行人导航系统主要用于行人在已知或未知环境下的自主导航和实时定位。当GPS信号丢失或强度较弱无法完成导航任务时,基于微机电系统(micro electro mechanical systems,MEMS)惯性器件的IMU可以为行人完成自主式导航的功能[1]。然而长时间导航时,IMU的误差随时间积累,导致导航精度降低[2]。为减小IMU引起的误差,Christoph等采用视觉陀螺辅助的IMU系统[3],Leppakoski等对Wi-Fi与IMU的组合系统进行了研究[4]。Delikostidis等分析了路标辅助的算法[5]。这些方法虽能提高导航精度,但均需提供外界信息,而且增加了系统成本。因此,研究在无外界信号情况下提高导航定位精度的算法显得尤为重要。故提出基于行人步幅和建筑方向的辅助算法,并利用RTS平滑算法对轨迹进行平滑处理,解决轨迹突变问题。
1 零速校正当IMU固定于行人脚部时[6],利用检测到的零速能有效修正系统的导航参数误差[7]。以速度误差为观测量时,航向误差是通过北向与东向加速度和速度误差相关联,而北向和东向加速度理论值应为零,这使得航向误差的可观测性非常差[8]。高阶IMU能够提高系统性能,但会增加系统成本和尺寸,且误差依然会累积。磁力计对应用环境有一定的要求。因此提出基于行人步幅和建筑方向的航向误差校正算法,以减小行人导航的定位误差。系统总体算法流程如图 1。
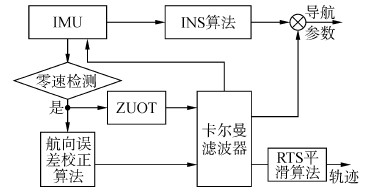
|
| 图 1 系统总体算法流程图 Fig. 1 The overall algorithm flowchart of system |
首先利用IMU的输出进行导航解算和零速检测,当行人步态处于零速状态时,应用零速校正和航向误差校正算法,通过卡尔曼滤波器估计状态向量,得到修正后的导航参数,同时保存滤波参数,利用RTS平滑算法得到平滑后的运动轨迹。
2 航向误差校正算法航向误差校正算法建立在行人步幅和建筑方向的基础上。首先需要利用行人的运动状态获得步幅航向和建筑方向,然后对原有观测量进行扩维,以速度误差和航向误差为观测量推导系统模型,最后采用卡尔曼滤波器对导航参数进行估计,并利用估计结果修正导航参数。
2.1 行人步幅和建筑方向分析在行人运动过程中,每运动一步均会产生步幅航向和步长。步长定义为一步的距离,步幅航向定义为两个连续步之间的角度[9],如下
| ${\varphi _s}\left(k \right)=\arctan \left({\frac{{p_y^k - p_y^{k - 1}}}{{p_x^k - p_x^{k - 1}}}} \right)$ | (1) |
式中:φs(k)为第k步时行人的步幅航向,p=[px py pz]T为行人的位置坐标,pxk、pyk分别为第k步时行人在x和y方向的位置坐标。步幅航向示意图如图 2所示。

|
| 图 2 步幅航向示意图 Fig. 2 Schematic diagram of stride heading |
在引入步幅航向之前,需要判断行人是否已经走出一步。只有当行人已经迈出一步,才可以根据式(1)得到步幅航向。由于行人运动的灵活性较大,本文利用广泛似然比检测算法判断行人的步态[10],相对于传统的阈值检测算法,此方法充分利用了传感器信息,并将零速检测问题模型化为假设检验问题,可对快走、跑步等运动状态进行准确检测。表 1给出了行人在正常、快走和跑步运动状态的步态检测结果,默认一步运动中只有一个零速区间,实验共有34个真实零速区间。
| 运动 状态 | 速度/(m·s-1) | 零速区间/个 | |
| 传统法 | GLRT法 | ||
| 正常 | 1.2 | 34 | 34 |
| 1.3 | 33 | 34 | |
| 快走 | 1.6 | 26 | 34 |
| 1.6 | 29 | 34 | |
| 跑步 | 2.3 | 10 | 33 |
| 2.3 | 7 | 34 | |
由表 1可知,传统算法只适用于正常步速情况,无法准确检测快走和跑步时的零速情况。GLRT检测算法则可对正常步速、快走和跑步等运动状态进行准确的检测,能够检测到较为完整的零速区间。
在零速检测的基础上,根据两个相邻的零速点即可计算行人步幅航向,计算得到的步幅航向将在下一步中用到[11]。零速检测结果可用二进制表示,如图 3所示,“0”为非零速状态,“1”为零速状态[12],图中黑点表示每个零速区间的第一个零速点,即用于计算步幅航向的时刻点。
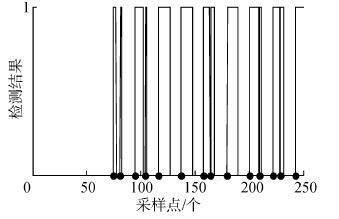
|
| 图 3 零速检测结果 Fig. 3 Result of zero velocity detection |
建筑方向通过2D地图获取,利用MATLAB对图像进行处理,根据追踪到的像素点即可计算建筑方向的值[13]。
建筑方向的获取方法为:首先利用Canny检测算子检测图像上的边缘;在边缘检测的基础上,采用Hough变换检测图像上的直线;根据直线起始点和结束点的像素值,即可获得建筑方向:
| ${\varphi _{bm}}=\arctan \left({\delta y/\delta x} \right)$ | (2) |
式中:φbm为获得的建筑方向,δx、δy分别为起始点和结束点在x和y方向上的像素差。图 4给出了图像处理得到的建筑方向。

|
| 图 4 建筑方向 Fig. 4 Building heading |
图 4中,黑色直线为检测到的一条直线,直线的起始点和结束点分别已在图中标注,将两点的像素值代入式(2),可得到该建筑方向为1.589 rad。
为得到更加准确的建筑方向φb,利用零速检测点处的导航参数对其修正,零速点如图 4中的黑点所示,分析相邻3个零速点的航向变化值:
| $\delta \theta={\theta _k} - \frac{{\alpha \theta {k_{m - 2}}+\beta \theta {k_{m - 1}}}}{2}$ | (3) |
式中:θk为采样时刻k时的航向值,km-1为前一个零速点的采样时刻,km-2为第1个零速点的采样时刻,α和β分别为前2个采样时刻对应航向的修正权值。当km-1和km-2时刻的滤波精度相同时,权值α和β相等。由式(3)可知,此时应取两时刻航向的平均值与k时刻的航向值进行比较,即满足α=β=1,故权值α和β应满足:
| $\alpha+\beta=2$ | (4) |
当两时刻的滤波精度不同时,其具体数值可根据对应时刻的滤波效果决定,即由km-1和km-2采样时刻的滤波协方差矩阵Pkm-1和Pkm-2决定。若km-2时刻的航向滤波精度高,则对应权值大;若滤波精度低,则其权值小。km-1时刻亦然。所以权值和对应时刻的航向滤波精度值成反比:
| $\frac{\alpha }{\beta }=\frac{{{P_{{k_{m - 1}}}}\left({9,9} \right)}}{{{P_{{k_{m - 2}}}}\left({9,9} \right)}}$ | (5) |
式中:Pkm-1(9,9)和Pkm-2(9,9)分别为对应时刻的航向估计精度。联立式(4)、(5),可得到权值α和β的具体值:
| $\left\{ \begin{array}{l} \alpha=\frac{{2{P_{{k_{m - 1}}}}\left({9,9} \right)}}{{{P_{{k_{m - 1}}}}\left({9,9} \right)+{P_{{k_{m - 2}}}}\left({9,9} \right)}}\\ \beta=\frac{{2{P_{{k_{m - 2}}}}\left({9,9} \right)}}{{{P_{{k_{m - 1}}}}\left({9,9} \right)+{P_{{k_{m - 2}}}}\left({9,9} \right)}} \end{array} \right.$ | (6) |
由式(3)可得到相邻3个零速点的航向变化值,利用此航向变化值可对建筑航向进行修正,得到修正后的建筑方向:
| ${\varphi _b}={\varphi _{bm}}+\delta \theta $ | (7) |
式中:φbm为由地图得到的建筑方向,δθ为航向变化值,φb为修正后的建筑方向。
2.2 系统模型在分析步幅航向和建筑方向后,即可推导系统模型。首先分析系统的状态空间模型,选取状态向量x为
| $x={\left({{p_{3{\rm{ \times 1}}}}\;\;\;{v_{3{\rm{ \times 1}}}}\;\;{a_{3{\rm{ \times 1}}}}\;\;\delta {w_{3{\rm{ \times 1}}}}\;\;\delta {f_{3{\rm{ \times 1}}}}} \right)^{\rm{T}}}$ | (8) |
式中:p3×1为位置向量,v3×1为速度向量,a3×1为姿态向量,δw3×1为陀螺零偏向量,δf3×1为加速度计零偏向量。状态转移矩阵F(t)如下
| $F\left(t \right)=\left[{\begin{array}{*{20}{c}} 0&I&0&0\\ 0&0&{\left[{c_b^t{f_b}{\rm{ \times }}} \right]}&0\\ 0&0&0&{ - \frac{1}{\tau }I}\\ 0&0&0&0 \end{array}\;\;\;\;\begin{array}{*{20}{c}} 0\\ {c_b^t}\\ 0\\ { - \frac{1}{\tau }I} \end{array}} \right]$ | (9) |
式中:[Cbtfb×]为加速度在导航系下的反对称矩阵,Cbt为载体系到导航系的旋转矩阵,τ为一阶马尔科夫模型中的时间常数。则系统状态模型为
| $\dot x\left(t \right)=F\left(t \right)x\left(t \right)+W\left(t \right)$ | (10) |
式中:W(t)为系统白噪声。
由融合零速校正和航向误差校正算法[12],得到系统的观测模型:
| $Z\left(t \right)=H\left(t \right)X\left(t \right)+V\left(t \right)$ | (11) |
观测量Z4×1=[δvx δvy δvz δφ]T由两部分组成:速度误差和航向误差。速度误差为INS算法计算得到的速度值;航向误差δφ由2.1节分析的步幅航向和建筑方向求得,航向误差[13]如下
| $\delta \varphi={\varphi _s} - {\varphi _b}$ | (12) |
由此得到量测矩阵H4×15:
| $\begin{array}{*{20}{c}} {H\left(t \right)=}\\ {\left[{\begin{array}{*{20}{c}} {{0_{3{\rm{ \times 3}}}}}&{{I_{3{\rm{ \times 3}}}}}&{{0_{{\rm{1 \times 3}}}}}&{{0_{3{\rm{ \times 3}}}}}&{{0_{3{\rm{ \times 3}}}}}\\ {{0_{{\rm{1 \times 3}}}}}&{{0_{{\rm{1 \times 3}}}}}&{\left[{0 - \sin \left({{x_{k - 1}}\left(9 \right)} \right)\;\;\;1} \right]}&{{0_{{\rm{1 \times 3}}}}}&{{0_{{\rm{1 \times 3}}}}} \end{array}} \right]} \end{array}$ | (13) |
式中:xk-1(9)为滤波更新得到的上一时刻的纵摇角,Vk为量测噪声。各协方差矩阵如下所示:
滤波协方差阵:
| $P={\rm{diag}}\left\{ {X\;\;\;Y\;\;Z\;\;M\;\;N} \right\}$ | (14) |
系统噪声协方差矩阵:
| $Q={\rm{diag}}\left\{ {U\;\;\;V\;\;W\;\;G} \right\}$ | (15) |
量测噪声协方差矩阵:
| $R={\rm{diag}}\left\{ {J\;\;K} \right\}$ | (16) |
其中
| $\begin{array}{*{20}{c}} {X={{\left({{{10}^{ - 5}}} \right)}^2}{\rm{ \times }}{I_3}}\\ {Y={{\left({{{10}^{ - 5}}} \right)}^2}{\rm{ \times }}{I_3},Z={{\left({0.1} \right)}^2}{\rm{ \times }}{I_3}}\\ {M={{\left({0.1} \right)}^2}{\rm{ \times }}{I_3},N={{\left({0.1} \right)}^2}{\rm{ \times }}{I_3}}\\ {U={{\left({0.5} \right)}^2}{\rm{ \times }}{I_3},V={{\left({0.5} \right)}^2}{\rm{ \times }}{I_3}}\\ {W={{\left({{{10}^{ - 7}}} \right)}^2}{\rm{ \times }}{I_3},N={{\left({{{10}^{ - 7}}} \right)}^2}{\rm{ \times }}{I_3}}\\ {I={{\left({0.01} \right)}^2}{\rm{ \times }}{I_3},K={{\left({0.01} \right)}^2}} \end{array}$ |
零速校正算法和航向误差校正算法均以零速检测为基础,在修正区间能有效限制误差增长,在非零速区间,误差依然持续增长,故会产生轨迹突变现象。为避免急剧修正现象的产生,本文在行人每个单步运动中利用RTS平滑算法对轨迹进行平滑,以得到平滑的运动轨迹。
RTS平滑算法包括前向滤波和后向平滑两部分。本文中前向滤波采用卡尔曼滤波,在滤波过程中,保存每个时刻的状态向量Xk、估计均方误差阵Pk、一步预测均方误差Pk,k-1以及状态转移矩阵Φk,k-1,保存值将在后向平滑过程中用到[14]。
前向滤波的卡尔曼滤波算法为
| $\begin{array}{*{20}{c}} {{{\hat X}_{k,k - 1}}{\Phi _{k,k - 1}}{{\hat X}_{k - 1}}}\\ {{{\hat X}_k}={{\hat X}_{k,k - 1}}+{K_k}\left({{Z_k} - {H_k}{{\hat X}_{k,k - 1}}} \right)}\\ {{K_k}={P_{k,k - 1}}+H_k^{\rm{T}}{{\left({{H_k}{P_{k,k - 1}} - H_{_k}^{\rm{T}}+{R_k}} \right)}^{ - 1}}}\\ {{P_{k,k - 1}}={\Phi _{k,k - 1}}{P_{k,k - 1}}\Phi _{_{k,k - 1}}^{\rm{T}}+{\Gamma _{k - 1}}{Q_{k - 1}}\Gamma _{_{k,k - 1}}^{\rm{T}}}\\ {{P_k}=\left({I - {K_k}{H_k}} \right){P_{k,k - 1}}}\\ {} \end{array}$ |
后向平滑过程按k=N,N-1,…1逆时针方向递推解算得到平滑估计结果。后向平滑算法为
| $\begin{array}{l} {{\hat X}_{k,s}}={{\hat X}_k}+{K_{k,s}}\left({{{\hat X}_{k+1,s}} - {\Phi _{k+1,k}}{{\hat X}_k}} \right)\\ {P_{k,s}}={P_k}+{K_{k,s}}\left({{P_{k+1,s}} - {P_{k+1,k}}} \right)K_{_{k,s}}^{\rm{T}}\\ \;\;\;\;\;\;\;\;\;\;\;{K_{k,s}}={P_k}\Phi _{_{k+1,k}}^{\rm{T}}P_{_{k+1,k}}^{ - 1} \end{array}$ |
为验证算法的有效性,利用荷兰Xsens公司的MTi-G型IMU进行场地试验。实物如图 5所示,其内部集成了三轴MEMS加速度计、陀螺和磁力计。其中,加速度计量程为±5.23 rad/s,陀螺量程为±50 m/s2,满足试验要求。

|
| 图 5 IMU实物图 Fig. 5 Figure of the IMU |
将IMU固定于鞋上,尽量与水平地面保持平行。利用自带数据采集软件XSENS MT Manager对传感器数据进行实时采集和存储,并可根据需要导出十进制或二进制的MEMS传感器数据。系统启动时,需对系统的采样频率、输出数据格式等参数进行设置。
试验时波特率设置为115 200,数据采样频率为100 Hz,传感器输出为标定后的数据,可直接用于导航解算。步行试验持续8 min左右,全程大约70 m,试验开始和结束的地点在同一位置,以确保得到返回时的位置误差。场地试验在哈尔滨工程大学军工操场内进行,如图 6所示,其中箭头代表开始点,圆点绘制的线路为试验时行人的运动轨迹。

|
| 图 6 试验场地图 Fig. 6 Map of the test field |
数据采集完成后,进行离线分析。单独采用INS算法得到的航向如图 7所示。由图 7可知,单独采用INS算法得到的航向波动较大,且呈发散趋势,需进行进一步修正。采用ZUPT+航向误差校正算法与单独采用ZUPT的航向对比图如图 8所示。
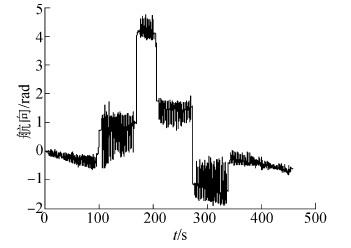
|
| 图 7 INS航向 Fig. 7 The heading of INS algorithm |
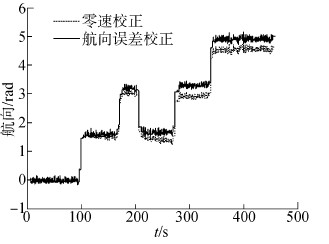
|
| 图 8 航向对比图 Fig. 8 The comparison chart of heading |
由图 8可以看出,采用航向误差校正算法能够有效减小航向误差。在前200 s内,零速校正算法能使航向保持在一定精度范围内。但在200 s之后,随着时间的推移,航向误差逐渐增大。表 2给出了航向误差的具体数值,表中数据为各时间段内的最大航向误差值。
| 时间/s | ZUPT/rad | ZUPT+航向辅助/rad |
| 212~270 | 0.182 | 0.060 |
| 270~334 | 0.262 | 0.129 |
| 334~500 | 0.203 | 0.163 |
由表 2可以看出,单独采用零速校正算法时的航向误差最大可达到0.262 rad,而且在各时间段内的误差均超过0.174 rad;采用航向误差校正算法后的最大误差减小为0.163 rad,各时间段内的误差最小为0.060 rad。由此可见,航向误差校正算法能有效提高航向的精度。
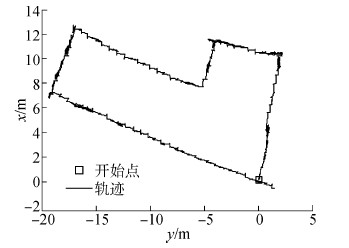
采用零速校正和航向误差校正算法得到的行人运动轨迹如图 9所示。
|
| 图 9 行人运动轨迹 Fig. 9 The trajectory for pedestrian |
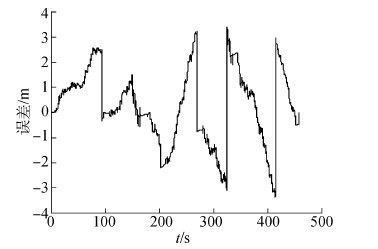
由图 9和图 6对比可以看出,此算法解算得到的行人运动轨迹与真实运动轨迹一致,故此算法能完成对行人的自主导航和定位功能。为更好的分析定位结果,以IMU/GPS组合系统得到定位结果为参考,进一步量化分析行人的定位误差,行人运动过程中的定位误差如图 10所示,误差的具体数值见表 3。
|
| 图 10 行人定位误差 Fig. 10 The positioning error for pedestrian |
| 误差类型 | 误差/m | 占总距离百分比/% |
| 最大误差 | 3.38 | 4.82 |
| 平均误差 | 1.21 | 1.72 |
| 返回误差 | 1.05 | 1.51 |
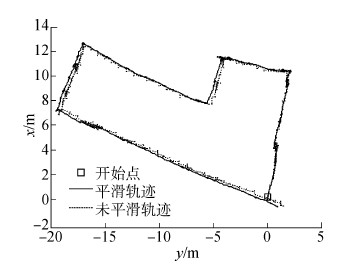
由图 10和表 3可以看出,在300~400 s,行人的位置误差达到最大值,为3.38 m。在整个运动过程中,其位置误差不超过运动总距离的5%,并且其位置误差不随时间累积,能够限制在一定范围内。由此可见,采用航向误差校正算法能有效减小行人的定位误差。利用RTS平滑算法后的行人运动轨迹对比图如图 11所示。
|
| 图 11 平滑运动轨迹对比图 Fig. 11 The comparison chart of smoothed trajectory |
由图 11可以看出,和平滑前的轨迹相比,平滑后的轨迹较为平滑,不存在轨迹突变现象。在保证定位精度的同时,采用RTS平滑算法能有效解决轨迹突变问题。
5 结论本文在零速校正的基础上,对步幅和建筑方向辅助的航向误差校正算法进行了研究,通过数据的离线分析可得到以下结论:
1)利用修正建筑方向和步幅航向之差作为观测量对导航参数实现滤波更新,由航向误差和定位误差的结果对比可以看出,该方法的定位精度较传统的零速校正算法有所提高;
2)在航向误差校正算法的基础上,采用RTS平滑算法对定位轨迹进行后向平滑,在保证了定位精度的同时,解决了只在零速区间内进行校正导致的轨迹突变问题;
3)此算法不需额外的信号源,这意味着不论试验场地大小,系统的成本不会增加,但其不足在于校正算法依赖于零速点的准确检测,当行人处于非静止状态时,误差仍然是累积的,未来的工作主要在于解决运动状态下误差累积的问题。
| [1] | 周启帆, 张海, 常艳红, 等. 基于MIMU的行人导航算法研究[J]. 系统仿真技术, 2010, 6(4): 281-286. ZHOU Qifan, ZHANG Hai, CHANG Yanhong, et al. Research of pedestrian navigation algorithm based on MIMU[J]. System simulation technology, 2010, 6(4): 281-286. |
| [2] | 陈述奇, 刘青峰, 冉龙明, 等. 低成本MIMU/编码器组合的高精度航姿系统[J]. 压电与声光, 2012, 34(3): 368-371. CHEN Shuqi, LIU Qingfeng, RAN Longming, et al. Design and test of low-cost MIMU/encoder integrated precision attitude heading reference system[J]. Piezoelectrics & acoustooptics, 2012, 34(3): 368-371. |
| [3] | KESSLER C, ASCHER C, FRIETSCH N, et al. Vision-based attitude estimation for indoor navigation using vanishing points and lines[C]//Position Location and Navigation Symposium (PLANS). Indian Wells, USA, 2010: 310-318. |
| [4] | LEPPÄKOSKI H, COLLIN J, TAKALA J. Pedestrian navigation based on inertial sensors, indoor map, and WLAN signals[J]. Journal of signal processing systems, 2013, 71(3): 287-296. |
| [5] | DELIKOSTIDIS I, ENGEL J, RETSIOS B, et al. Increasing the usability of pedestrian navigation interfaces by means of landmark visibility analysis[J]. Journal of navigation, 2013, 66(4): 523-537. |
| [6] | 张金亮, 秦永元, 梅春波. 基于MEMS惯性技术的鞋式个人导航系统[J]. 中国惯性技术学报, 2011, 19(3): 253-256. ZHAGN Jinliang, QIN Yongyuan, MEI Chunbo. Shoe-mounted personal navigation system based on MEMS inertial technology[J]. Journal of Chinese inertial technology, 2011, 19(3): 253-256. |
| [7] | PARK S K, SUH Y S. A zero velocity detection algorithm using inertial sensors for pedestrian navigation systems[J]. Sensors, 2010, 10(10): 9163-9178. |
| [8] | GODHA S, LACHAPELLE G. Foot mounted inertial system for pedestrian navigation[J]. Measurement science and technology, 2008, 19(7): 075202. |
| [9] | FENG Wenquan, ZHAO Hongbo, ZHAO Qi, et al. Integration of GPS and low cost INS for pedestrian navigation aided by building layout[J]. Chinese journal of aeronautics, 2013, 26(5): 1283-1289. |
| [10] | SKOG I, HANDEL P, NILSSON J O, et al. Zero-velocity detection-An algorithm evaluation[J]. IEEE Transactions on biomedical engineering, 2010, 57(11): 2657-2666. |
| [11] | JIMNEZ A R, SECO F, ZAMPELLA F, et al. Improved heuristic drift elimination with magnetically-aided dominant directions (MiHDE) for pedestrian navigation in complex buildings[J]. Journal of location based services, 2012, 6(3): 186-210. |
| [12] | JIMENEZ A R, SECO F, PRIETO J C, et al. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU[C]//Proceedings of the 7th Workshop on Positioning Navigation and Communication. Dresden, Germany, 2010: 135-143. |
| [13] | ABDULRAHIM K, HIDE C, MOORE T, et al. Aiding MEMS IMU with building heading for indoor pedestrian navigation[C]//Proceedings of Ubiquitous Positioning Indoor Navigation and Location Based Service(UPINLBS). Kirkkonummi, Finland, 2010: 1-6. |
| [14] | 宫晓琳, 张蓉, 房建成. 固定区间平滑算法及其在组合导航系统中的应用[J]. 中国惯性技术学报, 2012, 20(6): 687-693. GONG Xiaolin, ZHANG Rong, FANG Jiancheng. Fixed-interval smoother and its applications in integrated navigation system[J]. Journal of Chinese inertial technology, 2012, 20(6): 687-693. |



