微动是发生在法向加载力作用下两个接触表面之间微小的切向位移时。微动现象不仅会存在于机构中材料之间的微动磨损,也会由微动疲劳产生。微动会引起机械零部件的接触表面受到破坏,也会引起裂纹的萌生、扩展与断裂,最终导致机构无法正常运行。微动与其他的接触方式不同,往往存在于机构内紧配合部位,不易被发现。目前,微动摩擦学的研究越来越受到国内外学者的广泛重视,已经成了摩擦学中的一个重要分支,在当今世界科学和经济发展中具有非常重要意义。
对于MEMS/NEMS系统的材料微动磨损研究,影响的因素很多,如法向加载力和微动频率的变化[1]以及不同材料表面的质量[2]。关于微动磨损的研究,当前主要是基于实验的方法。例如,文献[3]进行了微观摩擦与表面形貌相关性研究,采用了美国CETR公司生产的UMT-2MT摩擦试验机,加载范围为0~10-3N,分辨率为0.1 mN,摩擦方式为直径3 mm的氮化硅陶瓷球与圆盘的匀速直线运动;文献[4]基于自制的微动磨损实验装置,观察各种表面材料组合对微动磨损的影响。但是这类实验设备比较昂贵。为此,英国华威大学的Derek教授领导他的团队研制了通用于一般机构和MEMS/NEMS材料的微观摩擦特性检测的电磁加载微摩擦测量头装置及其试验系统[3]。
本文在此研究的基础上,结合摩擦学的测试方法和原理。介绍了一种新型微摩擦测试系统,开发了低频往复摆动模拟运动平台,并在该平台上进行了金属、非金属和高分子材料的变载荷、变频率的微动摩擦测试,分析了不同材料的摩擦特性规律,以检验系统工作的基本性能和可靠性。
1 低频往复式模拟平台的设计新型微摩擦测试系统主要由微摩擦测量头装置和低频往复式模拟平台组成,如图1所示。其中,微摩擦测量头[5]是由英国华威大学Dr.Alsoufi研发,主要用于样本的切向、法向载荷加载以及瞬时摩擦力的测量。其原理是通过线圈电流控制与较硬的饱和磁铁相互作用的磁场来产生作用在样本上的垂直和侧向力,以及利用无屏蔽非接触式涡流传感器测得的悬臂梁偏转来计算摩擦力。该设计的优点在于适用于样本的多种移动方式、达到100 nm的位移分辨率以及超过160 Hz的工作带宽。

|
| 图1 新型微摩擦测试系统 Fig.1 A novel micro-tribological testing system 注:1.磁铁线圈;2.非接触式涡流传感器;3.电磁力驱动器;4.摆动架; 5.样本;6.激光位移传感器 |
本文设计了低频往复模拟平台,其原理是由电磁力驱动摆动机构,并通过改变电压信号频率和幅值来控制机构的摆动频率和振幅。它主要是由激光位移传感器、摆动机构、电磁力驱动装置和功率振荡器组成。其中,激光位移传感器主要是用于测量样本的水平移动距离;电磁力驱动装置能使摆动架在水平方向上往复摆动,并应用功率振荡器来设定不同的摩擦测试条件。该平台具体的设备参数为:驱动电压信号频率范围从0~25 Hz,激光位移传感器的可测行程为0~6.35 mm,摆动机构的刚度为2 680 N/m,摆动机构的共振频率达到69.9 Hz,摆动台的总质量为32.4 g。
图1中标注的样本[5],上试样可为圆球或圆筒,它固定于悬臂梁端部的样本架上;下试样的形状可为一个平面或者圆筒,并与摆动机构固连。因此,通过更换上、下试样,可以模拟样本间不同摩擦副的摩擦,用于分析材料表面的摩擦特性。
2 摆动平台工作原理及运动数学模型
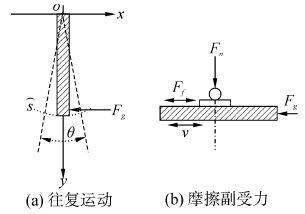
图2中的下试样与摆动架一起作往复运动。如图3所示,垂直加载力Fn对上试样加载,交变驱动载荷Fg作用于摆动架端部一侧。摆动架在Fg驱动下,做往复式摆动运动,设其端部的轨迹为弧线,摆动角度为θ,将摆动架视作一个杆件。为了模拟实际微动工况,使得两个接触表面之间产生微小振幅的振动,设定Fg的信号形式为正弦周期信号:
$${F_g} = {F_0}\sin (2\pi ft + \varphi )$$
(1)

|
| 图2 平台装置 Fig.2 Diagram of reciprocating platform |
|
| 图3 摆动架及摩擦副受力 Fig.3 Diagram of oscillation mechanism and friction pair |
图1中传感器[6]输出信号频率应该等于电磁驱动力信号频率f,其幅值等于摆动架摆动一个周期行程的1/2。下试样受到的力有摩擦力Ff和电磁驱动力Fg。因当摆动角度θ较小时,sin θ≈θ,故可以认为下试样与摆动台一起近似作直线运动。
根据振动理论,摆动架(含下试样)的运动是正弦力作用下的有阻尼受迫振动,其振动微分方程为
$$m\ddot x + c\dot x + kx = {F_0}\cos (pt + \varphi )$$
(2)
$$x(t) = {x_1}(t) + A{e^{ - \delta t}}\cos ({\omega _1}t + \varphi )$$
(3)
$$x(t) = {x_{0\cos }}(pt)$$
(4)
$${x_0} = \frac{{{F_0}}}{{\sqrt {{{({\omega ^2} - {\varphi ^2})}^2} + 4{p^2}{\delta ^2}} }},{\omega ^2} = \frac{m}{k},\delta = \frac{c}{{2m}}$$
(5)
$$v(t) = \dot x(t) = - p{X_0}\sin (pt)$$
(6)
| $$a(t) = \ddot x(t) = - {p^2}{X_0}\cos (pt)$$ | (7) |
由式(5)可以算出摆动架振幅。本文用激光传感器直接测得摆动架位移振幅值,则由式(4)、(6)、(7)直接求出最大位移、最大速度、最大加速度值,并且可以看出,它们与Fg的圆频率和振幅F0有关。
3 摩擦特性测试实验分析在室温为(22±1) ℃和相对湿度为(40±5)%的环境中,对新型微摩擦测试系统进行了标定和实验条件设定,其结果为:法向载荷的施加范围为0~60 mN,测法向载荷和摩擦力的传感器灵敏度标定结果分别为42.730 μm/V和47.640 μm/V,悬臂梁的垂直和横向加载标定刚度为1 917 N/m和1 930 N/m,摆动机构的半周期行程、最大摆动速度、最大加速度和半角分别为75 μm、341 μm/s、3.575 μm/s2和0.031 054°。
为了验证本文设计的低频往复式模拟平台的工作稳定性和可靠性,需要通过摩擦测试实验结果来分析样本表面的摩擦特性。实验中,上试样为直径1 mm的小钢球,下试样选取了钢、玻璃和聚四氟乙烯(PTFE)这三种不同的金属、非金属、高分子材料,尺寸均为10 mm×10 mm×1 mm。实验前,应用Bruker公司提供的ContourGT-I型3D光学显微镜对样本进行了3D表面测量实验,如图4、5所示,分别为钢和PTFE表面形貌和参数,其中钢的表面粗糙度为Ra=87.803 nm,PTFE的表面粗糙度为Ra=2.221 μm。

|
| 图4 不锈钢试样的表面形貌和参数 Fig.4 Surface topography and parameters of steel specimen |

|
| 图5 PTFE试样的表面形貌和参数 Fig.5 Surface topography and parameters of PTFE specimen |
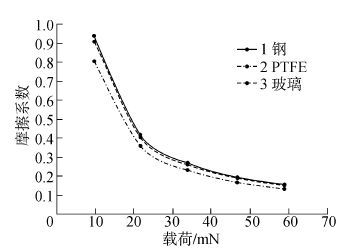
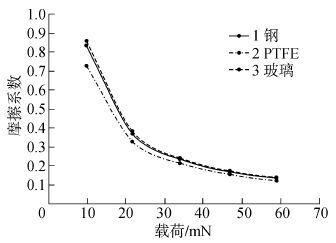
设定电磁驱动力信号周期分别为250 ms(频率为4 Hz)和400 ms(频率为2.5 Hz)。每次实验中,在样本的卸载和加载后,均由异丙酮对上、下试样进行清洗。测试系统采样频率为200 Hz,摆动循环次数设定为20 000,法向载荷分别设定为9.65、21.66、33.78、46.68、58.83 mN的5次加载。选取采集测试数据中的一个周期为计算样本,计算出瞬时滑动摩擦系数-法向载荷曲线(见图6、7)。
|
| 图6 摆动频率为2.5 Hz时摩擦系数与法向载荷的变化曲线 Fig.6 The variation of CoF with normal load(f=2.5 Hz) |
|
| 图7 摆动频率为4 Hz时摩擦系数与法向载荷的变化曲线 Fig.7 The variation of CoF with normal load(f=4 Hz) |
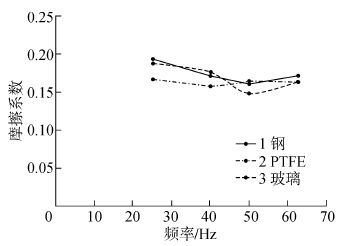
增加摆动频率,选取电磁驱动信号周期分别为400、250、200、160 ms(频率依次为2.5、4、5、6.25 Hz)。选用与3.1节中相同的清洗条件、采样频率和摆动循环次数,并选取较高的法向载荷(46.68 mN和58.83 mN)进行测试,得到瞬时摩擦系数与摆动频率的关系曲线(见图8、9)。
|
| 图8 法向载荷为46.68 mN时摩擦系数与摆动频率变化曲线 Fig.8 The curves between CoF and frequency(Fn=46.68 mN) |
|
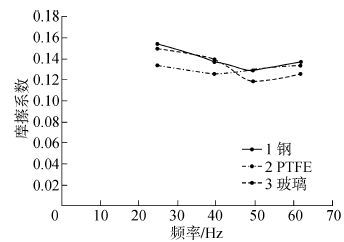
| 图9 法向载荷为58.83 mN时摩擦系数与摆动频率变化曲线 Fig.9 The curves between CoF and frequency(Fn=58.83 mN) |
在完成摩擦测试实验后,对选取的样本再一次进行了3D表面测量实验,得到了钢和PTFE表面形貌和参数值,如图10、11所示,其中钢的表面粗糙度为Ra=97.376 nm,PTFE的表面粗糙度为Ra=2.056μm。

|
| 图10 不锈钢试样的表面形貌和参数(实验后) Fig.10 Surface topography and parameters of steel specimen (post-experiment) |

|
| 图11 PTFE试样的表面形貌和参数(实验后) Fig.11 Surface topography and parameters of PTFE specimen (post-experiment) |
由以上实验结果可以看出材料的表面形貌、法向载荷、摆动频率对瞬时滑动摩擦系数的影响,分析如下:
1)法向载荷与瞬时摩擦系数之间的关系。在图5、6中,无论是金属和非金属材料,在两种不同的摆动频率下,其瞬时滑动摩擦系数均随着法向载荷的变小而迅速的上升,且当摆动频率为2.5 Hz时,样本的上升趋势更为明显。这与文献[6, 7]中的论述相一致。另外,高分子材料PTFE的滑动摩擦系数值相对较低,这与文献[8, 9, 10]中阐述的“PTFE有较小的摩擦,易于划损从而影响测量”的论述相符,且这种现象归因于表面化学效应和较软表面的改性。
2)摆动频率与瞬时摩擦系数之间的关系。从图8和图9中可以看出,在法向载荷为46.68 mN时,随着摆动频率的增加,三种样本基本维持在摩擦系数0.15~0.2;而在58.83 mN加载力的作用下,样本的摩擦系数变化范围更小。这与文献[11]中摩擦系数不依赖于滑动速度的说法相吻合。
3)同一材料在不同表面粗糙度下进行实验测量对摩擦系数的影响。通过对实验前后,两次样本表面形貌的测量结果进行对比,发现样本表面的粗糙度变化不是非常明显。其中,PTFE可能受到划损的影响,其表面粗糙度只是稍有变化。因此,证明了在微动摩擦测试中,样本表面的磨损量几乎可以忽略不计,对滑动摩擦系数影响较小。
由此看出,通过摩擦测试实验,在分析样本表面摩擦特性的基础上,结合相关文献的结论,验证了本文设计的低频往复式模拟平台具有工作稳定性和使用可靠性。
4 结论本文在文献[3]的基础上,对新研制的低频往复式模拟平台,进行了微小法向载荷下不同材料的高副摩擦副的瞬时滑动摩擦系数测试实验。在变法向载荷和不同的摆动频率下,分析了样本形貌、法向载荷和摆动频率对瞬时滑动摩擦系数的影响。得到了如下结论:
1)金属和非金属材料,在两种不同的摆动频率下产生的摩擦系数变化与文献[6, 7]中的论述相一致。而PTFE的较低摩擦系数是由于材料表面化学效应和较软表面改性的原因而易于划损。
2)在法向载荷为46.68 mN和58.83 mN时,得到与文献[11]中的摩擦系数不依赖于滑动速度的相一致的论证结果。
3) 同一材料在不同表面粗糙度下的磨损量几乎可以忽略不计,对滑动摩擦系数影响较小。
以上结论表明了往复摆动平台可以模拟金属或非金属固体摩擦副的微动振动,在微小法向载荷作用下,低频往复摆动微动磨损测试平台的摩擦特性与文献中的结论相一致,样本的磨损测试实验可靠,通过增加摆动频率还可以进行一定的加速寿命试验。而对于提高精度测试、优化摩擦副结构和增加试样类型等仪器方面的改进还需进一步的研究。
| [1] | KU I S Y, REDDYHOFF T, CHOO J H, et al. A novel tribometer for the measurement of friction in MEMS[J]. Tribology international, 2010, 43(5/6): 1087-1090. |
| [2] | CHETWYND D G, ALSOUFI M S. A novel micro-friction measuring-head using force-feedback compensation[C]//6th International Symposium on Precision Engineering Measurements and Instrumentation. Hangzhou, China, 2010: 754417-9. |
| [3] | LAI Tianmao, HUANG Ping. Study on microscale adhesion between solid surfaces with scanning probe[J]. Science China technological sciences, 2013, 56(12): 2934-2952. |
| [4] | CHO Y J, KIM T W. Measurement of wear and friction coefficients for the prediction of fretting wear[J]. Journal of the korean society of tribologists and lubrication engineers, 2012, 28(3): 124-129. |
| [5] | ALSOUFI M S, CHETWYND D G. A novel design of multi-function micro-tribometer for MEMS/NEMS materials [C]//The 4th Saudi International Conference. Manchester, UK, 2010. |
| [6] | Bhushan B. Nanotribology and nanomechanics[J]. Wear, 2005, 259(7-12): 1507-1531. |
| [7] | BRAIMAN Y, BARHEN J, PROTOPOPESCU V. Control of friction at the nanoscale[J]. Physical review letters, 2010, 90(9): 094301. |
| [8] | MYSHKIN N K, PETROKOVETS M I, KOVALEV A V. Tribology of polymers: Adhesion, friction, wear, and mass-transfer[J]. Tribology international, 2005, 38(11/12): 910-921. |
| [9] | WEI C, WANG C I, TAI F C, et al. The effect of CNT content on the surface and mechanical properties of CNTs doped diamond like carbon films[J]. Diamond and related materials, 2010, 19(5/6): 562-566. |
| [10] | REES B L. Static friction of bulk polymers over a temperature range[J]. Research, 1957, 10: 331-338. |
| [11] | GRILEC K, IVUŠIĆ V. A brief history of tribology[C]//International Conference on Materials, Tribology, Recycling MATRIB 2013. Vela Luka, Hrvatska, 2013. |



