目前军用舰船向大平台、高航速、低振动方向发展,而民船方面,EEDI(新船能效设计指数)等规则的不断生效使得船舶的节能减排、减震降噪成为船东、船舶设计者及总装厂的关注重点之一[1]。国外对桨舵干扰进行了系统的理论研究、数值仿真、模型试验机实船验证[2, 3, 4, 5, 6],并推出一种新型的一体化推进装置,该系统将舵球、扭曲舵及襟翼合理地结合在一起,通过各装置间的有利干扰达到了节约燃油消耗、改善桨后尾流场、减少推进器表面空泡的作用。文献[7, 8]讨论了舵球、扭曲舵等组合型节能装置的水动力性能计算,但仅基于水动力性能开展了数值仿真,未考虑空泡的影响。文献[9]开展了最大舵阻力减额的扭曲舵设计及性能预报,文献[10, 11]开展了一体化推进器设计方法研究,并完成了水动力性能及空泡性能数值仿真,但未开展过模型试验验证。总体而言,目前国内对一体化推进器的研究较少,研究处于起步阶段。
本文基于推进及空泡性能平衡设计思想,采用基于速度势的低阶面元法,通过速度场的迭代计算考虑桨舵之间的相互干扰,设计了一体化推进器,完成了一体化推进器与传统桨舵推进器的快速性、空泡性能对比模型试验。
1 面元法理论
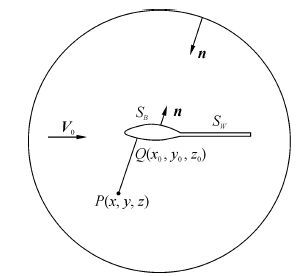
考虑在来流速度为V0的无旋、无粘、不可压缩势流中的任意一升力体,取一外部无穷远控制面将其封闭在内。如图1所示,流域的边界面为物面SB,升力体尾涡面SW和外边界面${S_\infty }$。在该流域中可由扰动速度势φ来表示升力体的扰动。根据格林公式及边界条件,物面上的积分方程为
\[\begin{array}{l}
2\pi \varphi P) = (\frac{1}{{{R_{PQ}}}})ds + \\
\varphi ({Q_1})\frac{\partial }{{\partial {n_{Q1}}}}(\frac{1}{{{R_{PQ}}}})ds + (\frac{1}{{{R_{PQ}}}})ds
\end{array}\]
(1)
|
| 图1 升力体及计算域 Fig.1 Lifting body and calculation domain |
对式(1)同时取梯度得到扰动速度的表达式:
\[\begin{array}{l}
4\pi VP) = ({Q_1}){\nabla _p}\frac{\partial }{{\partial {n_Q}}}(\frac{1}{{{R_{PQ}}}})ds + \\
\varphi ({Q_1}){\nabla _p}\frac{\partial }{{\partial {n_Q}}}(\frac{1}{{{R_{PQ}}}})ds + \\
{n_Q}){\nabla _p}(\frac{1}{{{R_{PQ}}}})ds
\end{array}\]
(2)
本文综合权衡推进及空泡性能,完成了一体化推进器的理论设计。一体化推进器包括舵球和扭曲舵,舵球的主要参数为长度及直径,其中舵球长度需根据舵与毂帽的相对位置确定。对不同舵球直径时的桨舵系统性能进行数值仿真,对比分析舵球直径对效率的影响确定最优的舵球直径。扭曲舵设计主要以桨舵相互干扰的流场计算为基础,通过不同展向剖面偏转实现阻力最小,并结合适伴流Eppler剖面设计方法,优化舵剖面压力分布,实现在舵效基本不变的情况下,降低舵的阻力、优化舵空泡性能的目标。
2.1 舵球设计方法舵球的设计以桨舵相互干扰的数值仿真为基础,采用基于速度势的低阶面元法,建立桨舵推进系统的坐标系并对物面进行双曲面元划分,坐标系及网格划分如图2所示。计算中桨舵之间的相互干扰通过在桨、舵的求解方程中分别计入二者之间诱导速度实现,并通过迭代计算逐步收敛该相互干扰。
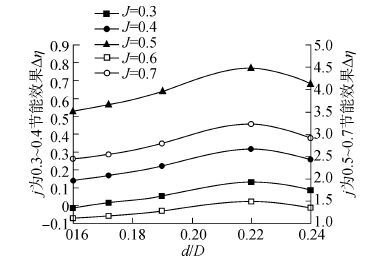
对不同舵球直径时桨舵推进系统的水动力性能进行预报,通过计算结果的分析确定舵球直径对节能效果的影响,其中节能效果定义为$\Delta \eta = \frac{{{\eta _1} - {\eta _0}}}{{{\eta _0}}} \times $100%,结果如图3所示。

|
| 图2 一体化推进器坐标系及网格划分 Fig.2 Coordinate system and mesh of integrative propulsor |
|
| 图3 舵球直径对节能效果的影响 Fig.3 Effect of rudder ball diameters on energy saving |
由于船体、附体特别是螺旋桨旋转的影响,即使在零度舵角时,常规舵的剖面与来流也存在一定的夹角,传统的设计并未充分考虑该问题,因此容易出现舵剖面与流场的不匹配而出现舵阻力大、空泡性能差的问题,而合理设置舵的偏转及扭曲是解决上述问题的有效方法。
假设船速为Vs,螺旋桨转速为n,船体伴流场在舵剖面位置处三向分量分别为wx、wθ、wr,则当舵角为零时舵剖面处的来流速度为
\[\begin{array}{l}
{V_R} = {V_{Rx}} + {V_{Ry}} = \\
[{V_s} \cdot (1 - {w_x}) + {u_{Rx}}] + [{V_s} \cdot {w_R} + {u_{Ry}}]
\end{array}\]
(3)
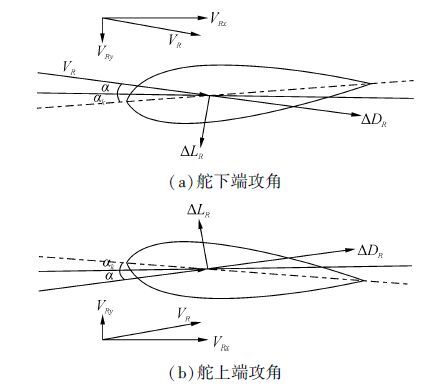
在来流VR作用下,舵剖面产生的升力定义为ΔLR,产生的阻力定义为ΔDR,在舵角为零的情况下,舵的附加推力定义为
\[\Delta {T_R} = \Delta {L_R}\sin \alpha - \Delta {D_R}\cos \alpha \]
(4)
剖面的升阻比是随攻角而变化的,因此扭曲舵的设计实际上是根据桨舵之间相互干扰的流场确定舵剖面的最佳偏转角αk使得舵的推力最大,其数学实质是求解式(5)的极大值:
\[\begin{array}{l}
{T_R} = \int_0^S {[\Delta {L_{R(\alpha + \alpha k)}}\sin \alpha - \Delta {D_{R(\alpha + \alpha k)}}\cos \alpha ]{\rm{ds}}} = \\
\int_0^S {[{C_{L(\alpha + \alpha k)}}} \sin \alpha - {C_{D(\alpha + \alpha k)}}\cos \alpha ]{\rm{ds}}
\end{array}\]
(5)
|
| 图4 舵剖面受力示意图 Fig.4 Force on rudder section |
根据伴流场可确定舵最大附加推力对应的剖面偏转角,但随着剖面的偏转其压力分布也发生了较大的变化,可能会导致侧向力减小而影响舵效或者出现大的吸力峰而恶化舵的空泡性能,而Eppler方法可以优化舵的压力分布,在满足舵受力基本不变基础上,使得舵的表面压力分布均匀。
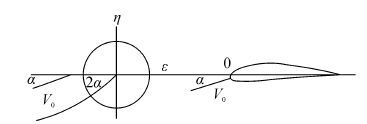
Eppler方法是根据指定的速度分布形式通过保角变换来得到所需的翼型剖面。保角变换如图5所示。该方法可以将翼型表面分为若干部分,在每一部分上指定一个攻角和速度分布形式,可以考虑翼型剖面在多个工况下工作的情况,是一种多点设计方法。翼型表面在单位圆上的区域划分及对应的攻角设置如图6所示。
|
| 图5 保角变换示意图 Fig.5 Sketch map of conformal mapping |

|
| 图6 单位圆上圆弧划分及攻角示意图 Fig.6 Arc limit define and attack angle on unit circle |
在进行扭曲舵剖面设计时,需要根据伴流场计算结果确定舵剖面的攻角变化范围,并参考普通舵的剖面升力系数确定设计剖面的负荷,以免引起侧向力的明显降低。 ζ-平面:ζ=ζ+iη, z-平面:z=x+iy
2.4 一体化推进器设计方案选择某双桨双舵船为研究对象,其螺旋桨为5叶桨,直径1.56 m,盘面比为0.74,毂径比0.189。舵为传统的直舵,位于螺旋桨正后方,剖面为NACA0020,舵高1.35 m,下端面弦长0.893 m,上端面弦长1.08 m。
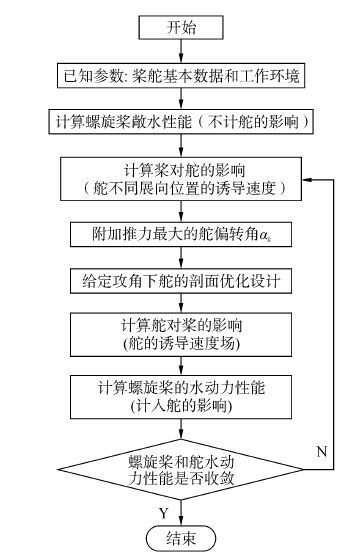
通过不同舵球直径对桨舵系统效率的影响分析,确定最佳舵球尺寸,结果见图3。随着舵球直径由小变大,桨舵系统的节能效果由小变大,在d/D=0.22时节能效果最优,舵球直径进一步增加则节能效果迅速减小,因此取舵球直径d=0.22D,D为螺旋桨直径。为保证舵球与毂帽光顺过渡,舵球前端直径与桨毂帽后端直径相等。根据扭曲舵的设计原理开展一体化推进器设计,设计流程如图7所示。
|
| 图7 桨舵一体化推进器设计流程 Fig.7 Flow chart of integrative propulsor design |
根据桨舵一体化推进器设计流程迭代计算,获得最大附加推力的舵偏转角及适伴流扭曲剖面,扭曲舵偏转角见表1,其中,z为舵剖面距桨盘中心的高度,L为舵的展长。给定攻角下的适伴流剖面优化结果见图8,桨舵一体化设计方案见图9。

|
| 图8 舵剖面对比 Fig.8 Comparison of rudder section |

|
| 图9 一体化推进器方案 Fig.9 Integrative propulsor |
| 序号 | z/L | αk/(°) | 序号 | z/L | αk/(°) | |
| 1 | -0.295 | -9.90 | 12 | 0.255 | 9.70 | |
| 2 | -0.245 | -9.60 | 13 | 0.305 | 9.60 | |
| 3 | -0.195 | -9.20 | 14 | 0.355 | 9.00 | |
| 4 | -0.145 | -8.30 | 15 | 0.405 | 7.50 | |
| 5 | -0.095 | -6.80 | 16 | 0.455 | 5.00 | |
| 6 | -0.045 | -4.00 | 17 | 0.505 | 2.50 | |
| 7 | 0.000 | 0.00 | 18 | 0.555 | 1.00 | |
| 8 | 0.055 | 4.20 | 19 | 0.605 | 0.00 | |
| 9 | 0.105 | 7.00 | 20 | 0.655 | 0.00 | |
| 10 | 0.155 | 8.40 | 21 | 0.705 | 0.00 | |
| 11 | 0.205 | 9.30 |
为了验证一体化推进器的节能、抑制空泡效果,开展了传统桨舵推进器与一体化桨舵推进器的快速性试验及空泡试验。
快速性试验主要开展了不同桨舵方案的自航试验,对不同航速下的螺旋桨及舵的受力进行了测量,其中舵的受力包括轴向力及侧向力,试验的缩尺比为1∶11。
空泡对比试验在空泡水筒中进行,为了真实模拟螺旋桨工作环境,采用假体对船后非均匀流场进行模拟,假体形状见图10。螺旋桨模型直径为220 mm,材料为铝合金,传统舵模型与一体化推进器模型分别见图11和图12。试验采用模型桨与实桨等推力系数及等空泡数的相似条件进行。

|
| 图10 假体模型伴流 Fig.10 Wake simulation by dummy model |

|
| 图11 传统舵模型 Fig.11 Test model of traditional rudder |

|
| 图12 一体化推进器模型 Fig.12 Test model of integrative propulsor |
桨舵系统的受力包括螺旋桨受力及舵的受力,表2列出了传统桨舵推进器及一体化推进器的螺旋桨受力对比。由试验结果可得,新型一体化推进器使得螺旋桨的推力增加,而扭矩减小,因此螺旋桨的效率增加。
| Fn | 传统桨舵推进器 | 一体化推进器 | ||
| T/N | Q/(N·m) | T/N | Q/(N·m) | |
| 0.246 | 25.936 | 0.713 | 26.115 | 0.712 |
| 0.271 | 33.977 | 0.929 | 34.439 | 0.923 |
| 0.296 | 42.743 | 1.159 | 43.295 | 1.151 |
| 0.320 | 52.860 | 1.419 | 53.399 | 1.413 |
| 0.345 | 64.957 | 1.729 | 65.467 | 1.724 |
| 0.369 | 76.975 | 2.032 | 77.178 | 2.030 |
| 0.394 | 96.303 | 2.528 | 96.830 | 2.520 |
为了检验一体化推进器设计方法在降低舵的阻力及保持舵效方面的效果,进行了舵力测量试验,表3列出了不同航速下舵的受力对比。
| Fn | 传统桨舵推进器 | 一体化推进器 | 轴向力 变化/% | 侧向力 变化/% | ||
| FX/N | FX/N | FY/N | FX/N | |||
| 0.246 | -0.85 | -0.88 | -0.74 | -0.83 | 12.9 | 5.7 |
| 0.271 | -1.08 | -1.11 | -0.92 | -1.06 | 14.8 | 4.5 |
| 0.296 | -1.35 | -1.34 | -1.14 | -1.29 | 15.6 | 3.7 |
| 0.320 | -1.66 | -1.56 | -1.44 | -1.46 | 13.3 | 6.4 |
| 0.345 | -2.07 | -1.8 | -1.81 | -1.69 | 12.6 | 6.1 |
| 0.369 | -2.6 | -2.08 | -2.28 | -1.98 | 12.3 | 4.8 |
| 0.394 | -3.4 | -2.5 | -3.06 | -2.38 | 10.0 | 4.8 |
由舵的受力对比可得,一体化推进器的舵阻力比传统舵降低10%~15%,而侧向力变化较小,降低5%左右,这主要是由于通过舵的偏转及扭曲设计,舵与螺旋桨尾流场的匹配性更优。
定义桨舵推进系统的效率为
| Fn | 传统桨舵推进器 | 一体化推进器 | 效率变化% |
| 0.246 | 0.695 0 | 0.704 1 | 1.3 |
| 0.271 | 0.683 6 | 0.702 2 | 2.7 |
| 0.296 | 0.678 0 | 0.696 1 | 2.7 |
| 0.320 | 0.674 1 | 0.688 5 | 2.1 |
| 0.345 | 0.669 5 | 0.680 7 | 1.7 |
| 0.369 | 0.668 4 | 0.674 6 | 0.9 |
| 0.394 | 0.653 9 | 0.662 7 | 1.3 |
由桨舵推进系统的效率对比可得,一体化推进器的效率较传统桨舵最大提高约2.7%,而随着航速的增加节能效果减弱,到16 kn时节能效果约1%。
3.3 空泡试验结果及分析在给定的进速及空泡数下进行了传统桨舵推进器与一体化推进器的螺旋桨空泡形态对比试验,图13为桨叶处于50°位置时的空泡形态对比。

|
| 图13 螺旋桨空泡对比 Fig.13 Comparison of propeller cavitation |
由相同工况下螺旋桨的空泡形态对比可知,普通桨舵系统与一体化推进器的螺旋桨空泡形态基本一致,表明一体化推进器对螺旋桨的空泡性能影响较小,这主要是由于舵位于螺旋桨后方,扭曲舵与普通舵对螺旋桨的影响不大,而舵球主要影响螺旋桨内半径区域,该区域桨叶未发生空化。
在对应工况下,普通舵的两侧均产生了空化,空泡的面积及形态差别不大,但是左侧面时空泡发生在轴线下方,而右侧面时空泡发生在轴线上方,这主要是因为试验时螺旋桨右旋,对于轴向下方的剖面,来流存在向左的诱导速度,左侧面为剖面的叶背,随着攻角增加左侧面上产生吸力峰而出现空化,而轴向上方的剖面处存在向右的诱导速度,因此空泡发生位置相应的为右侧面。
在对应工况下,一体化推进器的舵未发生空化,表明通过多特性均衡设计,一体化推进器可在保持舵效不变,增加螺旋桨推力及推进系统节能效果基础上,有效改善舵的空泡性能。

|
| 图14 普通舵的空泡形态 Fig.14 Comparison of traditional rudder cavitation |

|
| 图15 一体化推进器舵空泡 Fig.15 Comparison of integrative propulsor cavitation |
从节能、改善空泡及保持舵效的特性平衡设计理念出发,建立了一体化推进器设计方法,通过快速性及空泡性能试验验证了设计方法的正确性。通过本文研究可得出如下结论:
1)一体化推进器可增加螺旋桨推力、减小螺旋桨扭矩,扭曲后舵阻力减小10%以上,最大效率可提高约2.7%。
2)舵的扭曲对螺旋桨空泡性能的影响较小,但通过剖面优化可实现在不改变舵效情况下,舵空泡性能的有效改善。
3)建立的一体化推进器多特性均衡设计方法可全面考虑桨舵之间的相互干扰,实现推进器与流场的匹配,达到在不改变舵效情况下的节能、抑制空泡的效果。
| [1] | 刘飞. EEDI对船舶总体设计影响分析研究[D]. 大连: 大连理工大学, 2011: 11-36. LIU Fei. The research of EEDI impact on the basic ship design[D]. Dalian: Dalian University of Technology, 2011: 11-36. |
| [2] | GHASSEMI H, GHADIMI P. Computational hydrodynamic analysis of the propeller-rudder and the AZIPOD systems[J]. Ocean engineering, 2008, 35(1): 117-130. |
| [3] | COLLAZO A C, FERNÁNDEZ A S. Flow adapted rudder geometry for energy efficiency improvement[R]. Vigo, Spain: First International Symposium on Fishing Vessel Energy Efficiency E-Fishing, 2010. |
| [4] | DI MASCIO A, DUBBIOSO G, MUSCARI R, et al. CFD Analysis of Propeller-Rudder Interaction[C]//Proceedings of the Twenty-fifth (2015) International Ocean and Polar Engineering Conference. Hawaii, USA, 2015: 946-950. |
| [5] | BADOE C E, PHILLIPS A B, TURNOCK S R. Influence of drift angle on the computation of hull-propeller-rudder interaction[J]. Ocean engineering, 2014, 103: 64-77. |
| [6] | KIM J H, CHOI J E, CHOI B J, et al. Twisted rudder for reducing fuel-oil consumption[J]. International journal of naval architecture & ocean engineering, 2014, 6(3): 715-722. |
| [7] | 马骋, 钱正芳, 张旭, 等. 螺旋桨-舵-舵球推进组合体水动力性能的计算与仿真研究[J]. 船舶力学, 2005, 9(5): 38-45. MA Cheng, QIAN Zhengfang, ZHANG Xu, et al. Numeric computation and simulation on the hydrodynamic performance of the propeller-rudder-rudder bubble combination[J]. Journal of ship mechanics, 2005, 9(5): 38-45. |
| [8] | 何苗, 王超, 郭春雨, 等. 舵球几何参数对螺旋桨水动力性能的影响[J]. 武汉理工大学学报, 2011, 33(7): 69-70.HE Miao, WANG Chao, GUO Chunyu, et al. Effect of rudder ball geometric parameters on propeller hydrodynamic performance[J]. Journal of Wuhan University of Technology, 2011, 33(7): 69-70. |
| [9] | WANG Chao, HE Miao, WANG Guoliang, et al. Design and performance analysis of twisted rudder based on the maximum reduction of rudder resistance[J]. Journal of ship mechanics, 2014, 18(3): 238-247. |
| [10] | 王超, 何苗, 郭春雨, 等. 一体化节能推进装置定常水动力性能的数值模拟分析[J]. 哈尔滨工程大学学报, 2013, 34(6): 674-679. WANG Chao, HE Miao, GUO Chunyu, et al. Steady hydrodynamic performance simulation of integrative energy-saving propulsion system[J]. Journal of Harbin Engineering University, 2013, 34(6): 674-679. |
| [11] | 何苗. 一体化节能推进装置的构型设计及水动力性能预报[D]. 哈尔滨: 哈尔滨工程大学, 2012: 13-60. HE Miao. Design and hydrodynamic performance simulation of integrative energy-saving propulsion system[D]. Harbin: Harbin Engineering University, 2012: 13-60. |



