2. Education Ministry Key Laboratory of High-efficiency and Clean Mechanical Manufacture, Shandong University, Ji'nan 250061, China
喷丸是一种常用的提高零部件疲劳寿命的表面强化方法。在喷丸过程中,通过向零部件表层引入残余压应力从而改善其抗疲劳性能。喷丸残余压应力对其表面疲劳裂纹的萌生及扩展的抑制作用研究是目前喷丸强化领域的热点研究方向。很多学者分别从实验、解析分析和数值模拟方面做了大量研究工作,结果表明喷丸强化所产生的加工硬化层可使流动应力升高,并可有效阻滞裂纹张开,抑制裂纹扩展以提高工件的疲劳寿命[1, 2]。虽然近期涉及残余应力对裂纹扩展疲劳寿命影响的数值仿真研究较多,但针对喷丸残余应力场的相对较少且其研究不够完善、深入。Guagliano M[3]针对旋转弯曲试样通过计算裂纹应力强度因子幅值评价其抗裂纹扩展能力,但其模型是基于经典的线弹性裂纹扩展理论。周建忠等[4]对应力比分别为0.1、0.3、0.5的紧凑拉伸(CT)试样进行了激光喷丸强化疲劳裂纹扩展的数值研究,也是基于线弹性断裂力学理论,利用应力线性叠加方法建立其裂纹扩展模型。Liu Jinxiang [5]利用CZM模型建立裂纹扩展疲劳寿命预测模型,表明不同的荷载幅值和不同喷丸强度都会影响疲劳裂纹扩展,着重阐述了不含喷丸残余应力场的疲劳裂纹寿命预测模型,而未涉及喷丸残余应力引起的裂纹闭合效应。Liu Hu[6]认为在循环变幅载荷作用下,张开应力强度因子为常值,当考虑残余应力时,仅需考虑其对张开应力强度因子的影响,并将其代入裂纹扩展模型预测疲劳寿命。
针对上述数值仿真研究的不足,本文开展了喷丸残余应力场对裂纹扩展疲劳寿命影响的数值仿真预测模型的研究,所提出的预测模型涉及喷丸残余应力场的分布、塑性诱导裂纹闭合效应、裂纹张开力的确定、裂纹表面的接触定义、材料运动硬化属性等非线性因素。
1 有限元建模喷丸或其他塑性变形处理引起的疲劳寿命提高主要是由于残余压应力可阻滞微裂纹的扩展,而不是阻止疲劳裂纹的萌生。残余应力将引起裂纹闭合效应,其结果将改变实际应力强度因子幅值。在研究过程中需要考虑喷丸残余应力场的真实分布及循环载荷对裂纹表面接触状况的影响,忽略裂纹表面的接触闭合现象将导致不准确的预测结果,故传统的利用线性叠加技术计及残余应力影响的方法不再适用。故在喷丸残余应力场中求解真实的裂纹张开力尤为重要,本节基于计及裂纹闭合效应的非线性有限元模型对其求解,为后续裂纹扩展疲劳寿命准确预测创造条件。
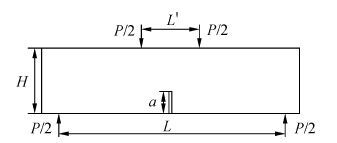
1.1 算例描述研究结果表明,表面强化对提高拉-拉疲劳性能作用不大,有时甚至会降低拉-拉疲劳性能,因此在工程应用上一般不采用表面强化来提高拉-拉疲劳性能。本文针对De los Rios E. R.的四点弯曲实验[7]建立相应的有限元模型,如图1所示。
|
| 图1 四点弯曲试样 Fig.1 Four point bending specimen |
试样材料、尺寸及加载情况均参考文献[7],其材料为2024-T351铝合金,尺寸为:厚度B=6.5 mm,宽H=4.6 mm,总长80 mm,L′=21.8 mm,L=66 mm。应力比为0.1,对于受喷试样与未喷试样,最大外载取值范围分别为270~320 MPa和 223.6~310 MPa。针对上述试样进行有限元建模及仿真分析是为了便于对照实验结果和仿真结果以验证仿真模型及结果的正确性及有效性。
1.2 材料属性采用双线性各向同性随动强化模型建立2024-T351铝合金试样的弹-塑性本构关系,取von-Mises屈服准则,其弹性模量为73 774 MPa,塑性模量为530 MPa,泊松比μ=0.33,屈服应力为372 MPa [8]。该材料本构模型可较好地反映材料的循环塑性和包申格效应。
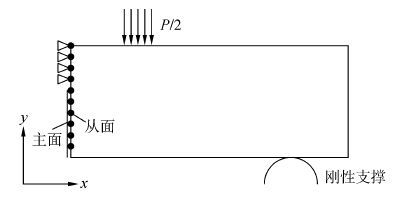
1.3 边界条件及载荷施加利用ABAQUS软件通过建立有限元模型计算裂纹张开力,进而预测裂纹扩展疲劳寿命。利用对称性,取矩形试样的右侧1/2建立有限元模型,如图2所示。设裂纹沿y轴方向扩展,初始裂纹长度a为0.05 mm,预定义裂纹扩展长度范围为3 mm,沿y轴定义一条刚性线,该刚性线与预定裂纹扩展长度范围内的模型左侧边界线形成裂纹扩展面,在其上分别定义主从接触面。y轴预设裂纹长度以外的边界节点采用对称约束。初始状态时将从面节点与主面(刚性线)绑定在一起。将试样底部的支撑圆柱面定义为刚体表面,并定义其与试样下表面的接触关系。在模型上表面局部区域内施加循环面载荷。
|
| 图2 边界条件及载荷施加 Fig.2 Boundary conditions and loading |
采用CPE4R四节点平面应变减缩积分单元划分网格。为保证数值分析精度,需在裂尖前部微小塑性区域内至少包含2~3个单元。利用式(1)估算裂尖塑性区大小以确定该处的网格尺寸:
$$2{r_f} = \frac{1}{{\alpha \pi }}{\left( {\frac{{{K_{\max }}}}{{{\sigma _0}}}} \right)^2}$$
(1)
|
| 图3 网格划分 Fig.3 Finite element meshing |
为了模拟喷丸残余应力场对裂纹扩展疲劳寿命的影响,通过ABAQUS用户子程序SIGINI直接将实测喷丸残余应力导入四点弯曲试样有限元模型中。喷丸残余应力场沿深度方向的分布通常可用Robertson公式[9]表示:
$$Y = A\exp \left( {\frac{{ - 2{{\left( {x - {x_d}} \right)}^2}}}{{{W^2}}}} \right) + B$$
(2)
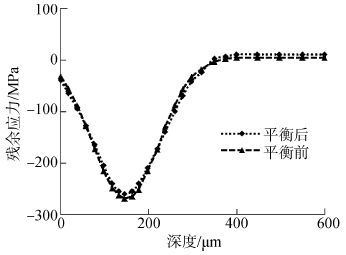
为满足喷丸残余应力在特定边界条件下的自平衡,在导入残余应力后需先进行一次静平衡分析,使得所施加的预应力既符合喷丸残余应力特征又满足应力平衡状态。图4为平衡前后喷丸残余应力的分布状况,两者基本一致,故可用平衡后的喷丸残余应力研究其对裂纹扩展疲劳寿命的影响。 满足自平衡条件的残余应力分量Sx沿y轴的分布如图5所示。
|
| 图4 喷丸残余应力分布 Fig.4 Distribution of shot peening residual stress |
|
| 图5 喷丸残余应力分布 Fig.5 Distribution of shot peening residual stress |
由Elber[10]提出的有效应力强度因子幅值法可预测计及塑性裂纹闭合条件下的裂纹扩展。Elber认为,在裂纹扩展过程中,裂纹扩展路径上的材料塑性变形可导致裂纹闭合现象,只有当施加的外力所产生的应力大于某一水平时,裂纹才能完全张开,该应力水平下的外力称为裂纹张开力。因为裂纹只有在完全张开之后才能向前扩展,故在载荷循环过程中最大外载荷与裂纹张开力之差是驱动裂纹扩的载荷因素,将其定义为有效应力幅值$\Delta {P_{{\text{eff}}}}$,$\Delta {P_{{\text{eff}}}} = {P_{\max }} - {P_{{\text{op}}}}$。故需首先确定裂纹张开力Pop。
采用Newman[11]提出的裂纹张开力计算方法,该方法用裂纹尖端后部第一个节点与刚性线的接触状态确定裂纹的实际开合状态,设在每个加载步的开始解除一个裂纹单元的绑定状态,但这并不意味裂纹实际扩展一个单元长度,如此时裂纹尖端后部第一个节点为闭合接触状态,说明裂纹并未扩展;反之,当该节点为非接触的张开状态,则说明裂纹发生扩展。为精确计算裂纹长度和裂纹张开力,对裂纹张开前后的两个载荷增量步进行线性插值以提高裂纹张开力的求解精度。
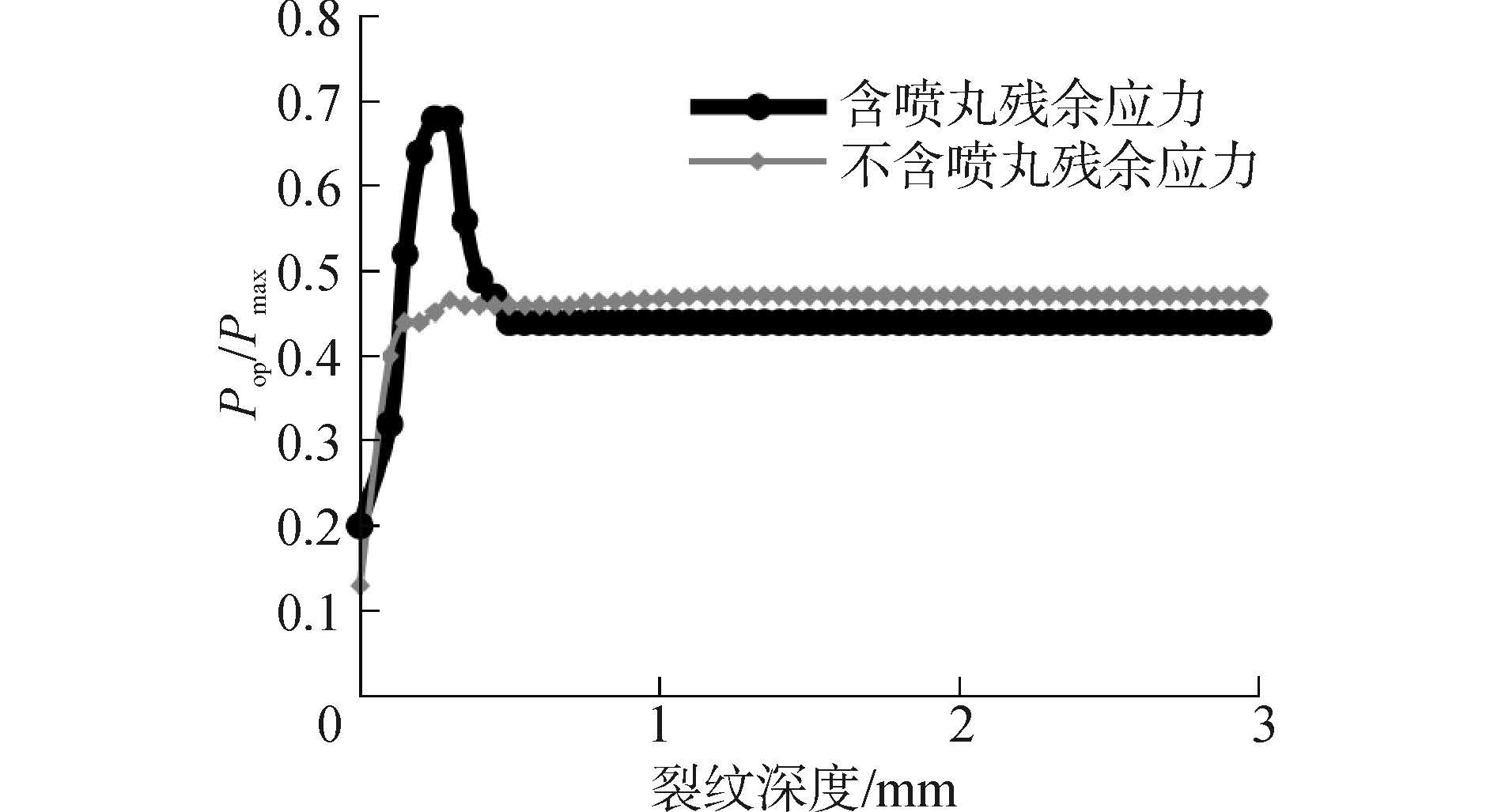
通过上述有限元模型及裂纹开合判定方法可数值计算裂纹张开力,用于研究喷丸残余压应力场对裂纹扩展的影响。图6为其数值计算结果,当试样次表层存在喷丸残余压应力时,裂纹张开力的变化趋势与喷丸残余压应力的分布趋于一致,说明喷丸残余压应力确对裂纹张开力产生直接影响。
|
| 图6 裂纹张开力 Fig.6 Open force of crack |
在距受喷表面0~0.3 mm裂纹张开力呈显著上升趋势,随后下降并趋于稳定。裂纹张开力的显著上升表明喷丸残余压应力的存在可有效减缓裂纹扩展。裂纹张开力在距试样受喷表面约0.6 mm处开始趋于稳定且该稳定值略低于未喷丸的。这是因为喷丸残余压应力的分布范围为距受喷表面0~0.6 mm的次表层,深度大于0.6 mm的试样内部基本不含喷丸残余压应力,故当深度大于0.6 mm时裂纹张开力趋于稳定。由于喷丸残余应力在试样内部对应给定边界条件是处于平衡状态的,导致与残余压应力次表层相邻的内部区域存在少许拉应力与次表层中的压应力平衡,使得裂纹张开力较未喷丸的试样略低。无论是否包含喷丸残余应力,稳定后的裂纹张开力均约为0.4Pmax,说明喷丸与未喷丸试样中均存在由于塑性变形导致的裂纹闭合现象,而在喷丸时该现象更加突出。
2.2 有效应力强度因子幅值计算
在得到上述裂纹张开力的基础上,即可利用Elber 的有效应力强度因子幅值法研究喷丸残余应力场对裂纹扩展的作用及影响。设对应裂纹张开时的应力强度因子为Kop,则有效应力强度因子幅值为$\Delta {K_{{\text{eff}}}} = {K_{\max }} - {K_{{\text{op}}}}$。代入四点弯曲试样的应力强度因子计算公式得
$\eqalign{
& \Delta {K_{{\text{eff}}}} = f\Delta {K_0} = f\frac{{\Delta {K_{{\text{eff}}}}\left( {L - L'} \right)}}{{4B{H^{\frac{3}{2}}}}} = \cr
& f\frac{{({P_{\max }} - {P_{{\text{op}}}})\left( {L - L'} \right)}}{{4B{H^{\frac{3}{2}}}}} \cr} $
(3)
$\left\{ \begin{array}{l}
f = 11.94{\left( {\frac{a}{H}} \right)^{1/2}} - 14.82{\left( {\frac{a}{H}} \right)^{3/2}} + 77.82{\left( {\frac{a}{H}} \right)^{5/2}} - \\
139.02{\left( {\frac{a}{H}} \right)^{7/2}} + 148.8{\left( {\frac{a}{H}} \right)^{9/2}},a/H \le 0.5\\
f = 3.976/{(1 - \frac{a}{H})^{3/2}},a/H \ge 0.5
\end{array} \right.$
(4)
|
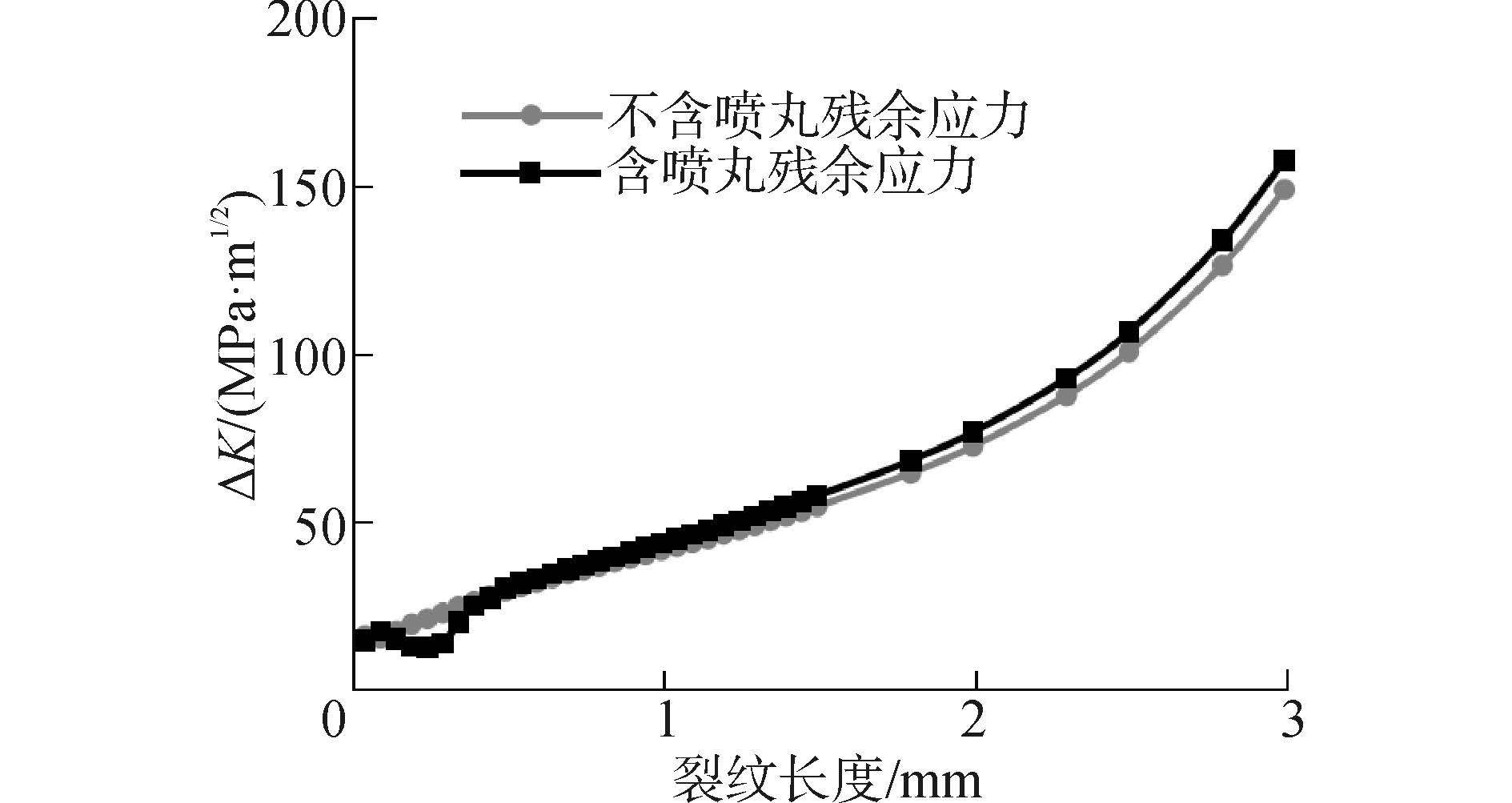
| 图7 应力强度因子幅值 Fig.7 Amplitude of stress intensity factors |
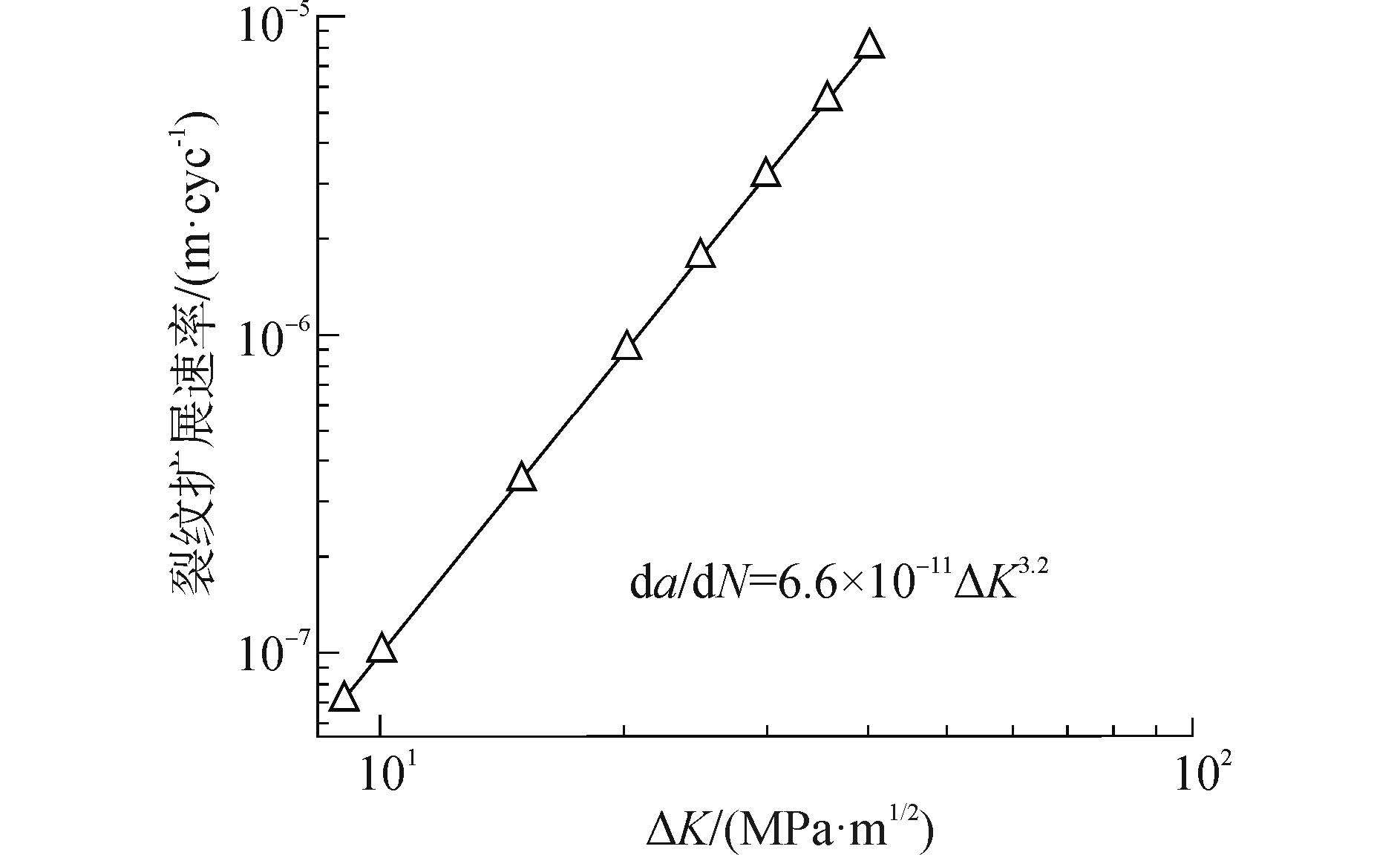
利用图7有效应力强度因子幅值结果,基于Paris公式(5)可预测裂纹扩展疲劳寿命:
${\text{d}}a/{\text{d}}N = C{\left( {\Delta {K_{{\text{eff}}}}} \right)^m}$
(5)
|
| 图8 裂纹扩展速率曲线 Fig.8 The curve of crack growth rate |
将式(5)表示为如下积分形式:
$\Delta N = {\int_{a - \Delta a}^a {{C^{ - 1}}\left( {\Delta {K_{{\text{eff}}}}} \right)} ^{ - m}}{\text{d}}a$
(6)
基于式(6)预测裂纹扩展疲劳寿命时,需划分裂纹扩展步,在各裂纹扩展步中给定裂纹扩展增量Δa,由式(6)可得到裂纹扩展增量Δa所对应的载荷循环次数增量ΔN。图9所示为整个裂纹扩展过程中各裂纹扩展步所对应的循环次数增量变化趋势。在不含喷丸残余应力时,当裂纹长度大于0.5 mm时,裂纹扩展单位长度时的循环次数急剧下降随后趋于平稳;而在含有喷丸残余应力时,当裂纹长度约为0~0.3 mm时,循环次数急剧上升到最大值,随后急剧下降,当裂纹长度大于0.5 mm时,喷丸与未喷丸试样扩展单位长度所需循环次数趋于一致。这与喷丸残余应力的大小及位置分布联系紧密。
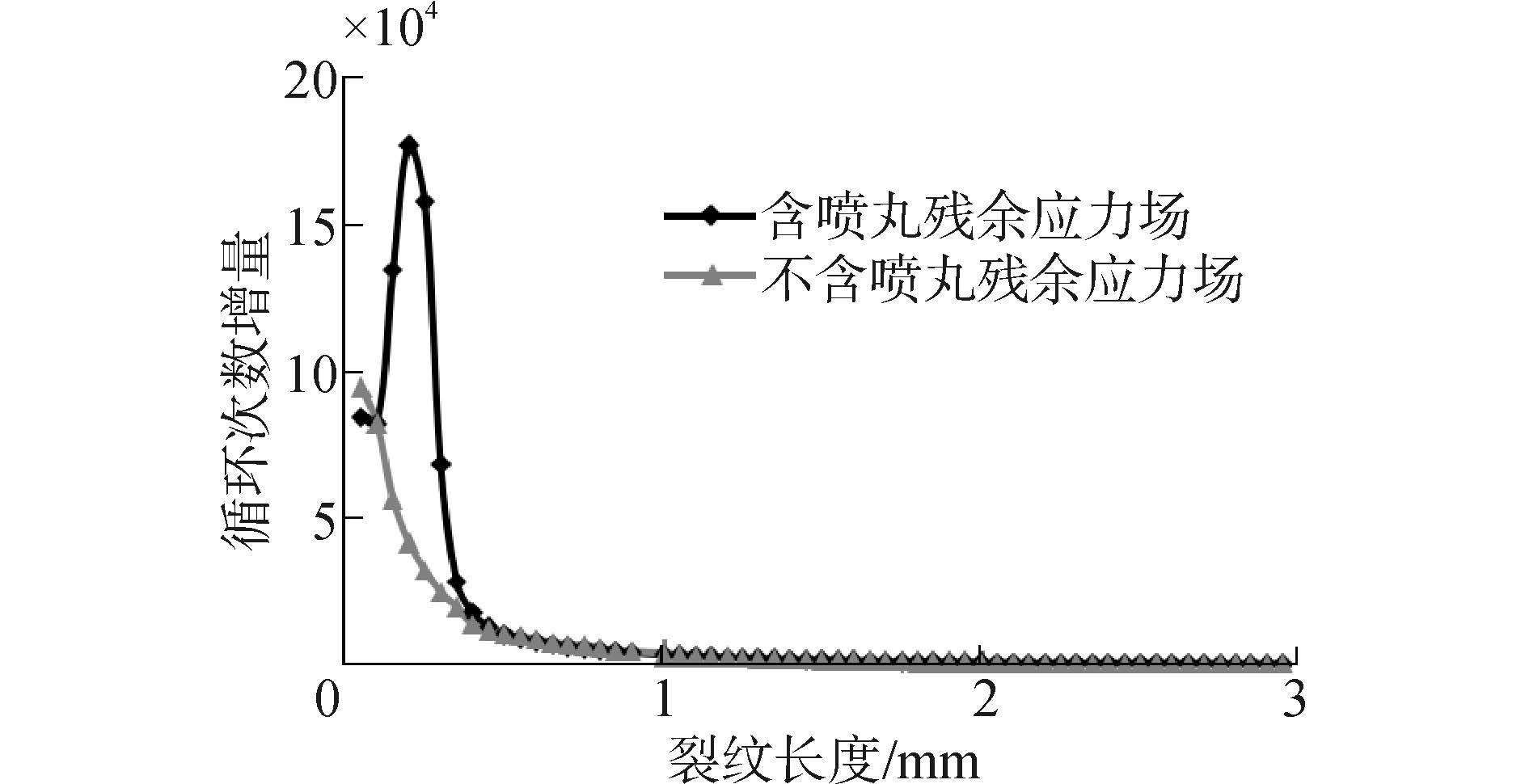
|
| 图9 循环次数增量与裂纹长度的关系 Fig.9 Cycle number increment vs. crack length |
图10为同一载荷作用下含喷丸残余应力和不含喷丸残余应力的试样裂纹扩展疲劳寿命预测结果与文献[7]给出的实验结果对比图,图11所示为不同外载荷水平作用下的预测疲劳寿命结果与文献[7]的实验结果对比图。由图10和图11可以看出,预测结果与实验结果的变化趋势基本一致且数值吻合度较高,说明本文所给出的研究方法是正确有效的。由图10可知,经过喷丸处理后的试样裂纹扩展3 mm的循环次数约为未喷丸试样的2.5倍,说明喷丸处理可有效提高试样的高周疲劳寿命。
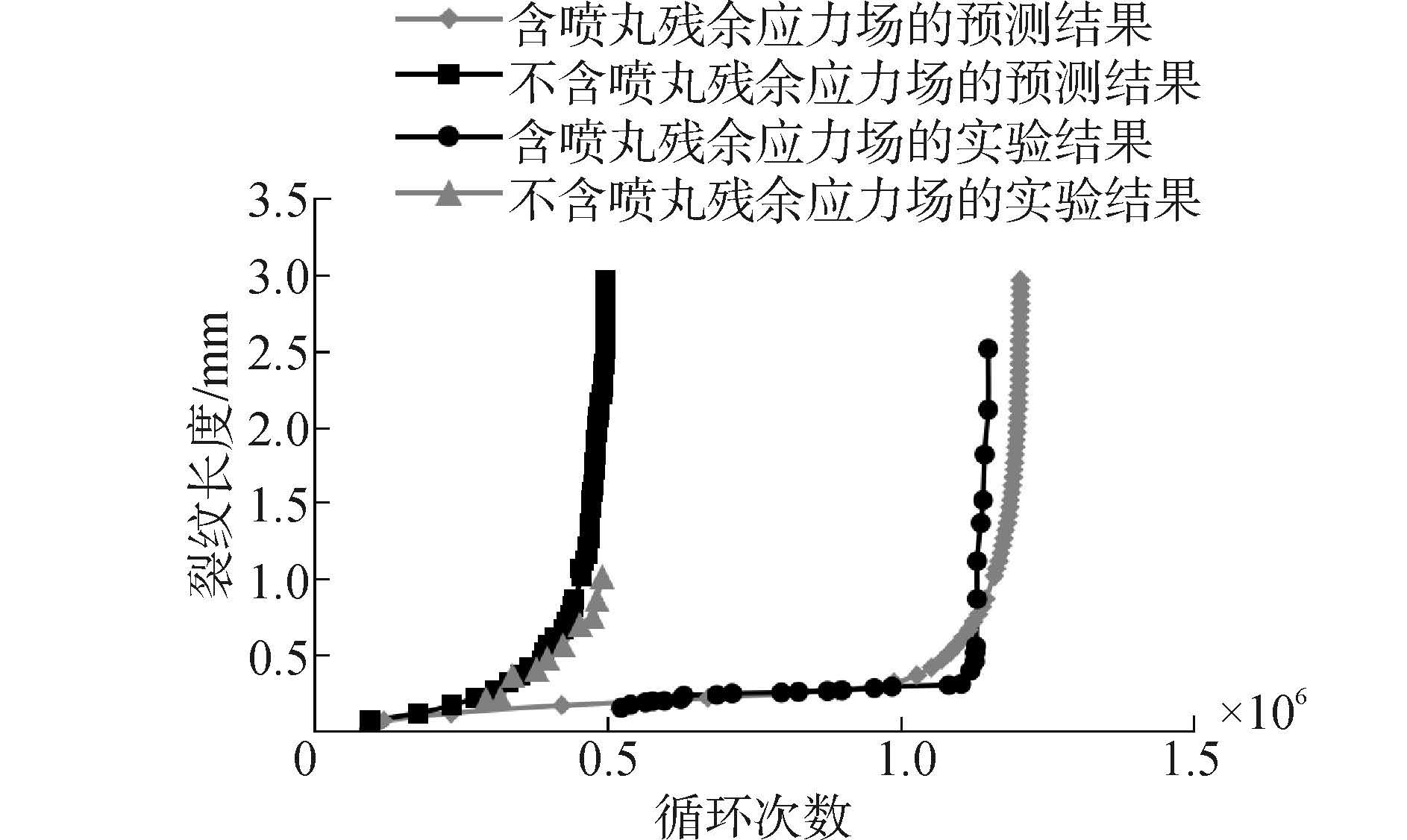
|
| 图10 裂纹扩展疲劳寿命 Fig.10 Crack growth fatigue life |
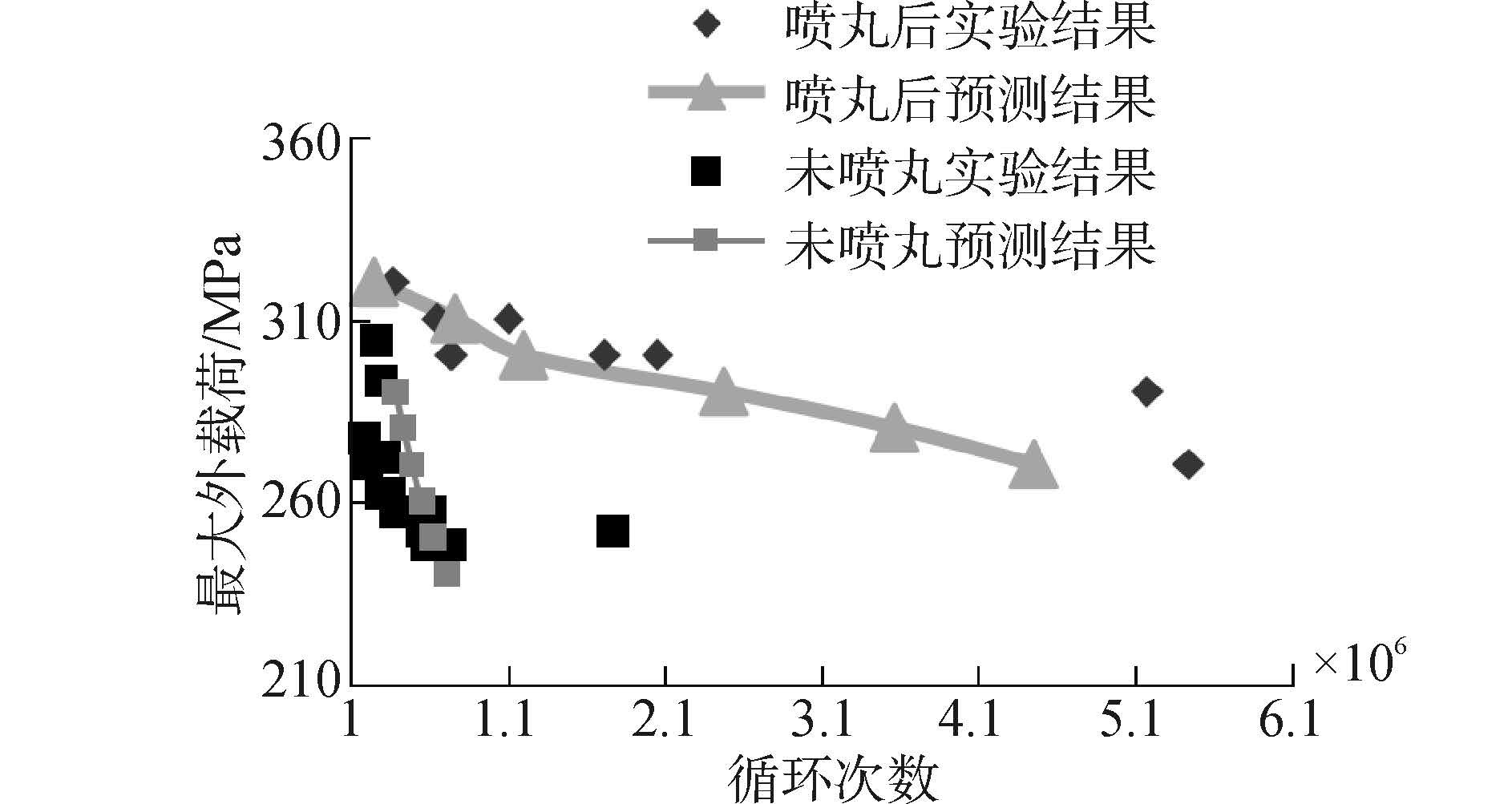
|
| 图11 裂纹扩展疲劳寿命 Fig.11 Crack growth fatigue life |
众所周知,影响裂纹扩展疲劳寿命的因素众多,如材料参数、加载方式、应力比等。而经喷丸处理的试样,其裂纹扩展疲劳寿命除与上述因素有关外,还与喷丸工艺密切相关。本文着重研究应力比和不同喷丸处理工艺对裂纹扩展疲劳寿命的影响。表1为不同应力比下的Paris公式相关参数[12]。
| R | C | m |
| 0.05 | 5.75×10-11 | 3.09 |
| 0.10 | 6.60×10-11 | 3.20 |
| 0.50 | 5.29×10-11 | 3.29 |
| 0.75 | 3.28×10-12 | 4.59 |
图12为不同应力比条件下,裂纹扩展到3 mm时的疲劳寿命预测曲线。由图可知,应力比越小,裂纹闭合效应越明显,从而疲劳寿命越长;经喷丸后的试样寿命均比未喷丸试样的预测寿命要长,说明喷丸可有效延长试样的裂纹扩展疲劳寿命,特别在裂纹长度小于0.5 mm时,其抑制裂纹扩展的作用尤为显著,该裂纹长度正对应于喷丸试样中残余压应力的分布深度。当裂纹长度超过该深度后,其扩展速率陡然上升,迅速进入快速扩展阶段。不同应力比条件下,喷丸试样的裂纹扩展疲劳寿命均约为未喷丸试样的2.5倍。
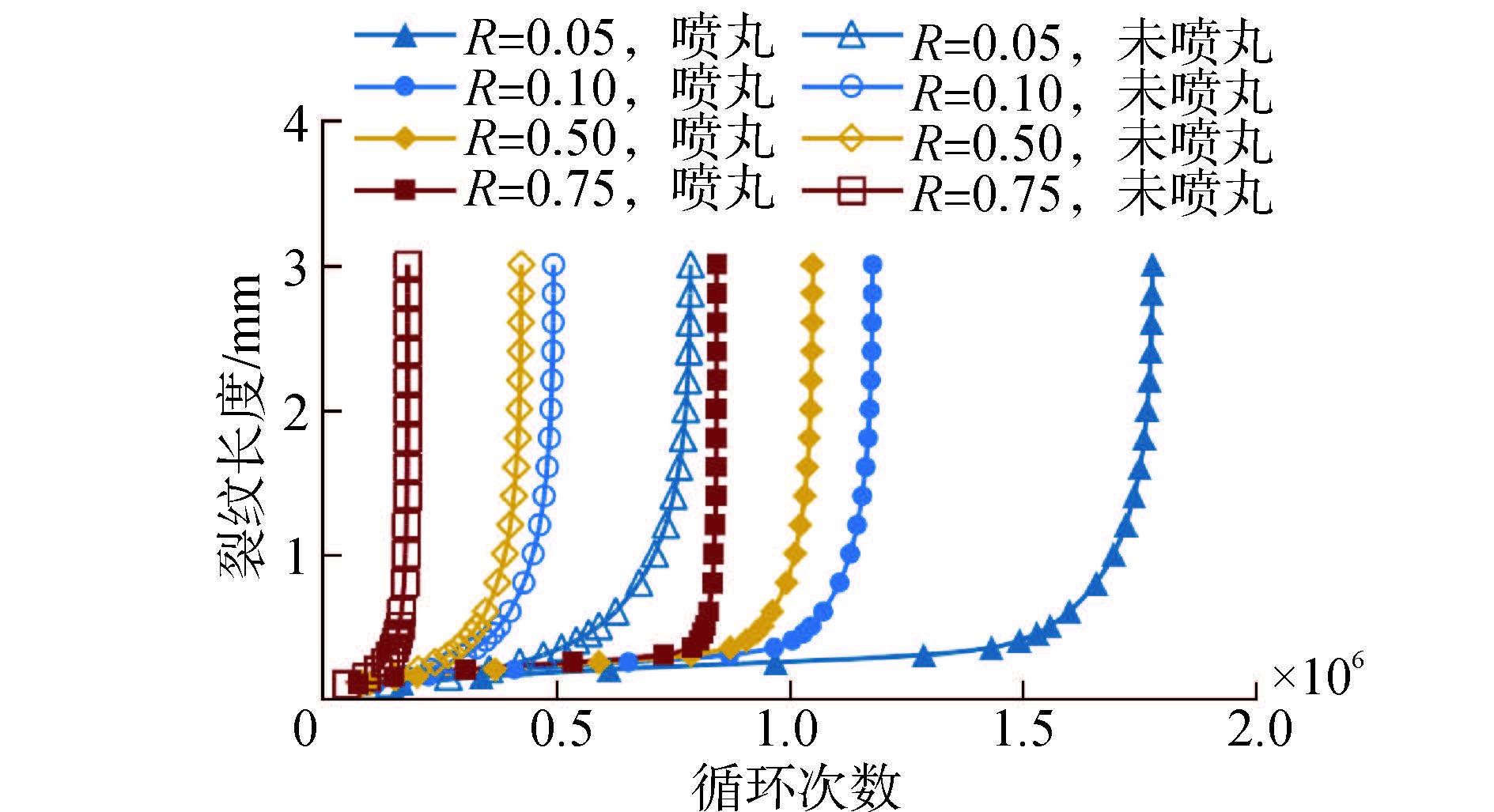
|
| 图12 不同应力比条件下的裂纹扩展疲劳寿命 Fig.12 Crack growth fatigue life of different stress ratio |
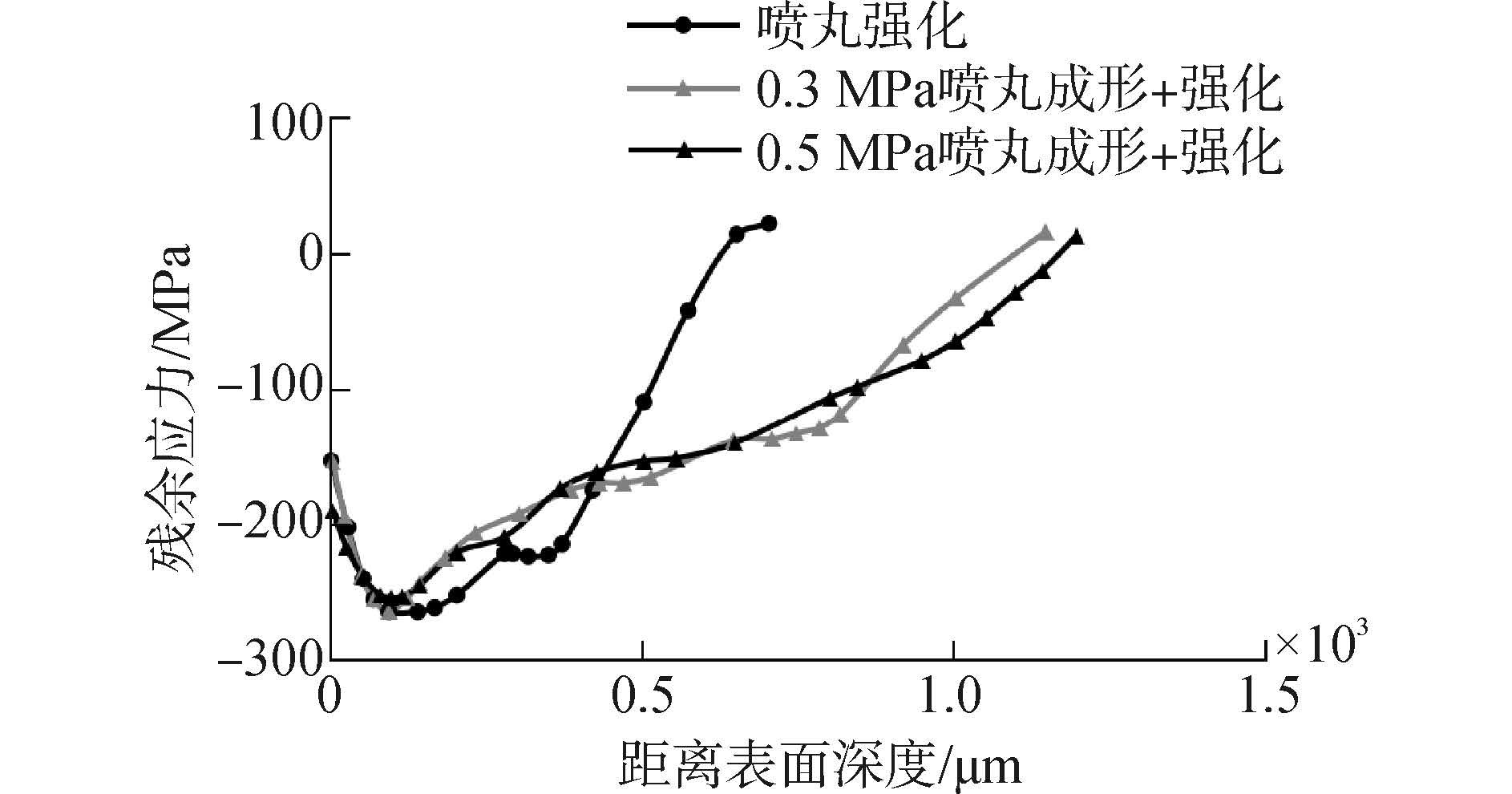
喷丸的另一应用场合是喷丸成形。文献[13]针对2024-T351铝合金进行直径为3 mm的大弹丸作用喷丸成形实验,图13所示为对应不同喷丸工艺条件下铝合金次表层残余应力分布实验曲线。由图13可知,相较于喷丸强化,大弹丸喷丸成形扩大了残余压应力层的深度,但喷丸强化和喷丸成形两者所形成的最大残余压应力值差别不显著,这是由于最大残余压应力值受材料屈服强度限制。下面研究不同喷丸工艺所形成的不同残余应力分布对裂纹扩展疲劳寿命的影响。
|
| 图13 不同喷丸工艺条件下的残余应力 Fig.13 Residual stress under different peening technology |
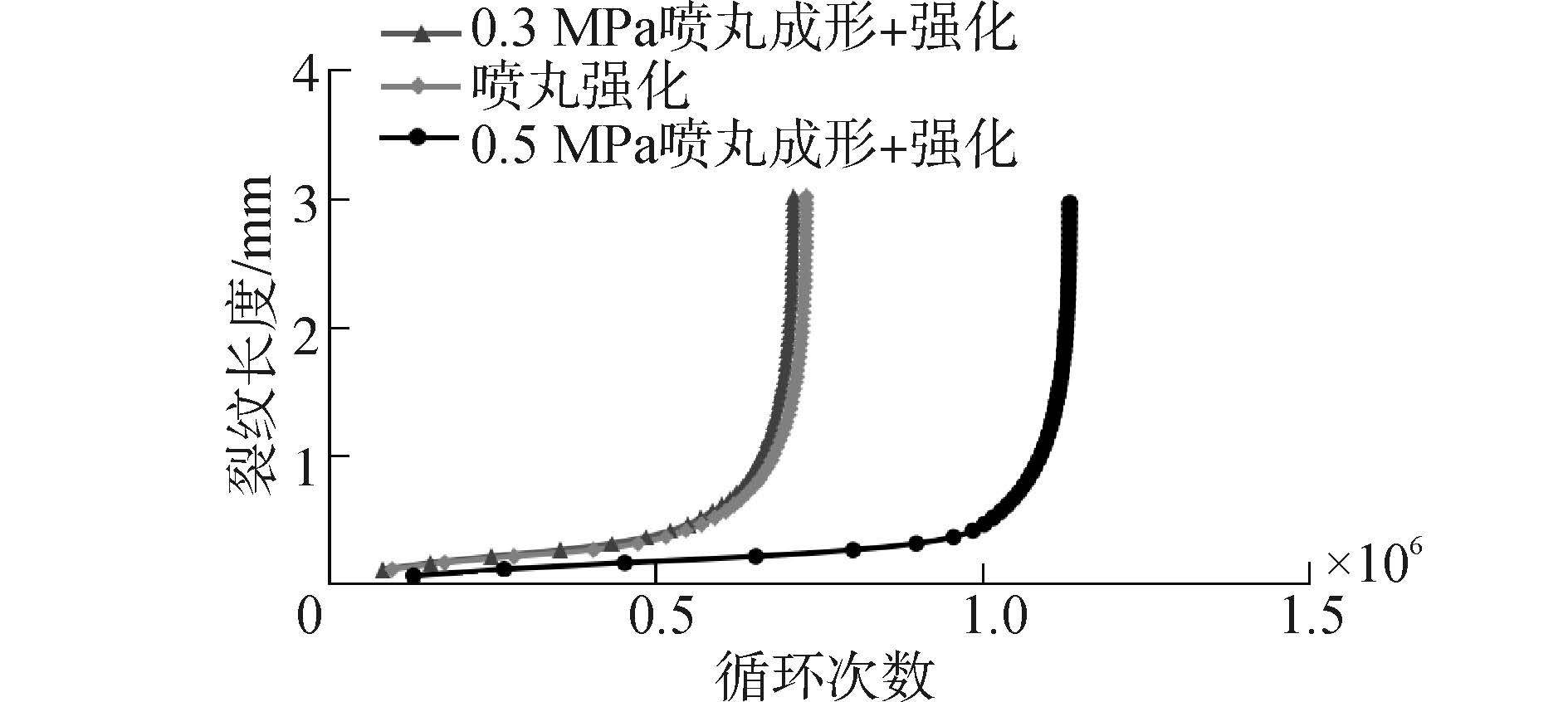
针对图13给出不同喷丸工艺所对应的残余应力分布,仿真得到相应裂纹扩展疲劳寿命变化趋势如图14所示。由该图可知,单独喷丸强化对裂纹扩展疲劳寿命的提高效果优于喷丸成形与强化的共同作用效果。分析其主要原因,在距离表面0~0.4 mm的深度范围内,喷丸强化的残余压应力整体上大于喷丸成形与强化的残余压应力。而此时裂纹长度较短,每个裂纹扩展步对应的循环次数增量较大,残余压应力对裂纹扩展的抑制作用较为明显,使得喷丸强化对提高试样疲劳寿命的效果较之喷丸成形加强化好的多。此外,不同强度下的喷丸成形所形成的残余应力分布不完全一致,导致对裂纹扩展疲劳寿命的影响略有差别。
|
| 图14 不同喷丸工艺条件下的疲劳裂纹扩展寿命 Fig.14 Fatigue crack growth life of different peening technology |
本文针对De los Rios E. R.的四点弯曲实验参数及条件建立有限元仿真模型,并形成疲劳寿命预测方法。通过预测结果与实验结果的对比,验证了所建有限元模型与疲劳寿命预测方法的正确性。基于该模型及算法,研究了不同应力比及不同喷丸工艺对裂纹扩展疲劳寿命的影响规律。结果表明:
1)喷丸强化处理可有效改善不同应力比条件下试样的疲劳寿命,且应力比越小,裂纹闭合效应越明显,试样疲劳寿命越长;
2)单独喷丸强化在试样次表层产生的残余压应力大于喷丸成形与强化共同作用所产生的残余压应力,从而导致单独喷丸强化对裂纹疲劳寿命的改善程度优于喷丸成形与强化共同作用的效果。
| [1] | 高玉魁. 喷丸强化对TC21高强度钛合金疲劳性能的影响[J]. 金属热处理, 2010, 35(8): 30-32. GAO Yukui. Influence of shot peening on fatigue property of TC21 titanium alloy[J]. Heat treatment of metals, 2010, 35(8): 30-32. |
| [2] | DE LOS RIOS E R, TRULL M, LEVERS A. Modelling fatigue crack growth in shot-peened components of Al 2024-T351[J]. Fatigue & fracture of engineering materials & structures, 2000, 23(8): 709-716. |
| [3] | GUAGLIANO M, VERGANI L. An approach for prediction of fatigue strength of shot peened components[J]. Engineering fracture mechanics, 2004, 71(4-6): 501-512. |
| [4] | 周建忠, 徐增闯, 黄舒, 等. 基于不同应力比下激光喷丸强化6061-T6铝合金的疲劳裂纹扩展性能研究[J]. 中国激光, 2011, 38(9): 0903006-1-0903006-6. ZHOU Jianzhong, XU Zengchuang, HUANG Shu, et al. Effects of different stress ratios on fatigue crack growth in laser shot peened 6061-T6 aluminum alloy[J]. Chinese journal of lasers, 2011, 38(9): 0903006-1-0903006-6. |
| [5] | LIU Jinxiang. Numerical analysis for effects of shot peening on fatigue crack growth[J]. International journal of fatigue, 2013, 50: 101-108. |
| [6] | LIU Hu, SHANG Deguang, LIU Jianzhong, et al. Fatigue life prediction based on crack closure for 6156 Al-alloy laser welded joints under variable amplitude loading[J]. International journal of fatigue, 2015, 72: 11-18. |
| [7] | DE LOS RIOS E R, TROOLL M, LEVERS A. Improving the fatigue crack resistance of 2024-T351 aluminium alloy by shot peening[C]//Proceedings Ceas Forum: Life Extension-Aerospace Technology Opportunities. Cambridge: Churchill College, 1999, 26.1-26.8. |
| [8] | 李亚智, 王启, 张自鹏, 等. 残余应力场中疲劳裂纹闭合的数值分析[J]. 西北工业大学学报, 2011, 29(1): 97-102.LI Yazhi, WANG Qi, ZHANG Zipeng, et al. Exploring further fatigue crack closure in residual stress field through numerical simulation[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 97-102. |
| [9] | ROBERTSON G T. The effect of shot size on the residual stresses resulting from shot peening[J]. The shot peener, 1997, 11(3): 46-48. |
| [10] | 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002: 167-179. |
| [11] | NEWMAN JR J C. A finite element analysis of fatigue crack closure[J].ASTM international, 1976: 281-301. |
| [12] | 杨光. 不同应力比下2024-T4铝合金疲劳裂纹扩展速率试验研究及数值模拟[D]. 杭州: 浙江工业大学, 2012: 7-13. YANG Guang. Experimental and numerical investigation of fatigue crack growth of 2024-T4 aluminum alloy under different R-ratios[D]. Hangzhou: Zhejiang University of Technology, 2012: 7-13. |
| [13] | 王明涛, 曾元松, 黄遐. 大尺寸弹丸喷丸成形2024-T351铝合金表面质量研究[J]. 航空制造技术, 2012(5): 92-94. WANG Mingtao, ZENG Yuansong, HUANG Xia. Research on surface quality of 2024-T351 aluminum alloy by peen forming with large ball[J]. Aeronautical manufacturing technology, 2012(5): 92-94. |



