无源雷达是利用非合作的外辐射源发出的信号作为探测信号,接收经过目标反射的信号,提取目标的方位、速度等参数的雷达系统[1]。它具有不可探测性、反隐身潜力、结构简单和造价低廉等优点,近年来在国内外引起广泛关注[2]。由于GPS的全天候、抗干扰、实时性等特点,将GPS信号作为辐射源的无源雷达系统逐渐成为研究热点[3, 4]。但是,GPS经过反射的回波通道不可避免的存在直达波、多径信号、杂波旁瓣等干扰[5, 6],微弱的目标回波通常被掩盖在噪声背景下,很难实现对目标的直接测向。因此如何在抑制干扰中进行多目标的DOA估计成为需要解决的重要内容。
为了实现目标测向时抑制干扰,人们提出了一些方法。文献[7]提出的批处理抵消ECA(extensive cancellation algorithm)算法不需要对干扰参数进行估计,根据多径干扰的多普勒频移特点实现干扰抑制,但不能完成测向问题。文献[8]提出利用距离-多普勒二维相关法提高回波信噪比实现测向方法,虽然抑制了直达波和多径干扰,但没有考虑强目标回波旁瓣对弱目标的干扰。针对阵元间噪声的空间相关性未知或无法估计的情况,文献[9]提出了MUSIC-like方法进行测向,它利用阵列输出的全部四阶累积量,计算复杂度较高。压缩感知是近几年流行起来建立在信号稀疏表示和重建基础上的一个介于数学和信息科学的新方向,它作为一个新的采样理论,在远小于奈奎斯特采样定律的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法完美的重建信号[10]。根据文献[10]对空间稀疏性的分析,当回波天线阵元数目足够大于需测定距离-多普勒单元函数关系时,目标空间满足稀疏性的定义,本文利用稀疏模型进行多目标的DOA估计,通过需测定距离-多普勒单元内的方位向压缩感知稀疏重构,获得目标DOA信息。这种方法将求解四阶累积量的复杂度降低,提高运算速度。同时,为了在低信噪比环境下获得更准确的求解结果,对L1范数最小化约束的权重值进行了改进以达到抑制噪声的效果。
1 无源雷达系统模型将GPS信号作为辐射源的无源雷达系统不主动发射信号,利用空中已有的GPS卫星发射的非合作信号进行目标检测、估计、跟踪及定位。利用GPS信号作为外辐射源的收发分置系统,接收站由参考通道和回波通道两部分组成[11, 12]。参考通道主要用于接收直达波,由于波束最大增益对准直达波方向,因而杂波较弱。回波通道用于接收目标的反射信号,同时干扰也不可避免的进入通道。为了消除干扰,首先利用ECA算法进行时域干扰相消和距离-多普勒二维相关处理,消除天线各阵元的直达波和多径干扰并提高目标回波的信噪比。再对多目标利用L1范数作为约束条件,建立稀疏模型进行DOA估计,处理过程如图1所示。
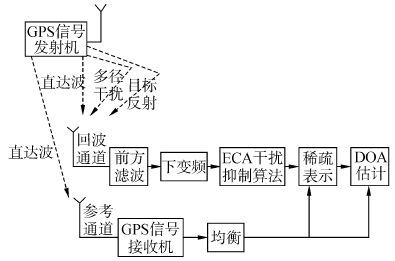
|
| 图1 系统模型 Fig.1 System model |
| $${s_{{\text{ref}}}}{\text{(t) = }}\sqrt {{\text{2}}{{\text{P}}_{\text{A}}}} {\text{C(t)D(t)}}{{\text{e}}^{{\text{j(}}{\omega _0}t + {\varphi _0})}}$$ | (1) |
由于直达波信号由参考通道的主瓣接收,因此忽略了目标回波和杂波。式中,PA为参考通道接收的信号功率;C(t)为带宽为1.023 MHz的伪码;D(t)为带宽为50 Hz的卫星导航数据;ω0为载波频率;φ0为GPS信号初始相位。
在回波通道中,进入通道的信号包括目标回波、直达波干扰、多径干扰和噪声等。在t时刻,回波通道的信号为
$$\eqalign{
& {s_{{\text{ref}}}}{\text{(t) = }}{s_{ref}} + \sum\limits_{i = 1}^{{N_m}} {{A_{mi}}s(t - {\tau _{mi}})} + \cr
& \sum\limits_{i = 1}^{{N_i}} {{A_i}s(t - {\tau _i})} {e^{j\pi p\sin {\theta _i}}} + {n_{sur}}(t) \cr} $$
(2)
ECA算法将回波天线接收的信号投影到由基站直达波及其时延展开空间的正交子空间中,同时通过采用分段相消的方式,不仅可以消除零频的直达波和多径干扰,还能够消除零频附近的杂波。采样后的多目标回波与参考信号的距离-多普勒相关函数为
$${s_{sur}}(\tau ,{f_d}) = \sum\limits_{i = 1}^N {{G_i}} (\tau ,{f_d}){e^{j\pi p\sin {\theta _i}}} + {Q_p}(\tau ,{f_d})$$
(3)
波达方向的估计方法,以MUSIC(multiple signal classification)算法为代表的基于矩阵特征空间分解的方法突破了瑞利限,可以达到很高的精度。但是原型MUSIC算法以阵元间的噪声不相关为前提,如果阵元间的噪声具有空间相关性,尤其在这种相关性未知或无法估计的情况下,用MUSIC法得到的方向估计结果就很差。针对一个距离-多普勒包含多个目标情况,文献[9]提出的MUSIC-like方法,它利用了输出阵列的全部四阶累积量和子空间方法进行多于阵元个数的信号测向,但该方法需要进行解相干处理才能应用到相干信号上,信息冗余度和计算复杂度高。
由式(3)可以看出,对目标回波信号直达波和多径干扰进行抑制后,还包括需要抑制的其他回波旁瓣干扰,回波天线阵元数P与距离-多普勒目标个数N0满足P≥uN0ln(N/N0)时,即认为目标空间是稀疏的[13, 14],就可以通过稀疏重构以较少的计算获得多目标方向信息,式(3)的向量化处理可以表示为
$$y = vec({s_{sur - E}}(\tau ,{f_d})) = A\beta + n$$
(4)
\[\begin{align}
& \operatorname{minnimize}||\hat{\beta }|{{|}_{1}},{{s}_{\centerdot }}{{t}_{\centerdot }}||y-A\hat{\beta }||<\varepsilon \\
& ||Re(\hat{\beta }(i),\operatorname{Im}(\hat{\beta }(i))|{{|}_{2}}<{{b}_{i}} \\
\end{align}\]
(5)
\[\begin{align}
& \operatorname{minnimize}||\omega \hat{\beta }|{{|}_{1}},{{s}_{\centerdot }}{{t}_{\centerdot }}||y-A\hat{\beta }||<\varepsilon \\
& ||Re(\hat{\beta }(i),\operatorname{Im}(\hat{\beta }(i))|{{|}_{2}}<{{b}_{i}} \\
\end{align}\]
(6)
$${\omega _i} = \frac{{{\xi _1}{\xi _2}}}{{|{{\hat \beta }_i}| + {\xi _2}}}$$
(7)
算法首先采用ECA方法在零多普勒平面消除直达波和多径干扰,将直达波和多径干扰消除,再针对目标回波旁瓣和相关后噪声等干扰,在目标对应的距离-多普勒单元处进行基于压缩感知方位向稀疏重构,利用稀疏正则化方法,同时采用了改进加权L1范数约束稀疏表示模型,以较少的计算复杂度和较高的准确度进行单元内目标DOA的有效估计,具体算法流程为:
1)利用ECA算法根据式(4)构建矩阵A;
2)定义代价函数:$J(\hat \beta ) = ||y - A\hat \beta ||_2^2 + ||\omega \hat \beta |{|_1},\hat \beta = \arg \min (J(\hat \beta )){\text{ }}$;
3)初始化ω0、${{\hat \beta }^0}$、ξ1、ξ2,终止条件δ=0.01;
4)更新式(7)$\omega _i^{k + 1} = \frac{{{\xi _1}{\xi _2}}}{{|\hat \beta _{_i}^k| + {\xi _2}}}$代入式(6)求解${\hat \beta ^{k + 1}}$;
5)更新ξ1、ξ2;
6) k=k+1;
7)判断终止条件若k>K或$|J({{\hat \beta }^{k + 1}}) - ({{\hat \beta }^k})| < \delta $,迭代结束,否则转至4)。
利用迭代算法求解最优化的问题,迭代终止条件非常重要,本算法中利用对偶空隙,因为对偶理论和方法是最优化的基本工具,也是内容最丰富、应用最广泛的松弛方法之一,即原问题与对偶问题之差来判断算法是否达到收敛。在求解迭代搜索方向时,首先获得代价函数J的梯度向量和海塞矩阵利用牛顿迭代法求解每一步的迭代方向。根据迭代方向,最后利用线性回波搜索的方法求解最优迭代步长。
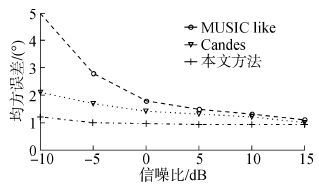
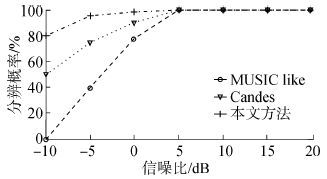
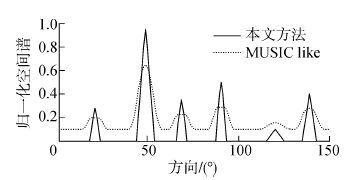
4 仿真及复杂度分析构造GPS信号作为辐射源,8路多径干扰都分布在0~20 km距离内,干噪比为0~30 dB,直达波干扰的干噪比为50 dB,4个目标的距离、多普勒频移、DOA和信噪比为:(20 km,1 MHz,20°,-8.04 dB),(40 km,3 MHz,50°,-10.07 dB),(70 km,2 MHz,80°,-17.28 dB),(80 km,-2 MHz,100°,-23.92 dB)。未抑制干扰前回波信号与参考信号相干累积的距离-多普勒相关图如图2所示。此时无法输出目标回波,对接收信号在0~100 km采用ECA算法抑制直达波和多径干扰进行相干累积得到目标位置等高线如图3所示,可以检测出部分目标。图4是DOA的估计结果,可见经过本文方法处理后,能检测出全部目标。图5是均方根误差随信噪比变化曲线,从DOA估计的经典MUSIC-like方法入手,进而分析稀疏理论Candes方法与本文方法,可以看出在低信噪比条件下,本文方法和Candes方法都具有较高的估计精度,性能优于MUSIC-like算法。图6是分辨概率随信噪比的变化曲线,可以看出本文的分辨率高于Candes方法和MUSIC-like算法。图7是目标个数多于阵元数的DOA估计,针对20°、50°、70°、90°、120°和140°六个信号源的四阵元阵列,对比本文方法和MUSIC-like算法的空间谱,可以看出两种方法都能进行多于阵元数的DOA估计,而本文方法检测目标的精准度较高。
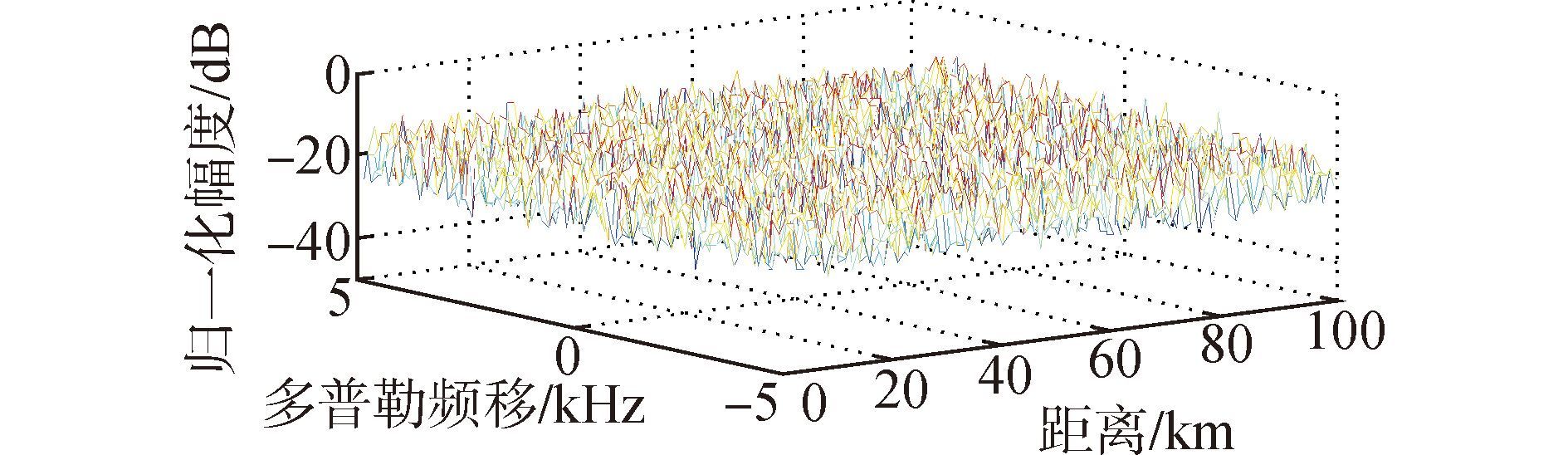
|
| 图2 抑制前二维相关 Fig.2 2D correlation before cancellation |
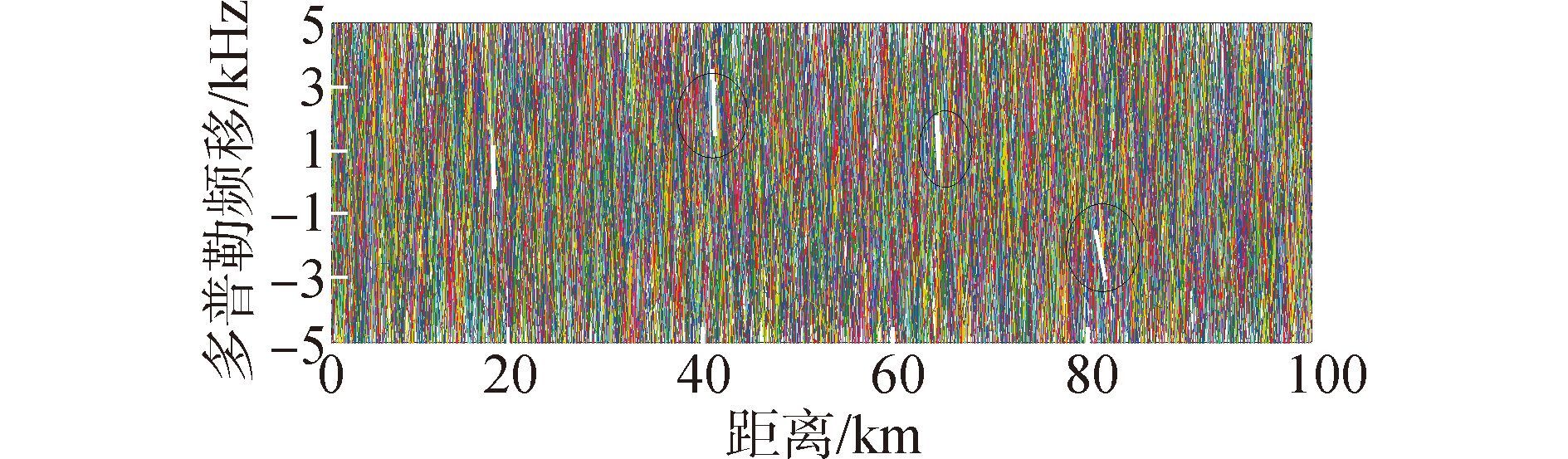
|
| 图3 ECA抑制后的二维相关 Fig.3 2D correlation after ECA |
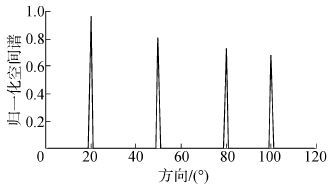
|
| 图4 DOA 估计 Fig.4 DOA estimation |
|
| 图5 均方误差变化曲线 Fig.5 Mean square error curves |
|
| 图6 分辨概率变化曲线 Fig.6 Resolution probability curves |
|
| 图7 多信号源DOA 估计 Fig.7 Multi signal source DOA estimation |
假设M元天线阵列接收了L次快拍,在式(3)ECA算法中需要进行若干次乘法和加法,其复杂度为O(L),式(4)的计算复杂度为O(M2),而长度N的稀疏重构部分复杂度为O(N3logN),所以文本算法的总复杂度为O(LM2+N3logN),而MUSIC-like方法的L次快拍四阶累积量为O(LM4),矩阵特征值分解的复杂度为O(NM2),所以其总复杂度为O(M10+LM4+NM4)。由此可见,当过完备字典长度N不过大,即回波天线阵元数P与距离-多普勒目标个数N0满足P≥uN0ln(N/N0)时,本文方法的计算复杂度优势明显,表1给出了计算复杂度和计算时间对比,可以看出由于使用了稀疏模型,本文方法的计算量和计算复杂度明显降低。
| 算法 | 计算时间/s | 计算复杂度 |
| 本文方法 | 0.75 | O(LM3+N3logN) |
| MUSIC-like方法 | 1.93 | O(M10+LM4+NM4) |
本文讨论GPS辐射源的多目标DOA估计问题,通过分析外辐射源雷达的干扰因素,得到了利用稀疏模型估计DOA的方法,得到如下结论:
1) 采用ECA和L1范式稀疏重构方法,抑制8路信噪比为-25 dB以内的多径干扰信号,可准确检测0~20 km距离的回波信号。
2)该方法以天线阵元满足稀疏完备字典为前提,在降低计算复杂度的同时提高准确度。
基于本文结论,下一阶段的研究重点在于多辐射源的组网联合探测问题,目标检测、跟踪、识别问题,以及快速高效的稀疏分解算法研究。
| [1] | TUYSUZ B, URBINA J, LIND D. Development of a passive VHF radar system using software-defined radio for equatorial plasma instability studies[J]. Radio science, 2013, 48(4): 416-426. |
| [2] | JIN Wei, LYU Xiaode, XIANG Maosheng. Research on performance influence of direct-path signal for DVB-S based passive radar[J]. Journal of electronics (China), 2013, 30(2): 111-117. |
| [3] | 何德波, 汪学刚. 一种基于GPS信号的外辐射源雷达目标定位研究[J]. 全球定位系统, 2011, 36(4): 19-22, 28. HE Debo, WANG Xuegang. A study on passive radar target location using GPS singal[J]. GNSS world of China, 2011, 36(4): 19-22, 28. |
| [4] | 万莉莉, 左伟华. 基于GPS无源雷达干扰抑制研究[J]. 电子设计工程, 2011, 19(8): 103-105, 109. WAN Lili, ZUO Weihua. Research on interference mitigation of GPS-based passive radar[J]. Electronic design engineering, 2011, 19(8): 103-105, 109. |
| [5] | 王伟, 李强, 徐定杰, 等. 一种矢量跟踪环路及其抗干扰性能分析[J]. 电子与信息学报, 2013, 35(7): 1581-1586.WANG Wei, LI Qiang, XU Dingjie, et al. A Design Method and anti-jamming performance analysis for vector tracking loop[J]. Journal of electronics & information technology, 2013, 35(7): 1581-1586. |
| [6] | 胡毅, 宋茂忠, 孟斌. 一种基于压缩采样与相关幅值估计的GPS抗多径方法[J]. 电子与信息学报, 2013, 35(12): 2889-2895.HU Yi, SONG Maozhong, MENG Bin. A method for GPS multipath mitigation based on the compressed sampling and the auto-correlation function amplitude estimation[J]. Journal of electronics & information technology, 2013, 35(12): 2889-2895. |
| [7] | COLONE F, O'HAGAN D W, LOMBARDO P, et al. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar[J]. IEEE transactions on aerospace and electronic systems, 2009, 45(2): 698-722. |
| [8] | CHALISE B K, ZHANG Y D, AMIN M G, et al. Target localization in a multi-static passive radar system through convex optimization[J]. Signal processing, 2014, 102: 207-215. |
| [9] | WANG Jun, WANG Haitao, ZHAO Yong. Direction finding in frequency-modulated-based passive bistatic radar with a four-element Adcock antenna array[J]. IET radar, sonar & navigation, 2011, 5(8): 807-813. |
| [10] | LIU Wei, XU Yougen, LIU Zhiwen. DOA estimation of coexisted noncoherent and coherent signals via sparse representation of cleaned array covariance matrix[J]. Journal of Beijing institute of technology, 2013, 22(2): 241-245. |
| [11] | 王德周, 李耀民. 基于GPS技术辅助雷达引导系统设计[J]. 计算机测量与控制, 2013, 21(1): 139-141.WANG Dezhou, LI Yaomin. Design of radar guidance system based on GPS[J]. Computer measurement & control, 2013, 21(1): 139-141. |
| [12] | 沈方芳, 李雅祥, 赵光辉, 等. 双基地MIMO雷达高分辨角度估计[J]. 西安电子科技大学学报: 自然科学版, 2013, 40(5): 33-37, 106.SHEN Fangfang, LI Yaxiang, ZHAO Guanghui, et al. High resolution angle estimation of the bistatic MIMO radar[J]. Journal of Xidian University: natural science edition, 2013, 40(5): 33-37, 106. |
| [13] | CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE transactions on information theory, 2006, 52(2): 489-509. |
| [14] | QI Chenhao, WU Lenan. A study of deterministic pilot allocation for sparse channel estimation in OFDM systems[J]. IEEE communications letters, 2012, 16(5): 742-744. |
| [15] | CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE signal processing magazine, 2008, 25(2): 21-30. |
| [16] | LIANG Jing, LIANG Qilian. Design and analysis of distributed radar sensor networks parallel and distributed systems[J]. IEEE transactions on parallel and distributed systems, 2011, 22(11): 1926-1933. |



