混沌是非线性科学研究的重要课题,国内外学者围绕混沌的应用、控制和识别等问题开展了广泛的研究[1]。但是,由于受到测量工具以及外界环境等影响,实际采集到的混沌信号不可避免地混有噪声,掩盖了混沌信号的真实动力学行为,并且混沌复杂的动力学行为使其具有功率谱宽带性和似噪声性,其频带与叠加的噪声频带往往全部或部分重叠,传统的线性降噪方法很难实现有效滤波,甚至会严重歪曲干净的混沌信号[2]。
小波变换具有时频局部化、多分辨率、解相关等特点,因而被广泛应用在信号降噪等领域[3]。其中,小波阈值去噪方法[4]由于实现简单、计算量小等特点,应用最为广泛。但小波阈值去噪方法虽能够有效地去除混沌信号中的白噪声,却对脉冲噪声的抑制效果不明显[5],并且利用小波阈值去噪时需考虑以下三方面的影响:最优小波基函数的选取,小波分解层数的确定,阈值函数的确定。在小波基选取问题上,大部分方法需要信号的先验信息,并易忽视信号与小波基的相似性[6, 7, 8, 9];针对分解层数的确定,最常用的方法是基于高频分量的噪声分布检验,然而去相关白化检验对大样本事件比较适用,小波系数的个数Nj=N/2j随分解层数成指数下降,故高尺度的小波系数数量达不到精度的最低要求,会直接影响对总体的正确判断[10]。
结合以上,本文从小波基函数、分解层数和阈值处理三方面对原始的小波降噪方法进行改进,并建立改进小波和S-G混合降噪模型。利用所提方法对含噪声的Lorenz混沌时间序列及实测机械式混沌振动信号进行了去噪分析,结果表明所提方法能非常有效地滤除混沌信号中的白噪声和脉冲噪声。
1 小波去噪及改进方法 1.1 小波去噪方法混沌信号去噪的目的是从含噪信号x(t)中提取干净信号s(t),设x(t)=s(t)+w(t),w(t)为噪声信号。
小波变换是一种线性变换,因此含噪信号x(t)经小波分解后的小波系数模型可以表示为
| $x\left( i \right) = s\left( i \right) + w\left( i \right)$ | (1) |
式中:x(i)、s(i)、w(i)分别为含噪信号、干净信号以及噪声信号的小波系数。
小波阈值去噪算法的主要思想是:在不同小波分解尺度上选择一个合适的阈值,绝对值小于该阈值的小波系数认为是噪声引起的,将其置零,而绝对值大于该阈值的认为是由信号引起的,予以保留,通过阈值函数的映射,得到小波系数的估计,最后利用二进离散小波逆变换,对保留的小波系数进行重构达到去噪目的。
1.2 最优小波函数的选取小波熵是小波变换与表达系统复杂度信息熵理论融合的产物,能够对时频域上能量分布特性进行定量描述。可以度量系统的未知程度,因而特别适用于混沌系统未知的情况,实际应用性强[11]。为了能同时兼顾第j层近似信号的能量损失最小,本文将小波变换和能量对数熵进行融合,以第j层和第j-1层近似信号的小波能量对数熵Ej(ψX)绝对值比值最大为依据,选择最优小波基。
由于第j层小波分解近似信号小波能量对数熵Ej(ψX)是用其小波系数计算,这需要考虑第一层最优小波基的选择问题。根据能量守恒性质有[12]
| $\sum\limits_{i = 1}^N {{{\left| {\left\langle {X,{\psi _{i,j}}\left( t \right)} \right\rangle } \right|}^2}} = {\left\| X \right\|^2}$ | (2) |
因此,原始信号X的能量对数熵可表示为
| ${E_0} = - \sum\limits_i^N {\lg {{\left| {{x_i}} \right|}^2}} $ | (3) |
式中:xi为原始信号第i分量,N为信号长度。
尺度j下的小波低频分量的能量对数熵Ej为
| ${E_j} = - \sum\limits_i^N {\lg {{\left| {{a_{ij}}} \right|}^2}} $ | (4) |
式中:aij为尺度j下的第i个小波低频分量的小波系数,n为低频分量长度。
第j层近似信号的小波能量对数熵Ej和第j-1层近似信号小波能量对数熵Ej-1的绝对值比值可以表示为
| ${e_j}\left| {{E_j}} \right|/\left| {{E_{j - 1}}} \right|\;\;\;\;\;\;j = 1,2,\ldots ,J$ | (5) |
式中:J为分解总层数。
由于小波基函数种类繁多,经过大量仿真实验分析,混沌信号经小波分解需满足精确重构、能量集中、局部化能力强和计算复杂程度低等要求,因此选用正交紧支集函数Daubechies(dbN)和Symlets(symN)小波函数库为选择对象,以提高最优小波基的选择速度。为了克服传统单一选择小波基处理复杂信号的局限性,本文利用逐层确定最优小波的方法,即从一簇小波中选取各层最优的小波,以达到自适应选择最佳小波基函数的目的。
1.3 小波分解层数的确定文献[13]指出:含噪信号经小波分解,随分解尺度的增加,有用信号的小波系数增大,噪声的小波系数减小。因此当有用信号在高频分量中占主要成分时,其样本极差会发生跃变,此时高频分量中信号的小波系数高能量、高幅值的特性显现出来,并且随着小波分解层数的增加越发明显。为了尽可能保留高频分量中有用信号的特征,所以选择发生跃变点为最佳分解层数。
设Xj =(x1,x2,…,xn)是j尺度高频分量的小波系数样本,则其样本极差可以表示为
| ${R_j} = _{1 \le i,j \le n}^{\;\;\;\max }\left| {{x_i} - {x_j}} \right|$ | (6) |
由式(6)可以看出,样本极差的观测值是样本中最大值和最小值之差,是反映观测值分散程度的数量指标。在机械振动信号采集过程中,通常受到脉冲噪声的干扰,而脉冲噪声的小波系数较大,会直接影响高频分量极差的计算。为了减小这种不确定干扰,对j尺度高频分量的小波系数进行排序,求最大的k个分量和最小的k分量的均值,记为xmax、xmin,根据大量仿真实验分析,k值不宜过大,否则样本极差曲线经过平均处理后为一条接近于零的直线。则样本极差可以表示为
| ${R_j} = {x_{\max }} - {x_{\min }}$ | (7) |
S-G滤波算法是一种移动窗口的加权平均算法,其加权系数是通过在移动窗口内对给定高阶多项式的最小二乘拟合得出[14]。对于信号{x1,x2,…,xn},点xi的光滑数值gi是由xi附近固定个数的点通过多项式拟合得出。用nl、nr分别表示xi左边、右边点的个数,pi(x)表示相对于点xi的一个M次多项式,用其在最小二乘意义下拟合nl+nr+1个点,因此
| ${g_i} = \sum\limits_m^M {{b_m}} \left( {\frac{{x - {x_i}}}{{\Delta x}}} \right)m$ | (8) |
假设横坐标xi具有xi+1-xi≡Δx的均匀间距。设实测数据为yi,为了使用pi(x)拟合测试数据,必须定义系数bm,使下式达到最优:
| $\min {\sum\limits_{i = 1}^{i + {n_r}} {\left[{{p_i}\left( {{x_j} - {y_j}} \right)} \right]} ^2}$ | (9) |
由于S-G平滑滤波算法可以有效平滑信号中的脉冲噪声[15],因此,本文利用S-G平滑滤波算法对第1~J尺度的高频系数进行平滑处理,以降低高频系数中的脉冲噪声。然而,S-G平滑滤波算法在去除高频系数的脉冲噪声的同时也会导致高频系数中部分有用信号的流失。文献[16]提出了对高频系数做加权处理的方法,可以减少部分有用信号细节的流失,为了更合理地降低脉冲噪声和白噪声,本文利用噪声分量随分解层数增加而递减的关系这一特性对文献[16]的加权方法按下式
| $\bar s = \frac{{s + \hat s\left( {J - i + 1} \right)}}{{J - i + 2}}$ | (10) |
加以改进,高频系数经式(10)处理后,不仅可以有效地降低高频系数中的脉冲噪声,而且可以恢复大部分有用信号。最后对1~J尺度平滑和加权处理后的高频系数进行阈值处理。
鉴于通用阈值在实际应用中效果并不理想,会产生过扼杀现象。本文采用Penalty阈值[17]对高频系数进行处理。
改进的小波去噪算法的具体步骤是:
1)计算原始信号X={x1,x2,…,xN}的能量对数熵E0;
2)从基小波库中选择基小波ψ={ψ1,ψ2,…,ψn},将原始信号X进行一层小波分解,计算低频系数的小波能量对数熵E1;
3)计算e=E1/E0;
4)从基小波库中选择另一基小波,重复步骤1~3,计算低频系数的小波能量对数熵{E1,E2,…,En},并且计算相应的{e1,e2,…,en},选用最大的e值对应的基小波作为第一层分解的最优小波对信号进行分解,分解后的低频系数记为A1,高频系数记为D1;
5)计算高频系数D1的样本极差记为R1;
6)重复步骤1~5,计算高频系数极差并绘制曲线图,根据样本极差曲线图第一次出现跃变点为最佳分解层数,记为J。则第J层小波分解的低频系数记为AJ,第1~J层小波分解的高频系数记为{D1,D2,…,DJ};
7)对各层高频系数用SG滤波算法进行平滑处理,并对平滑处理后的高频系数按式(10)处理。
8)对经步骤7处理后的高频系数进行阈值量化处理;
9)重构信号。
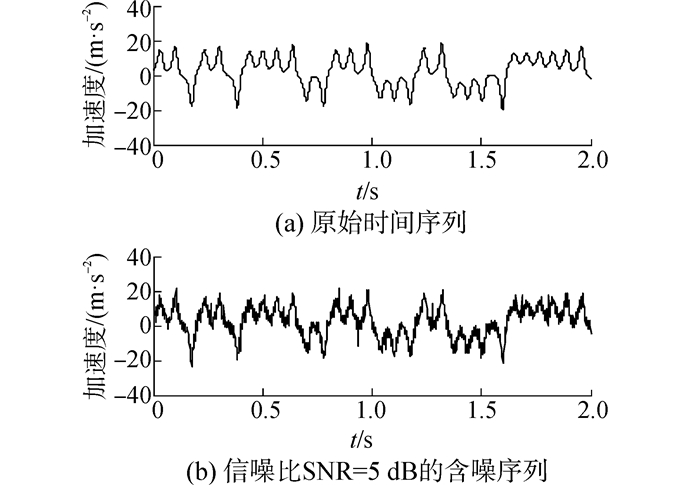
2 仿真实验实验信号为Lorenz方程产生的混沌信号,如图 1所示,脉冲噪声由Matlab的gauspuls函数叠加。
|
| 图 1 Lorenz时间序列图 Fig. 1 Lorenz time series |
经大量实验证实,db2~20和sym2~8基小波去噪效果好,效率高,一个完整的去噪过程只需0.098 14 s左右。因此,本文以db2~20和sym2~8为基小波库,含噪Lorenz时间序列的3层小波分解低频信号的小波能量对数熵比值见表 1,并以sym8和db5小波为单一基小波和逐层最优基小波作对比分析,逐层最优基小波依次为db8、db15、db16。由表 1可以看出,与单一小波分解结果相比,选用逐层最优小波基对信号进行去噪,去噪后信号的信噪比最大,均方误差最小,显示了逐层选择最优小波基的优越性。
| sym8 | db5 | 逐层最优小波/基小波 | |
| 尺度1 | 0.592 5 | 0.596 7 | 0.616 6/db8 |
| 尺度2 | 0.599 2 | 0.594 4 | 0.605 0/db15 |
| 尺度3 | 0.578 1 | 0.570 4 | 0.616 4/db16 |
| 信噪比 | 19.234 2 | 18.937 3 | 20.037 9 |
| 均方差 | 0.935 6 | 1.001 8 | 0.777 5 |
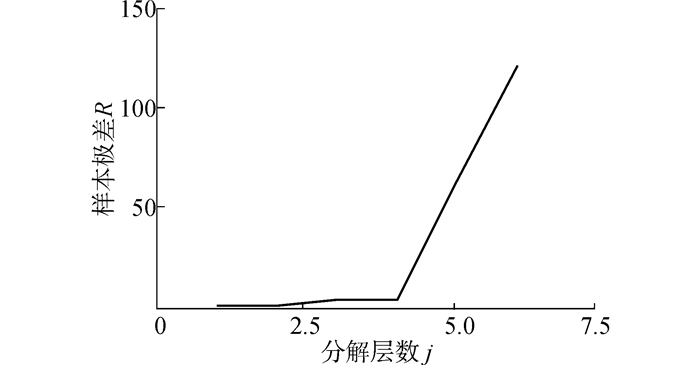
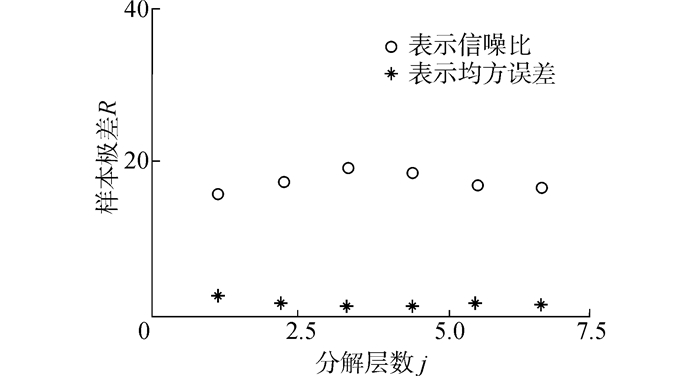
对信噪比为5 dB的Lorenz混沌序列利用sym8小波进行6尺度小波分解,样本长度为2 000。考虑到高频分量样本数随着尺度的增大成指数减少,所以本文取k1=100,k2=50,k3=25,k4=k5=k6=10。其高频分量的样本极差和分解层数的关系如图 2所示,从第3层到第4层极差发生跃变,此时高频分量中信号的小波系数高能量、高幅值的特性显现出来,所以选择最佳分解层数为4。图 3为分解层数J和阈值处理后信号的信噪比和均方误差的关系,可以看出分解层数为4时,去噪后信号的信噪比最大,均方误差最小,并且分解层数的不同,信噪比和均方误差差别很大。
|
| 图 2 R与j关系图 Fig. 2 Relationship of R and j |
|
| 图 3 不同分解层数降噪效果对比 Fig. 3 Denoising effect comparison of different decomposition levels |
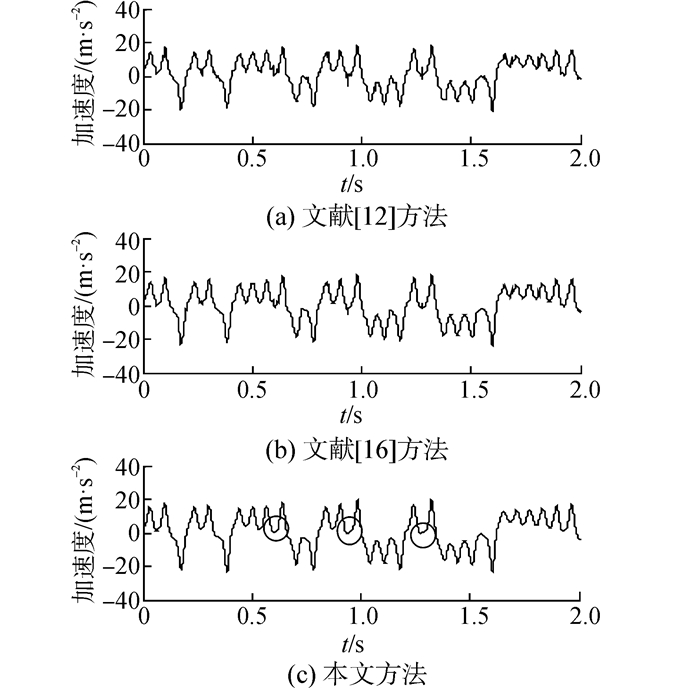
本文从信噪比(SNR)和均方误差(MSE)对文献[12, 16]和本文方法的降噪效果进行评价。3种方法去噪后的时间序列图如图 4所示。去噪后信号的信噪比及均方误差如表 2所示。
|
| 图 4 3种方法的去噪结果比较图 Fig. 4 Denoising results comparison diagrams of the three methods above |
由图 4和图 1(a)比较可以看出,文献[12]方法(图 4(a))仅是提升对白噪声的抑制能力,脉冲噪声残余还较多;文献[16] 方法(图 4(b))对阈值处理后的信号和原信号加权再处理对白噪声和脉冲噪声只是起削弱作用,并不能完全剔除;而本文方法(图 4(c))降噪后的Lorenz时间序列图更接近于原信号,图 4(c)中圆圈标注处,脉冲噪声明显得到抑制。从表 2可知,本文方法降噪后的信噪比最大,而均方误差最小,进一步显示了所提方法的优越性。
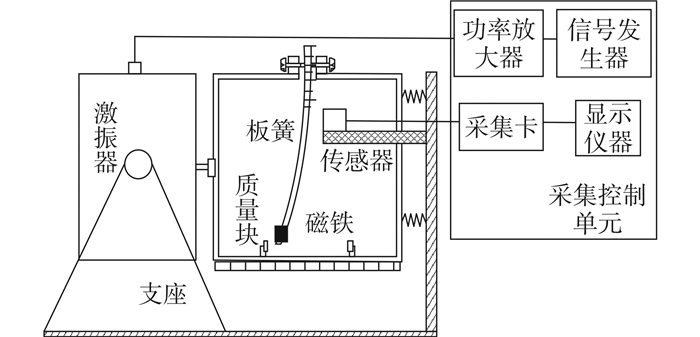
2.4 实测机械式混沌振动信号处理为了进一步验证本文所提方法对于模型未知的混沌信号的去噪效果,本文基于双势阱理论的单端磁吸式混沌振动试验装置产生的振动信号为对象,双势阱单端磁吸式混沌振动装置如图 5所示,装置由如下部分组成:激振器、支座、板簧、磁铁、质量块。
|
| 图 5 双势阱单端磁吸式混沌振动装置 Fig. 5 The chaotic vibration experimental rig of two-well potential single end magnetic |
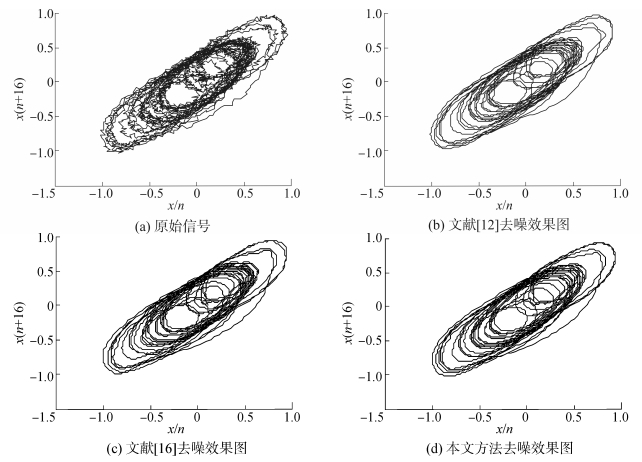
实验本质为正弦信号的慢速频率扫描实验,扫描频率范围为5~25 Hz,采样频率为2 kHz,数据采集时长为5 s。调节功率放大器增益为1、激励频率为13 Hz时,重构相空间参数中嵌入维数为4,延迟时间为16,得到的重构相图如图 6(a)所示。分别使用文献[12]、[16]以及本文方法对原始信号进行降噪处理,去噪后的二维相图如图 6(b)、(c)、(d)所示,通过比较可以看出,本文方法降噪后的二维相图曲线更加光滑,更能清晰地展现原信号吸引子的几何结构。由于原始信号为机械式振动信号,其信号和噪声未知,不能利用信噪比和均方误差进行定量比较,但是对于混沌信号,其自相关函数值比较大,且远远大于噪声的自相关函数值[18],因此可以用3种方法去噪后的自相关函数值评价去噪效果。
|
| 图 6 振动信号去噪前后二维相图 Fig. 6 The two-dimensional phase diagrams of noisy and denoised vibration signals |
自相关函数的定义如下:
${R_{xcorr}}\left( \tau \right) = \frac{1}{{N - \tau }}\sum\limits_{n = 1}^{N - \tau } {x\left( n \right)x\left( {n + \tau } \right)} $
式中:τ表示延迟,N为信号长度。
3种方法去噪前后的部分自相关函数值如表 3所示,可以看出,原始信号受到噪声的干扰,其自相关函数值相比去噪后要小很多,而本文所提方法降噪后序列的自相关函数值最大,进一步展现了其降噪的优越性。
改进小波和SG混沌信号去噪方法的时间花费主要分成2大部分:
1)基小波簇中选取基小波对信号进行分解的时间开销。由1.1和1.2节中小波分解和基小波选择方法可知,原始信号需进行N+M次分解,N、M分别为db和sym小波簇个数;对分解得到的低频小波系数和原始信号进行(N+M)次小波对数能量熵的计算,然后选择e最大值对应的基小波为最优基小波,对于e的计算和排序次数和小波需要分解的层数一致,由最优基小波分解得到的低频小波系数重复1.4节的算法步骤2~4,设小波分解层数为J,则分解得到的低频小波系数为AJ、高频小波系数D1,D2,…,DJ。设小波进行一次分解的时间为Δt1,小波对数能量熵的计算时间为Δt2,计算e值大小并进行排序处理的时间消耗为Δt3,则总的时间消耗为[(N+M)(Δt1+Δt2)+ Δt3](J+1)。
2)对分解得到的小波高频系数处理的时间开销。由1.4节的算法步骤5~8可知,对分解得到的小波高频系数主要进行4个方面的处理:计算样本极差、SG滤波、加权处理、阈值处理,设这4个部分的时间消耗分别为Δt4、Δt5、Δt6、Δt7。计算样本极差是为了确定分解层数J,根据2.2节分析,若样本极差突然变大,则选择上一次分解层数为总分解层数,所以小波需要分解的次数应为(J+1),也就是样本极差的计算次数,而SG滤波、加权处理和阈值处理仅需进行J次即可。所以小波高频系数处理总的时间开销为Δt4(J+1)+( Δt5+Δt6+Δt7)J。
因此,利用本文方法对混沌信号进行去噪时,总的时间开销约为
$\begin{array}{l} T \approx \left[{\left( {N + M} \right)\left( {\Delta {t_1} + \Delta {t_2}} \right) + \Delta {t_3} + \Delta {t_4}} \right]\left( {J + 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\Delta {t_5} + \Delta {t_6} + \Delta {t_7}} \right)J \end{array}$
本文仿真实验中,由2.1、2.2可知N=19,M=7,J=4,实验运行环境为MATLAB 7.9.0,PC机内存为2 G,CPU主频为3.06 GHz,Lorenz时间序列的长度为2 000,使用MATLAB中的时耗运算方法计算出仿真实验的总时间开销约为1.277 5 s,对于长度为3 900的实测混沌振动信号去噪的时间开销约为1.732 5 s。
3 结论针对小波阈值法在混沌信号去噪中存在的不足,分别从小波基选取、分解层数和阈值处理三方面对原始小波降噪方法进行改进,并结合S-G滤波算法的消除脉冲噪声的能力,建立小波-S-G去噪模型,分别对Lorenz混沌时间序列及实测双势阱机械式混沌振动信号进行了去噪分析,结果表明:
1)对已知的混沌系统,如Lorenz混沌时间序列,所提方法相比其他降噪方法能提高信号信噪比近1 dB。
2)对未知的实测混沌信号,所提方法能将信号自相关函数提高近0.01,表明对于有或无先验知识的混沌振动信号,所提方法都有较好的降噪效果,具有广泛的应用前景。
| [1] | NEACSU C, CHESARU V, DAN C, et al. An autonomous chaos generator using oscillator structure[C]//Proceedings of International Semiconductor Conference (CAS). Sinaia: IEEE, 2011, 2: 431-434. |
| [2] | LIM T P, PUTHUSSERYPADY S. Chaotic time series prediction and additive white Gaussian noise[J]. Physics letters A, 2007, 365(4): 309-314. |
| [3] | SAN EMETERIO J L, RODRIGUEZ-HERNANDEZ M A. Wavelet denoising of ultrasonic A-scans for detection of weak signals[C]//Proceedings of the 19th International Conference on Systems, Signals and Image Processing. Vienna: IEEE, 2012: 48-51. |
| [4] | LIU Lei, YU Miao, YANG Ruijuan, et al. Wavelet denoising applied in optical fiber Raman temperature sensor system[J]. Chinese journal of lasers, 2013, 40(6): 1-5. |
| [5] |
滕军, 朱焰煌, 周峰, 等. 自适应分解层数的小波域中值滤波振动信号降噪法[J]. 振动与冲击, 2009, 28(12): 58-62. TENG Jun, ZHU Yanhuang, ZHOU Feng, et al. Vibration signal denoising method based on median filter in wavelet domain with self-adaptive level decomposition[J]. Journal of vibration and shock, 2009, 28(12): 58-62. |
| [6] |
李月琴, 栗苹, 闫晓鹏, 等. 无线电引信信号去噪的最优小波基选择[J]. 北京理工大学学报, 2008, 28(8): 723-726. LI Yueqin, LI Ping, YAN Xiaopeng, et al. Selection of optimal wavelet basis for radio fuze signal denoising[J]. Transactions of Beijing institute of technology, 2008, 28(8): 723-726. |
| [7] |
张华, 陈小宏, 杨海燕. 地震信号去噪的最优小波基选取方法[J]. 石油地球物理勘探, 2011, 46(1): 70-75. ZHANG Hua, CHEN Xiaohong, YANG Haiyan. Optimistic wavelet basis selection in seismic signal noise elimination[J]. Oil geophysical prospecting, 2011, 46(1): 70-75. |
| [8] |
李剑, 杨洋, 程昌奎, 等. 变压器局部放电监测逐层最优小波去噪算法[J]. 高压电技术, 2007, 33(8): 56-60. LI Jian, YANG Yang, CHENG Changkui, et al. Optimum wavelet denoising algorithm for partial discharge online monitoring of transformers[J]. High voltage engineering, 2007, 33(8): 56-60. |
| [9] |
李化, 杨新春, 李剑, 等. 基于小波分解尺度系数能量最大原则的GIS局部放电超高频信号自适应小波去噪[J]. 电工技术学报, 2012, 27(5): 84-91. LI Hua, YANG Xinchun, LI Jian, et al. The maximum energy of wavelet decomposition approximation related adaptive wavelet denoising for partial discharge UHF pulse in GIS[J]. Transactions of China electrotechnical society, 2012, 27(5): 84-91. |
| [10] |
杜文辽, 朱茹敏, 李彦明. 小波滤波分解层数的自适应确定方法[J]. 光电子·激光, 2010, 21(9): 1408-1411. DU Wenliao, ZHU Rumin, LI Yanming. Adaptive selection of optimal decomposition level in filtering algorithm based on wavelet transform[J]. Journal of optoelectronics · laser, 2010, 21(9): 1408-1411. |
| [11] | MIIKKA E. Methods for the classification of biosignals applied to the detection of epileptiform waveforms and to the recognition of physical activity[D]. Tampere: Tampere University of Technology, 2009. |
| [12] |
李文, 刘霞, 段玉波, 等. 基于小波熵和相关性的高分辨率阈值去噪方法[J]. 数据采集与处理, 2013, 28(3): 371-375. LI Wen, LIU Xia, DUAN Yubo, et al. High-resolutiont threshold denoising method based on wavelet entropy and correlation[J]. Journal of data acquisition and processing, 2013, 28(3): 371-375. |
| [13] | YAQUB M F, GONDAL I, KAMRUZZAMAN J. Resonant frequency band estimation using adaptive wavelet decomposition level selection[C]//Proceedings of the 2011 International Conference on Mechatronics and Automation. Beijing: IEEE, 2011: 376-381. |
| [14] | JIANG Shubo, LIN Jinhuo. Octane number detection based on Raman spectra[C]//Proceedings of International Conference on Electrical and Control Engineering. Wuhan: IEEE, 2010: 5365-5368. |
| [15] | ZHOU Zengguang, TANG Ping. VI-quality-based Savitzky-Golay method for filtering time series data[J]. Remote sensing technology and application, 2013, 28(2): 232-239. |
| [16] |
位秀雷, 林瑞霖, 刘树勇, 等. 基于改进小波变换方法的混沌信号去噪研究[J]. 武汉理工大学学报: 交通科学与工程版, 2013, 37(5): 1062-1065. WEI Xiulei, LIN Ruilin, LIU Shuyong, et al. Denoising for chaotic signal based on an improved wavelet transform method[J]. Journal of Wuhan university of technology: transportation science & engineering, 2013, 37(5): 1062-1065. |
| [17] | STARK A J, HSUEH Y T, SEARCY S, et al. Scaling 112 Gb/s optical networks with the nonlinear threshold metric[J]. Journal of lightwave technology, 2012, 30(9): 1291-1298. |
| [18] |
刘云侠, 杨国诗, 贾群. 基于双提升小波的自适应混沌信号降噪[J]. 电子学报, 2011, 39(1): 13-17. LIU Yunxia, YANG Guoshi, JIA Qun. Adaptive noise reduction for chaotic signals based on dual-lifting wavelet transform[J]. Acta electronica sinica, 2011, 39(1): 13-17. |



