船舶分段堆场是为了协调船舶生产过程中由于生产和管理的原因造成分段在不同加工工序之间无法即时周转的问题用于临时存放分段的场所。分段通过舾装、喷漆等工艺处理后运输至堆场进行预处理作业(预舾装、检验和修补等)或暂存等待后续的加工作业。由于分段体积和重量都十分庞大,无法进行垂直方向上的吊运,因此只能通过平板车进行平面方向上的运输,并且平板车一次只能运输一个船舶分段。在船舶堆场调度操作过程中,根据作业流程可分成3种分段:进场分段、出场分段和临时阻挡分段。对于进场分段需要安排一个空的存储单元和一条可行的路径,对于出场分段则需要规划一条可行的路径,而在分段进出堆场的路径上会遇到挡道的分段,需要先将挡道的分段临时移至空地,待平板车运输完目标分段后,挡道分段可重回原位、重新选位或移至临时暂存场所。这些操作对于堆场调度来说都是非增值操作,因此在分段移动中临时阻挡分段的数量是影响移动路径优劣的重要因素。此外,还有其他很多因素也会对移动路径的优劣产生影响,如分段的几何属性,因此如何设定一个较为合理、综合的移动路径评价指标尤为重要。
国内外针对船舶分段堆场调度问题的研究较少。Changkyu等以临时分段移动数量最少为目标建立优化模型,并运用遗传算法和改进动态启发式算法对模型进行求解[1, 2]。然而该优化模型是在假定堆场场地固化的生产环境中建立,限定分段在堆场中的移动路径和移动方向,导致分段只能按直线进出堆场,大大增加了临时分段的移动量。Tao等[3]在此基础上考虑了分段进出堆场的任务顺序对调度方案的影响,并运用启发式算法和禁忌搜索对结果进行优化。申钢等[4]以最小化临时分段移动量和平板车在堆场中的行驶距离为优化目标建立优化模型,并运用分支定界法和启发式规则来确定分段的移动路径和停放位置。徐建祥等[5]提出临时场地用于暂时存放临时移动分段,采用改进遗传算法选择分段在堆场中停放位置的最优方案,并构建启发式规则来确定分段在堆场中的最优进、出场路径。但上述研究对分段堆场调度方案的评价因素单一,并且假设分段堆场的场外道路确定且唯一,脱离了船舶生产的实际情况。
除了临时阻挡分段数量这一影响因素,本文还考虑了平板车转向次数和移动距离对移动路径选择的影响,并确定了较为全面的评价指标,以综合移动难度为优化目标,利用智能算法和启发式规则建立分段堆场调度优化模型。确定分段在堆场中最佳的停放位置,规划进、出场平板车最优的移动路径,合理的安排出场任务的顺序,从而提高堆场的运作效率。论文还对堆场的尺寸规格、道路开放程度和初始负载率进行对比优化,提高了对堆场资源的利用率,并用某船厂的实际数据对模型进行验证。
1 问题描述与解决方法 1.1 问题描述平板车是船厂中最主要的运输工具,作为中间产品的分段在各个生产车间和分段堆场间的运输都依赖于它。常用的平板车是一种具有液压提升装置,有65个轮子的特殊车辆[6]。它通过液压装置将分段提升,通过堆场中的可行路径,将分段移动至目标存储单元并放置支撑杆上。除了提升、移动和放置,转向也是平板车在堆场中的重要操作,通过转向可以避开挡道分段较多的路径,从而有效降低临时阻挡分段的数量,但转向对于体型庞大的平板车在空间有限的堆场道路上是十分不易的,因此,有必要将平板车的转向次数这一指标加入平板车移动路径优劣的评价标准之中。
船舶分段存在紧前、紧后的搭载顺序,因此这些分段的出场顺序需要满足一定的先后顺序,而有些分段出场时间是柔性的,因此对于具有柔性出场时间的分段,可以根据其所在的堆场位置选择适当的出场时间,从而对分段的调度方案进行优化。
考虑到堆场运作的实际情况和研究问题的方便,本文作了以下的假设:1)船舶分段堆场由若干个面积相等的正方形场地组成,每个正方形场地为一个存储单元;2)分段用最小包络矩形近似;3)一个存储单元只能存放一个分段;4)存储单元能容下各种不同形状的分段;5)每天分段的出场任务优先于进场任务;每日出场分段除具有紧前、紧后关系的分段,其他的分段出场顺序可随意调整。
要解决的问题有:1)为进场分段分配一个合适的存储单元;2)为进出场分段确定一条最优的移动路径;3)确定同一天出场各个分段之间的调度顺序。
1.2 解决方法本文针对以上问题,首先制定一个同时考虑临时阻挡分段数量、平板车转向次数和移动距离的分段综合移动难度的评价标准。然后以使其最小化为目标函数,利用遗传算法[7](genetic algorithm,GA)为进场分段选择一个合适的存储单元位置,并用启发式规则根据评价指标,为进、出场分段选择一条最优的移动路径。对于同一天出场的具有柔性出场时间的分段,需要运用禁忌搜索(tabu search,TS)优化其出场顺序。最后综合考虑调度周期内所有的分段,制定一个整体最优的分段调度计划。
2 建立船舶分段堆场调度模型 2.1 堆场状态二进制矩阵为了表示分段在堆场中的停放位置及分段堆场存储单元的状态,建立堆场状态二进制矩阵Ht。Ht的每个元素bVxy表示此时调度t时刻堆场中存储单元位置为Vxy(位于堆场的第x行第y列)的状态,bVxy=1表示存储单元内已有分段停放,bVxy=0表示该时刻存储单元状态为空,进场分段可以分配至该位置。
| ${H_t} = \left[ {\begin{array}{*{20}{c}} {{b_{{V_{11}}}}}&{{b_{{V_{12}}}}}& \cdots &{{b_{{V_{1N}}}}}\\ {{b_{{V_{21}}}}}&{{b_{{V_{22}}}}}& \cdots &{{b_{{V_{2N}}}}}\\ \cdots & \cdots & \cdots & \cdots \\ {{b_{{V_{M1}}}}}&{{b_{{V_{M2}}}}}& \cdots &{{b_{{V_{MN}}}}} \end{array}} \right]$ |
随着船舶分段调度任务的进行,堆场中存储单元的状态也会随之改变。若位于Vxy位置的分段在t时刻有调度任务,那么堆场状态矩阵对应位置的元素要满足bVxyt-1+bVxy=1t,即原来存储单元停放有分段的,出场后状态由1变为0;原来空存储单元,分段进出停放至该位置后,状态由0变为1。
2.3 分段移动路径优劣的评价标准评价分段移动路径优劣的因素主要有:1)路径中的临时分段的数量;2)存取分段时,为了到达目标位置平板车在该路径中的转向次数;3)平板车在该路径中移动的距离。
表1将上述评价因素按其对分段调度作业的影响程度排序。因此,建立分段综合移动难度p的评价标准:p=αx+βy+γz,根据评价分段移动路径优劣因素的重要程度,为了区分设定α=1,β=0.1,γ=0.01,在路径搜索时,移动路径中每一个挡道分段便累加α,平板车每进行一次转向便累加β,每移动经过一个存储单元便累加γ。最后得到每条路径的移动难度p。若p=2.36,则表示该分段进(出)堆场临时阻挡分段的数量为2个,平板车的转向次数为2次,平板车需要移动6个存储单元的距离。
堆场分段调度计划以分段综合移动难度最小为优化目标建立堆场调度模型,并采用改进的启发式算法进行优化。
定义决策变量如下:
$O_{ixy}^{{t_{Si}}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{\rm{在}}{t_{Si}}{\rm{时进场分段}}i{\rm{存放到}}{V_{xy}}{\rm{的储位上}}}\\ {0,}&{{\rm{其他}}} \end{array}} \right.$
$O_{jxy}^{{t_{Rj}}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{\rm{在}}{t_{Rj}}{\rm{时进场分段}}j{\rm{存放到}}{V_{xy}}{\rm{的储位上}}}\\ {0,}&{{\rm{其他}}} \end{array}} \right.$
以最小化分段综合移动难度为目标,建立以下目标函数:
$\begin{array}{l}
\min \left\{ {\sum\limits_{t \in {t_{Si}}} {\sum\limits_{i \in {S_{{i^x}}}} {\sum\limits_{y \in {V_{xy}}} {\min \left\{ {\sum\limits_{k = 1}^h {pl_{ik}^{xy} \cdot O_{ixy}^{{t_{Si}}}} } \right\}} } } } \right.\\
\sum\limits_{t \in {t_{Rj}}} {\sum\limits_{i \in {S_{{j^x}}}} {\sum\limits_{y \in {V_{xy}}} {\min \left\{ {\sum\limits_{k = 1}^h {pl_{jk}^{xy} \cdot O_{jxy}^{{t_{Si}}}} } \right\}} } }
\end{array}$
(1)
$\sum\limits_{i = 1}^m {O_{ixy}^{{t_{Si}}}} = 1\forall x \in M,y \in N$
(2)
$\sum\limits_{x = 1}^m {\sum\limits_{y = 1}^n {O_{ixy}^{{t_{Si}}}} } = 1\forall i = 1,2 \ldots m$
(3)
$\sum\limits_{i,i' = 1}^n {\left( {O_{jxy}^{{t_{Si}}} + O_{i'xy}^{{t_{Si'}}}} \right)} = 1\forall i \ne i',{t_{Si}} = {t_{Si'}}$
(4)
$\sum\limits_{j,j' = 1}^n {\left( {O_{jxy}^{{t_{Ri}}} + O_{j'xy}^{{t_{Rj'}}}} \right)} = 1\forall j \ne j',{t_{Rj}} = {t_{Rj'}}$
(5)
$\sum\limits_{i,i = 1}^n {\left( {O_{ixy}^{{t_{Sj}}} + O_{jxy}^{{t_{Rj}}}} \right)} = 1\forall {t_{Si}} = {t_{Rj}}$
(6)
$0 \le {t_s} \le {t_{Si}} \le {t_e}$
(7)
$0 \le {t_s} \le {t_{Rj}} \le {t_e}$
(8)
$0 \le {L_g}{W_g} \le {S_0}$
(9)
本文根据目标函数(1)依次计算调度计划中分段移动的可选路径,选择每个分段最优的移动路径,从而使整体综合移动难度最小,然后利用遗传算法,得到一个基于位置选择的整体最优的分段调度方案。最后运用禁忌搜索,优化每天具有柔性出场时间的分段出场顺序。
约束(2)说明堆场中一个存储单元只能存放一个分段;约束(3)确保一个分段只能分配到一个确定的储位;约束(4)~(6)限制堆场每次只能执行一个调度任务;约束(7)规定计划进场的分段其进场时间在调度周期内;约束(8)限定计划出场的分段其出场时间在调度周期内;约束(9)保证分段的几何投影尺寸能够在一个存储单元内放下。
3 模型求解船舶分段堆场调度模型的遗传算法设计如下:
1)初始化。以调度开始时的堆场状态作为初始状态建立堆场初始状态二进制矩阵。
2)产生初始种群。将进场分段在堆场中可能放置的存储单元的位置(出场分段则为出场前分段所在位置)按照调度计划组合形成一种调度方案(染色体)。
3)编码。根据堆场的大小,若堆场大小M×N,遗传算法的染色体可以采取如图1的编码方式。

|
| 图1 染色体 Fig.1 Chromosome |
染色体的基因位数为调度周期内所有需调度的分段数量,基因中的整数部分用来表示分段在堆场中的位置,而小数部分则用于表示调度周期内分段的时间属性(最小单位以天计)。没有整数部分的基因位置表示进场分段,整数部分根据分段可能存放的存储单元位置随机生成,为堆场状态二进制矩阵中bVxy=0的存储单元的序号(按从左到右,从上到下依次为bVxy=0的存储单元编号,随机生成为第a个零的位置,整数部分则为a)。负数则表示原先进入堆场的分段此时要出堆场,例如-8.03则表示位于染色体第8个位置的进场分段,需要出堆场,它的出场时间为调度周期的第3天。通过这样的编码,可以更好的反应调度任务的时间属性,使算法最后呈现的调度计划更加直观,也便于后续的禁忌搜索。
4)解码。利用改进的路径搜索启发式算法搜索得到调度周期内每个分段的最优移动路径,通过计算每个分段的堆场调度计划产生的综合移动难度,并进行累加。具体过程如下:
①将目标位置(出场分段为出场前分段所在存储单元的位置)放入已搜索集合S;
②搜索与S集合中各个位置直接相邻并且bVxy=0的位置,计算移动到该位置所需的综合移动难度p并记录;
③将已标有p的位置放入集合S中,同时记录到达该位置的前一个位置的节点r(父节点),如图2(a)所示。
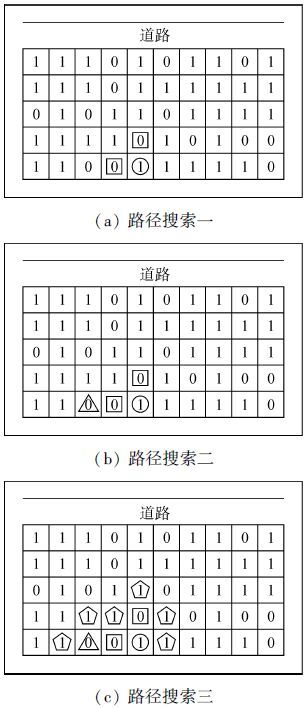
|
| 图2 路径搜索 Fig.2 Moving path searching |
④继续搜索与S集合中各个位置直接相邻的位置,若遇到bVxy=0的位置则继续搜索并累加综合移动难度p,并将这些位置放入已搜索集合S中,同时记录每个位置所对应的父节点r。重复④直到所有与S集中各个位置相邻的位置的bVxy=1为止。如图2(b)所示。
⑤将所有与S集合中各个位置相邻的位置(bVxy=1)放入已搜索集合S,累加综合移动难度并记录各个位置的父节点r。如图2(c)所示。
⑥重复②~⑤,当计算各个新搜索位置的p时,检查p的值是否有更新,若有更小的p值,则对其进行修正,并更新该位置的父节点r,直到已搜索集合S中的位置临近道路,算法便停止搜索。
依次比较路径搜索启发式算法搜索产生各条路径的综合移动难度,选取具有最小综合移动难度的路径,并记录下该路径。
根据堆场的调度计划来依次安排分段,每调度一个分段更新相应的堆场二进制矩阵Ht。
5)选择。本文采用精英保留战略,把适应度好的个体保留下来,并利用其好的性质繁殖后代。同时采用比例选择算子,使个体按照与适应度倒数成正比的概率向下一代群体繁殖。
6)交叉。随机产生一个以二进制编码的染色体E,将其基因位置与双亲的位置一一对应,将染色体E上基因值为1所对应的双亲染色体基因互换,若1所对应的位置为出场分段,则不作交叉。如图3所示。
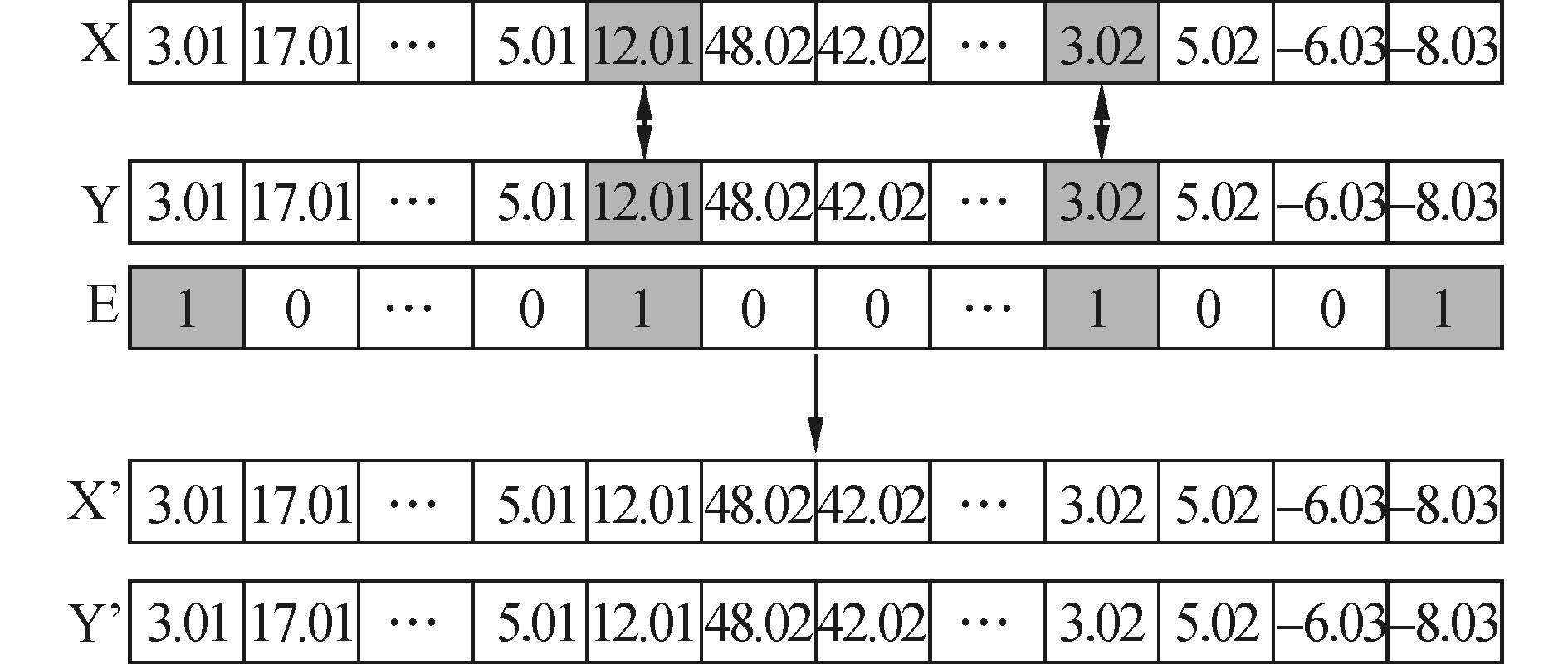
|
| 图3 染色体交叉 Fig.3 Crossover of chromosome |
7)变异。随机产生一个以二进制编码的染色体E,将染色体E上基因值为1所对应基因用重新随机生成的a来代替,a的上限为当前堆场状态下堆场中空闲的存储单元的个数。若染色体E基因1所对应的位置为出场分段,则不变。如图4所示。
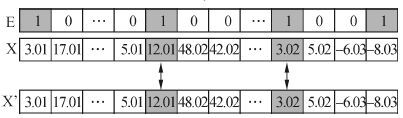
|
| 图4 染色体变异 Fig.4 Mutation of chromosome |
由于具有紧前、紧后搭载顺序的分段出场顺序是固定的,而禁忌搜索的禁忌表就可以避免这些分段顺序的调换,因此本文采用禁忌搜索[8, 9]对柔性出场时间的分段进行调度顺序的优化。算法设计如下:
1)用遗传算法求得的最优调度序列作为一个初始可行解xnow。并计算当前序列下总的综合移动难度p,将具有紧前、紧后出场顺序的分段放入禁忌表H中。令Ino=0,NIno=0,其中Ino为总的交换次数,NIno为交换后结果没有优化的次数。
2)若满足Ino≥MaxIno或者NIno≥MaxNIno,转至3);否则,搜索xnow的邻域(邻域产生方法由图5所示)N(xnow) 并计算该邻域序列总的综合移动难度p’,若p’<p,那么Ino=Ino+1,NIno=0,否则Ino=Ino+1,NIno= Nino+1。将当期得到的调度序列作为当前最优的解,并更新禁忌表H。
3)输出分段调度的最优序列,算法结束。
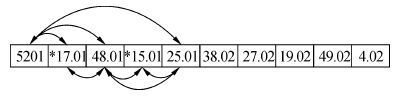
|
| 图5 邻域搜索 Fig.5 Neighborhood search |
为了验证本文所建模型以及算法的可行性与正确性,以上海某大型船厂一周内的分段调度为例,利用Microsoft Visual Studio 2010软件,在处理器为2.40 GHz,内存为4 GB的计算机上进行求解。实验包括以下输入参数:1)堆场初始状态的二进制矩阵;2)调度周期T内计划进出场分段的数量和进出场的日期;3)每日出场时间固定的分段以及出场时间较为柔性的出场分段;4)遗传算法的参数设置:种群规模为100,染色体个体长度为50,交叉概率为0.9,变异概率为0.1,算法终止代数为100;5)禁忌搜索的参数设置:算法终止条件MaxIno=100,Nino=15,禁忌表长度为10,某分段堆场初始状态如图6所示,该堆场有6×10个存储单元构成,其中42个存储单元已有分段存放,Ax为暂存在堆场不同存储单元上的分段编号。
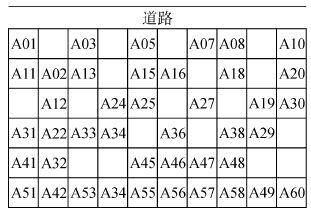
|
| 图6 堆场初始状态 Fig.6 Stockyard initial state |
按调度日期顺序排列的一周内堆场调度计划如表2所示。表中共有25个进场分段(从B1至B25依次编号),25个出场分段(Ax出场分段的编号,C1至C6为调度周期T内进入堆场暂存一段时间后又从堆场中取出的分段)。分段停放位置Vxy则表示分段停放的位置,x表示行,y表示列,例如V48则表示该分段位于堆场的第4行第8列的存储单元上。由于C1至C5的分段出场位置是由先前分段进入堆场的位置所决定的,因此Vz中的z则表示进入堆场中的序号所对应的停放位置,例如V6表示序号为6的B1分段进入堆场所停放的存储单元的位置。标有*号的出场分段表示这些分段由于生产的紧前、紧后关系出场先后顺序是固定的,不可进行随意的调整。
| 序号 | 调度日期 | 分段编号 | 任务属性 | 分段停放位置数 |
| 1 | 1 | *A42 | 出场 | V52 |
| 2 | 1 | A18 | 出场 | V28 |
| 3 | 1 | *A24 | 出场 | V34 |
| … | … | … | … | … |
| 23 | 3 | A55 | 出场 | V65 |
| 26 | 3 | B11 | 进场 | - |
| 27 | 3 | B12 | 进场 | - |
| 28 | 3 | B13 | 进场 | - |
| … | … | … | … | … |
| 48 | 5 | B23 | 进场 | - |
| 24 | 3 | A57 | 出场 | V67 |
| 49 | 5 | B24 | 进场 | - |
| 25 | 3 | A36 | 出场 | V46 |
| 50 | 5 | B25 | 进场 | - |
通过算法程序确定进场分段在堆场中的停放位置、出场分段的出场顺序以及进出场分段进出堆场的路径,得到一种较优的堆场调度方案如表3所示。随着程序的运行,个体的多样性在55代后逐渐消失,解开始收敛,收敛时间为291.95 s,收敛曲线如图7所示。
| 序号 | 调度日期 | 分段编号 | 任务属性 | 分段停放位置数 |
| 1 | 1 | A18 | 出场 | V28-V29-V19-V0 |
| 2 | 1 | *A42 | 出场 | V52-V53-V54-V44-V34-V24-V14-V0 |
| 3 | 1 | *A24 | 出场 | V34-V24-V14-V0 |
| … | … | … | … | … |
| 23 | 3 | A36 | 出场 | V46-V36-V35-V34-V24-V14-V0 |
| 24 | 3 | A55 | 出场 | V65-V55-V54-V44-V34-V24-V14-V0 |
| 25 | 3 | A57 | 出场 | V67-V66-V65-V55-V54-V44-V34-V24-V14-V0 |
| 26 | 3 | B11 | 进场 | V510-V410 |
| 27 | 3 | B12 | 进场 | V67-V66-V65-V55-V54-V44-V34-V24-V14-V0 |
| 28 | 3 | B13 | 进场 | V58-V48-V47-V46-V36-V35-V34-V24-V14-V0 |
| … | … | … | … | … |
| 48 | 5 | B23 | 进场 | V19-V0 |
| 24 | 3 | A57 | 出场 | V67 |
| 49 | 5 | B24 | 进场 | V38-V28-V18-V0 |
| 50 | 5 | B25 | 进场 | V36- V37-V27-V17-V0 |
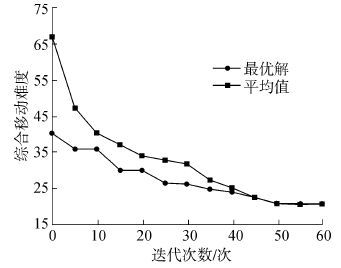
|
| 图7 算法收敛曲线 Fig.7 Algorithm convergence curves |
为了验证堆场尺寸、初始负载率、道路开放程度对综合移动难度的影响,本文进行以下试验:
1)调度分段数量:50个
2)堆场尺寸:4×15、5×12、6×10
3)初始负载率:60%、70%、80%、90%
4)道路开放程度:一条、两条、四条
针对以上不同参数一共试验了36种组合试验,对于每种情况,为了保证更好的试验效果,对每种情况进行5次试验,并取平均值。
通过图8对比分析可得
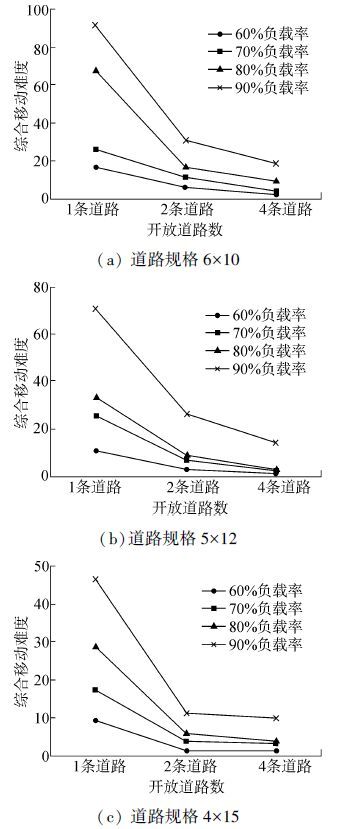
|
| 图8 不同规格堆场调度实验分析 Fig.8 Analysis of stockyard scheduling experiments with different specification |
1)相同堆场规格的情况下,提高堆场的初始负载率,分段总的综合移动难度会相应的增加。
2)堆场初始负载率相同的情况下,随着场外道路开放程度的增加,分段总的综合移动难度会相应的减少。
3)堆场场外道路开放程度的增加,在较高初始负载率的堆场状态下,总的综合移动难度的下降更为明显。说明在较高初始负载率的堆场状况下,适当的增加开放道路的数量,能有效的提高堆场的运作效率。
4)堆场的道路由两条增加至四条,对提升堆场的运作效率作用并不明显,尤其是堆场在较低初始负载率的情况下运作。
5)对于场外道路数为一条,不同规格的堆场,分段总的综合移动难度与初始负载率由以下关系:
①对于堆场规格为6×10(图8(a)) 当堆场的初始负载率由70%提高至80%时,分段的综合移动难度提高164.83%,因此在该堆场规格下,将堆场的初始负载率定为70%左右较为合理;
②对于堆场规格为5×12(图8(b)) 当堆场的初始负载率由80%提高至90%时,分段的综合移动难度提高109.98%,因此在该堆场规格下,将堆场的初始负载率定为80%左右较为合理;
③对于高负荷(堆场初始负载率90%)的分段堆场,堆场的布局规格设计为4×15较为合理。
4.2.2 算法比较分析求解分段进出场的路径问题是平面堆场调度问题中最为关键的问题,对于路径的求解可以用Dijkstra算法[10, 11, 12]进行求解,Dijkstra算法能得出最短路径的最优解,但本文需要综合考虑临时阻挡分段数量、平板车的转向次数和移动距离,若使用Dijkstra算法需要遍历所有可能的路径再筛选出最优的进出场路径,大大增加了算法的时间。因此本文在Dijkstra算法的基础上,利用堆场的二进制矩阵,以起始点为中心,对状态为0、1的存储单元进行交替的搜索,直至搜索到终点,该算法只对路径上的相关存储单元进行搜索,在能够求得最短路径最优解的情况下大大减少算法的搜索范围,有效的降低路径搜索的时间。如图9所示,随着调度分段数量的增加,两种算法的运行时间都相应的增加,但本文的算法明显小于Dijkstra算法,且调度的规模越大,本文的算法的优越性更加明显。
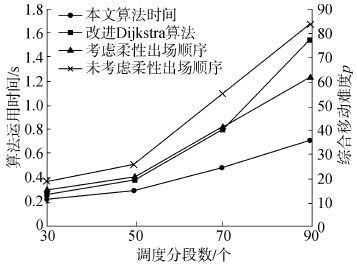
|
| 图9 算法比较分析 Fig.9 Comparison and analysis of algorithms |
对于出场分段,本文考虑对出场时间柔性的分段进行重新安排出场顺序,使用禁忌搜索算法,根据出场分段所停放的位置,安排分段的出场顺序。如图9所示,在考虑分段出场顺序的情况下,分段的综合移动难度相比于原来有明显的下降,并随着调度分段数的增加,优化的效果也明显增加。
5 结论本文通过对船舶分段堆场的调度过程进行研究,得出以下结论:
1)综合考虑临时阻挡分段数量、平板车转向次数和移动距离对堆场调度成本的影响,确定了分段移动路径优劣的综合评价指标;
2)通过确定的评价指标运用智能算法对堆场的分段调度计划进行优化;
3)通过对不同堆场尺寸、初始负载率和道路开放程度的实验分析比较,得出不同堆场环境下堆场的较优配置,提高了堆场的实际运作效率。
由于研究只考虑了一辆平板车的调度计划,多辆平板车的协同调度情况将会复杂很多,需要作进一步的研究。
| [1] | PARK C, SEO J. Mathematical modeling and solving procedure of the planar storage location assignment problem[J]. Computers & Industrial Engineering, 2009, 57(3):1062-1071. |
| [2] | PARK C, SEO J. Comparing heuristic algorithms of the planar storage location assignment problem[J]. Transportation Research Part E:Logistics and Transportation Review, 2010, 46(1):171-185. |
| [3] | TAO Ningrong, JIANG Zuhua, QU Shipeng. Assembly block location and sequencing for flat transporters in a planar storage yard of shipyards[J]. International Journal of Production Research, 2013, 51(14):4289-4301. |
| [4] | 张志英, 申钢, 刘祥瑞, 等. 基于最短路算法的船舶分段堆场调度[J]. 计算机集成制造系统, 2012, 18(9):1982-1990. ZHANG Zhiying, SHEN Gang, LIU Xiangrui, et al. Block storage yard scheduling of shipbuilding based on shortest path algorithm[J]. Computer Integrated Manufacturing Systems, 2012, 18(9):1982-1990. |
| [5] | 张志英, 徐建祥, 计峰. 基于遗传算法的船舶分段堆场调度研究[J]. 上海交通大学学报, 2013, 47(7):1036-1042.ZHANG Zhiying, XU Jianxiang, JI Feng. Shipbuilding yard scheduling approach based on genetic algorithm[J]. Journal of Shanghai Jiaotong University, 2013, 47(7):1036-1042. |
| [6] | ROH M I, CHA J H. A block transportation scheduling system considering a minimisation of travel distance without loading of and interference between multiple transporters[J]. International Journal of Production Research, 2011, 49(11):3231-3250. |
| [7] | REEVES C R. A genetic algorithm for flowshop sequencing[J]. Computers & Operations Research, 1995, 22(1):5-13. |
| [8] | 符卓. 带装载能力约束的开放式车辆路径问题及其禁忌搜索算法研究[J]. 系统工程理论与实践, 2004, 24(3):123-128. FU Zhuo. The capacitated open vehicle routing problem and its tabu search algorithm[J]. Systems Engineering-Theory & Practice, 2004, 24(3):123-128. |
| [9] | JIA Shuai, HU Zhihua. Path-relinking Tabu search for the multi-objective flexible job shop scheduling problem[J]. Computers & Operations Research, 2014, 47:11-26. |
| [10] | FAN Yuezhen, LU Dunmin, WANG Qingchun, et al. Notice of retraction an improved Dijkstra algorithm used on vehicle optimization route planning[C]//Proceedings of the 2nd International Conference on Computer Engineering and Technology. Chengdu:IEEE, 2010,3:V3-693-696. |
| [11] | KAMBAYASHI Y, YAMACHI H, TSUJIMURA Y, et al. Dijkstra beats genetic algorithm:Integrating uncomfortable intersection-turns to subjectively optimal route selection[C]//Proceeding of International Conference on Computational Cybernetics. Spain:IEEE, 2009:45-50. |
| [12] | 李擎, 谢四江, 童新海, 等. 一种用于车辆最短路径规划的自适应遗传算法及其与Dijkstra和A*算法的比较[J]. 北京科技大学学报, 2006, 28(11):1082-1086. LI Qing, XIE Sijiang, TONG Xinhai, et al. A self-adaptive genetic algorithm for the shortest path planning of vehicles and its comparison with Dijkstra and A* algorithms[J]. Journal of University of Science and Technology Beijing, 2006, 28(11):1082-1086. |
| [13] | PHANTHONG T, MAKI T,URA T, et al. Application of A*algorithm for real-time path replanning of an unmanned surface vehicle avoiding underwater obstacles[J]. Journal of Marine Science and Application,2014, 13(1):105-116. |



