2. Beijing Institute of Long March Vehicle, Beijing 100076, China;
3. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
高超声速飞行器由于其飞行速度高、飞行空域大、射程远等优点,近年来已成为各国学者的研究热点。与传统飞行器不同,高超声速飞行器飞行环境复杂多变,气动参数和结构参数存在较大摄动,使得飞行器具有激烈快时变、严重非线性、强耦合和不确定的特点,因此所设计的控制系统必须在满足精度要求的条件下具有较强的鲁棒性[1, 2, 3]。
为了满足飞行器姿态控制的鲁棒性和抗干扰性要求,众多学者提出了大量的鲁棒控制方法。如,文献[3, 4]针对高超声速飞行器在爬升段与巡航段之间切换的控制问题,设计了h∞姿态控制器;文献[5]为了继承传统PID控制的优点并使其具有更好的控制品质,设计了鲁棒分数阶PID自动驾驶仪;文献[6]针对吸气式高超声速飞行器的纵向运动,提出了一种非线性的鲁棒自适应控制方法。文献[7, 8]利用滑模控制技术,为可重复使用的航天运载飞行器X-33设计了飞行控制系统,取得了良好的控制效果。
上述控制方法使得飞行器在存在系统摄动和外界干扰的情况下,均具有较强的鲁棒性和抗干扰能力,而其中滑模控制由于设计简单,控制精度高等优点,在航天控制领域中得到了广泛的应用[7, 8, 9, 10, 11, 12, 13]。文献[7, 8]中的滑模控制采用线性函数作为滑动超平面,这种情况下,系统到达滑模面后跟踪误差只能渐近的收敛到零。为了使系统跟踪误差在有限时间内收敛到零,一些学者以非线性函数构建滑模面,提出了终端滑模控制方法。文献[9]针对高超声速飞行器六自由度再入模型,基于终端滑模对再入过程中姿态角进行了跟踪控制;为了消除稳态误差,文献[10]设计了基于积分滑模面的控制方法,但是降低了系统响应的快速性;为了增强在线逼近干扰及系统不确定的能力,文献[11]提出了一种基于快速模糊干扰观测器的终端滑模控制方案,但是增加了控制器的复杂度。在上述滑模控制方法中,符号函数的存在会引起控制系统的抖振,而在工程实际中,必须对抖振问题进行去除或削弱。采用饱和函数是常用的抑制抖振的方法,该方法虽然行之有效,但却降低了控制性能。在保证控制系统性能且尽可能不增加控制器复杂度的前提下,本文设计一种连续的终端滑模控制器,有效的避免了抖振问题的产生。
针对高超声速飞行器再入过程中的姿态跟踪问题,本文考虑系统模型不确定性和有界干扰的影响,设计连续的快速终端滑模控制器,并对控制系统的有限时间收敛性进行了数学证明,最后通过数值仿真验证本文算法的在高超声速条件下的有效性。
1 高超声速飞行器姿态运动模型高超声速飞行器的运动可以分解为质心的平动和绕质心的转动2部分,即轨道运动和姿态运动。通常由于轨道运动比姿态运动慢得多,因此在研究姿态控制问题时可以忽略描述轨道运动的量。基于上述假设,并考虑系统参数摄动及外界干扰的影响,得到如下简化的姿态运动方程:
| $\dot q = Rw + f$ | (1) |
| $J\dot \omega = - \omega \times J\omega + M + d$ | (2) |
式中:q=[α β γc]T表示攻角、侧滑角和倾侧角,ω=[ωx ωy ωz]T表示飞行器转动角速度,f表示姿态运动学方程中的广义不确定性和干扰,d表示干扰力矩,J=J0+ΔJ为飞行器的转动惯量矩阵,J0为转动惯量的标称部分,ΔJ表示系统模型的不确定性,M=[Mx My Mz]T表示飞行器三通道的控制力矩,R可表示为
| $R\left( \cdot \right) = \left[ {\begin{array}{*{20}{c}} 0&0&1\\ {\sin \alpha }&{\cos \alpha }&0\\ {\cos \alpha }&{ - \sin \alpha }&0 \end{array}} \right]$ |
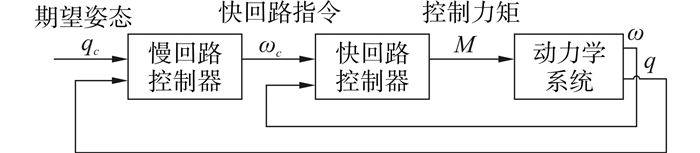
如图 1所示,基于多时间尺度划分姿态模型,可以将飞行器的控制系统分为快回路和慢回路,即认为慢回路带宽比快回路小得多,在快回路跟踪结束后,慢回路响应还没有达到稳态。因此,可以将控制器设计分为2部分:1)用于产生快回路制导指令的慢回路控制器设计;2)用于产生控制力矩的快回路设计。
|
| 图 1 姿态控制系统结构框图 Fig. 1 Schematic diagram of attitude control system |
在设计控制器之前,给出如下定理和引理:
定理1 假设存在连续可微函数V:U→R,使得其满足下列条件:
1) V为正定函数;
2)存在正实数λ>0和a∈(0,1),以及一个包含原点的开邻域U0U,使得下列条件成立
| $\dot V\left( x \right) + \gamma {V^\alpha }\left( x \right) \le 0,x \in {U_0}\backslash \left\{ 0 \right\}$ | (3) |
则系统为有时间稳定的。
引理1 对于任意向量x=[x1 x2 … xn]T,存在0 < p < 2,使得下列不等式成立
| ${\left\| x \right\|^p} \le \sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^p}} $ | (4) |
慢回路控制器的设计目标是设计快回路的制导指令ωc,使得飞行器的姿态角q在有限时间内收敛到需要跟踪的制导指令qc,即使得姿态跟踪误差qe=q-qc在有限时间内收敛到零。
为了实现上述控制目标,选取如下终端滑模面:
| $\tau = {q_e} + \int_0^t {\left( {{A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right)} {\rm{d}}t$ | (5) |
式中:A1、B1为对角矩阵,且对角线的每个元素均为正实数;p1、q1为正奇数,且满足q1 < p1 < 2q1
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;q_e^{{q_1}/{p_1}} = \\ \left[ {{\mathop{\rm sgn}} \left( {{q_{e1}}} \right){{\left| {{q_{e1}}} \right|}^{{q_1}/{p_1}}},{\mathop{\rm sgn}} \left( {{q_{e2}}} \right){{\left| {{q_{e2}}} \right|}^{{q_1}/{p_1}}},{\mathop{\rm sgn}} \left( {{q_{e3}}} \right){{\left| {{q_{e3}}} \right|}^{{q_1}/{p_1}}}} \right] \end{array}$ |
基于式(5)所示的滑模面,设计如下连续的终端滑模控制器:
| ${\omega _c} = {R^{ - 1}}\left( {{{\dot q}_c} - {A_1}{q_e} - {B_1}q_e^{{q_1}/{p_1}} - {K_1}\tau - {G_1}{\tau ^{{q_1}/{p_1}}}} \right)$ | (6) |
其中,K1、G1为对角矩阵,其对角线的每个元素均为正实数,且对于K1的每个元素都有|K1i|>|fi|,这里fi为广义干扰f的元素。
定理2 针对慢回路系统模型(1),假设其广义干扰f是有界的,采用控制器(6),系统状态q将在有限时间内从初始位置收敛到期望的制导指令qc,且跟踪误差qe能在有限时间内收敛到零。
证明:1)证明滑模面τ能够在有限时间内收敛到零。取如下Lyapunov函数:
| $V = \frac{1}{2}{\tau ^{\rm{T}}}\tau $ | (7) |
采用控制器(6),沿式 (1)对V求一阶导数可得
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\dot V = {\tau ^{\rm{T}}}\dot \tau = \\ \;\;\;{\tau ^{\rm{T}}}\left( {{{\dot q}_e} + {A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right) = \\ {\tau ^{\rm{T}}}\left( {\dot q - {{\dot q}_c} + {A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right) = \\ \;\;\;\;{\tau ^{\rm{T}}}\left( {f - {K_1}\tau - {G_1}{\tau ^{{q_1}/{p_1}}}} \right) \end{array}$ | (8) |
由引理1可得
| $\begin{array}{l} \dot V = \sum\limits_{i = 1}^3 {\left[ {\left( {\left| {{f_i}} \right| - \left| {{K_{1i}}} \right|} \right){{\left| {{\tau _i}} \right|}^2} - \left| {{G_{1i}}} \right|{{\left| {{\tau _i}} \right|}^{1 + {q_1}/{p_1}}}} \right]} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \sum\limits_{i = 1}^3 {\left| {{G_{1i}}} \right|{{\left| {{\tau _i}} \right|}^{1 + {q_1}/{p_1}}}} \le \\ \;\;\;\;\;\;\;\;\;\; - {g_1}{\left\| \tau \right\|^{1 + {q_1}/{p_1}}} \le - {g_1}{V^{\frac{{1 + {q_1}/{p_1}}}{2}}} \end{array}$ | (9) |
式中:g1=min(|G1i|)。再由定理1可知,滑模面τ能够在有限时间内收敛到零。
2)证明在系统状态到达滑模面后,跟踪误差可以在有限时间内收敛到零。当系统状态到达滑模面后,有
| ${q_e} + \int_0^t {\left( {{A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right)} {\rm{d}}t = 0$ | (10) |
两边同时求导可得
| ${{\dot q}_e} = - \left( {{A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right)$ | (11) |
取Lyapunov函数V=qeTqe/2,对其求导得
| $\begin{array}{l} \dot V = - q_e^{\rm{T}}{{\dot q}_e} = - q_e^{\rm{T}}\left( {{A_1}{q_e} + {B_1}q_e^{{q_1}/{p_1}}} \right) \le \\ - q_e^{\rm{T}}{B_1}q_e^{{q_1}/{p_1}} \le - {b_1}{\left\| {{q_e}} \right\|^{1 + {q_1}/{p_1}}} \le {b_1}{V^{\frac{{1 + {q_1}/{p_1}}}{2}}} \end{array}$ | (12) |
式中:b1=min(|B1i|)。由定理1可知,系统状态跟踪误差qe能够在有限时间内收敛到零。证毕。
2.2 快回路控制器设计快回路控制器的设计目标是设计控制力矩指令M,使得飞行器的姿态角速度ω能够在有限时间内收敛到慢回路输出的制导指令ωc,即使得姿态角速度跟踪误差ωe=ω-ωc在有限时间内收敛到零。
为了实现上述控制目标,选取如下终端滑模面:
| $s = {\omega _e} + \int_0^t {\left( {{A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right)} {\rm{d}}t$ | (13) |
式中:A2、B2为对角矩阵,且每个元素均为正实数;p2、q2为正奇数,且满足q2 < p2 < 2q2、ωeq2/p2与qeq1/p1的定义类似。
基于式(13)所示的滑模面,设计如下连续的终端滑模控制器:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;M = \left( {\omega \times {J_0}\omega } \right) + \cdots + \\ {J_0}\left( {{{\dot \omega }_c} - {A_2}{\omega _e} - {B_2}\omega _e^{{q_2}/{p_2}} - {K_2}s - {G_2}{s^{{q_2}/{p_2}}}} \right) \end{array}$ | (14) |
式中:K2、G2为对角矩阵,其每个元素均为正实数,且对于K2的每个元素都有|K2i|>|ηi|,这里ηi表示矢量J0-1D的元素,D表示包括模型不确定性和干扰力矩的广义干扰,即
| $D = - \Delta J\dot \omega - \omega \times \Delta J\omega + d$ |
定理3 针对快回路系统(2),假设其广义干扰D是有界的,采用控制器(14),系统状态ω将在有限时间内从初始位置收敛到需要跟踪的制导指令ωc,且跟踪误差ωe能在有限时间内收敛到零。
证明:
1)证明滑模面s能够在有限时间内收敛到零。取如下Lyapunov函数:
| $V = \frac{1}{2}{s^{\rm{T}}}s$ | (15) |
采用控制器(14),沿系统(2)对V求一阶导数可得
| $\begin{array}{l} \;\dot V = {s^{\rm{T}}}\dot s = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{s^{\rm{T}}}\left( {{{\dot \omega }_e} + {A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;{s^{\rm{T}}}\left( {\dot \omega - {{\dot \omega }_e} + {A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right) = \\ {s^{\rm{T}}}\left[ {J_0^{ - 1}\left( { - \omega \times \Delta J\omega - \Delta J\dot \omega + d} \right) - {K_2}s - {G_2}{s^{{q_2}{p_2}}}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{s^{\rm{T}}}\left[ {J_0^{ - 1}D - {K_2}s - {G_2}{s^{{q_2}{p_2}}}} \right] \end{array}$ | (16) |
由引理1可得
| $\begin{array}{l} \;\;\;\;\;\dot V = \sum\limits_{i = 1}^3 {\left[ {\left( {\left| {{\eta _i}} \right| - \left| {{K_{2i}}} \right|} \right){{\left| {{s_i}} \right|}^2} - \left| {{G_{2i}}} \right|{{\left| {{s_i}} \right|}^{1 + {q_2}/{p_2}}}} \right]} \le \\ - \sum\limits_{i = 1}^3 {\left[ {\left| {{G_{2i}}} \right|{{\left| {{s_i}} \right|}^{1 + {q_2}/{p_2}}}} \right]} \le - {g_2}{\left\| s \right\|^{1 + {q_2}/{p_2}}} \le - {g_2}{V^{\frac{{1 + {q_2}/{p_2}}}{2}}} \end{array}$ | (17) |
式中:g2=min(|G2i|)。再由定理1可知,滑模面s能够在有限时间内收敛到零。
2)证明在系统状态到达滑模面后,跟踪误差可以在有限时间内收敛到零。当系统状态到达滑模面后,有
| ${\omega _e} + \int_0^t {\left( {{A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right)} {\rm{d}}t = 0$ | (18) |
两边同时求导可得
| ${{\dot \omega }_e} = - \left( {{A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right)$ | (19) |
取Lyapunov函数V=1/2ωeTωe,对其求导得
| $\begin{array}{l} \dot V = - \omega _e^{\rm{T}}{{\dot \omega }_e} = - \omega _e^{\rm{T}}\left( {{A_2}{\omega _e} + {B_2}\omega _e^{{q_2}/{p_2}}} \right) \le \\ - \omega _e^{\rm{T}}{B_2}\omega _e^{{q_2}/{p_2}} \le - {b_2}{\left\| {{\omega _e}} \right\|^{1 + {q_2}/{p_2}}} \le {b_2}{V^{\frac{{1 + {q_2}/{p_2}}}{2}}} \end{array}$ | (20) |
同样的,由定理1可知,系统状态跟踪误差ωe能够在有限时间内收敛到零。证毕。
注1 对于本文所采用的快速终端滑模面,当系统状态远离原点时,滑模面的线形部分-ax提供较快的收敛速度,而当系统状态在原点附近时,相比于线形部分,其非线性部分-bxq/p提供较快的收敛速度。因此结合这两部分的优势,快速终端滑模控制器无论在距离原点较远还是较近时都能提供较快的收敛速度。
注2 如式(6)和式(14)所示,控制器中并未出现符号函数等非连续项,因此本文所设计的控制器是连续的。由于避免了符号函数的使用,使得本文所设计的控制器可以有效防止抖振现象的产生,相比于传统的终端滑模控制器,其工程实用意义更强。
3 数学仿真及结果分析为验证本文控制方法的有效性,在高超声速条件下,将控制器(6)和(14)用于飞行器的姿态角跟踪控制问题中。仿真中,采用式(1)和式(2)所示的运动模型,其中,飞行器的转动惯量为
| $J = {\rm{diag}}\left( {1.1 \times {{10}^6},1.78 \times {{10}^7},1.71 \times {{10}^7}} \right){\rm{kg}} \cdot {{\rm{m}}^2}$ |
姿态角和姿态角速度的初始参数为
| $\begin{array}{l} \alpha \left( 0 \right) = 0^\circ ,\beta \left( 0 \right) = 1^\circ ,{\gamma _c}\left( 0 \right) = 1^\circ ;\\ {\omega _x}\left( 0 \right) = 0,{\omega _y}\left( 0 \right) = 0,{\omega _z}\left( 0 \right) = 0 \end{array}$ |
姿态运动学的广义干扰为
| $f = \left[ \begin{array}{l} 2 \times {10^{ - 4}}\left( {1 + \sin \left( {0.1\pi t} \right)} \right)\\ 2 \times {10^{ - 4}}\left( {1 + \sin \left( {0.1\pi t} \right)} \right)\\ 1 \times {10^{ - 3}}\left( {1 + \sin \left( {0.1\pi t} \right)} \right) \end{array} \right]$ |
动力学方程中的广义干扰为
| $d = \left[ \begin{array}{l} {10^5}\left( {1 + \sin \left( {0.1\pi t} \right)} \right)\\ {10^6}\left( {1 + \sin \left( {0.1\pi t} \right)} \right)\\ {10^6}\left( {1 + \sin \left( {0.1\pi t} \right)} \right) \end{array} \right]$ |
假设制导指令为常值攻角,仿真中取期望姿态角和角速度分别为
| $\begin{array}{l} \alpha \left( t \right) = 1^\circ ,\beta \left( t \right) = 0^\circ ,{\gamma _c}\left( 0 \right) = 0^\circ ,\\ {\omega _x}\left( 0 \right) = 0,{\omega _y}\left( 0 \right) = 0,{\omega _z}\left( 0 \right) = 0 \end{array}$ |
控制器(6)中的参数选取如下:
| $\begin{array}{l} {A_1} = {\rm{diag}}\left( {0.1,0.1,0.1} \right)\\ {B_1} = {\rm{diag}}\left( {0.3,0.3,0.3} \right)\\ \;\;\;{K_1} = {\rm{diag}}\left( {1,1,1} \right)\\ \;\;\;\;{G_1}{\rm{ = diag}}\left( {2,2,2} \right)\\ \;\;\;\;\;{p_1} = 9,{q_1} = 7 \end{array}$ |
控制器(14)中的参数选取如下:
| $\begin{array}{l} {A_2} = {\rm{diag}}\left( {0.1,0.1,0.1} \right)\\ {B_2} = {\rm{diag}}\left( {0.3,0.3,0.3} \right)\\ \;\;\;{K_2} = {\rm{diag}}\left( {3,3,3} \right)\\ \;\;\;\;{G_2}{\rm{ = diag}}\left( {4,4,4} \right)\\ \;\;\;\;\;{p_2} = 9,{q_2} = 7 \end{array}$ |
仿真时间为20 s,仿真步长为Ts=0.01 s。仿真结果如图 2~7所示。
|
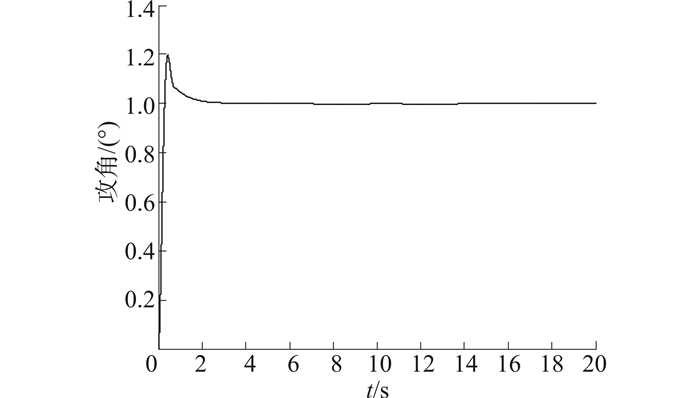
| 图 2 攻角随时间变化曲线 Fig. 2 Time history of the angle of attack |
|
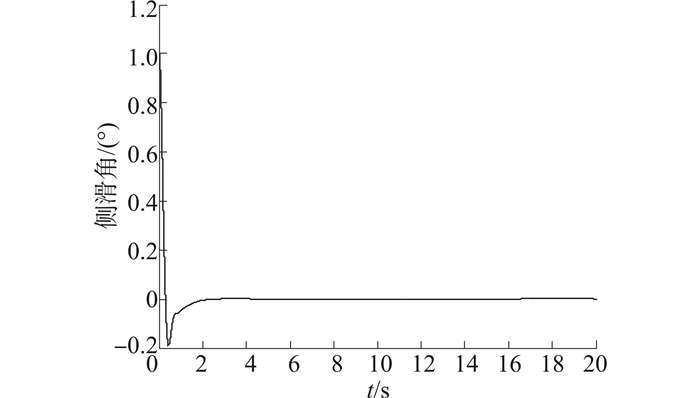
| 图 3 侧滑角随时间变化曲线 Fig. 3 Time history of the angle of side slip |
|
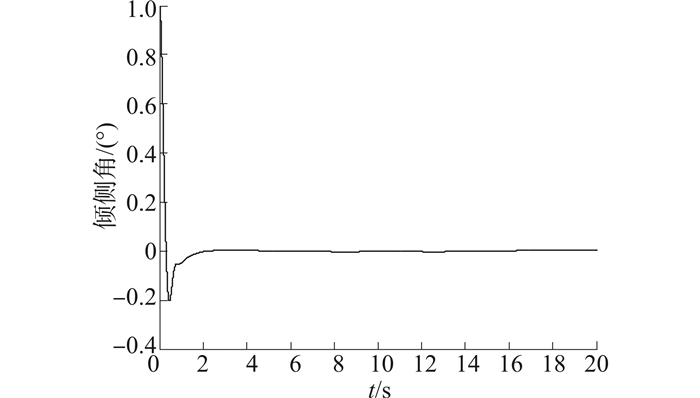
| 图 4 倾侧角随时间变化曲线 Fig. 4 Time history of the angle of heel |
|
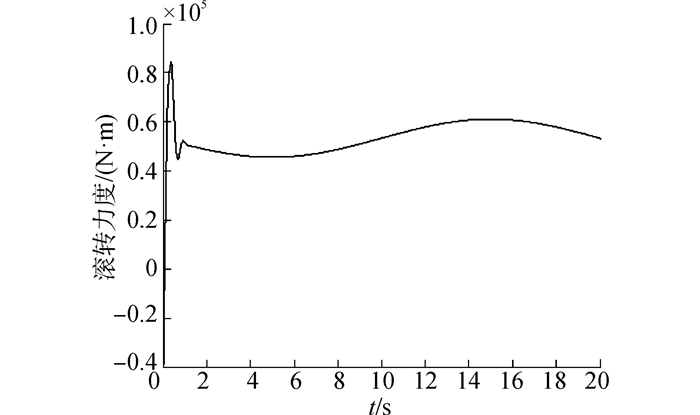
| 图 5 滚转力矩随时间变化曲线 Fig. 5 Time history of rolling moment |
|
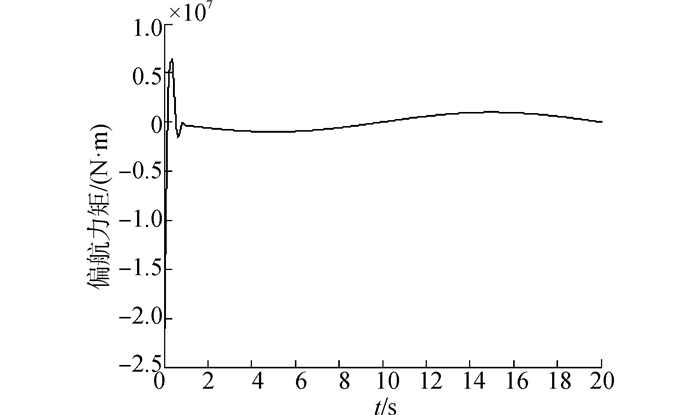
| 图 6 偏航力矩随时间变化曲线 Fig. 6 Time history of yawing moment |
|
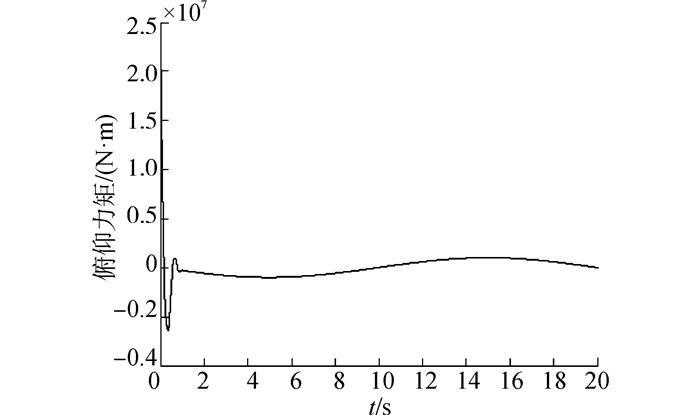
| 图 7 俯仰力矩随时间变化曲线 Fig. 7 Time history of pitching moment |
由图 2~4可以看出,在2 s内,飞行器的攻角、侧滑角和倾侧角均以较高的精度收敛至期望状态;由图 5~7可以看出,3个方向的控制力矩曲线均变化平滑,无抖振现象产生。上述仿真结果表明,在考虑外界干扰的情况下,采用本文所设计的控制器仍能够实现对期望姿态的快速、精确跟踪,体现了控制器良好的鲁棒性,且控制力矩平滑无抖振,易于工程实现。
4 结论本文研究了高超声速飞行器的姿态控制问题,所设计的连续终端滑模控制器可以在考虑系统模型不确定性以及外界干扰的情况下,使得姿态跟踪误差在有限时间内收敛。数值仿真结果表明,本文的控制算法具有良好的鲁棒性,可以实现高精度快速控制,并可以有效去除传统滑模控制带来的抖振问题,具有良好的工程实现价值。
| [1] | MARRISON C I, STENGEL R F. Design of robust control systems for a hypersonic aircraft[J]. Journal of guidance, control, and dynamics, 1998, 21(1): 58-63. |
| [2] | SIGTHORSSON D O, JANKOVSKY P, SERRANI A, et al. Robust linear output feedback control of an air-breathing hypersonic vehicle[J]. Journal of guidance, control, and dynamics, 2008, 31(4): 1052-1066. |
| [3] | SACHS G, SCHODER W. Robust control of the separation of hypersonic lifting vehicles[C]//Proceedings of the 4th AIAA, International Aerospace Planes Conference. Orlando, FL, USA, 1992. |
| [4] |
王延, 周凤岐, 周军, 等. 高超声速飞行器非线性H∞姿态控制设计[J]. 哈尔滨工业大学学报, 2011, 43(9): 128-133. WANG Yan, ZHOU Fengqi, ZHOU Jun, et al. Design of nonlinear H∞ controller for hypersonic vehicle system[J]. Journal of Harbin Institute of Technology, 2011, 43(9): 128-133. |
| [5] |
齐乃明, 秦昌茂, 宋志国. 导弹鲁棒分数阶PID自动驾驶仪设计[J]. 控制工程, 2011, 18(5): 715-718. QI Naiming, QIN Changmao, SONG Zhiguo. Robust fractional PID missile autopilot design[J]. Control engineering of China, 2011, 18(5): 715-718. |
| [6] |
张天翼, 周军, 郭建国. 高超声速飞行器鲁棒自适应控制律设计[J]. 宇航学报, 2013, 34(3): 384-388. ZHANG Tianyi, ZHOU Jun, GUO Jianguo. A study on robust adaptive control method for hypersonic vehicle[J]. Journal of astronautics, 2013, 34(3): 384-388. |
| [7] | SHTESSEL Y, MCDUFFIE J, JACKSON M, et al. Sliding mode control of the X-33 vehicle in launch and re-entry modes[C]//Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit. Reston, VA, 1998: 1352-1362. |
| [8] | SHTESSEL Y, HALL C, JACKSON M. Reusable launch vehicle control in multiple-time-scale sliding modes[J]. Journal of guidance, control, and dynamics, 2000, 23(6): 1013-1020. |
| [9] |
韩钊, 宗群, 田柏苓, 等. 基于Terminal滑模的高超声速飞行器姿态控制[J]. 控制与决策, 2013, 28(2): 259-263, 268. HAN Zhao, ZONG Qun, TIAN Boling, et al. Hypersonic vehicle attitude control using Terminal sliding mode control[J]. Control and decision, 2013, 28(2): 259-263, 268. |
| [10] | TOURNES C, JOHNSON C D. Reusable launch vehicle control using linear-adaptive subspace-stabilization techniques[J]. Journal of guidance, control, and dynamics, 2001, 24(2): 278-286. |
| [11] |
黄国勇, 姜长生, 王玉惠. 基于快速模糊干扰观测器的UASV再入Terminal滑模控制[J]. 宇航学报, 2007, 28(2): 292-297, 304. HUANG Guoyong, JIANG Changsheng, WANG Yuhui. Research of Terminal sliding mode control based on fast fuzzy disturbance observer for UASV re-entry[J]. Journal of astronautics, 2007, 28(2): 292-297, 304. |
| [12] | WANG Jianying, LIANG Haizhao, SUN Zhaowei, et al. Finite-time control for spacecraft formation with dual-number-based description[J]. Journal of guidance, control, and dynamics, 2012, 35(3): 950-962. |
| [13] | WU Shunan, RADICE G, GAO Yongsheng. Quaternion-based finite time control for spacecraft attitude tracking[J]. Acta astronautica, 2011, 69(1/2): 48-58. |



