频谱感知是认知无线电技术一个重要的组成部分，其主要作用是可靠地感知频谱是否被主用户使用，以不对主用户造成干扰的方式进行频谱接入，提高了频谱的利用率。已有很多典型的频谱感知算法^{[1, 2, 3, 4, 5]}，如能量检测^{[6, 7, 8, 9]}、匹配滤波器检测^{[9, 10]}、循环平稳特征检测^{[11, 12]}和协方差检测^[13]等。这些典型频谱感知算法在感知时间、复杂度和检测性能有不同的权衡。在研究频谱感知算法时，隐主用户问题是认知无线电面临的主要挑战之一^[1]。该问题造成认知用户信号和主用户信号共存于同一授权频段(主从信号共存)，认知用户在使用频谱时对主用户造成了有害干扰。

在主从信号共存时，现有的频谱感知算法感知主用户信号存在一定的困难。能量检测和协方差检测等非相关频谱感知算法可以感知信号的存在，但是无法区分是主用户信号还是认知用户信号。匹配滤波器检测和循环平稳特征检测等相关频谱感知算法在主从信号共存时可以检测主用户信号，但是需要一个存储各种主用户信号先验信息的专用滤波器。而在现实的认知无线电环境中，多种类型信号共存，限于复杂度的要求，存在具有所有主用户信号的专用滤波器的可能性较小。而且，在同一授权频段可能还存在其他认知无线电系统，这些其他认知无线电系统的先验信息可能也不会被本文研究的认知无线电系统掌握。而认知用户的先验信息是已知的，可以利用此先验信息消除认知用户信号对主用户信号检测的影响，因此本文提出一种联合频谱感知算法，利用认知用户已知的先验信息，消除认知用户信号对频谱感知算法的影响，以解决现有频谱感知算法在主从信号共存时感知主用户信号存在困难的问题。

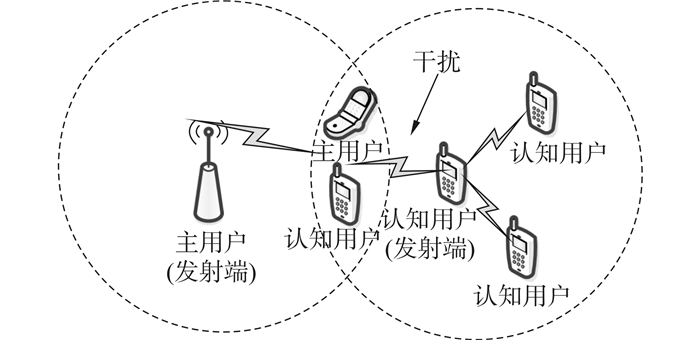
1 联合频谱感知算法设计

认知无线电中的隐主用户问题与CSMA中隐终端问题相似，图 1给出认知无线电中隐主用户问题的示例，图中的虚线圆表示主用户信号和认知用户信号的覆盖范围。由图可见，在这种情况下，认知用户将对主用户信号造成有害干扰。

因此，本文提出一种联合频谱感知算法，在主从信号共存时感知主用户信号，从而使认知用户及时解除认知占用，避免对主用户信号造成有害干扰。在本算法中，假设认知用户本地先验信息信号与接收到的认知用户信号同步。在此基础上，对联合频谱感知算法进行理论分析。

1.1 算法理论分析

主从信号共存时，频谱感知接收机的接收信号如下

$y\left[ n \right] = \left\{ \begin{gathered} w\left[ n \right],{H_{00}} \hfill \\ {h_{su}}{s_{su}}\left[ n \right] + w\left[ n \right],{H_{01}} \hfill \\ {s_{pu}}\left[ n \right] + w\left( n \right),{H_{10}} \hfill \\ {s_{pu}}\left[ n \right] + {h_{su}}{s_{su}}\left[ n \right] + w\left[ n \right],{H_{11}} \hfill \\ \end{gathered} \right.$

(1)

式中：y[n]是接收信号，w[n]是噪声信号，s_pu[n]是主用户信号，s_su[n]是认知用户信号，h_su是认知用户信号的信道增益，H₀₀表示主用户信号和认知用户信号都不存在的状态，H₀₁表示不存在主用户信号但存在认知用户信号的状态，H₁₀表示存在主用户信号但不存在认知用户信号的状态，H₁₁表示主从信号共存的状态。

对接收到的信号进行处理：

$\begin{gathered} {Y_{su}} = \sum\limits_N {y\left[ n \right]s_{su}^*\left[ n \right]} = \hfill \\ \sum\limits_N {\left( {{s_{pu}}\left[ n \right] + {h_{su}}{s_{su}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]} \hfill \\ \end{gathered} $

(2)

式中：Y_su表示对接收信号处理的结果，N表示检测长度。由本文假设可知，认知用户本地先验信息信号与接收到的认知用户

$\begin{gathered} {{\hat h}_{su}} = \frac{{{Y_{su}}}}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }} = \hfill \\ {h_{su}} + \frac{{\sum\limits_N {\left( {{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]} }}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }} \hfill \\ \end{gathered} $

(3)

式中：${\hat h_{su}}$表示认知用户信号信道增益的估计值。令r_x(m)表示认知用户信号的自相关函数，r_xy(m)表示认知用户信号的互相关函数：

$\begin{gathered} {r_x}\left( m \right) = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {{s_{su}}\left[ n \right]s_{su}^*\left[ {n + m} \right]} \hfill \\ E\left( {{s_{su}}\left[ n \right]s_{su}^*\left[ {n + m} \right]} \right) \hfill \\ \end{gathered} $

(4)

$\begin{gathered} {r_{xy}}\left( m \right) = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {\left( {{s_{pu}}\left[ {n - m} \right] + w\left[ {n + m} \right]} \right){s_{su}}\left[ n \right] = } \hfill \\ E\left[ {\left( {{s_{pu}}\left[ {n - m} \right] + w\left[ {n + m} \right]} \right)s_{su}^*\left[ n \right]} \right] \hfill \\ \end{gathered} $

(5)

式中：m表示信号的偏移量。由本文假设可知，m等于0。本文研究的主用户信号、认知用户信号和噪声是互相独立且均值为0的高斯信号，因此，如果N足够大，可以得到

$\begin{gathered} \frac{{{r_{xy}}\left( 0 \right)}}{{{r_x}\left( 0 \right)}} = \frac{{\sum\limits_N {\left( {{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]} }}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }} = \hfill \\ o\left( {\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} } \right) \hfill \\ \end{gathered} $

(6)

式中：ο(·)是无穷小量。基于式(3)、(6)对接收信号y[n]进行去认知用户信号处理：

$\begin{gathered} {y_{{\text{SUR}}}}\left[ n \right] = y\left( n \right) - {{\hat h}_{su}}{s_{su}}\left[ n \right] = \hfill \\ {s_{pu}}\left[ n \right] + w\left[ n \right] - o\left( {\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} } \right){s_{su}}\left[ n \right] \hfill \\ \end{gathered} $

(7)

式中：y_SUR[n]表示进行去认知用户信号处理之后的输出信号。在此基础上，进行主用户信号感知，由于在实际频谱感知过程中，检测长度N不可能无穷大，这决定了ο(·)将受主用户信号s_pu[n]和噪声w[n]的影响，因此ο(·)是一个小量，但不会是无穷小量。但是，在研究联合频谱感知算法时发现，当检测长度N>1 000时，对主用户信号感知采用基于能量检测的感知算法时，可以消除ο(·)大小变化对联合频谱感知算法性能的影响。对y_SUR[n]进行基于能量检测的主用户信号感知：

$\begin{gathered} {Y_{pu}} = \sum\limits_N {y_{{\text{SUR}}}^2\left[ n \right]} \hfill \\ \sum\limits_N {{{\left( {{s_{pu}}\left[ n \right] + w\left[ n \right] - o\left( {\sum\limits_N {{s_{su}}} \left[ n \right]s_{su}^*\left[ n \right]} \right){s_{su}}\left[ n \right]} \right)}^2}} \hfill \\ \end{gathered}$

(8)

式中：Y_pu表示感知主用户信号的检测统计量。根据式(1)、(8)，可得

${Y_{pu}} = \left\{ \begin{gathered} \sum\limits_N {{{\left( {w\left( n \right) - \alpha } \right)}^2}} ,{H_{00}} \hfill \\ \sum\limits_N {{{\left( {w\left( n \right) - \alpha } \right)}^2}} ,{H_{01}} \hfill \\ \sum\limits_N {{{\left( {{s_{pu}}\left( n \right) + w\left[ n \right] - \beta } \right)}^2}} ,{H_{10}} \hfill \\ \sum\limits_N {{{\left( {{s_{pu}}\left( n \right) + w\left[ n \right] - \beta } \right)}^2}} ,{H_{11}} \hfill \\ \end{gathered} \right.$

(9)

其中

$\left\{ \begin{gathered} \alpha = \frac{{\sum\limits_N {w\left[ n \right]s_{su}^*\left[ n \right]} }}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }}{s_{su}}\left[ n \right] \hfill \\ \beta = \frac{{\sum\limits_N {\left( {{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]} }}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }}{s_{su}}\left[ n \right] \hfill \\ \end{gathered} \right.$

(10)

当N足够大时，α和β对算法性能的影响可以消除，因此，当N足够大(N>>1)时，Y_pu服从如下分布：

$\frac{{{Y_{pu}}}}{{\sigma _{{\text{SUR}}}^2}} = \left\{ \begin{gathered} \frac{{{Y_{pu}}}}{{\sigma _n^2}} \sim \chi _N^2,{H_{_{00}}} \hfill \\ \frac{{{Y_{pu}}}}{{\sigma _n^2}} \sim \chi _N^2,{H_{01}} \hfill \\ \frac{{{Y_{pu}}}}{{\sigma _{pu}^2 + \sigma _n^2}} \sim \chi _N^2,{H_{10}} \hfill \\ \frac{{{Y_{pu}}}}{{\sigma _{pu}^2 + \sigma _n^2}} \sim \chi _N^2,{H_{11}} \hfill \\ \end{gathered} \right.$

(11)

式中：σ_SUR²是信号y_SUR[n]的方差，σ_pu²和σ_n²分别是主用户信号和噪声的方差。由式(11)可知，在消除α和β对算法性能的影响后，检测统计量Y_pu服从开方分布。式(11)还可以表示为

$\frac{{{Y_{pu}}}}{{\sigma _{signal}^2}} = \left\{ \begin{gathered} \frac{{{Y_{pu}}}}{{\sigma _n^2}} \sim \chi _N^2,{H_{_{0x}}} \hfill \\ \frac{{{Y_{pu}}}}{{\sigma _{pu}^2 + \sigma _n^2}} \sim \chi _N^2,{H_{1x}} \hfill \\ \end{gathered} \right.$

(12)

式中：H_0x表示不存在主用户信号，H_1x表示存在主用户信号。由式(12)可知，基于能量检测的联合频谱感知算法在主从信号共存的情况下进行主用户信号感知时，其检测统计量只与主用户信号和噪声的方差有关，消除了认知用户信号的影响，达到了本文研究的预期目的。

1.2 算法性能分析

检测概率、虚警概率和漏检概率是衡量频谱感知算法感知性能的指标。漏检概率和检测概率之和为1，因此漏检概率可由检测概率获得。

联合频谱感知算法的检测统计量服从开方分布，由式(12)可得联合频谱感知算法的检测概率和虚警概率：

$\left\{ \begin{gathered} {P_d} = P\left( {{Y_{pu}} \geqslant \lambda |{H_{1x}}} \right) = \hfill \\ \Gamma \left( {\frac{N}{2},\frac{\lambda }{{2\left( {\sigma _{pu}^2 + \sigma _n^2} \right)}}} \right)/\Gamma \left( {\frac{N}{2}} \right) \hfill \\ {P_f} = P\left( {{Y_{pu}} \geqslant \lambda |{H_{0x}}} \right) = \hfill \\ \Gamma \left( {\frac{N}{2},\frac{\lambda }{{2\sigma _n^2}}} \right)/\Gamma \left( {\frac{N}{2}} \right) \hfill \\ \end{gathered} \right.$

(13)

式中：P_d表示联合频谱感知算法的检测概率，P_f表示虚警概率，λ是检测门限，Γ(·)和Γ(·,·)是完全和非完全Gamma函数。

联合频谱感知算法的检测门限λ和检测长度N是算法的重要参数，通过这两个参数控制算法的频谱感知性能，λ和N通过式(13)获得。基于式(13)获得λ和N的严格表达式有点困难，根据中心极限定理，把开方分布近似转化成高斯分布。先计算检测统计量Y_pu的期望和方差：

$\left\{ \begin{gathered} E\left( {{Y_{pu}}} \right) = N\sigma _n^2 \hfill \\ D\left( {{Y_{pu}}} \right) = 2N\sigma _n^4,{H_{0x}} \hfill \\ E\left( {{Y_{pu}}} \right) = N\left( {\sigma _{pu}^2 + \sigma _n^2} \right) \hfill \\ D\left( {{Y_{pu}}} \right) = 2N{\left( {\sigma _{pu}^2 + \sigma _n^2} \right)^2},{H_{1x}} \hfill \\ \end{gathered} \right.$

(14)

研究发现，在一定信噪比下为了达到一定的感知性能，检测长度N通常取值很大(N>>1)，因此可以根据中心极限定理，简化λ和N的计算。式(12)可转化为

${Y_{pu}} \sim \left\{ \begin{gathered} N\left( {N\sigma _n^2,2N\sigma _n^4} \right),{H_{0x}} \hfill \\ N\left( {N\left( {\sigma _{pu}^2 + \sigma _n^2} \right),2N{{\left( {\sigma _{pu}^2 + \sigma _n^2} \right)}^2}} \right),{H_{1x}} \hfill \\ \end{gathered} \right.$

(15)

基于式(15)，式(13)可转化为

$\begin{gathered} {P_d} = P\left( {{Y_{pu}} > \lambda |{H_1}} \right) = Q\left( {\frac{{\lambda - N\left( {\sigma _{pu}^2 + \sigma _n^2} \right)}}{{\sqrt {2N{{\left( {\sigma _{pu}^2 + \sigma _n^2} \right)}^2}} }}} \right) \hfill \\ {P_f} = P\left( {{Y_{pu}} > \lambda |{H_0}} \right) = Q\left( {\frac{{\lambda - N\sigma _n^2}}{{\sqrt {2N\sigma _n^4} }}} \right) \hfill \\ \end{gathered} $

(16)

检测门限λ通常是由给定的虚警概率来决定的，因此检测门限λ可由下式计算得到

$\lambda = \left( {{Q^{ - 1}}\left( {{P_f}} \right)\sqrt {2N} + N} \right)\sigma _n^2$

(17)

对式(16)两边取反并进行相关运算，可以获得N的表达式：

$N \geqslant 2{\left[ {\left( {{Q^{ - 1}}\left( {{P_f}} \right) - {Q^{ - 1}}\left( {{P_d}} \right)} \right)\frac{{\sigma _n^2}}{{\sigma _{pu}^2}} - {Q^{ - 1}}\left( {{P_d}} \right)} \right]^2}$

(18)

如果给定了虚警概率P_f，可以确定检测门限λ，就可以得出检测概率P_d，从而确定联合频谱感知算法的最小检测长度。

2 认知用户信号不同步的影响

当认知用户本地先验信息信号与接收到的认知用户信号不同步时，本文分析这种不同步对联合频谱感知算法感知性能的影响。

2.1 频率不同步的影响

假设认知用户本地先验信息信号的频率和接收到的认知用户信号之间存在频率偏差:

${\tilde s_{su}}\left[ n \right] = {s_{su}}\left[ n \right]{e^{j\omega n}}$

(19)

式中：ω是频率偏差。基于上一节的分析，可得

${Y_{su}} = \sum\limits_N {\left( {{s_{su}}\left[ n \right] + {h_{su}}{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]{e^{ - j\omega n}}} $

(20)

${\hat h_{su}} = \left( {{h_{su}} + \frac{{\sum\limits_N {\left( {{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)s_{su}^*\left[ n \right]} }}{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ n \right]} }}} \right){e^{ - jwn}}$

(21)

当N足够大时：

${y_{{\text{SUB}}}}\left[ n \right] = {s_{pu}}\left[ n \right] + w\left[ n \right] + \left( {1 - {e^{ - jwn}}} \right){h_{su}}{s_{su}}\left[ n \right]$

(22)

${y_{pu}} = {\sum\limits_N {\left[ {{s_{pu}}\left[ n \right] + w\left[ n \right] + \left( {1 - {e^{ - jwn}}} \right){h_{su}}{s_{su}}\left[ n \right]} \right]} ^2}$

(23)

当$N \ll 2\pi /\omega $时，即2ωN≈0时，频率偏差ω对联合频谱感知算法性能的影响可以忽略。

2.2 相位不同步的影响

假设认知用户本地先验信息信号的相位和接收到的认知用户信号之间存在相位偏差:

${\tilde s_{su}}\left[ n \right] = {s_{su}}\left[ {n + m} \right]$

(24)

式中：m是相位偏差。可得：

${Y_{su}} = \sum\limits_N {\left( {{s_{su}}\left[ n \right] + {h_{su}}{s_{pu}}\left[ n \right] + w\left[ n \right]} \right)} s_{su}^*\left[ {n + m} \right]$

(25)

$\begin{gathered} {{\hat h}_{su}} = {h_{su}}\frac{{\sum\limits_N {{s_{su}}\left[ n \right]} s_{su}^*\left[ {n + m} \right]}}{{\sum\limits_N {{s_{su}}\left[ {n + m} \right]} s_{su}^*\left[ {n + m} \right]}} + \hfill \\ o\left( {\sum\limits_N {{s_{su}}\left[ {n + m} \right]} s_{su}^*\left[ {n + m} \right]} \right) \hfill \\ \end{gathered} $

(26)

当N足够大时：

$\begin{gathered} {y_{{\text{SUR}}}}\left[ n \right] = {s_{pu}}\left[ n \right] + w\left[ n \right] + \hfill \\ \left( {1 - \frac{{\sum\limits_N {{s_{su}}\left[ n \right]s_{su}^*\left[ {n + m} \right]} }}{{\sum\limits_N {{s_{su}}\left[ {n + m} \right]s_{su}^*\left[ {n + m} \right]} }}} \right){h_{su}}{s_{su}}\left[ n \right] \hfill \\ \end{gathered} $

(27)

由式(27)可知，当认知用户本地先验信息信号的相位与接收到的认知用户信号相位不同步时，联合频谱感知算法的检测性能将受到影响。随相位偏差m的变大，联合频谱感知算法的检测性能会急剧恶化。因此，主从信号共存时，采用联合频谱感知算法检测主用户信号需要保证认知用户本地先验信息信号的相位与接收到的认知用户信号的相位同步。

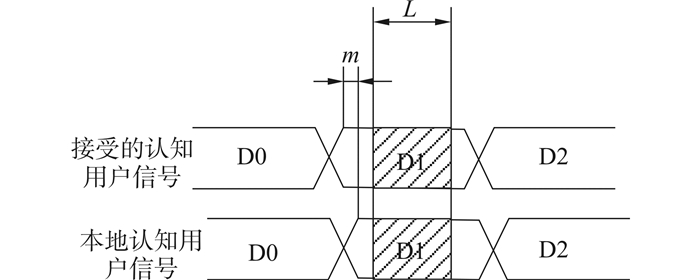
在实际应用中，可以通过信号同步模块对认知用户信号进行信号同步，在此基础上对接收到的认知用户信号进行再处理，如可以抛弃不同步的部分，对同步部分进行联合频谱感知。如图 2所示，经过同步模块的同步之后，接收到的认知用户信号与本地认知用户信号存在相位偏差m，对这两个信号进行截取L长度部分进行频谱感知，如图中阴影部分所示。

通过这种处理可以保证接收到的认知用户信号与本地认知用户信号严格同步，从而消除了相位偏差m对联合频谱感知算法检测性能的影响。

3 联合频谱感知算法验证和分析 3.1 联合频谱感知算法性能

本文设噪声的方差σ_n²为1，联合频谱感知算法的虚警概率P_f为1%。同时假设联合频谱感知算法在主用户信号的信噪比为-10 dB时检测概率为100%，则由式(18)可得最小检测长度N等于4 926。因此，对联合频谱感知算法的检测性能仿真时，设置其检测长度N为5 000。

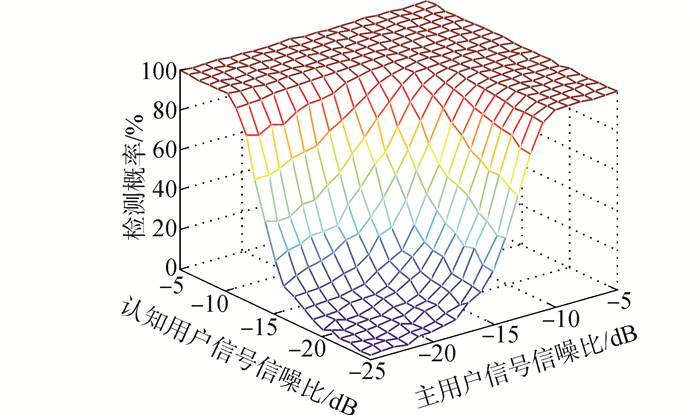
由图 3分析可知，能量检测算法的检测概率不仅受主用户信号信噪比的影响，而且还受到认知用户自身信号信噪比的影响。能量检测的检测概率随主用户信号或认知用户信号信噪比的变大而变大。这说明认知用户的频谱感知接收机如果采用能量检测算法，将无法区分接收到的信号是主用户信号还是认知用户自身的信号，从而无法判断认知用户占用的频段是否有主用户信号出现，从而使得认知用户的信号可能对主用户信号造成有害干扰。

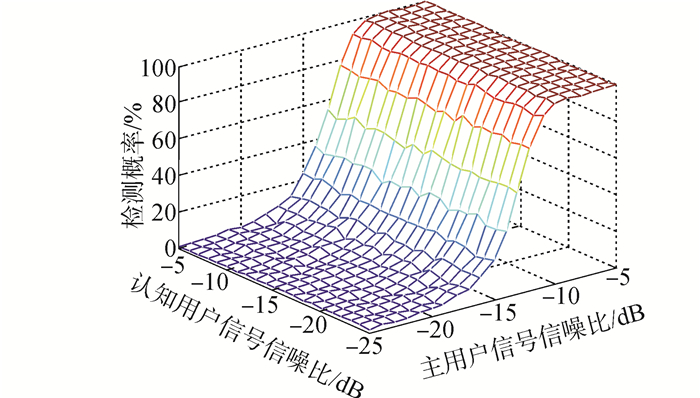
由图 4分析可知，联合频谱感知算法的检测概率仅受主用户信号信噪比的影响，不受认知用户自身信号信噪比的影响。联合频谱感知算法的检测概率仅随主用户信号信噪比的变化而变化，认知用户自身信号信噪比的变化对联合频谱感知算法的检测概率没有影响。由分析可知，联合频谱感知算法的检测概率和能量检测算法在只存在主用户信号时的检测概率一样。这说明认知用户的频谱感知接收机如果采用联合频谱感知算法，在主从信号共存时可以检测主用户信号，消除了认知用户自身信号对算法检测概率的影响。当认知用户占用授权频段时，认知用户的频谱感知接收机可以判断认知用户占用的频段是否有主用户信号出现，从而避免认知用户对主用户信号造成有害干扰。

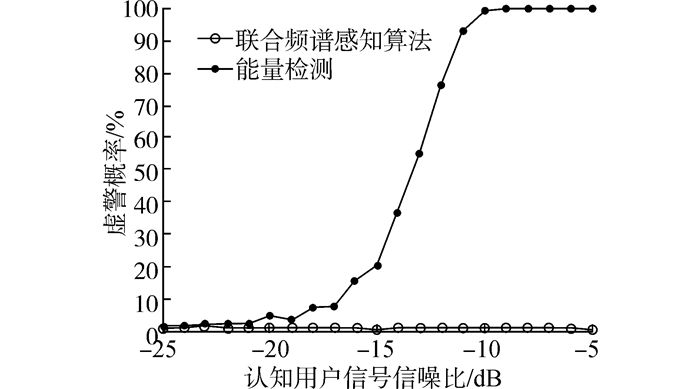
由图 5分析可知，当认知用户没有占用授权频段时，即没有认知用户信号时，联合频谱感知算法的虚警概率和经典能量检测算法的虚警概率都为1%。但当认知用户占用授权频段时，也即存在认知用户信号时，经典能量检测算法的虚警概率随认知用户信号信噪比的变大而变大，因为能量检测算法只能检测授权频段中信号的能量，而无法区分主用户信号和认知用户信号。而不管是否存在认知用户信号，联合频谱感知算法的虚警概率一直维持在1%，这说明联合频谱感知算法的虚警概率不受认知用户信号的影响。

由上述分析可知，能量检测算法的检测概率和虚警概率受认知用户自身信号信噪比的影响，随认知用户信号信噪比变化而变化，这说明能量检测算法可以感知信号，但是不能区分感知到的是主用户信号还是认知用户信号。而联合频谱感知算法的检测性能不受认知用户自身信号的影响，可以在主从信号共存的情况下感知主用户信号，其感知性能与能量检测算法在只存在主用户信号的情况下的感知性能一样，使得认知用户在占用授权频段时感知主用户信号的出现，从而停止对授权频段的占用，避免对主用户信号造成有害干扰。

3.2 信号不同步对算法性能的影响

当本文中认知用户本地先验信息信号与接收到的认知用户信号同步的假设不成立时，以认知用户本地先验信息信号与接收到的认知用户信号之间存在相位差为例，进行算法检测性能仿真和分析。

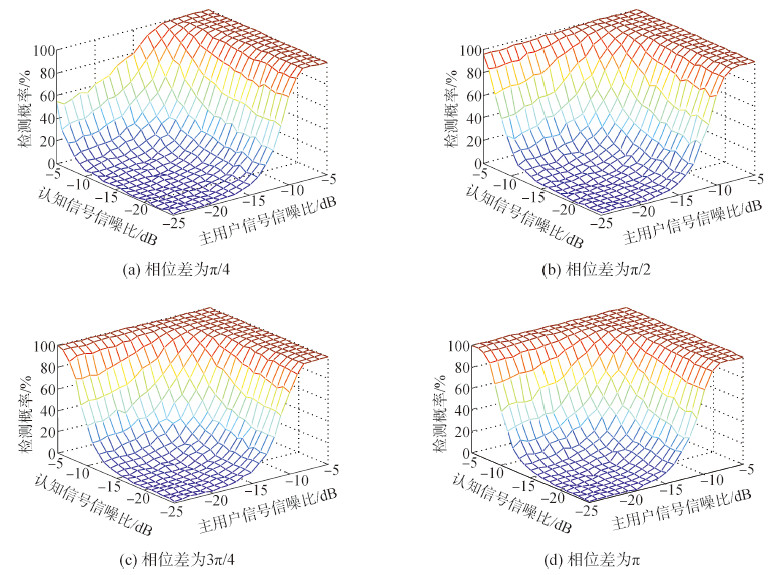
由图 6分析可知，存在相位差时，联合频谱感知算法的检测概率随着认知用户信号信噪比变大而变大。而且随着相位差的变大，联合频谱感知算法的检测概率变大的幅度也随之增加。这说明，联合频谱感知算法的检测概率受相位差的影响，而且这种影响与相位差和认知用户信号信噪比的大小成正向变化。

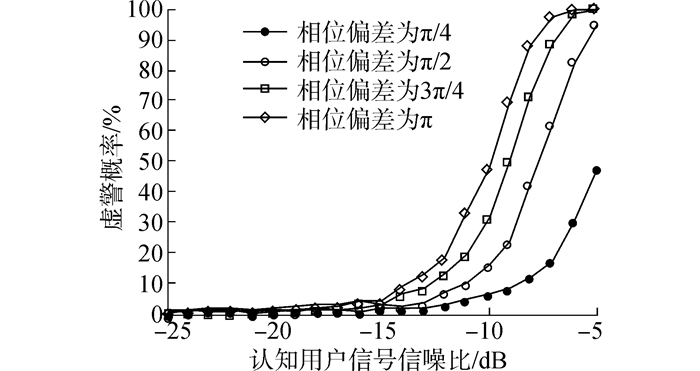
图 7给出了认知用户本地先验信息信号与接收到的认知用户信号之间存在不同相位差时联合频谱感知算法的虚警概率。由图 7分析可知，此时联合频谱感知算法不能消除认知用户信号的影响，其虚警概率受认知用户信号信噪比和相位差的影响。随着相位差或认知用户信号信噪比的增加，联合频谱感知算法的虚警概率越来越大。

由上分析可知，联合频谱感知算法的检测性能受相位差的影响。这种相位差的存在使得联合频谱感知算法无法消除认知用户自身信号对检测性能的影响，尤其是在认知用户信号的高信噪比情况下恶化了联合频谱感知算法的检测性能。因此，联合频谱感知算法应工作在认知用户信号同步的情况下。

4 结束语

本文提出一种联合频谱感知算法，用以解决认知无线电技术中主从信号共存时感知主用户信号的问题。基于认知用户掌握自身信号先验信息的这一条件，当主从信号共存时，联合频谱感知算法利用本地已知的认知用户先验信息对接收到的信号进行预处理，复现接收到的信号中认知用户的信号，进而从接收信号中剔除认知用户信号，然后对预处理之后的接收信号进行主用户信号的感知。理论分析和仿真结果表明，本文提出的联合频谱感知算法不仅能够在主从信号共存的条件下有效地感知主用户信号，消除了认知用户信号对主用户信号感知的影响，同时其感知性能与在只存在主用户信号的条件下典型频谱感知算法的感知性能相同。