船体曲线曲面生成技术是计算机辅助船舶设计CASD领域最活跃最的学科分支之一，是实现船舶数字化造型的关键技术之一，它可以辅助进行船舶总体性能计算、适航性计算、流体力学分析、结构设计和船舶的生产设计。船体曲面通常是非常复杂的几何曲面，特别是在艏艉区域具有双向曲度，因此如何快速精确的表达船体曲面一直是困扰很多造船工作者的难题，也是他们一直努力的目标。

船体曲线曲面生成是船舶设计制造重要的技术基础，自从国际标准化组织(ISO)正式将NURBS作为定义工业产品几何形状的唯一数学方法^[1]，曲线曲面几何造型实现了表达形式的统一。国内外学者对船体曲线曲面生成算法原理进行了大量研究，David F. Rogers^[2]首次提出采用B样条曲线和曲面来表达船体；Nam^[3]在船体曲面设计过程中运用NURBS方法表达；Le T-H等^[4]采用遗传算法，以数据点和曲面的最近距离作为适应度函数来拟合曲面；WANG Hu等^[5]通过迭代的方式使得曲面在两个参数方向各自具有相同的控制顶点数和节点矢量，然后得到整个船体曲面。周超骏等^[6]采用B样条构造船体曲面；林焰等^{[7, 8, 9, 10]}对船体曲面的NURBS表达和设计进行了系列研究；陈宾康等^{[11, 12]}对NURBS 在船舶设计中的应用进行了相关研究。

在目前的船舶设计过程中，设计人员工作的出发点大多是船体型值点，所关心的是船体型值。但是，船体曲面的重构需要用到的是NURBS 曲线、曲面的控制顶点。基于NURBS的船体曲面重构解决的是NURBS曲面的“反算”问题，即根据已知船体曲面上的一些型值点，构造出NURBS曲面，且保证曲面通过或逼近这些型值点。

本文以NURBS为船体曲线曲面的数学表达工具，采取由点—线—面的方式来获得整个船体曲面，其中点为现有型值点，线为通过本文方法所构造的广义站线，面则为最终通过改进放样法得到的船体曲面。研究表明，本方法能够根据有限的离散型值获得较为精确和光顺的船体曲面，利于对船体进行后续的CAD/CAE/CAM处理。

1 船体NURBS曲线的插值和逼近

本文中NURBS曲线曲面均采用齐次坐标表示^[13]，次数取为三次和双三次。

1.1 曲线插值

可以将NURBS曲线的插值视为简单的插值四维带权型值点的问题，即求解出插值带权型值点的非有理B样条曲线的带权控制顶点，它和传统的B样条插值方法一致，然后取其在的超平面ω=1上的投影，便得到所求的NURBS曲线的控制顶点。

已知待插值的型值点为p_i0(i₀=0,1,…,n₀)，其对应的权因子为h_i0，插值问题的目标就是求解该曲线的控制顶点d_i(i=0,1,…,n)和对应的权因子ω_i，使之定义的曲线插值这些型值点，其中n=|n₀+2|。具体的插值反算过程如下：

1)根据权因子将三维型值点转化为四维带权型值点P_i0=[h_i0p_i0,h_i0]；

2)采用累加弦长参数化法计算型值点对应的参数值${\bar u_{{i_0}}}$=[i₀=0,1,…,n₀]，对型值点进行参数化：

$\left\{ \begin{gathered} {{\bar u}_0} = 0 \hfill \\ {{\bar u}_{{i_0}}} = {{\bar u}_{{i_0} - 1}} + \frac{{\left| {{P_{{i_0}}} - {P_{{i_0} - 1}}} \right|}}{L},{i_0} = 1,2,\cdots ,{n_0} - 1 \hfill \\ {{\bar u}_{{n_0}}} = 1 \hfill \\ \end{gathered} \right.$

(1)

式中：$L = \sum\limits_{j = 1}^{{n_0}} {\left| {{P_j} - {P_{j - 1}}} \right|} $。

3)将2)计算的参数值作为节点矢量U={u₀,u₁,…,u_n0+6}定义域[u_k,u_n0+3]内的节点值，同时取两端节点重合度为k+1=4，使得曲线两端的控制顶点与首尾型值点重合且在曲线首尾端点处与控制多边形首尾边相切，即

$\left\{ \begin{gathered} {u_0} = {u_1} = {u_2} = {u_3} = 0 \hfill \\ {u_i} = {{\bar u}_{i - 3}},i = 4,5,\cdots ,{n_0} + 2 \hfill \\ {u_{{n_0} + 3}} = {u_{{n_0} + 4}}{ = _{{n_0} + 5}}{ = _{{n_0} + 6}} = 1 \hfill \\ \end{gathered} \right.$

(2)

4)曲线的分段连接点分别依次与NURBS曲线定义域内的节点一一对应，因此按照式(1)可建立插值方程组，目前该方程组中仅包含n₀+1个方程，而未知控制顶点为n₀+3个，因此还需要添加2个边界条件使方程组封闭。常用的边界条件包括端切矢条件、自由端条件、抛物线条件、非节点条件等^[14]。结合边界条件将方程组写成矩阵形式，以自由端边界条件为例：

$P = ND$

(3)

式中：

$\begin{gathered} {P^T} = \left[{0{P_0}{P_1} \cdots {P_{{n_0}}}0} \right] \hfill \\ {D^T} = \left[{{D_0}{D_1} \cdots {D_{{n_0} + 2}}} \right] \hfill \\ N = \left[\begin{gathered} N_{0,3}^\left( {{u_3}} \right)N_{1,3}^\left( {{u_3}} \right) \cdots N_{{n_0} + 2,3}^\left( {{u_3}} \right) \hfill \\ {N_{0,3}}\left( {{u_3}} \right){\text{ }}{N_{1,3}}\left( {{u_3}} \right){\text{ }} \cdots {\text{ }}{N_{{n_0} + 2,3}}\left( {{u_3}} \right) \hfill \\ {N_{0,3}}\left( {{u_4}} \right){\text{ }}{N_{1,3}}\left( {{u_4}} \right){\text{ }} \cdots {\text{ }}{N_{{n_0} + 2,3}}\left( {{u_4}} \right) \hfill \\ {\text{ }} \vdots {\text{ }} \vdots {\text{ }} \ddots {\text{ }} \vdots \hfill \\ {N_{0,3}}\left( {{u_{{n_0} + 3}}} \right){\text{ }}{N_{1,3}}\left( {{u_{{n_0} + 3}}} \right){\text{ }} \cdots {\text{ }}{N_{{n_0} + 2,3}}\left( {{u_{{n_0} + 3}}} \right) \hfill \\ N_{_{0,3}}^\left( {{u_{{n_0} + 3}}} \right){\text{ }}N_{_{1,3}}^\left( {{u_{{n_0} + 3}}} \right){\text{ }} \cdots {\text{ }}N_{_{{n_0} + 2,3}}^\left( {{u_{{n_0} + 3}}} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $

注意N中的元素大部分值为零，每一行只有4个为非零值，求解式(3)便可以得到相应的带权控制顶点：

$\ = {N^{ - 1}}P$

(4)

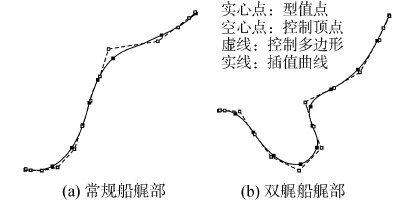
5)将求得的四维控制顶点D_i=[ω_id_i,ω_i]向超平面ω=1上投影，得到控制顶点d_i及其权因子ω_i。在计算的初始阶段，型值点的初始权因子h_i0可以全部取1，后期可以根据曲线的曲率变化进行调整，重新反算。图 1为某常规单体船和某双艉船艉部的插值横剖线。

1.2 曲线逼近

事实上往往由于测量误差、录入错误等原因，很多情况下得到的型值点都不是百分百准确的。以此作为后续工作的基础，会使误差得以保留、传递，因此，应该对型值点进行处理，降低误差，即采用逼近而非插值的方式得到曲线往往更有效。

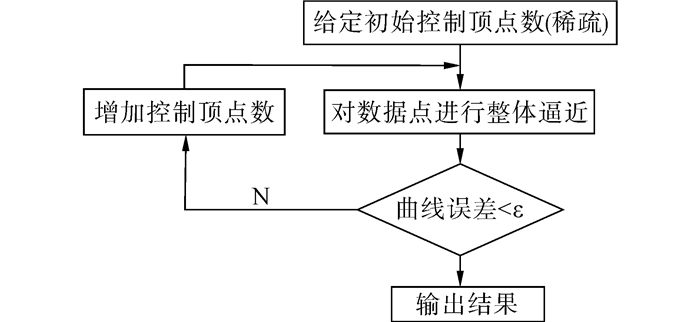
已知待逼近的型值点为p_i0(i₀=0,1,…,n₀)，其对应的权因子为h_i0，逼近问题的目标就是求解该曲线的n_app+1个控制顶点d_i(i=0,1,…,n_app)和对应的权因子ω_i，使其定义的曲线在给定的误差界限ε内逼近这些型值点，其中3 < n_app < n₀。逼近过程的流程图如图 2所示。

具体的插值反算过程如下：

1)根据权因子将三维型值点转化为四维带权型值点P_i0=[h_i0p_i0,h_i0]；

2)采用累加弦长参数化法计算型值点对应的参数值$\bar u$_i0(i₀=0,1,…,n₀)，对型值点进行参数化：

$\left\{ \begin{gathered} {{\bar u}_0} = 0 \hfill \\ {{\bar u}_{{i_0}}} = {{\bar u}_{{i_0} - 1}} + \frac{{\left| {{P_{{i_0}}} - {P_{{i_0} - 1}}} \right|}}{L},{i_0} = 1,2,\cdots ,{n_0} - 1 \hfill \\ {{\bar u}_{{n_0}}} = 1 \hfill \\ \end{gathered} \right.$

(5)

式中：$L = \sum\limits_{j = 1}^{{n_0}} {\left| {{P_j} - {P_{j - 1}}} \right|} $。

3)此时需要寻找一条三次NURBS曲线：

${C^\omega }\left( u \right) = \sum\limits_{i = 0}^{{n_{app}}} {{D_i}{N_{i,3}}\left( u \right)}$

(6)

满足：

${P_0} = {C^\omega }\left( 0 \right) = {D_0},{P_{{n_0}}} = {C^\omega }\left( 1 \right) = {D_{{n_{pp}}}}$

剩下的型值点则以最小二乘的方式的逼近，即

$\sum\limits_{{i_0} = 1}^{{n_{_0}}_{ - 1}} {{{\left| {{P_{{i_0}}} - {C^\omega }\left( {{{\bar u}_{{i_0}}}} \right)} \right|}^2}} $

(7)

达到最小，需要注意的是C^ω($\bar u$_i0)并非曲线上离P_n0最近的点。

令R_i0=P_i0-N_0,3($\bar u$_i0)D₀-N_npp,3($\bar u$_i0)D_n0，定义函数：

$\begin{gathered} f = \sum\limits_{{i_0} - 1}^{{n_0} - 1} {{{\left| {{P_{{i_0}}} - {C^\omega }\left( {{{\bar u}_{{i_0}}}} \right)} \right|}^2}} \hfill \\ \sum\limits_{{i_0} - 1}^{{n_0} - 1} {{{\left| {{R_{{i_0}}} - \sum\limits_{i = 1}^{{n_{{\text{app}}}} - 1} {{N_{i,3}}\left( {{{\bar u}_{{i_0}}}} \right){D_i}} } \right|}^2}} \hfill \\ \end{gathered} $

式中：f为一个包含n_app-1个变量D₁,D₂,…,D_npp-1的标量函数。应用标准的线性最小二乘拟合技术，欲使f最小，则其关于未知变量D_l的导数为零，即

$\frac{{\partial f}}{{\partial {D_l}}} = \sum\limits_{{i_0} - 1}^{{n_0} - 1} {\left( {2{N_{l,3}}\left( {{{\bar u}_{{i_0}}}} \right){R_{{i_0}}} + 2{N_{l,3}}\left( {{{\bar u}_{{i_0}}}} \right)\sum\limits_{i = 1}^{{n_{{\text{app}}}} - 1} {{N_{i,3}}\left( {{{\bar u}_{{i_0}}}} \right){D_i}} } \right)} = 0$

对上式进行简单变换可得

$\begin{gathered} \sum\limits_{i = 1}^{{n_{{\text{app}}}} - 1} {\left( {\sum\limits_{{i_0} - 1}^{{n_0} - 1} {{N_{l,3}}\left( {{{\bar u}_{{i_0}}}} \right){N_{i,3}}\left( {{{\bar u}_{{i_0}}}} \right)} } \right)} \hfill \\ {D_i} = \sum\limits_{{i_0} - 1}^{{n_0} - 1} {\left( {{N_{l,3}}\left( {{{\bar u}_{{i_0}}}} \right){R_{{i_0}}}} \right)} \hfill \\ \end{gathered} $

(8)

式(8)为关于未知控制顶点的线性方程，由于l=1,2,…,n_app-1，因此便得到一个包含n_app-1个变量和n_app-1的方程的方程组。写成矩阵形式为

$\left( {{N^T}N} \right)D = R$

(9)

式中：

$\begin{gathered} N = \left[\begin{gathered} {N_{1,3}}\left( {{{\bar u}_1}} \right) \cdots {N_{{n_{app}} - 1,3}}\left( {{{\bar u}_1}} \right) \hfill \\ {N_{1,3}}\left( {{{\bar u}_2}} \right) \cdots {N_{{n_{app}} - 1,3}}\left( {{{\bar u}_2}} \right) \hfill \\ \vdots \ddots \vdots \hfill \\ {N_{1,3}}\left( {{{\bar u}_{{n_0} - 1}}} \right) \cdots {N_{{n_{app}} - 1,3}}\left( {{{\bar u}_{{n_0}1}}} \right) \hfill \\ \end{gathered} \right],\hfill \\ R = \left[\begin{gathered} {N_{1,3}}\left( {{{\bar u}_1}} \right){R_2} + {N_{1,3}}\left( {{{\bar u}_2}} \right){R_2} + \cdots + {N_{1,3}}\left( {{{\bar u}_{{n_0}1}}} \right){R_{{n_0} - 1}} \hfill \\ {N_{2,3}}\left( {{{\bar u}_1}} \right){R_2} + {N_{2,3}}\left( {{{\bar u}_2}} \right){R_2} + \cdots + {N_{2,3}}\left( {{{\bar u}_{{n_0}1}}} \right){R_{{n_0} - 1}} \hfill \\ \vdots \hfill \\ {N_{{n_{{\text{app}}}}1,3}}\left( {{{\bar u}_1}} \right){R_2} + {N_{{n_{{\text{app}}}}1,3}}\left( {{{\bar u}_2}} \right){R_2} + \cdots + {N_{{n_{{\text{app}}}}1,3}}\left( {{{\bar u}_{{n_0}1}}} \right){R_{{n_0} - 1}} \hfill \\ \end{gathered} \right] \hfill \\ {D^{\text{T}}} = \left[{{D_1}{D_2} \cdots {D_{{n_{{\text{app}}}}1}}} \right] \hfill \\ \end{gathered} $

由于N和R都包含基函数的表达式，因此还需要确定其节点矢量，令g=(n₀+1)/(n_app-2)，则节点矢量可根据下式定义^[13]：

$\left\{ \begin{gathered} {u_0} = {u_1} = {u_2} = {u_3} = 0 \hfill \\ \alpha = jg - i \hfill \\ {u_{3 + j}} = \left( {1 - \alpha } \right){{\bar u}_{i - 1}} + \alpha \hfill \\ {{\bar u}_i}{u_{{n_{{\text{app}}}} + 1}} = {u_{{n_{{\text{app}}}} + 2}} = {u_{{n_{{\text{app}}}} + 3}} = {u_{{n_{{\text{app}}}} + 4}} = 1 \hfill \\ \end{gathered} \right.$

(10)

式中：i=int(jg),int()为向下取整函数；j=1,2,…,n_app-3。这样取节点矢量可以保证每一个节点矢量区间至少包含一个型值点的参数值，防止了方程组出现奇异的情况。得到节点矢量以后，求解方程组(9)便可以得到相应的带权控制顶点：

$D = {\left( {{N^T}N} \right)^{ - 1}}R$

(11)

4)将求得的四维带权控制顶点D_i=[ω_id_i,ω_i]向超平面ω=1上投影，得到控制顶点d_i及其权因子ω_i。

5)计算求得的逼近曲线与型值点之间的偏差，可以用最大欧几里得范数距离来表达：

$\xi = \mathop {\max }\limits_{1 \leqslant {i_0} \leqslant {n_0} - 1} \left( {\mathop {\min }\limits_{0 \leqslant u \leqslant 1} \left| {{P_{{i_0}}} - {C^\omega }\left( {{{\bar u}_{{i_0}}}} \right)} \right|} \right)$

(12)

如果ξ≤ε，则输出结果，如果ξ>ε，则取n_app=n_app+1然后转到第3)步继续执行。

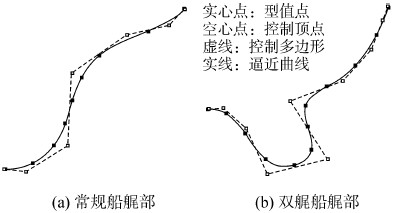
图 3为某常规单体船和某双艉船的艉部逼近横剖线。图 3(a)和(b)曲线与型值点的最大相对误差分别为0.24%和0.18%。

对于实际应用中具体是采用插值还是逼近一方面要考虑型值点的精度，另一方面要考虑型值点的个数。如果型值点不存在测量误差或录入误差且每个横截面的型值点数量不多并分析较为均匀，建议采用插值方法，否则作者建议采用逼近的方法。插值能保证精度但是控制顶点数相对较多，而逼近能够保证在规定误差范围内的情况下进行数据压缩，设计者可根据具体情况进行选择。

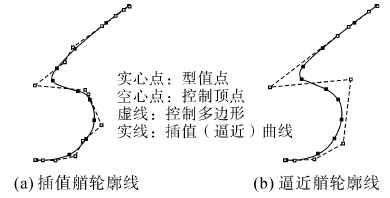
图 4为某船型艏轮廓线的插值和逼近NURBS曲线对比。型值点数为12个，图 4(a)插值曲线的控制顶点为14个，曲线精确通过每个型值点，图 4(b)逼近曲线的控制顶点个数为10个，曲线与型值点的最大相对误差为0.17%。从图中可知，对于型值点较多且分布不太均匀的型值点，逼近曲线要比插值曲线光顺。因此对于允许存在一定误差的情况下，逼近曲线的效果要优于插值曲线。

2 广义站的构造和曲线重构 2.1 构造广义站线

显然，常规的站线无法构成完整表达船体曲面的设计截面，还需要艏艉轮廓线和反应艏艉曲率变化特征的特征曲线，本文以纵向设计法为基础，将船体的艏艉轮廓线和反映艏艉曲率变化特征的特征曲线统称为广义站线，本节将主要介绍这些广义站线的构造方法。

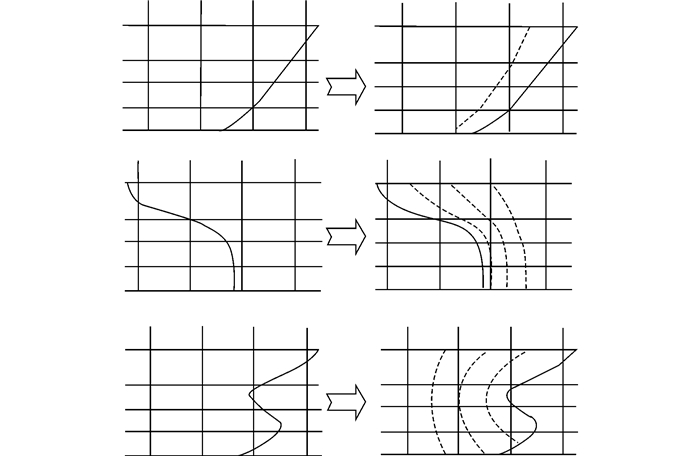
艏艉轮廓线的构造相对简单，只要根据中纵剖线上的型值点插值或逼近即可得到，而反映艏艉曲率变化特征的特征曲线的构造则相对复杂，首先这些特征曲线往往并非平面曲线，如图 5中左列所示，平面广义站线通常无法准确反映艏艉部的曲率变化与过渡，因此本文采用三维空间曲线作为广义站线，以便于较好的反映艏艉曲面的走势，如图 5中右列虚线所示，这些曲线便是所谓的广义站线。

由于仅根据常规站线无法获得空间广义站线的信息，所以要借助于水线或纵剖线，由于水线相对纵剖线更符合一般的设计思路，因此本文主要借助水线来构造广义站线，具体的构造方法如下：

1)根据型值点，依照第1节提出的插值或逼近方法，得到各条常规横剖站线和水线的NURBS表达式。

2)确定广义站线的纵向范围：以艏部为例：对于不包含球艏的简单船型，如图 5中最上面一行图所示，可以将离艏轮廓线最近的站线作为艏部广义站线的左边界，对于带球艏的船型，如图 5中最下面一行图所示，此时球艏和船体曲面主体的过渡部分存在双向曲度，通常需要相对较长的纵向范围且较多的广义站线，因此将离艏轮廓线次近的站线作为艏部广义站线的左边界。艉部广义站线纵向范围的确定方式则与艏部类似，如图 5中中间一行图所示。

3)为了获得构造广义站线的广义型值点，需要在步2)确定的纵向范围内对每条水线进行等数分割，分割的方式可以是等弧长分割也可以是其他不等弧长分割例如等比分割、指数分割等^[15]。本文采取等弧长的等数分割来构造广义型值点，弧长计算表达式如下：

$s\left( u \right) = \int_{{u_B}}^{{u_E}} {\left| {W'\left( u \right)} \right|{\text{d}}u\sqrt {x'{{\left( u \right)}^2} + y'{{\left( u \right)}^2}{\text{d}}u} } $

(13)

式中：W(u)=(x(u),y(u))为水线的NURBS表达式，u_B和u_E分别为水线在纵向范围内起点和终点对应的参数值。艏艉处各自的广义站线的条数即等数分割的内点个数可取为3~5，视艏艉曲面的复杂程度而定。

4)根据第1节提出的方法，对广义型值点进行插值或逼近得到广义站线。

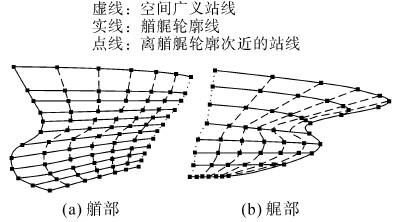
将艏艉广义站线纵向范围内的空间广义站线取代该范围内的常规站线，配合艏艉轮廓线以及艏艉空间广义站线之间的中间常规站线，共同构成了后续生成船体曲面的截面曲线。图 6为本方法构造的带球艏和球艉船型的艏艉部广义站线。

2.2 基于等数弧长均分的曲线重构

对曲线进行放样生成船体曲面之前，首先就是对截面曲线进行一致化处理，对于传统的曲面放样方法，如果直接对未处理的截面曲线进行放样，一致化过程中由于需要对各条截面曲线进行升阶和节点插入处理，一般来说，如果有k条截面曲线，每条截面线平均有n个控制点，则一致化处理后每条曲线的控制点数目为ο(kn)，从而最终曲面的控制点数目为ο(k²n)。这样会造成大量的控制顶点冗余，一方面会极大的影响曲面生成的速度，另一方面会使曲面存在大量过小的面元，对后续的建造和水动力性能分析造成不良影响。

大量控制顶点的引入使得经典的曲面放样算法很难直接应用到实际的CAD系统中，因此本文提出一种新的一致化处理方法：首先对各条截面曲线(包括常规站线和广义站线)进行等数弧长均分采样以获得广义型值点，然后采用相同次数和节点矢量的一组相容的的NURBS曲线来插值采样点，从而对截面曲线进行一致化的重构。经过该处理过程，各条重构的截面曲线便具有相同的次数、控制顶点数和节点矢量，这样不仅构造了一致化的截面曲线，同时大大减少了控制顶点的冗余，从而为后续的放样曲面过程提供了良好的基础。注意此处采用等数弧长均分的方式采样和2.1节中对水线进行等数弧长均分的目的是不一样的，后者是为了获得足够数量的广义站线以反映曲面在艏艉的走势，而前者是为了构造一致化的截面曲线。

具体的截面曲线一致化重构过程如下：

1)对各截面曲线进行等数弧长均分，设重构前的原截面曲线为

${C^{\left( 0 \right)}}\left( u \right) = \sum\limits_{i = 0}^n {D_{^i}^{\left( 0 \right)}{N_{i,3}}\left( u \right)} $

(14)

式中：$D_i^{\left( 0 \right)} = \left[{\omega _i^{\left( 0 \right)}d_i^{\left( {} \right)},\omega _i^{\left( 0 \right)}} \right]\left( {i = 0,1,\cdots ,n} \right)$，节点矢量为${U^{\left( 0 \right)}} = \left\{ {u_0^{\left( 0 \right)},u_1^{\left( 0 \right)},\cdots ,u_{n + k + 1}^{\left( 0 \right)}} \right\}$，均分的数目m由用户给定的精度ε确定，类似于逼近的思路，显然当m→+$\infty $时，重构曲线收敛于原截面曲线。首先先取一个较小的m，此时均分得到的广义型值点个数为m+1。

2)对各条截面曲线的广义型值点进行NURBS插值，次数取为三次，节点矢量则取准均匀节点矢量：

$\left\{ \begin{gathered} {u_0} = {u_1} = {u_2} = {u_3} = 0 \hfill \\ {u_i} = \left( {i - 3} \right)/m,i = 4,5,\cdots ,m + 2 \hfill \\ {u_{m + 3}} = {u_{m + 4}} = {u_{m + 5}} = {u_{m + 6}} = 1 \hfill \\ \end{gathered} \right.$

(15)

由于是采用等数弧长均分进行广义型值点的采样，因此取准均匀节点矢量是合理的，基本上近似于弧长参数化。边界条件取为切矢条件，由重构前的原截面曲线C_u⁽⁰⁾确定：

$\begin{gathered} C'\left( 0 \right) = \frac{3}{{{u_4}}}\frac{{\omega _1^{\left( 0 \right)}}}{{\omega _0^{\left( 0 \right)}}}\left( {d_1^{\left( 0 \right)} - d_1^{\left( 0 \right)}} \right) \hfill \\ C'\left( 1 \right) = \frac{3}{{1 - {u_n}}}\frac{{\omega _{n - 1}^{\left( 0 \right)}}}{{\omega _n^{\left( 0 \right)}}}\left( {d_n^{\left( 0 \right)} - d_{n - 1}^{\left( 0 \right)}} \right) \hfill \\ \end{gathered} $

3)采用1.1节叙述的插值方法对广义型值点进行插值，得到重构后的一致化截面曲线：

$C\left( u \right) = \sum\limits_{i = 0}^{m + 2} {{D_i}{N_{i,3}}\left( u \right)} $

(16)

4)计算重构曲线与原截面曲线之间的偏差，同样用最大欧几里得范数距离来表达：

$\xi = \max \left| {C\left( u \right) - {C^{\left( 0 \right)}}\left( u \right)} \right|$

如果ξ≤ε，则输出结果，如果ξ>ε，则取m=m+1然后转到第2)步继续执行。

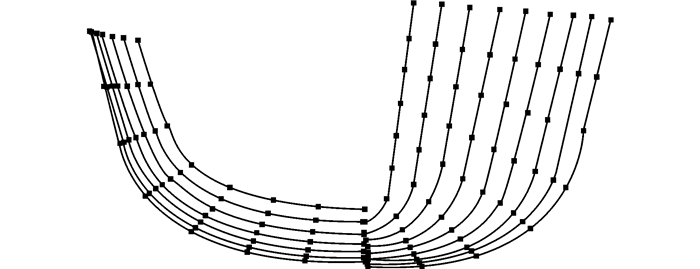
图 7为一游艇重构前和重构后的船体曲线对比。

从图中可知重构曲线几乎跟原曲线重合，相对误差为ε=0.05%，弧长等分数为7，而且满足后续生成曲面的一致化要求。

3 船体NURBS曲面的重构

不同的船型，外型有不同的特点。船体外型的传统描述与表达是船舶型线图和型值表。经过实船的NURBS描述已证明，仅通过船舶型线图和型值表是不能够得到光顺的船体曲面，原因是船舶型线图的站线、水线均太稀疏，不足以来表达光顺的船体曲面。而船体曲面造型包含了一条船的完整的形状信息，它的信息量较船舶型线图或肋骨型线图更完整、全面。

本节的目的便是通过上节重构的截面曲线(包括广义站线和常规站线)来构造船体曲面，采用的曲面生成方法为改进的放样曲面(lofting surface)方法^[16]，该方法将截面曲线定义为参数曲面的等参数线并插值通过这些截面曲线。由于重构后的各截面曲线已经满足一致化要求，因此可直接跳过对曲线的预处理过程而直接进行曲面生成，将截面曲线的参数方向取为u向，不失一般性，设共有q+1条截面曲线：

${C_s}\left( u \right) = \sum\limits_{i = 0}^n {{{\bar D}_{i,s}}{N_{i,3}}\left( u \right)} $

(17)

式中：${\bar D_{i,s}} = \left[{{{\bar \omega }_{i,s}}{{\bar d}_{i,s}},{{\bar \omega }_{i,s}}} \right]$为第s条截面曲线的控制顶点，v向则取船体纵向方向。i=0,1,…,n、s=0,1,…,q。根据NURBS插值和曲面放样理论，需要找到一个NURBS曲面插值通过这些截面曲线，即通过将截面曲线的带权控制顶点作为新的“型值点”，对这些“型值点”沿v向插值得到的控制顶点网格，便是该NURBS曲面的控制点网格。

对于传统的曲面放样方法而言，由于它只是单纯的对截面曲线进行插值，并没有考虑到所生成曲面的光顺性，文中对传统的放样法做出改进，采用基于光顺原则的放样法进行船体曲面的建模，即在曲面生成的过程中考虑v向即纵向曲线的光顺性，在对q+1条截面曲线的带权控制顶点$\bar D$_i,s插值时，设生成v向纵向曲线为L_i(v)，控制顶点数量为m+1，取为3次，则其可以表示为

${L_i}\left( v \right) = \sum\limits_{j = 0}^m {{D_{i,j}}{N_{j,3}}\left( v \right)} $

(18)

式中：D_i,j(j=0,1,…,m)为各条纵向曲线L_i(v)(i=0,1,…,n)的带权控制顶点，也是整个NURBS曲面的控制顶点。曲线L_i(v)在定义域节点v_s(s=0,1,…,q)上的值等于相应截面曲线上的控制顶点：

${L_i}\left( {{v_s}} \right) = \sum\limits_{s = 0}^m {{D_{i,j}}{N_{j,3}}\left( {{v_s}} \right)} = {\bar D_{i,s}}$

(19)

对v向的各行截面曲线控制顶点采用累加弦长参数化方法计算其对应的v向参数值，取各个对应控制顶点参数值的平均值作为统一的v向参数值v_s^[13]：

${v_0} = 0,{v_q} = 1,{v_s} = {v_{s - 1}} + \frac{1}{{n + 1}}\sum\limits_{i = 0}^n {\frac{{\left| {{{\bar D}_{i,s}} - {{\bar D}_{i,s - 1}}1} \right|}}{{{L_i}}}} $

(20)

式中：${L_i} = \sum\limits_{s = 1}^q {\left| {{{\bar D}_{i,s}} - {{\bar D}_{i,s - 1}}} \right|} $。

若采用传统的曲面放样法，则m=q+2，即每条纵向曲线的位置控制顶点数为q+3个，而式(19)共有q+1个方程，和曲线插值方法类似，如果要求解该问题，必须要额外再添加两个边界条件。并且传统的曲面放样法只是单纯的对截面曲线进行插值，并没有考虑到所生成曲面的光顺性，因此对于v向纵向曲线式(18)，根据NURBS曲线的端点性质，曲线在首尾端点与首尾控制顶点重合，同时保证纵向曲线在节点参数处的值即为相应横剖面的控制顶点，并将其作为等式约束条件，从而，就共有4×(q-1)个约束条件，此时便可将基于光顺原则的曲面放样法转化为

$\begin{align} & \min {{F}_{i}}={{E}_{i}}+{{B}_{i}}= \\ & \int{{{\left| L_{i}^{''}\left( v \right) \right|}^{2}}\text{d}v}+\sum\limits_{j=1}^{q-1}{b_{ij}^{2}}=\int{\left\{ \sum\limits_{j=0}^{m}{D_{i,j}^{''}{{N}_{j,3}}\left( {{v}_{s}} \right)} \right\}\text{d}v}+ \\ & {{\sum\limits_{j=1}^{q-1}{\left| \frac{\left| L_{i}^{''}\left( {{v}_{j+1}} \right) \right|-\left| L_{i}^{''}\left( {{v}_{j}} \right) \right|}{{{l}_{i,j}}}-\frac{\left| L_{i}^{''}\left( {{v}_{j}} \right) \right|-\left| L_{i}^{''}\left( {{v}_{j-1}} \right) \right|}{{{l}_{i,j-1}}} \right|}}^{2}} \\ \end{align}$

(21)

式中：D=[D_x,D_y,D_z,ω]为纵向曲线的坐标分量。∫|L″_i(v)²dv为第i条纵向曲线的应变能，$\sum\limits_{j = 1}^{q - 1} {b_{ij}^2} $为其剪力跃度平方和，二者均为曲线的光顺性判别式，前者表征曲线的总曲率和，后者表征曲线的曲率变化^[16]。此时曲面放样法转化为一个以插值条件为约束条件的约束优化问题，只要保证该纵向曲线插值通过所有的截面曲线控制顶点，就可以专注于它的光顺性，同时纵向曲线的控制顶点也不再依赖于截面曲线的数量q+1，不仅可以通过增加节点矢量和控制顶点数目来使纵向曲线具有更高的自由度，也不需要添加额外的边界条件，只需保证纵向曲线首尾端控制顶点通过首尾截面曲线的控制顶点以及满足相应的等式约束条件即可。

求解出上述的优化问题(21)，便可以得到船体曲面的控制顶点，然后根据NURBS曲面的表达式(2)得到船体曲面。

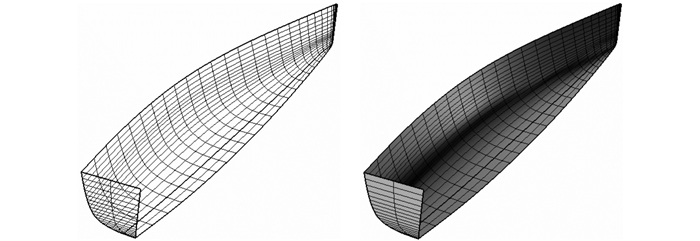
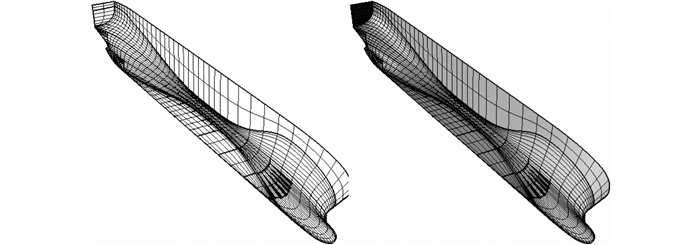
图 8和图 9分别为按照本文提出的船体曲面重构方法得到的船体曲面，图 8为一简单船型，图 9为带球艏和球艉的复杂船型，从结果可知该重构方法得出的船体曲面具有较好的精度和光顺性。

4 结论

以插值和逼近方式拟合型值为基础，引入广义站线来构造船体曲面的截面曲线，通过改进的曲面放样法构造了船体曲面，研究表明：

1)广义站线相对传统站线能够更好的体现出船体曲面在艏艉处的曲率变化和过渡，也为后续的船体曲面重构提供了更为合理的截面曲线；

2)基于等数弧长均分的曲线重构能够在精度范围内很好的拟合船体型线，而且具有良好的数据压缩效果，避免了控制顶点冗余；

3)改进放样法所构造的船体曲面具有较高的拟合精度和光顺性，有效避免了后期大量的人工干预和手动光顺处理；

4)由于曲面重构的过程考虑的是两个参数方向曲线的光顺性，并未从曲面整体来考虑，今后的工作需要对这方面内容进行改进。