2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China
水深是海图上反映海底地形地貌的最基本要素[1, 2, 3]。海图水深的选取作为海图制图综合中的核心环节,其作业质量的高低将直接影响到舰船海上航行的安全性和海底地形表达的准确性[4, 5, 6]。
当前的水深选取,通常由制图作业员采用手工方式对各个水深逐一分析并完成选取的,这一方面造成作业效率的低下,另一方面,其结果质量在很大程度上也取决于制图员的业务水平和细致程度。为此,如何实现水深注记的自动选取,一直是国内外学者广泛关注并为之不懈探索的问题[6, 7, 8, 9, 10]。Zoraster将水深分为首选水深、背景水深和限定水深,根据重要性顺序进行选取优化[6];王家耀和田震采用层次信息模型,提出了海图水深综合的人工神经元网络方法[7];陆毅、刘颖等从水深综合的基本原则出发,模拟人在制图综合时的思维方式,探索海图水深的自动综合[8, 9];张立华等采用模型面控制的思想,设计水深自动选取策略,确保了水深在保证航海安全方面的质量,为真正实现水深的自动综合带来了新的希望[10]。
但以上关于海图水深的自动综合研究,只是考虑了水深自身在保证航海安全、准确显示航道和表达清晰美观等方面的要求,缺少与其他海部要素间相互协调的考虑。而在水深的自动选取中,与其他要素的相互协调,特别是与等深线的协调,是一个不可或缺的环节[1, 4]。在与等深线协调的水深选取过程中,通常需注意3个方面:1)水深与等深线凸凹处的协调匹配;2)水深与等深线平直处的协调匹配;3)水深注记尽量不要中断等深线。然而,从目前公开的文献来看,仅有一些文献提及了在等深线的重要凸凹处需注意水深点的优先选取[8, 9],并没有专门针对水深自动选取中与等深线协调的问题,提出一种实际可用的具体方法。
为此,针对水深与等深线协调问题,通过使用道格拉斯普克算法来自动识别等深线的弯曲特征,并通过量化分析水深协调度,设计相应的水深选取策略,实现与等深线协调的水深自动选取。
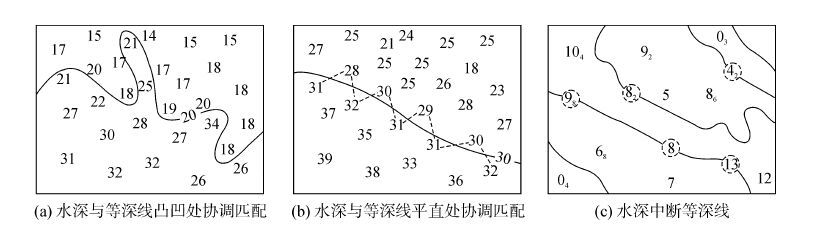
1 与等深线协调的水深自动选取在与等深线协调的水深选取过程中,通常需注意3个方面,对应的基本要求如下[4]:1)在等深线凸凹处[11]附近应优先选取水深点,用于确定等深线的基本轮廓,如图1(a)中所示的水深;2)在等深线平直处两侧附近交错选取水深点,用来进一步控制等深线的轮廓形状,如图1(b)中所示的水深;3)不宜选取离等深线太近的水深,避免过多地中断等深线,如图1(c)中所示的水深。
|
| 图1 与等深线协调的水深选取 Fig.1 Soundings selection harmonizing with depth-contours |
在与等深线协调的水深自动选取中,首先需自动识别出等深线上特征点,确定等深线的凸凹处和平直处,为后续建立水深选取策略奠定基础。
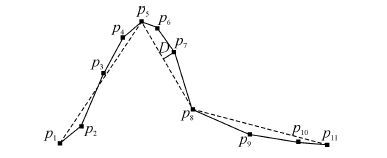
目前,对于曲线上特征点识别的算法较多,其中以道格拉斯普克算法最为常用[12]。它不仅可实现曲线特征的分解与组合,还可给出曲线的形态与拓扑特征[11]。如图2所示,等深线是由一系列二维点p1p2…p11依次连接而成的连续折线段,具体的处理步骤如下:1) 设定阈值为D,使用道格拉斯普克算法,识别出特征点p5、p8,如图2所示;2) 将等深线上特征点的位置视作等深线的凸凹处,其余二维点的位置视作等深线的平直处。
阈值D会影响到道格拉斯普克算法的识别结果,进而影响到后续协调水深选取策略的选择。阈值D一般可选取一个经验值,如图上0.3 cm,其最合理的取值通常可通过试验统计分析来得到。
|
| 图2 等深线弯曲特征点识别 Fig.2 A recognition of curving feature nodes in |
在确定出等深线凸凹处的基础上,设计相应的水深选取策略:首先,根据水深与等深线协调的基本要求,确定等深线凸凹处的水深协调条件;然后,量化分析这些条件,计算出等深线凸凹处的水深协调度;最后,从中优选水深协调度最高的水深点。
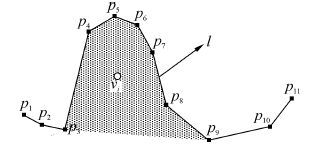
1.2.1 凸凹处水深协调条件确定如图3所示,等深线l是由p1p2…p11连接而成的折线段,等深线上的特征点为p5,由于点p3、p9与点p2、p10的凹凸性相反,故折线段p3p4…p9是等深线l的一个弯曲[11]。将该折线段p3p4…p9的首尾点相连,形成一个闭合区域(如图3所示),定义该区域为特征点p5所在弯曲的内部区域。
|
| 图3 凸凹处的协调水深点 Fig.3 a sounding harmonizing with a local range of a depth-contour being scraggy |
对于等深线l上特征点p5对应的凸凹处,需选取一个协调的水深点。该水深点应符合以下条件:
①协调水深点必须位于特征点所在弯曲的内部区域;②协调水深点注记应尽量避免中断等深线;③协调水深点与等深线上对应特征点p5的平面距离合适;④协调水深点到折线段p3p4p5和p5p6…p9的最短距离应尽可能相近。其中,水深点到折线段的最短距离是指水深点到该折线段上各点距离的最小值。
上述条件的重要性等级由高到低依为条件①、条件②、条件③(或条件④)。
1.2.2 凸凹处水深协调度计算
为便于计算机进行自动处理上述条件,综合考虑上述条件及其重要性等级,采用凸凹处水深协调度这一指标,量化评估水深点与等深线凸凹处的协调质量。如图3所示,以水深点vi为例,其与等深线凸凹处(对应特征点p5)的协调度w(vi,p5)为:
\[w\left( {{v}_{i}},{{p}_{5}} \right)=\frac{1}{2}{{\lambda }_{i}}\left( {{\gamma }_{i}}+\frac{1}{1+{{\left( d\left( {{v}_{i}},{{p}_{5}} \right)-{{d}_{lbest}} \right)}^{2}}+\left( d\left( {{v}_{i}},{{l}_{5,9}} \right) \right)-d{{\left( {{v}_{i}},{{l}_{5,9}} \right)}^{2}}} \right)\times 100%\]
(1)
从式(1)可以看出:若水深点vi必须位于等深线凸凹处的外侧,λi=0,则w(vi,p5)=0,从而此水深点就不可能与等深线协调,所以,反过来,λi=1是一个“必须”的条件;由于γi是根据水深点vi是否中断等深线取值0(或1),未中断则γi=1,中断则γi=0,另一方面,其后一项分式取值变化范围是(0,1),故不论后一项分式的数值如何变化,如果水深点未中断等深线,则上述两项和的变化范围是(1,2),如果中断等深线,则上述两相和的变化范围是(0,1),因此未中断等深线的水深点协调度必然要大于中断等深线的水深点协调度,也就符合了条件②中关于“水深点尽量避免中断等深线”的描述;将条件③、④的量化式同时置于同一分式的分母部分,且形式上相同,以符合对条件③、④重要性相同的描述要求,并且若d(vi,p5)与d1best(或d(vi,l3,5)与d(vi,l5,9))相差越小,则协调度越高。
通过分析等深线凸凹处水深协调条件,量化评估各水深点与等深线凸凹处的协调质量,并从中优选出协调度最高的水深点,从而实现等深线凸凹处协调水深的自动选取。
1.3 平直处协调水深点的选取在选取完等深线凸凹处附近的水深点后,接下来,应围绕等深线平直处的两侧,再“交错”选取一定数量的水深点,进一步控制等深线的走向变化。水深在等深线平直处协调选取的基本要求是:首先,确定等深线平直处的水深协调条件;然后,量化分析这些条件,计算出等深线平直处的水深协调度;最后,从中选取水深协调度最高的水深点。
1.3.1 平直处水深协调条件确定如图4(a)所示,等深线凸凹处附近有已选的协调水深点q1、q5,首先在已选水深点q1基础上,从等深线另一侧选取出一个协调的水深点,与q1构成交错形态,定义为单点交错。与q1构成交错形态的协调水深点应符合以下条件:
①协调水深点与已选水深点q1必须位于等深线的两侧;②协调水深点到q1的平面距离必须在规范要求的间隔范围内;③协调水深点的注记应尽量避免中断等深线;④协调水深点到等深线的最短距离应尽可能合适(水深点到等深线的最短距离是指水深点到该等深线上各点距离的最小值)。
上述条件的重要性等级由高到低依为条件①(或条件②)、条件③、条件④。
如图4(b)所示,在与q1构成交错、选取出协调水深点q2后,继续在点q2的基础上,交错选取出协调水深点q3。之后,需注意的是,在交错选取下一个协调水深点时,该点既要与水深点q3“交错”,还要与已选取的水深点q5“交错”。也就是说,选取出的协调水深点q4必须同时满足与q3、q5交错的4个条件,定义为双点交错。
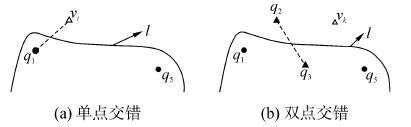
|
| 图4 平直处的协调水深点 Fig.4 A sounding harmonizing with a local range of a depth-contour being smooth |
为便于计算机自动处理,综合考虑上述条件及其重要性等级高低,采用平直处水深协调度,来量化评估水深点与等深线平直处的协调质量。如图4所示,等深线l平直处附近的某个水深点为vi,该点与已选水深点q1单点交错的协调度w(vi,q1)为:
\[\begin{align}
& w\left( {{v}_{i}},{{q}_{i}} \right)=\frac{1}{2}{{\lambda }_{i}}.{{\mu }_{i}}* \\
& \left( {{\gamma }_{i}}+\frac{1}{1+{{\left( d\left( {{v}_{i}},l \right)-{{d}_{2best}} \right)}^{2}}} \right)\times 100% \\
\end{align}\]
(2)
从式(2)可以看出:若水深点vi与水深点p同时位于等深线的一侧,λi=0,则w(vi,q1)=0,则此水深点不可能与等深线协调,反之λi=1,故是一个“必须”的条件;水深点vi与水深点q1的平面距离应在规范要求范围,即ui=1,为一个“必须”的条件;水深点是否中断等深线的分析与式(1)类似;将条件④的量化公式置于末尾,若d(vi,l)与d2best相差越小,则水深点到等深线的距离就越合适。
量化分析双点交错条件。如图4(b)所示,若等深线平直处附近的某水深点vk,计算点vk与已选水深点q3、q5双点交错的协调度w(vk,q3,q5)为:
\[w\left( {{v}_{k}},{{q}_{3}},{{q}_{5}} \right)=w\left( {{v}_{k}},{{q}_{3}} \right).w\left( {{v}_{k}},{{q}_{5}} \right)\times 100%\]
(3)
在等深线凸凹处水深点选取的基础上,通过分析等深线平直处水深协调条件,评估各水深点与等深线平直处的协调质量,自动选取协调度最高的水深点,即可实现与等深线协调的水深自动选取。
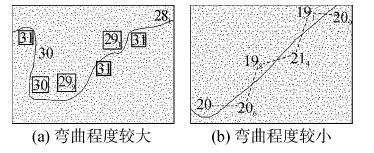
2 试验与分析 2.1 可行性验证选取如图5所示的等深线弯曲程度不同的两个局部区域,采用所提方法,进行与等深线协调的水深自动选取验证。由于资料水深数据密度较大,全部用注记显示会造成注记相互压盖,故用黑色像素点表示,选取的水深点用注记表示。所提方法中3个关键参数先采用一组经验数值:阈值D=0.3 cm,等深线凸凹处和平直处的最协调距离d1best=0.4 cm和d2best=0.3 cm,具体的试验结果如图5所示。
|
| 图5 与等深线协调的水深选取结果 Fig.5 Soundings selection harmonizing with a depth-contour |
从图5中可以看出,所提方法能较好地识别出等深线上的特征点,并在等深线上对应的凸凹处附近选取一个合适的匹配水深点,如图5(a)所示;在等深线的平直处附近,所提方法也能可以较好地实现水深点的交错选取,如图5(b)所示。
2.2 阈值对水深选取结果的影响分析进一步分析阈值D对水深选取与等深线协调结果的影响,采用5个试验区域进行统计分析。试验通过调查10名实际作业人员,比较试验结果,确定该参数取0.3 cm最为合理,具体结果如表1。不失一般性,选取一组典型试验进行更直观、详细的阐述,如图6某等深线所在的局部区域,设定不同大小的阈值进行试验,具体结果如图7。
| 阈值D /cm | 0.1 | 0.2 | 0.3 | 0.4 |
| 区域1认为结果最合理的人数 | 0 | 1 | 9 | 0 |
| 区域2认为结果最合理的人数 | 0 | 2 | 8 | 0 |
| 区域3认为结果最合理的人数 | 0 | 1 | 8 | 1 |
| 区域4认为结果最合理的人数 | 0 | 2 | 7 | 1 |
| 区域5认为结果最合理的人数 | 0 | 1 | 8 | 1 |

|
| 图6 阈值分析的试验区域 Fig.6 Experimental area for analyzing threshold |
|
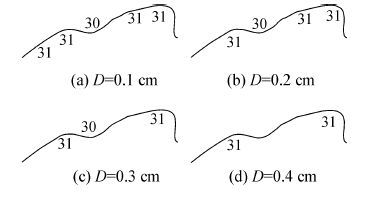
| 图7 阈值的试验比对 Fig.7 Sea area for analyzing threshold |
从图7中可以看出,采用阈值为0.3 cm时,所提方法自动选取出3个协调的水深点,对等深线上特征点的识别结果最为符合实际情况,如图7(c)所示。而采用阈值为0.1、0.2、0.4 cm时,所提方法对等深线特征点的识别结果与实际情况均略有不符(特征点识别数量偏多或偏少),致使协调水深点的选取结果不够合理。故确定0.3 cm作为道格拉斯算法的阈值。
2.3 最协调距离对水深选取结果的影响分析在计算水深点在等深线凸凹处和平直处的协调度中(如式(1)~(3)所示),最协调距离d1best、d2best是两项影响最终水深选取结果的关键参数。然而,目前尚无规范明确水深点应距离等深线多远最为合适,实践中制图员多是根据个人经验而定。为此,通过调查10名制图员,比较试验结果,确定d1best=0.4 cm和d2best=0.3 cm时选取结果最为合理。
不失一般性,选取其中两组典型区域进行更直观、详细的阐述(如图8所示),采用不同大小的数值进行试验,具体的试验结果如图9、10所示。
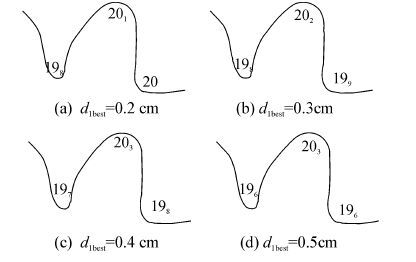
如图9所示,当d1best=0.4 cm时,与等深线凸凹处协调的水深选取结果与实际情况最为相符。当d1best=0.2 cm时,水深点注记点中断等深线,故水深点的协调质量最差;当d1best=0.3、0.5 cm时,水深点到等深线凸凹处的距离稍偏近(或偏远),故确定凸凹处的最协调距离为0.4 cm。
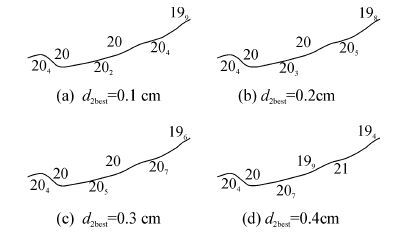
如图10所示,当d2best=0.3 cm时,与等深线平直处协调的水深选取结果与实际情况最为相符。当d2best=0.1、0.2、0.4 cm时,水深点到等深线平直处的距离稍偏近(或偏远),故确定平直处的最协调距离为0.3 cm。

|
| 图8 试验区域 Fig.8 Experimental area |
|
| 图9 最协调距离d1best的试验比对 Fig.9 Comparison of best distance d1best |
|
| 图10 最协调距离d2best的试验比对 Fig.10 Comparison of best distance d2best |
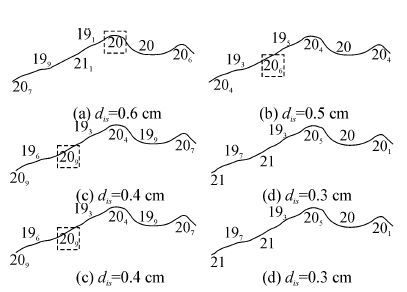
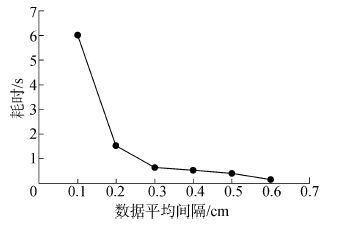
进一步分析资料水深数据密度对水深选取结果的影响,在某海图上同一区域内选取不同密度的资料水深数据(平均间隔dis依次为0.6、0.5、0.4、0.3、0.2、0.1 cm),采用所提方法进行比对试验。实验所用计算机CPU主频2.4 GHz,内存4 G。具体的试验结果如图11所示。图12为资料水深数据平均间隔与运算耗时的关系图。
|
| 图11 水深选取结果比较 Fig.11 Comparison of sounding selection |
|
| 图12 运算耗时 Fig.12 Processing time |
从图11、图12中还可以看出,资料水深数据间隔越小(即资料水深数据量越大),所提方法在与等深线协调的水深选取效果上就越好,但运算耗时也就随之增加。对比图11中的6组水深选取结果可以看出,资料水深数据间隔为0.1、0.2、0.3 cm时,与等深线协调的水深选取结果要相对较好,其余3组(资料水深数据间隔为0.4、0.5、0.6 cm)的水深选取结果与等深线的协调匹配效果略差(在某些水深点上与等深线协调不够理想,如图11(a)、图11(b)、图11(c)中所示水深点距离等深线过近)。这表明:资料水深数据间隔越小,可用于提供给算法分析的水深点数量也就越多,从而有可能挑选出更协调的水深点。然而,过大的资料水深数据量将会直接影响到算法的效率。从图12中可以看出,当资料水深数据间隔由0.1 cm增大到0.3 cm时,所提方法的运算耗时会明显降低。
3 结论通过理论推导与试验分析,得结论如下:
1) 所提方法能在等深线凸凹处选取出协调的水深点,同时在等深线平直处使选取的水深点构成相互交错的形态,还能较好地避免水深注记中断等深线的情况。
2) 通过试验统计分析可确定出所提算法中3项关键参数的合理取值(道格拉斯普克算法的阈值为0.3 cm,等深线凸凹处和平直处的最协调距离分别为0.4 cm和0.3 cm),从而进一步保证了所提方法在水深点与等深线协调中的水深选取效果。
3) 通常来说,资料图水深数据密度越大,所提方法选取出与等深线协调的水深点就越合理,但密度过大的资料水深数据会降低算法的运行效率
当然,限于论文篇幅和数据来源,仅针对一些典型区域进行了试验论证,并从中对部分试验结果进行了比对分析,对于文中所提的三个水深协调度计算公式及其中有关参数的取值等,这些都需要更多的试验进行全面的验证。另外,本文仅考虑了与单条等深线协调的水深自动匹配,对于水深点与多条等深线间的相互协调配置,这也有待于进一步的探索。
| [1] | 国家质量技术监督局. GB 12320-1998, 中国航海图编绘规范[S]. 北京:中国标准出版社, 1999.The State Bureau of Quality and Technical Supervision. GB 12320-1998, Specifications for Chinese nautical charts[S]. Beijing:Chinese Standards Press, 1999. |
| [2] | SMITH S. The navigation surface:A multipurpose bathymetric database[D]. Durham:University of New Hampshire, 2003:1-9. |
| [3] | 贾帅东, 张立华, 宋国大, 等. 基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3):454-460. JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A method for constructing an adaptive grid digital depth model based on mean vertical uncertainty of area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):454-460. |
| [4] | 王厚祥, 李进杰. 海图制图综合[M]. 北京:测绘出版社, 1999:114-126. WANG Houxiang, LIU Jinjie. Generalization of nautical charts[M]. Beijing:Surveying and Mapping Press, 1999:114-126. |
| [5] | 张立华, 贾帅东, 元建胜, 等. 一种基于不确定度的水深控浅方法[J]. 测绘学报, 2012, 41(2):184-190. ZHANG Lihua, JIA Shuaidong, YUAN Jiansheng, et al. A method for controlling shoal-bias based on uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2):184-190. |
| [6] | ZORASTER S, BAYER S. Automated cartographic sounding selection[J]. International Hydrographic Review, Monaco, 1992(3):103-116. |
| [7] | 王家耀, 田震. 海图水深综合的人工神经元网络方法[J]. 测绘学报, 1999, 28(4):334-339. WANG Jiayao, TIAN Zhen. The cartographic generalization of soundings on chart by artificial neural network techniques[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4):335-339. |
| [8] | 刘颖, 翟京生, 陆毅, 等. 数字海图水深注记的自动综合研究[J]. 测绘学报, 2005, 34(2):179-184. LIU Ying, ZHAI Jingsheng,LU Yi, et al. Automatic generalization of sounding in digital chart[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2):179-184. |
| [9] | 陆毅, 翟京生, 杜景海. 海底地形的识别与水深的综合[J]. 测绘学院学报, 2000, 17(4):296-300. LU Yi, ZHAI Jingsheng, DU Jinghai. Sounding selection based on recognition of submarine topography features[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4):296-300. |
| [10] | 张立华, 贾帅东, 王涛, 等. 一种不漏水深浅点的海图水深自动选取方法:中国, 201410184190[P]. 2014-07-30. |
| [11] | 翟京生, 陆毅. 数字海图线性特征的识别、量测与综合[J]. 测绘学报, 2000, 29(3):273-279. ZHAI Jingsheng, LU Yi. Recognition, measurement and generalization for line features in digital nautical chart[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3):273-279. |
| [12] | DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. The Canadian Cartographer, 1973, 10(2):112-122. |



