船舶设计作为一个复杂的过程,设计方案往往需要在诸多建议之间反复协调[1, 2]。随着计算机技术不断发展,大量研究工作投入到计算机辅助设计中。计算机辅助船舶设计技术,目前处在国际领先水平的有美国的先进舰船综合模型开发与评估工具ASSET和英国的舰船概念设计工具Paramarine。然而实际上计算机辅助设计在船舶领域并未受到足够的重视,与其他领域存在差距,在已有船舶舱室布置设计的研究中,Lee等所建立的模型存在考虑因素不全面和只顾及到局部布置的问题[3, 4, 5],胡玉龙建立的模型只考虑到了舰船纵剖面的舱室布置[6]。本文从船舶舱室全局布置考虑,针对舱室在船舶某一层带有主要结构的甲板上的区域分布问题,提出了数学模型。引入引力搜索算法(GSA)[7]并基于小生境技术[8, 9]进行改进,和数学模型构成舱室分布设计模型。
1 需求分析舰船舱室分布设计主要考虑技术要求、重量分布、面积及某些环境因素方面等的要求[10, 11]。
技术要求方面包括安全性、通达性[3]。某些舱室如弹药储备舱室需要布置在安全性较高的位置,避免被击中导致爆炸造成二次伤害。舱室的通达性也是在日常生活和紧急状态时需要保证的。
重量分布应保证舰船的稳心高及舰船的重量平衡。同时考虑到船身强度的问题,在单层甲板中应使重量尽量集中在船身的中央位置[6]。
面积需满足每个舱室的需求,同时不超过甲板总面积。
环境因素方面的要求,包括噪音、振动、运动、湿度、温度等。在舱室布置设计完成之前该方面因素并不能主导方案设计过程,因为其中大部分因素可通过后续技术手段改善[12],不过优秀的设计会尽量减少后续的工作。
2 数学模型的建立 2.1 变量有待分配舱室I个,若舱室数量过多,也可将I个舱室按照功能和属性相似性分为K个不同的舱室组,将甲板划分为区域J个。设每个舱室的分布区域为变量。本文模型中待分配的舱室并没有给出具体尺寸形状,仅具有面积、估算设备总重等属性。 X=[xi] 式中:i=1,2,···,I;xi=1,2,…,J。
2.2 目标函数 2.2.1 环境因素目标函数
确定每一个甲板区域中的指标评价值:
$${\mu _{n,j}} = {{{L_{n,j}} - {L_{n\min }}} \over {{L_{n\max }} - {L_{n\min }}}}$$
(1)
$${\mu _{n,j}} = 1 - {{{L_{n,j}} - {L_{n\min }}} \over {{L_{n\max }} - {L_{n\min }}}}$$
(2)
当较大值代表比较好的情况时采用式(1),反之则采用式(2)。
设cn,k表示舱室组k的第n种指标的标准要求值,得出舱室组k对甲板区域j中第n种指标的评价函数vn,j(k):
vn,j(k)=μn,j/cn,k
(3)
为全面考虑舱室对各个指标的要求,运用式(4)对N种指标的评价值进行加权平均得到舱室组k对甲板区域j的总评价值u1kj:
$${u_{1kj}} = \sum\limits_{n = 1}^N {{\omega _{n,k}}} {\upsilon _{n,j}}(k)$$
(4)
从而得到舱室组k对某甲板区域的评价值:
U1k=[u1kj]
(5)
得到U1k后,由于舱室i与舱室组k存在对应关系,同时考虑变量xi与u1kj的对应关系,不难得到U1i,由式(6)得环境因素目标函数U1:
$${U_1} = {1 \over I}\sum\limits_{i = 1}^I {{U_{1i}}} $$
(6)
安全性目标函数与环境因素目标函数建立方法相同,将式(1)或(2)中L替换成安全性评价值即可。每个甲板区域安全性评价值在不同情况下有不同的评定,应根据实际方案需要制定。
通达性目标函数的建立需先将舱室间的距离要求进行等级划分并定量表示,对应关系如表1所示。表中,disij为舱室i与舱室j之间的距离;dismax为布置方案中最远的舱室间距离。舱室间距离采用舱室所在的甲板区域间的距离,其计算精度高低根据甲板区域的划分精细程度而定,甲板划分的区域越精细,其计算精度越高。此处甲板区域间的距离采用两个甲板区域矩形几何中心间的距离。
| 等级 | 很远 | 远 | 一般 | 近 | 很近 |
| 定量表示 | 5 | 4 | 3 | 2 | 1 |
| disij /dismax | 0.8~1 | 0.6~0.8 | 0.4~0.6 | 0.2~0.4 | 0~0.2 |
通达性目标函数UACC为:
$${U_{ACC}} = \min (1 - 0.25\left| {f(di{s_{ij}}) - c\_di{s_{ij}}} \right|)$$
(7)
U2=ωSAFUSAF+ωACCUACC
(8)
利用高斯曲面函数作为模糊建模算子,可以使函数较好地描述舰船舱室布置设计对重量分布的要求。设Q=[qi],qi为舱室i重量。
$$\eqalign{
& {U_{3i}} = {1 \over 2}\exp \left\{ { - {1 \over 2}\left[ {{{{{({q_i} - {\mu _1})}^2}} \over {2\sigma _1^2}} + {{{{({d_i} - {\mu _2})}^2}} \over {2\sigma _2^2}}} \right]} \right\} + \cr
& {1 \over 2}\exp \left\{ { - {1 \over 2}\left[ {{{{{({q_i} - {\mu _1})}^2}} \over {2\sigma _1^2}} + {{{{({b_i} - {\mu _3})}^2}} \over {2\sigma _3^2}}} \right]} \right\} \cr} $$
(9)
$${U_3} = {1 \over I}\sum\limits_{i = 1}^I {{U_{3i}}} $$
(10)
最后由式(10)确定重量分布目标函数。重量分布应保证舰船左右对称,约束条件设为: 0.75≤Qleft/Qright≤1.25
2.2.4 面积目标函数
设A=[Aj],Aj为甲板区域j的面积;a=[ai],ai为舱室i的面积,且与xi对应。当xi =j时,设与xi对应的ai的和为Amj,Amj即为分布在第j甲板区域里所有舱室面积的和。选用下式模拟每个甲板区域的面积利用率评价值:
$${U_{4j}} = {{\mathop{\rm e}\nolimits} ^{ - {{{{({s_j} - \mu )}^2}} \over {2{\sigma ^2}}}}} + R \times \min ({S_j} - 0.5,0)$$
(11)
Sj从μ值变小时,开始评价值并不会快速下降,因为剩余的面积可用于通道布置,随着通道数量和宽度的增加会使人流和物流变得更加通畅[13]。
面积目标函数取式(11)所得最小值。
U4=min(U4j)
(12)
布置于某一甲板区域内的舱室的总面积不能超过该甲板区域的面积,即约束条件为:Sj≤1。
3 基于小生境的多目标引力搜索算法 3.1 引力搜索算法引力搜索算法拥有较好的全局寻优能力和较快的收敛速度[7]。其迭代规则如下式所示:
vdi(t+1)=randi×vdi(t)+adi(t)
xdi(t+1)=xdi(t)+vdi(t+1)
式中:randi是在区间[0,1]之间的随机数;xid表示个体i在第d维空间上的位置;i=1,2,…,N,d=1,2,…,n。在t时刻,个体i和j之间的欧式距离Rij(t): Rij(t)=‖Xi(t),Xj(t)‖2,万有引力常数G(t): G(t)=G(t0)(t0/t)β 式中:t0为初始时刻;β为小于1的常数。
个体i的质量Mi(t)根据目标函数值计算得到:$$mi(t) = {{fi{t_i}(t) - worst(t)} \over {best(t) - worst(t)}}$$ $${M_i}(t) = {{{m_i}(t)} \over {\sum\nolimits_{j = 1}^N {{m_j}(t)} }}$$ 式中:fiti(t)表示个体i在t时刻的目标函数值。worst(t)和best(t)的值,分别取fiti(t)的最差和最优值。 个体i和个体j之间第d维空间上的力Fijd(t): $$F_{ij}^d(t) = G(t){{{M_j}(t) \times {M_i}(t)} \over {{R_{ij}}(t) + \varepsilon }}(x_j^d(t) - x_i^d(t))$$ 式中:ε是一个比较小的常数。
作用在个体i上的第d维空间上的合力Fid(t): $$F_i^d(t) = \sum\limits_{j = Kbest,j \ne i} {ran{d_j}F_{ij}^d(t)} $$ 式中:Kbest开始时被初始化为K0,K0等于N,随着时间的推移Kbest逐渐减小至1;randj是在区间[0,1]之间的随机数。 个体i在第d维空间上的加速度aid(t)为:$$a_i^d(t) = {{F_i^d(t)} \over {{M_i}(t)}}$$
3.2 多目标引力搜索算法本文所建立的数学模型为多目标优化模型,为使引力搜索算法适用于多目标优化问题,将小生境技术[8, 9]引入其中,提出了一种多目标引力搜索算法。
设多目标优化问题中任意两个目标向量u和v,维数为m,根据定义有:若存在i∈{1,2,…,m},使得ui=vi,则u=v;使得ui≥vi,则u≥v;使得ui>vi,则u≥v∧u≠v。设多目标优化问题中任意两个变量a和b,根据定义有:若f (a)>f (b),则a优于b;若f (a)≥f (b),则a弱优于b;若f (a)≯f (b)∧f(a)≮f (b),则a无差别于b。对于最小化多目标优化问题,也可有类似定义。当选取非劣解时,按照以上定义进行判断,若在可行解空间中不存在比x更优的解,则x是该多目标优化问题的最优解或非劣解。
在可行解目标空间中均匀随机初始化群体,选取其中非劣解个体作为“精英集”(elitism)。通过小生境技术给精英集中的非劣解个体分配适应度值,聚集程度越大的个体适应度越小,精英集中第i个个体的适应度为: $$F(i) = {1 \over {\sum\limits_{j = E} {s(dist(i,j))} }}$$ 式中:E为精英集,s(dist(i,j))为精英集中第i个个体和第j个个体适应度分享函数: $$s(dist(i,j)) = \left\{ {\matrix{ {1 - {{({{dist(i,j)} \over {{\sigma _{{\rm{share}}}}}})}^\alpha },} & {d(i,j) < {\sigma _{{\rm{share}}}}} \cr {0,} & {22} \cr } } \right.$$ 式中:dist(i,j)为第i个和第j个个体目标向量之间的欧式距离;σshare为小生境半径;α为调节参数,一般取1左右。
以轮盘赌概率选取精英集中的个体参与单次迭代过程,选出单次迭代后群体中的非劣解,加入精英集,并删除其中的劣解;若精英集中非劣解个数超过精英集的容量,则删除其中适应度较小的个体,保证前沿分离度;迭代多次后的精英集即最终的非劣解集。
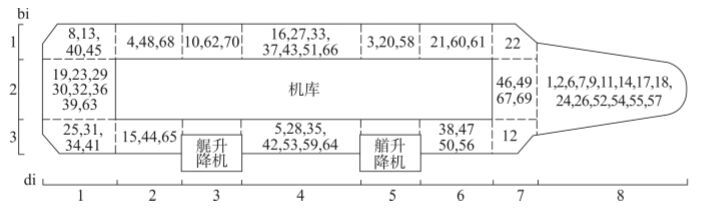
4 算例检验 4.1 参数输入 4.1.1 变量参数输入算例为如图1所示甲板,机库与升降机等主要结构位置已确定,各甲板区域左上角数字为区域编号。有待分配舱室70个,按照功能要求与固有属性相似性分为6组,将待布置甲板划分为15个区域,即I=70,K=6,J=15。若想得到更细致的方案则需要划分更多的区域,甲板区域的划分应考虑实际需要与船体主要舱壁位置。
|
| 图1 舱室区域分布方案图 Fig.1 Sketch of cabin layout design |
考虑噪声、振动、运动3个环境因素的要求,即N=3。舱室布置时,可根据经验和已布置好的设备或结构推测出船体环境因素大致的分布情况。本算例各甲板区域的3种指标评价值如表2所示。
| 甲板区域 | 噪声 | 振动 | 运动 | 安全性 |
| 1 | 0.60 | 0.33 | 0 | 0 |
| 2 | 0.40 | 0.17 | 0.25 | 0.20 |
| 3 | 0.20 | 0.33 | 0.50 | 0.40 |
| 4 | 0.40 | 0.50 | 0.75 | 0.60 |
| 5 | 0.60 | 0.67 | 0.50 | 0.40 |
| 6 | 0.80 | 0.83 | 0.25 | 0.20 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 0.40 | 0.17 | 0.25 | 0.20 |
| 9 | 0.80 | 0.83 | 0.25 | 0.20 |
| 10 | 0.90 | 0.90 | 0.13 | 0.80 |
| 11 | 0.60 | 0.33 | 0 | 0 |
| 12 | 0.40 | 0.17 | 0.25 | 0.20 |
| 13 | 0.40 | 0.50 | 0.75 | 0.60 |
| 14 | 0.80 | 0.83 | 0.25 | 0.20 |
| 15 | 1 | 1 | 0 | 0 |
6组舱室对各指标的标准要求值与权重见表3。由式(3)~(6)求得U1。
| 舱室组 | 1 | 2 | 3 | 4 | 5 | 6 |
| 舱室号 | 1~10 | 11~15 | 16~25 | 26~45 | 46~60 | 61~70 |
| 噪声 | 1 | 0.8 | 0.7 | 0.35 | 0.25 | 0 |
| ω1,k | 0.4 | 0.65 | 0.3 | 0.35 | 0.2 | 0 |
| 振动 | 0.3 | 1 | 0.8 | 0 | 0.7 | 0.5 |
| ω2,k | 0.3 | 0.35 | 0.4 | 0 | 0.6 | 0.5 |
| 运动 | 0.85 | 0 | 0.5 | 1 | 0.25 | 0.65 |
| ω3,k | 0.3 | 0 | 0.3 | 0.65 | 0.2 | 0.5 |
| 安全性 | 0.1 | 0.6 | 0.8 | 0.5 | 1 | 0.3 |
| 重量 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| 面积 | 42 | 54 | 50 | 34 | 43 | 45 |
每一个甲板区域的安全性评价值如表2所示,每组舱室对安全性的要求值如表3所示,由式(3)~(6)求得USAF。
出于验证模型合理性的目的,同时考虑篇幅问题,设舱室1、2、11、16、 26、27、46、61共8个舱室之间有通达性要求,要求矩阵c_dis为: \[c\_dis=\left[ \begin{matrix} 0 & 1 & 1 & 0 & 2 & 2 & 1 & 2 \\ {} & 0 & 1 & 3 & 2 & 2 & 0 & 2 \\ {} & {} & 0 & 0 & 2 & 2 & 0 & 3 \\ {} & {} & {} & 0 & 3 & 2 & 2 & 2 \\ {} & {} & {} & {} & 0 & 2 & 0 & 0 \\ {} & {} & {} & {} & {} & 0 & 0 & 0 \\ {} & {} & {} & {} & {} & {} & 0 & 0 \\ {} & {} & {} & {} & {} & {} & {} & 0 \\ \end{matrix} \right]\] 此矩阵为对称阵,其中0代表舱室间无通达性要求。
甲板的尺寸如图1所示。由式(7)求得UACC。设ωSAF=0.4,ωACC=0.6,由式(8)求得U2。
4.1.4 重量分布参数输入式(9)的控制参数μ1、σ1、μ2、σ2、μ3、σ3分别取0.5、0.2、4、1.2、2、0.3。每个舱室组的舱室具有相似的重量,见表3。由式(9)、(10)求得U3。
4.1.5 面积参数输入A=[220180 160 340 170 200 70 440 260 840 220 180 340 200 70];每个舱室组的舱室具有相似的面积,见表3;μ=0.84。由式(11)、(12)求得U4。
4.1.6 引力搜索算法参数输入设置粒子维数70,粒子规模50,G0=1 000,β =0.6,α =0.9。
4.2 结果及分析选取结果中的一个解,目标函数U1=0.700,U2=0.687,U3=0.377,U4=0.717。得到70个舱室的区域分布方案如图1所示,各甲板区域中方框外的数字为分布其中的舱室编号。方案中各甲板区域的面积利用率和总重量统计见表4。甲板面积利用率均保持在84%以下,甲板左侧总重量为11.6,甲板右侧总重量为9.6,符合约束条件。
| 甲板区域 | 面积利用率/% | 总重量 | 甲板区域 | 面积利用率/% | 总重量 | |
| 1 | 74.6 | 1.5 | 9 | 67.7 | 2.6 | |
| 2 | 72.2 | 1.5 | 10 | 80.2 | 5.7 | |
| 3 | 82.5 | 1.6 | 11 | 69.1 | 1.9 | |
| 4 | 80.6 | 3.7 | 12 | 73.9 | 1.5 | |
| 5 | 79.4 | 1.2 | 13 | 80.9 | 3.6 | |
| 6 | 69 | 1.7 | 14 | 81.5 | 2.3 | |
| 7 | 71.4 | 0.4 | 15 | 77.1 | 0.3 | |
| 8 | 71.6 | 4.0 |
计算舱室1、2、11、16、26、27、46、61之间的通达性等级并列出矩阵如下: \[\left[ \begin{matrix} 0 & 1 & 1 & 3 & 1 & 3 & 1 & 2 \\ {} & 0 & 1 & 3 & 1 & 3 & 1 & 2 \\ {} & {} & 0 & 3 & 1 & 3 & 1 & 2 \\ {} & {} & {} & 0 & 3 & 1 & 3 & 2 \\ {} & {} & {} & {} & 0 & 3 & 1 & 2 \\ {} & {} & {} & {} & {} & 0 & 3 & 2 \\ {} & {} & {} & {} & {} & {} & 0 & 1 \\ {} & {} & {} & {} & {} & {} & {} & 0 \\ \end{matrix} \right]\]
与通达性要求矩阵中的等级符合程度较好,部分舱室距离和要求相差1个评级。
以甲板区域14为例进行分析,其内分布有舱室38、47、50、56。其中47、50、56号舱室的标准值与该甲板区域的评价值符合较好,38号舱室的振动、运动和安全性三项指标符合度不高,若希望提高其符合度,可进一步调整各指标权重。指标标准值低于评价值表示舱室对该指标要求不高。甲板区域14内舱室的面积和与甲板区域面积的比为81.5%,接近84%。
5 结束语本文针对舱室在带主要结构的甲板上的区域分布问题建立了数学模型;基于小生境技术将引力搜索算法改进成多目标引力搜索算法,并引入到提出的数学模型中,构成了舱室分布设计模型。通过算例检验,结果与输入的要求基本符合,验证了模型的合理性,模型所得结果可用于指导后续具体的舱室布置。模型尚限于单一甲板内的舱室分布设计,不适用于详细舱室布置设计,还需进一步完善。
| [1] | PAPANIKOLAOU A. Holistic ship design optimization[J]. Computer-Aided Design, 2010, 42(11):1028-1044. |
| [2] | CUI Hao, TURAN O, SAYER P. Learning-based ship design optimization approach[J]. Computer-Aided Design, 2012, 44(3):186-195. |
| [3] | LEE K Y, ROH M I, JEONG H S. An improved genetic algorithm for multi-floor facility layout problems having inner structure walls and passages[J]. Computers & Operations Research, 2005, 32(4):879-899. |
| [4] | 王文全, 黄胜, 胡玉龙, 等. 舰船通道布局优化模型及其粒子群算法[J]. 武汉理工大学学报, 2012, 34(9):52-56. WANG Wenquan, HUANG Sheng, HU Yulong, et al. Ship passage layout optimization model and PSO algorithm[J]. Journal of Wuhan University of Technology, 2012, 34(9):52-56. |
| [5] | 胡耀, 姜治芳, 熊治国, 等. 基于SLP和遗传算法的容积型船舶内部舱室位置布局设计优化[J]. 中国舰船研究, 2013, 8(5):19-26. HU Yao, JIANG Zhifang, XIONG Zhiguo, et al. The optimized layout design of volume type ship cabins based on SLP and GA[J]. Chinese Journal of Ship Research, 2013, 8(5):19-26. |
| [6] | 胡玉龙, 黄胜, 侯远杭, 等. 舰船舱室分布的多目标优化设计模型研究[J]. 华中科技大学学报:自然科学版, 2011, 39(12):41-45.HU Yulong, HUANG Sheng, HOU Yuanhang, et al. Research on multi-objective optimization design model for distribution of cabins in naval ships[J]. Journal of Huazhong University of Science & Technology:Natural Science Edition, 2011, 39(12):41-45. |
| [7] | REEVES C R. A genetic algorithm for flowshop sequencing[J]. Computers & Operations Research, 1995, 22(1):5-13. |
| [8] | LIN C Y, WU Wenhong. Niche identification techniques in multimodal genetic search with sharing scheme[J]. Advances in Engineering Software, 2002, 33(11/12):779-791. |
| [9] | URSEM R K. Multinational evolutionary algorithms[C]//Proceedings of Congress of Evolutionary Computation. Washington, D.C., 1999. |
| [10] | HU Yulong, HUANG Sheng, HOU Yuanhang. The application of fuzzy modeling and PSO in spaces allocation of naval ship[J]. Advanced Materials Research, 2011, 201-203:1238-1242. |
| [11] | PARSONS M, CHUNG H, NICK E. Intelligent ship arrangements:A new approach to general arrangement[J]. Journal of the American Society of Naval Engineers, 2008, 120(3):51-65. |
| [12] | 丁建. SIKA敷料在降低船舶舱室噪声上的应用[J]. 广东造船, 2009(5):45-47. DING Jian. Application of SIKA cufadan deck coverings in interior noise reduction[J]. Guangdong Shipbuilding, 2009 (5):45-47. |
| [13] | LEE D, KIM H, PARK J H, et al. The current status and future issues in human evacuation from ships[J]. Safety Science, 2003, 41(10):861-876. |



