风能作为一种清洁的可再生能源,越来越受到世界各国的关注与重视,风力发电机也在近年来得到快速的发展与应用。叶片作为风力机捕获风能的关键部件,其成本也占到整个风力机的20%左右,对叶片的研究设计也变得十分重要。Kamoun Badreddinne等[1]以风轮输出功率为优化目标,运用升力线理论对Glauert模型进行改进,在此基础上对叶片进行了优化,并将此与Glauert模型进行了对比;Wang Xudong等[2, 3]以风力机单位能量的输出成本为目标,对叶片的外形参数进行优化设计,提高了风力机的工作性能和效率,降低了风力机的发电成本;张嘉麟等[4]采用Hicks-Henne函数对美国可再生能源实验室设计的Phases II-IV叶片进行了改进设计,并用CFD软件对改进设计的叶片进行校验计算,得到在低风速下具有较高气动性能的叶片;国内外还有一些学者对此做了很多研究[5, 6, 7, 8, 9, 10, 11, 12],都值得借鉴参考。
上述学者在设计风力机叶片的气动外形时,都将叶片看作是刚性的,并未考虑叶片弹性变形对风力机性能的影响,在实际运转中,叶片会产生弹性变形,从而造成作用在叶片上的载荷变化。柔性叶片与变化的载荷之间的耦合作用会影响叶片变形,如果忽略这种耦合作用将使叶片性能偏离原设计值,影响风力机的实际性能。针对这一情况,在设计叶片形状参数时必须考虑气动弹性对风力机性能的影响。
文中以风力机空气动力学理论为基础,结合气动弹性对风力机性能的影响,通过对叶片的原始外形参数进行优化设计,以提高风力机在实际运转中的性能,为风力机叶片的研发提供理论依据。
1 考虑气动弹性的风力机空气动力学模型基于一维动量理论建立的风力机空气动力学模型是假设风轮由无限多个叶片组成,而实际中风轮是由有限数量的叶片来组成。普朗特针对轴向质量流量损失提出了普朗特叶尖修正模型,引入修正因子F,推力与转矩[13]表示为
| ${\rm{d}}T = 4\pi \rho v_0^2aF\left( {1 - aF} \right)r{\rm{d}}r$ | (1) |
| ${\rm{d}}M = 4\pi \rho \omega {v_0}a'F\left( {1 - aF} \right){r^3}{\rm{d}}r$ | (2) |
式中:$F = \frac{2}{\pi }\arccos \left[{\exp \left( { - \frac{{B\left( {R - r} \right)}}{{2r\sin \varphi }}} \right)} \right],\rho $为空气密度,v0为来流风速,a为轴向诱导因子,F为普朗特叶尖损失修正因子,r为叶片展向位置,ω为风轮转动角速度,a'为周向诱导因子,φ为入流角,B为叶片个数,R为风轮半径。
Shen加入修正因子F1,进一步的修正了风轮叶素中的法向力系数和切向力系数[14],并代入经典的叶素理论中得到推力与转矩为
| ${\rm{d}}T = \frac{1}{2}B\rho cv_{{\rm{rel}}}^2{F_1}{C_{\rm{n}}}{\rm{d}}r$ | (3) |
| ${\rm{d}}M = \frac{1}{2}B\rho cv_{{\rm{rel}}}^2{F_1}{C_1}r{\rm{d}}r$ | (4) |
式中:${F_1} = \frac{2}{\pi }\arccos \left[{\exp \left( { - g\frac{{B\left( {R - r} \right)}}{{2r\sin \varphi }}} \right)} \right],g = \exp \left[{ - 0.125\left( {B\lambda - 21} \right)} \right] + 0.1,c$为叶片弦长,vrel为入流相对风速,λ为叶尖速比,Cn为法向力系数,Ct为切向力系数。
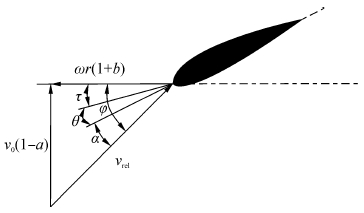
式(3)、(4)中,Ct和Cn的计算与攻角有关,考虑气动弹性时风轮平面内的速度如图 1所示,τ是指叶片受到气动载荷时发生扭转的变形量,逆时针为正。θ 表示该位置翼型的气动扭角,α 表示该姿态下翼型的攻角:
| $\alpha = \varphi - \tau - \theta $ | (5) |
|
| 图1 考虑气动弹性时风轮平面内的速度 Fig.1 Velocity of a section of blade with aeroelastic effect |
当不考虑气动弹性时,τ=0;当考虑气动弹性即叶片受到载荷发生变形时,τ ≠0,此时,翼型的攻角会受到叶片扭转变形的影响,相应地也会影响Ct和Cn。
联立式(1)~(5),可以得到考虑气动弹性情况下轴向诱导因子a和周向诱导因子a'为
| $a = \frac{{2 + {Y_1} - \sqrt {4{Y_1}\left( {1 - F} \right) + Y_1^2} }}{{2\left( {1 + F{Y_1}} \right)}}$ | (6) |
| $a' = \frac{1}{{\left( {1 - aF} \right){Y_2}/\left( {1 - a} \right) - 1}}$ | (7) |
其中
$$\begin{array}{c} {Y_1} = 4F{\sin ^2}\varphi /\left( {\sigma {C_n}{F_1}} \right)\\ {Y_2} = 4F\sin \varphi \cos \varphi /\left( {\sigma {C_t}{F_1}} \right)\\ \sigma = Bc/\left( {2\pi r} \right) \end{array}$$当轴向诱导因子a>0.3时,叶素理论将不再适用,此时就需要引入修正因子对风力机的推力进行修正。那么轴向诱导因子a和周向诱导因子a'为
| $\begin{array}{l} a = \left[{2 + \left( {1 - 2{a_c}F} \right){Y_1} - } \right.\\ \left. {\sqrt {{{\left( {1 - 2{a_c}F} \right)}^2}Y_1^2 + 4{Y_1}\left( {1 - 2{a_c}F + a_c^2F} \right)} } \right]/2 \end{array}$ | (8) |
| $a'\frac{1}{{\left( {1 - aF} \right){Y_2}/\left( {1 - a} \right) - 1}}$ | (9) |
式中:ac=1/3。
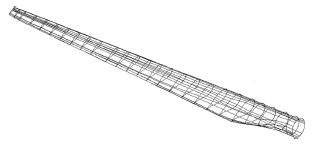
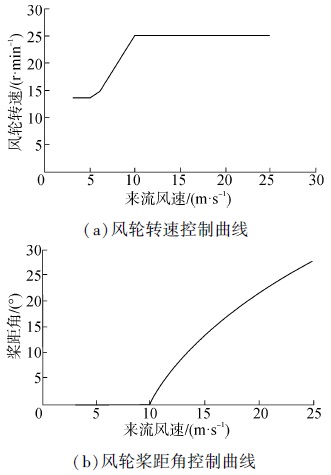
2 气动弹性对风力机性能的影响 2.1 风力机叶片模型选用国内某850 kW风力机叶片作为参考叶片进行计算分析,叶片总长30 m,最大弦长为2.65 m,叶尖弦长为0.72 m。叶片的相对厚度从最大弦长处的40%沿着展向递减到叶尖处的18%。在叶根处,叶片的扭角为12°,叶尖处为0°。叶片外形如图 2所示。变桨变速型风力机,其风轮转速和变桨距控制曲线如图 3所示。
|
| 图2 参考叶片外形 Fig.2 The shape of reference blade |
|
| 图3 风力机运行条件 Fig.3 Operating conditions of wind turbine |
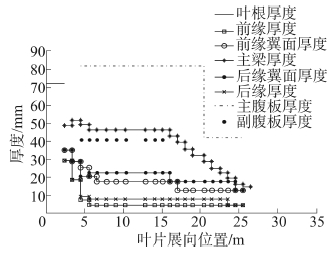
叶片内部采用2个剪切横梁的截面形式[15],这种构造形式通过腹板将叶片内部分成5个部分,从左至右依次为前缘增强、前缘翼面、主梁、后缘翼面及后缘增强,主梁由2个腹板连接。叶片内部铺层由单向布、双向布和三向布的聚酯玻纤铺设而成,翼型前、后缘和腹板采用“三明治”夹芯结构,其外层为正交编织的双向布,中间为PVC泡沫,其中翼面承受部分剪切和弯曲载荷,腹板则维持叶片整体稳定性,以防止叶片在受载时发生失稳破坏;前、后缘加强为内部沿展向铺设若干单向布,以保证该处有足够的强度;此外为使叶片表面光滑,减少由于生产制造而造成的表面粗糙度问题,还需在叶片表面铺设一层胶衣布。图 4展示叶片各个部分厚度分布。
|
| 图4 叶片各个部位厚度分布 Fig.4 Thickness distribution of each part of blade |
文中利用风力机专用软件RFOIL[16]计算叶片的气动载荷,RFOIL是荷兰代尔夫特理工大学开发的一款专门用于风力机翼型设计和气动性能分析的软件,与目前广泛被运用的XFOIL相比,其优点是改进了失速区域的翼型气动性能的计算稳定性和准确性,其计算结果也通过了相应的实验验证[17]。自行编制的MATLAB程序将RFOIL计算的结果解耦成载荷函数,在有限元软件中将气动载荷函数加载到叶片模型上并计算叶片的变形,并通过自编程序计算变形后的气动载荷,再次加载并计算叶片的变形;如此反复迭代计算,直到满足收敛条件(前后两次叶尖位移插值小于1 mm)为止,得到叶片变形收敛时的转角τ 。求解叶片扭转角τ的过程,实际上就是求解叶片与流体双向流固耦合的过程。在多种风速工况下,运用该方法,计算得到参考叶片在考虑气动弹性前后的性能如图 5所示。
|
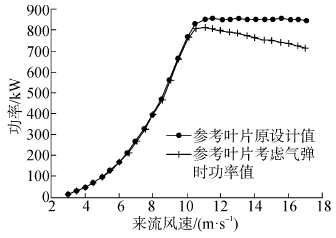
| 图5 参考叶片考虑气弹前后功率 Fig.5 Power of reference blade with/without aeroelastic effect |
由图 5可知,随着风速的增大,风力机原设计功率逐渐增大,并达到额定功率;当考虑气动弹性时,功率先随着风速的增大而增大,同时,风轮受到载荷增大,扭转变形量随之增加,导致叶片各截面局部攻角减小,功率降低。风速越大,功率降低越严重。在大风速大载荷工况下,气动弹性对风轮性能有明显的负面影响,并且风速越大,这种影响越明显。因此,在设计叶片的气动外形时,必须考虑气动弹性对风力机性能的影响。
3 优化模型的建立 3.1 目标函数对与变速型风力机而言,风力机的年发电量与风轮的风能利用率成正比,因此,将风力机额定风速下风能利用率作为优化目标:
| $F\left( X \right) = \max \left( {{C_P}} \right)$ | (10) |
根据风力机风能利用系数的定义有表达式:
| ${C_P} = \frac{P}{{\rho {V^3}A/2}}$ | (11) |
根据修正的叶素动量理论,将式(11)经过变换,得到风能利用系数的另外一种表达式:
| ${C_P} = \frac{{8{\lambda ^2}}}{{{R^4}}}\int_0^R {a'\left( {1 - a} \right){r^3}{\rm{d}}r} $ | (12) |
风力机捕获风能的效率由叶片的表面形状来决定,而叶片的长度、弦长、扭角及相对厚度共同构成了叶片的基本外形。翼型、翼型沿展向的位置及相对厚度的分布于叶片原设计值保持一致,风轮的运行条件如图 2所示。前文分析可知,叶片受载扭转变形直接影响叶片有效攻角,对叶片性能影响较大,由式(5)可知,扭角也会影响有效攻角,进而将叶片的扭角作为设计变量;另外,叶片的扭转变形量与风速和叶片弦长有关,同等情况下,叶片弦长越大,风速越大,叶片受载就越大,扭转变形量随之增大,气动弹性影响就越明显,因此,将叶片的弦长也作为设计变量。
对于叶片的弦长和扭角分布,为了保证其拥有良好的气动性能及连续光滑的表面,本文选取关键的6个点(沿叶片展向位置分别为18%、46%、61%、74%、92%、100%),采用贝塞尔曲线对弦长及扭角沿叶片展向的分布进行控制,设计变量总共有12个,其取值范围控制如下(表 1给出了优化设计变量的约束范围):
| ${X_{i\min }} \le {X_i} \le {X_{i\max }},i = 1,2$ | (13) |
| 弦长c/m | 扭角θ/(°) | 相对厚度δ/% | |
| 最大值 | 2.65 | 12.0 | 40 |
| 最小值 | 0.72 | -0.7 | 18 |
除叶片形状需要设置约束限制外,在优化过程中,还需对叶片的载荷进行约束。根据风力机空气动力学理,叶片的法向力系数Cn和切向力系数Ct表示为
| $\left\{ \begin{array}{l} {C_n} = L\cos \varphi + D\sin \varphi \\ {C_t} = L\sin \varphi - D\cos \varphi \end{array} \right.$ | (14) |
式中:L为翼型的升力系数,D为翼型的阻力系数。
在风轮工作时,叶片的法向力表现为推力形式,而叶根处的弯矩是由推力而产生,叶根处弯矩的增加会直接影响着叶片强度及风力机的疲劳寿命,因此,对叶根弯矩进行约束:
| ${M_{\rm{m}}} = \frac{1}{2}\rho B\int_0^R {\frac{{V_0^2{{\left( {1 - a} \right)}^2}}}{{{{\sin }^2}\varphi }}c{C_n}r{\rm{d}}r \le {M_{{\rm{m}}\;\max }}} $ | (15) |
式中:Mm max由参考叶片决定。
另一方面,叶片所受的切向力形成风轮的扭矩,而风力机的输出功率与转矩成正比关系。但是,过大的转矩会使风力机传动系统的载荷增加,不利于机械传动系统的使用寿命。因此,对风轮的扭矩也进行约束控制:
| ${M_{\rm{T}}} = \frac{1}{2}\rho B\int_0^R {\frac{{{V_0}\left( {1 - a} \right)wr\left( {1 + a'} \right)}}{{\sin \varphi \cos \varphi }}} c{C_t}r{\rm{d}}r \le {M_{{\rm{T}}\;{\rm{max}}}}$ | (16) |
式中:MT max由参考叶片决定。
在设计过程中,由于采用叶片的真实结构,为了减少叶片的成本,还需要对叶片的质量进行约束:
| $m \le {m_{\max }}$ | (17) |
式中:mmax由参考叶片决定。
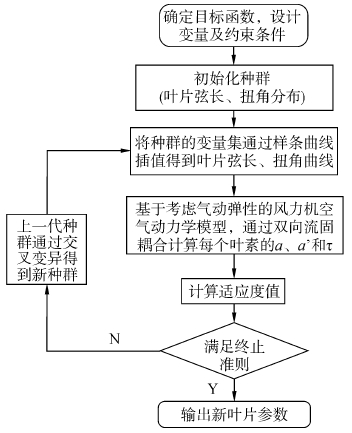
3.3 优化设计程序与方法风力机的功率与载荷采用前文建立的基于气动弹性的风力机空气动力学模型来求解。通过优化模型可以看出,本次优化是一个非线性单目标多约束问题。应用自行编制的改进遗传算法程序[18],进行自动优化求解。该改进算法的基本参数如下:交叉概率为0.7,变异概率为0.3,变量维数为12,种群大小为30,最大迭代次数为80。叶片优化设计流程图如图 6所示。
|
| 图6 优化设计流程图 Fig.6 Flow chart of the blade optimized design algorithm |
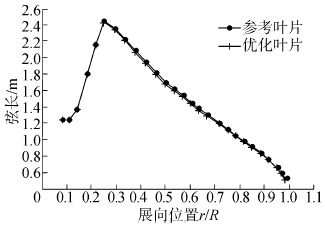
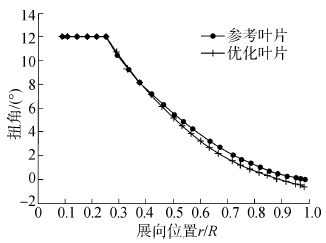
图 7、8分别为叶片优化后的弦长和扭角分布图。由图 7可以看出,优化叶片的弦长小于参考叶片。优化前叶片质量为3 992.9 kg,优化后叶片质量为3 918.7 kg,优化叶片的质量相比参考叶片减少了1.85%;由图 8可以看出,优化叶片的扭角在叶片根部附近与参考叶片相差不太,在叶片中后端扭角比参考叶片小,这是由于优化叶片在受载扭转变形的反方向上有一定的预扭,可使叶片在受载变形后处于最佳扭角位置,以减小气动弹性对叶片性能的影响。
|
| 图7 弦长分布 Fig.7 The distribution of the chord length |
|
| 图8 扭角分布 Fig.8 The distribution of the twist angle |
|
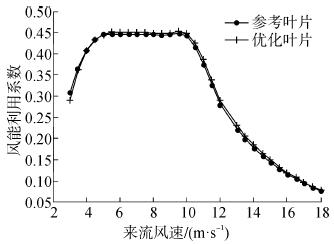
| 图9 风能利用系数特性 Fig.9 The characteristics of the power coefficient |
表 2为优化叶片与参考叶片在不同风速下的功率与效率的对比。
| 风速/(m·s-1) | 叶尖速比 | Po/kW | P1/kW | η1/% | P2/kW | η2/% |
| 注:Po表示参考叶片设计功率;P1表示考虑气弹时参考叶片的功率;η1表示考虑气弹时参考叶片的效率,是P1与Po的比值;P2表示考虑气弹时优化叶片的功率;η2表示考虑气弹时优化叶片的效率,是P2与Po的比值。 | ||||||
| 3 | 13.6 | 13.85 | 14.14 | 102 | 14.31 | 103 |
| 5 | 8.14 | 95.70 | 94.44 | 98.69 | 94.99 | 99.26 |
| 8 | 7.3 | 394 | 387 | 98.39 | 391 | 99.31 |
| 10 | 7.3 | 769 | 755 | 98.19 | 763 | 99.21 |
| 11 | 6.66 | 851 | 814 | 95.91 | 833 | 97.83 |
| 13 | 5.64 | 852 | 783 | 92.44 | 806 | 94.62 |
| 15 | 4.31 | 852 | 747 | 88.97 | 765 | 89.8 |
效率按照下式进行计算:
| $\eta = \frac{{{P_1}}}{{{P_o}}} \times 100\% $ | (18) |
式中:η为功率发挥效率,Po为原设计功率,P1为考虑气弹后计算功率。效率计算大于100%时,表明气动弹性对风轮产生正影响;反之,则为负影响。效率数值越偏离100%,表明影响较明显;反之,表明影响较小。
由表 2的数据可知,在任意风速下,优化叶片的功率与效率相比参考叶片有提高,特别在风速为13 m/s时,功率提高23 kW,效率提高2.18%。综合可知,在叶片质量减少的同时,风轮的功率与输出效率都有所提高。
5 结论1) 通过运用考虑气动弹性的风力机空气动力学模型对某850 kW风力机叶片进行分析计算,结果表明在大风速大载荷工况下,气动弹性对风轮有负面影响,并且这种影响随风速增大而更加明显。
2) 在考虑气动弹性的风力机空气动力学模型的基础上,提出了以额定风速下风能利用率为目标的优化模型,运用改进的遗传算法对风力机叶片弦长和扭角分布进行了优化设计,结果表明,相比参考叶片,优化后的850 kW风力机叶片质量降低了1.85%,同时,其风能利用系数最大提高了2.9%,使得风力机的输出功率得到提高,最大提高23 kW。该叶片的设计方法为设计出高性能轻质量低成本的风力机叶片提供了理论依据。
| [1] | BADREDDINNE K, ALI H, DAVID A. Optimum project for horizontal axis wind turbines ‘OPHWT’[J]. Renewable energy, 2005, 30(13): 2019-2043. |
| [2] | WAND Xudong, SHEN Wenzhong, ZHU Weijun, et al. Shape optimization of wind turbine blades[J]. Wind energy, 2009, 12(8): 781-803. |
| [3] | 陈进, 王旭东, 沈文忠, 等. 风力机叶片的形状优化设计[J]. 机械工程学报, 2010, 46(3): 131-134. CHEN Jin, WANG Xudong, SHEN Wenzhong, et al. Optimization design of blade shapes for wind turbines[J]. Journal of mechanical engineering, 2010, 46(3): 131-134. |
| [4] | 章嘉麟, 周正贵, 雷延生. 基于并行遗传算法的低风速高性能风力机叶片优化设计[J]. 太阳能学报, 2011, 32(8): 1275-1280. ZHANG Jialin, ZHOU Zhenggui, LEI Yansheng. Optimization for high performance wind turbine blades at low wind velocity based on parallel genetic algorithm[J]. Acta energiae solaris sinica, 2011, 32(8): 1275-1280. |
| [5] | 汪泉, 陈进, 郭小峰, 等. 基于性能及轻量化的新型风力机叶片优化设计研究[J]. 空气动力学学报, 2014, 32(1): 77-84. WANG Quan, CHEN Jin, GUO Xiaofeng, et al. Optimal design of a new wind turbine blade based on performance and light weight[J]. Acta aerodynamic sinica, 2014, 32(1): 77-84. |
| [6] | 刘雄, 陈严, 叶枝全. 遗传算法在风力机风轮叶片优化设计中的应用[J]. 太阳能学报, 2006, 27(2): 180-185. LIU Xiong, CHEN Yan, YE Zhiquan. Application of genetic algorithms to HAWT rotor blades optimization[J]. Acta energiae solaris sinica, 2006, 27(2): 180-185. |
| [7] | SINGH P M, CHOI Y D. Shape design and numerical analysis on a 1 MW tidal current turbine for the south-western coast of Korea[J]. Renewable energy, 2014, 68: 485-493. |
| [8] | DO RIO VAZA D A T D, PINHEIRO VAZA J R, MESQUITA A L A, et al. Optimum aerodynamic design for wind turbine blade with a Rankine vortex wake[J]. Renewable energy, 2013, 55: 296-304. |
| [9] | VITALE A J, ROSSI A P. Computational method for the design of wind turbine blades[J]. International journal of hydrogen energy, 2008, 33(13): 3466-3470. |
| [10] | DING Jiaojiao, WANG Hao, SUN Liping, et al. Optimal design of wind turbine blades with Wilson and BEM method integrated[J]. Applied mechanics and materials, 2013, 404: 286-291. |
| [11] | 汪泉. 风力机叶片气动外形与结构的参数化耦合设计理论研究[D]. 重庆: 重庆大学, 2013: 75-99. WANG Quan. Study on the parameterized coupled design theory of wind turbine blade aerodynamic shape and structure[D]. Chongqing: Chongqing University, 2013: 75-99. |
| [12] | 张石强. 风力机专用翼型及叶片关键设计理论研究[D]. 重庆: 重庆大学, 2010: 75-95. ZHANG Shiqiang. Study on the key theory of wind turbine blade and dedicated airfoils[D]. Chongqing: Chongqing University, 2010: 75-95. |
| [13] | 贺德馨. 风工程与工业空气动力学[M]. 北京: 国防工业出版社, 2006: 80-96. HE Dexin. Wind Engineering and Industrial Aerodynamics[M]. Beijing: National Defense Industry Press, 2006: 80-96. |
| [14] | SHEN Wenzhong, MIKKELSEN R, SRENSEN J N, et al. Tip loss corrections for wind turbine computations[J]. Wind energy, 2005, 8(4): 457-475. |
| [15] | 陈进, 马金成, 汪泉, 等. 基于ANSYS二次开发的风力机叶片结构优化[J]. 哈尔滨工程大学学报, 2014, 35(7): 895-900. CHEN Jin, MA Jincheng, WANG Quan, et al. Structural optimization of the wind turbine blade combining the ANSYS secondary development[J]. Journal of Harbin engineering university, 2014, 35(7): 895-900. |
| [16] | 陈进, 张石强, 王旭东, 等. 基于粗糙度敏感性研究的风力机专用翼型设计[J]. 空气动力学学报, 2011, 29(2): 142-149. CHEN Jin, ZHANG Shiqiang, WANG Xudong, et al. Dedicated wind turbine airfoil design based on the roughness sensitivity considerations[J]. Acta aerodynamica sinica, 2011, 29(2): 142-149. |
| [17] | TIMMER W A, VAN ROOIJ R P J O M. Summary of the delft university wind turbine dedicated airfoils[J]. Journal of solar energy engineering, 2003, 125(4): 488-496. |
| [18] | 陈明杰, 刘胜. 改进自适应遗传算法在函数优化中的应用研究[J]. 哈尔滨工程大学学报, 2007, 28(8): 875-879. CHEN Mingjie, LIU Sheng. An improved adaptive genetic algorithm and its application in function optimization[J]. Journal of Harbin engineering university, 2007, 28(8): 875-879. |



