通过对旋转弹的角运动特性进行分析发现,以俯仰轴为敏感轴安装的单轴陀螺所敏感的角速度由俯仰、偏航和滚转速率耦合而成,在短时间内,该耦合角速度信号可以看成是以俯仰角速度为幅值、滚转角为相位和滚转角频率为角频率的周期信号与一个幅值远小于俯仰角速度的周期信号之和,总体幅值约等于俯仰角速度、总体角频率约等于滚转角频率且在低量程陀螺测量带宽内,因此可以利用低量程陀螺测量该耦合角速度信号并将其近似为正弦信号进行处理。锁相跟踪是对具有周期特性的信号进行相位跟踪锁定,进而得到信号的频率和相位的算法,锁相跟踪算法对这种短时间内可以近似为周期信号的信号具有良好的跟踪特性。因此,利用锁相跟踪方法提取上述耦合角速度中含有的滚转姿态信息是可行的。因此,本文在对锁相跟踪原理及三阶锁相环特性进行深入研究的基础上,提出利用三阶锁相环对旋转弹滚转角进行跟踪,进而获取滚转姿态的旋转弹滚转姿态测量方法。
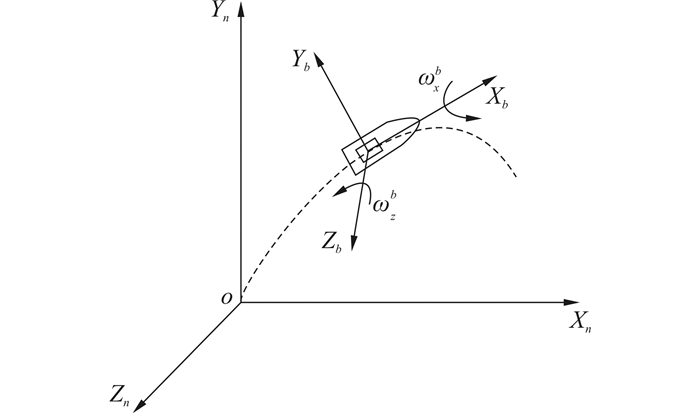
1 弹体耦合角运动信号特性研究 1.1 弹体角运动耦合采用单轴陀螺测量弹体俯仰角运动时,单轴陀螺在弹体上的安装方式如图 1所示,图中XbYbZb轴为弹体坐标系三个轴,弹体旋转轴为Xb轴,陀螺敏感轴Zb感受角速度ωzb。
|
| 图 1 单轴陀螺安装位置及敏感轴示意图 Fig. 1 The installation of single-axis gyroscope |
陀螺受到弹体滚转运动和偏航运动的影响,测到的数据受到滚转角速度和偏航角速度的调制,根据旋转弹体坐标系、非旋转弹体坐标系与地面惯性坐标转换关系可得:
| $ \omega _z^b = \dot \theta \cos \gamma + \dot \psi \sin \gamma \cos \theta $ | (1) |
如式(1)所示单轴陀螺所测弹体角速度ωzb,受到非旋转弹体坐标系俯仰角θ,非旋转弹体坐标系俯仰角速度 $\dot \theta $、非旋转弹体坐标系滚转角γ和非旋转弹体坐标系偏航角速度 ${\dot \psi }$的影响,需要分析这些参数对耦合角速度ωzb的影响。
式(1)可根据三角函数关系改写为
| $ \left\{ \begin{array}{l} \omega _z^b = \dot \theta \cos \varphi + \dot \psi \sin \varphi \cos \theta = A\sin \left( {\gamma + \zeta } \right)\\ A = \sqrt {{{\dot \theta }^2} + {{\left( {\dot \psi \cos \theta } \right)}^2}} \end{array} \right. $ | (2) |
因此本文提出的利用单轴陀螺测量耦合角速度信号ωzb,利用锁相跟踪对该耦合角速度信号进行处理,得到该信号中所含频率和相位信息。因为偏航角速度 ${\dot \psi }$小于俯仰角速度 $\dot \theta $,ζ的值很小,以锁相跟踪获得的γ+ζ作为旋转弹滚转角γ,以耦合角速度 ${\kern 1pt} {\kern 1pt} \dot \gamma $+ ${\dot \zeta }$作为旋转弹滚转角速度 ${\kern 1pt} {\kern 1pt} \dot \gamma $是合理的。
2 三阶锁相跟踪环路研究三阶锁相环能跟踪频率加加信号,但有恒定的跟踪误差,其跟踪更高阶激励信号将导致发散,会导致跟踪失锁。其特性由其特征频率ωn和阻尼系数ξ决定,若环路所采用的特征频率ωn越高,则其达到稳态所需时间就越少,即较高的ωn能让系统具有相应较快的跟踪性能。若阻尼系数ξ越大,则环路的通带增益显得越为平坦,但是增益幅度在阻带段下降得越慢,环路对噪声的滤波效果越不理想。噪声带宽越窄,则由于越少频率成分的噪声被允许进入环路,因而环路的滤波效果越好,环路对信号的跟踪效果就越精确,若噪声带宽越宽,则环路的噪声性能越差,信号跟踪就越不准确。
因为弹体运动特别是弹体章动会引起弹体角运动的急剧变化,进而引起频率和相位跟踪误差的激烈震荡,所以环路带宽BL能保证适应弹体的这种激烈运动导致的频率和相位的正常波动,以保证环路对信号的持续跟踪;否则,如果BL过小,则由弹体高动态应力所致的频率和相位变化中有用的高频信号成分可能会同噪声一起被滤除,进而破坏信号的真实性,使环路容易发生信号失锁。因此,环路带宽BL是锁相环的一个重要参数,越大的环路带宽使锁相跟踪环路具有满足较强动态运动测试的能力,但也同时降低其噪声性能。
参考文献[10]取三阶锁相跟踪环路的二阶环路滤波器的各参数如下:
$$ \begin{array}{l} {a_3} = 1.1,{b_3} = 2.4,\\ {B_L} = \frac{{{a_3}{b_3} + a_3^2 - {b_3}}}{{4\left( {{a_3}{b_3} - 1} \right)}}{\omega _n} = 0.7845{\omega _n} \end{array} $$上述参数是ξ=0.707时计算得出的,当选定带宽BL,则可以确定ωn的值,即可实现环路滤波器设计。
|
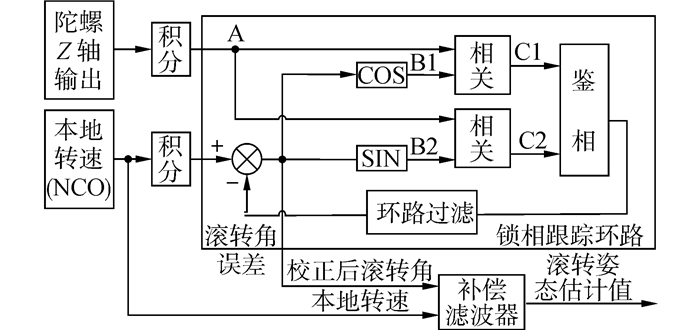
| 图 2 基于三阶锁相环和陀螺的滚转姿态信息提取方法 Fig. 2 Roll attitude solve method based on three phase-locked loops and low-range gyroscope |
由于弹丸在全弹道非旋转弹体坐标系俯仰、偏航角速度幅值比较小,在各种气动干扰的条件下,传感器测量信号还会产生较多噪声,因此如何从惯性传感器的低信噪比信号中提取出有用信号是本文的关键。将借鉴在数字通信信号处理中普遍采用的锁相跟踪技术,该技术的优点能在信噪比低的条件下实现对信号的跟踪和锁定,提取出滚转姿态数据。
基于以俯仰轴为敏感轴的单轴陀螺所测数据及锁相跟踪算法,设计弹体滚转姿态测量模型。以图 1安装方式安装的陀螺敏感到的角速度测量值积分作为A路信号,本地生成转速(NCO)经积分作为本地滚转角,经误差校正后,生成两路相互正交的正弦信号B1和B2作为本地参考信号,分别与A路信号进行相关运算(乘加),两路相关运算结果C1和C2通过鉴相得到滚转相位误差估计值,经环路滤波器进一步估计后,形成滚转角误差校正值,对本地滚转角进行校正,经过若干次循环后最终可达到对陀螺测量值中所含滚转相位的锁定,再经过误差校正后的滚转姿态接近真实值。为提高滚转姿态估计精度,进一步采用补偿滤波器,根据本地转速对经校正后的滚转角估计值。
4 补偿滤波器补偿滤波算法是根据三阶锁相环路稳态误差模型和相关参数估计进行补偿滤波,以提高锁相跟踪输出结果精度。根据锁相跟踪结果误差特性,将补偿滤波分为锁相跟踪稳态常值偏置误差补偿和呈正弦规律变化误差的线性递推最小二乘滤波补偿。
(1)稳态常值偏置误差补偿。根据旋转稳定弹运动特性,俯仰角速度 $\dot \theta $大于偏航角速度 ${\dot \psi }$,由反正切函数性质可得
| $ \zeta = \frac{{\dot \psi \cos \theta }}{{\dot \theta }} $ | (3) |
由于旋转稳定弹的俯仰角速度和偏航角速度变化较小,可以近似为直线,而滚转角速度变化较大,所以在短时间内,假定旋转稳定弹角运动如式(4)所示。
| $ \left\{ \begin{array}{l} \theta = {a_0} + {a_1}t,\psi = {c_0} + {c_1}t\\ \gamma = {d_0} + {d_1}t + {d_2}{t^2} + {d_3}{t^3} \end{array} \right. $ | (4) |
由式(4)可知
| $ \dot \theta = {a_1},\dot \psi = {c_1},\zeta = \frac{{{c_1}\cos \left( {{a_0} + {a_1}t} \right)}}{{{a_1}}} $ | (5) |
| $ \dddot \gamma = 6{d_3},\dddot \zeta = {a_1}^2{c_1}\sin \left( {{a_0} + {a_1}t} \right) $ | (6) |
| $ \dddot \varphi = \dddot \gamma + \dddot \zeta = 6{d_3} + {a_1}^2{c_1}\sin \left( {{a_0} + {a_1}t} \right) $ | (7) |
则由三阶锁相环的稳态输出可得
| $ \mathop {\lim }\limits_{n \to \infty } {\theta _e}\left( n \right) = \frac{{{T_s}^2{\Delta _\omega }}}{{{b_0} + {b_1} + {b_2}}} = \frac{{{T_s}^2\left[ {6{d_3} + {a_1}^2{c_1}\sin \left( {{a_0} + {a_1}t} \right)} \right]}}{{{b_0} + {b_1} + {b_2}}} $ | (8) |
根据实际弹道计算出a0、a1、d3和c1的值,根据锁相环特性和参数确定b0、b1和b2的值即可计算出稳态跟踪误差θe(n),用该稳态误差对锁相跟踪误差进行补偿,即可得到更加精确的输出结果。
(2)线性递推最小二乘滤波。如式(2)所示的信号,经过积分清除和锁相跟踪计算后其稳态误差存在如(8)式所示的误差,可以将这种沿真值附近正负变化的误差通过线性递推最小二乘滤波法滤除,滤波结果即为锁相跟踪最终补偿后的计算结果,该结果精度更高,满足锁相跟踪的要求。
经按阶递推最小二乘滤波,得到锁相跟踪频率误差和相位误差,再经过稳态常值偏置补偿得滤波估计值,即最佳误差量,再通过本地生成频率和相位进行误差补偿后得到载体滚转速度和相位结果。
5 弹体滚转姿态跟踪实验对于上述滚转姿态跟踪算法,采用两组弹道数据模拟出垂直于弹轴安装的陀螺测量数据进行跟踪运算,计算弹体滚转角速度和滚转相位,根据跟踪误差对所提姿态跟踪算法进行验证。
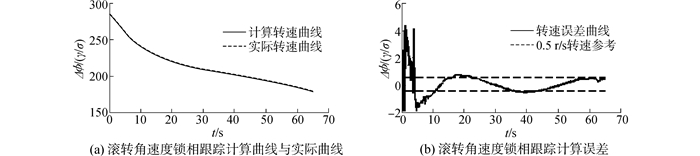
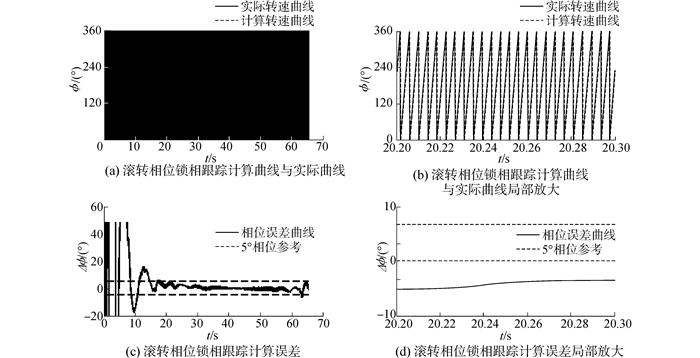
第一组弹道数据为初速为780m/s、射角为45°、转速为252r/s且随机风干扰较大的弹体角运动数据,锁相跟踪结果如图 3~5所示。第二组弹道数据为初速为900 m/s、射角为45°、转速为286 r/s且随机风干扰较大的弹体角运动数据,锁相跟踪结果如图 6~8所示。可见,与采用第一组弹道数据进行滚转姿态检测仿真的结果相比,第二组弹道数据的速度较高,转速较大,但滚转姿态检测误差相差不大, 转速跟踪误差也为0.5 r/s,相位稳态误差也可达2°以内。
|
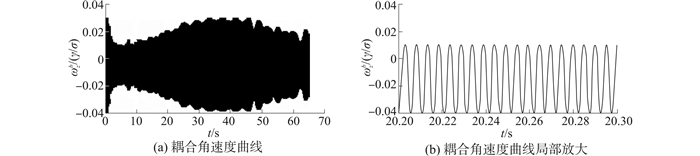
| 图 3 第一组弹道耦合角速度曲线及局部放大图 Fig. 3 The coupled angular rate and its partial curve of the first group trajectory |
|
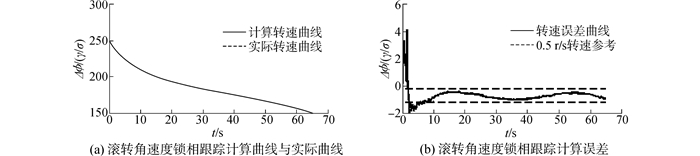
| 图 4 第一组弹道滚转角速度锁相跟踪计算结果 Fig. 4 The roll angular rate calculated results of the first group trajectory |
|
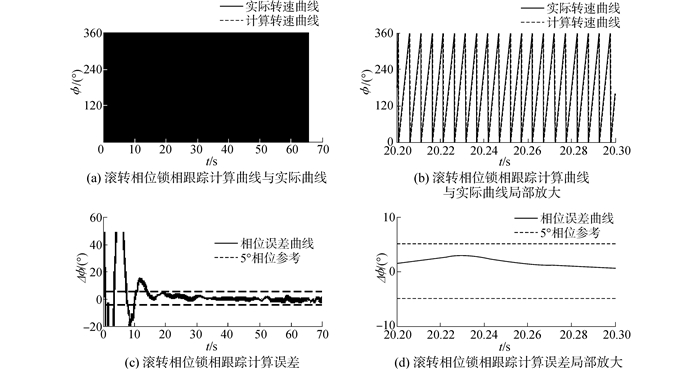
| 图 5 第一组弹道滚转相位锁相跟踪计算结果及局部放大图 Fig. 5 The roll phase calculated results and its partial curve of the first group trajectory |
|
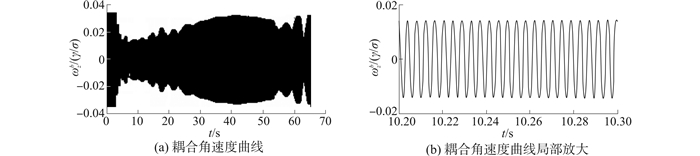
| 图 6 第二组弹道耦合角速度曲线及局部放大图 Fig. 6 The coupled angular rate and its partial curve of the second group trajectory |
|
| 图 7 第二组弹道滚转角速度锁相跟踪计算结果 Fig. 7 The roll angular rate calculated results of the second group trajectory |
|
| 图 8 第二组弹道滚转相位锁相跟踪计算结果及局部放大图 Fig. 8 The roll phase calculated results and its partial curve of the second group trajectory |
由图 3可以看出耦合角速度曲线具有明显的周期特性,其包络与俯仰角速度相似,包络细节与偏航角速度相似;由图 4可知转速跟踪误差在0.5 r/s以内,相对误差可达3‰;由图 5可知实际相位曲线和计算相位曲线基本重合,误差在8 s内达到5°以内,稳态误差可达2°以内。由图 3~8可知,该滚转姿态锁相跟踪方法能对弹丸的俯仰和滚转耦合信号进行有效跟踪,但对于动态性较高的弹丸,其初始跟踪误差较大,收敛时间较长,但总体收敛时间10 s左右, 跟踪精度在2°左右。
6 结论1)弹丸的运动参数变化较为缓慢,以俯仰轴为敏感轴的陀螺所测的弹体角运动耦合信号具有明显的周期特性,其幅值受俯仰角速度调制,可以借鉴所限跟踪算法对其进行处理,提取出耦合信号中的滚转角运动信息,实现弹体滚转姿态测量。
2)三阶锁相环路具有跟踪滚转角加加速度的能力,且具有较高的跟踪精度和跟踪稳定性,能有效跟踪弹体滚转运动,满足跟踪弹体滚转运动的要求。因此,本研究所提的基于锁相跟踪原理的滚转姿态提取方法是可行的,能解决弹体滚转姿态测量的难题。
| [1] | BEST R E. Phase-locked loops design, simulation and applications[M]. 5th ed. New York: McGraw-Hill, 2003: 1-5. |
| [2] | GUSTAFSON D E, LUCIA D J. Autonomous local vertical determination for guided artillery shells[C]//Proceedings of the 52nd Annual Meeting of the Institute of Navigation. Cambridge, MA, USA, 1996. |
| [3] | DOTY J H. Advanced spinning-vehicle navigation——a new technique in navigation of munitions[C]//Proceedings of the 57th Annual Meeting of the Institute of Navigation. Albuquerque, NM, USA, 2001. |
| [4] | RATKOVIC J A. Projectile guidance with accelerometers and a GPS receiver: US, US6779752[P]. 2004-08-24. |
| [5] | GÉRARD L. Process to control the trajectory of a spinning projectile: US, US7105790[P]. 2006-09-12. |
| [6] | PARK H Y, KIM K J, LEE J Y, et al. Roll angle estimation for smart munitions[C]//Proceedings of the 17th IFAC Symposium on Automatic Control in Aerospace. Universitas Studii Toulouse, France, 2007. |
| [7] | MANSUKHANI A. Phase lock loop stability analysis[R]. Applied Microwave and Wireless, 2000. |
| [8] | KINGSTON D, BEARD R W. Real-time attitude and position estimation for small UAVs using low-cost sensors[C]//Proceedings at AIAA 3rd "Unmanned Unlimited" Technical Conference, Workshop and Exhibit. Chicago, Illinois, 2004. |
| [9] | CHHEDA B, CRASSIDIS A. L, WALTER W W. Attitude estimation using an accelerometer and rate gyro based device[C]//Proceedings at AIAA Atmospheric Flight Mechanics Conference and Exhibit. Keystone, Colorado, 2006. |
| [10] | KAPLAN E D, HEGARTY C J. Understanding GPS: principles and applications[M]. 2nd ed. Boston: Artech House, Inc., 2006. |



