镍钛形状记忆合金(shape memory alloys,SMAs)因其独特的超弹性和形状记忆效应被广泛地应用在航空航天,交通运输和生物医学等多个领域[1, 2, 3]。然而这些器件不可避免的就会受到循环载荷的影响,为了能完善的设计形状记忆合金工作元件并且评估其可靠性,有必要深入地研究循环载荷条件下的形状记忆合金超弹性变形特性和建立适合工程应用的本构模型。
近20年来,许多学者对镍钛合金的循环变形进行了实验观察,其中所得出来的主要共同特点有三个[4, 5]: 1)随着循环圈数的增加迟滞环变小,当循环圈数到达特定的值时,迟滞环大小不变;2)残余应变(残余塑性应变)随着循环圈数的增加逐渐减小,直至减小到0不变;3)相变临界应力或者相变驱动力随着循环圈数的增加逐渐减小,当循环圈数到达一特定值后保持不变。
根据实验观察所得到数据及现象,研究者建立了许多与循环圈数N有关的形状记忆合金本构关系,这些本构关系大致可以分为两类,即宏观唯象模型和细观力学模型。比较有代表性的宏观唯象模型有Tanaka模型,他通过引入三个内变量残余应力,残余应变和马氏体体积分数来描述形状记忆合金在一维情况下受到循环载荷的本构关系[6]。其中循环载荷包括机械载荷和温度热载荷。Lexcellent等[7]在简单循环载荷下定义新的内变量,引入瞬时残余马氏体的概念进而改变自由能函数提出新的动力学方程来描述本构关系。Abeyaratne等[8]则是通过引入内变量来控制相变驱动力来影响多晶体的成核程度,使得相变改变的发生较为准确。Auricchio[9]则考虑了温度的影响,相变临界应力和残余永久变形来建立了一个在循环加载下一维超弹性的本构关系。Zaki等[10]定义了三个状态变量内应力,残余应变和累积马氏体体积分数来构造循环相变方程和应力屈服函数来进行数值模拟和模型确认。近年来也有学者通过唯象理论来构造镍钛合金循环本构关系[11]。这些模型形式相对简单便于计算和工程应用及有限元分析,但是却无法描述形状记忆合金的微观相变的机理。细观力学模型考虑微结构的物理机理,以热力学和细观力学等为原理出发,通过对相变转变发生过程中的能量变化来建立模型,同时可以为唯象模型提供相应的理论依据。典型的细观力学模型有Bo and Lagoudas模型[12, 13, 14],他们从热力学原理出发定义了一个包含马氏体、奥氏体和塑性应变的代表性体积单元(RVE),结合定义的几个内变量得到Gibbs自由能并给出马氏体增量的能量增量形式,给出支配相变转化中硬化效应的四种基本机制。Patoor等[15, 16]从晶体学出发给出了单晶相变的运动学描述并利用自洽方法建立多晶模型。Thamburaja等[17]则考虑了马氏体重定向和孪晶来建立单晶体模型通过Taylor方法和有限元程序来实现对多晶体的模拟。Stupkiewicz等[18]则基于层状微结构的假设,通过孪晶和惯习面方程来得到由应力加载本构方程。Yu等[19]通过引入三个界面间的状态变量来得到单晶的Helmholtz自由能和相变驱动力,通过尺度变换得到可以描述多晶NiTi合金循环变形的本构关系。
本文考虑奥氏体与马氏体在相变过程中具有层状微结构,利用理想界面连续的条件并忽略界面的相互作用及局部热效应,推导出宏观应力应变与微观应力应变之间的变化和相变的控制方程[20, 21],并推广到多晶体上[22]。本文在此基础上,引入累积残余应变,累积残余马氏体体积分数等状态变量,通过构造与循环次数N有关的表达式以及控制相变临界驱动力来构造关于循环变形的本构模型。最后通过数值模拟来证明此模型的有效性。
1 单晶本构模型 1.1 本构关系假设在相变过程中马氏体与奥氏体是以层状微结构构成。取体积为V的代表性体积单元,在相变过程中马氏体的体积分数为λ,其应力应变分别为σm和εm,奥氏体的体积分数为1-λ,应力应变为σa和εa。通过体积平均的方法可以得到代表性体积单元的宏观应力和应变:
| $\bar \sigma = \int_v {\sigma {\rm{d}}v = \lambda {\sigma ^m} + \left( {1 + \lambda } \right)} {\sigma ^a}$ | (1) |
| $\bar \varepsilon = \int_v {\varepsilon {\rm{d}}v = \lambda {\varepsilon ^m} + \left( {1 + \lambda } \right)} {\varepsilon ^a}$ | (2) |
相变应变可以表述为
| ${\varepsilon _t} = 0.5g\left( {m \otimes n + n \otimes m} \right)$ | (3) |
式中:g为相变变形量,m、 n分别为相变切变和惯习面法线方向。这些参数很容易通过相变唯象晶体学理论得到。为了便于计算,采用Kelvin矩阵的记法将应力及应变分为面内及面外向量表示[19]。
理想界面条件可表示为
| $\varepsilon _i^m - \varepsilon _i^a = 0$ | (4) |
| $\sigma _o^m - \sigma _o^a = 0$ | (5) |
分别由马氏体与奥氏体各相的本构关系可得
| $\left\{ \begin{array}{l} \varepsilon _i^m\\ \varepsilon _o^m \end{array} \right\} = \left[{\begin{array}{*{20}{c}} {M_{ii}^m}&{0_{io}^m}\\ {0_{oi}^m}&{1_{oo}^m} \end{array}} \right]\left\{ \begin{array}{l} \sigma _i^m\\ \sigma _o^m \end{array} \right\} + \left\{ \begin{array}{l} \varepsilon _i^t\\ \varepsilon _o^t \end{array} \right\}$ | (6) |
| $\left\{ \begin{array}{l} \varepsilon _i^a\\ \varepsilon _o^a \end{array} \right\} = \left[{\begin{array}{*{20}{c}} {M_{ii}^a}&{0_{io}^q}\\ {0_{oi}^a}&{1_{oo}^a} \end{array}} \right]\left\{ \begin{array}{l} \sigma _i^a\\ \sigma _o^a \end{array} \right\}$ | (7) |
代入理想界面条件可以得到
| ${\sigma ^m} = {P^m}\bar \sigma - \left( {1 - \lambda } \right)Q{\varepsilon ^t}$ | (8) |
| ${\sigma ^a} = {P^a}\bar \sigma + \lambda Q{\varepsilon ^t}$ | (9) |
式中:Pm和Pa分别为马氏体与奥氏体的应力集中矩阵,Q为相变应变集中矩阵:
$$\begin{array}{c} {P^m} = \\ \left[{\begin{array}{*{20}{c}} {I - \left( {1 - \lambda } \right)\left( {M_{ii}^m - M_{ii}^a} \right){M^*}}&{\left( {1 - \lambda } \right){M^*}\left( {M_{io}^a - M_{io}^m} \right)}\\ O&I \end{array}} \right]\\ {P^a} = \left[{\begin{array}{*{20}{c}} {\lambda \left( {M_{ii}^m - M_{ii}^a} \right){M^*} + I}&{\lambda {M^*}\left( {M_{io}^a - M_{io}^m} \right)}\\ O&I \end{array}} \right]\\ Q = \left[{\begin{array}{*{20}{c}} {{M^*}\varepsilon _i^t}&0\\ 0&0 \end{array}} \right]\;{M^*} = {\left[{\left( {1 - \lambda } \right)M_{ii}^m + \lambda M_{ii}^a} \right]^{ - 1}} \end{array}$$将σm和σa代入各相的本构方程有
| ${\varepsilon ^m} = {M^m}{P^m}\bar \sigma - \left( {1 - \lambda } \right){M^m}Q{\varepsilon ^t} + {\varepsilon ^t}$ | (10) |
| ${\varepsilon ^a} = {M^a}{P^a}\bar \sigma + \lambda {M^a}Q{\varepsilon ^t}$ | (11) |
将σm,σσa,εm和εa分别代入式(1)、(2)有
| $\bar \sigma = \lambda {P^a}\bar \sigma + \lambda Q{\varepsilon ^t} + \left( {1 - \lambda } \right){P^m}\bar \sigma - {\left( {1 - \lambda } \right)^2}Q{\varepsilon ^t}$ | (12) |
以及宏观总体应力应变的本构关系:
| $\begin{array}{c} \bar \varepsilon = \left[{\left( {1 - \lambda } \right){M^a}{P^a} + \lambda {M^m}{P^m}} \right]\bar \sigma + \\ \lambda \left( {1 - \lambda } \right)\left( {{M^a} - {M^m}} \right)Q{\varepsilon ^t} + \lambda {\varepsilon ^t} \end{array}$ | (13) |
式(12)为应力与马氏体体积分数的表达式,取每一次循环加载后残余马氏体体积分数累加在一起即为相应循环次数的累积残余马氏体体积分数。所以只需要把逆相变结束的应力代入即可得到相应循环加载圈数的累积残余马氏体体积分数。式(13)即为代表性体积单元的本构关系。
1.2 相变驱动力在相变的过程中涉及到能量的变化,通过定义相变驱动力fc来控制相变的改变,只有当 f=fc 时正相变才发生,当f=-fc时逆相变才会发生。
奥氏体与马氏体两相的Helmholtz自由能密度和为
| $\psi = \left( {1 - \lambda } \right){\psi ^a} + \lambda {\psi ^m}$ | (14) |
其中ψa和ψm表示为
$$\begin{array}{c} {\psi ^a} = \psi _o^a + \frac{1}{2}{\sigma ^a}{M^a}{\sigma ^a}\\ {\psi ^m} = \psi _o^m + \frac{1}{2}{\sigma ^m}{M^m}{\sigma ^m} + {E_c} \end{array}$$化学能Ec=B(T-To),B为常数,To热力学的相变平衡温度,ψom和ψoa分别为两相的初始自由能。
Gibbs自由能可以通过Helmholtz变换得到:
| $G = \psi - \bar \sigma :\bar \varepsilon $ | (15) |
所以相变驱动力的表达式为
| $\begin{array}{l} f = - \frac{{\partial G}}{{\partial \lambda }} = \bar \sigma :{\varepsilon ^t} - \bar \sigma :\left[{\left( {I - \frac{1}{2}{{\left( {{P^a}} \right)}^{\rm{T}}}} \right)} \right.:\\ \left. {{M^a}{P^a} - \left( {I - \frac{1}{2}{{\left( {{P^m}} \right)}^{\rm{T}}}:{M^m}{P^m}} \right)} \right]\bar \sigma - {E_c} \end{array}$ | (16) |
材料的每一次加载卸载后都会存在一个残余应变,把第N次加载后残余应变与之前N-1次加载后残余应变相加即为N次加载后的累积残余应变。相应的累积残余应变在循环加载到一定圈数时,其值维持在一定值不变。原因在于循环加载中奥氏体与马氏体的界面产生了塑性滑移,随圈数的增加而达到饱和。相应的可取如下指数形式的演化方程[9]:
| ${\varepsilon _r} = \alpha \left( {1 - \exp \left( {N/\beta } \right)} \right)$ | (17) |
其中α、β为常数。
1.4 临界应力临界应力分为正相变的临界应力与逆相变的临界应力,当应力达到正相变临界应力时发生正相变,同理有相应逆相变临界应力。同累积残余应变类似,随循环加载次数的增加,趋于一个稳定值。临界应力变化的原因在于循环加载中内部位错密度的改变和马氏体的重定向导致产生了内应力,从而使得发生相变的应力减小,最终趋于稳定[9]。
由于在试验中所用形状记忆合金常为多晶体,相应的单晶体在工艺上是很难制备出来,所以对于单晶体的一些实验数据很难直接通过实验得到,Thamburaja[16]证明得到多晶体的相变驱动力近似与单晶体的相变驱动力相等,由式(16)可以得到多晶体的临界应力近似与单晶体的临界应力相等。
同样临界应力可取指数形式的如下表达式[9]:
| ${\sigma _c} = a\left( {1 - \exp \left( { - N/b} \right)} \right)$ | (18) |
将临界应力的表达式代入相变驱动力表达式就可以得到相变驱动力随循环次数N变化的表达式:
| $\begin{array}{c} f = {\sigma _c}:{\varepsilon ^t} - {\sigma _c}:\left[{\left( {I - \frac{1}{2}{{\left( {{p^a}} \right)}^{\rm{T}}}} \right):{M^a}{p^a} - } \right.\\ \left. {\left( {I - \frac{1}{2}{{\left( {{p^m}} \right)}^{\rm{T}}}} \right):{M^m}{p^m}} \right]{\sigma _c} - {E_c} \end{array}$ | (19) |
在众多多晶体均匀化方法中,Taylor方法与有限元方法得到的结果较为接近,而且计算简便[23]。所以本文采用Taylor方法将单晶模型推广到多晶模型。假设每个晶粒的局部和宏观变形都是均匀的,且多晶体是由晶体体积相等的单晶体构成,采用欧拉角(β,θ,φ)来表示每个晶粒的取向,相应的转换公式如下表示:
| ${R^k} = \left( {\begin{array}{*{20}{c}} {\cos \theta \cos \beta \cos \varphi - \sin \beta \sin \varphi }&{ - \cos \theta \cos \beta \cos \varphi - \sin \beta \sin \varphi }&{\sin \theta \cos \beta }\\ {\cos \theta \cos \beta \cos \varphi - \sin \beta \sin \varphi }&{ - \cos \theta \cos \beta \cos \varphi + \sin \beta \sin \varphi }&{\sin \theta \sin \beta }\\ { - \sin \theta \cos \varphi }&{\sin \theta \sin \varphi }&{\cos \theta } \end{array}} \right)$ | (20) |
则每个晶粒的局部应变就可以通过对宏观应变E-进行旋转得到即:
| ${\bar \varepsilon ^k} = {R^k}\bar E{\left( {{R^k}} \right)^{\rm{T}}}$ | (21) |
宏观应力可以由局部应力进行旋转得到:
| $T = \frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {{R^k}} \right)}^{\rm{T}}}{{\bar \sigma }^k}{R^k}} $ | (22) |
本文所取得实验数据取自Ren等[24]人所做30圈循环加载的实验,在计算单晶相变时马氏体相的弹性常数取为母相的1/2,具体的单晶材料参数如表 1所示[16]。
| C11A/GPa | C12A/GPa | CA44/GPa | B0/MJ·m-3 | Tms/K | Tmf/K | Tas/K | Taf/K |
| 130.0 | 98.0 | 34.0 | 0.7 | 251.3 | 213.0 | 260.3 | 268.5 |
实验温度为室温,所以在实验开始时材料完全处在奥氏体相。通过累积残余应变的表达式对实验数据的拟合(图 1),可以确定出参数α、β进而得到累积残余应变数值表达式为
$${\varepsilon _r} = 0.00624 - 0.00624 \cdot \exp \left( { - N/7.405} \right)$$
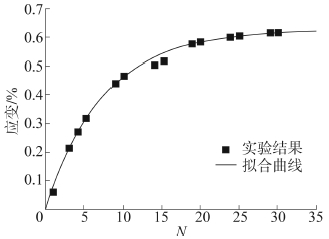
|
| 图1 累积残余应变的实验与拟合结果 Fig.1 Cumulative residual strain experiment and fitting results |
同理,可以得到临界相变应力的表达式。临界应力的表达式可以分为两个部分。
正相变临界应力的表达式为
$$\sigma = 476.328 + 166.398 \cdot \exp \left( { - N/6.10} \right)$$逆相变临界应力的表达式为
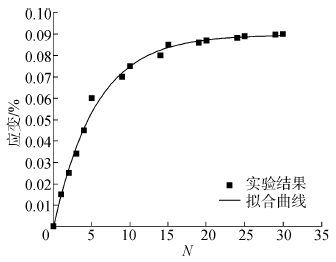
$$\sigma ' = 343.748 + 32 \cdot \exp \left( { - N/4.99} \right)$$相应的临界相变应力实验结果与拟合曲线如图 2所示。利用式(12)、(16)可得到残余马氏体体积分数与循环次数N的模拟图(如图 3所示)。只需取实验中逆相变结束时的应力代入其中就可得到相应数据。

|
| 图2 临界相变应力的实验数据与拟合曲线 Fig.2 The critical stress of experiment and simulation |
|
| 图3 累积残余马氏体体分比与循环次数关系 Fig.3 The relationship of the Cumulative residual martensite volume and cycles |
利用式(12)很难得到关于累积残余马氏体体积分数的显示表达式,而累积残余马氏体体积分数与逆相变结束的应力有关,在循环加载中逆相变结束的应力同逆相变开始的应力均与循环次数有关,所以可以利用指数函数来构建累积残余马氏体体积分数与循环次数N之间的关系,与通过实验计算得到的结果吻合较好。具体的表达式如下:
$$\lambda = 0.09\left( {1 - \exp \left( { - N/5.53} \right)} \right)$$为了验证本模型对超弹性的预测能力,对应力应变的关系进行了数值模拟,在对多晶的计算中选取2000个晶粒,通过3个欧拉角在晶体学给定范围中随机取值来确定每一个晶粒的取向来进行模拟并实验结果进行了对比。取其中的四圈结果进行了对比,结果如图 4所示。
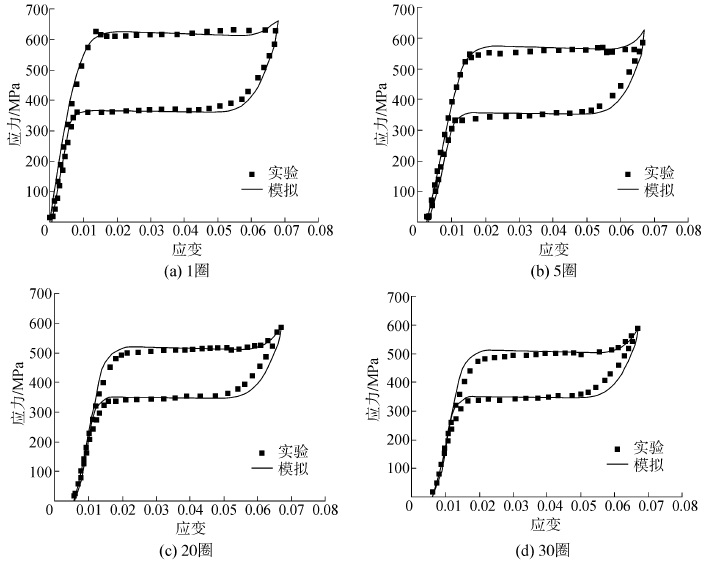
|
| 图4 应力应变曲线的实验与模拟 Fig.4 Stress strain curve of experiment and simulation |
从图 4中可以看出,模拟的曲线与实验结果较为接近,可以很好的反映镍钛合金的超弹性演化规律。从应力应变曲线图中可以得到当循环圈数为20时累积残余应变趋于一个稳定值,当循环圈数为30时残余应变趋于0,而且迟滞环也趋于稳定状态。表明材料倾向于稳定的超弹性状态。
4 结论本文是基于SMA具有层状微结构的假设,通过实验结果来构造累积残余应变和临界应力的表达式。利用热力学原理推导出相变驱动力随循环次数N变化的表达式进而来得到相变演化的控制方程。利用Taylor假设推广到多晶体得到应力应变曲线并与实验结果进行了对比,得到如下结论:
1)本文构造了指数形式的累积残余应变和临界应力的表达式,并推导出相变驱动力随循环圈数变化的表达式。通过数值模拟可知,累积残余应变、临界应力和残余马氏体都是随循环圈数的增加趋于一个稳定值,反应出材料经过训练后可以得到稳定的超弹性能力。
2)利用本模型进行的数值模拟很好地表明材料在循环加载到一定的圈数后趋于稳定的超弹性状态。同时与实验结果进行了对比,结果较为接近,说明本模型能够很好的预测SMA的稳定超弹性。
| [1] | 王心美, 岳珠峰, 王亚芳, 等. NiTi合金的超弹性力学特性及其应用[M]. 北京: 科学出版社, 2009: 187-220. |
| [2] | MIYAZAKI S, FU Yongqing, HUANG Weimin. Thin film shape memory alloys: fundamentals and device applications[M]. Cambridge: Cambridge University Press, 2009: 437-455. |
| [3] | 彭刚, 姜袁. 利用SMA开发耗能阻尼器的实验研究[J]. 工程力学, 2004, 21(2): 183-187. PENG Gang, JIANG Yuan. Experimental investigation of development of SMA damper[J]. Engineering mechanics, 2004, 21(2): 183-187. |
| [4] | WANG X M, ZHOU Q T, LIU H, et al. Experimental study of the biaxial cyclic behavior of thin-wall tubes of NiTi shape memory alloys[J]. Metallurgical and materials transactions A, 2012, 43(11): 4123-4128. |
| [5] |
商泽进, 王忠民, 尹冠生, 等. 循环加载条件下TiNi形状记忆合金棒材的超弹性行为[J]. 实验力学, 2008, 23(4): 305-310. SHANG Zejin, WANG Zhongmin, YIN Guansheng, et al. Superelastic behavior under cyclic loading for TiNi shape memory alloy bars[J]. Journal of experimental mechanics, 2008, 23(4): 305-310. |
| [6] | TANAKA K, NISHIMURA F, HAYASHI T, et al. Phenomenological analysis on subloops and cyclic behavior in shape memory alloys under mechanical and/or thermal loads[J]. Mechanics of materials, 1995, 19(4): 281-292. |
| [7] | LEXCELLENT C, BOURBON G. Thermodynamical model of cyclic behaviour of Ti-Ni and Cu-Zn-Al shape memory alloys under isothermal undulated tensile tests[J]. Mechanics of materials, 1996, 24(1): 59-73. |
| [8] | ABEYARATNE R, KIM S J. Cyclic effects in shape-memory alloys: a one-dimensional continuum model[J]. International journal of solids and structures, 1997, 34(25): 3273-3289. |
| [9] | AURICCHIO F, MARFIA S, SACCO E. Modelling of SMA materials: training and two way memory effects[J]. Computers and sructures, 2003, 81(24-25): 2301-2317. |
| [10] | ZAKI W, MOUMNI Z. A 3D model of the cyclic thermomechanical behavior of shape memory alloys[J]. Journal of the mechanics and physics of solids, 2007, 55(11): 2427-2454. |
| [11] | ZHOU Bo, YOON S H. A macroscopic constitutive model of shape memory alloy considering cyclic effects[J]. Science China: physics, mechanics and astronomy, 2013, 56(4): 755-764. |
| [12] | BO Zhonghe, LAGOUDAS D C. Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part I: Theoretical derivations[J]. International journal of engineering science, 1999, 37(9): 1089-1140. |
| [13] | BO Zhonghe, LAGOUDAS D C. Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part III: evolution of plastic strains and two-way shape memory effect[J]. International journal of engineering science, 1999, 37(9): 1175-1203. |
| [14] | BO Zhonghe, LAGOUDAS D C. Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part IV: Modeling of minor hysteresis loops[J]. International journal of engineering science, 1999, 37(9): 1205-1249. |
| [15] | PATOOR E, LAGOUDAS D C, ENTCHEV P B, et al. Shape memory alloys, Part I: General properties and modeling of single crystals[J]. Mechanics of materials, 2006, 38(5-6): 391-429. |
| [16] | LAGOUDAS D C, ENTCHEV P B, POPOV P, et al. Shape memory alloys, Part II: Modeling of polycrystals[J]. Mechanics of materials, 2006, 38(5-6): 430-462. |
| [17] | THAMBURAJA P, ANAND L. Polycrystalline shape-memory materials: effect of crystallographic texture[J]. Journal of the mechanics and physics of solids, 2001, 49(4): 709-737. |
| [18] | STUPKIEWICZ S, PETRYK H. Modelling of laminated microstructures in stress-induced martensitic transformations[J]. Journal of the mechanics and physics of solids, 2002, 50(11): 2303-2331. |
| [19] | YU Chao, KANG Guozheng, KAN Qianhua, et al. A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloys[J]. International journal of plasticity, 2013, 44: 161-191. |
| [20] |
朱祎国, 赵聃. 具有层状微观结构的NiTi单晶本构模型[J]. 力学学报, 2011, 43(6): 1117-1124. ZHU Yiguo, ZHAO Dan. Constitutive model of NiTi single crystal with laminated microstructure[J]. Chinese journal of theoretical and applied mechanics, 2011, 43(6): 1117-1124. |
| [21] | HU Yiguo, ZHANG Yang, ZHAO Dan. Softening micromechanical constitutive model of stress induced martensite transformation for NiTi single crystal shape memory alloy[J]. Science china physics, mechanics and astronomy, 2014, 57(10): 1946-1958. |
| [22] |
朱祎国, 张杨, 赵聃. 多晶NiTi形状记忆合金相变的细观力学本构模型[J]. 金属学报, 2013, 49(1): 123-128. ZHU Yiguo, ZHANG Yang, ZHAO Dan. Micromechanical constitutive model for Phase transformation of NiTi Polycrystal SMA[J]. Acta metallurgica Sinica, 2013, 49(1): 123-128. |
| [23] | SENGUPTA A, PAPADOPOULOS P, TAYLOR R L. Multiscale finite element modeling of superelasticity in Nitinol polycrystals[J]. Computational mechanics, 2009, 43(5): 573-584. |
| [24] | REN Wenjie, LI Hongnan, SONG Gangbing. Phenomenological modeling of the cyclic behavior of superelastic shape memory alloys[J]. Smart materials and structures, 2007, 16(4): 1083-1089. |



