超高性能混凝土(ultrahigh-performance concrete,UHPC)具有很高的强度和优异的耐久性,由于强度很高,脆性明显。纤维增强聚合物(fiber reinforced polymer,FRP)约束是改善UHPC柱变形能力、承载力和抗震性能的有效方法之一。过去对5层以下纤维布约束普通混凝土研究较多,建立了相应的本构模型[1, 2, 3],但关于较多层数纤维布约束UHPC轴压性能的研究鲜见报道。本文试验研究了碳纤维布、芳纶纤维布、玻璃纤维布约束UHPC试件的轴压性能,探讨了纤维布层数对约束效果的影响。试验发现FRP约束是改善UHPC变形能力的有效方法。在试验基础上,建立了强度和极限应变的预测公式,分析了3种常见FRP约束混凝土本构模型对于FRP约束UHPC的适用性问题。
1 原材料及试验方法 1.1 试件及材料共制作30个圆柱体试件,其中27个为FRP管约束UHPC试件,3个为无约束UHPC试件。UHPC圆柱体高度为200 mm,直径为100 mm。FRP管采用纤维布缠绕加工而成,分别为芳纶纤维(AFRP)、碳纤维(CFRP)和玻璃纤维布(GFRP)。纤维布厚度及其力学指标列于表 1。纤维增强聚合物板轴拉试验测得的力学指标列于表 2。FRP管的纤维缠绕层数分别为3、5、7层,每种纤维布层数的FRP管约束UHPC 3个试件。试件编号见表 3,其中第一个字母为FRP品种,其后数字为纤维布层数,如A2代表 2层芳纶纤维布管约束试件。
| 纤维布品种 | 厚度/mm | 抗拉强度/MPa | 弹性模量/GPa | 延伸率/% |
| 碳纤维 | 0.167 | 3640 | 240 | 1.70 |
| 芳纶纤维 | 0.93 | 2000 | 125 | 2.0 |
| 玻璃纤维 | 0.436 | 1800 | 55 | 5.3 |
| FRP板 品种 | 厚度/mm | 抗拉强度/MPa | 弹性模量/GPa | 极限应变/% |
| CFRP | 0.98 | 615 | 50.7 | 0.012 |
| AFRP | 1.05 | 401 | 38.1 | 0.011 |
| GFRP | 1.01 | 390 | 223.3 | 0.017 |
| 试件编号 | 纤维布 名称 | 纤维布层数 | 试件数量 |
| C3 | 碳纤维 | 3 | 3 |
| C5 | 碳纤维 | 5 | 3 |
| C7 | 碳纤维 | 7 | 3 |
| A3 | 芳纶纤维 | 3 | 3 |
| A5 | 芳纶纤维 | 5 | 3 |
| A7 | 芳纶纤维 | 7 | 3 |
| G3 | 玻璃纤维 | 3 | 3 |
| G5 | 玻璃纤维 | 5 | 3 |
| G7 | 玻璃纤维 | 7 | 3 |
UHPC的组份及配合比见表 4。其中水泥为PO.42.5硅酸盐水泥,磨细高炉矿渣为S95,比表面积408m2/kg。天然石英砂粒径40-70目。聚羧酸高效减水剂,固体含量60%。钢纤维为上海贝尔卡特有限公司生产的微细高强平直钢纤维,直径0.12mm,长径比66.7,抗拉强度大于2850MPa。
| 普通水泥 | 硅灰 | 高炉矿渣 | 石英砂 | 水胶比 | 减水剂 | 钢纤维体积率 |
| 0.684 | 0.184 | 0.132 | 0.737 | 0.16 | 1.2% | 2% |
将搅拌均匀的UHPC混合料导入内径100mm、高200mm的PVC管中,在常温下静置3d后,然后放入混凝土加速养护箱中养护2d,养护温度为80℃。之后用切割机切掉PVC外壳,并用打磨机打磨试件的两个端部,使试件两个端部平整光滑,便于施加轴心压力。最后在纤维布上涂刷浸渍胶,将浸渍胶树脂浸透的纤维布缠绕在混凝土圆柱体表面,纤维布搭接长度160 mm。将FRP管UHPC试件在常温下放置10 d,然后开始轴压试验。
1.3 加载装置与测试设备在FRP管表面中部对称粘贴4个应变片,分别测定环向和纵向应变。在试验机承压板上下分别安装2个位移计和1个力的传感器,分别量测试件竖向位移和荷载值。观察加载过程中约束试件的破坏过程与形态。用3000 kN的电液伺服实验机加载,加载速率110 kN/min。
2 试验结果及分析 2.1 试件破坏特征未约束UHPC试件的破坏过程为:加载初期,试件环向变形小,UHPC处于弹性阶段。当加载至0.3Nu(Nu极限荷载)时,试件表面萌生纵向裂缝,荷载增加,裂缝不断扩展;加载至0.75 Nu时,纵向裂缝延伸至全试件高度,试件中部向外鼓出,环向变形增大;当加载至极限荷载时,由于钢纤维桥联作用,试件完整性较好,如图 1(a)所示。

|
| 图 1 试件破坏形态 Fig. 1 Typical failure mode of specimens |
约束试件过程为:加载初期,FRP布环向应变很小,约束作用甚小。随着荷载增加,核心UHPC逐渐向外膨胀,FRP布约束作用逐渐被激活,此时听到胶体“啪啪”的响声。加载至0.9 Nu时,FRP布中部横向断裂,并向上下端延伸,试件中部明显外鼓,此时听见较大的FRP管断裂声音,碳纤维、芳纶纤维布层数多时破坏响声大。FRP布约束试件的破坏过程比未约束试件缓慢。约束试件破坏形态如图 1所示。
2.2 试验结果 2.2.1 强度与极限应变FRP管对UHPC的约束应力fr为
| ${{f}_{r}}=2{{f}_{j}}{{t}_{j}}/D$ | (1) |
式中,fj为FRP环向抗拉强度;tj为FRP管厚度;D 为核心UHPC直径。
各试件的抗压强度、极限应变平均值列于表 5。表中约束比为约束应力与未约束UHPC抗压强度fco'的比值;约束效率比为约束试件抗压强度fcc'与未约束试件抗压强度的比值。纵向应变为位移计、纵向应变片应变值的平均值,环向应变为应变片读数。
| 试件 | 层数 | fr/MPa | 纵向 应变 | 环向 应变 | 抗压强度/MPa | 约束比 | 约束效率比 |
| UHPC | N/A | N/A | 0.0028 | 0.0006 | 106.57 | N/A | N/A |
| C3 C5 C7 A3 A5 A7 G3 G5 G7 | 3 | 36.16 | 0.0052 | 0.0035 | 174.65 | 0.34 | 1.64 |
| 5 | 60.27 | 0.0093 | 0.0040 | 217.83 | 0.57 | 2.04 | |
| 7 | 84.38 | 0.0189 | 0.0105 | 285.50 | 0.79 | 2.68 | |
| 3 | 25.26 | 0.0076 | 0.0058 | 127.88 | 0.24 | 1.20 | |
| 5 | 42.11 | 0.0129 | 0.0066 | 179.62 | 0.40 | 1.69 | |
| 7 | 58.95 | 0.0254 | 0.0084 | 266.81 | 0.55 | 2.50 | |
| 3 | 23.63 | 0.0032 | 0.0038 | 117.49 | 0.22 | 1.10 | |
| 5 | 39.39 | 0.0045 | 0.0074 | 167.01 | 0.37 | 1.57 | |
| 7 | 55.15 | 0.0136 | 0.0079 | 256.24 | 0.52 | 2.40 |
由表 5可见,FRP约束UHPC显著提高了圆柱体抗压强度,纤维布层数越多,提高幅度越大。3、5、7层CFRP布约束试件比未约束试件抗压强度分别提高63.88%、104.40%和167.90%;3、5、7层AFRP布约束试件抗压强度分别提高20.0%、68.55%和150.36%;3、5、7层GFRP布约束试件抗压强度分别提高10.25%、56.71%和140.44%。
2.2.2 应力-应变曲线未约束UHPC试件变形曲线如图 2示,应力-应变曲线在达到峰值荷载之前几乎呈直线上升,达到极限抗压强度后,试件迅速丧失承载力,曲线下降很陡,呈脆性破坏。
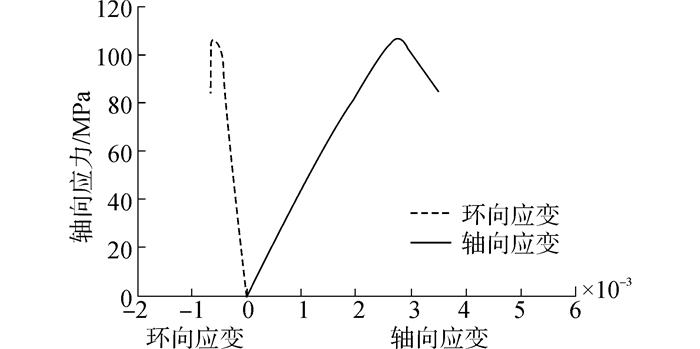
|
| 图 2 未约束UHPC试件应力-应变曲线 Fig. 2 Average stress-strain cures for unconfined specimens |
图 3(a-c)为3种纤维布约束试件的轴压应力-应变曲线。可见应力-应变曲线具有双线性的特征,可分为3个变形阶段:加载初期,变形曲线与未约束试件相似,UHPC横向膨胀变形很小,FRP布约束作用未显现出来;荷载再增大,核心区UHPC开始产生许多纵向裂缝,膨胀变形增大,FRP被逐渐激活;最后一个阶段是破坏阶段,FRP被完全激活,变形呈线性关系。文献[4]研究了FRP管约束高强混凝土的强度和变形,发现FRP管对于高强混凝土极限变形改善作用不大。而FRP管约束UHPC对强度和变形均有明显改善作用,这是由于钢纤维增强UHPC具有明显的横向变形能力,使FRP管约束作用完全发挥出来。
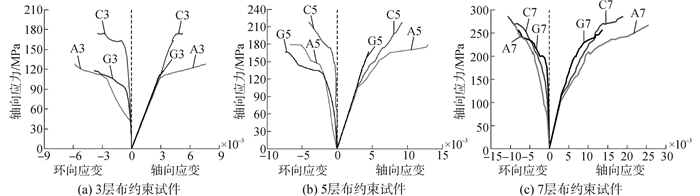
|
| 图 3 不同层数纤维布约束UHPC应力-应变曲线 Fig. 3 Average stress-strain curves for specimens confined with different number fiber sheets |
由图 3看出,当UHPC缠绕的纤维布层数相同时,如A3、C3、G3或A5、C5、G5,碳纤维布对改善UHPC的强度的效果最好;而芳纶布可显著提高UHPC试件极限应变;玻璃纤维布对UHPC强度和极限应变的改善效果低于碳纤维、芳纶纤维布。3种纤维布约束试件,强度和极限应变随纤维布层数的增加而提高。当荷载达到fco'之后,3层布约束试件(如G3)首先出现明显的刚度退化,σ-ε曲线呈直线上升,但斜率减小,纵向和环向变形迅速增加,抗压强度和极限应变比5、7层布约束试件小;5层和7层的试件(如A5、A7、C5、C7)在FRP布与核心约束UHPC应力重分布后仍能保持较高的刚度,σ-ε曲线强化段直线斜率较大,变形增加相对缓慢,破坏时fcc'和εcc较大。这是由于FRP厚度增加,侧向约束应力fr提高,能更有效地约束核心区UHPC的侧向变形从而提高试件的抗压强度fcc'和极限应变εcc。
3 FRP约束混凝土本构模型 3.1 FRP约束混凝土的应力-应变关系模型目前常用的约束混凝土本构模型有:Graybeal[5],Lam-Teng[6],Samaan[7]模型等。对这些典型模型预测曲线与试验曲线均进行了比较。图 4是部分试件试验曲线与理论曲线的比较。
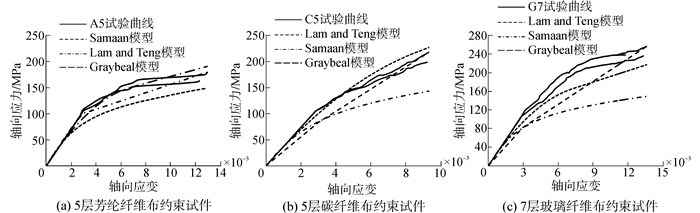
|
| 图 4 应力-应变试验曲线与理论曲线比较 Fig. 4 Comparison between stress-strain models and test curves |
由图 4可见,理论曲线与试验曲线有较大差异。用拟合曲线的相对误差值反映其预测精度,各理论模型拟合曲线的相对误差值列于表 6。Lam-Teng[6]、Samaan[7]和Graybeal[5]模型预测曲线相对误差依次为8.53%、20.31%和15.01%。Lam-Teng比Samaan、Graybeal模型预测曲线更接近实测曲线。已有模型是据FRP管约束普通混凝土试验结果建立的,不完全合适于UHPC试件。
| % | |||
| 试件 | Samaan模型 | Lam-Teng模型 | Graybeal模型 |
| A3 | 16.37 | 11.95 | 4.08 |
| A5 | 14.45 | 4.84 | 6.52 |
| A7 | 16.29 | 13.88 | 11.33 |
| C3 | 28.73 | 7.58 | 13.27 |
| C5 | 21.75 | 4.85 | 14.65 |
| C7 | 15.89 | 6.85 | 21.51 |
| G3 | 18.15 | 7.84 | 25.25 |
| G5 | 20.91 | 5.02 | 19.38 |
| G7 | 30.28 | 13.92 | 19.08 |
| 平均 | 20.31 | 8.53 | 15.01 |
对试验数据进行拟合后得到抗压强度的公式为:
| $\frac{f{{'}_{cc}}}{f{{'}_{co}}}=1+2.53{{\left(\frac{{{f}_{r}}}{f{{'}_{co}}} \right)}^{1.32}}\left({{R}^{2}}\text{=}0.82 \right)$ | (2) |
已有的FRP约束混凝土极限应变模型大多采用以下形式:
| $\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=1+\beta {{\left(\frac{{{f}_{r}}}{f{{'}_{co}}} \right)}^{n}}$ | (3) |
若不分纤维布种类,回归得到式(3)中的参数β和n,但预测精确度较差。经分析发现影响极限应变的不但与约束应力有关,且与纤维布种类密切相关,为提高预测精度,对每种FRP管约束试件分别回归得到统计意义的公式见表 7。
从表 7见,FRP约束UHPC轴向极限应变不但依赖于约束应力,还依赖于FRP管的种类;而约束试件的抗压强度,主要与约束应力有关。试验发现:AFRP、GFRP约束试件,当约束比大于0.4时,极限应变随着约束比的提高显著提高;约束比大于0.6时,CFRP约束试件极限应变随着约束比的提高明显提高。
此外,将Lam-Teng[6]极限应变预测式(4)与试验值进行了回归拟合,拟合结果列于表 8。
| $\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=\alpha+\beta \left(\frac{{{f}_{r}}}{f{{'}_{co}}} \right){{\left(\frac{{{\varepsilon }_{rup}}}{{{\varepsilon }_{co}}} \right)}^{r}}$ | (4) |
| 纤维种类 | 公式 | R2 | εcc试验值与计算值之比 | ||
| 平均值 | 标准差 | 变异系数 /% | |||
| 芳纶纤维 | $\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=1+21.4{{\left( \frac{{{f}_{r}}}{f{{'}_{co}}} \right)}^{1.93}}$ | 0.91 | 1.03 | 0.14 | 13.59 |
| 碳纤维 | $\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=1+10.1{{\left( \frac{{{f}_{r}}}{f{{'}_{co}}} \right)}^{2.53}}$ | 0.92 | 1.03 | 0.14 | 13.59 |
| 玻璃纤维 | $\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=1+22.6{{\left( \frac{{{f}_{r}}}{f{{'}_{co}}} \right)}^{2.6}}$ | 0.91 | 0.96 | 0.17 | 17.71 |
| 纤维种类 | 参数 | R2 | εcc试验值与计算值之比 | ||||
| α | β | γ | 平均值 | 标准差 | 变异系数 /% | ||
| 芳纶纤维 | 1.45 | 0.60 | 2.93 | 0.99 | 1.06 | 0.06 | 5.66 |
| 碳纤维 | 0.80 | 2.68 | 0.76 | 0.99 | 1.06 | 0.08 | 7.55 |
| 玻璃纤维 | 1.20 | 0.01 | 6.32 | 0.92 | 1.06 | 0.16 | 15.09 |
比较表 7、8可见,$\frac{{{\varepsilon }_{cc}}}{{{\varepsilon }_{co}}}=\alpha+\beta \left(\frac{{{f}_{r}}}{f{{'}_{co}}} \right){{\left(\frac{{{\varepsilon }_{rup}}}{{{\varepsilon }_{co}}} \right)}^{r}}$模型预测精度更高。
4 结论1)FRP管约束UHPC圆柱体轴压变形曲线,具有双线性的特点。
2)FRP约束UHPC提高了强度和变形能力,特别是对极限应变的改善效果显著。
3)FRP约束UHPC的极限应变受FRP种类影响较大,本文回归得到了FRP管约束UHPC的极限应变计算公式,其预测精度较高。
4)与3个常用FRP约束混凝土本构模型进行对比后发现,Lam-Teng模型与实测应力-应变曲线最为接近,但目前已有模型是在FRP约束普通混凝土试验结果的基础上建立的,不完全适用于UHPC。
| [1] | SAAFI M, TOUTANJI H A, LI Zongjin. Behavior of concrete columns confined with fiber reinforced polymer tubes[J]. ACI materials journal, 1999, 96(4): 500-509. |
| [2] | AHMAD S H, SHAH S P. Stress-strain curves of concrete confined by spiral reinforcement[J]. ACI journal, 1982, 79(6): 484-490. |
| [3] | MIRMIRAN A, SHAHAWY M. A new concrete-filled hollow FRP composite column[J]. Composites part B: engineering, 1996, 27(3/4): 263-268. |
| [4] | XIAO Y, WU H. Compressive behavior of concrete confined by carbon fiber composite jackets[J]. Journal of materials in civil engineering, 2000, 12(2): 139-146. |
| [5] | GRAYBEAL B A. Compressive behavior of ultra-high-performance fiber-reinforced concrete[J]. ACI materials journal, 2007, 104(2): 146-152. |
| [6] | TENG J G, HUANG Y L, LAM L, et al. Theoretical model for fiber reinforced polymer confined concrete[J]. Journal of composites for construction, 2007, 11(2): 201-210. |
| [7] | SAMAAN M, MIRMIRAN A, SHAHAWY M. Model of concrete confined by fiber composites[J]. Journal of structural engineering, 1998, 124(9): 1025-1031. |



