2. Department of Civil Engineering, Nanchang Institute of Technology, Nanchang 330099, China
针对大跨钢管结构的分析目前仍然采用传统的理想化节点假定来建立计算模型的现状,国内外学者对于钢管相贯节点的非刚性性能进行了较深层次的研究,对于考虑钢管节点刚度对于节点性能的影响有了一定程度的了解并且在钢管结构模型分析中引入节点刚度分析结构的整体性能。《钢结构设计规范》[1]给出了桁架弦杆和腹杆受压时计算长度的规定。国际管结构发展与研究委员会(CIDECT)给出矩形钢管桁架腹杆任一平面内的计算长度为0.75l[2]。《矩形钢管混凝土结构技术规程》[3]对压杆计算长度的规定,指出受压腹杆的计算长度为0.75l。Ueda[4]提出了分别受支管轴力、支管平面内弯矩作用下的节点刚度参数公式,基于弹性和理想弹塑性荷载-位移关系采用杆系线单元组成的简单模型近似模拟管节点。陈以一[5]进行了相贯节点抗弯刚度和承载力的实验研究。试验表明在一定条件下,节点可以作为全刚接抗弯节点看待。王伟[6, 7]提出了相贯节点分别受支管轴力、平面内弯矩作用下的节点刚度的参数公式。以刚架弹性稳定理论为基础给出了半刚性节点钢桁架受压腹杆计算长度。蔡健[8]以经典的刚架弹性稳定理论及相关研究成果为基础,推导了考虑节点刚度和相邻腹杆刚度对受压腹杆影响的杆件群稳定方程及腹杆计算长度系数的计算方程。武振宇[9] 分析了不同参数对方管搭接支杆平面内计算长度影响,指出采用理想铰接条件进行桁架杆件的稳定设计偏于保守。蔡健[10]分析了相邻节间弦杆内力比对受压弦杆计算长度的影响,提出了矩形钢管混凝土桁架受压弦杆计算长度系数。童乐为、王新毅[11]对钢管混凝土节点抗弯刚度和承载力的实验研究。试验表明在一定条件下,节点可以作为全刚接抗弯节点看待,节点抗弯强度能保证杆件承载能力的充分发挥。张建军[12]对单层折面空间网格结构钢屋盖中的复杂边界条件杆件计算长度进行了研究,指出杆件计算长度受节点刚度影响较大,杆件计算长度系数小于或接近1.0。林彦[13]分析了圆管桁架节点参数对受压腹杆平面内计算长度的影响,给出了圆管桁架受压腹杆平面内计算长度系数的建议值。
在实际工程中,大多把采用圆钢管混凝土相贯节点用于桁式或拱式结构,作为平面的或空间的铰接杆件体系看待;当圆钢管混凝土相贯节点用于空腹桁架或单层网壳时,设计时必须采用刚性节点假定[14]。而国内外对于圆钢管混凝土节点刚度的研究较少,如何评价钢管混凝土节点刚度对结构整体性能的影响没有理论依据可循。
1 T/Y型节点抗弯刚度参数公式 1.1 节点抗弯刚度的定义当节点的支管受到平面内弯矩作用时,除主管由于弯矩作用下的整体转动外,在支管和主管连接处的主管管壁发生局部凹陷(凸突),连接处产生局部转动,如图 1所示。

|
| 图 1 平面内弯矩作用下的节点局部变形图 Fig. 1 Local deformation of joints under in-plane bending moment 注:β=d/D, γ=D/2T, τ=t/T |
节点的抗弯刚度定义为发生单位局部变形对应的外荷载,对于T型、Y型节点,其公式为:
| ${K_M} = \frac{M}{{{\theta _r}}}$ | (1) |
式中:KM表示节点的抗弯刚度;M表示为支管轴线与主管表面相交处的弯矩;θr表示在支管平面内弯矩M作用下主管相贯面的局部转角(不包括主管作为梁承受弯矩产生的转角)。
1.2 节点抗弯刚度公式模型分析采用非线性拟合的方法,对节点进行多元回归,T/Y型节点的抗弯刚度公式如下[15]:
| ${K_M} = 0.116{E_{\rm{s}}}{D^3}\left( {\sin \theta \theta } \right) - 2.16{\gamma ^{ - 0.90}}{\tau ^{0.12}}{\beta ^{2.65}}$ | (2) |
其中,30°≤θ≤90°,0.3≤β≤1.0,0≤γ≤40,0.4≤τ≤1.0。
当腹杆受弯矩作用时,腹杆与弦杆连接部位的节点域的弯矩可简化为一对间距为(d-t)的力偶作用在腹杆与弦杆相贯线的冠点位置,节点的抗弯刚度取决于弦杆的径向刚度和弦、腹杆相贯面的表面积。并且弦杆内填充混凝土后,弦杆的径向抗压刚度得到极大的提高,弦杆管壁受压侧冠点的的局部变形明显减小,弦杆管壁受拉侧冠点的局部变形主要依靠弦杆的抗弯刚度以及混凝土与钢管之间的粘结力。
在弦杆管径保持不变的情况下,当γ增大时,弦杆壁厚减小,弦杆的抗弯刚度减小,节点刚度降低;当β增大时,腹杆管径增大,弦、腹杆相贯面的表面积增大,节点刚度增大;当τ增大时,腹杆管径不变,腹杆壁厚增大,弦、腹杆相贯面的表面积增大,节点刚度增大;当腹杆与主管之间的夹角θ增大时,弦、腹杆相贯面的表面积减小,节点刚度降低。
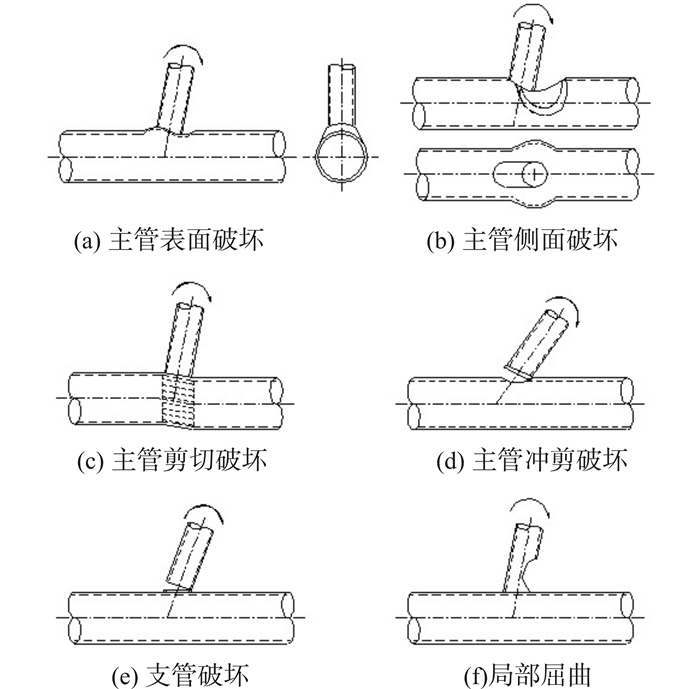
2 CHS节点与CFCHS节点抗弯性能比较根据以往对于空心圆钢管CHS(Circle Hollow Section)节点抗弯性能的研究,其节点在承受支管弯矩时,其节点的破坏形式见图 2,其具体的破坏形式取决于节点参数[16]。
|
| 图 2 弯矩作用下钢管节点的破坏模式 Fig. 2 Failure mode of joints under In-plane bending moment |
空心圆钢管节点的支管轴向刚度远远大于相贯线处的主管径向刚度,当支管上作用弯矩时,在弦杆相贯线附近受压一侧管壁局部凹陷,受拉一侧管壁局部凸突,连接处产生局部转动,即“失圆”现象。相比较而言,圆钢管混凝土CFCHS节点的弦杆内填充混凝土以后,弦杆的径向刚度得到了极大程度的提高,对于弦杆管壁的局部变形起到明显的约束作用。
对于T型节点(β=0.6,γ=25,τ=0.7,D=400mm)在平面内弯矩作用下的节点力学性能进行了数值分析,比较弦杆内填充混凝土后对于节点抗弯性能的影响。图 3、图 4给出了两类节点的的变形图,从图中可以看到:CHS节点的弦杆相贯线附近受压侧弦杆管壁局部凹陷,受拉侧管壁局部凸突,表现出明显的“失圆”特征;而CFCHS节点受拉侧钢管与混凝土局部脱开,由于内填充混凝土极大程度的提高了弦杆的径向刚度,受压侧支管管壁局部屈曲。

|
| 图 3 钢管节点区变形 Fig. 3 Joint deformation of CHS joints |
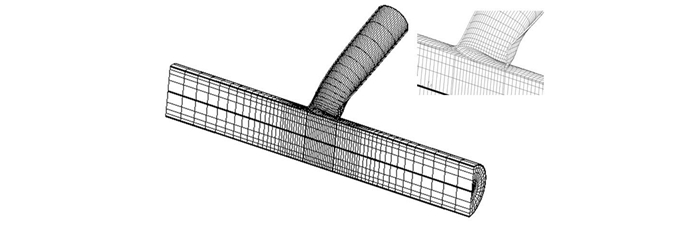
|
| 图 4 钢管混凝土节点区变形 Fig. 4 Joint deformation of CFCHS joints |
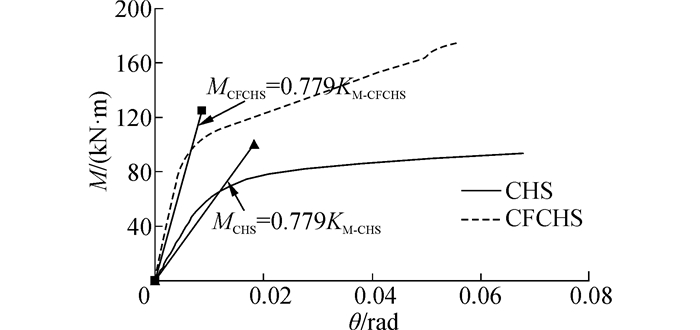
图 5给出了CHS节点和CFCHS节点的M-θ曲线,其中M为腹杆轴线与弦杆表面相交处的弯矩。图中同时标出了按日本《钢管结构设计施工指南》[17]规定的节点的屈服承载力,即斜率为0.779KM(节点初始刚度)的割线与M-θ曲线的交点对应的弯矩和转角作为节点的屈服弯矩My和屈服转角θy。从图中可以看到:CHS节点的抗弯刚度和抗弯承载力明显小于CFCHS节点。
|
| 图 5 钢管节点与钢管混凝土节点M-θ曲线的比较 Fig. 5 moment -deformation of chord tube curves compared CHS joints with CFCHS joints |
《钢结构设计规范》基于腹杆和弦杆完全刚接的假定下给出了受压腹杆的计算长度:端部斜腹杆取0.90l,中间斜腹杆取0.80l。而对于圆钢管混凝土桁架的腹杆长度取值没有明确规定。
桁架结构的稳定问题比较复杂,为了简化,分析中针对钢管混凝土桁架的钢管混凝土弦杆和钢管腹杆的不同特点,腹杆的稳定性分析作如下假定:
1) 受压弦杆有足够刚度,受压腹杆失稳先于受压上弦杆;
2) 因为腹杆刚度一般较小,略去其他腹杆的约束作用;
3)弦杆对受压腹杆的约束看做不移动弹簧铰;
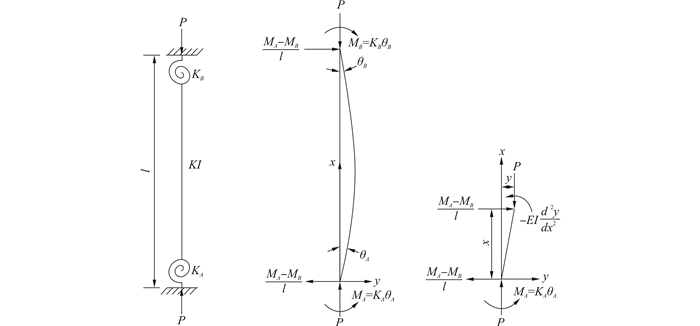
由图 6得任一截面的弯曲平衡方程为
| $EI\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} + Py - \frac{{{M_B} - {M_A}}}{l} - {M_A} = 0$ | (3) |
| $y = A\sin \left( {\theta kx} \right) + b\cos \left( {kx} \right) + \frac{{{M_B} - {M_A}}}{{Pl}}x + \frac{{{M_A}}}{P}$ | (4) |
|
| 图 6 两端不移动弹簧受压腹杆计算简图 Fig. 6 Calculation model of compression brace |
考虑边界约束条件,引入EI/l=i,受压腹杆的屈曲方程为:
| $\begin{array}{l} {k^2}{l^2}\left( {\frac{i}{{{K_{\rm{A}}}}}\sin \left( {\theta kl} \right) + \frac{i}{{{K_{\rm{B}}}}}\sin \left( {\theta kl} \right) - \frac{i}{{{K_{\rm{A}}}}}kl\cos \left( {kl} \right) - } \right.\\ \left. {\;\;\;\;\;\;\frac{i}{{{K_{\rm{B}}}}}kl\cos \left( {kl} \right)} \right) + \frac{i}{{{K_{\rm{A}}}}}\frac{i}{{{K_{\rm{B}}}}}{k^4}{l^4}\sin \left( {\theta kl} \right) + \\ \;\;\;\;\;\;\;\;kl\left( {2 - 2\cos \left( {kl} \right) - kl\sin \left( {\theta kl} \right)} \right) = 0 \end{array}$ | (5) |
引入计算长度系数
| $kl = \frac{\pi }{\mu }$ | (6) |
代入式(5)得到
| $\begin{array}{l} \frac{{{\pi ^2}}}{{{\mu ^2}}}\left( {\frac{i}{{{K_{\rm{A}}}}}\sin \theta \frac{\pi }{\mu } + \frac{i}{{{K_{\rm{B}}}}}\sin \theta \frac{\pi }{\mu } - \frac{i}{{{K_{\rm{A}}}}}\frac{\pi }{\mu }\cos \frac{\pi }{\mu } - } \right.\\ \left. {\;\;\;\;\;\frac{i}{{{K_{\rm{B}}}}}\frac{\pi }{\mu }\cos \frac{\pi }{\mu }} \right) + \frac{i}{{{K_{\rm{A}}}}}\frac{i}{{{K_{\rm{B}}}}}\frac{{{\pi ^4}}}{{{\mu ^4}}}\sin \theta \frac{\pi }{\mu } + \\ \;\;\;\;\;\;\;\frac{\pi }{\mu }\left( {2 - 2\cos \frac{\pi }{\mu } - \frac{\pi }{\mu }\sin \theta \frac{\pi }{\mu }} \right) = 0 \end{array}$ | (7) |
表 1给出了腹杆线刚度/节点抗弯刚度(i/KM)的受压腹杆计算长度。受压腹杆的计算长度与腹杆的线刚度相关,引入节点抗弯刚度公式(2),则腹杆线刚度/节点抗弯刚度(i/KM)可以表述为:
| $\frac{i}{{{K_M}}} = \frac{{E{I_{br}}}}{{{l_{br}}}}\frac{1}{{0.116{E_s}{D^3}\left( {\sin \theta \theta } \right) - 2.16{\gamma ^{ - 0.90}}{\tau ^{0.12}}{\beta ^{2.65}}}}$ | (8) |
| i/KAi/KB | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 2 | 3 |
| 0 | 0.5 | 0.54561 | 0.57768 | 0.59939 | 0.61472 | 0.62641 | 0.63472 | 0.64156 | 0.64710 | 0.65167 | 0.65551 | 0.67503 | 0.68249 |
| 0.1 | 0.54561 | 0.59194 | 0.62533 | 0.64849 | 0.66510 | 0.67751 | 0.68708 | 0.69469 | 0.70087 | 0.70601 | 0.71032 | 0.73246 | 0.74099 |
| 0.2 | 0.57768 | 0.62533 | 0.65982 | 0.68397 | 0.70144 | 0.71457 | 0.72474 | 0.73285 | 0.73948 | 0.74497 | 0.74960 | 0.77349 | 0.78278 |
| 0.3 | 0.59939 | 0.64849 | 0.68397 | 0.70894 | 0.72707 | 0.74073 | 0.75136 | 0.75987 | 0.76678 | 0.77255 | 0.77743 | 0.80261 | 0.81243 |
| 0.4 | 0.61472 | 0.66510 | 0.70144 | 0.72707 | 0.74573 | 0.75983 | 0.77081 | 0.77959 | 0.78678 | 0.79275 | 0.79780 | 0.82400 | 0.83422 |
| 0.5 | 0.62641 | 0.67751 | 0.71457 | 0.74073 | 0.75983 | 0.77427 | 0.78554 | 0.79456 | 0.80192 | 0.80806 | 0.81327 | 0.84025 | 0.85080 |
| 0.6 | 0.63472 | 0.68708 | 0.72474 | 0.75136 | 0.77081 | 0.78554 | 0.79701 | 0.80624 | 0.81378 | 0.82005 | 0.82537 | 0.85298 | 0.86381 |
| 0.7 | 0.64156 | 0.69469 | 0.73285 | 0.75987 | 0.77959 | 0.79456 | 0.80624 | 0.8156 | 0.82327 | 0.82966 | 0.83506 | 0.86322 | 0.87427 |
| 0.8 | 0.64710 | 0.70087 | 0.73948 | 0.76678 | 0.78678 | 0.80192 | 0.81378 | 0.82327 | 0.83104 | 0.83753 | 0.84302 | 0.87162 | 0.88284 |
| 0.9 | 0.65167 | 0.70601 | 0.74497 | 0.77255 | 0.79275 | 0.80806 | 0.82005 | 0.82966 | 0.83753 | 0.84411 | 0.84965 | 0.87862 | 0.89002 |
| 1 | 0.65551 | 0.71032 | 0.74960 | 0.77743 | 0.79780 | 0.81327 | 0.82537 | 0.83506 | 0.84302 | 0.84965 | 0.85527 | 0.88458 | 0.89609 |
| 2 | 0.67503 | 0.73246 | 0.77349 | 0.80261 | 0.82400 | 0.84025 | 0.85298 | 0.86322 | 0.87162 | 0.87862 | 0.88458 | 0.91565 | 0.9279 |
| 3 | 0.68249 | 0.74099 | 0.78278 | 0.81243 | 0.83422 | 0.85080 | 0.86381 | 0.87427 | 0.88284 | 0.89002 | 0.89609 | 0.9279 | 0.94046 |
引入无量纲参数:腹、弦杆直径比β=d/D,弦杆径厚比γ=D/(2T),腹、弦杆厚度比τ=t/T后上式为:
| $\begin{array}{l} \frac{i}{{{K_M}}} = \frac{\pi }{{64}}\frac{{{\beta ^3}\left[ {1 - {{\left( {1 - \tau /\left( {\beta \lambda } \right)} \right)}^4}} \right]}}{{{l_{br}}/d}} \cdot \\ \frac{1}{{0.116\left( {\sin \theta \theta } \right) - 2.17{\gamma ^{ - 0.90}}{\tau ^{0.12}}{\beta ^{2.65}}}} \end{array}$ | (9) |
引入记号λbr=lbr/(0.35d),代入公式(9)后得:
| $\begin{array}{l} \frac{i}{{{K_M}}} = \frac{\pi }{{64}}\frac{{\left[ {1 - {{\left( {1 - \tau /\left( {\beta \gamma } \right)} \right)}^4}} \right]}}{{0.35{\lambda _{br}}}} \cdot \\ \frac{1}{{0.116\left( {\sin \theta \theta } \right) - 2.17{\gamma ^{ - 0.90}}{\tau ^{0.12}}{\beta ^{ - 0.35}}}} \end{array}$ | (10) |
考虑常见的工程参数范围以及钢管混凝土节点刚度公式的适用范围:30°≤θ≤90°,0.3≤β≤1.0,10≤γ≤40,0.4≤τ≤1.0,30≤λbr≤150,可以界定腹杆线刚度/节点抗弯刚度(i/KM)的取值为
| $2.14 \times {10^{ - 3}} \le i/{K_M} \le 0.215$ | (11) |
而对于圆钢管桁架节点,腹杆线刚度/节点抗弯刚度(i/KM)的取值可参考文献[7]:
| $2.22 \times {10^{ - 3}} \le i/{K_M} \le 0.74$ | (12) |
桁架受压杆件的计算长度受节点刚度影响较大。节点刚度越大,压杆失稳时其它杆件随之产生的变形也越大,从而对压杆产生约束作用。对于钢管混凝土桁架,由于节点灌注混凝土,其刚度大大提高从而对压杆产生较大的约束作用,若其压杆的计算长度沿用《钢结构设计规范》或者钢管桁架规范,则可能偏于保守。根据本文的分析,根据式(11)、(12),参照受压腹杆的计算长度表,可得到:
1)对于上、下弦杆均为为圆钢管混凝土杆件,受压腹杆的计算长度可近似的取0.7l;
2)对于受压弦杆为圆钢管混凝土杆件,受拉弦杆为圆钢管杆件,受压腹杆的计算长度可近似的取0.8l。
4 结论1)由于弦杆内混凝土的原因,钢管混凝土节点的抗弯刚度、抗弯承载力明显优于圆钢管节点;
2)内填充混凝土后,钢管混凝土节点在平面内弯矩作用下的破坏模式与钢管节点有很大程度的不同,支管受拉侧主管冲剪破坏或支管受压侧局部屈曲是钢管混凝土节点主要破坏形式;内填充混凝土强度的变化对节点的抗弯刚度影响较小。
3)抗弯刚度取决于弦杆的径向刚度和弦杆、腹杆相贯面的表面积,节点刚度随管径比β、壁厚比τ的增大而提高,随径厚比γ、主支管夹角θ的增大而降低。
4)由于节点灌注混凝土,其刚度显著提高,从而对压杆产生较大的约束作用。对于上、下弦杆均为为圆钢管混凝土杆件,受压腹杆的计算长度可近似的取0.7l;对于受压弦杆为圆钢管混凝土杆件,受拉弦杆为圆钢管杆件,受压腹杆的计算长度可近似的取0.8l。
| [1] | 中华人民共和国建设部和中华人民共和国国家质量监督检验检疫总局. GB 50017-2003 钢结构设计规范[S]. 北京: 中国计划出版社, 2003. |
| [2] | PACKER J A, HENDERSON J E, CAO J J. Design direction of hollow structural section connection[M]. Beijing: Science and Technology Press, 1997: 42-49. |
| [3] | 中国工程建设标准化协会. CECS 159-2004 矩形钢管混凝土结构技术规程[S]. 北京: 中国计划出版社, 2004. |
| [4] | UEDA Y, RASHED S M H, NAKACHO K. An improved joint model and equations for flexibility of tubular joints[J]. Journal of offshore mechanics and arctic engineering, 1990, 112(2): 157-168. |
| [5] |
陈以一, 王伟, 赵宪忠, 等. 圆钢管相贯节点抗弯刚度和承载力实验[J]. 建筑结构学报, 2001, 22(6): 25-30. CHEN Yiyi, WANG Wei, ZHAO Xianzhong, et al. Experiments on bending rigidity and resistance of unstiffened tubular joints[J]. Journal of building structures, 2001, 22(6): 25-30. |
| [6] |
王伟, 陈以一. 圆钢管相贯节点局部刚度的参数公式[J]. 同济大学学报, 2003, 31(5): 515-519. WANG Wei, CHEN Yiyi. Parametric formulas for local rigidity of unstiffened tubular joints[J]. Journal of Tongji University, 2003, 31(5): 515-519. |
| [7] |
王伟, 陈以一. 节点半刚性钢桁架受压腹杆计算长度分析[J]. 工程力学, 2005, 22(5): 131-135, 125. WANG Wei, CHEN Yiyi. Analysis of effective length of compressive braces in semi-rigid steel trusses[J]. Engineering mechanics, 2005, 22(5): 131-135, 125. |
| [8] |
蔡健, 陈国栋. 相邻腹杆刚度对桁架受压腹杆计算长度的影响[J]. 华南理工大学学报:自然科学版, 2008, 36(6): 1-5. CAI Jian, CHEN Guodong. Influence of adjacent brace rigidity on effective length of compressive brace in trusses[J]. Journal of South China University of Technology: natural science edition, 2008, 36(6): 1-5. |
| [9] |
刘娟, 武振宇. 方管搭接支杆平面内计算长度有限元分析[J]. 哈尔滨工业大学学报, 2008, 40(6): 851-854, 890. LIU Juan, WU Zhenyu. Finite element analysis on in-plane effective length of overlap brace in SHS truss[J]. Journal of Harbin Institute of Technology, 2008, 40(6): 851-854, 890. |
| [10] |
蔡健, 陈国栋. 矩形钢管混凝土桁架受压弦杆的计算长度[J]. 钢结构, 2009, 24(4): 23-25, 29. CAI Jian, CHEN Guodong. The effective length of compressive chord members in concrete-filled rectangular steel tubular truss[J]. Steel construction, 2009, 24(4): 23-25, 29. |
| [11] |
童乐为, 王新毅, 陈以一, 等. 广州新电视塔环梁-立柱-支撑-牛腿焊接节点抗弯刚度性能研究[J]. 土木工程学报, 2010, 43(7): 22-28. TONG Lewei, WANG Xinyi, CHEN Yiyi, et al. Bending rigidity of welded beam-column-brace-bracket joints in Guangzhou New TV Tower[J]. China civil engineering journal, 2010, 43(7): 22-28. |
| [12] |
张建军, 刘琼祥, 郭满良, 等. 深圳大运中心体育场空间钢结构杆件计算长度研究[J]. 建筑结构学报, 2011, 32(5): 63-69. ZHANG Jianjun, LIU Qiongxiang, GUO Manliang, et al. Research on effective length of bar of space steel structure of the Shenzhen Universiade Sports Center[J]. Journal of building structures, 2011, 32(5): 63-69. |
| [13] |
林彦, 周学军. 圆管桁架受压腹杆平面内计算长度有限元分析[J]. 建筑钢结构进展, 2013, 15(1): 45-49. LIN Yan, ZHOU Xuejun. Finite element analysis on in-plane effective length of compressive web members in CHS truss[J]. Progress in steel building structures, 2013, 15(1): 45-49. |
| [14] | 董石麟, 罗尧治, 赵阳, 等. 新型空间结构分析、设计与施工[M]. 北京: 人民交通出版社, 2006: 23-27. |
| [15] |
王新毅, 童乐为. 圆钢管混凝土节点平面内抗弯刚度研究[J]. 钢结构, 2016, 31(1): 15-19. WANG Xinyi, TONG Lewei. Analysis on the flexural rigidity of CHS-CFCHS joints under in-plane bending moment[J]. Steel building structures, 2016, 31(1): 15-19. |
| [16] | KUROBANE Y, MAKINO Y, OCHI K, Ultimate resistance of unstiffened tubular joints[J]. Journal of structural engineering, 1984, 110(2): 385-400. |



