2. School of Naval Architecture, Dalian University of Technology, Dalian 116024, China;
3. Department of Civil Engineering, Dalian University of Technology, Dalian 116024, China
海底地震具有很强的不确定性与随机性,其频谱特性通常不同。具有不同频谱特性的地震作用会导致平台结构的振动响应发生变化,这种变化会影响结构各构件本身以及构件与构件之间的力学行为,导致不同地震作用下的内部破坏过程有所差异,最终发展为平台失效模式的不同。为掌握不同地震作用下结构的破坏行为与塑性发展规律,有必要尽可能多地获取平台主体可能出现的杆件破坏规律,进而获取不同地震作用下结构失效模式可能会呈现的共同特征或差异,有助于制定平台抗地震破坏控制策略,进而降低不同地震对结构倒塌的影响,从而有根据的延缓结构的倒塌行为。对于海洋平台地震破坏的研究一般为基于采用静力倒塌分析或强震下动力分析的结构破坏特性与状态。魏巍[1]采用时变的方法模拟地震作用下的杆件破坏过程与平台倒塌过程;Honarvara等[2]对一个小规模钢架进行了动力破坏试验,并将数值模拟与试验结果进行了对比;Adelson等[3]基于INTRA程序以及模型试验研究了强震作用下的承载力与延性性能。这些研究虽然能够获取结构的破坏过程,但一般属于单载荷记录作用下的一次破坏过程,很少触及“倒塌”这一结果。FEMA[4]提出PBEE抗震设计理念来指导结构的相关设计,同时建议采用IDA方法[5]对结构进行地震倒塌分析。近年来,该方法逐渐应用于海洋平台结构的抗震性能分析中[6]。这种方法能够有效地获取杆件在不同强度地震波下的弹塑性结果,并提供一个“大体”的塑性发展路径,因此可用于结构地震破坏特性的相关研究。为了得到地震作用下结构动力特性与破坏过程,深入了解结构的薄弱环节与失效模式,本文采用不同频谱特性的地震波,对某导管架平台进行动力增量分析,并在分析中记录结构的响应结果、杆件状态信息,以及塑性点、倒塌临界载荷水平。然后,对所有地震波下的塑性发展过程进行汇总与总结,采用秩和比法获取杆件的塑性影响系数以及最易出现的平台主体结构塑性发展路径。
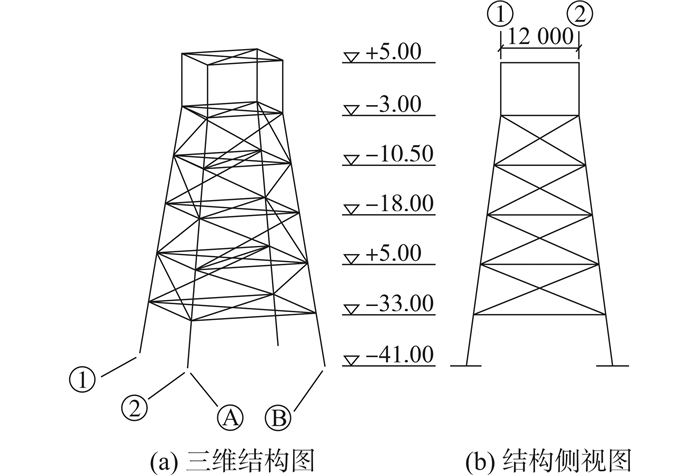
1 平台模型本文所选择的导管架平台结构如图 1所示,结构杆件标号如图 2所示。
|
| 图 1 平台几何模型 Fig. 1 Model of Platform Structure |
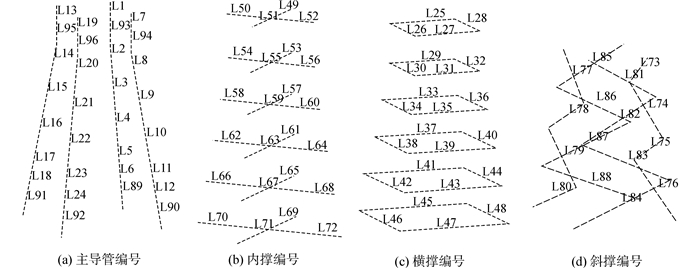
|
| 图 2 模型杆件标号 Fig. 2 No. of Members |
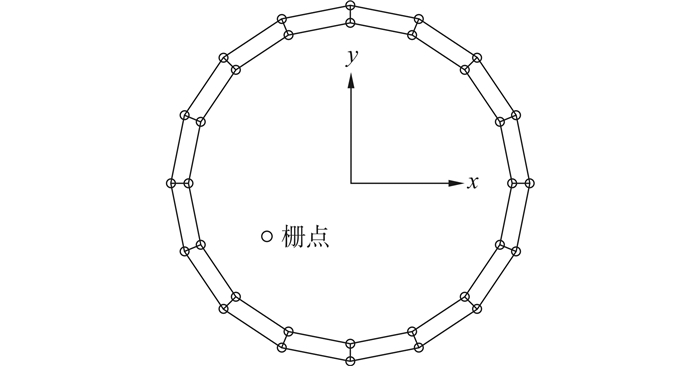
结构主体为6层钢架结构,整体结构由四根主导管支撑。平台的X、Y方向结构几何布置一致,降低了由于结构本身特性所导致不同方向的响应差异。平台的设计水深为33.8m,平台建模时不考虑桩-土相互作用以及海水对结构振动的影响,边界条件为泥线以下6倍桩径处固结。为方便计算,平台上部结构以集中质量作用于4根主导管顶端的相应节点上;整体结构钢材强度为235MPa,主要的几何参数如表 1所示。为记录各杆件截面的塑性状态,在杆件截面上取32个栅点并记录其塑性应变状态,栅点位置如图 3所示。
| 杆件类别 | 位置 | 外径 (m) | 壁厚 (m) |
| 1类 | 泥面上导管架主导管 | 1.20 | 0.050 |
| 2类 | 泥面下导管架主导管 | 1.20 | 0.050 |
| 3类 | 导管架层间横支撑 | 0.78 | 0.038 |
| 4类 | 导管架斜撑杆 | 0.51 | 0.025 |
|
| 图 3 杆件截面 Fig. 3 Member Cross Section |
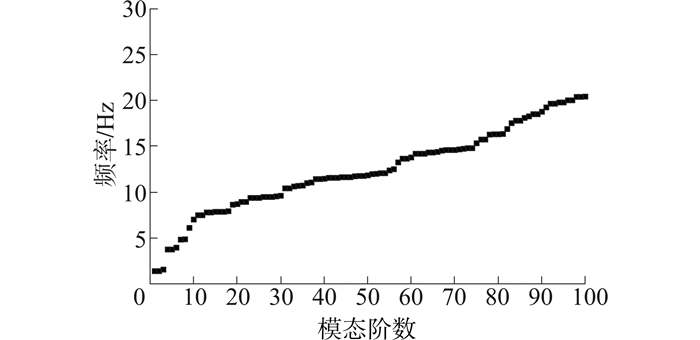
模态分析可以确定结构的自振频率、振型等振动特性,确定结构在不同激振频率下结构的变形趋势,是进行结构动力分析的基础。对于导管架平台结构,我们常常关注的是其前几阶振动特性。结构前100阶固有频率见图 4。
|
| 图 4 结构前100阶固有频率 Fig. 4 Natural Frequencies of First 100 Modes |
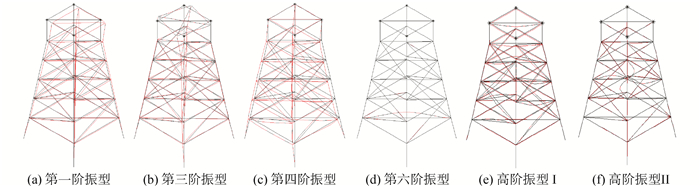
可见,平台的前三阶自振频率与随后的频率相差较大,对应于平台的两个对称水平振型与Z向扭转振型(图 5中a,b);此后在前10阶范围内的固有频率发展较快,主要包括整体水平振型与局部竖向振型(图 5中c,d);第10阶的平台固有频率大小均处于20Hz以内较低的频率范围,主要包括竖向振动、杆件振动或面内振动振型(图 5中e,f)。由自振频率分析可见,平台结构杆件繁多,自由度数较高,结构频谱特性较为密集。
|
| 图 5 平台结构振型 Fig. 5 Certain Modal Shapes of Platform |
本文选择了26条具备不同频谱特性的地震波[7],均截取含较大波段的1000子步。地震记录的震级、PGA等信息如表 2所示。
| 编号 | 地震 | 震级 | PGA (g) | 编号 | 地震 | 震级 | PGA (g) | |
| 1 | Imperial Valley-07, 1979 | 5.01 | 0.0822 | 14 | San Fernando, 1971 | 6.61 | 0.3297 | |
| 2 | Imperial Valley-07, 1979 | 5.01 | 0.0502 | 15 | Northridge,1994 | 6.7 | 0.593 | |
| 3 | Borah Peak, ID-01, 1983 | 6.88 | 0.0474 | 16 | San Fernando, 1971 | 6.61 | 0.1008 | |
| 4 | Westmorland, 1981 | 5.90 | 0.1571 | 17 | Point Mugu, 1973 | 5.65 | 0.0946 | |
| 5 | Tabas, Iran, 1978 | 7.35 | 0.3505 | 18 | San Fernando, 1981 | 6.61 | 0.0653 | |
| 6 | Lytle Creek, 1970 | 5.33 | 0.1348 | 19 | San Fernando, 1971 | 6.61 | 0.0324 | |
| 7 | Imperial Valley, 1940 | 6.9 | 0.34 | 20 | Westmorland, 1981 | 5.90 | 0.2193 | |
| 8 | Norcia, Italy, 1979 | 5.90 | 0.0314 | 21 | Nahanni,1985 | 6.76 | 1.0556 | |
| 9 | Norcia, Italy, 1979 | 5.90 | 0.1856 | 22 | Tabas, Iran, 1978 | 7.35 | 0.0270 | |
| 10 | Norcia, Italy, 1979 | 5.90 | 0.0417 | 23 | San Fernando, 1971 | 6.61 | 0.0389 | |
| 11 | Imperial Valley-06, 1979 | 6.53 | 0.1382 | 24 | San Fernando, 1971 | 6.61 | 0.0681 | |
| 12 | Imperial Valley-06, 1979 | 6.53 | 0.1212 | 25 | San Fernando, 1971 | 6.61 | 0.0146 | |
| 13 | Imperial Valley-06, 1979 | 6.53 | 0.2165 | 26 | Kern County, 1952 | 7.6 | 0.156 |
本文采用增量动力分析(Incremental Dynamic Analysis,IDA)方法对导管架平台结构进行倒塌全过程分析。用于评估地震载荷下结构性能的IDA方法近年来受到广泛的重视并被应用于基于性能的抗震设计(performance based earthquake engineering,PBEE)研究中[8, 9],成为结构整体倒塌性能分析的新方法。IDA方法通过对地震动时程乘以一系列不同大小的比例系数(scale factor,SF),并分别在这一系列不同强度地震动下对结构进行非线性动力时程分析,然后绘制结构性能参数(damage measure,DM)与地震动强度(ground motion intensity measure,IM)的关系曲线,研究结构在地震作用下的倒塌全过程。
将所有地震波调幅为PGA=0.01g (1g=9.8 m/s2),以PGA为地震动强度指标,通过不断调整调幅因子来调整作用于结构的载荷水平。计算过程中分析塑性结果不断调整调幅因子(scale factor,SF),获取结构最初进入塑性时的载荷水平,即“结构塑性点”;然后从该水平载荷下逐级提高载荷水平(提高调幅因子)直到结构发生倒塌,并获得结构倒塌时对应的极限载荷水平。文中倒塌点被定义为“结构顶点突然出现较大位移时的载荷水平”,并获取其前一载荷水平下的结构状态为结构倒塌前的结构状态。在计算过程中记录了每一步载荷水平下结构的动力响应信息与结构状态信息,并通过计算结果的汇总与讨论,研究结构的动力性能。
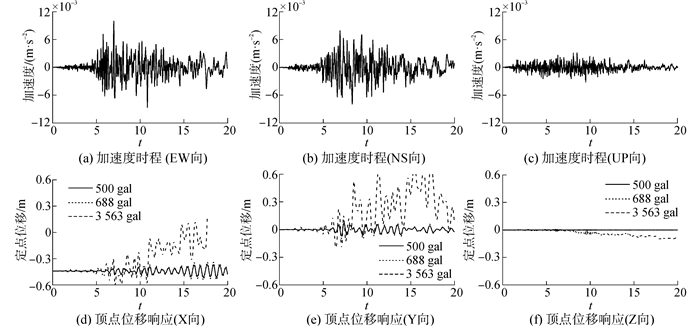
以Imperial Valley-06 (1979-2) 地震波为例,对导管架平台进行全过程倒塌分析。地震波三向加速度时程(PGA=1g)以及结构分别在弹性范围、塑性点以及临倒塌载荷水平下的顶点位移响应见图 6。从分析来看,塑性点对应载荷水平时顶点位移平衡位置的偏移并不明显,但倒塌临界状态的平衡位置产生了较大偏移,且出现多次的偏移过程,意味着结构在极限载荷下会出现多次明显的结构杆件破坏与应力重分布过程。
|
| 图 6 地震加速度时程与结构顶点位移时程 Fig. 6 Acceleration History of earthquake and Top Dis History of structure |
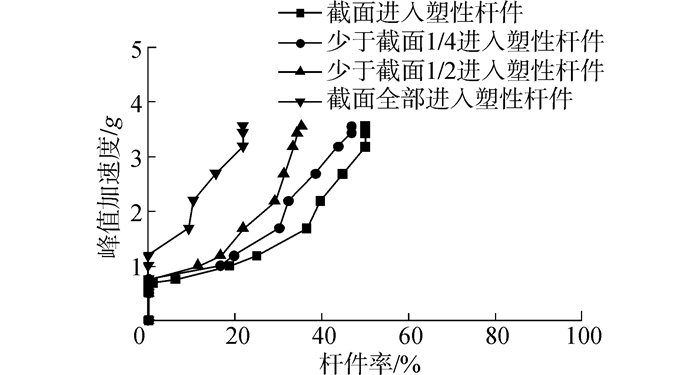
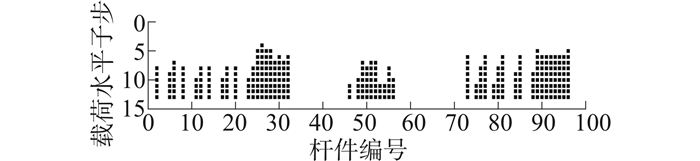
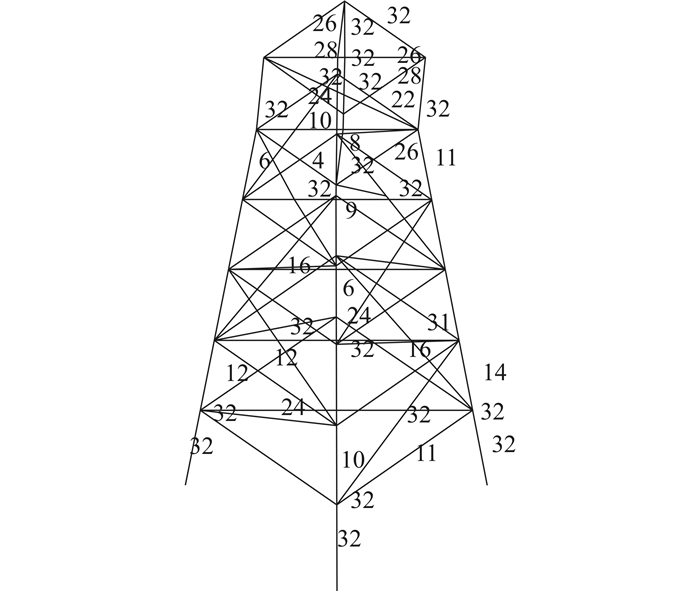
1)单地震记录下的动力计算为深入了解塑性发展过程,对于不同载荷水平下进入塑性杆件状态进行记录,得到杆件截面进入塑性的状态与进入塑性的程度。随载荷水平增加,结构的屈服杆件发展比例见图 7。由图中可以看出,塑性点位置为PGA=0.7g左右,在结构进入塑性后,会呈现一个塑性快速发展的过程,在截面进入塑性、1/4以内截面进入塑性、1/2以内截面进入塑性,以及全截面进入塑性的杆件数量均快速增长然后在PGA=1.2g左右开始缓慢增长,直到PGA=3.5g左右时到达极限状态。图 8由上至下表达了结构在由低载荷水平到高载荷水平下每根构件的塑性状态,能够在一定程度上反映结构进入塑性的发展过程。对比结构的杆件编号图可见,平台首次进入塑性的杆件为26与28号杆件,即第6层的横撑杆件,然后26号附近的杆件25、27和28号也随之进入塑性状态;在五层以上腿柱(96号杆件)与泥面以上腿柱(89号杆件)进入塑性以后,结构在下一载荷水平发生了塑性急剧发展的过程,塑性发展呈现由最上层与最下方向中间位置发展的趋势,当发展到某一阶段时,结构进入倒塌极限状态。最终有约50%的杆件进入塑性,20%的杆件全截面进入塑性,最终倒塌前的结构进入塑性程度如图 9所示。
|
| 图 7 地震幅值-屈服杆件比例 Fig. 7 PGA-Plastic Member Rate |
|
| 图 8 结构杆件的塑性发展过程 Fig. 8 Plastic Development of Structural Members |
|
| 图 9 倒塌塑性程度 Fig. 9 Plastic development |
b) IDA计算结果汇总
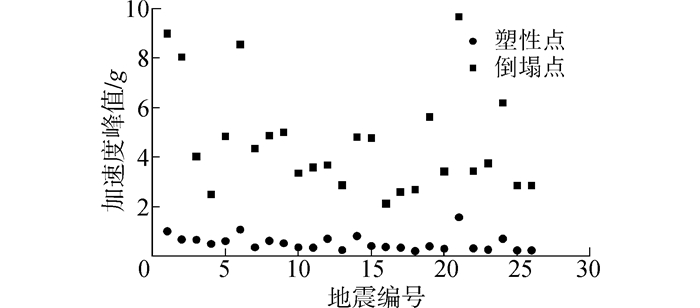
对所有地震波下的结构塑性点、倒塌点载荷水平、顶点位移进行了汇总与整理,如图 10。可以看出,塑性出现时对应的载荷水平一般较低,远低于结构倒塌状态时的载荷水平,其中23号地震波的倒塌极限与塑性时刻对应的PGA比最高,为15左右,而4号地震波的倒塌极限与塑性时刻对应的PGA比最低,为5.1左右。可见结构在进入塑性后,还可保持较高的冗余度与安全储备。除21号地震波外,其他地震动记录作用下的塑性点均在1g以内,而倒塌点在不同地震波作用下变异性较高,在塑性点大小相近的情况下,极限点之间的差距能够达到1倍以上(如16、18号地震波),可见结构在不同地震作用下的抗倒塌能力差异性较大。
|
| 图 10 塑性点与倒塌点汇总 Fig. 10 Summary of Plastic Point and Collapse Point |
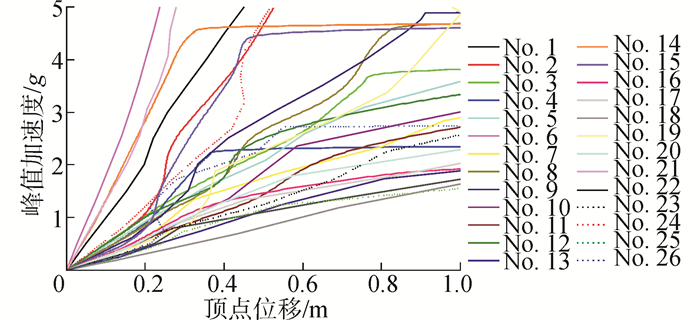
图 11描述了位移与载荷水平的关系。一般认为,以PGA作为地震动强度指标(IM)时此类曲线的离散程度较高,因此这里只讨论位移发展过程的特点。从图中可以看出:1)产生较大位移变化的位置一般高于该地震波的塑性点,即结构出现明显非线性位移变化的时候,结构的塑性程度已达到高于塑性点的水平;2)位移随地震波的不同,发展速度不同,同时产生非线性的发展过程,有时甚至呈现多次的“震荡”发展过程。这种现象从工程上来说,结构有时会经历DM积累率的加速提高过程,但其他时刻降速的发生能够暂时停止甚至逆转位移的积累,并因此拉动IDA曲线,使DM的值相对降低并成为IM相关的非单调函数。最终,随着DM的积累速率越来越高,一个最终的“软化”段的发生,标志着结构动力不稳定性的出现。
|
| 图 11 顶点位移-峰值加速度汇总 Fig. 11 Summary of PGA and Top_Dis Curves |
导致结构倒塌的直接原因是结构整体稳定性的丧失,这种稳定性的丧失从整体上表现为结构承载能力的下降,即结构整体刚度的退化。而导致结构整体刚度降低的原因实际上是结构内部杆件进入塑性程度的不断提高与破坏杆件的数量不断增加,因此,结构中所有杆件的破坏与塑性发展规律是结构失效过程的一个重要特性,有重要的研究意义。
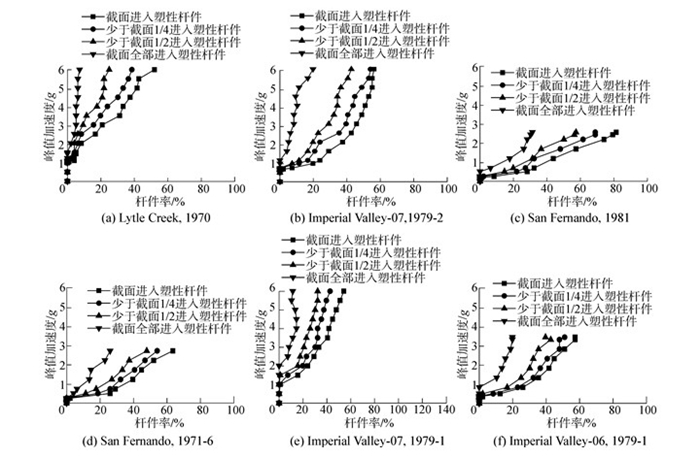
观察所有地震波下的所有构件截面进入塑性、1/4以内截面进入塑性、1/2以内截面进入塑性,以及截面进入全塑性的杆件率发展过程如图 12,在首次出现塑性后,结构中不同进入塑性程度的杆件数量均呈一个急剧增长的过程。而此后这个发展过程在不同地震波作用下的有较大差异。例如:Lytle Creek (1970) 记录下塑性急剧发展过程后斜率升高,塑性发展减缓,Imperial Valley-07 (1979-2) 仅在截面1/2以内进入塑性杆件率中出现了一次显著提高;San Fernando (1981) 作用下杆件塑性发展持续一个较快的水平,直至结构倒塌;San Fernando (1971-6) 记录下杆件塑性率在斜率平缓后再次出现了斜率降低的过程,表示地震峰值达到一定水平后结构塑性发展再次加剧的过程。同时,发现Imperial Valley-07 (1979-1)、Imperial Valley-06 (1979-1) 等记录作用下的塑性杆件率发生了一定的下降,可考虑为不同载荷水平下的时程动力分析对于结构的破坏过程不同所致。
|
| 图 12 地震幅值-屈服杆件比例 Fig. 12 PGA-Plastic Member Rate |
对所有地震作用下结构塑性点、倒塌临界水平对应的所有杆件状态进行汇总,见表 3。截面进入塑性程度被分为截面进入塑性、1/4以内截面进入塑性、1/2以内截面进入塑性,以及截面进入全塑性。可以看出,不同地震波作用下进入塑性杆件数均在40以上,最高达到78根,最低为43根;杆端截面进入全塑性的杆件数最高可达38根,最低为10根,可见结构进入塑性的程度较高,同时也意味着极限状态与塑性点之间有着较大的塑性发展过程,从侧面反映了塑性点与极限点之间存在着较大的整体冗余度与安全储备水平。从单条地震来看,不同地震波下的进入塑性程度有着较大的变异性。说明不同地震波特性对于结构的塑性发展趋势与倒塌过程有着较大的影响,而结构的倒塌并不完全受到结构进入塑性程度的控制。
| 地震 编号 | 进入 塑性 | 1/4进入 塑性 | 1/2进入 塑性 | 全进入 塑性 | 地震 编号 | 进入 塑性 | 1/4进入 塑性 | 1/2进入 塑性 | 全进入 塑性 | |
| 1 | 62 | 56 | 42 | 22 | 14 | 45 | 35 | 24 | 13 | |
| 2 | 65 | 55 | 47 | 20 | 15 | 69 | 60 | 48 | 21 | |
| 3 | 57 | 46 | 42 | 21 | 16 | 47 | 45 | 33 | 19 | |
| 4 | 43 | 29 | 24 | 10 | 17 | 51 | 42 | 32 | 12 | |
| 5 | 57 | 54 | 42 | 24 | 18 | 78 | 66 | 55 | 30 | |
| 6 | 66 | 52 | 33 | 13 | 19 | 75 | 66 | 49 | 27 | |
| 7 | 64 | 52 | 49 | 28 | 20 | 53 | 50 | 42 | 22 | |
| 8 | 61 | 50 | 46 | 23 | 21 | 62 | 48 | 34 | 18 | |
| 9 | 66 | 59 | 41 | 21 | 22 | 61 | 55 | 54 | 31 | |
| 10 | 70 | 62 | 54 | 24 | 23 | 67 | 61 | 53 | 38 | |
| 11 | 55 | 49 | 38 | 19 | 24 | 63 | 56 | 45 | 19 | |
| 12 | 48 | 45 | 34 | 21 | 25 | 61 | 52 | 46 | 25 | |
| 13 | 69 | 64 | 55 | 32 | 26 | 51 | 46 | 36 | 19 |
为观察各杆件在不同地震作用下进入塑性几率,定义杆件出现塑性的比率为
| ${\rm{Peecentage = }}\frac{{{\rm{count}}\left( \sigma \right)}}{N},\left( {\sigma = 0} \right)$ | (1) |
式中:N为地震波数,σ为构件进入塑性的程度。将计算结果与结构位置进行对照,得到结构不同位置在不同地震波下进入塑性的几率,如表 4所示。
| Percentage>90% | 40% < Percentage < 90% | 0 < Percentage < 40% | Percentage=0 |
| 二层以下的腿柱; 与五层相连接的腿柱; 五、六层X斜撑, 五、六层横撑, 一、二层间斜撑; 四、五层间斜撑。 | 一层横撑; 一层X型斜撑; 四层X型斜撑; 一、二层间斜撑; 三、四层间斜撑。 | 与六层连接腿柱; 二、三层间腿柱; 三、四层间腿柱; 二、三层X型斜撑; 第四层横撑。 | 二层横撑; 三层横撑。 |
从构件层次上来说,腿柱更容易进入塑性,其次为层间斜撑,然后是X型斜撑,而横撑结构虽然在最高层进入速度较快,但其它层横撑的塑性程度一般较低。从整体来看,结构的最上层,以及结构与泥面的接触部分进入塑性的程度最高,然后呈由上下两端向中间发展的趋势。
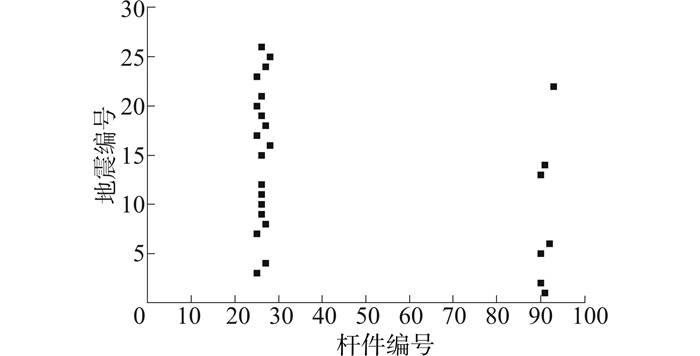
图 13为结构在塑性点处对应的进入塑性杆件编号。可以看出,结构首次进入塑性的位置主要集中于25~28,以及90~94处。结合图 3中的杆件位置,发现这些位置主要分布于最高层的横撑位置,以及腿柱与泥面固结的连接处。这是一个较为共性的结果,意味着结构的塑性发展一般从平台结构的最上端与最下端开始。
|
| 图 13 首次进入塑性杆件汇总 Fig. 13 Summary of Members into Plastic Initially |
进一步了解各杆件在塑性发展过程中的贡献,采用秩和比法对杆件的塑性结果进行了影响系数的计算。对于第i个杆件,影响系数可以取为:
| $W = \frac{{\sum\limits_{k = 1}^E {\frac{{{N_k} - j + 1}}{{{N_k}}}} }}{E}$ | (2) |
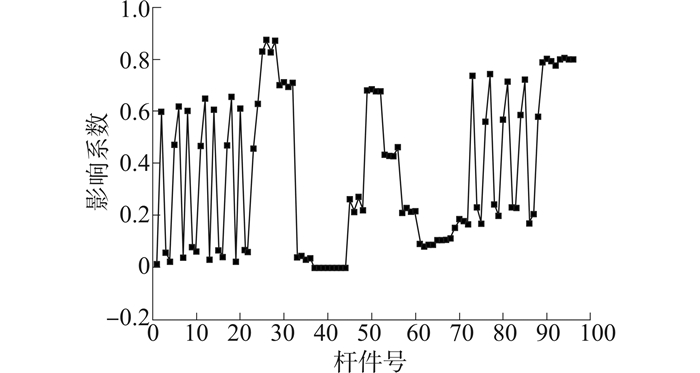
其中,N为从出现塑性到结构倒塌的总载荷步数;j为结构开始进入塑性后,杆件首次出现塑性应变所对应步数;E为地震动记录总数;k为地震编号。计算结果见图 14。
|
| 图 14 杆件塑性发展影响系数 Fig. 14 Plastic Development Influence Factors of Members |
杆件塑性发展影响系数实际上是不同地震波下失效模式的综合性描述。不同构件间系数的大小比较,能够在一定程度上反映出杆件截面最可能出现塑性的先后顺序,在初始塑性点位置同样可以得出与图 13相似的结论。同时,虽然系数顺序并不意味着结构在某地震记录下的实际失效模式,但由于不同杆件系数的大小明确,其顺序可以体现最易出现的平台主体结构塑性发展过程。
进一步研究不同地震动下失效模式与最易出现塑性发展过程的差异,本文采用了余弦相似度算法对失效模式之间的相似度进行描述。定义相似度系数[10]为:
| $\cos \theta = \frac{{a \cdot b}}{{\left| a \right|\left| b \right|}}$ | (3) |
式中:a·b为2个n维样本点,其相似性结果在从-1~1。-1意味着a·b指向的方向恰好相反,而1表示a·b的指向完全相同,0通常表示a·b之间相互独立,而在这之间的其它值则表示一定程度的相似或相异性。
由孙爱伏[11]等人提出的最弱失效模式可知,结构的最弱失效模式为16号地震波作用下的杆件破坏模式。通过上文得到的综合塑性发展参与系数与各地震动下该系数的分析,以及通过最弱失效模式的杆件参与系数与所有地震动下该系数的分析计算得到相似性系数如表 5所示。
| 地震波 编号 | 相似性系数 | 地震波 编号 | 相似性系数 | |||
| 本文 | 最弱 | 本文 | 最弱 | |||
| 1 | 0.971 | 0.934 | 14 | 0.933 | 0.914 | |
| 2 | 0.970 | 0.925 | 15 | 0.965 | 0.923 | |
| 3 | 0.978 | 0.954 | 16 | 0.972 | 1.000 | |
| 4 | 0.930 | 0.909 | 17 | 0.967 | 0.949 | |
| 5 | 0.984 | 0.958 | 18 | 0.963 | 0.900 | |
| 6 | 0.922 | 0.846 | 19 | 0.971 | 0.923 | |
| 7 | 0.979 | 0.949 | 20 | 0.968 | 0.982 | |
| 8 | 0.966 | 0.948 | 21 | 0.970 | 0.945 | |
| 9 | 0.979 | 0.935 | 22 | 0.976 | 0.964 | |
| 10 | 0.946 | 0.900 | 23 | 0.968 | 0.942 | |
| 11 | 0.985 | 0.975 | 24 | 0.972 | 0.926 | |
| 12 | 0.974 | 0.966 | 25 | 0.977 | 0.971 | |
| 13 | 0.975 | 0.947 | 26 | 0.975 | 0.982 | |
通过两类失效模式下相似度的对比,可以看出基于影响系数的失效模式与各地震动倒塌失效模式相似度最大值为0.985,最小为0.922;最弱失效模式与其他倒塌失效模式下相似度最大值为0.982,最小为0.846。经过计算,不同相似度大小的平均值与变异系数如表 6所示。可以看出,基于影响系数的失效模式平均值较高,且变异系数较低。可见基于影响系数的失效模式与所有失效模式均更为相近,且离散度较小,更具备统计意义,便于实际工程应用。
| 基于影响系数的失效模式 | 最弱失效模式 | |
| 平均值 | 0.967 | 0.941 |
| 变异系数 | 0.017 | 0.034 |
本文采用IDA分析方法,选择26条三向地震波时程记录,对某海洋平台结构进行了动力倒塌分析,并在全过程分析中记录结构响应与杆件的塑性状态,进而探讨了平台结构的塑性发展规律,并根据秩和比法获得统计规律下的结构失效模式,得出以下结论:
1) 结构进入塑性对应载荷水平普遍较低,远低于临界倒塌时刻对应的载荷水平。不同地震波下的塑性点、临界倒塌对应载荷水平差距较大,结构响应的发展在地震作用下会受到结构非线性、地震动时程与频谱特性的影响。随着载荷作用水平的提高,结构会经历多次的杆件失效与应力重分布过程。在不同地震作用下的结构性能参数与载荷水平曲线的发展特性并不一致且差别较大;
2) 平台结构从完好状态进入塑性状态时的初始杆件位置具有一定的共性,一般为顶层水平支撑,或与泥线相接的桩腿位置,结构塑性率的发展在结构进入塑性后呈现急剧加快的趋势,而后的发展过程在不同地震波记录之间存在较大差异;
3)通过计算塑性发展影响系数,找到最易出现的平台主体结构塑性发展过程。通过计算相似性系数,得到与综合发展影响系数最相近的倒塌失效模式,该方法获取的失效模式与所有真实倒塌失效模式均较为接近且相似度离散性较小,具有统计意义,可以为抗地震倒塌设计提供基础。
| [1] |
魏巍. 导管架式海洋平台地震破坏状态分析研究[D]. 青岛: 中国海洋大学, 2004: 56-77. WEI Wei. Research on seismic damage states of jacket offshore platform structures[D]. Qingdao: Ocean University of China, 2004: 56-77. |
| [2] | HONARVAR M R, BAHAARI M R, ASGARIAN B, et al. Cyclic inelastic behavior and analytical modelling of pile-leg interaction in jacket type offshore platforms[J]. Applied ocean research, 2007, 29(4): 167-179. |
| [3] | ADELSON B L, STEINMETZ R L. Earthquake ductility study for offshore structures[J]. Journal of waterway, port, coastal, and ocean engineering, 1984, 110(4): 393-412. |
| [4] | MAHONEY M, HANSON R D. Effects of strength and stiffness degradation on seismic response[M]. Washington, D.C.: Federal Emergency Management Agency, Department of Homeland Security, 2009: 89-101. |
| [5] | ASGARIAN B, AJAMY A. Seismic performance of jacket type offshore platforms through incremental dynamic analysis[J]. Journal of offshore mechanics and arctic engineering, 2010, 132(3): 031301. |
| [6] | SKREKAS P, GIARALIS A. On the use of incremental dynamic analysis for evaluating the earthquake-resistant performance of off-shore jack-up platforms[C]//Proceedings of the 6th International ASRANet 2012 Conference for Integrating Structural Analysis, Risk and Reliability. Croydon, London, UK, 2012. |
| [7] | Pacific Earthquake Engineering Research Center. PEER Strong Motion Database[EB/OL].[2014-03-16].Berkeley, CA: PEER. http://peer.berkeley.edu/smcat. |
| [8] | BERTERO V V. Strength and deformation capacities of buildings under extreme environments[J]. Structural engineering and structural mechanics, 1977, 53(1): 29-79. |
| [9] | GHOBARAH A. Performance-based design in earthquake engineering: state of development[J]. Engineering Structures, 2001, 23(8): 878-884. |
| [10] | GOWER J C. A general coefficient of similarity and some of its properties[J]. Biometrics, 1971, 27(4): 857-871. |
| [11] |
孙爱伏, 欧进萍, 侯爽. 高层钢框架结构的薄弱层加强与最弱失效模式控制[J]. 地震工程与工程振动, 2011, 30(6): 49-55. SUN Aifu, OU Jinping, HOU Shuang. Weak story strengthening and weakest failure mode control of tall steel frame buildings[J]. Journal of earthquake engineering and engineering vibration, 2011, 30(6): 49-55. |



