2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
高速、高性能的水声通信是近年来水声领域的研究热点之一。随着通信速率的增加,浅水信道的多途效应[1]所引起的码间干扰会影响几十甚至上百个码元,这极大地影响了通信性能。为了抑制严重的码间干扰,传统的水声通信往往采用复杂的自适应均衡技术[2]。近年来,时反技术由于其结构的简单性和良好的空时聚焦性[3],被广泛的应用于水声通信领域[4, 5, 6, 7, 8, 9]。
时反技术主要可分为主动时反(active time reversal,ATR)和被动时反(passive time reversal,PTR)。与ATR相比,PTR仅需要单向传输,探测信号和信息信号的间隔时间短,更能保证估计的信道和实际信道的匹配性,因此得到了更广泛地研究。时反技术与空间分集技术相结合,可以获得较高的空间处理性能,进而提高通信性能[3]。现有研究中,PTR主要与接收分集相结合,但是当接收平台的尺度较小、阵元数较少时,能够获得空间处理性能较低,为了进一步提高通信性能,可以利用发射分集。文献[8]对基于发射分集的PTR水声通信进行了初步的研究,但是该方法PTR处理后的信号不能实现最大比合并,因此通过发射分集获得空间处理性能较低。本文提出了时反空时分组编码(time-reversal space-time block coding,TR-STBC) 多输入多输出(multiple-input-multiple-output,MIMO)水声通信方法。所提方法根据正交空时分组编码的原理[10, 11],设计了码率为1/2的TR-STBC方案,使小尺度接收平台PTR处理后的信号实现最大比合并,从而获得较高的空间处理性能,进而提高通信性能。
1 TR-STBC MIMO水声通信方法 1.1 发射端的信号处理为了便于表达,以下分析中信号矩阵A(t)=[akl(t)m×n和B(t)=bkl(t)n×s的卷积为
| $A\left( t \right)*B\left( t \right) = {\left[{\sum\limits_{r = 1}^n {{a_{kr}}\left( t \right)*{b_{rl}}\left( t \right)} } \right]_{n \times s}}$ |
信号a(t)与矩阵B(t)的卷积为
| $a\left( t \right)*b\left( t \right) = {\left[{a\left( t \right)*{b_{rl}}\left( t \right)} \right]_{n \times s}}$ |
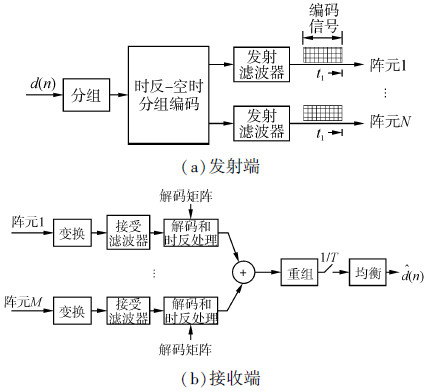
图 1给出了TR-STBC MIMO水声通信方法的信号处理原理框图。由图 1 (a)知,发射端首先根据发射阵元数N,将信息码元d(n)划分成长度相同的L=min$\left\lfloor {{2^{4c + d}}} \right\rfloor $个码组dl(n),l=1,…,L,其中最小化运算是对集合{c≥0,d≥0|8c+2d≥N}中所有可能的整数c和d进行的,划分后的码组dl(n)经过TR-STBC和发射滤波处理后可得
| $S\left( t \right) = \left[\begin{array}{l} \sum\limits_{l = 1}^L {{s_l}\left( t \right)} {E_l}\\ \sum\limits_{l = 1}^L {{s_l}\left( { - t} \right)} {E_l} \end{array} \right]$ | (1) |
|
| 图 1 发射-接收方案原理框图 Fig. 1 Block diagram of transmitter and receiver |
式中:${s_l}\left( t \right) = \sum\limits_n {{d_l}\left( n \right){g_l}\left( {t - nT} \right)} $为第l个发射子信号,gt(t)为发射滤波器的响应,El为L×N的实矩阵,其满足:
| $\left\{ \begin{array}{l} E_l^T{E_l}' + E_l^{T'}{E_l} = {0_N},\;\;\;l \ne l'\\ E_l^T{E_l} = {I_N},\;\;\;\;l = 1,2,\cdots ,L \end{array} \right.$ | (2) |
式中:0N是一个N×N的零矩阵。
由式(1)、(2)知,S(t)为2L×N的矩阵,其每一列表示同一个阵元在不同时隙发射的信号,每一行表示不同阵元在同一时隙发射的信号,L个信息子信号通过2L个时隙发送,因此码率为1/2。
1.2 接收端的信号处理第j个阵元接收的信号为
| $\begin{array}{*{20}{c}} {{X^j}\left( t \right) = }\\ {\left[\begin{array}{l} X_1^j\left( t \right)\\ X_2^j\left( t \right) \end{array} \right] = \left[\begin{array}{l} \sum\limits_{l = 1}^L {{s_l}\left( t \right)} {E_l}*{H^j}\left( t \right)\\ \sum\limits_{l = 1}^L {{s_l}\left( { - t} \right)} {E_l}*{H^j}\left( t \right) \end{array} \right] + \left[\begin{array}{l} N_1^j\left( t \right)\\ N_2^j\left( t \right) \end{array} \right]} \end{array}$ | (3) |
式中:Xj(t)为2L×1的信号矩阵,X1j(t)和X2j(t)为Xj(t)的2个L×1的分块矩阵; N1j(t)和N2j(t)为2个L×1的分块矩阵,其第k元素分别表示第k个和第L+k个时隙接收到的信道噪声;Hj(t)为N×1的矩阵,其第i个元素为第i个发射阵元与第j个接收阵元间的信道响应hij(t)。
对Xj(t)进行变换,可以得到Yj(t):
| ${Y^j}\left( t \right) = \left[{{{\left( {X_1^j\left( t \right)} \right)}^{\rm{T}}},{{\left( {X_2^j\left( { - t} \right)} \right)}^{\rm{T}}}} \right]$ | (4) |
Yj(t)经过接收滤波器处理可得
| ${R^j}\left( t \right) = {g_r}\left( t \right)*{Y^j}\left( t \right)$ | (5) |
式中:gr(t)为接收滤波器的响应。
由图 1(b)知,为了进行解码和时反处理,必须构造解码矩阵。解码矩阵的形式为Ωj(t)=Zj(t),Zj(-t),Zj(t)和Zj(-t)均为L×L的矩阵,其第l行分别为
| $\left\{ \begin{array}{l} z_l^j\left( t \right) = {\left( {{H^j}\left( t \right)} \right)^{\rm{T}}}E_l^{\rm{T}}\\ z_l^j\left( { - t} \right) = {\left( {{H^j}\left( { - t} \right)} \right)^{\rm{T}}}E_l^{\rm{T}} \end{array} \right.$ | (6) |
式中:El为式(2)定义的矩阵,Hj(-t)为N×1的矩阵,其第i个元素为信道响应的时反hij(-t),分析中不考虑信道估计所产生的误差。
在第j个接收阵元,利用解码信号矩阵Ωj(t)对矩阵Rj(t)进行解码和时反处理,可得
| $\begin{array}{*{20}{c}} {R_c^j\left( t \right) = {R^j}\left( t \right)*{{\left( {{\Omega ^j}\left( { - t} \right)} \right)}^{\rm{T}}} = }\\ {\sum\limits_{i = 1}^N {2{h_{ij}}\left( t \right)} *{h_{ij}}\left( { - t} \right)*{g_r}\left( t \right)*\left[{{s_1}\left( t \right),\cdots ,{s_L}\left( t \right)} \right] + }\\ {{g_r}\left( t \right)*\left[{{{\left( {N_1^j\left( t \right)} \right)}^{\rm{T}}},{{\left( {N_2^j\left( { - t} \right)} \right)}^{\rm{T}}}} \right]*{{\left( {{\Omega ^j}\left( { - t} \right)} \right)}^{\rm{T}}}} \end{array}$ | (7) |
并将M个接收阵元处理后的信号合并可得
| $\begin{array}{*{20}{c}} {{R_c}\left( t \right) = \left[{{r_{c1}}\left( t \right),\cdots ,{r_{cL}}\left( t \right)} \right] = }\\ {\left[{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\sum\limits_n^{} {2{d_1}\left( n \right){f_{ij}}\left( {t - nT} \right),\cdots ,} } } } \right.}\\ {\left. {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\sum\limits_n^{} {2{d_L}\left( n \right){f_{ij}}\left( {t - nT} \right)} } } } \right] + \left[{{n_{c1}}\left( t \right),\cdots ,{n_{cL}}\left( t \right)} \right]} \end{array}$ | (8) |
其中
| $\begin{array}{*{20}{c}} {{f_{ij}}\left( t \right) = {g_t}\left( t \right)*{g_r}\left( t \right)*{h_{ij}}\left( t \right)*{h_{ij}}\left( { - t} \right) = }\\ {g\left( t \right)*{h_{ij}}\left( t \right)*{h_{ij}}\left( { - t} \right)} \end{array}$ | (9) |
式中:rcl(t)为Rc(t)的第l个元素,ncl(t)为$\sum\limits_{j = 1}^M {{g_r}\left( t \right)*\left[{{{\left( {N_1^j\left( t \right)} \right)}^{\rm{T}}},{{\left( {N_2^j\left( { - t} \right)} \right)}^{\rm{T}}}} \right]*{{\left( {{\Omega ^j}\left( { - t} \right)} \right)}^{\rm{T}}}} $的第l个元素,g(t)为发射滤波器和接收滤波器的组合响应,其频谱为升余弦谱。
由式(8)、(9)知,N个发射信号的副本在接收端实现了最大比合并。此外,式(8)等号右端第1项包含了系数2,这是因为1/2码率的TR-STBC使每个子信号都发射了2次。
在无线电通信中,若N个发射信号的副本在接收端实现了最大比合并,则可判断通信系统实现了全发射分集,空间处理性能提高了10lg(N) dB,但是在浅水通信中,这一结论不能直接使用。这是因为无线电通信的结论是基于平坦瑞利信道,并且认为信道之间满足互不相关,而浅水信道是一个典型的频率选择性衰落信道,并且不同阵元间的信道响应具有相关性。以下结合浅水信道的具体特性,对所提方法的空间处理性能进行分析。
2 空间处理性能 2.1 理论推导无线电通信中,多元收发对空间处理性能的提高通过空间分集增益:
| ${G_d} = \mathop { - \lim \lg }\limits_{\gamma \to \infty } \left( {{P_e}} \right)/\lg \left( \gamma \right)$ |
来衡量,式中:γ表示输入信噪比,Pe表示错误概率。浅水通信中错误概率尚未有统一公式,但是浅水通信中错误概率与输出信号干扰噪声比(signal-to-interference-noise ratio,SINR)有一定关系,因此以下通过分析输入信噪比和输出SINR的关系来衡量所提方法的空间处理性能,即在输入信噪比的不变条件下,输出SINR越高,空间处理性能就越高。
将式(8)中信号矩阵进行重组,并按码元速率1/T进行采样可得
| $2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\sum\limits_{n \ne 0}^{} {d\left( {m - n} \right){f_{ij}}\left( {nT} \right) + {n_c}\left( {mT} \right)} } } $ | (10) |
式(10)右端第1项仅与第m时刻发射的信息码元有关,第2项为其他码元对第m个码元产生码间干扰,第3项为噪声干扰。
由式(10)可得,所提方法的输出SINR为
| $\begin{array}{*{20}{c}} {{\rm{SIN}}{{\rm{R}}^c} = \frac{1}{{{{\left( {{\rm{SI}}{{\rm{R}}^c}} \right)}^{ - 1}} + {{\left( {{\rm{SN}}{{\rm{R}}^c}} \right)}^{ - 1}}}} = }\\ {\frac{{{\rm{E}}\left[{{{\left| {2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {d\left( m \right){f_{ij}}\left( 0 \right)} } } \right|}^2}} \right]}}{{{\rm{E}}\left[{{{\left| {2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\sum\limits_{n \ne 0}^{} {d\left( {m - n} \right){f_{ij}}\left( {nT} \right) + {n_c}\left( {mT} \right)} } } } \right|}^2}} \right]}}} \end{array}$ | (11) |
式中:SIRc和SNRc分别表示所提方法的输出信干比和输出信噪比。
由文献[3]知,仅使用接收分集的PTR水声通信方法的输出SINR为
| $\begin{array}{*{20}{c}} {{\rm{SIN}}{{\rm{R}}^t} = \frac{1}{{{{\left( {{\rm{SI}}{{\rm{R}}^t}} \right)}^{ - 1}} + {{\left( {{\rm{SN}}{{\rm{R}}^t}} \right)}^{ - 1}}}} = }\\ {\frac{{{\rm{E}}\left[{{{\left| {\sum\limits_{j = 1}^M {d\left( m \right){f_j}\left( 0 \right)} } \right|}^2}} \right]}}{{{\rm{E}}\left[{{{\left| {\sum\limits_{j = 1}^M {\sum\limits_{n \ne 0}^{} {d\left( {m - n} \right){f_j}\left( {nT} \right) + {n_t}\left( {mT} \right)} } } \right|}^2}} \right]}}} \end{array}$ | (12) |
式中:fj(t)表示单发射阵元到第j个接收阵元的组合信道响应,nt(mT)表示多元接收阵时反处理后的噪声。
由式(11)、(12)知,要分析所提方法的有效性,只需要在信噪比不变的条件下,将SINRc和SINRt进行对比。要定量对比SINRc和SINRt,必须结合fij(t)和fi(t)的表达式,然而浅水信道尚未有统一的表达式,因此本文将结合多途信道模型进行仿真分析。
2.2 仿真分析仿真基于浅海信道的多途模型,每个信道都包括P个传播路径,每个路径都通过路径增益cp、时延τp和到达角θp共同表达。cp的相位为φcp=-2πfcτp,其中fc为载波频率,仿真中fc=12 kHz。cp的幅度为|cp|=Γp/A(lp),其中Γp=|vs|ns|vb|nb为界面反射损失,ns、nb分别为海面、海底反射次数,仿真中海面反射损失|vs|=1,海底反射损失|vb|=0.6,A(lp)=lpk[a(fc)]lp为传播损失,lp为传输距离,仿真中k=1.5,吸收系数a(fc)根据文献[1]计算。仿真水域为平坦水域,水深75 m,声速为1 500 m/s且为均匀分布。小尺度接收平台与发射阵的水平距离为3 000 m,其阵元数为2,分别放置于距离水面25 m和26 m处。发射阵布放在距离水面15~45 m处,阵元间距为d=0.3 m,阵元数为101。
由于在浅水环境中,空间分集所能获得的空间处理性能与不同阵元间的信道响应的相关性有关,因此为了分析所提方法的空间处理性能,必须分析信道间的相关性。本文利用相关系数[12]来衡量信道间的相关性。
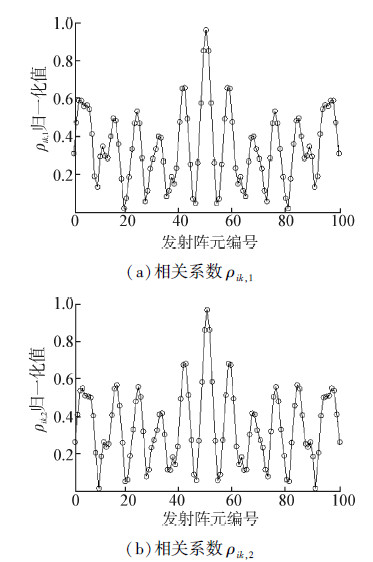
图 2给出了发射阵元间距为d时,以第k=51个发射阵元为参考,hi1(t)(i=1,…,N)与hk1(t)(k=51)之间的相关系数ρik,1,以及hi2(t)与hk2(t)(k=51)之间的相关系数ρik,2。由图 2知,当阵元间距为4d时相关系数相对较低,因此可认为仿真条件下,信道的垂直相关长度为4d。
|
| 图 2 发射阵元与接收阵元间信道的相关系数 Fig. 2 Correlation coefficients of channels between transmitter elements and receiver elements |
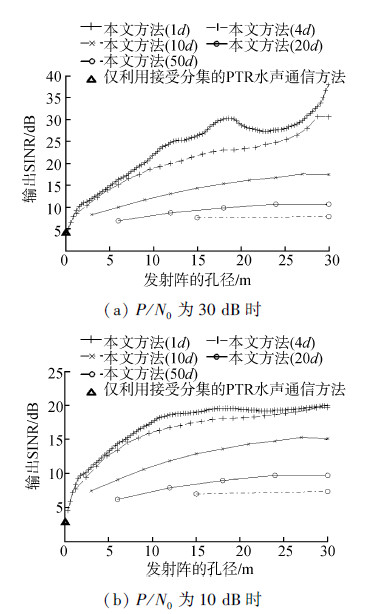
仿真中的信道噪声功率谱密度为N0的高斯白噪声,且与信号互不相关,图 3给出了当单位码元的发射能量P与噪声的功率谱密度N0的比值分别为30 dB和10 dB时,所提方法的SINRc,图中同时用“▲”标出了同等信噪比P/N0条件下,仅使用接收分集的PTR水声通信方法的SINRt。计算SINRc和SINRt时,fij(t)和fj(t)均相对于其最大值进行了归一化。
|
| 图 3 2种通信方法输出SINR Fig. 3 Output SINR of two communication methods |
由图 3知,与仅使用接收分集的PTR水声通信方法相比,由于所提方法利用了发射分集,所以SINRc更高。此外值得注意的是,对于所提方法而言,当发射孔径相同、阵元间距分别为d和4d时,虽然发射阵元数相差较大,但是SINRc的值却非常接近,而当阵元间距增大到10d后,SINRc则出现明显的降低;而当发射阵元数相同时,阵元间距为4d时SINRc最高。这是因为(如图 2所示)仿真环境中信道的垂直相关长度为4d,因此当阵元间距小于4d时,信道间的强相关性会降低发射分集所能提供的空间处理性能,而当阵元间距大于4d时,发射分集所能提供的空间处理性能又受制于实际所用的发射阵元数N。因此在发射阵元数固定的条件下,发射阵元间距等于信道的垂直相关长度时,所提方法能够获得的空间处理性能达到最佳。
3 水池试验验证试验在四壁消声的信道水池内进行,池底为沙底。接收阵由无指向性的标准水听器R1和R2组成,其分别距离水面1 m和2 m。发射阵与接收阵的水平距离为L=6.5 m,由2个无指向性发射换能器T1和T2组成,其中T1距离水面1.5 m,T2距离水面1.7 m。
发射信息码元总数为5 100,码率为2 400 symbol/s,其中,前200个码元用于训练。载波频率为12 kHz,接收端的采样频率为60 kHz。试验中后处理所用的均衡器为直接判决均衡器,采样间隔为符号间隔,抽头数为nt,所用算法为RLS算法,遗忘因子为λ=0.999。
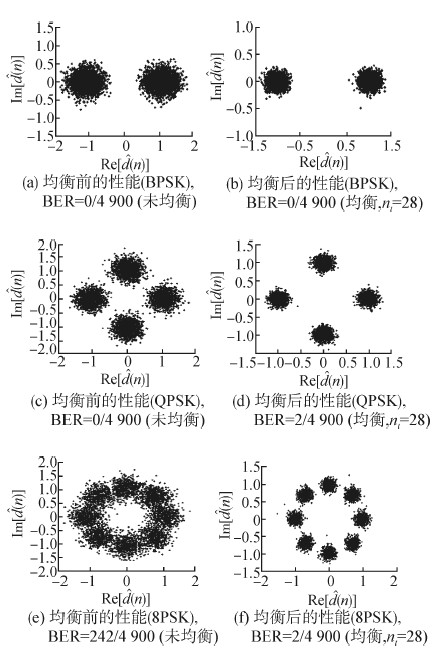
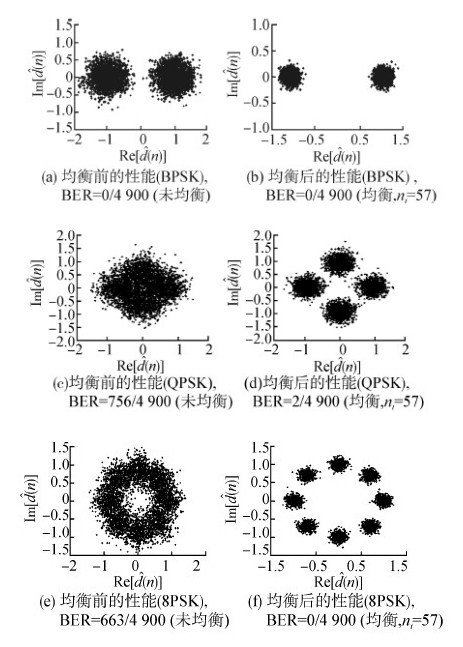
图 4、5分别给出了在接收信噪比为24.0 dB时,本文方法和仅使用接收分集的PTR水声通信方法的试验结果。对比图 4、5的结果可知,在未使用自适应均衡时,与仅使用接收分集的PTR水声通信方法相比,由于所提方法利用发射分集提高了系统的空间处理性能,因此误码率BER更低,星座图分布更好;在自适应均衡处理后,由于所提方法利用发射分集提高了系统的空间处理性能,降低了时反处理后的残余干扰,因此在均衡后的误码率相似的情况下,所提方法所用的均衡器的抽头数降低了一半。
|
| 图 4 所提方法的性能 Fig. 4 Performance of the proposed method |
|
| 图 5 仅使用接收分集的PTR水声通信方法的性能 Fig. 5 Performance of the PTR acoustic communication method exploiting receiver diversity alone |
本文提出了基于TR-STBC的MIMO水声通信方法,阐述了方法的原理,并有针对性地构建了浅海信道模型和水池试验系统对方法的有效性进行了验证。结果表明:
1) 所提方法利用设计的码率为1/2的TR-STBC方案可以使多元发射信号在接收端实现最大比合并,从而获得较高的空间处理性能;
2) 与仅使用接收分集的PTR水声通信方法相比,由于所提方法提高了系统的空间处理性能,因此其误码率和后处理所用自适应均衡器的复杂度更低,通信性能更优;
3) 当发射阵元数固定时,令发射阵元间距等于信道的垂直相关长度,可以使所提方法获得的空间处理性能达到最佳。
下一步工作是开展湖上试验,验证所提方法的稳定性。
| [1] | STOJANOVIC M, PREISIG J. Underwater acoustic communication channels: Propagation models and statistical characterization[J]. IEEE communications magazine, 2009, 47(1): 84-89. |
| [2] | WEN Qian, RITCEY J A. Spatial diversity equalization applied to underwater communications[J]. IEEE journal of oceanic engineering, 1994, 19(2): 227-241. |
| [3] | STOJANOVIC M. Retrofocusing techniques for high rate acoustic communications[J]. Journal of acoustical society America, 2005, 117(3): 1173-1185. |
| [4] | EDELMANN G F, AKAL T, HODGKISS W S, et al. An initial demonstration of underwater acoustic communication using time reversal[J]. IEEE journal of oceanic engineering, 2002, 27(3): 602-609. |
| [5] | ROUSEFF D, JACKSON D R, FOX W L J, et al. Underwater acoustic communication by passive-phase conjugation: Theory and experimental results[J]. IEEE journal of oceanic engineering, 2001, 26(4): 821-831. |
| [6] |
殷敬伟, 张晓, 赵安邦, 等. 时间反转镜在水声通信网上行通信中的应用[J]. 哈尔滨工程大学学报, 2011, 32(1): 1-5. YIN Jingwei, ZHANG Xiao, ZHAO Anbang, et al. The application of a virtual time reversal mirror to upstream communication of underwater acoustic networks[J]. Journal of Harbin engineering university, 2011, 32(1): 1-5. |
| [7] | CHO S E, SONG H C, HODGKISS W S. Asynchronous multiuser underwater acoustic communications (L)[J]. Journal of acoustical society America, 2012, 132(1): 5-8. |
| [8] |
孙琳, 李若, 周天. 基于被动时反的时分复用下行通信研究[J]. 哈尔滨工程大学学报, 2013, 34(10): 1254-1260. SUN Lin, LI Ruo, ZHOU Tian. A research of time division multiplexed downlink communications using passive time reversal[J]. Journal of Harbin engineering university, 2013, 34(10): 1254-1260. |
| [9] | SUN Lin, CHEN Baowei, LI Haisen, et al. Time reversal acoustic communication using filtered multitone modulation[J]. Sensors, 2015, 15(9): 23554-23571. |
| [10] | XIAO Pei, CARRASCO R, WASSELL I. Time reversal space-time block coding for FWA systems[C]//Proceedings of the ICWMC'06 International Conference on Wireless and Mobile Communications. Bucharest: IEEE, 2006: 51. |
| [11] | JAFARKHANI H. Space-time coding: theory and practice[M]. Cambridge: Cambridge University Press, 2005: 45-95. |
| [12] | YANG T C. A study of spatial processing gain in underwater acoustic communications[J]. IEEE journal of oceanic engineering, 2007, 32(3): 689-709. |



