众所周知,由于其简单实用性,马斯京根模型是众多洪水演算模型中应用最为广泛的方法之一,它利用河段水量槽蓄方程代替复杂的水动力方程从而使计算过程极大简化,同时又能取得满足实用的演算精度,从而被国内外广泛应用,在洪水预报和防洪规划中具有重要意义。然而,该方法在实际应用中的一个重要难点即是模型的参数优选问题。Gill[1]采用最小二乘方法求解非线性马斯京根模型的三个参数值;Tung[2]将Hook-Jeeves模式搜索方法分别和线性回归方法、共轭梯度方法、DFP方法相结合应用于马斯京根模型的参数识别问题,得到了较好的结果;Yoon等[3] 讨论了马斯京根模型参数估计的多种方法,如:基于最小二乘方法的线性及非线性回归法、非线性迭代方法、线性规划、二次规划等。但由于马斯京根模型本身的近似性和传统方法的局限性,上述方法较难得到全局最优解。而近些年来,随着各种智能优化算法的发展,其在马斯京根模型参数优化求解问题中的应用逐渐引起了众多专家学者的关注。Mohan[4] 采用遗传算法研究了马斯京根模型参数估计问题,结果显示方法的全局寻优性明显优于上述三种方法,并且不需要严苛的初始值猜测;Kim等[5]和程银才等[6]分别将和声搜索方法和混沌模拟退火方法用于相同问题的求解,确定参数x、n和K,有效地提高了收敛速度和模型精度;袁晓辉等[7]和鲁帆等[8]针对传统遗传算法的不足,分别提出了相应的改进遗传算法,用于非线性马斯京根模型参数估计,得到了较好的结果;马细霞等[9]和Chu等[10]分别提出采用粒子群算法对马斯京根模型参数进行率定,研究结果显示了粒子群算法较好的全局寻优能力。
粒子群优化算法[11] ( particle swarm optimization,PSO )是由Kennedy 和Eberhart等提出的一种基于种群搜索的自适应进化计算技术。该算法具有并行处理和鲁棒性好等特性。它不依赖于问题的具体领域,以粒子群个体作为运算对象,直接以目标函数作为寻优搜索的基本信息,可以使用整个种群的信息,并且占用计算机内存少,尤其适用于求解一些非线性、多参数复杂系统的全局优化问题。但在实际应用中,其存在两个主要的缺点,分别是容易陷入局部收敛和后期收敛速度慢。为了能够有效的解决上述问题,本文提出将小生境思想[12]和粒子群算法结合构造小生境粒子群算法,并将其应用于马斯京根模型的参数反演,同时为了提高方法的抗噪性,在反演过程中,加入了多尺度思想[13],有效提高了反演结果的计算精度,改善了方法的抗噪性。
1 马斯京根模型马斯京根法是河道洪水演算中广泛应用的方法,其采用的基本方程如下:
| $ \left\{ \begin{gathered} \frac{{dW}}{{dt}} = I - Q \hfill \\ W = K\left[ {xI + \left( {1 - x} \right)Q} \right] \hfill \\ \end{gathered} \right. $ | (1) |
该模型的解析解[8]为
| $ {Q_2} = {C_1}{I_1} + {C_2}{I_2} + {C_3}{Q_1} $ | (2) |
式中: I1、I2分别为时段始、末上断面的入流量,Q1为时段始下断面的出流量,Q2为时段末下断面的出流量, ${C_1} = \frac{{Kx + \frac{{\Delta t}}{2}}}{\delta },{C_2} = \frac{{ - Kx + \frac{{\Delta t}}{2}}}{\delta },{C_3} = \frac{{K\left( {1 - x} \right) - \frac{{\Delta t}}{2}}}{\delta },\delta = K\left( {1 - x} \right) + \frac{{\Delta t}}{2},{C_1} \geqslant 0,{C_2} \geqslant 0,{C_3} \geqslant 0$,且C1+C2+C3=1,Δt为演算时段。
式(1)中K值基本上反映的是河道稳定流的传播时间,理论上应随流量的增大而减小,不少实测资料也是这样的;x值反映的是楔蓄在河槽调蓄中的影响,对于某河段,x在洪水涨落的过程中基本稳定;Δt的选取要求摘录的洪水数值能比较真实地反映洪水的变化情况并且不要溜掉洪峰。
对于一个河段,只要确定参数K,x的值和演算时段Δt之后,就可以求出C1、C2、C3,代入式(2),再根据上站流量过程和下站起始流量从而计算出下站的流量过程。
当Δt=2Kx时则C2=0,则式(2)就变成:
| $ {Q_2} = {C_1}{I_1} + {C_3}{Q_1} $ | (3) |
小生境是来自于生物学的一个概念,它是指在特定环境下的一种生存环境,即生物居住生活的小范围或小栖息地。而应用于进化算法中的小生境技术就是把上述概念应用到进化算法中,产生小生境机制。主要的小生境机制有预选择机制(preselection)、排挤机制(crowding)与共享机制(sharing)。小生境技术具有较强的局部搜索能力,能够保持物种的多样性,防止过早收敛。将其与粒子群算法相结合,构造小生境粒子群算法,能够有效的促进粒子群算法跳出局部最优找到全局最优。 本文采用的是基于适应值共享的小生境技术[15]。
2.1 基于适应值共享的小生境粒子群算法小生境共享机制的基本思想为:利用共享函数去判断个体之间相似程度,对适应值进行调整。也就是当适应度值减小时,代表一个个体与其他个体比较相似,反之,当适应度值增大时,代表一个个体与其他个体相似程度较差。按照上述方式进行就可以有效的控制相似个体复制过多,从而形成一种较好的小生境进化环境。
本文的适应度计算基于适应值共享原则,要想实现适应值共享,首先要定义一种距离度量方式。常用的距离度量方式有两种:一种是在参数空间中被广泛采用的欧几里得距离,它也被称作是表现型距离;另一种是在编码空间中被广泛采用的基因距离,它也被称作是海明距离。采用第一种距离方式。
将粒子i与粒子j之间的距离记为符号dij,共享函数的表达式如下:
| $ Sh\left( {{d_{ij}}} \right) = {\left\{ \begin{gathered} 1 - \left( {\frac{{{d_{ij}}}}{\sigma }} \right) \hfill \\ 0,{d_{ij}} \geqslant \sigma \hfill \\ \end{gathered} \right.^\alpha },{d_{ij}} < \sigma $ | (4) |
| $ \sigma = \left( {1/\left( {2{q^{ - \frac{1}{n}}}} \right)} \right)\sqrt {\sum\limits_{k = 1}^n {\left( {x_k^u - x_k^l} \right)} } $ | (5) |
因此,依据上述处理,假如在一个小生境中存在非常多的个体,那么在该小生境中基于适应值共享后的所有个体的适应值会大大的降低,这样就会让那些存在较少个体的小生境能够存在并繁衍。
基于适应值共享原则的小生境粒子群算法优化的基本步骤为:
1)初始化粒子群体为X=X1,X2,…,XN并让其属于可行解范围内,其中每个粒子个体为Xi=(x1,x2,...,xm),其中i=1,2,…,N。设置算法中的参数,如粒子的数量,粒子维数,小生境个数,迭代次数等,再根据公式计算出小生境半径σ;
2)确定小生境种群个体。
首先,令i=1;
其次,计算两个粒子个体的距离dij;
最后,让上述距离dij小于小生境半径σ,进而确定小生境群体;
3)按照粒子群算法对小生境群体进行速度和适应度更新,再对更新后的粒子更新其适应度;
4)计算每个粒子的适应值,保留最优的适应值及个体,检查是否达到优化条件; 如果达到,则结束。否则,进入下一个粒子的小生境群体进行优化;
5)若没有找到最优值,则对每个粒子的小生境群体保留的最优个体组成新的群体空间,重复步骤2)~4)。
2.2 多模态函数优化为验证小生境粒子群算法的有效性,选取表 1所示的四个典型多模态函数作为测试函数,其中,F1为Rastrigrin 函数、F2为Griewangk's函数,F3为Branin函数、F4为Schaffer 函数,它们在自己所在的可行解范围内的全局最优值均为0。
| 函数名称 | 测试函数 | 变量取值范围 |
| F1 | f(x,y)=20+x2-10cos(2πx)+y2-10cos(2πy) | x,y∈[-5.12,5.12] |
| F2 | f(x,y)=(x2+y2)/4000-cos(x)cos(y/ $\sqrt 2 $)+1 | x,y∈[-600,600] |
| F3 | f(x,y)=(1-2y+ $\frac{1}{{20}}$sin(4πy)-x)2+(y-0.5sin(2πx))2 | x,y∈[-10,10] |
| F4 | f(x,y)=((x2+y2)0.25)((sin(50 (x2+y2)0.1)2)+1.0) | x,y∈[-100,100] |
选取的参数设定如下:迭代次数为100,多模态函数优化时的参数范围如表 1所示。对上述函数进行优化时,在基于适应值共享原则的小生境粒子群算法(NPSO)中,选取粒子个数为30,粒子维数为2,小生境个数为4,小生境半径可由式(5)计算求得。同时,采用基本粒子群算法(PSO)对上述4个函数也进行了计算,选取参数和小生境粒子群算法(NPSO)完全一致。为克服算法随机性的影响,所有计算结果都是进行30次计算后的平均结果。迭代寻优结果的对比如表 2和图 1所示。
| 算法函数名 | NPSO | PSO | ||||
| 最优解 | 收敛次数 | 收敛时间/s | 最优解 | 收敛次数 | 收敛时间/s | |
| F1 | 0.0037 | 34 | 2.22×10-4 | 0.066 3 | 37 | 0.55×10-4 |
| F2 | 0.150 7 | 41 | 5.784 7×10-4 | 4.5055 | 41 | 6.637 3×10-4 |
| F3 | 2.61×10-4 | 20 | 1.077 0×10-4 | 0.003 4 | 32 | 1.492 0×10-4 |
| F4 | 3.57×10-5 | 85 | 4.633 0×10-4 | 9.58×10-4 | 81 | 4.208 0×10-4 |
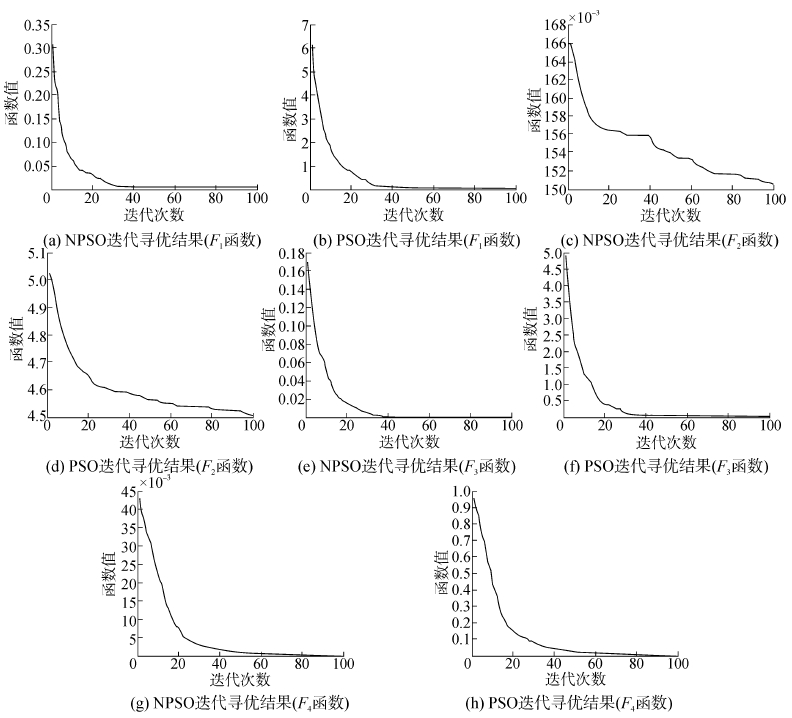
|
| 图 1 NPSO与PSO的迭代寻优结果 Fig. 1 The iterative results of algorithm NPSO and algorithm PSO |
从表 2和图 1中,可以清晰地看到对于四个测试函数,NPSO在解的精确性上都明显高于PSO,而在迭代次数和收敛时间上,前三个测试函数有明显的提升,而对于函数F4则相差不大。总的来说,相比于基本粒子群算法,小生境粒子群算法在全局寻优方面更具有优势。
3 马斯京根模型参数反演首先给出马斯京根模型参数反演的小生境粒子群算法的基本步骤:
算法1:基于适应值共享原则的小生境粒子群算法
1)收集某一河段不同时段流量的实测数据,测量河流中的实测流量值,并将之记为Q2i(m),符号中的m表示该值为实测值,测量时段序号用i表示(i=1,2,…,n)。
2)利用模型(1),计算该河段的流量数据并记为Q2(Δti,x,K),其中Δti为i个不同的时段。
3)这样便得到了不同时段上Q2的计算值与实测值,将他们作差后平方相加得出误差的平方和,形式如下:
| $ J\left( {x,K} \right) = \sum\limits_{i = 1}^n {{{\left( {{Q_2}\left( {\Delta {t_i},x,K} \right) - Q_{2i}^{\left( m \right)}} \right)}^2}} $ | (6) |
4)把J(x,K)作为小生境粒子群算法的适应值函数,适时调整参数x,K,使式(6)达到最小,即可得到参数的全局最优值。
为了检验上述方法的可行性,选取以下算例进行验证。
假设对某均匀河段,在给定不同时段的I1,I2,Q1,K,x后,可由式(2)得到Q2的值,并把它作为实测数据Q2i(m),i=1,2,…,16,如表 3所示。
| Δt(h) | 7.3.2 | 7.3.8 | 7.3.14 | 7.3.20 | 7.4.2 | 7.4.8 | 7.4.14 | 7.4.20 |
| I1/(m3·s-1) | 24266. 69093 | 27766. 69443 | 32900. 03290 | 38733. 37207 | 43166. 70983 | 47133. 38047 | 49933. 38327 | 52033. 38537 |
| I2/(m3·s-1) | 38850. 03885 | 43400. 04340 | 47250. 04725 | 50050. 05005 | 52150. 05215 | 53200. 05320 | 53900. 05390 | 53200. 05320 |
| Q1/(m3·s-1) | 22015. 02202 | 23030. 02303 | 24920. 02492 | 27790. 02779 | 30940. 03094 | 34720. 03472 | 38850. 03885 | 42350. 04235 |
| Q2i(m)=Q2/(m3·s-1) | 27790. 02779 | 30880. 03087 | 34720. 03472 | 38840. 03884 | 42240. 04223 | 45320. 04532 | 47900. 04790 | 49600. 04960 |
| Δt(h) | 7.5.2 | 7.5.8 | 7.5.14 | 7.5.20 | 7.6.2 | 7.6.8 | 7.6.14 | 7.6.20 |
| I1/(m3·s-1) | 54153. 43654 | 57015. 32658 | 61235. 78542 | 64256. 23263 | 67365. 30254 | 70124. 32654 | 74136. 69841 | 77562. 36254 |
| I2/(m3·s-1) | 54296. 58946 | 56324. 12458 | 55216. 21654 | 59126. 02541 | 62154. 65402 | 65847. 31042 | 70125. 36985 | 75584. 26589 |
| Q1/(m3·s-1) | 46326. 203145 | 49325. 65487 | 54897. 23645 | 58125. 69587 | 62145. 35421 | 66859. 03248 | 70926. 65298 | 74326. 56984 |
| Q2i(m)=Q2/(m3·s-1) | 51957. 98498 | 54620. 79123 | 57704. 89461 | 61038. 87721 | 64385. 13201 | 67969. 38077 | 72073. 44870 | 76072. 67987 |
依据上述模型分别对槽蓄系数K、流量比重因子x进行了反演,其真值为K=18,x=0.1。
算法参数设定如下:粒子数量为30,迭代次数为100次,小生境个数为4个,粒子维数为1,小生境半径可由式(5)计算求得。为克服算法随机性的影响,所有计算结果都是进行30次计算后的平均结果。参数K和x的反演结果如表 4所示,从表中可以看到在待反演参数初始范围分别是5≤K≤25和0≤x≤0.5时,反演结果精度很高,和真值的相对误差达到了分别达到了10-8和10-6数量级,反演值和真值几乎完全吻合。为了验证所提算法的抗扰动性,在加噪5%的情况下对两个参数进行反演。加噪方式为:Q2i(m)*=Q2i(m)*1+δ×random,其中δ=0.05,random为满足标准正态分布的随机数。其他参数的选择和上述算例相同,反演结果见表 5,从表中可以看到在添加了5%的噪声后,反演结果精度大幅下降,和真值的相对误差分别达到了21%和36%,显示了单纯的小生境粒子群算法在抗噪性方面的不足。
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% | 收敛代数 | 收敛计算时间/s |
| K | 17.999 999 998 654 21 | 18 | 1.345 789 968×10-8 | 7.476 610 935×10-8 | 8 | 0.0010223 |
| x | 0.100 000 001 568 | 0.1 | 1.567 999 994×10-9 | 1.567 999 994×10-6 | 65 | 0.001 209 |
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% | 收敛代数 | 收敛计算时间/s |
| K | 14.156 329 852 014 1 | 18 | 3.843 670 1 47 985 900 | 21.353 72 3 044 366 1 | 5 | 0.001 523 5 |
| x | 0.136 154 8 65 289 32 | 0.1 | 0.036 154 865 289 32 | 36.154 8 65 289 32 | 45 | 0.000 956 4 |
为了进一步提高算法的抗噪性,将多尺度反演策略和小生境粒子群算法相结合,提出了多尺度小生境粒子群算法。其主要求解思路如下:
算法2:多尺度小生境粒子群算法
1) 将算法1中的实测值Q2i(m)进行多尺度分解,得到不同尺度下的子实测值Q(mj)2i,j=1,2,…N,其中N为最粗糙分解尺度;
2)设定待反演参数初始选择区间(15≤K≤25和0≤x≤0.5),以最粗糙尺度为起始尺度,采用小生境粒子群算法求解,目标函数为
$$ J\left( {x,K} \right) = \sum\limits_{i = 1}^n {{{\left( {{Q_2}\left( {\Delta {t_i},x,K} \right) - Q_{2i}^{\left( {{m_N}} \right)}} \right)}^2}} $$3)将尺度加细,依据上一尺度的反演结果来确定下一尺度的待反演参数区间。具体来说即是:采用二分法将上一尺度的待反演参数区间划分为两等份,判断上一尺度的反演结果落在哪一个子区间,以包含反演结果的子区间作为下一尺度的待反演参数区间;
4)在较细尺度下,采用小生境粒子群算法求解,目标函数为
$$ J\left( {x,K} \right) = \sum\limits_{i = 1}^n {{{\left( {{Q_2}\left( {\Delta {t_i},x,K} \right) - Q_{2i}^{\left( {{m_j}} \right)}} \right)}^2}} $$5)重复上述步骤3)和4)直至最精确的尺度,得到最终反演结果。
在加噪5%的情形下,将多尺度小生境粒子群算法应用于马斯京根模型的参数反演。尺度分解工具选用Matlab小波工具箱中的相关命令(尺度分解函数:wavedec,系数提取函数:appcoef,信号重构函数:wrcoef),分解及重构基函数选用Daubechies小波,本文中分解为5个尺度。参数反演结果如表 6和表 7所示。表 6是槽蓄系数K和流量比重因子x的最终反演结果。从表 6中可以看到两个参数的计算精度都有了较好的提升,和真值的相对误差分别由21%提升到了4%和由36%提升到了接近10%。表 7给出了在各个不同尺度下的反演结果。从表 7中可以看到随着尺度的减小,反演结果的精度在不断的改善。但需要引起注意的是,在槽蓄系数K的多尺度反演过程中,最好的反演结果并没有出现在原始尺度,而是出现在了第四层,因此在多尺度算法的实现过程中,要留意保留不同尺度下的数值计算结果,并通过最终比较给出最好的反演值。
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% | 收敛计算时间/s |
| K | 17.265 98 5 522 201 4 | 18 | 0.734 014 477 798 6 | 4.077 858 209 992 22 | 0.014 067 12 |
| x | 0.109 895 422 566 3 | 0.1 | 0.009 895 422 566 3 | 9.895 4 22 566 3 | 0.0272 99 |
| 参数名称 | 层数 | 区间 | 反演值 | 反演时间 |
| K | 5 | (15,25) | 16.236 598 974 111 2 | 0.002 356 |
| 4 | (15,20) | 16.956 665 984 158 4 | 0.002 958 | |
| 3 | (15,17.5) | 17.023 658 954 555 2 | 0.003 026 5 | |
| 2 | (16.25,17.5) | 17.265 985 522 201 4 | 0.003 156 8 | |
| 1 | (16.875,17.5) | 17.236 598 528 688 52 | 0.002 569 82 | |
| x | 5 | (0,0.5) | 0.155 252 314 368 | 0.007 256 |
| 4 | (0,0.25) | 0.124 563 255 822 | 0.005 344 | |
| 3 | (0,0.125) | 0.120 895 241 411 | 0.006 235 | |
| 2 | (0.0625,0.125) | 0.115 956 258 478 | 0.005 896 | |
| 1 | (0.09375,0.125) | 0.109 895 422 566 | 0.002 568 |
算法参数设定如下:粒子数量为30,迭代次数为100次,小生境个数为4个,粒子维数为2。同样的,为克服算法随机性的影响,所有计算结果也都是进行30次计算后的平均结果。同时对参数K和x进行反演,待反演参数初始范围分别是5≤K≤25和0≤x≤0.2,反演结果如表 8所示,从表中可以看到反演结果精度较高,相对误差可以控制在4%之内。表 9给出了在对实测值添加5%的噪声情形下,采用小生境粒子群算法得到的反演结果,结果显示反演的精度明显降低,参数K的相对误差达到了5%以上,参数x的相对误差达到18%以上。表 10给出了结合了多尺度策略后的反演结果,两个参数反演值的精度都有所提高,和真值的相对误差分别达到了3.08%和13.26%。反演结果显示相比于单参数反演,双参数反演的多尺度小生境粒子群算法的抗噪性有所欠缺,这还有待于进一步研究。
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% |
| K | 17.906 2 36 152 2 | 18 | 0.093 763 8 47 799 998 | 0.520 910 265 555 5 |
| x | 0.096 0 36 258 4 | 0.1 | 0.003 963 7 41 600 000 | 3.963 741 6 |
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% |
| K | 18.995 6 82 143 2 | 18 | 0.995 682 1 43 200 000 | 5.531 567 462 222 2 |
| x | 0.118 56 4 215 52 | 0.1 | 0.018 56 4 215 52 | 18.564 215 52 |
| 参数名称 | 反演值 | 真值 | 绝对误差 | 相对误差/% |
| K | 17.445 523 621 | 18 | 0.554 476 379 | 3.080 42 43 277 778 |
| x | 0.113 256 3487 | 0.1 | 0.013 256 3487 | 13.256 348 7 |
1)本文将基于适应值共享原则的小生境策略与传统粒子群算法相结合,提出了一种改进粒子群算法—小生境粒子群算法,并应用于基于马斯京根模型的参数反演中。通过对槽蓄系数和流量比重因子进行单参数和双参数反演计算实验,结果显示:如果不考虑噪声的话,小生境粒子群算法具有理想的计算精度和收敛速度。单参数的反演值和真值的相对误差可以达到10-6,和真值几乎完全吻合;双参数的反演结果的相对误差也可以控制在4%之内。但是,该方法的抗噪性却是不甚理想。
2)为进一步提高算法的抗噪性,将基于小波多分辨分析的多尺度反演策略和小生境粒子群算法相结合构造了多尺度小生境粒子群算法,并将之应用于带有5%随机噪声的马斯京根模型参数反演,使反演结果的精度得到了明显的改善,有效的提升了小生境粒子群算法的抗噪性。
3)数值模拟实验显示提出的小生境粒子群算法能够有效的改善传统粒子群算法的全局寻优性,而多尺度反演策略的加入能够有效的改进算法的抗噪性。因此在进行实际河道洪水演进计算时,两者结合所构造的多尺度小生境粒子群算法能够为马斯京根模型的参数估计问题提供一种高效的计算方法。
| [1] | GILL M A. Flood routing by the Muskingum method[J]. Journal of Hydrology, 1978, 36(3/4): 353-363. |
| [2] | TUNG Y K. River flood routing by nonlinear Muskingum method[J]. Journal of hydraulic engineering, 1985, 111(12): 1447-1460. |
| [3] | YOON J, PADMANABHAN G. Parameter estimation of linear and nonlinear Muskingum models[J]. Journal of water resources planning and management, 1993, 119(5): 600-610. |
| [4] | MOHAN S. Parameter estimation of nonlinear Muskingum models using genetic algorithm[J]. Journal of hydraulic engineering, 1997, 123(2): 137-142. |
| [5] | KIM J H, GEEM Z W, KIM E S. Parameter estimation of the nonlinear Muskingum model using harmony search[J]. Journal of the American Water Resources Association, 2001, 37(5): 1131-1138. |
| [6] |
程银才, 李明华, 范世香. 非线性马斯京根模型参数优化的混沌模拟退火法[J]. 水电能源科学, 2007, 25(1): 30-33. CHENG Yincai, LI Minghua, Fan Shixiang. Application of Chaotic simulated annealing algorithm to parameter optimization of nonlinear Muskingum model[J]. Water resources and power, 2007, 25(1): 30-33. |
| [7] |
袁晓辉, 张双全, 张勇传, 等. 非线性马斯京根模型参数率定的新方法[J]. 水利学报, 2001, 32(5): 77-81. YUAN Xiaohui, ZHANG Shuangquan, ZHANG Yongchuan, et al. Parameter estimation of nonlinear Muskingum Model using mixed genetic algorithm[J]. Journal of hydraulic engineering, 2001, 32(5): 77-81. |
| [8] |
鲁帆, 蒋云钟, 王浩, 等. 多智能体遗传算法用于马斯京根模型参数估计[J]. 水利学报, 2007, 38(3): 289-294. LU Fan, JIANG Yunzhong, WANG Hao, et al. Application of multi-agent genetic algorithm to parameter estimation of Muskingum model[J]. Journal of hydraulic engineering, 2007, 38(3): 289-294. |
| [9] |
马细霞, 舒丹丹, 黄渝桂. 基于PSO的非线性马斯京根模型参数率定新方法[J]. 郑州大学学报: 工学版, 2007, 28(4): 122-125. MA Xixia, SHU Dandan, HUANG Yugui. Parameter estimation method of nonlinear Muskingum model based on PSO[J]. Journal of Zhengzhou University: engineering science, 2007, 28(4): 122-125. |
| [10] | CHU H J, CHANG L C. Applying particle swarm optimization to parameter estimation of the nonlinear Muskingum model[J]. Journal of hydrologic engineering, 2009, 14(9): 1024-1027. |
| [11] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, WA: IEEE, 1995: 1942-1948. |
| [12] | HUTCHINSON G E. Concluding remarks[J]. Cold spring harbor symposium on quantitative biology, 1957, 22: 415-427. |
| [13] | ZHANG Xinming, ZHOU Chaoying, LIU Jiaqi, et al. Multiparameter identification of fluid-saturated porous medium with the wavelet multiscale method[J]. Journal of porous media, 2009, 12(3): 255-264. |
| [14] | GOLDBERG D E, RICHARDSON J. Genetic Algorithms with sharing for multimodal function optimization[C]//Proceedings of the 2nd International Conference on Genetic Algorithms on Genetic Algorithms and Their Application. Hillsdale: Lawrence Erlbaum Associates, 1987: 41-47. |



