可回转双桨电力推进船舶是一种新型电力推进船舶,区别于常规的尾轴推进船舶的是其动力和舵向均由推进电机提供。由于取消了船舵,可回转螺旋桨在船舶作回转运动时通过桨的回转或桨的转速差(推力差)产生不同的舵效,即可看作船舶的“等效舵”,因此研究在此“等效舵”作用下电力推进船舶的运动具有实用价值和现实意义。
对于艉轴电力推进船舶,其运动模型可从单桨单舵船舶的运动模型扩展而来。例如可以通过研究单桨单舵运动模型和船模试验得到了双桨双舵船舶运行参数,并据此提出了适合双桨双舵船舶的运动数学模型[1, 2]。双桨双舵船舶的操纵性能也是研究的重点,比如其系泊操纵试验研究,静水中的操纵运动模型数值模拟等[3, 4, 5, 6]。
但是,电力推进船舶的可回转螺旋桨推进与常规艉轴推进方式有着根本性的区别。在可回转双桨作用下,船舶的推进运动与回转运动高度耦合,双桨的回转作用产生舵效;而双桨不作回转,但在双桨转速(推力)不等时也将产生舵效,给船舶的操纵控制带来了难度。这方面的研究未见有公开文献报道。
本文根据船舶分离型运动建模方法,建立了可回转双桨船舶的运动方程,分析船舶常规舵受力情况,导出了可回转双桨作用下的船舶等效舵效模型。
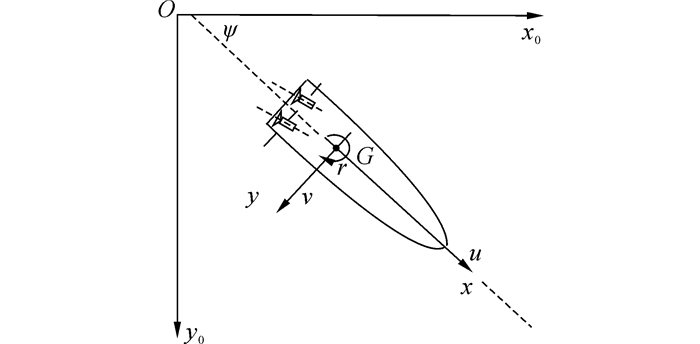
1 可回转双桨作用下的船舶运动设固定坐标系O-x0y0z0,船舶运动坐标系G-xyz固定于船舶上,以船舶质心G作为原点,随船舶运动而运动,如图 1所示。
|
| 图 1 固定坐标系O-x0y0z0和运动坐标系G-xyz Fig. 1 Fixed coordinates system O-x0y0z0and moving coordinates systemG-xyz |
若仅考虑船舶的水平面运动(纵荡、横荡和艏摇),根据MMG的研究方法[7],将作用于船舶的外力分离开来表示,则船舶运动方程可以表示为
| $\left\{ \begin{array}{l} \left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)rv = {X_H} + {X_P}\\ \left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ru = {Y_H} + {Y_P}\\ \left( {{I_z} + {J_z}} \right)\dot r = {N_H} + {N_P} \end{array} \right.$ | (1) |
式中:XP、YP和NP分别为推进器(螺旋桨)作用于船舶的前进力、横移力和转船(艏摇)力矩,XH、YH和NH分别为除推进器外作用于船舶的其他一切外力(风浪流等),m为船舶质量,mx和my分别为运动坐标系x轴和y轴上的附加质量,Iz和Jz分别为船舶绕z轴的转动惯量和附加转动惯量,u和v分别为船舶在x轴和y轴方向上的速度(前进速度和横移速度),r为船舶绕z轴的转船角速度(艏摇角速度)。
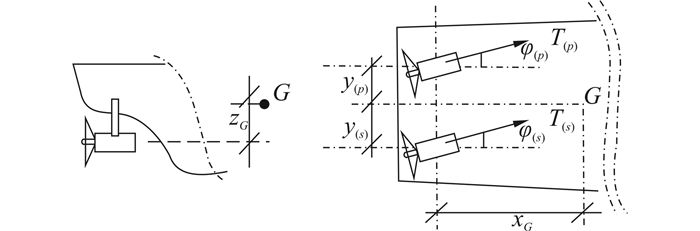
对于电力推进船舶,以可回转螺旋桨替代艉轴固定螺旋桨及其常规舵,实现了桨舵合一,通常将回转双螺旋桨左、右舷对称布置于船艉,如图 2所示。左、右舷可回转螺旋桨立柱平面距船舶重心G处距离为xG;船舶重心与两个螺旋桨轴系所处平面的垂直距离为zG,距船舶艏艉线距离为yP;xG/yP=Kxy定义为结构系数。
|
| 图 2 可回转双桨船舶 Fig. 2 Rotatable twin-propeller ship |
设下标(P)和(S)为左、右舷推进螺旋桨,桨盘面直径为D,由此产生在螺旋桨轴向方向上的推力T(P)和T(S)为
| $\left\{ \begin{array}{l} {T_{\left( P \right)}} = \rho n_{\left( P \right)}^2{D^4}{k_{{T_{\left( P \right)}}}}\\ {T_{\left( S \right)}} = \rho n_{\left( S \right)}^2{D^4}{k_{{T_{\left( S \right)}}}} \end{array} \right.$ | (2) |
式中:r为水密度;n(P)和n(S)分别为螺旋桨转速;kT(P)和kT(S)分别为螺旋桨推力系数,它是进速系数的函数,由经验公式给出。设左、右桨水平回转角分别为j(P)和j(S)(顺时针为正),根据图 2所示的关系,可以得到螺旋桨推力在运动坐标系G-xyz上的投影分量[8]。对于左桨(P)有
| $\left\{ \begin{array}{l} {X_{\left( P \right)}} = \left( {1 - {t_{\left( P \right)}}} \right){T_{\left( P \right)}}\cos {\varphi _{\left( P \right)}}\\ {Y_{\left( P \right)}} = \left( {1 - {d_{Y\left( P \right)}}} \right){T_{\left( P \right)}}\sin {\varphi _{\left( P \right)}}\\ {N_{\left( P \right)}} = \left( {1 - {d_{N\left( P \right)}}} \right){T_{\left( P \right)}}\left( { - {y_{\left( P \right)}}\cos {\varphi _{\left( P \right)}} + {x_G}\sin {\varphi _{\left( P \right)}}} \right) \end{array} \right.$ | (3) |
式中:t(P)为左桨推力在x轴方向上的常规推力减额系数;dY(P)和dN(P)是左桨作为船舶附体对横漂力和转船力矩的影响系数,可以通过试验给出。同理,对于右桨(S)有:
| $\left\{ \begin{array}{l} {X_{\left( S \right)}} = \left( {1 - {t_{\left( S \right)}}} \right){T_{\left( S \right)}}\cos {\varphi _{\left( S \right)}}\\ {Y_{\left( S \right)}} = \left( {1 - {d_{Y\left( S \right)}}} \right){T_{\left( S \right)}}\sin {\varphi _{\left( S \right)}}\\ {N_{\left( S \right)}} = \left( {1 - {d_{N\left( S \right)}}} \right){T_{\left( S \right)}}\left( { - {y_{\left( S \right)}}\cos {\varphi _{\left( S \right)}} + {x_G}\sin {\varphi _{\left( S \right)}}} \right) \end{array} \right.$ | (4) |
式中:t(S)为右桨推力在x轴方向上的常规推力减额系数;dY(S)和dN(S)是右桨作为船舶附体对横漂力和转船力矩的影响系数,可以通过试验给出[6]。
合并式(3)和(4),若双桨结构相同,对称安装,则t(S)=t(P)=tP、dY(S)=dY(P)=dYP、dN(S)=dN(P)=dNP、y(S)=y(P)=yP于是得到左、右双桨同时作用下的船体运动控制力:
| $\left\{ \begin{array}{l} {X_P} = {X_{\left( S \right)}} + {X_{\left( P \right)}} = \left( {1 - {t_P}} \right) \cdot \\ \;\;\;\;\;\;\;\left( {{T_{\left( S \right)}}\cos {\varphi _{\left( S \right)}} + {T_{\left( P \right)}}\cos {\varphi _{\left( P \right)}}} \right)\\ {Y_P} = {Y_{\left( S \right)}} + {Y_{\left( P \right)}} = \left( {1 - {d_{YP}}} \right) \cdot \\ \;\;\;\;\;\;\;\left( {{T_{\left( S \right)}}\sin {\varphi _{\left( S \right)}} + {T_{\left( P \right)}}\sin {\varphi _{\left( P \right)}}} \right)\\ {N_P} = {N_{\left( S \right)}} + {N_{\left( P \right)}} = \left( {1 - {d_{NP}}} \right) \cdot \\ \;\;\;\;\;\;\;\left( {{T_{\left( S \right)}}\left( {{y_P}\cos {\varphi _{\left( S \right)}} + {x_G}\sin {\varphi _{\left( S \right)}}} \right) + } \right.\\ \;\;\;\;\;\left. {{T_{\left( P \right)}}\left( { - {y_P}\cos {\varphi _{\left( P \right)}} + {x_G}\sin {\varphi _{\left( P \right)}}} \right)} \right) \end{array} \right.$ | (5) |
式中:tP为运动坐标系x方向的常规推力减额系数,且tP=t(P)+t(S)。
由式(5)可知,船舶在左、右桨推进力T(P)和T(S)作用下,由于左、右桨回转,产生在y方向上的分力T(P)sinj(P)和T(S)sinj(S),造成船舶横漂。由于左、右桨回转以及推力不等而产生舵效,即使螺旋桨不作回转(概念上的不动舵)j(P)=j(S)=0,但当左、右螺旋桨转速不同n(P)≠n(S)时,也将产生实际舵效(转船力矩),使船舶航向发生改变。
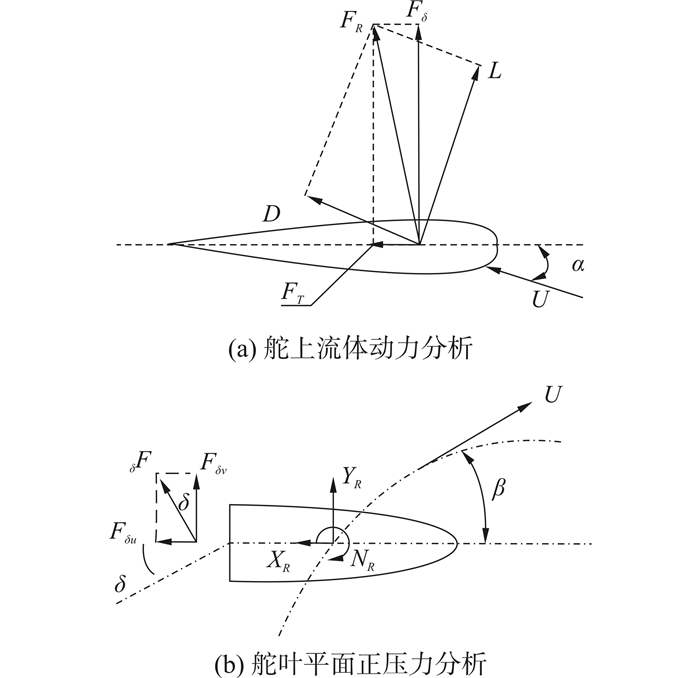
2 船舶常规舵的作用力分析采用全回转双桨推进方式的船舶是通过双桨回转以及通过双桨转速差实现其转船运动的。先就常规单舵进行研究分析,进而结合电力推进无舵双桨实际操控情况,推导出“等价舵”的概念,即通过对双桨的控制实现操舵效果,图 3所示为常规单舵的受力分析图。
|
| 图 3 常规舵效分析 Fig. 3 Traditional rudder analyse 注:U-水流方向上的流速,a-冲角,D-沿流速方向的阻力,L-垂直于流速方向的升力,FR-舵上产生的流体动力,Fd-舵叶平面的正压力,FT-沿舵叶平面的切向力。 |
舵叶平面正压力为
| ${F_\delta } = {C_\delta }\rho {A_R}{U^2}/2$ | (6) |
式中:Cδ为正压力系数,可由升力系数[9]计算得
| ${C_\delta } = \frac{{\partial {C_L}}}{{\partial \alpha }}\left| {_{\alpha = 0}} \right. \cdot \sin \alpha $ | (7) |
式中:升力系数为CL=2L/ρU2AR,于是有
| ${F_\delta } = \frac{1}{2}\rho {A_R}U_A^2{f_\alpha }\sin \alpha $ | (8) |
式中:水流方向与舵叶之间的夹角(冲角)a,在敞水中等同于舵角a=d;fa为升力系数在a =0时的斜率,可由近似公式计算;uA为流速,当水流方向并行于船的艏艉线时,流速等同于船的前进速度uA= U;r为水密度;AR为舵面积。
不考虑横摇运动的影响,将Fd分解为在X、Y、N上的分量XR、YR、NR:
| $\left\{ \begin{array}{l} {X_R} = - {F_\delta }\sin \delta \\ {Y_R} = \left( {1 + {d_{YR}}} \right){F_\delta }\cos \delta \\ {N_R} = \left( {1 + {d_{NR}}} \right){x_R}{F_\delta }\cos \delta \end{array} \right.$ | (9) |
式中:d 为舵角;dYR和dNR是舵作为船舶附体对横漂力和回转力矩的影响系数,可以通过试验给出;xR为舵柱至船舶质心G的水平距离。
式(9)表示了常规舵作用于船舶的控制力和力矩,船舶转动舵后,舵力在x方向(船艏向)上的分量XR,表现为对船的阻力,使船舶前进速度降低;而在y方向上的分量YR,造成船舶横漂;产生的NR为回转力矩,它直接影响船舶运动的操纵性和稳定性。
从船舶操纵性角度看,舵桨合一的可回转双桨电力推进船舶实施转船操作或进行航向控制时,主要根据式(5)中的第3式。根据相似性原理,考察常规舵作用的式(9)中的第3式,应使二者相等,即
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\left( {1 + {d_{NR}}} \right){x_R}{F_\delta }\cos \delta = \\ \left( {1 + {d_{NR}}} \right)\left( {{T_{\left( P \right)}}\left( { - {y_P}\cos {\varphi _{\left( P \right)}} + {x_G}\sin {\varphi _{\left( P \right)}}} \right)} \right. + \\ \left. {\;\;\;\;\;\;{T_{\left( S \right)}}\left( {{y_P}\cos {\varphi _{\left( S \right)}} + {x_G}\sin {\varphi _{\left( S \right)}}} \right)} \right) \end{array}$ | (10) |
将式(2)和式(6)的关系代入到式(8)中,整理得
| $\begin{array}{l} \sin \left( {2\delta } \right) = {K_B}\frac{1}{{u_A^2}}\left( {n_{\left( P \right)}^2{k_{T\left( P \right)}}\left( { - \frac{{{y_P}}}{{{x_G}}}\cos {\varphi _{\left( P \right)}} + \sin {\varphi _{\left( P \right)}}} \right)} \right. + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {n_{\left( S \right)}^2{k_{F\left( S \right)}}\left( {\frac{{{y_P}}}{{{x_G}}}\cos {\varphi _{\left( S \right)}} + \sin {\varphi _{\left( S \right)}}} \right)} \right) \end{array}$ | (11) |
式中:${K_B} = \frac{{4\left( {1 + {d_{NP}}} \right){D^4}}}{{\left( {1 + {d_{NR}}} \right){A_R}{f_\alpha }}}$为等效系数,其中fα=$\frac{{6.13\lambda }}{{2.25 + \lambda }}$,λ∈[0.5,3.0]。
船舶在给定航向定速航行时,双桨在回转角不大的情况下,角的正弦和余弦可以近似为sina ≈a和cosa ≈1-a2/2。令螺旋桨基准转速为n=(n(S)+n(P))/2,基准推力系数为kT=(kT(S) +kT(P))/2,流速uA= u,于是有
| $\begin{array}{l} \delta \approx \frac{1}{2}{K_B}{k_T}\left( {^)2\left( {\frac{{{y_P}}}{{{x_G}}}\left( {{i_{\left( S \right)}} - {i_{\left( P \right)}}} \right) - \frac{{{y_P}}}{{{x_G}}}\left( {{i_{\left( S \right)}}\varphi _{\left( S \right)}^2 - } \right.} \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {{i_{\left( P \right)}}\varphi _{\left( P \right)}^2} \right)/2 + \left( {{i_{\left( S \right)}}{\varphi _{\left( S \right)}} + {i_{\left( P \right)}}{\varphi _{\left( P \right)}}} \right)} \right) \end{array}$ | (12) |
式中:${i_{\left( S \right)}} = \frac{{n_{\left( S \right)}^2{k_{T\left( S \right)}}}}{{{n^2}{k_F}}}$和${i_{\left( P \right)}} = \frac{{n_{\left( P \right)}^2{k_{T\left( S \right)}}}}{{{n^2}{k_F}}}$定义为左、右舷螺旋桨对于基准推力下的相对推力值。
在左、右舷螺旋桨转速相差不大的情况下,认为推力系数近似相等kT(S) ≈ kT(P) = kT ,则i(S)≈n(S)2/n2,i(P)≈n(P)2/n2,即相对推力值简化为基准转速下的相对转速值。
3 可回转双桨的等价舵效通过对等效舵效的分析,根据式(12)的等价舵效表达式,讨论以下4种典型工况。
3.1 双桨同回转且转速相等当双桨同时回转j(S)=j(P)=jP,且转速相等n(S)=n(P)=nP时,i(S)=i(P)=iP,此时等价舵效的表达较为简洁,由式(10)简化得到
| $\delta \approx {K_B}{k_T}{\left( {n/u} \right)^2}{\varphi _P}{i_P}$ | (13) |
式(11)表明,双桨同回转且转速相等时,舵效值的大小仅决定于双桨的回转角jP及其推力值iP(转速值)。等价舵效是双桨推力和回转角共同作用的结果,在双桨推力一定(转速一定)情况下,回转角jP(-p/2 < jP < p/2)的绝对值愈大,舵效愈显著;而在回转角一定情况下,双桨推力愈大,舵效愈显著。
可回转双桨的电力推进船舶在正常运行工况时,均为左、右桨转速相同(推力值相等),通过双桨同时回转实现转船操作(或航向控制)。
3.2 双桨不回转但转速不相等如果双桨不作回转j(S)=j(P)=0,但转速不相等n(S)≠n(P)时,i(S)≠i(P)。由式(10)简化得到的等价舵效为
| $\delta \approx \frac{1}{2}{K_B}{k_T}{\left( {\frac{n}{u}} \right)^2}\frac{{{y_P}}}{{{x_G}}}\left( {{i_{\left( S \right)}} - {i_{\left( P \right)}}} \right)$ | (14) |
式(14)表明,即使在双桨不作回转情况下,由于双桨的转速值不相等而造成双桨的推力不等,同样会产生舵效,且此时的等价舵效与双桨的转速差(推力差)成正比。
当i(P) < i(S),即右舷螺旋桨转速(推力)大于左舷螺旋桨时,舵效值d为正(顺时针),相当于打左舵;反之,当i(P)>i(S) 时,舵效值d为负(逆时针),相当于打右舵。
电力推进船舶的另一种推进方式——双桨固定艉轴推进方式,可以看作是上述可回转双桨推进方式在双桨不作回转(即回转角为零)情况下的特例。由此说明,在桨舵独立的双桨固定艉轴推进方式下,左、右螺旋桨的转速不相等将形成舵效,为了保持给定航向,必须通过压舵来消除此不希望的舵效,而压舵的舵角值正是式(14)所获得的等价舵效值。
3.3 仅单桨回转但转速相等当双桨非同时回转仅单浆回转,此时j(S)≠0、jP=0,或j(S) =0、 jP≠0,双桨转速相等n(S)=n(P)= nP≠0时,i(S)=i(P)=iP。由式(10)得到的等价舵效为
| $\left\{ \begin{array}{l} \delta \approx \frac{1}{2}{K_B}{k_T}{\left( {\frac{n}{u}} \right)^2}\left( {\frac{1}{2}\frac{{{y_P}}}{{{x_G}}}\varphi _{\left( P \right)}^2{i_P} + {\varphi _{\left( P \right)}}{i_P}} \right)\\ \left( {{\varphi _{\left( S \right)}} = 0,{\varphi _{\left( P \right)}} \ne 0} \right)\\ \delta \approx - \frac{1}{2}{K_B}{k_T}{\left( {\frac{n}{u}} \right)^2}\left( {\frac{1}{2}\frac{{{y_P}}}{{{x_G}}}\varphi _{\left( S \right)}^2{i_P} + {\varphi _{\left( S \right)}}{i_P}} \right)\\ \left( {{\varphi _{\left( P \right)}} = 0,{\varphi _{\left( S \right)}} \ne 0} \right) \end{array} \right.$ | (15) |
式(15)所表示的等价舵效值大小决定于双桨 的回转角j(S)或j(P)及其推力值iP(转速值)。
3.4 仅单桨作用特别当其中一桨因故停机,转速为零时,成为单 桨运行状态,此时n(S)≠ 0,n(P)=0或n(S)=0,n(P)≠0,即仅有一桨可回转且转速不为零,此工况 可看作为上一工况的特例,此时等效舵效为
| $\left\{ \begin{array}{l} \delta \approx - \frac{1}{2}{K_B}{k_T}{\left( {\frac{n}{u}} \right)^2}\frac{{{y_P}}}{{{x_G}}}{i_{\left( P \right)}}\;\;\;\;\left( {{n_{\left( S \right)}} = 0,{n_{\left( P \right)}} \ne 0} \right)\\ \delta \approx \frac{1}{2}{K_B}{k_T}{\left( {\frac{n}{u}} \right)^2}\frac{{{y_P}}}{{{x_G}}}{i_{\left( S \right)}}\;\;\;\;\;\left( {{n_{\left( P \right)}} = 0,{n_{\left( S \right)}} \ne 0} \right) \end{array} \right.$ | (16) |
根据简化的等价舵效表达式(12),以及式(1)的船舶运动方程,对可回转双桨电力推进船舶的等价舵效及其转船操纵进行计算机数值仿真试验。仿真实船数据取自一艘内河216客位电力推进客渡轮,主要参数:船长36.00m,型宽8.40m,型深1.90m,吃水1.10m,排水量120t,额定航速10kn,推进电动机额定功率2×90kW。
电力推进仿真参数:双机双桨可回转推进系统,四叶定距桨,盘面直径0.90m,额定转速500r/m,双桨立柱间距5.60m,重心距螺旋桨回转立柱距离15.2m,最大回转角±30°。
根据文献[10]的计算公式,船舶x轴附加质量mx=21.32t,y轴附加质量my=0.58t,船舶绕z轴转动惯量Iz=19707.1kg·m2,附加转动惯量Jz=713.477 kg·m2。等效系数取值范围KB∈[0.476,1.494],此处可取为1。
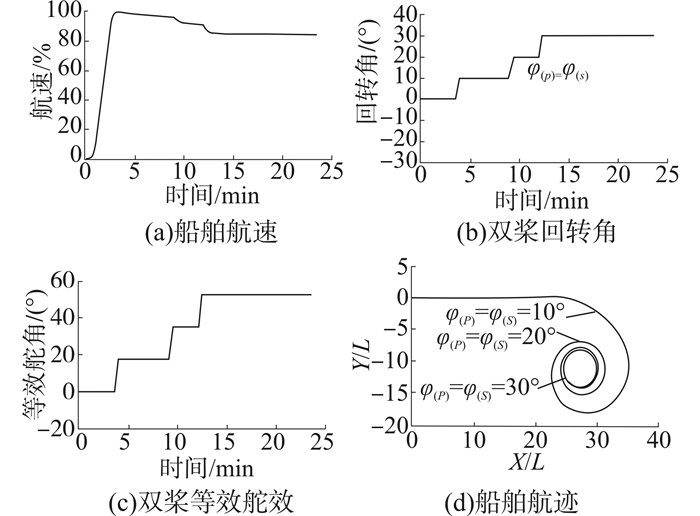
4.1 双桨同回转且转速相等此时双桨同时回转j(S)=j(P)=jP,且转速相等n(S)=n(P)=nP时,i(S)=i(P)=iP,特别地当双桨回转角等于零时,其运动轨迹为一直线。当回转角不为零时仿真结果如下图 4所示。本文设定右舵回转角为正,左舵回转角为负。
此时仿真中螺旋桨转速不变为额定值,设置回转角分别为10°、20°、30°,从图 4中可以看出当回转角变大时,船舶的等效舵角也随之变大,且等效舵角增加更快,舵效很明显。此时船舶回转半径随着回转角的增大而变小,回转角速度变大,船速一部分产生切向航速,一部分产生船舶回转的角速度,回转角速度变大时,船舶航速会随之减小。
|
| 图 4 双桨同回转且转速相等时 Fig. 4 Twin-propeller rotating and rotating speed equality |
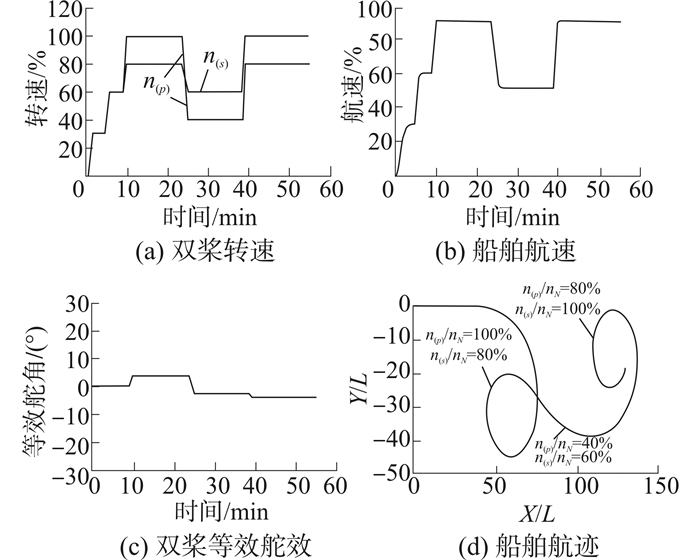
此时双桨不作回转j(S)=j(P)=0,但转速不相等n(S)≠n(P)时,i(S)≠i(P)。如图 5所示。此时设置双桨在额定转速30%和60%时同转速,可以看出船舶航迹为一条直线,但当左桨转速升至100%,右桨转速升至80%时船舶发生回转,10min后将左桨转速降为40%,右桨降为60%,此时回转方向发生明显变化,船舶航速也因为转速降低推力减小而快速下降。而后右桨转速升至100%,左桨转速升至80%,船舶航速也随之上升。此时可以看出等效舵角很小,且舵效的大小取决于双桨推力以及推力差。
|
| 图 5 双桨不回转但转速不相等时 Fig. 5 Twin-propeller not rotating and rotating speed not equality |
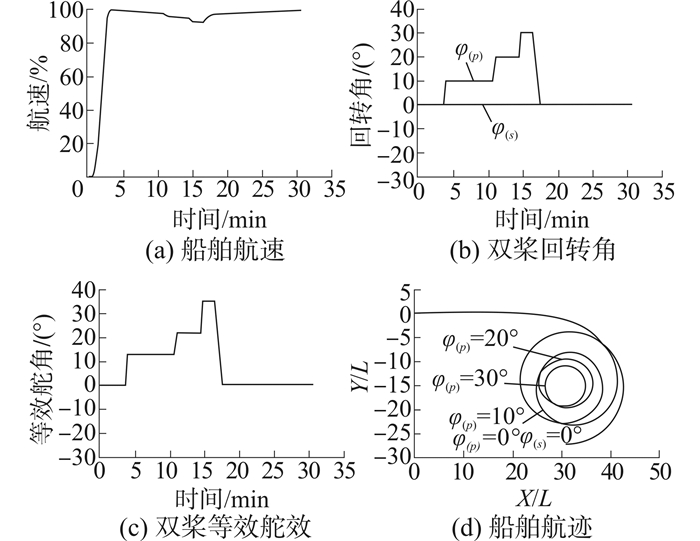
此时j(S) ≠0、jP=0,或j(S) =0、jP≠0,双桨转速相等n(S)=n(P)= nP时,i(S)=i(P)=iP。如图 6所示。此时仿真设置右桨不回转,左桨回转角分别为10°、20°、30°,可以看出船舶回转半径随着回转角变大而变小,航速也因为回转角速度变大而下降,但下降幅度小于图 4所示的双桨回转。当左桨回转角回复到0°后,此时船舶直线航行,航速也随之上升至正常状态。
|
| 图 6 仅单浆回转但转速相等时 Fig. 6 Only one propeller rotating and rotating speed equality |
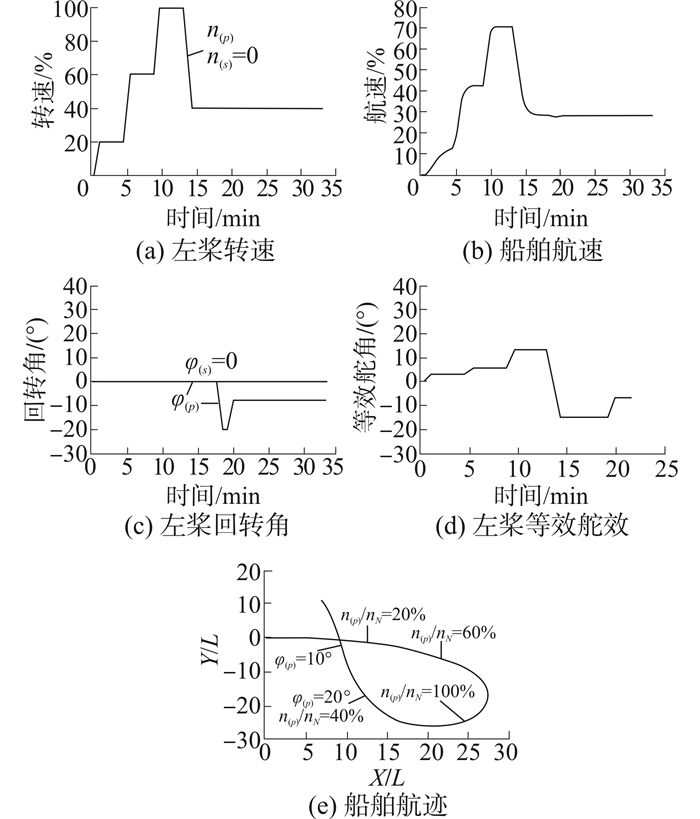
此状态为上一状态的特例,设置右桨不作用,仅左桨回转。如图 7所示。此时设置左桨转速分别为额定转速的20%、60%、100%,但回转角等于0,可以看出随着转速增加船舶航迹回转半径有变小的趋势。转速回到40%并保持不变,螺旋桨向内侧回转,首先回转20°再减到10°,可以看出船舶回转方向不变,但回转半径随着回转角度减小而增大。可以看出由推力差产生的舵效远小于螺旋桨回转产生的舵效。
|
| 图 7 仅单浆回转时 Fig. 7 Only one propeller action |
以上4种为可回转双桨电力推进船舶的典型工况,回转角和螺旋桨转速还有其他组合,但都可归到这4种工况中。从以上分析可以看出可回转双桨可以产生更强的船舶舵效,机动性远强于一般船舶,且依靠双桨推力差产生的船舶舵效远不如螺旋桨回转产生的舵效。其中第1种为正常状态下船舶的运行工况,第2、3种工况可作为船舶离靠码头时姿态的修正,第4种工况一般不会出现,可作为一种故障工况研究。
5 结论本文研究了可回转双桨电力推进船舶的四种典型运动工况,回转角和螺旋桨转速还有其他组合,但都可归到这四种工况中。从上文分析可以得出以下结论:
1)可回转双桨可以产生更强的船舶舵效,机动性远强于一般船舶,且依靠双桨推力差产生的船舶舵效远不如螺旋桨回转产生的舵效。
2)第一种工况为正常状态下船舶的运行,第二、三种工况可作为船舶离靠码头时姿态的修正,第四种工况一般不会出现,可作为一种故障研究。对于故障状态下可回转双桨船舶的运动还需进一步研究。
3)可回转双桨船舶是一类新型船舶,相对于双桨双舵船舶操纵控制更复杂,也有进一步研究的必要。
4)仿真结果验证了可回转双桨船舶在等效舵效作用下船舶运动的可靠性,为船舶推进系统的设计和航向控制研究提供了依据。
| [1] | LEE S K, FUJINO Masataka. Assessment of a mathematical model for the manoeuvring motion of a twin-propeller twin-rudder ship[J]. International shipbuilding progress, 2003, 50(1/2): 109-123. |
| [2] | KIM Y G, KIM S Y, KIM H T, LEE S W, YU B S. Prediction of the maneuverability of a large container ship with twin propellers and twin rudders[J]. Journal of marine science and technology, 2007,12(3): 130-138. |
| [3] | TERESA A G. Experimental study on the hydrodynamic forces induced by a twin-propeller ferry during berthing[J]. Ocean engineering, 2008, 35(3/4): 323-332. |
| [4] |
王化明, 邹早建. 双桨双舵船舶操纵性预报研究[J]. 武汉理工大学学报, 2006, 30(1): 124-127. WANG Huaming, ZOU Zaoming. Manoeuvrability prediction for a ship with twin propellers and twin rudders[J]. Journal of Wuhan university of technology, 2006, 30(1): 124-127. |
| [5] | UENO M, MIYAZAKI H, TSUKADA Y. On course stability of ships of different stern types[C]//11th International Symposium on Practical Design of Ships and Other Floating Structures, 2010: 182-189. |
| [6] | SAHBI K, KAZUHIKO H, VISHWANATH N et al. Manoeuvring characteristics of twin-rudder systems: Rudder-hull interaction effect on the manoeuvrability of twin-rudder ships[J]. Journal of marine science and technology, 2011, 16(4): 472-490. |
| [7] | OGAWA A, KASAI H. On the mathematical model of manoeuvring motion of ships[J]. International shipbuilding progress, 1978, 25(292): 306-319. |
| [8] |
康伟, 褚建新, 黄辉, 等. 可回转双桨电力推进船舶运动模型的研究[J]. 中国造船, 2012, 53(1): 173-183. KANG Wei,CHU Jianxin,HUANG Hui,et al.Study on propulsion and rotary motion model of the rotatable twin-propeller electric propulsion ship[J].Shipbuilding of China, 2012,53(1):107-116. |
| [9] | 贾欣乐,杨盐生. 船舶运动数学模型-机理建模与辨识建模[M].大连:大连海事大学出版社,1999: 33-42. |
| [10] |
周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21-36. ZHOU Zhaoming, SHENG Ziyin, FEN Wushi. On Maneuverability prediction for multipurpose cargo ship[J]. Ship engineering, 1983(6): 21-36. |



