2 Institute of Geology and Geophysics, Chinese Academy of Sciences, Key Laboratory of Petroleum Resources Research, Chinese Academy of Sciences, Beijing 100029, China;
3 Research Institute of Petroleum Exploration & Development, Petro China, Beijing 100083, China
For the risk exploration of carbonate rocks in the west of China, clarifying the small-scale cavities, fractures and other geological structures plays an important role in reservoir analysis. Thus, performing research on detecting these discontinuous and inhomogeneous geological structures has an important value in evaluating the conditions of oil and gas. In the petroleum industry, there have been many available methods for fault detection and among them the seismic coherence technique provides a solid foundation for automatic identification. The first generation of coherent volume algorithm (Bahoric et al., 1998) is based on the classical normalized crosscorrelation theory but with the requirements of a higher S/N of seismic data. In order to deal with the low S/N data, Marfurt et al., (1998) proposed the second generation of coherent volume algorithm for improving noise immunity that introduces a multi-channel similarity of covariance matrix. However, the averaging effect will reduce the lateral resolution of seismic interpretation. The third generation coherent volume algorithm was developed (Gersztenkorn et al., 1999) by calculating the eigenvalues of covariance matrix. This algorithm can improve seismic interpretation by eliminating noise and increasing lateral resolution. Some other seismic discontinuity detection methods inspirited by the coherent volume technology, also grow up rapidly, such as the seismic attribute method (Li et al., 2005 ; Zhang et al., 2010 ; Li et al., 2011 ; Fang et al., 2013 ; Huo et al., 2014 ; Wang et al., 2014 ; Chen et al., 2014), the spectral decomposition method (Liao et al., 1990 ; Wei, 2009 ; Zhu et al., 2009 ; Chen et al., 2010 ; Chen et al., 2011 ; Huang et al., 2012 ; Yu et al., 2013 ; Cai et al., 2014 ; Zhang et al., 2014 ; Wang et al., 2015), the ant tracking technique (Zhang, 2010 ; Wang et al., 2013 ; Huo et al., 2014). In order to eliminate the scattering and diffraction effect generated from fault zones, some scholars (Wang, 2009) even introduced the chaotic theory for measuring the regularity and chaos properties of seismic amplitudes. Liao et al.(1990) proposed a fault identification method based on the spectral decomposition. Zhang et al.(2006) applied the spectral decomposition technique to study the carbonate reservoir.
In fact, in the stage of analyzing carbonates, in addition to caring about tiny faults and other discontinuities, the inhomogeneity related to the inner conditions of reservoirs, such as cavities should also be paid attention to. Therefore, in this paper, we propose a method based on the L1 non-smooth norm that can provide a mathematical mode for dealing with both the discontinuous and inhomogeneous information.
2 METHODOLOGYThe seismic strong reflections from large-scale structures generally will mask the existence of small-scale discontinuous and inhomogeneous geological structures, because the energy difference between them can be one or two orders of magnitude. Thus, the hidden small-scale information can be extracted if we remove the strong reflections. The plane wave destruction filter that uses a local plane wave model to characterize seismic structure has a good potential in predicting linear events and will be adopted for estimating reflections. After subtracting the predicted reflections from seismic imaging data, the residual data will include nonlinear structural features and noises. Then, a L1 sparse inversion method will be developed for inversing the inhomogeneous information.
2.1 Plane Wave Destruction Method for Smooth InformationThe reflections with stable amplitudes are corresponding to large-scale smooth structural characteristics of seismic imaging data. The plane wave destruction method (PWD)(Fomel, 2002) can take a job for estimating reflections and is given by

|
(1) |
where d is a vector of seismic residual data, s = [s1, s2, …, sN, ]T is the given seismic imaging data, R (σ) is a nonlinear plane wave prediction operator, σ is the local slope of seismic imaging data. The formula (1) can be expressed as

|
(2) |
where I is the identity matrix, σ is the local slope vector, the filter Pi, j (σi) means a prediction of trace j from trace i according to the plane wave equation and local slopes.
In solving seismic local slopes, the initial local slopes will be given and then the conjugate gradient method is used to update the local slopes. For prediction reflections, the low-order term of the filter Pi, j (σi) is used because only the smooth information of seismic imaging data is considered, and its form is given as
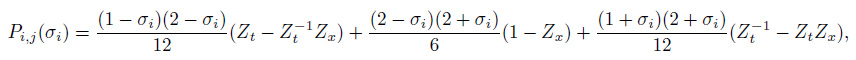
|
(3) |
where Zt, Zx are the Z transform of t, x respectively.
As seismic local slopes corresponding to the locations of faults, fractures, cavities and other geological anomalies cannot be estimated accurately by the PWD method, the discontinuous and inhomogeneous geological information will be left into the seismic residual data d.
2.2 Seismic Sparse Inversion Method for Detecting Discontinuities and InhomogeneitiesIn order to extract the useful discontinuous and inhomogeneous information from the seismic residual data, the nonlinear structure-enhancing filtering method (Liu et al., 2014 ; Liu et al., 2010) is required. Here, the operator D (σ) can be a Gaussian similar mean filter (Liu et al., 2009) or lower-upper-middle filter (Hardie et al., 1993). In this paper we apply the lower-upper-middle filter (Liu et al., 2010):
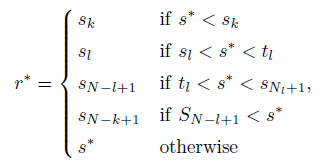
|
(4) |
where, r* is the result of the lower-upper-middle filter, k is the smoothness parameter, l is the sharpening parameter, N is the number of sample point, s* is the intermediate value of sample point.
The magnitude of seismic energy from small-scale discontinuities and inhomogeneities is usually comparable with noises, therefore the inversion method will be considered for accomplishing a higher S/N image. Since the discontinuous and inhomogeneous information has a characteristic of sparsity, a L1 norm model will be constructed and the minimization problem can be written as

|
(5) |
where m is the inversion model. The above equation is equivalent to solving an unconstrained problem using the Lagrange operator:

|
(6) |
where α is an adjustable regularization parameter, and Ω(m) is defined as (Wang et al., 2011a)
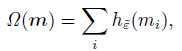
|
(7) |
where ${{h}_{{\tilde{\varepsilon }}}}$ is defined as a piecewise function:
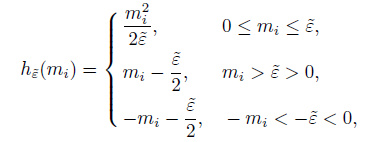
|
(8) |
where $\tilde{\varepsilon }$ is a small constant parameter. Obviously, as $\tilde{\varepsilon }$ → 0, Ω(m) approximates the L1 norm very well.
Supposing H (m) is the Hessian matrix of the function Jα(m), quasi-Newton methods can be used to solve this minimization problems. The benefit of the quasi-Newton method lies in only the requirement of the first-order partial derivatives to ensure a fast convergence, which is more appropriate for solving the large-scale computation problem.
The objective function Jα(m) is a nonlinear function and its gradient can be calculated:
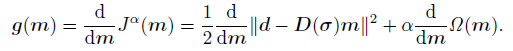
|
(9) |
The above equation can be rewritten as
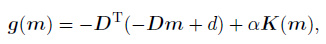
|
(10) |
where the function K (m) is defined as
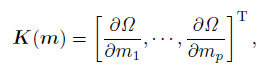
|
(11) |
where 
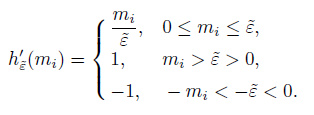
|
(12) |
Supposing B ≈ H-1(m), the gradient of the function Jα(m) at the k-th iteration is defined as gk = g (mk), and the direction for updating inversion parameters is defined as sk =(m) k+1 -(m) k. Therefore, the next inversion parameters can be updated by the following equations (Wang et al., 2011b):
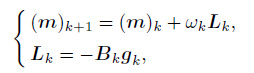
|
(13) |
where the matrix Bk is calculated:

|
(14) |
The parameter ωk is the step size for a line search, which can be solved by the Armijo-Goldstein criterion (Yuan and Sun, 1997).
The iteration steps of the quasi-Newton algorithm can be described as follows:
Step 1: Given initial inversion parameters m0, a constant parameter r and a symmetric positive definite matrix B0 = I, and set k = 0.
Step 2: If k 6 ≠ 0, compute mk and Bk.
Step 3: Compute g (mk). If 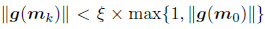
Step 4.

|
Step 5: Set k = k + 1, and update mk and Bk; GOTO Step 3.
Remark: Stopping criteria is a key issue for an inversion algorithm. For general inverse problems, the accuracy of a solution should be dictated by the error of input data (Wang, 2007). If we consider the conventional gradient energy value as a stopping criterion, it will fall into many iterations and lead to the accumulation of computation errors. Therefore, we choose 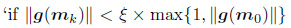
In order to test the performance of the proposed seismic sparse detection method for detecting discontinuities and inhomogeneities, a fracture-cavity model is designed that includes breakpoints, cavities and rough reflectors. Seismic diffractions will be generated from this kind of small-scale geological structures or elements and will be imaged after migration. However, compared with the reflections, diffractions are generally much weaker. So it is difficult to observe the weak diffraction information in conventional migration images. The conventional migration result of the fracture-cavity model is shown in Fig. 1, where the large-scale structures are clearly imaged but the small-scale fractures and cavities seem invisible because of their weak energies. Therefore, strong reflections corresponding to large-scale structures must be removed for releasing the high-resolution diffraction details. The estimated reflections by the plane-wave prediction method are shown in Fig. 2. After subtracting the estimated reflections, we get the seismic residual data that concludes the non-smooth information. The sparse inversion result of the seismic residual data is shown in Fig. 3. The four series of cavities in the shallow parts, three series of cavities in the deep part, and discontinuous information of the breakpoints and faults can be clearly seen in Fig. 3. In this sparse inversion process, the regularization parameter α in the objective function plays a key role: if α is chosen larger, the effect of sparsity constraint will become stronger; if α is chosen smaller, it will become a smoother constraint model. The purpose of using L1 sparsity norm is to protect the discontinuous and inhomogeneous information. Compared with the conventional migration result, the proposed method has advantages in imaging the breakpoints, fractures and cavities. The migration noises also get suppressed in this sparse inversion process. Although there are some linear events left in Fig. 3, the amplitudes along them change dramatically, which in some way demonstrate the sensitivity of the proposed method to amplitude variations. After removing the smooth large-scale geological information, the sedimentary discontinuities, faults, cavities, rough reflection interfaces and other information are separated and enhanced. This kind of small-scale geological information can be used for studying the inner conditions of oil and gas reservoirs.

|
Fig. 1 Depth migration of a fracture-cavity model |

|
Fig. 2 Reflection information predicted by plane-wave method |

|
Fig. 3 Discontinuous and inhomogeneous geological information extracted by the seismic sparse inversion method |
The testing result of the fracture-cavity model shows that the proposed seismic sparse inversion method can clearly reveal small-scale geological structures or elements that are related to the migration channel or accumulation of oil and gas.
4 FIELD DATA APPLICATIONThe high-capacity carbonate reservoirs in abroad are generally related to homogeneous reefs, complete structures of dolomite weathering crusts and are less involved with heterogeneity properties. However, in China, a typical feature of the majority of effective carbonate reservoirs is strong discontinuity or inhomogeneity, such as cavities or fractures, as they suffered from a long history of tectonic movements and weathering. In this case, detecting karst fractures or cavity groups has a significant value in discovering a large-scale oil and gas reservoir, especially for the risk exploration in the west of China. In this given example, we will try to clarify the distributions of such small-scale discontinuous and inhomogeneous geological information along the Ordovician layer in the Tarim basin.
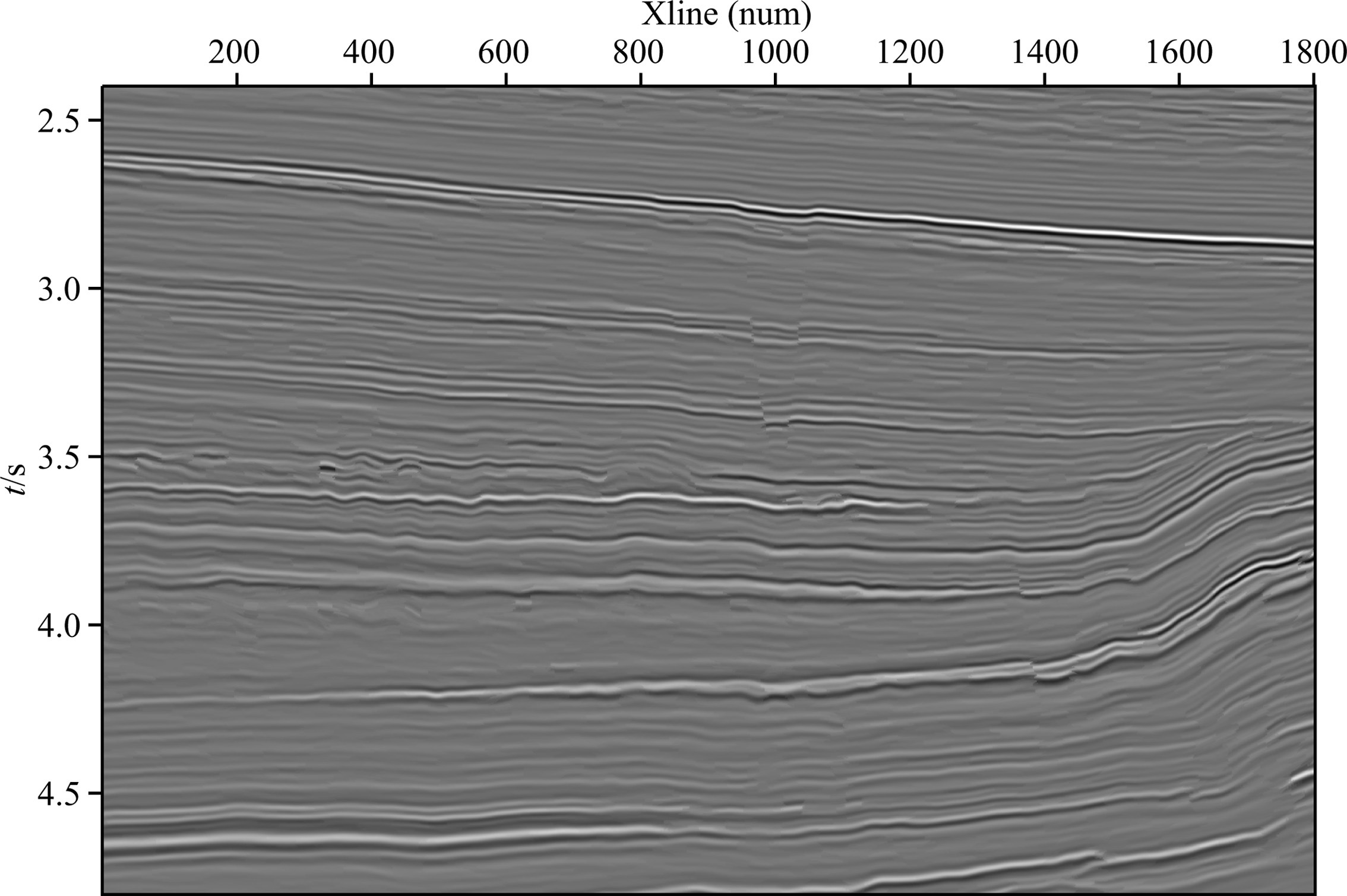
One inline image of the 3D prestack time migration result is shown in Fig. 4, where the vertical location of weathering crusts is at 3.5 seconds and the vertical position corresponding to bead-shaped cavities is at 4 seconds. Although Fig. 4 can show the changes of amplitudes, the shapes of weathering crusts and even the shadows of cavities in a certain extent, it is not clear enough to describe the small-scale karst cavities in the deep part. We provide the linear prediction result of Fig. 4 by the plane-wave destruction method in Fig. 5 that mainly describes the macro-scale smooth events but not for the small-scale fractures, karst cavities and other geological units. The discontinuous and inhomogeneous geological information extracted by the proposed seismic sparse inversion method is shown in Fig. 6. After removing the smooth and strong reflections, the tiny faults and small-scale cavities in the deep part can be clearly showed and even for the breaking points along the weathering crusts. More important is its ability to depict the development of the karst zones along the Ordovician layers.
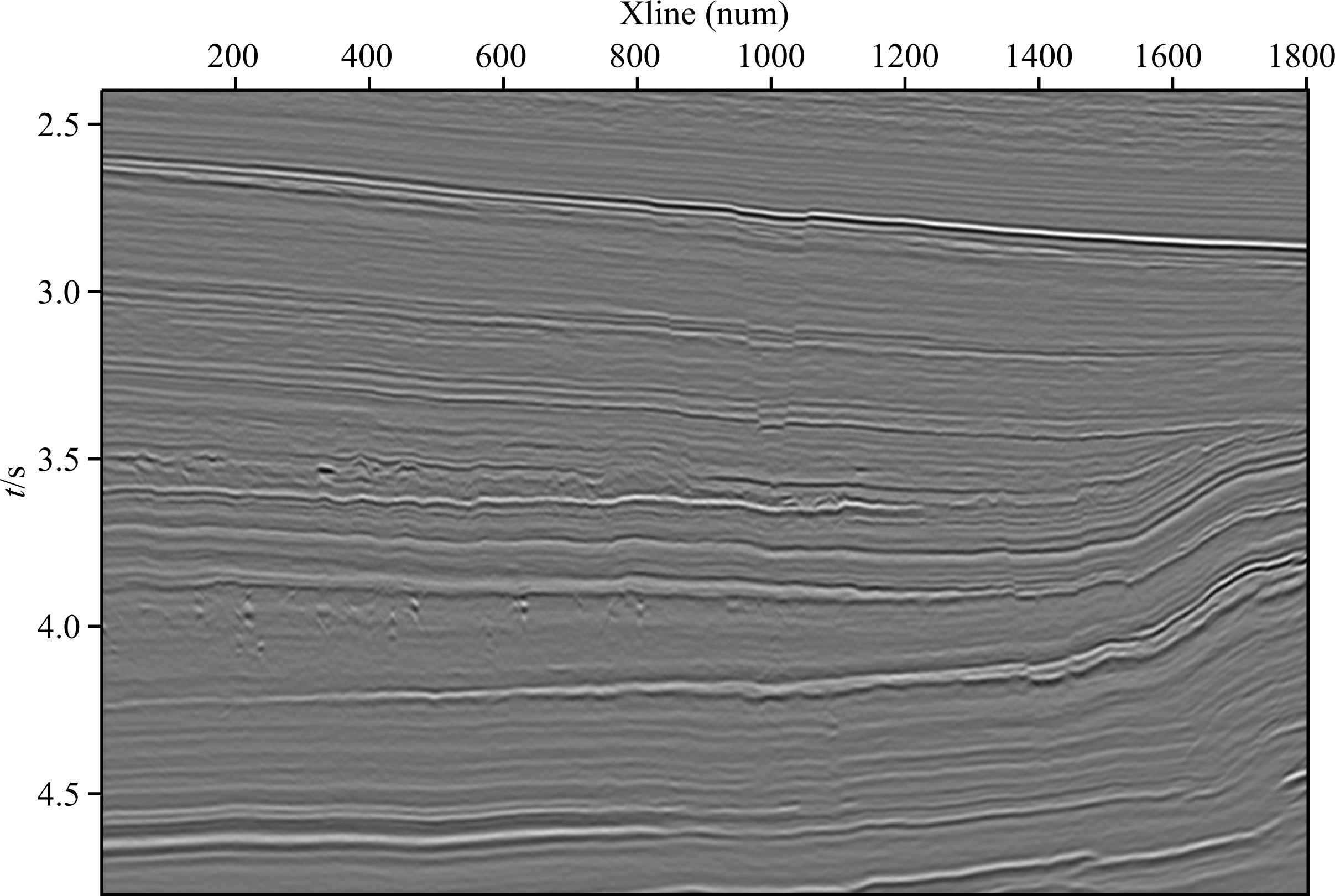
|
Fig. 4 Three-dimensional pre-stack time migration profile in inline direction |
|
Fig. 5 Smooth reflection profile obtained by the plane wave destruction method |

|
Fig. 6 Discontinuous and inhomogeneous geological information extracted by the seismic sparse inversion method |
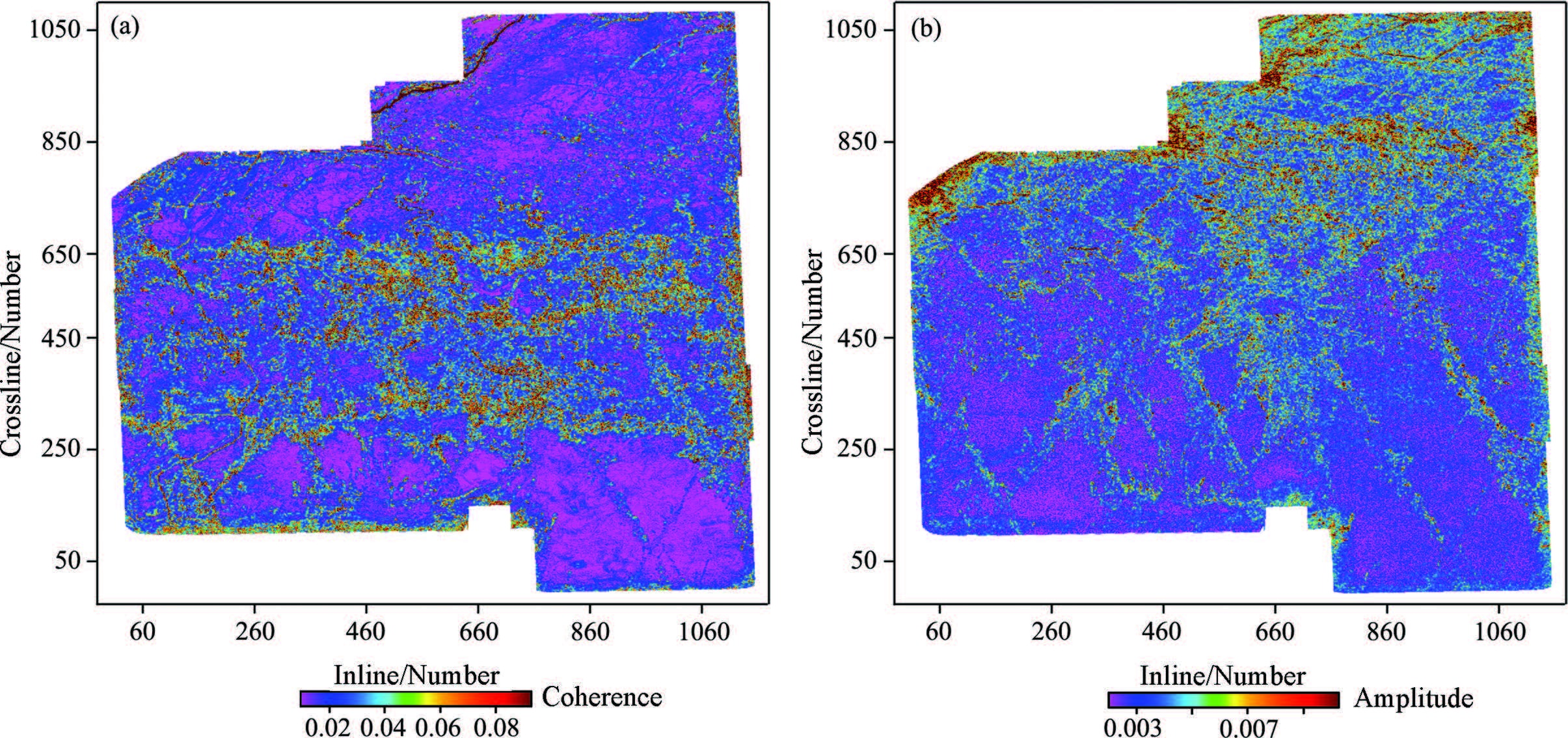
In order to further study the planar distribution of fractures and karst cavities, some seismic attribute analysis is performed along the Ordovician layer. One of the important seismic attributes is the coherent volume that can highlight the non-correlation information, corresponding to faults, fractures and so on, by transforming seismic imaging data into similar coefficients and the result is shown in Fig. 7a. The shape of an ancient river can be clearly shown in Fig. 7a, but the small-scale geological bodies such as karst cavities and tiny faults are difficult to be found. After calculating the root-mean-square (RMS) amplitudes of the seismic sparse inversion data, we present Fig. 7b that can clearly show the planner distribution of the small-scale karst cavities and even the development characteristics of fractures.
|
Fig. 7 Seismic attribute maps along the Ordovician layer (a) Coherence attribute;(b) RMS amplitude attribute of seismic sparse inversion data. |
The 3D seismic field application in the Tarim basin confirms the ability of the proposed seismic sparse inversion method for detecting the discontinuous structures, such as tiny faults and fractures, and small-scale inhomogeneous elements, such as karst cavities.
5 CONCLUSIONBy constructing a L1 sparsity-constraint inversion model, this paper presents a method for detecting the small-scale discontinuous and inhomogeneous geological information. The proposed method demonstrates a good performance in extracting the small-scale geological structures or elements, such as tiny faults and cavities. For practical application of the method, some valuable notes should be considered:
(1) In this paper, the plane-wave destruction filter is used to predict the linear and smooth reflection information. Some other methods, such as F-K filter or median filter, can achieve a similar technical effect.
(2) In order to improve the S/N of the discontinuous and inhomogeneous geological information, this paper constructs a sparsity-constraint model and then uses the piecewise function approximation method and the quasi Newton algorithm to achieve a high-preformation computation. Thus, the proposed method has a capability for processing 3D high-density seismic imaging data.
(3) One application condition of the proposed method is the requirement of seismic imaging data to have the discontinuous and inhomogeneous information imaged. Otherwise, some additional seismic data processing should be performed.
(4) In the future, an issue that how to individually discriminate the small-scale discontinuous or inhomogeneous information, and then only use the extracted small-scale inhomogeneous information to study "beaded" reservoir, can be further explored.
ACKNOWLEDGMENTSThis work is supported by National Key Research and Development Program (2016YFC0501102), National Science and Technology Major Project (2016ZX05066-001), Coal United Project of National Natural Science Foundation (U1261203), Shanxi Natural Science Funds Project (2013012001). We are grateful to the editor and reviewers for kind comments and suggestions which greatly improved the quality of our paper.
| [] | Bahorich M, Farmer S. 1995. 3-D seismic discontinuity for faults and stratigraphic features:The coherence cube. The Leading Edge , 14 (10) : 1053-1058. DOI:10.1190/1.1437077 |
| [] | Cai H P, He Z H, Li Y L, et al. 2014. Instantaneous spectrum decomposition and fast interpretation of broadband seismic data. Oil Geophysical Prospecting (in Chinese) , 49 (5) : 932-939. |
| [] | Chen B, Wei X D, Ren D Z, et al. 2010. Small fault identification based on spectrum decomposition technique. Oil Geophysical Prospecting (in Chinese) , 45 (6) : 890-894. |
| [] | Chen H, Peng Z M, Wang J, et al. 2011. Spectral decomposition of seismic signal based on fractional Gabor transform and its application. Chinese J. Geophys. (in Chinese) , 54 (3) : 867-873. |
| [] | Chen H Q, Bai J, Zou W, et al. 2014. Fractured reservoir prediction in Liugouzhuang with seismic attribute approaches provided by GeoEast. Oil Geophysical Prospecting (in Chinese) , 49 (S1) : 154-159. |
| [] | Fang H F, Zhou S, Wang Y L, et al. 2013. Geometric attribute improved-processing in fault interpretation. Oil Geophysical Prospecting (in Chinese) , 48 (S1) : 120-124. |
| [] | Fomel S. 2002. Application of plane-wave destruction filters. Geophysics , 67 (6) : 1946-1960. DOI:10.1190/1.1527095 |
| [] | Gersztenkorn A, Marfurt K J. 1999. Eigenstructure based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics , 64 (5) : 1468-1479. DOI:10.1190/1.1444651 |
| [] | Hardie R C, Boncelet C G. 1993. LUM filters:A class of Rank-Order-Based filters for smoothing and sharpening. IEEE Transactions on Signal Processing , 41 (3) : 1061-1076. DOI:10.1109/78.205713 |
| [] | Huang H D, Guo F, Wang J B, et al. 2012. High precision seismic time-frequency spectrum decomposition method and its application. Oil Geophysical Prospecting (in Chinese) , 47 (5) : 773-780. |
| [] | Huo L N, Zhang J J, Zheng L H, et al. 2014. Fault interpretation with multiple attributes in coalbed methane interpretation. Oil Geophysical Prospecting (in Chinese) , 49 (S1) : 221-227. |
| [] | Li C F, Liner C. 2005. Singularity exponent from wavelet-based multiscale analysis:A new seismic attribute. Chinese J. Geophys. (in Chinese) , 48 (4) : 882-888. |
| [] | Li J X, Cui Q Z, Wei X D. 2011. Application of seismic attributes in micro-fault interpretation. Oil Geophysical Prospecting(in Chinese) , 46 (6) : 925-929. |
| [] | Liao X H, Yan P F, Chang T. 1990. Automatic faults recognition using spectrum decomposition. Acta Geophysica Sinica(in Chinese) , 33 (2) : 220-226. |
| [] | Liu G C, Fomel S, Jin L, et al. 2009. Stacking seismic data using local correlation. Geophysics , 74 (3) : V43-V48. DOI:10.1190/1.3085643 |
| [] | Liu Y, Fomel S, Liu G C. 2010. Nonlinear structure-enhancing filtering using plane-wave prediction. Geophysical Prospecting , 58 (3) : 415-427. DOI:10.1111/(ISSN)1365-2478 |
| [] | Liu Y, Wang D, Liu C, et al. 2014. Structure-oriented filtering and fault detection based on nonstationary similarity. Chinese J. Geophys. (in Chinese) , 57 (4) : 1177-1187. DOI:10.6038/cjg20140415 |
| [] | Marfurt K J, Kirlin R L, Farmer S L, et al. 1998. 3-D seismic attributes using a semblance-based Coherence algorithm. Geophysics , 63 (4) : 1150-1165. DOI:10.1190/1.1444415 |
| [] | Wang H Q, Yang W Y, Xie C H, et al. 2014. Azimuthal anisotropy analysis of different seismic attributes and fracture prediction. Oil Geophysical Prospecting (in Chinese) , 49 (5) : 925-931. |
| [] | Wang J, Li Y D, Gan L D. 2013. Fracture characterization based on azimuthal anisotropy of ant-tracking attribute volumes. Oil Geophysical Prospecting (in Chinese) , 48 (5) : 763-769. |
| [] | Wang W. 2009. Technology of seismic geometric attributes for fault identification and its application[Master thesis] (in Chinese). Qingdao:China University of Petroleum. |
| [] | Wang Y F. 2007. Computational Methods for Inverse Problems and Their Applications (in Chinese)[M]. Beijing: Higher Education Press . |
| [] | Wang Y F, Stepanova I E, Titarenko V N, et al. 2011. Inverse Problems in Geophysics and Solution Methods (in Chinese)[M]. Beijing: Higher Education Press . |
| [] | Wang Y F, Yagola A G, Yang C C. 2011. Optimization and Regularization for Computational Inverse Problems and Applications[M]. New York: Springer . |
| [] | Wang Y P, Xie J P, Han W G, et al. 2014. Thin bed prediction based on spectral decomposition. Oil Geophysical Prospecting (in Chinese) , 49 (3) : 561-566. |
| [] | Wei Z P. 2009. Application of spectrum-decomposition tuning body technique to quantitatively predict thin reservoir. Oil Geophysical Prospecting (in Chinese) , 44 (3) : 337-340. |
| [] | Yu H, Li J S, Zhang Y, et al. 2013. Spectral decomposition in fault and reservoir identifications. Oil Geophysical Prospecting(in Chinese) , 48 (6) : 954-959. |
| [] | Yuan Y X, Sun W Y. 1997. Optimization Theory and Method (in Chinese)[M]. Beijing: Science Press . |
| [] | Zhang G D, Liu X, Tian L H, et al. 2010. Integrated application of seismic attribute and seismic inversion in reservoir characterization. Oil Geophysical Prospecting (in Chinese) , 45 (S1) : 137-144. |
| [] | Zhang X. 2010. Application of ant tracing algorithm in fault automatic interpretation:a case study on Fangheting structure in Pinghu Oilfield. Oil Geophysical Prospecting (in Chinese) , 45 (2) : 278-281. |
| [] | Zhang X Y, Peng Z M, Zhang P, et al. 2014. Spectral decomposition of seismic signal based on fractional Wigner Ville distribution. Oil Geophysical Prospecting (in Chinese) , 49 (5) : 839-845. |
| [] | Zhang Y Z, Zhao Y H, Lu X B, et al. 2006. Application of spectral factorization technique to predict carbonate fracturevuggy reservoir in TH area of northern Tarim basin. Oil Geophysical Prospecting (in Chinese) , 41 (S1) : 16-20. |
| [] | Zhu Z Y, Lü D Y, Sang S Y, et al. 2009. Research of spectrum decomposition method based on physical wavelet transform and its application. Chinese J. Geophys. (in Chinese) , 52 (8) : 2152-2157. DOI:10.3969/j.issn.0001-5733.2009.08.025 |
 2016, Vol. 59
2016, Vol. 59

