2 Material Testing Exploration Institute of Liaoning Province, Shenyang 110121, China;
3 Exploration and Development Institute of the Changqing Oilfield, PetroChina, Xi'an 710018, China;
4 First Branch of the Logging Company, Shengli Petroleum Engineering Co. Ltd., Dongying 257200, China
An optimization log interpretation method is a new technology which was developed in the early 1980s. It compiles all of the logging information, measurement and response equation errors, and some of the geological experience into a multi-dimensional information complex, and using mathematical optimization methods for multi-dimensional processing, solves the optimal solutions of the complexes (Yong, 1995). The selection of the mathematical optimization method is the key to the accuracy of the optimization log interpretation method, which is closely related to the logging interpretation results. The objective function of an optimal log interpretation is complex, and traditional algorithms based on gradient cannot meet this requirement. Since the 1970s, there has been a series of bionics-based swarm intelligence optimization algorithms, also known as the “heuristic algorithms”. These include genetic, ant colony optimization, particle swarm optimization, bacterial foraging algorithms, and so on (Liu, 2011).
Bacterial foraging algorithms (BFA) have attracted the attention of experts in various fields since they were first proposed by Passino (2002). These algorithms, along with their improved algorithms, are widely used in practical problems such as job shop scheduling, industrial instrument design, image compression, and predictive control, and they have achieved good results (Tripathy et al., 2006; Zhang, 2007; Kim and Cho, 2005, 2006; Chu et al., 2008). However, BFA algorithms have not yet been applied to the optimization of well logging interpretation. A complex algorithm (CM) is an optimization algorithm which has strong local search ability. It was developed from an improved simplex algorithm introduced by Box MJ in 1966. This algorithm is widely used in the mechanical engineering field (Zhang et al., 2003). Han (2012) combined the complex algorithm with a genetic algorithm, and the combined algorithm was applied to the optimization log interpretation of a sand conglomerate. It was determined that this combined algorithm had a higher precision.
The Sulige area has complex lithology composition and diverse pore structures, which presented difficulties when a conventional logging interpretation method was used for determining the reservoir parameters (Wang, 2013). However, an optimization of the logging interpretation method was able to effectively evaluate the complex lithology reservoir. Since its objective function is complex, the requirements of the optimization algorithm are high. Many researchers have chosen to use hybrid optimization algorithms to solve geophysical inversion problems. For example, Tan and Zou (2012) applied hybrid optimization algorithms to 2D NMR (Nuclear Magnetic Resonance) log inversions, and the fluid identification of oil and gas reservoirs. Also, Gong et al. (2012) used hybrid optimization algorithms to locate earthquake source locations in coal mines. Furthermore, Luo et al. (2003) applied hybrid optimization algorithms to three-dimensional implicit method migrations. In this study, a BFA algorithm was introduced for the first time for the purpose of solving the optimization of logging interpretation. It was combined with a complex algorithm (CM), which then constituted a BFA-CM hybrid algorithm. This new algorithm was then applied in the Sulige area.
2 BASIC PRINCIPLES AND IMPLEMENTATION PROCESS OF A BFA-CM ALGORITHM 2.1 Bacterial Foraging Algorithm (BFA)A bacterial foraging algorithm (BFA), with microorganisms as its imitating object, simulates the behavior of Escherichia coli’s constant movements to locate food by flagella in the human intestine. The results of this study showed that, when the bacteria are in an environment where food is inadequate, the bacteria will randomly choose one movement direction. If the mobile food is rich, it will continue to move in that direction. However, if there is not enough mobile food, it will randomly choose a different direction, and go on searching for food. The survival of the bacteria adheres to Darwin’s “survival of the fittest” theory, which signifies that only the high-energy bacteria can divide to produce new individuals, and the low-energy bacteria will die (You and Lei, 2013).
A bacterial foraging algorithm searches for the optimal solution through three operators of chemotaxis, reproduction, and the migration as follows:
(1) Chemotaxis operator: During the course of the chemotaxis, the bacteria become close to the foodintensive area through the two basic movements of turning and swimming. Turning is the movement in which the bacteria can change their direction, as well as the movements of the unit step. After the bacteria turn, if their fitness is improved they will continue to move along the same direction for a number of steps, until the fitness is no longer improved, or they has achieved the required threshold Ns. This becomes the swimming process.
P (i, j, K, ell) indicates the location of the ith bacteria, jth time chemotaxis cycle, Kth reproductive cycle, and ellth migration cycle, respectively. The changes in the positions of the bacteria during the course of the chemotaxis can be expressed as follows:
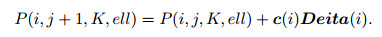
|
(1) |
In the formula, c(i) is the step size vector moving in the direction of motion; and Deita(i) is the randomly generated direction vector.
(2) Reproduction operator: The chemotaxis cycle Nc is set for the full life cycle of the bacteria. When the bacteria complete a life cycle, the bacteria enter the reproduction stage. The reproduction stage then reflects the “survival of the fittest” theory of Darwin. The fitness J(i, j, K, ell) of each bacterium in a life cycle is accumulated and used as the energy of the bacteria Jhealth(i). The S bacteria are accordingly sorted by energy from large to small. The Sr=S/2 high-energy bacteria are retained, and each of these bacteria is copied into two bacteria. The Sr=S/2 low-energy bacteria die. When the reproduction process is completed, the total number of bacteria remains unchanged.
(3) Migration operator: In order to avoid diversification of the bacterial population, the migration operator simulates the biological phenomena where the bacteria move to a new environment with the water. Following the reproductive cycle, the algorithm will randomly generate a probability P. If the generated random probability P is less than the predetermined migration probability Ped, then all of the bacteria will be randomly assigned to a space in any position. The migration operator can improve the global search ability of the algorithm, and can also prevent the algorithm from falling into local extreme points.
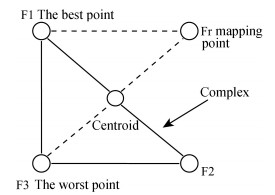
2.2 Complex Algorithm (CM)When solving optimization problems by using complex algorithms, complex k vertices in an n-dimensional space must be built. Fig. 1 shows the schematic diagram of a complex algorithm (n=2, k=3). The complex algorithm uses the value of the objective function to evaluate the quality of the points. The point of the maximum value of the objective function becomes the worst point, and the point of the minimum value of the objective function becomes the best point. After the initial complex shape is established, the objective function values of the F1, F2, F3 points must be calculated. It is assumed that the calculated values of the objective function are F3, F2, and F1, which are sorted from large to small. By removing the worst point F3, the F1 and F2 point centroids can be used as the mapping center in order to determine the mapping point Fr of the removed worst point F3. The mapping point Fr is used instead of the previous worst point F3 to constitute a new complex. In this way, the continuous iteration and complexity are constantly shrinking. When the centroid of each vertex is sufficiently close to each vertex, the iteration is stopped. Then, the point of the minimum objective function value in the complex shape is used as the optimal solution.
|
Fig. 1 Complex algorithm’s schematic |
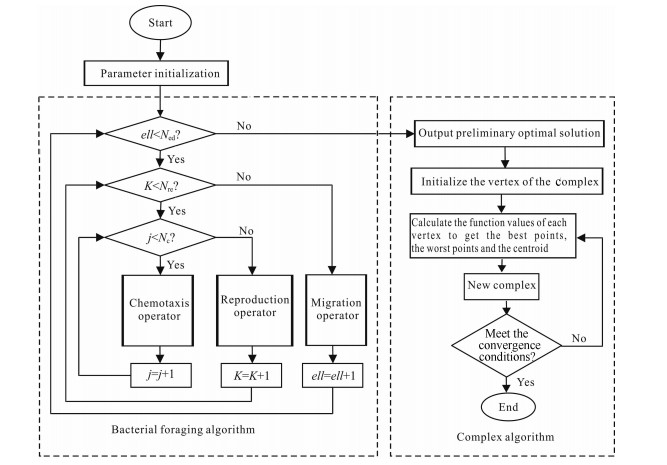
This study’s results showed that the convergence speed of the BFA algorithm will slow down during the later searching stages of the optimal solution (Zhang, 2013). The CM algorithm does not need to calculate the objective function derivative. Therefore, it is able to avoid the degeneration phenomenon in the iteration process with a strong local search ability. The BFA-CM hybrid algorithm was constituted by combining the BFA algorithm with the CM algorithm. The fusion method was simple, and the operation efficiency was found to be high. Fig. 2 illustrates the flow chart of the BFA-CM hybrid algorithm. The initial optimization results which were calculated by the BFA algorithm were among the initial values of the CM algorithm for the two-time optimization. Its specific implementation steps are as follows:
|
Fig. 2 Flow diagram of the BFA-CM hybrid algorithm |
(1) The parameter initialization included the following:
① The bacterial foraging algorithm: Chemotaxis times Nc; swimming times Ns; reproduction times Nre; migration times Ned; number of bacteria S; and migration probability Ped.
② The complex algorithm included the number of vertex k.
(2) The bacteria location was initialized, and the fitness of each bacterium was calculated.
(3) The bacterial foraging algorithm searched for the optimal solution through the three operators of chemotaxis, reproduction, and migration. Within the three layers, the outermost layer was the migration cycle, the middle layer was the reproductive cycle, and the inner layer was the chemotaxis cycle.
During the process of chemotaxis, the operation was executed, and the position of the bacteria was updated by the two basic movements of turning and swimming. The reproduction operator followed the chemotactic cycle, and the migration operator followed the reproductive cycle.
(4) When the bacterial foraging algorithm optimization process was completed, the output of the preliminary optimal solution p was found to be the highest.
(5) The best point of the bacterial foraging algorithm was determined as one of the initial vertexes of the complex, and the rest of the compound shape vertexes were initialized.
(6) The complex initial objective function values of each vertex were calculated to obtain the best points, worst points, and centroid.
(7) The mapping points were calculated, and the new complex shape was formed.
(8) The judgment of the end of the cycle condition was completed. If this was not satisfied, Step (6) was returned to. If the iteration was met, then the process was ended, and the output results were recorded.
3 BFA-CM OPTIMIZATION LOG INTERPRETATION METHOD 3.1 Basic Principles of the Optimal Log InterpretationIn this study, the optimization log interpretation was in accordance with the generalized inversion theory, and was based on the well logging value ai after the correction of the environmental impact, with the parameters of the reservoir, and the relative volume of the minerals as independent variables x. The objective function was established using a proper interpretation model and well logging response equation fi(x, z), and based on the nonlinear least square principle and error theory, as shown in Formula (2). Then, by selecting interpretation parameters Z, and reservoir parameter initial value x0, the value of the objective function was minimized using the optimization method. The independent variable x value was the optimized log interpretation results (Duan et al., 2012).
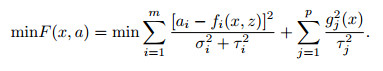
|
(2) |
In the formula, m is the number of log curves involved in the calculation; σi is the measurement error of the various logging methods in the measurement process; τi is the response equation error which was caused by the model; p is the number of constraint conditions; and gj(x) and τj are the j-th constraint and the constraint error, respectively.
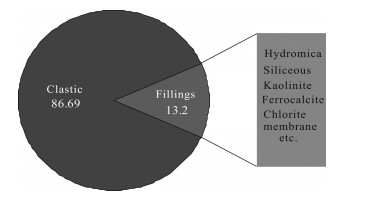
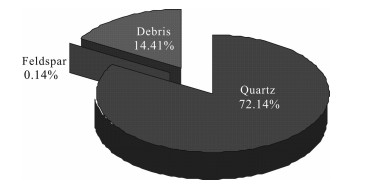
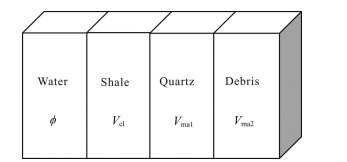
3.2 Establishment of the Mathematical ModelIn accordance with the complex characteristics of the Surige tight sandstone reservoir, this study chose a multicomponent model as the logging interpretation model of the area. The formation was composed of local uniform components (Tian, 2006). Figs. 3 and 4 show the rock component pie chart and clastic composition pie chart, respectively, of the He8 and Shan1 areas in the Sulige gas field zone. The main composition of the reservoir was quartz, and the second most dominant was the cutting, with the feldspar content observed to be minimal. The cuttings mainly included phyllite, metamorphic sandstone, schist, aphanite, and so on. The main components of the fillings were clay minerals, such as hydromica, kaolinite, and siliceous. In this study, in order to simplify the model, it was assumed that water was the only fluid in the pore. A multicomponent model was established for the study area (Fig. 5), which was composed of four parts: water, shale, quartz, and debris. Also, φ, Vcl, Vma1, and Vma2 were the four components of the volume content, respectively.
|
Fig. 3 Pie chart of the rock composition |
|
Fig. 4 Pie chart of the clastic composition |
|
Fig. 5 Schematic of the multi-component model |
The logging response equation was determined according to the multicomponent model established in the study area. Since the BFA-CM hybrid algorithm was used as the algorithm of the optimization log interpretation, the number of equations, and the number of unknown variables were not strictly required. In this study, the number of unknown reservoirs was four, and the number of response equations was three, which included the density logging (DEN), acoustic logging (AC), and compensated neutron logging (CNL). Their well logging response equations could be expressed as follows:
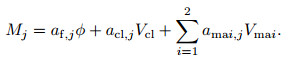
|
(3) |
In the formula, j=1, 2, 3 represent the density, acoustic wave, and neutron logging methods, respectively; Mj represents the actual measured value of the j logging method; af, j represents the response value of the pore fluid to the j logging method; acl, j represents the response value of the shale to the j logging method; and amai, j represents the response value of the i skeletal components to the j logging method.
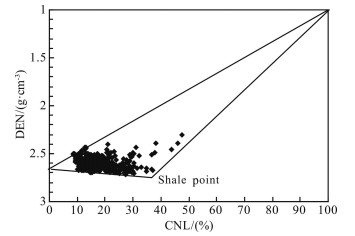
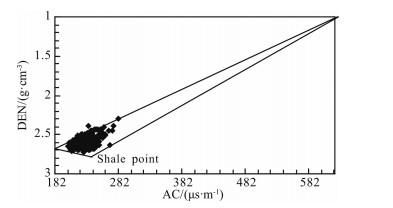
3.4 Determination of Interpretation ParametersThe response values of the shale (ρcl, φNcl, ∆tcl) for density, neutron, and sonic logging were determined as 2.75 g·cm−3, 37%, and 240 µs·m−1, respectively, by drawing the neutron-density cross plot (Fig. 6), and acoustic wave-density cross plot (Fig. 7) of a well in the study area. From the table of the well logging characteristics of the main minerals (Yong, 1995) and the main igneous rock logging response characteristics (Serra, 1986) the characteristic logging values of pore fluid and skeletal components were determined, as shown in Table 1.
|
Fig. 6 Neutron-density cross plot |
|
Fig. 7 Acoustic wave-density cross plot |
|
|
Table 1 Logging response characteristic values of the pore fluid and skeletal components |
In order to obtain a reasonable explanation of the results during the process of searching for the optimal solution, constraints should be put on the unknown quantity x. Also, generally speaking, the constraint conditions of the multicomponent interpretation model included mathematical physics constraints, regional geological constraints, and continuity constraints (Yong, 1995). The main purpose of this study was to examine the BFA-CM hybrid algorithm, with the purpose of improving the efficiency of the operation. Therefore, this study only considered the mathematical physical constraints, as shown in Formula (4):
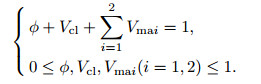
|
In this study, the optimization log interpretation method of the unknown reservoir parameters was solved using a genetic algorithm (GA), particle swarm optimization (PSO), bacterial foraging algorithm, and BFA-CM hybrid algorithm. The absolute errors are shown in Table 2. It was found that the accuracy of the BFA-CM hybrid algorithm results were significantly higher than those of the other algorithms. The GA and PSO algorithms were based on the higher organisms as the simulation objects, and the search for the optimal solution was through a method of “generating and testing”. The BFA algorithm used microorganisms as the simulation objects, and the competition and cooperation of the bacterial colony was utilized to achieve the optimization. When compared with the GA algorithm, the BFA algorithm was found to increase the direction information, and improve the search efficiency. When compared with the PSO algorithm, the BFA algorithm introduced the migration operator, thus avoiding entering local extreme points.
|
|
Table 2 Absolute errors of each algorithm |
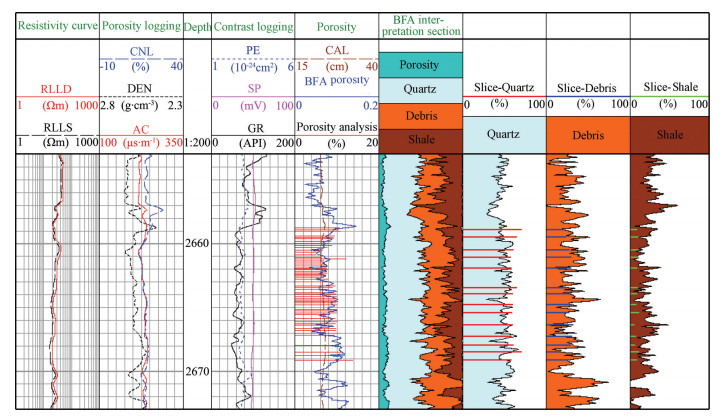
Figure 8 shows the results of the BFA algorithm after solving the optimization logging interpretation method of the unknown reservoir parameters. It was found that when using BFA algorithm alone to solve each of the reservoir parameters the curves presented more burrs. This was caused by the slow convergence rate in the later stage of the BFA algorithm. Fig. 9 shows the results of the BFA-CM hybrid algorithm in solving the optimization logging interpretation method of the unknown reservoir parameters. The BFA-CM hybrid algorithm overcame the shortcomings of the BFA algorithm, and improved the convergence rate in the later stage of BFA algorithm. The calculated results were found to be in agreement with the core and slice analysis data, and the porosity and curve of each component’s content were more stable.
|
Fig. 8 Results for the xx well using the BFA optimization log interpretation method |
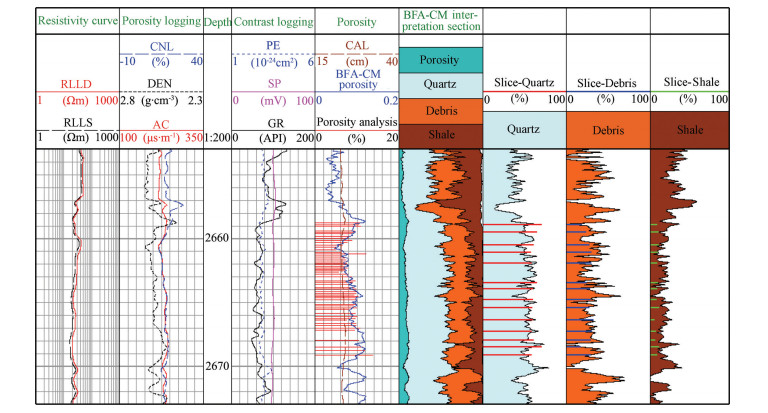
|
Fig. 9 Results for the xx well using the BFA-CM optimization log interpretation method |
Figure 10 is the BFA-CM optimization log interpretation processing test figure of the xx well. In the figure, F is the objective function of the optimization logging interpretation, and the unit is 10−8. The AC0, CNL0, DEN0 are the acoustic wave, density, and neutron theoretical well log curve, respectively. The AC, CNL, and DEN are the acoustic wave, density, and neutron actual well log curve, respectively. The black dashed lines on the right side of the three channels are the confidence intervals of the theoretical logging curve (AC0, CNL0, DEN0). In Fig. 10, the objective function value of the optimization log interpretation is F ≈ 0(3×10−9~3.797×10−6). This indicates that the results of the optimization calculation had high quality, and the interpretation model and interpretation parameter were reasonable. The AC0, CNL0, and DEN0 all fell within the confidence interval, which showed that there was no systematic deviation effect, and the optimization calculation results were reasonable and credible.
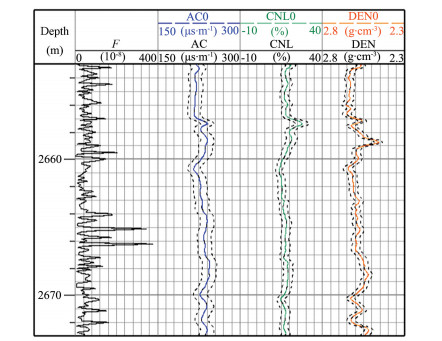
|
Fig. 10 Checking of the xx well using the BFA-CM optimization log interpretation method |
A bacterial foraging algorithm (BFA) is a new intelligent optimization algorithm. It has a strong global search capability, and does not need to solve the derivative of the objective function. However, the convergence rate of the algorithm is slow in the later period of the solution, and the search efficiency tends to become lower. In this study, a BFA algorithm was applied in the optimization log interpretation method. Also, it was combined with a CM algorithm to constitute a BFA-CM hybrid algorithm, for the purpose of improving the accuracy and efficiency of the solution. The experimental results confirmed that the BFA-CM hybrid algorithm was able to accurately and efficiently search for the optimal solution of the optimization log interpretation method, and could be extended to actual production practices.
ACKNOWLEDGMENTSThis paper was jointly funded by Major National Science and Technology Project (2011ZX05044) and the National Natural Science Foundation of China (41174096).
| [] | Chu Y, Shao Z B, Mi H, et al. 2008. An application of bacterial foraging algorithm in image compression. Journal of Shenzhen University Science and Engineering (Science & Engineering) (in Chinese) , 25 (2) : 153-157. |
| [] | Duan Y N, Pan B Z, Han X. 2012. Multi-component model and the optimize logging interpretation of glutenite reservoirs. World Well Logging Technology (in Chinese) , 33 (6) : 20-23. |
| [] | Gong S Y, Dou L M, Ma X P, et al. 2012. Study on the construction and solution technique of anisotropic velocity model in the location of coal mine tremor. Chinese J. Geophys. (in Chinese) , 55 (5) : 1757-1763. DOI:10.6038/j.issn.0001-5733.2012.05.033 |
| [] | Han X. 2012. Research on glutenite reservoirs with GA-CM hybrid optimization log interpretation method in Lishu Fault Depression[master's thesis] (in Chinese). Changchun:Jilin University. |
| [] | Kim D H, Cho J H. 2005. Adaptive tuning of PID controller for multivariable system using bacterial foraging based optimization.//Advances in Web Intelligence. Berlin Heidelberg:Springer, 231-235. |
| [] | Kim D H, Cho J H. 2006. A biologically inspired intelligent PID controller tuning for AVR systems. International Journal of Control, Automation, and Systems , 4 (5) : 624-636. |
| [] | Liu X L. 2011. Modification and application of bacterial foraging optimization algorithm[Ph. D. thesis] (in Chinese). Guangzhou:South China University of Technology. |
| [] | Luo M Q, Zhu G T, Liu H, et al. 2003. A hybrid method of matrix inversion suited for 3D implicit prestack depth migration. Chinese J. Geophys. (in Chinese) , 46 (5) : 684-689. |
| [] | Passino K M. 2002. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine , 22 (3) : 52-67. DOI:10.1109/MCS.2002.1004010 |
| [] | Serra O. 1986. Fundamentals of Well-log Interpretation:The Acquisition of Logging Data. Developments in Petroleum Science. Amsterdam:Elsevier Science. |
| [] | Tan M J, Zou Y L. 2012. A hybrid inversion method of (T2, D) 2D NMR logging and observation parameters effects. Chinese J. Geophys. (in Chinese) , 55 (2) : 683-692. DOI:10.3969/j.issn.0001-5733.2012.02.032 |
| [] | Tian Y Y, Xia H Q. 2006. Optimization log interpretation based on multi-mineral model analysis. Journal of Southwest Petroleum Institute (in Chinese) , 28 (4) : 8-11. |
| [] | Tripathy M, Mishra S, Lai L L, et al. 2006. Transmission loss reduction based on FACTS and bacteria foraging algorithm.//Parallel Problem Solving from Nature-PPSN IX. Berlin Heidelberg:Springer, 222-231. |
| [] | Wang C P. 2013. Quantitative evaluation of reservoir parameters and movable fluid in tight gas sandstone[master's thesis] (in Chinese). Changchun:Jilin University. |
| [] | Yong S H. 1995. Optimization Log Interpretation Method (in Chinese)[M]. Dongying: Petroleum University Press . |
| [] | You M L, Lei X J. 2013. An improved bacterial foraging algorithm for the traveling salesman problem. Journal of Guangxi University (Natural Science Edition) (in Chinese) , 38 (6) : 1436-1443. |
| [] | Zhang C. 2013. Improved bacterial foraging algorithm and its application to the structural optimal design[master's thesis] (in Chinese). Guangzhou:Guangdong University of Technology. |
| [] | Zhang N. 2007. Study on job-shop scheduling problems based on bacteria foraging optimization algorithm[master's thesis] (in Chinese). Changchun:Jilin University. |
| [] | Zhang X H, Zhang J F, Zeng J J. 2003. An improved algorithm of complex method in optimization. Journal of Sichuan University of Science and Technology (in Chinese) , 22 (2) : 21-23. |
 2016, Vol. 59
2016, Vol. 59




