2 Jiangsu Key Laboratory of Big Data Analysis Technology/B-DAT, Nanjing University of Information Science & Technology, Nanjing 210044, China;
3 Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing 100038, China;
4 Key Laboratory of Geoscience Spatial Information Technology, Ministry of Land and Resources, Chengdu University of Technology, Chengdu 610059, China;
5 Digital Land Key Lab of Jiangxi Province, Nanchang 330013, China
With the rapid growth of population, land resource is becoming increasingly important. Grasping the realtime status of land use accurately can protect and exploit the land resources more effectively and rationally. Remote sensing technology can choose different bands and remote sensors, get fast access to a wide range of the earth resource information, and is not restricted by the ground conditions, having the advantages that manual field measurement and aerial photography cannot match. Therefore, it has become an important technical means for land use and change detection and has a wide range of applications in the fields of stratigraphic analysis, disaster estimation, road traffic analysis, deforestation monitoring, and so on (Fan et al., 2012). Actually, the essence of change detection is extracting the change information from multi-temporal remote sensing images. Currently, change detection algorithms for multi-temporal remote sensing images can be mainly divided into two categories, namely algebraic operation based approaches and image transform based approaches. Algebraic operation based approaches include difference method (Fan et al., 2001), ratio method (Durucan and Ebrahimi, 2001), regression analysis method (Jha and Unni, 1994) and so on. Difference method and ratio method are intuitive and high-speed in change detection, but they are too simple to describe the change of the target region qualitatively and impossible to take into account the influence of the factors such as light, angle and atmospheric condition. The regression analysis method can reduce the adverse effects brought by these factors to some extent. However, we need to select the exact regression equation and appropriate band before detection, resulting in low accuracy in practical applications. Image transform based change detection algorithms are implemented mostly using the principal component analysis (PCA)(Qiu et al., 2004; Zhang and Wang, 2008), independent component analysis (ICA)(Hyvarinen et al., 2004; Zhong and Wang, 2006) or the like. PCA is a multi-dimensional orthogonal linear transform based on second-order statistical property. The first principal component obtained by transform contains most of the background information of the original remote sensing image, while the second principal component contains most of the change information. But only when the signal statistical distribution is Gaussian distribution, the relevant information between signals can be completely eliminated. However, the spectral characteristics of targets in remote sensing images do not satisfy the Gaussian distribution. Thus PCA cannot completely eliminate the higher-order related information between the various components, which affects the accuracy of change detection. As a recently proposed blind source separation technology, ICA not only can remove the second order correlation between information sources, but also can eliminate higher-order-related information (Xie et al., 2001; Berg et al., 2005). Therefore, ICA can obtain better detection results than PCA in change detection for remote sensing images.
ICA-based change detection algorithms are more sensitive to the background in the image. While detecting the changing region, they are liable to mistake the changes of background as the changes of target region due to radiation differences, resulting in the inaccuracy of change detection. Thus the wavelet transform is applied to change detection (Huang et al., 2010; Li, 2011). The image data is decomposed by the wavelet transform, which can preserve the edges, textures and fine structures while reducing the image noise, and finally improve the detection accuracy and computing efficiency. However, wavelet transform is not the optimal sparse representation of the image since it is restricted to only horizontal, vertical and diagonal directions. To a certain degree, the lack of directionality would lose the useful information of the image, and cannot accurately reflect the image edge contours and texture details. As a new extension of wavelet transform, contourlet transform has multi-resolutional, localized, directional and anisotropic properties, which has special advantages in representing the image edge contours and texture details. Therefore, if we apply contourlet transform to change detection, it is expected to improve detection accuracy. In addition, the existing ICA algorithm has disadvantages such as great computational burden, slow convergence and so on. Compared with the existing ICA algorithm, we adopt an improved ICA algorithm which can accelerate the convergence and meet the requirement of real-time processing. Moreover, there is no need to adjust the learning rate factor or other dynamic parameters, which enhances the reliability.
Based on the above analysis, a change detection algorithm for multi-temporal remote sensing images is proposed in this paper based on contourlet transform and ICA. Firstly, a multi-scale decomposition is applied to the multi-temporal remote sensing image by contourlet transform. Utilizing its features, the image block division could be implemented better in order to reduce the complexity of the ICA algorithm. Then, we use an improved ICA algorithm to process the decomposed data to improve the accuracy and efficiency of change detection. Detailed experimental results are presented. The proposed method is compared with the existing PCA based algorithm, ICA based algorithm, wavelet transform and ICA based algorithm. According to subjective visual quality and objective quantitative indicators such as misjudged error of changed pixels, misjudged error of unchanged pixels, overall accuracy and running time, the proposed algorithm is superior to the above-mentioned algorithms.
2 PRINCIPLE OF ICA AND CONTOURLET TRANSFORMICA is a multi-dimensional signal processing algorithm developed from blind source signal separation technology in recent years (Yu et al., 2010; Khaparde, 2012). Its basic principle is to establish an objective function based on equal independence measurement criterion, making the separated independent component approximate to the source signals as much as possible. Given a set of observed signals X = [x1, x2, …, xm]T and mutually independent source signals S = [s1, s2, …, sn]T, the i-th observed signal xi is formed by the linear combination of n independent source signals:
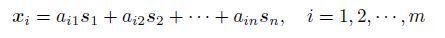
|
(1) |
where aij is the signal mixing coefficient. The observed signal X can be expressed as the product of source signal S and linear mixing matrix A:
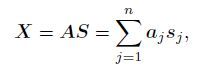
|
(2) |
where linear mixing matrix A = [a1, a2, …, an], aj is the base vector of mixing matrix. The source signal S is recovered from the observed signal X under the condition that mixing matrix A and source signal S are unknown in ICA. Unmixing matrix H is defined to make the output signal Y = HX = HAS unmixed by matrix H has the largest independence. The principle diagram of ICA is given in Fig. 1.

|
Fig. 1 The principle diagram of ICA |
ICA algorithm needs to make the following assumptions (Marchesi and Bruzzone, 2009). First, source signal S is a mutually independent stationary stochastic process. Second, the number of observed signals is not less than that of source signals. Third, at most one source signal obeys Gaussian distribution. Actually, ICA is an optimization problem. Owing to the lack of unique solution, the approximate solution can only be sought on a criterion of independence measurement, and each component in Y is independent of each other as much as possible.
Contourlet transform (Bai et al., 2009; Li et al., 2012) is a multi-direction and multi-scale analysis algorithm based on the multi-scale analysis idea of wavelet. The image multi-scale decomposition is accomplished by Laplacian pyramid (LP) transform to capture the singular point. Then, singular points distributed in the same direction are synthesized into a coefficient by directional filter bank (DFB). Contourlet transform has the properties of multi-resolution, localization, multi-direction, neighbor boundary sampling and anisotropy, which could capture the singularities of lines and surfaces in two-dimensional image better and use fewer coefficients to describe the edge contours and directional texture information.
3 CHANGE DETECTION ALGORITHM BASED ON CONTOURLET AND ICA 3.1 Change Detection Algorithm Based on Improved ICAFor multi-temporal remote sensing images, each pixel is a mixture of many kinds of corresponding ground object information, where each signal source (spectral information of various substances) is independent of each other. Some of these signal sources are stationary and the others are changing. It can be assumed that the background image consists of stationary signal sources and the change image consists of changing signal sources. In the ICA model, the mixed signal constituted by former and latter temporal remote sensing images is a mixture of two independent signal sources, namely background image and change image. The specific separating process is as follows:
(1) First of all, by line-wise scanning, each remote sensing image is reshaped into one-dimensional signal xi(i = 1, 2, …, n), where n is the number of remote sensing images. Then the observed signal X =[x1, x2, …, xn]T is constructed.
(2) Unmixing process is achieved by two steps (Ma and Wang, 2010), namely sphering process (W) and orthogonal transform (U), as shown in Fig. 2. The sphering process is to pre-whiten the observed signal X, making the variance of the sphered vector z = [z1, z2, …, zn]T is 1 and its expected value is 0 to reduce the computational complexity and noise. The orthogonal transform U can make the output data Y = [y1, y2, …, yn]T independent of each other as much as possible.

|
Fig. 2 The unmixing diagram of ICA |
(3) The estimation of the original signal Y is obtained after unmixing. Then, the separated signal components yi(i = 1, 2, …, n) are converted to an image. Finally, the chosen change image is converted to binary image by thresholding and the change result is obtained.
Step (2) is the most important step in the entire change detection process, and how to seek the orthogonal transform matrix U = [u1, u2, …, un]T quickly is the most critical in Step (2). Most existing ICA algorithms use fixed point algorithm based on negentropy since it is the optimal tool for measuring the non-Gaussian property of random variables (Wang et al., 2006). It is used to find every component ui of orthogonal matrix U, making the projection yi = uiT z have the largest non-Gaussian property. The basic idea is as follows: the approximate Gaussian distribution function p (y)can be expressed as

|
(3) |
where y is the shorthand for unmixed output data yi, pc(y)is the standard Gaussian distribution, F(i)(y) is the selected non-polynomial function which meets properties of moment vanishing and orthonormalization, ci is the non-polynomial function coefficient. In order to simplify the calculation in Eq.(3), we can make N = 2. The negentropy of y is obtained by symmetry property of probability density function:
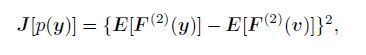
|
(4) |
where v is a random variable obeying N(0, 1) distribution. One component is obtained in each projection of the fixed point algorithm based on negentropy. The negentropy of the component yi obtained by the i-th projection is given as
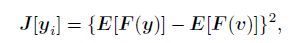
|
(5) |
where F is the shorthand for function F(2)in the Eq.(4). We can know yi = uiT z from the unmixing process, where uiT is the i-th row of the matrix U = [u1, u2, …, un]T, z is the sphered data. Take the derivative of J(yi) with respect to ui:
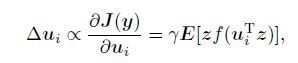
|
(6) |
where 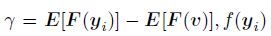
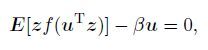
|
(7) |
where function f is the derivative of F, 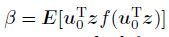

|
(8) |
After each extraction of an independent source, we should perform orthogonalization once more before next extraction, in order to ensure that the signal source to be extracted in each time has not been extracted yet. Because matrix inversion is involved in the process of calculating Jacobian matrix and its computational complexity is quite large, all the Jacobian matrices are generally replaced with Jac(u0) to reduce the computing burden. However, it would lower the convergence speed and may cause the algorithm unable to converge.
Aiming at the above problems, an improved fixed-point ICA algorithm based on Newton iterative algorithm is given (Zeng et al., 2003; Li et al., 2010). Assuming that ui(k) is obtained, we can gain ui(k +1) through the following process:
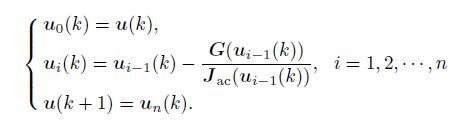
|
(9) |
The improved algorithm can accomplish n iterations by only calculating Jacobian matrix once. Compared with the general ICA algorithm, its convergence rate is faster, satisfying the requirement of real-time processing. Since there is no need to adjust the dynamic parameters like learning rate factor, its reliability is enhanced as well.
3.2 Procedure of Change Detection Algorithm Based on Contourlet and ICADue to the large size of image data matrix and the complexity of ICA algorithm, the image data is usually pre-processed before the independent component extraction to optimize the combination of the data blocks and make the subsequent data processing algorithm more efficient. In this paper, the image matrix is divided into blocks by contourlet transform, and then we apply independent component analysis to the divided image data and get the mutually independent components. Finally, the image data matrix is reconstructed by the inverse contourlet transform to obtain the change image. The implementation flowchart is shown in Fig. 3.
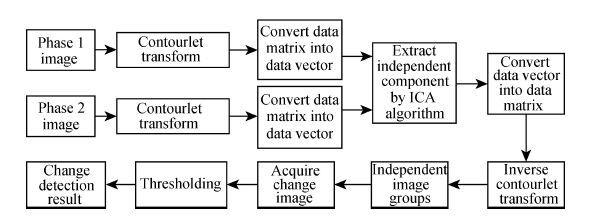
|
Fig. 3 Flowchart of change detection based on contourlet transform and ICA |
Specific implementation steps are as follows:
Step 1: Apply the multi-scale decomposition to the multi-temproal remote sensing image X1 by contourlet transform. Then the decomposition results are reshaped into vector form to get the block vector that consists of low-frequency component C1j and high-frequency components 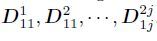
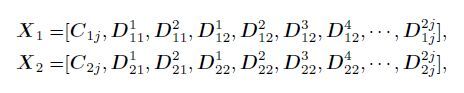
|
where j represents the decomposing layer.
Step 2: The data vectors gained by contourlet transform are taken as the input signal of the ICA algorithm. The extraction of the change region vector is achieved by the independent component analysis, namely
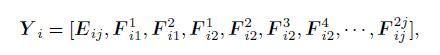
|
where Eij is the low-frequency component of the change image, 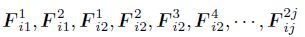
Step 3: The data vectors of change region are converted into a matrix. Then the change image is obtained by the inverse contourlet transform. The final change detection result is gained through thresholding.
Decomposing data block through contourlet transform makes the decomposed data blocks retain the characteristics of the original data in each frequency point and each direction, which optimizes the estimation of the source signal by ICA and reflects the changes of image blocks more accurately.
4 EXPERIMENT RESULTS AND ANALYSISTo verify the effectiveness of the algorithm proposed in this paper, change detection experiments are made on a large number of multi-temporal remote sensing images using the PCA based algorithm, the ICA based algorithm, the wavelet transform and ICA based algorithm and the proposed algorithm. The experimental environment is: Intel (R) Core (TM)2, 2.0 GHz, 1 GB memory, Matlab R2007b. In the wavelet transform part, the Daubechies orthonormal wavelet basis is adopted and the image is decomposed to the third layer. We select two real remote sensing image datasets to illustrate. The first real remote sensing image dataset consists of the images of the Red River in Vietnam taken in August 1996 and August 1998, which are SAR images obtained by ERS-2 remote sensor, as shown in Figd. 4a and Fig. 4b, respectively. The gray level of two remote sensing images are both 256, the size is 512×512 pixels and the change region is mainly caused by the flood.

|
Fig. 4 The first group of real remote sensing images |
The second remote sensing image dataset is the sample data from Erlas8.5, composed of SPOT images of a certain area taken in 1987 and 1992, as shown in Figs. 5a and Fig. 5b, respectively. Changes have occurred in several spots in this area, and the change type is complex. The gray level of the two remote sensing images is both 256 and the size is 512×512 pixels.

|
Fig. 5 The second group of real remote sensing images |
Aiming at the above two groups of real remote sensing images, the image components are separated by the PCA based algorithm, the ICA based algorithm, the wavelet transform and ICA based algorithm and the algorithm proposed in this paper, as shown in Fig. 6 and Fig. 7, respectively. Among them, Fig. 6a and Fig. 7a show the image components separated by the PCA based algorithm, where the left image is the first principal component of the image and the right one is the second principal component. Fig. 6b and Fig. 7b show the image components separated by the ICA based algorithm. Fig. 6c and Fig. 7c present the image components separated by the wavelet transform and ICA based algorithm. Fig. 6d and Fig. 7d display the image components separated by the proposed algorithm.
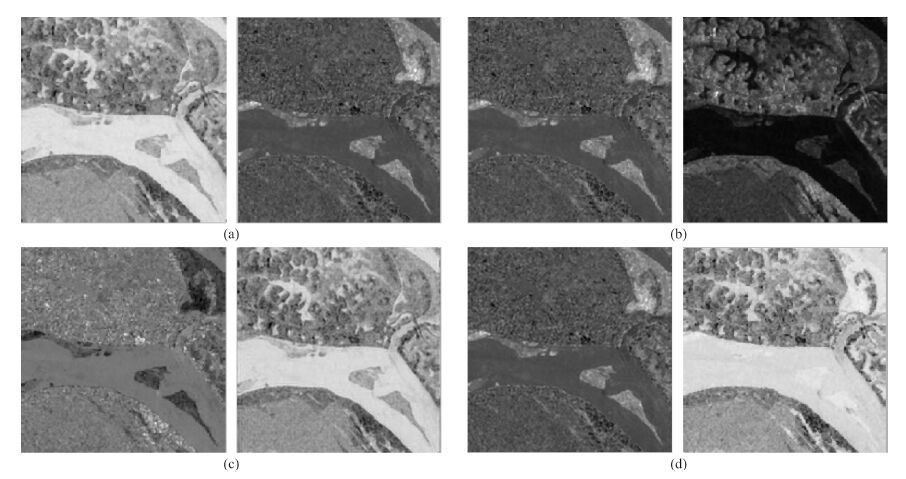
|
Fig. 6 The separated components of the first group of remote sensing images |

|
Fig. 7 The separated components of the second group of remote sensing images |
It can be seen from Fig. 6a and Fig. 6b that the first principal component separated by PCA is the background image while the second principal component is the change image. We can see from the separated component image that the ground object information of the image is partially mixed and the background image also contains the change information of incomplete separation, which shows PCA cannot completely eliminate the correlation between the various components in remote sensing images. Meanwhile, the ICA based algorithm, the wavelet transform and ICA based algorithm and the proposed algorithm can separate the change image better, which demonstrates that the ICA based algorithm has better ability than the PCA based algorithm in decorrelation and separating images. Then comparing Fig. 6b, Fig. 6c and Fig. 6d, it can be observed that there are still some contours of the change region in the background images of Fig. 6b and Fig. 6c while the background image of Fig. 6d hardly mixes any change information with fewer changes. In the background images of Fig. 7b and Fig. 7c, the dark region is the change region while the background image of Fig. 7d almost has no information of the change region and the change image is completely separated from the background image. Therefore, compared with the ICA based algorithm and the wavelet transform and ICA based algorithm, the proposed algorithm in this paper can separate the change information better.

|
Fig. 8 Change detection results of the first group of remote sensing images |

|
Fig. 9 Change detection results of the second group of remote sensing images |
In order to verify the effectiveness of the proposed algorithm, the Otsu image thresholding algorithm (Chen et al., 2010) is used to segment the change images in Fig. 6 and Fig. 7 and the change detection results are shown in Fig. 8 and Fig. 9. The final change detection results obtained by the PCA based algorithm, the ICA based algorithm, the wavelet transform and ICA based algorithm and the proposed algorithm are shown in Figs. 8- 9a, b, c and d, respectively. From the above results, we can see that the change detection results obtained by the PCA based algorithm contain a lot of pseudo change information caused by illumination factors in different temporal phases while the ICA based algorithm, the wavelet transform and ICA based algorithm and the proposed algorithm all get better change detection results. In addition, for the marked regions in Fig. 8, compared with the traditional ICA based algorithm, the wavelet transform and ICA based algorithm and the proposed algorithm can get finer detection results in the place of concave edge contours with better edge continuity. This demonstrates that the image decomposition through the contourlet transform or wavelet transform can optimize the processing of the edge details by ICA method. The isolating points in the change detection results obtained by the proposed algorithm are less than that obtained by the wavelet transform and ICA based algorithm, which shows that the change detection effect of the proposed algorithm is better. For the marked regions in Fig. 9, it can be seen from the marked regions at the top of figure that the change detection results obtained by the traditional ICA based algorithm have some broken points while the edge contours in the change detection results obtained by the proposed algorithm are more complete, demonstrating that the contourlet transform preserves more edge detail features in the image. Besides, it can be seen from the marked regions in the middle of the figure that the proposed algorithm detects a complete line-shaped unchanged region and it coincides with the change phenomena in the real remote sensing image while the other algorithms fail to detect it completely. This is because the proposed algorithm utilizes the properties of the multi-scale, multi-direction and anisotropy of the contourlet transform and the decomposed data blocks preserve the characteristics of the original data in different frequencies and directions, which could improve the estimation accuracy of source signals using ICA and reflect the change information more accurately.
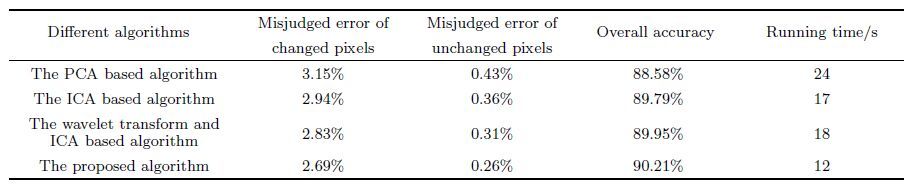
The four change detection algorithms are compared for two groups of real remote sensing images according to the objective quantitative evaluation indexes such as the misjudged error of changed pixels and misjudged error of unchanged pixels, the overall accuracy and running time. The change detection results of the remote sensing images in the second group are shown in Table 1. Compared with the PCA based algorithm, the ICA based algorithm and the wavelet transform and ICA based algorithm, the proposed algorithm improves the accuracy by 1.8%, 0.5% and 0.3%, respectively. Since the contourlet transform can better describe the contours and directional texture information in the images and make up for the deficiency of the wavelet transform well, the proposed algorithm can process the edge details better and achieve smaller false detection rate and higher overall accuracy. As for the running time, compared with three other methods, the proposed algorithm reduces 12 s, 5 s and 6 s, respectively. The wavelet transform and ICA based algorithm consumes more time than the ICA based algorithm since the wavelet transform merely rearranges the data better. Coupled with the time used for the wavelet transform, the former algorithm has no advantage in overall running time. In the proposed algorithm, the multi-direction and multi-scale decomposition and optimal combination are applied to the data by contourlet transform, and the improved fixed point ICA algorithm based on Newton iteration is adopted as well. Thus the running time is reduced a lot. Above all, compared with the PCA based algorithm, the ICA based algorithm and the wavelet transform and ICA based algorithm, the proposed algorithm has higher accuracy and running speed.
|
|
Table 1 Comparison of four change detection algorithms in accuracy |
A contourlet transform and ICA based change detection algorithm for multi-temporal remote sensing images is proposed in the paper. The accuracy of the change detection is improved and the computational complexity is reduced due to multi-resolution decomposition and better directionality and anisotropy of the contourlet transform. The computing efficiency is increased by the improved ICA algorithm. Experimental results show that, compared with three existing algorithms such as the PCA based algorithm, the ICA based algorithm and the wavelet transform and ICA based algorithm, the proposed algorithm can preserve the edges and details better. The change images obtained by the proposed algorithm have higher accuracy and better robustness. The proposed algorithm requires less running time and it can be extended to remote sensing image sequences with more temporal phases. The proposed algorithm is an accurate and effective change detection method for multi-temporal remote sensing images.
ACKNOWLEDGMENTSThis work was supported by the National Natural Science Foundation of China (61573183), Open Fund of Jiangsu Key Laboratory of Big Data Analysis Technology/B-DAT, Nanjing University of Information Science & Technology (KXK1403), Beijing Key Laboratory of Urban Spatial Information Engineering (2014203), Key Laboratory of Geo-spatial Information Technology, Ministry of Land and Resources, Chengdu University of Technology, China (KLGSIT2015-05), Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology (DLLJ201412) and Funding of Jiangsu Innovation Program for Graduate Education.
| [1] | Bai R, Yang W H, Zhang Y N. 2009. Remote sensing image fusion algorithm based on contourlet transform[J]. Journal of Image and Graphics , 14 (6): 1173–1177. |
| [2] | Berg M, Bondesson E, L ow, et al. 2005. A combined on-line PCA-ICA algorithm for blind source separation[J]. Asia-Pacific Conference on Communications, Perth, Western Australia : 969–972. |
| [3] | Chen Q, Xiong B L, Lu J, et al. 2010. Improved two-dimensional Otsu image segmentation method and fast recursive realization[J]. Journal of Electronics & Information Technology, 32 (5): 1100–1104. |
| [4] | Durucan E, Ebrahimi T. 2001. Change detection and background extraction by linear algebra[J]. IEEE Transactions on Image Processing, 89 (10): 1368–1381. |
| [5] | Fan H S, Ma A N, Li J. 2001. Case study on image differencing method for land use change detection using thematic data in Renhe district of Panzhihua[J]. Journal of Remote Sensing , 5 (1): 75–80. |
| [6] | Fan K G, Huang W G, He M X, et al. 2012. Marine atmospheric boundary layer depth retrieval by SAR in China Sea[J]. Chinese J. Geophys. , 55 (4): 1137–1143. |
| [7] | Huang S Q, Liu D Z, Hu M X, et al. 2010. Multi-temporal SAR image change detection technique based on wavelet transform[J]. Acta Geodaetica et Cartographica Sinica , 39 (2): 180–186. |
| [8] | Hyvrinen A, Karhunen J, Oja E. 2004. Independent Component Analysis. John Wiley and Sons Inc. |
| [9] | Jha C S, Unni N V M. 1994. Digital change detection of forest conversion of a dry tropical forest region[J]. International Journal of Remote Sensing, 15 (13): 2543–2552. |
| [10] | Khaparde. 2012. A study of ICA algorithm for separation of mixed images[J]. International Conference on Digital Information and Communication Technology : 82–86. |
| [11] | Li F F, Xiao B L, Zhang Q. 2010. New wetland change detection method based on improved independent component analysis[J]. Journal of Computer Applications , 30 (5): 1347–1350. |
| [12] | Li P. 2011. Multitemporal remote sensing images change detection based on wavelet transform and ICA[Master's thesis]. Xidian University. |
| [13] | Li S T, Fang L Y, Yin H T. 2012. Multitemporal image change detection using a detail-enhancing approach with nonsubsampled Contourlet transform[J]. IEEE Transactions on Geosciences and Remote Sensing, 9 (5): 836–840. |
| [14] | Ma C. 2010. Review of ICA based fixed-point algorithm for blind separation of mixed images[J]. International Conference on Bioinformatics and Biomedical Engineering, Xi'an, China : 1–3. |
| [15] | Marchesi S, Bruzzone L. 2009. ICA and kernel ICA for change detection in multispectral remote sensing images[J]. IEEE International Geoscience and Remote Sensing Symposium, Mantova, Italy : 980–983. |
| [16] | Pham D T, Cardoso J F. 2001. Blind separation of instantaneous mixtures of nonstationary sources[J]. IEEE Transactions on Signal Processing, 49 (9): 1837–1848. |
| [17] | Qiu B, Prinet V, Perrier E, et al. 2003. Multi-block PCA method for image change detection[J]. Proceedings of the 12th International Conference on Image Analysis and Processing Mantova, Italy : 385–390. |
| [18] | Wang C R, Du J, Zhang X L. 2006. Research of image separation based on improved independent component analysis[J]. Chinese Journal of Scientific Instrument , 27 (6): 785–786. |
| [19] | Xie D G, Zhang X D, Li X L, et al. 2007. Radar target recognition method based on independent component analysis[J]. Systems Engineering and Electronics , 29 (2): 164–166. |
| [20] | Yu X C, Cao T T, Hu D, et al. 2010. Blind image separation based on wavelet transformation and sparse component analysis[J]. Journal of Beijing University of Posts and Telecommunications , 33 (2): 58–63. |
| [21] | Zeng S G, Zhu N B, Bao Y, et al. 2003. A modified fast independent component analysis and its application to image separation[J]. Journal of Image and Graphics , 8 (10): 1160–1165. |
| [22] | Zhang H, Wang J G. 2008. A SAR image change detection algorithm based on principal component analysis[J]. Journal of Electronics & Information Technology , 80 (7): 1727–1730. |
| [23] | Zhong J Q, Wang R S. 2006. Multitemporal remote sensing images change detection based on ICA[J]. Journal of Electronics & Information Technology , 28 (6): 994–998. |
 2016, Vol. 59
2016, Vol. 59