Recently, owing to the good local property in time and frequency domain, wavelet is widely used in random noise suppression for seismic signal. The commonly used two-dimensional wavelet is the separable wavelet composed of the product of one-dimensional wavelet tensors. However, it merely works in the horizontal, vertical, and diagonal directions, and its filter kernels have no direction which results in the same degree of filtering for all directions. Filter coefficients of two-dimensional wavelet can hardly sparsely express directional information of seismic events, which can not make edge details clear. 2-D wavelet can hardly reflect the accurate time-frequency localization as in one-dimensional case (Zhang and Yin, 2004; Yu and Whitcombe, 2008). In order to overcome the omnidirectional deficiency of wavelet, Ridgelet transform was introduced, which first makes a Radon transform to map straight lines to points on the surface, then conducts a wavelet transform to improve the detection result of straight lines. However, in practice, most contours of seismic events in the record are not so straight that they cannot be transferred into concentrative points ideally, therefore, it is rarely used in processing the seismic signals. Later, subdivision of block structure was introduced and the curvature of the curve in localized part is small enough so that the curve can approximately be processed as the straight line, namely, Curvelet transform. Curvelet solved the deficiency of directionality in wavelet, and made sub-band partition. It has bases with clear directions, which could sparsely denote the smoothing areas in an image and also well sparsely represent the edges, and has a better applicability. But the directionality of Curvelet is improved by increasing the number of waves and direction filters, which results in the data redundancy for a huge data storage space and inevitably brings in edge effect (Candès and Donoho, 1999; Candès et al., 2006; Lin and Wang, 2009; Oliveira et al., 2012; Yuan et al., 2013). To achieve a low redundancy, after implementing Curvelet with discretization and making a multiscale and multi-direction analysis with Laplacian Pyramid, the Contourlet is got, which has a good effect on the seismic data processing. But it is still unable to overcome the deficiency of Curvelet itself (Do and Vetterli, 2002; Li et al., 2008).
We consider that if there’s a kind of filters which is continuous in directions, and it can yield arbitrary direction without interpolation calculation. Freeman and Adelson et al.(1991) proposed the theoretical framework of steerable filter, whose basic idea is that all the filters along arbitrary directions can be described as a set of linear combination of base filters. In this case, it looks like the filters could rotate along arbitrary direction, hence comes the name. According to the thought of steerable filter, the convolution of an input image and fixed base filters can estimate the convolution of the image and any rotation angle filter efficiently, which greatly reduces the amount of calculation. In the analysis of directional features (edges or ridge etc), steerable filters have many applications. By combining it with Hilbert transform for an orthogonal filter bank, Zheng et al.(2002) proposed a new image fusion method based on steerable filter; Shi et al.(2009) proposed an automatic calculation method of closed geometric figure; Zhang et al.(2005) combined steerable filter with wavelet analysis, which also achieved a good image fusion purpose, and demonstrated that this method had a better effect than conventional wavelet image fusion methods. Based on the steerable filter ideology, steerable filter is usually applied in the pyramid algorithm and conducts multi-scale and multiple directions analysis for an image. Dong and Lian (2008) proposed a modified model of visual information processing based on that thought, which effectively overcame an important problem in the face identification. Lin et al.(2011, 2012) applied steerable pyramid to the decomposition of 3-D seismic slices, which can not only analyze the features and the trend of fault in different scale directions, but also can obtain fault information. Getting the texture trend via steerable filters is applied to pattern recognition, such as palm grain (Wang and Ruan, 2008) and iris (Li, 2007). So steerable filter is mainly used in the image processing field. If it is introduced into the seismic signal preservation and random noise suppression successfully, it would be of great significance. This paper proposes a new kind of steerable filter for seismic signal denoising, which can separate different directional features and noise by analyze local mode angle signal of each pixel in an input image relying on its high directional selectivity, so as to enhance events and suppress noise.
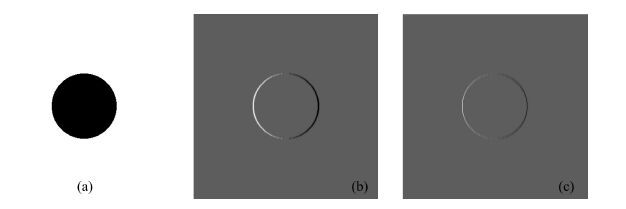
Freeman and Adelson (1991) adopted Hermite-Gauss Functions (HGFs) denoted by the product of Hermite polynomials and isotropic Gauss function. An inherent limitation of HGFs, which is caused by isotropic Gauss factor, is that it has a smoothing effect in all directions and can not protect details well. Thus, a parameter is introduced into Gauss function to elongate HGFs so as to get the Elongated Hermite-Gauss Functions (EHGFs), as shown in Fig. 1d. E-HGF has a clear directionality and reduces the smoothing effect on the gradient direction (Perona, 1995) while enhances the sensitivity for events as well. Fig. 1 gives a simple comparison of HGFs with E-HGFs. From the filtering results in Fig. 1e and 1f, E-HGFs can localize the event location better while it conducts denoising processing. However, a major defect of E-HGFs is that E-HGFs do not have the steerability, so it is necessary to design a steerable E-HGF fitting function to make E-HGFs have a steerable characteristic, and the fitting process is given in Section 2.2. With the high directional selectivity and efficiency, a local filtering processing can be done. According to the non-directionality of random noise, considering the directions of structure and sequence, combining statistical property, we can filter along the direction of events. The processing results of theoretical model and common shot record given in section 3 indicate that the proposed algorithm can achieve the purpose for random noise suppression and preservation of signal amplitude at the same time.

|
Fig. 1 Comparison of filters of HGFs and E-HGFs |
If a set of filters f(r, λ)(where r represents the vector in Cartesian coordinate and λ represents a filterdependent parameter) can be expanded into a linear combination of a finite number of basic filters Vn(r)(n = 1, 2, · · ·, N), with the linear coefficients a(λ) depending on λ only, then we say these filters have the property of steerability, i.e.,
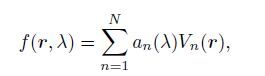
|
(1) |
where a(λ) is the function of λ and V(r) is the basic filter. In such a case, filtering an image I(r) with the filter kernel f (r, λ) can be exactly obtained by filtering I(r) with the basic filters Vn(r). This process can be expressed by Eq.(2), in which convolution is represented by symbol ‘*’.
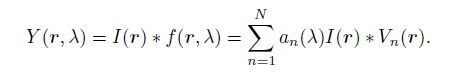
|
(2) |
As can be seen from the Eq.(2) that Y(r, λ) can be evaluated for any value of λ in case that the terms I(r)*Vn(r) and a(λ) are determined. Because convolution is a linear operation which avoids the discretization error caused by discretizing parameter λ. And the f(r, λ) could be considered as a continuous function of λ, which make f (r, λ) have exact integral and derivative feature by integrating or differentiating the linear coefficients a(λ). Compared with discretizing λ, steerable filters require a smaller number of convolutions for the same accuracy without discretization error.
Next, focus our study on the direction of rotation, i.e., the parameter λ is equal to the rotation angle θ. The rotation operation can be expressed as f(r, θ)= Rθ(f), where Rθ(·) is the rotation matrix Rθ =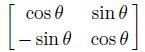
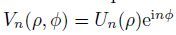
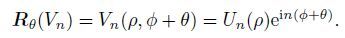
|
(3) |
Therefore, if a given filter kernel T(r) can be expanded into a sum of appropriate CHF Vn(r), shown in Eq.(4):
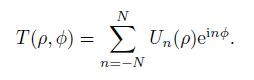
|
(4) |
Then the rotation operation of T(r) can be written as Eq.(5):
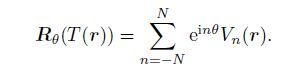
|
(5) |
Comparing the Eq.(5) with Eq.(1), it can be concluded that T(r) has the property of steerability. These filter kernels are called steerable filters. In actual process of images, the scheme is shown in Fig. 2(Perona, 1995).
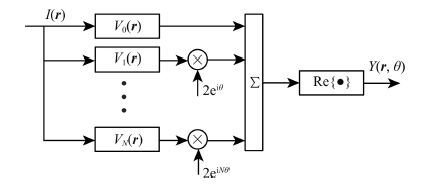
|
Fig. 2 Structure of processing an image in any orientation |
E-HGFs are the functions Hk, l (x, y; μ) that meet Eq.(6),
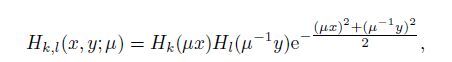
|
(6) |
where 
|
Fig. 3 Filter response to the first derivative of HGFs and E-HGFs for synthetic image |
A limitation of the E-HGFs is that they are not steerable, i.e., they need an infinite set of basic filters to be exactly represented in Eq.(5). Therefore, finding the steerable functions which best approximate the E-HGFs is required. LGT and SVD are two well-established frameworks to achieve this goal in literatures. The output of LGT is continuous spectrum function that cannot do a finite factorization. SVD overcomes the drawback of LGT by obtaining a discrete set of orthogonal steering functions. However, the analytical expressions are difficult to work out by SVD. Moreover, both methods can only get a somewhat imprecise decomposition. In this paper, the method proposed by Giuseppe Papari in 2012 is employed, which is based on the foundation of SVD framework and introduces an ad hoc matrix notation to generate compact wavelet functions.
Firstly, illustrate the shifting matrix S defined by Papari. For any vector r, {r}n denotes the nth element in r. Then we have {Skr}n = {r}n+k, i.e., the kth power of S produces a shift of k positions.
Then, Papari defined three notations for convenience:
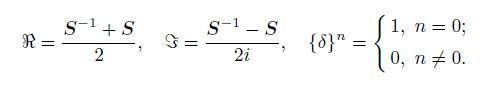
|
(7) |
Let 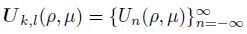
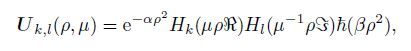
|
(8) |
where 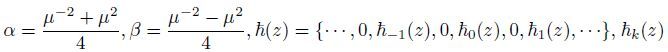
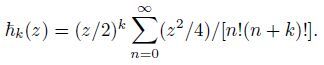
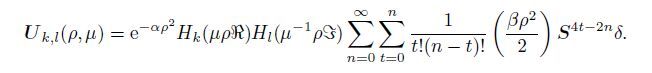
|
(9) |
In Eq.(9), 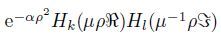
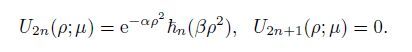
|
(10) |
Figure 4 lists the basic filter of n = {0, 1, 2, 3, 4, 5} with the parameter value k = 0, l = 0.

|
Fig. 4 Basic filters when k = 0, l = 0 and n = {0, 1, 2, 3, 4, 5} |
In this part, in order to obtain directional responses, the E-HGFs are used to filter the seismic data. First of all, according to the variance measure for each point directional responses, the valid signal is preliminarily distinguished from the noise. Then integrate local means to further extract the valid signal on the basis that random noise point has a smaller mean. Finally, do the nonlinear filtering for the directional data according to the size of the variance ratio. The essence of this processing is that the directional dimension is introduced into the signal and the filters filter along the in-phase axis of seismic data. The algorithm process is summarized as follows:
(1) Design the steerable filter with the method proposed by Papari et al.(2012).
(2) Input common shot seismic gathers to do direction filtering, which will construct the three-dimensional data of ‘Time-Space-Direcion’.
(3) According to the isotropic nature of noise, compute the variance in the directional dimension and suppress the point whose variance is lower than a threshold.
(4) Calculate the local means to further distinguish the valid signal from the noise, which will avoid misjudgments in the third step.
(5) Suppress the detected noise points and keep the biggest directional response for other points.
(6) Remove burrs by using a low pass filter with bandwidth wide enough.
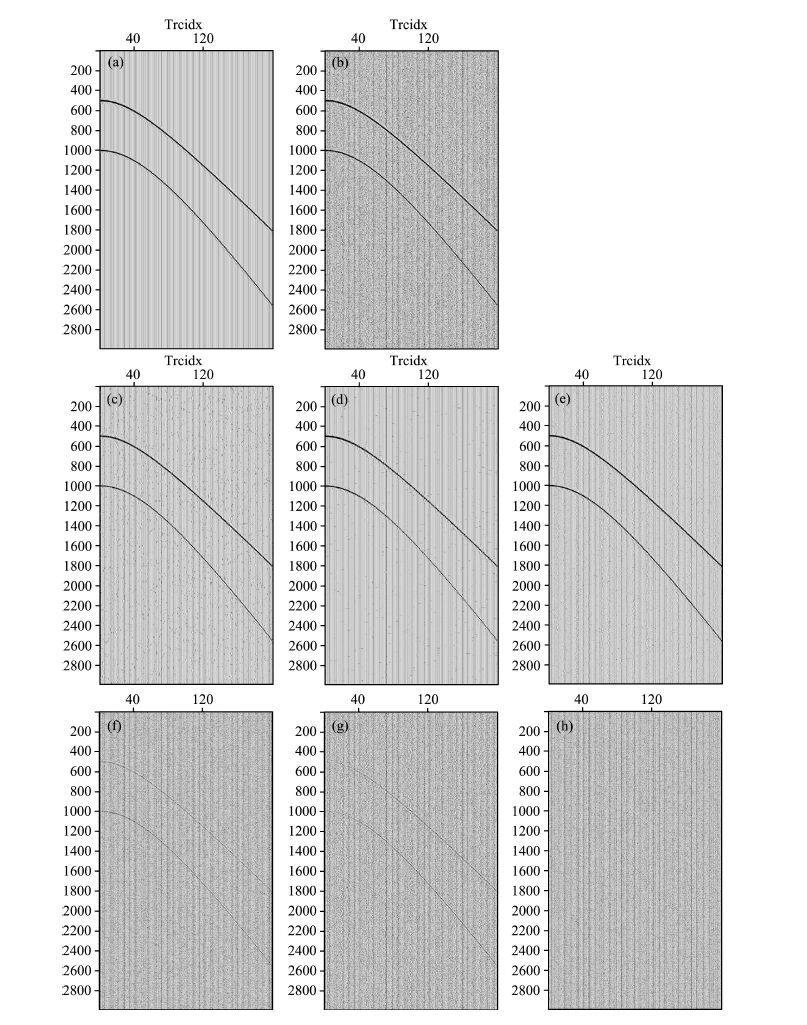
Figure 5a shows a pure synthetic record of 200 channels and the two reflection events with dominant frequencies of 30 and 23 Hz and velocities of 1800 and 2300 m·s-1, respectively, embedded in WGN with the SNR of -5 dB as shown in Fig. 5b. Figs. 5(c)(d)(e) show the de-noising results by the methods of traditional wavelet transform, Curvelet transform and the proposed method, respectively. To make the contrast even more remarkable, the difference images are posted in Figs. 5(f)(g)(h) for these three methods correspondingly. Theoretically, there are four classical choices to obtain the threshold for wavelet:(1) Stein unbiased likelihood estimation threshold;(2) Global threshold 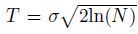
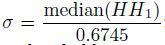
|
Fig. 5 (a) Raw seismic record with two reflection events. (b) Record with the SNR of –5 dB; (c), (d) and (e) Results after the conventional Wavelet transform, Curvelet transform and steerable filters; (f), (g) and (h) Difference diagrams of conventional wavelet transform, curvelet transform and steerable filters |
These four threshold methods are all used in the lab tests. And the signal is decomposed into three layers wavelet coefficients. Then we choose global threshold method in this paper for a compromise between de-noising and amplitude preservation. The hard threshold presented by Lin and Wang (2009) is employed in Curvelet transform, i.e., 
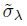
|
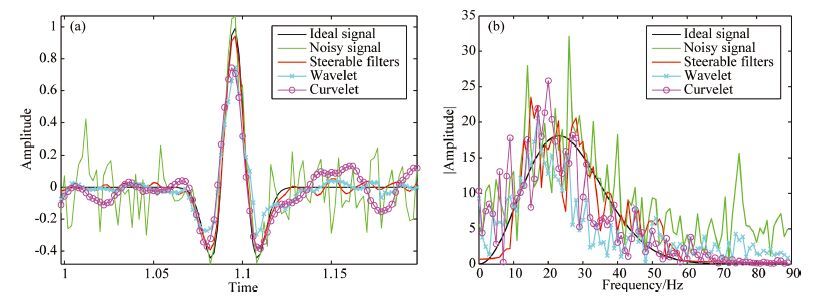
Fig. 6 (a) Waveforms of signal in the 102nd channel; (b) Spectrum of signal in 102nd channel |
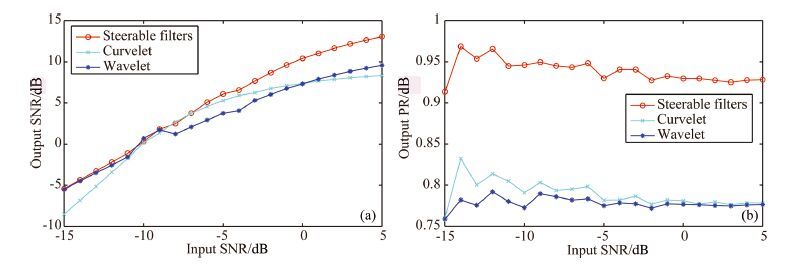
Figure 7a plots the SNR of filter results by these three methods under different background noise ranging from -15 dB to 15 dB with a one-dB interval. From Fig. 7a, it can be seen that all these methods can depress noise and obtain a high SNR. However, the output SNR of the proposed method is higher than that of the other two methods. Fig. 7b gives out the mean output amplitude curves of three methods under different background noise. It is clear that the proposed method is much better in maintaining signal amplitude. Moreover, Fig. 7b could explain that the capability of keeping signal depends on the algorithm itself rather than the background noise.
|
Fig. 7 (a) SNR after processing by different methods under different background noise; (b) Keeping average amplitudes after processing by different methods under different background noise |
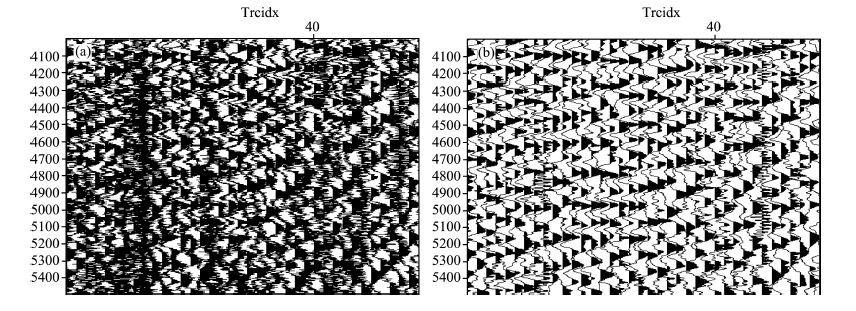
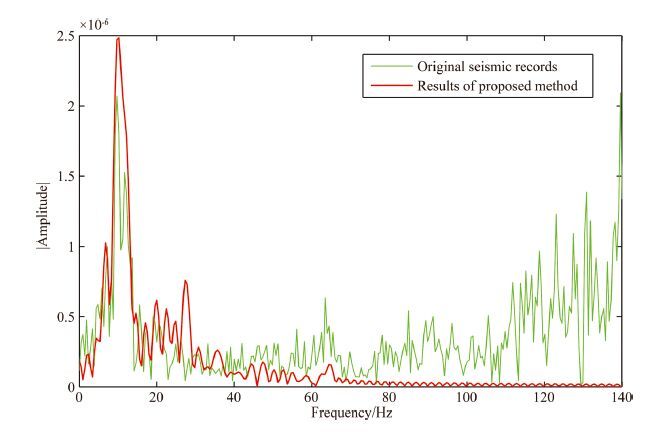
Simulation results demonstrate the effectiveness and feasibility of the proposed method. Then the proposed method is used for real seismic records. In practice, a real seismic shot gather with 168 channels, whose sample frequency is 1000 Hz and having 2501 data points for each channel, is provided to validate the capability of this proposed algorithm. Fig. 8a shows the collected signal. Fig. 8b presents the processed result of the proposed method. Compared with Fig. 8a, the random noise that manifests as the black background has been significantly suppressed in Fig. 8b. And the seismic events are more contiguous. Moreover, some events submersed in the intense background noises are restored. For a further detailed observation, the rectangle area ranging from 15~50 channels and 4000~5500 points of Fig. 8 is amplified as Fig. 9, respectively. After the processing by proposed method, the events can be seen in the Fig. 9b compared with Fig. 9a, visually. Finally, Fig. 10 shows the comparison of spectra of original seismic records and processed signal of the 22nd channel ranging from 3600~5000 points. The signal in frequency range of 5 Hz to 40 Hz is maintained and even enhanced. In reality, most of valid signal in seismic data is distributed in low frequency and noise is distributed in high-frequency mostly. Considering Fig. 10 together, we get that the proposed method can suppress random noise effectively as well as keep the amplitude.

|
Fig. 8 (a) Original seismic records; (b) Results of processing by proposed method |
|
Fig. 9 (a) Local original seismic records; (b) Results of processing by proposed method |
|
Fig. 10 Comparison of spectra of original seismic records and processed signals |
In this paper, the E-HGF steerable filters are firstly employed to analyze seismic data and remove noise. This algorithm takes geometric properties in space of events into account. Filters are designed to have a high directional resolution to precisely locate events by using the high orientation selectivity of E-HGFs. It can not only reduce calculation amount, but also can filter along the event to achieve the effect of suppressing random noise as well as maintaining signal amplitude. The record after processing by the proposed method has a higher SNR and the events get clearer and more continuous than those before processing. However, there is a limitation that the data reorganization is performed by local threshold based on statistical characteristics. In the future, we will study on how to select the data adaptively so as to get a better filtering result.
ACKNOWLEDGMENTSThis work was supported by the National Natural Science Foundation of China (41130421).Thanks for the help of senior colleagues in the lab.Particularly,I am very grateful to Li J W for her guiding.Sincere thanks to all friends for the support and assistance.
| [1] | Candès E J. 1998. Ridgelets:Theory and applications[Ph. D. Thesis]. USA:Stanford University. |
| [2] | Candès E J, Donoho L. 1999. Curvelets[M]. USA: Stanford University . |
| [3] | |
| [4] | |
| [5] | Do M N, Vetterli M. 2002. Contourlets.//Stoeckler J, V-Welland G. Beyond Wavelets. New York:Academic Press. |
| [6] | |
| [7] | |
| [8] | Li K, Gao J H, Wei W, et al. 2008. Local angle extraction and noise attenuation for seismic image using Contourlet transform.//ETT and GRS 2008. Shanghai:IEEE, 349-352. |
| [9] | Li Z H. 2007. Methodology on Feature Extraction and Descriptors in Iris Recognition[Ph. D. thesis] (in Chinese). Changchun:Jilin University. |
| [10] | |
| [11] | Lin C, Wang X B, Liu L H. 2012. Noise decaying of seismic data by Steerable Pyramid decomposition based on Laplace prior[J]. Computer Engineering and Applications , 48 (2): 222–226. |
| [12] | Lin C, Wang X B, Liu S B, et al. 2011. Steerable Pyramid decomposition method and its application in cracks imaging[J]. Journal of Lanzhou University (Natural Sciences) , 47 (1): 25–30. |
| [13] | |
| [14] | Papari G, Campisi P, Petkov N. 2012. New families of Fourier eigenfunctions for steerable filtering[J]. IEEE Transactions on Image Processing, 21 (6): 2931–2943. DOI: 10.1109/TIP.2011.2179060 |
| [15] | |
| [16] | Shi J, Xiao Z H, Chang Q. 2009. An algorithm for recognizing geometrical shapes automatically based on tunable filter[J]. Journal of North University of China (Natural Science Edition) , 30 (5): 467–471. |
| [17] | Teo P C, Hel-Or Y. 1998. Lie generators for computing steerable functions[J]. Pattern Recognition Letters, 19 (1): 7–17. DOI: 10.1016/S0167-8655(97)00156-6 |
| [18] | |
| [19] | Yu Z, Whitcombe D. 2008. Seismic noise attenuation using 2D complex wavelet transforms.//70th EAGE Conference & Exhibition. SPE, EAGE. |
| [20] | |
| [21] | |
| [22] | Zhang G Z, Yin X Y. 2004. Noise suppressing by wavelet transform in seismic data processing.//Proceedings of the 2004 7th International Conference on Signal Processing. Beijing:IEEE, 2553-2555. |
| [23] | Zheng L, Han C Z, Zuo D G, et al. 2002. An algorithm for noise image merging based on steerable filters[J]. Journal of Xi'an Jiaotong University , 36 (12): 1236–1239. |
 2016, Vol. 59
2016, Vol. 59


