With the development of exploration technologies, seismic anisotropy has been observed in many exploration areas, especially in sedimentary rocks. Transverse isotropy(TI)with a vertical symmetry axis(VTI)canprovide a good representation of intrinsic anisotropy induced by horizontally aligned parallel fractures and finelaminations. Reverse time migration for anisotropic media based on the full anisotropic elastic wave equationis computationally inefficient and requires at least five parameters. On the other h and , conventional P-waveseismic data, gathered at the earth’s surface, contain only the vertical component of the elastic wave. So, forpractical application of anisotropy, transverse isotropy is commonly adopted under the acoustic approximation.
In general, we can divide these acoustic approximations into two broad categories:(a)the coupled pseudoacoustic wave equations(Alkhalifah, 2000; Zhou et al., 2006; Hestholm, 2009; Fletcher et al., 2009; Fowler et al., 2010; Duveneck and Bakker, 2011; Zhang et al., 2011) and (b)the decoupled pure P-wave equations(Klié and Toro, 2001; Etgen and Br and sberg-Dahl, 2009; Liu et al., 2009; Crawley et al., 2010; Pestana et al., 2011; Chu et al., 2011, 2013; Zhan et al., 2011, 2013; Huang et al., 2011). The pseudo-acoustic equations areusually derived from the exact P-SV dispersion relation, simplified by setting the shear-wave velocity to zero(Alkhalifah, 2000). Although pseudo-acoustic wave equations yield kinematically accurate P-wave propagation, all these wave equations contain undesired shear-wave artifacts(Grechka et al., 2004). In addition, the pseudoacoustic wave equations become numerically unstable for anisotropic models with anisotropic parameters ε < δ.For these above mentioned reasons, the decoupled pure P-wave equations for modeling and migration in TImedia have attracted more attentions. The pure P-wave equations are also derived from the exact dispersionrelation by using a Taylor, Pad′e, or similar expansion to replace the square root with or without setting theshear-wave velocity to zero. The pure P-wave equations usually involve fractional pseudo-differential operatorsthat make the numerical implementation difficult when using the finite-difference(FD)method alone. The mostnatural choice to solve these equations is pseudospectral(PS)method(Kosloff and Baysal, 1982; Reshef et al., 1988a, 1988b). Besides, some other modified spectral methods are used to solve those special pure P-wave equations(Etgen and Br and sberg-Dahl, 2009; Crawley et al., 2010, Crawley Pestana and Stoffa, 2010). Although PSmethod requires only two nodes per wavelength, it is still computationally expensive because several fast Fouriertransforms(FFTs)are required in wavefield extrapolation at each time step. Zhan et al.(2013)proposed anefficient hybrid PS/FD scheme for solving second-order TTI pure P-wave equation.
Here, we propose the first-order form of the pure P-wave equation with stress and particle velocities aswavefield variables for heterogeneous VTI media. And we adopt the similar method to solve the proposed firstorder equation using hybrid PS/FD scheme. The proposed methods extend the pure P-wave equations fromthe cases of constant density to those of variable density. Moreover, another advantage of the velocity-stressequation is that we can use high-order staggered-grid finite difference in our numerical implementation to reducethe grid dispersion.
Stability of seismic numerical wave modeling is a dem and ing topic. The stability analysis for numericalsolutions of partial derivative equations is usually h and led using the von Neumann’s method. In numericalimplementation, spatial sampling is generally chosen to avoid grid dispersion in solutions and the temporalsampling is chosen to avoid numerical instability(Lines et al., 1999). The stability of the hybrid PS/FD schemeon central and staggered grids is investigated in this paper. The analysis shows that the staggered-grid hybridPS/FD scheme is more stable than central-grid hybrid PS/FD scheme. The hybrid PS/FD scheme on centralgrid is unstable when the anisotropy parameter is greater than δ. This instability problem is restricted towavenumbers near Nyquist. To deal with this problem, a low-pass filter is applied to the wavenumber operatorsin our numerical implementation.
2 VTI PURE P-WAVE EQUATIONWe start our derivation from the exact VTI phase velocity expression(Tsvankin, 1996):
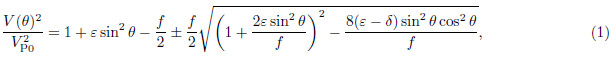
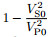 , VP0 and VS0 representthe P- and SV-wave velocities along the symmetry axis, respectively. Here, the plus sign corresponds to the Pwave and the minus sign to the SV wave. Letting VS0 = 0, then Eq.(1)reduces to
, VP0 and VS0 representthe P- and SV-wave velocities along the symmetry axis, respectively. Here, the plus sign corresponds to the Pwave and the minus sign to the SV wave. Letting VS0 = 0, then Eq.(1)reduces to
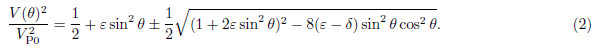
We only consider the plus sign. Using first-order Taylor expansion to replace the square root of Eq.(2)gives the following approximation for the P-wave phase velocity(Klié and Toro, 2001; Fowler, 2003):
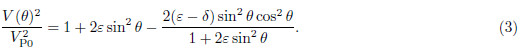
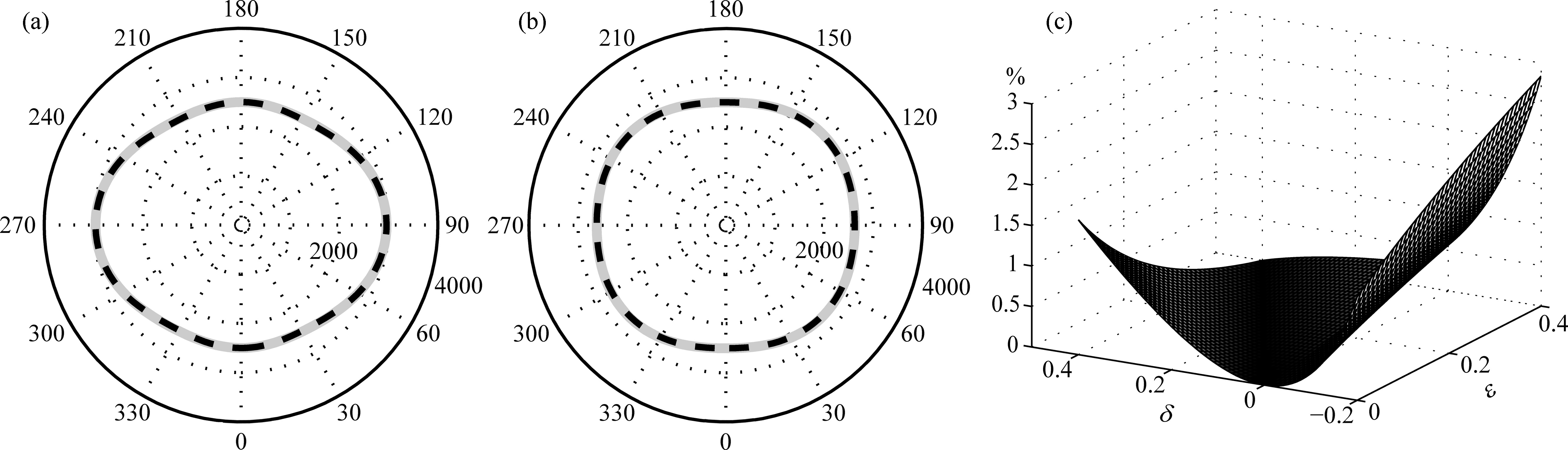
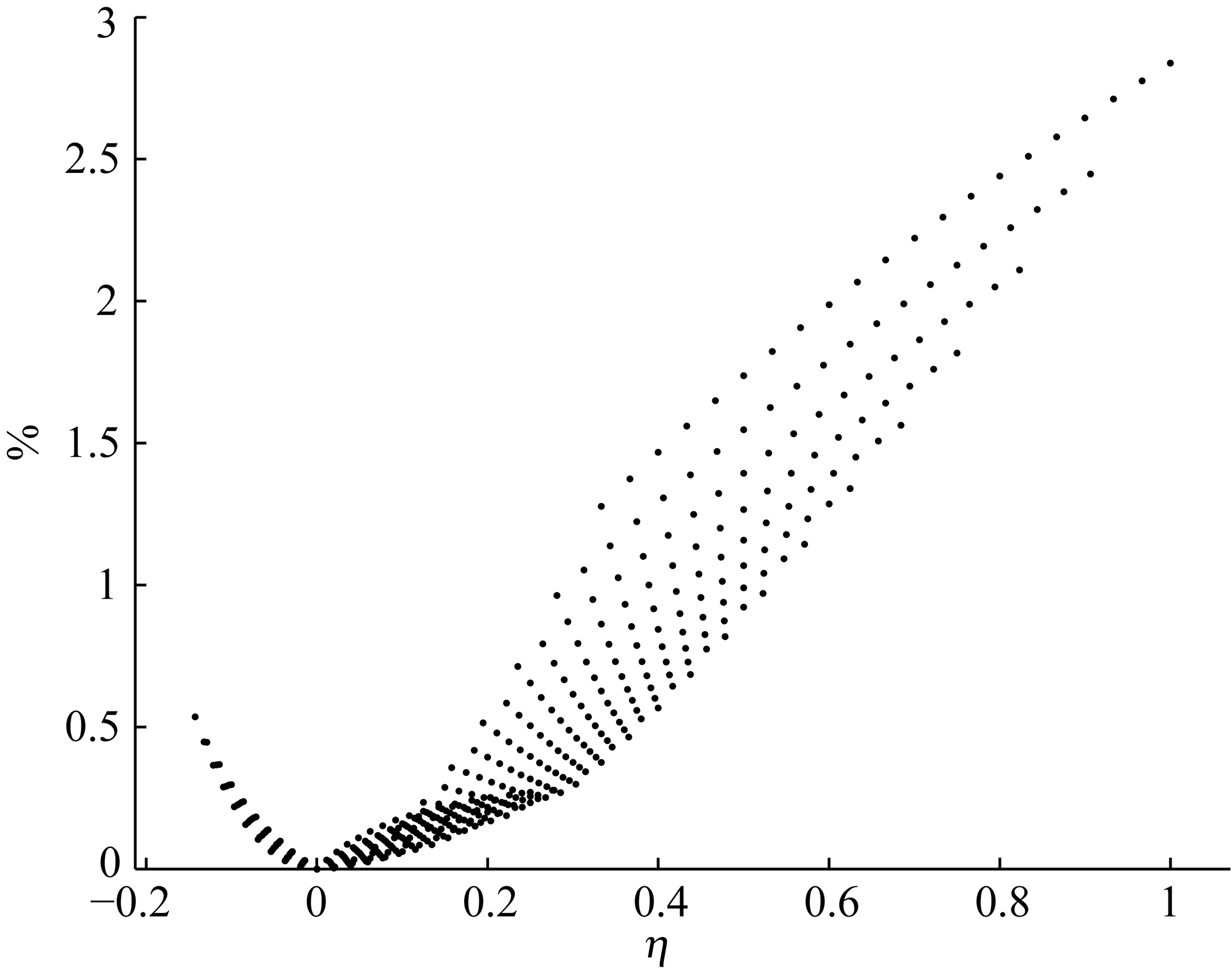
Figure 1 displays a comparison between the exact phase velocity(black dotted line) and the approximatephase velocity(gray solid line)governed by Eq.(3)with VP0 = 3500 m·s-1, VS0 = 2023 m·s-1 and anisotropyparameter(a)ε = 0.2, δ = -0.1, (b)ε = 0.05, δ = 0.3. Fig. 1c is the maximum relative errors of approximateP-wave phase velocity compared to the exact P-wave phase velocity for different anisotropy parameters ε varyingfrom 0 to 0.4 and ε varying from –0.2 to 0.4. Fig. 2 displays the maximum relative errors of approximate P-wavephase velocity for the effective anisotropy parameter η(Alkhalifah and Tsvankin, 1995). Fig. 1 and Fig. 2 showsthat the approximate P-wave phase velocity is very close to the exact phase velocity. For weak anisotropy(i.e. < 0.2), the relative phase velocity errors are below 1%. Note that Fig. 1c and Fig. 2 also indicate thatstrong anisotropy may lead to large error. Generally speaking, pure P-wave equation gives a reasonably good approximation to the exact phase velocity for weak anisotropy, but the accuracy decreases with the increase ofanisotropy.
|
(a) anisotropic parameters ε = 0.2, δ = -0.1; (b) anisotropic parameters ε = 0.05, δ = 0.3; (c) maximum relative errors for a wide range of ε and δ Fig.1 Comparison between exact (black dotted line) and approximate (gray solid line) phase velocities: |
|
Fig.2 Maximum relative error of pure P-wave equation versus the variation of η, where η = (ε - δ)/(1 + 2δ) |
Plugging the relations sin θ = 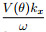 and cos θ =
and cos θ = 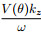 , where ω is angular frequency, kx and kzare spatial wavenumbers in x and z directions, into Eq.(2)gives the following VTI pure P-wave approximatedispersion relation(Fowler, 2003; Chu et al. 2011):
, where ω is angular frequency, kx and kzare spatial wavenumbers in x and z directions, into Eq.(2)gives the following VTI pure P-wave approximatedispersion relation(Fowler, 2003; Chu et al. 2011):
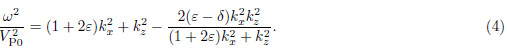
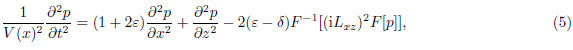
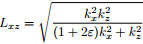 , i is square root of –1. Letting auxiliary wavefield
, i is square root of –1. Letting auxiliary wavefield 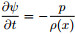 , we can obtain a hyperbolic system of first-orderequations as
, we can obtain a hyperbolic system of first-orderequations as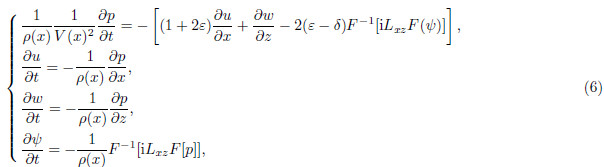
The stability problem is a very important aspectin seismic wave numerical simulations. Because of thefractional pseudo-differential operators, the stability offirst-order pure P-wave equation may be different fromthe isotropic acoustic or elastic equations. In this section, we focus our work on the stability analysis of thehybrid PS/FD scheme on central and staggered grids.
Eq.(6)takes the form as the following hyperbolicwave equation:

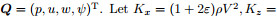
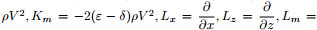
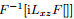 , and
, and 

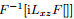
Replacing the time derivative of Eq.(9)with a second-order FD scheme, and applying spatial and temporalforward Fourier transform to wavefiled Q, we obtain
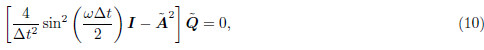
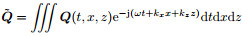 , I is identity matrix, and
, I is identity matrix, and
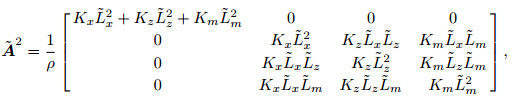
where 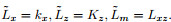 .
.
Since 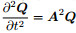 is a hyperbolic equation, there exists a nonsingular matrix S such that
is a hyperbolic equation, there exists a nonsingular matrix S such that 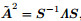 , where Λis a positive diagonal matrix composed of eigenvalues λi(Dong et al., 2000)of matrix
, where Λis a positive diagonal matrix composed of eigenvalues λi(Dong et al., 2000)of matrix 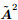 , and then
, and then
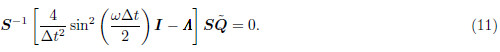
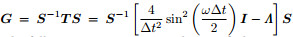 , then det(G)= det(T). If Eq.(11)has non-zerosolution, the following expression must be satisfied
, then det(G)= det(T). If Eq.(11)has non-zerosolution, the following expression must be satisfied
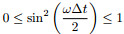 , we obtain the stability condition as
, we obtain the stability condition as
We first discuss the inequality 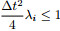 . The eigenvalues of matrix
. The eigenvalues of matrix 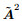 are λ1 = λ2 =
are λ1 = λ2 = 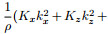
 , and λ3 = λ4 = 0. Since the sign of Km is uncertain, we use the following inequality
, and λ3 = λ4 = 0. Since the sign of Km is uncertain, we use the following inequality
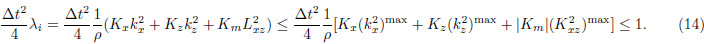
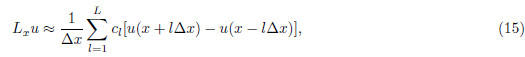
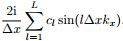 , and
, and 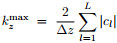 . Similarly, we have
. Similarly, we have 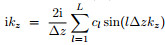 and
and 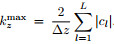 . We use PS method to calculate the fractional pseudo-differential operators. Thesampling theorem tells us that
. We use PS method to calculate the fractional pseudo-differential operators. Thesampling theorem tells us that 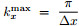 and
and 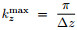 . Therefore the maximum value of Lxz is
. Therefore the maximum value of Lxz is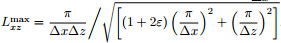 . Plugging kx max, kz max and Lxzmax into inequality(14)yields
. Plugging kx max, kz max and Lxzmax into inequality(14)yields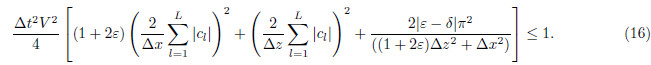
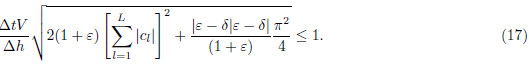
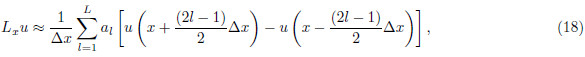
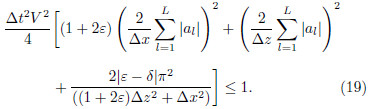
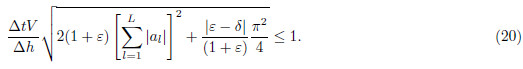
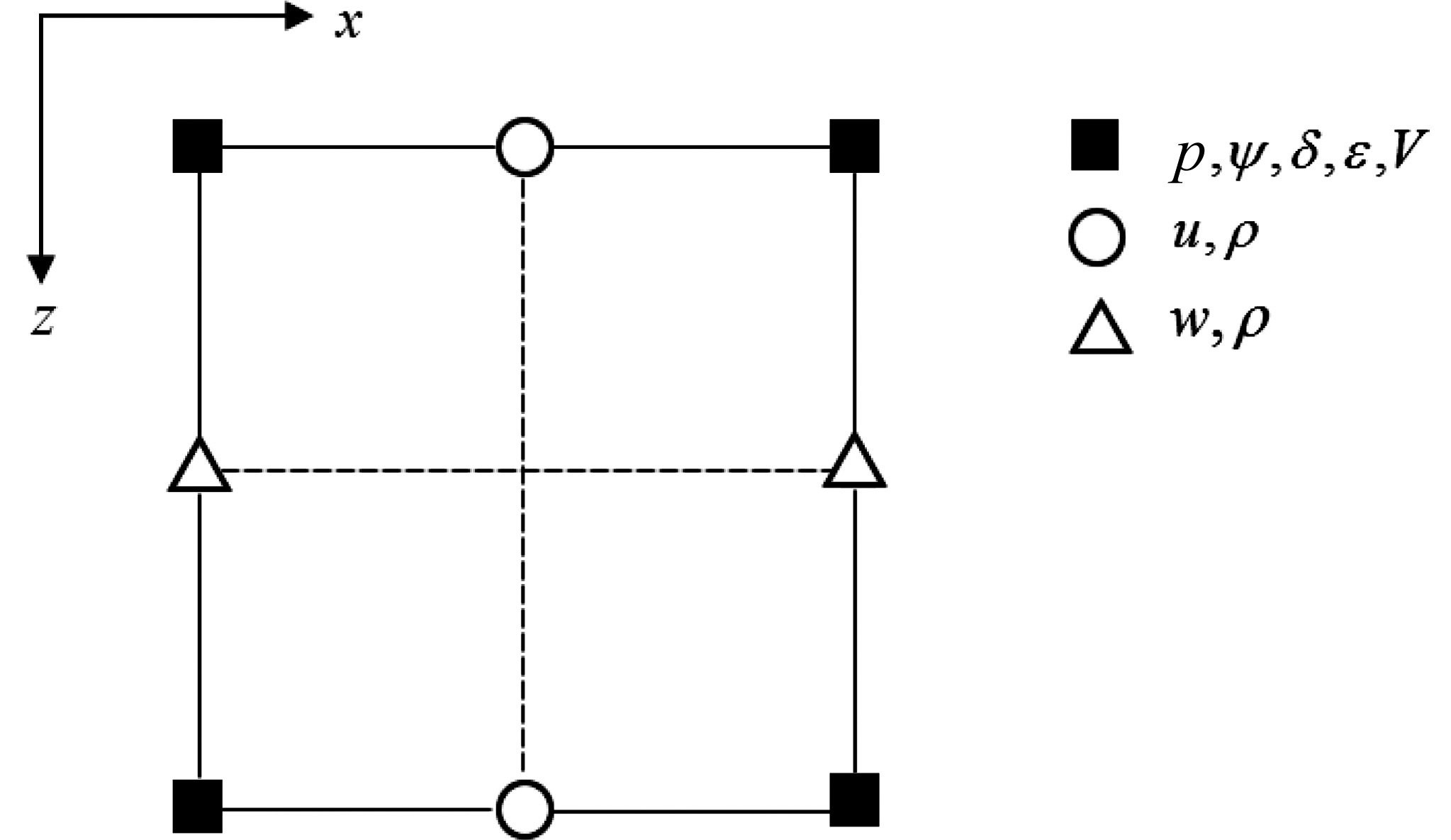
|
Fig.3 Staggered-grid geometries |
Next, we discuss the other inequality 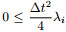 . As discussed above, the following inequality has to besatisfied
. As discussed above, the following inequality has to besatisfied
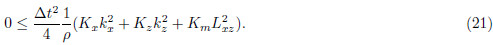
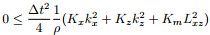 . So we only investigate the case where Km < 0. Let
. So we only investigate the case where Km < 0. Let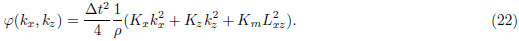
For central-grid finite-difference scheme, the Eq.(22)can be described as
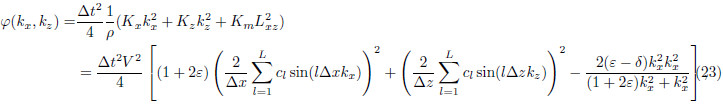
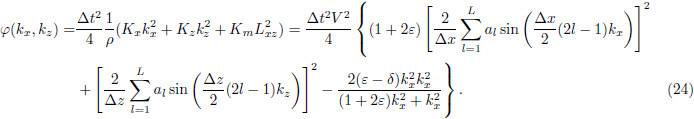
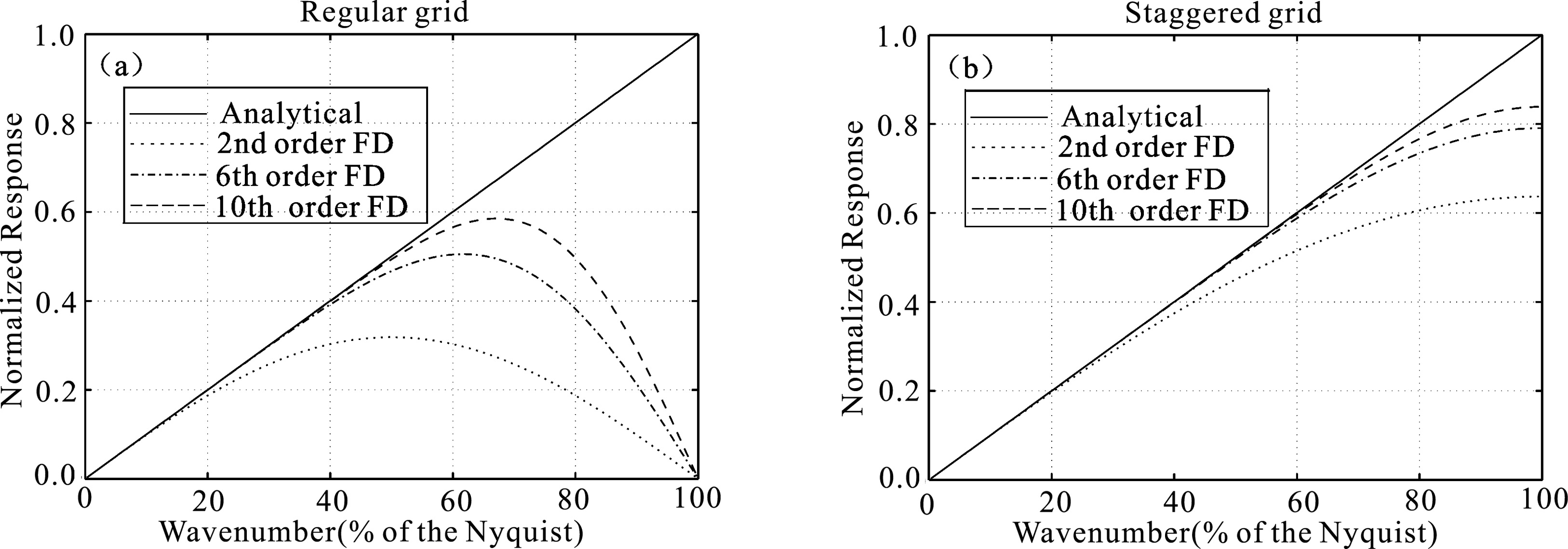
|
Fig.4 Dispersion curves for different finite-difference (FD) schemes to approximate first-order derivative |
|
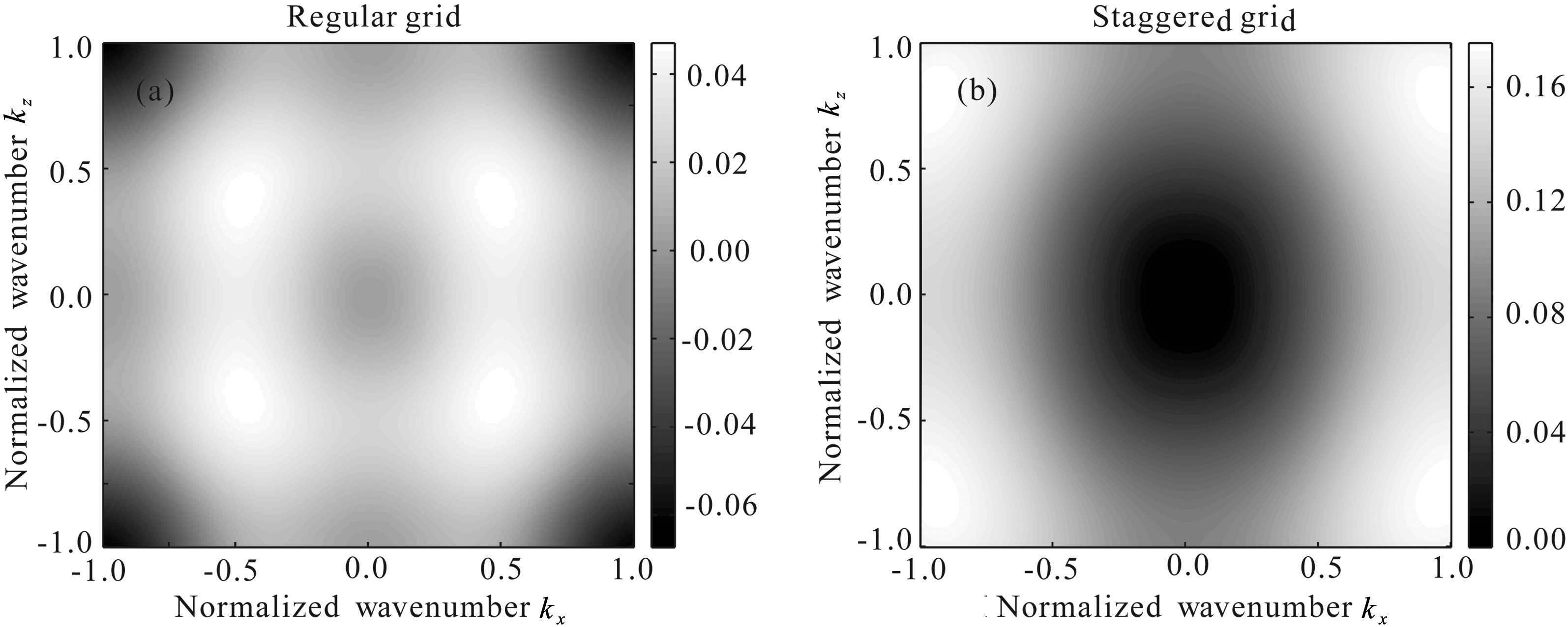
Fig.5 Numerical solution of φ(kx, kz) with ε = 0.3, δ = -0.1, L = 1 |
As shown in Fig. 4b, dispersion curves of staggered-grid FD scheme monotonically approach the theoreticalcurve with the increase of the order of finite difference scheme, i.e.,
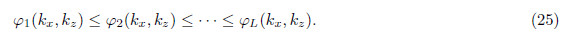
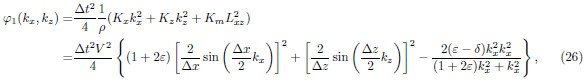
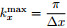 and
and 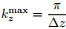 into Eq.(26)yields
into Eq.(26)yields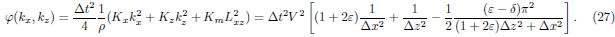
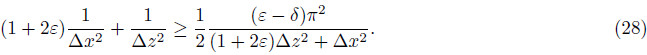

Figure 5a shows that the instability region is restricted to wavenumbers near Nyquist. So we can apply alow-pass filter to the wavenumber operators. Thus Eq.(6)can be rewritten as
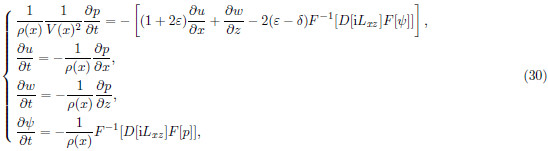
We use conventional Z transform to construct the wavenumber-domain weighting function(Yan and Sava, 2009). For the case of second-order centered derivatives, the stencil has the following Z transform representation



Here, the wavenumber k is normalized. Similarly, we can construct weights for fourth-, sixth-, and eighthorder weighting functions:
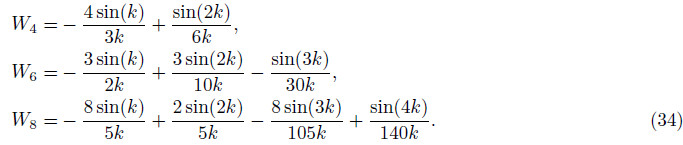
|
Fig.6 Filter function |
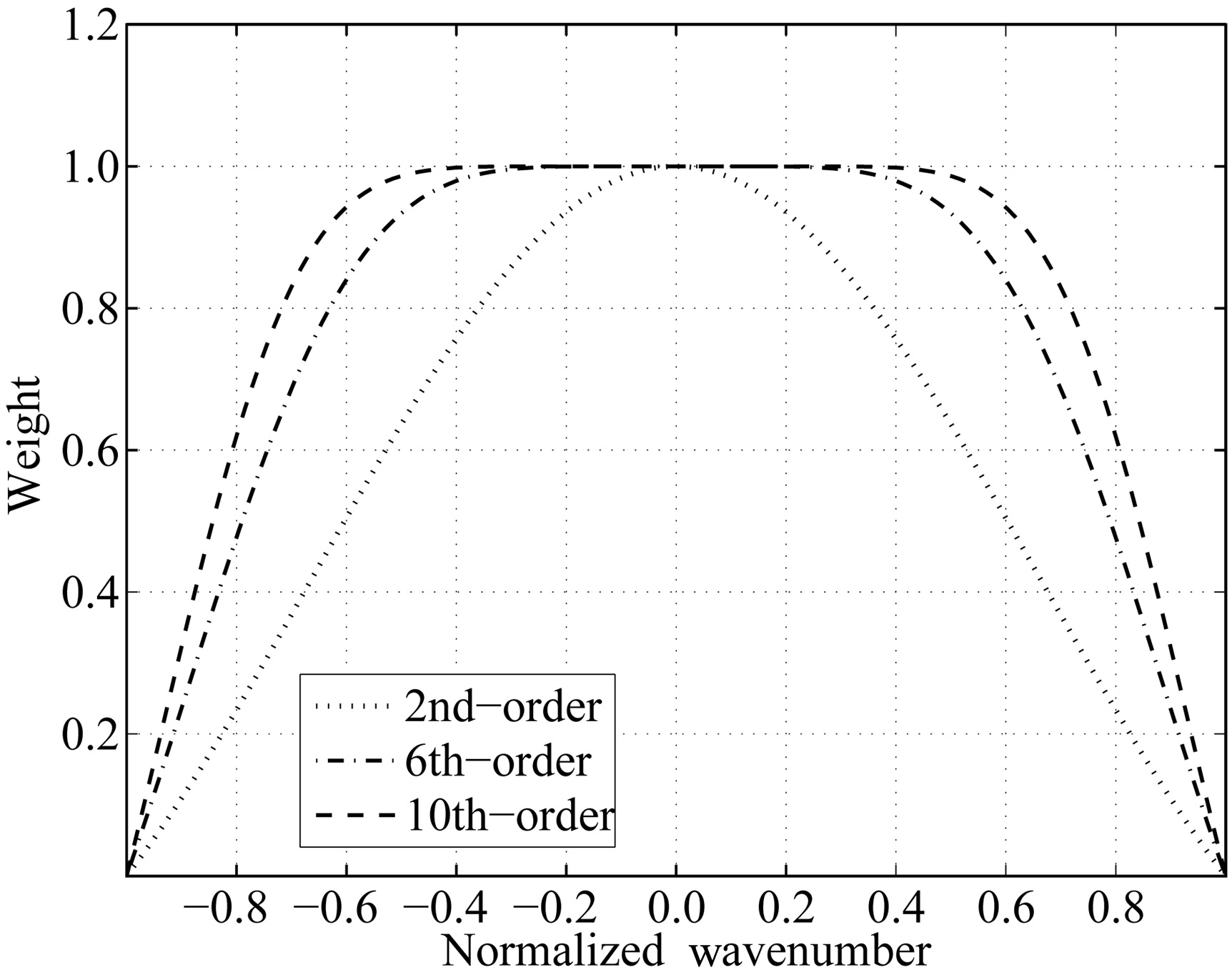
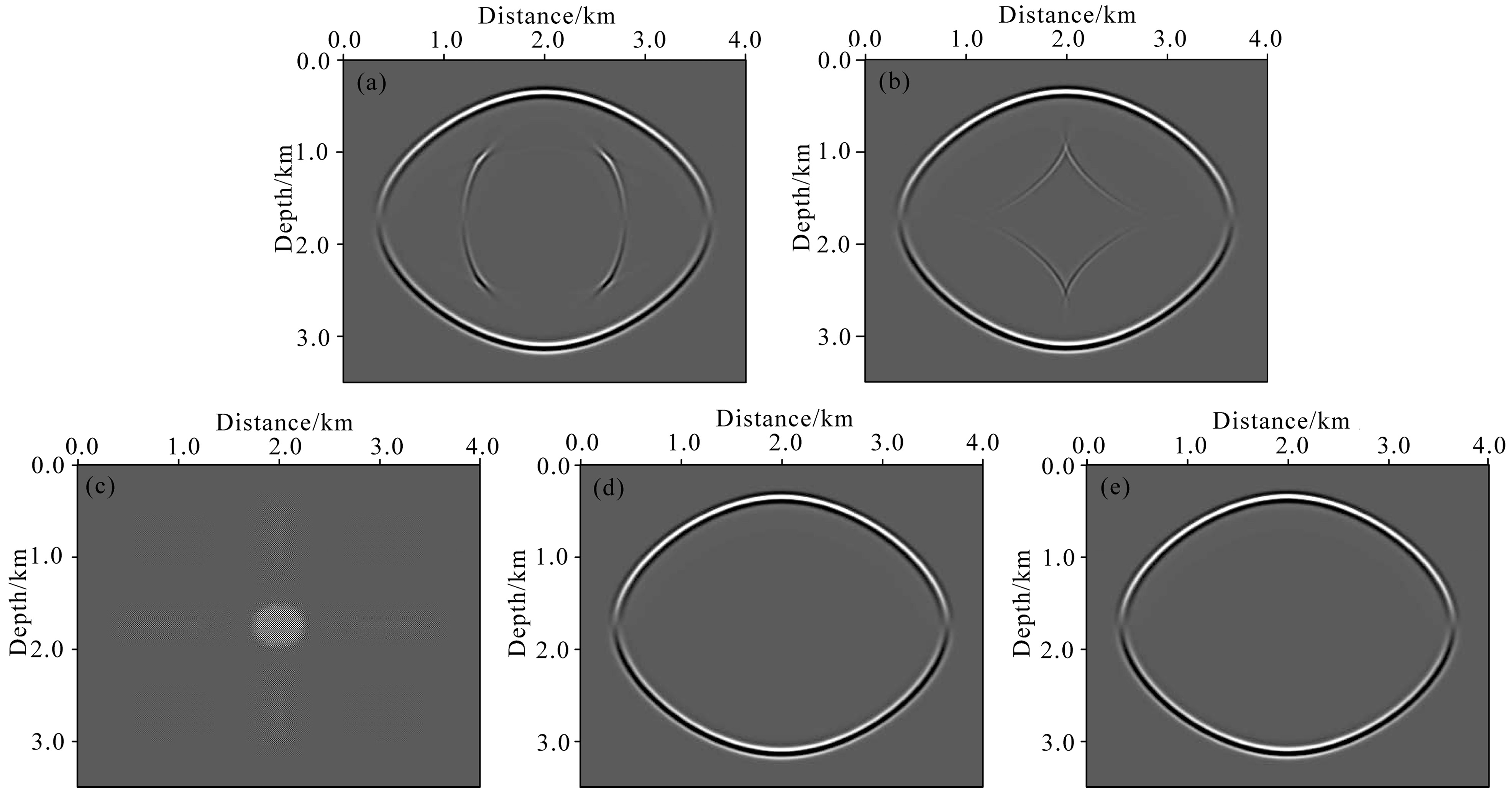
In this section, some synthetic examples are usedto validate the proposed algorithm. We first use homogeneous models with the vertical velocity V = 3000m·s-1 to test pure P-wave Eq.(6) and compare it withanisotropic elastic equation and pseudo-acoustic equation(Duveneck et al., 2008)using an impulse response.The source wavelet for this example is Ricker waveletwith a peak frequency fm=25 Hz located at middleof model. We use a 10 m grid space and a 1 mstime step size. Fig. 7 shows the vertical componentsin first homogeneous model with anisotropic parameters ε = 0.2, δ = -0.05, computed by anisotropicelasticequation(Fig. 7a), pseudo-acoustic equation(Fig. 7b), and pure P-wave equation using central-grid hybridPS/FD scheme(Fig. 7c and 7d) and staggered-grid hybrid PS/FD scheme(Fig. 7e). The difference betweenFig. 7c and 7d is that Fig. 7d is obtained by filtering the wavenumber operator with an eight-order filter functionin numerical implementation. From Fig. 7, we can clearly see that:(1)Pure P-wave equation is completely freefrom shear-wave compared with elastic wave equation and conventional pseudo-acoustic VTI equation;(2)Thehybrid PS/FD scheme on a central grid suffers from some numerical instabilities when the anisotropy parametersε > δ and low-pass filtering method significantly alleviate instability problem;(3)The staggered-grid hybridPS/FD scheme provides a stable pure P-wave propagator. The second example is still a homogeneous VTImodel but with anisotropic parameters ε = 0.05, δ = 0.2. Fig. 8 displays the stable wavefiled snapshots obtainedby anisotropic elastic equation(Fig. 8a) and pure P-wave equation using hybrid central-grid PS/FD scheme(Fig. 8b) and staggered-grid hybrid PS/FD scheme(Fig. 8c). These two examples testify our stability analysis. Both hybrid schemes are stable for VTI model with anisotropic parameters ε ≤ δ, but for the case ε > δ, thecentral-grid hybrid PS/FD scheme can’t provide stable numerical results.
|
Fig.7 Wavefield snapshots in a VTI model with ε=0.2,δ=-0.05:(a) Elastic wave equation;(b) Pseudoacoustic wave equation;(c) P-wave equation using central-grid hybrid PS/FD scheme;(d) As for (c), |
|
Fig.8 Wavefield modeling in a VTI model with ε = 0.05, δ = 0.2: (a) Elastic wave equation; (b) Pure P-wave equation using central-grid hybrid PS/FD scheme; (c) As for (b), except using staggered-grid scheme |
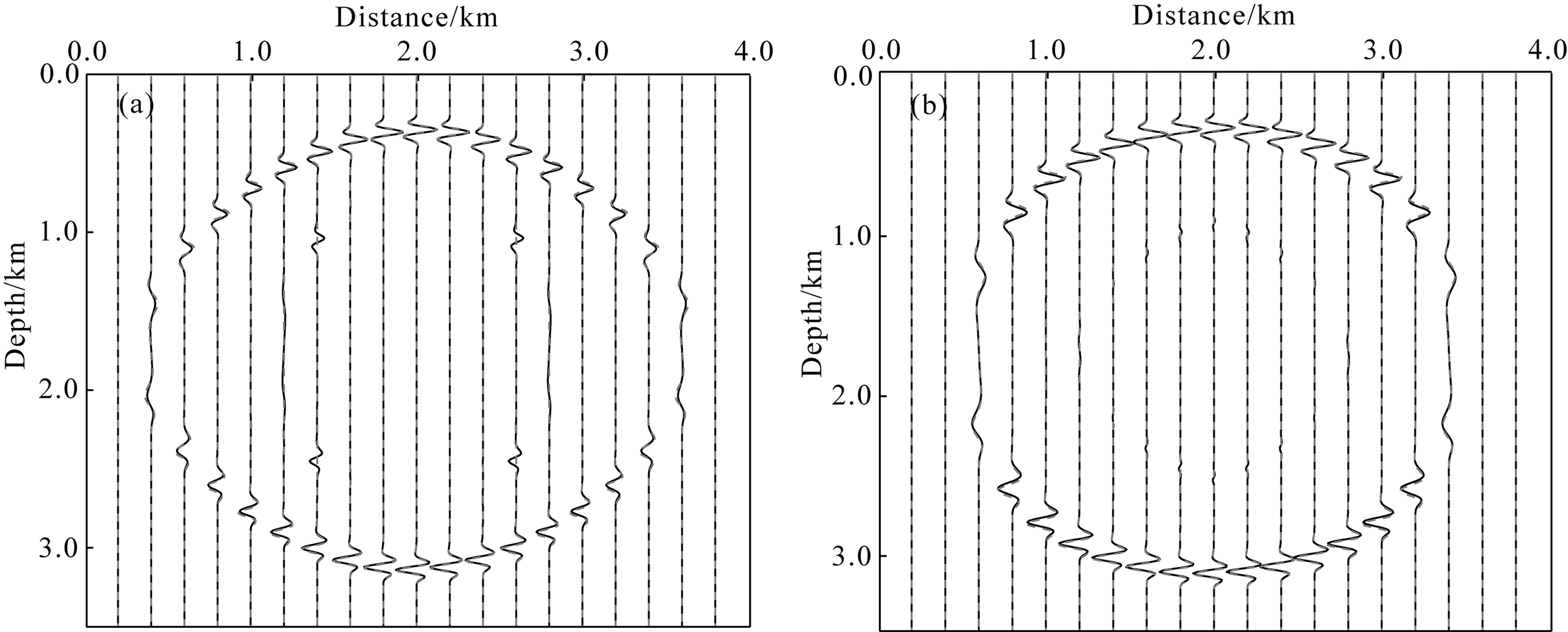
Figure 9 displays direct comparison between elastic wave(solid black line) and pure P wave(dashed grayline)seismograms. The pure P-wave simulation result is practically same as that from the elastic equation inkinematic and dynamic respects, except that the latter is completely free from shear wave. But note that, theamplitude behavior of P-wave equation do not match that of the elastic equation for heterogeneous media sincepure P-wave can’t h and le the converted waves. Further investigation in this area remains to be a research topic.
|
Fig.9 Comparison between elastic wave (solid black line) and pure P wave (dashed gray line) seismograms |
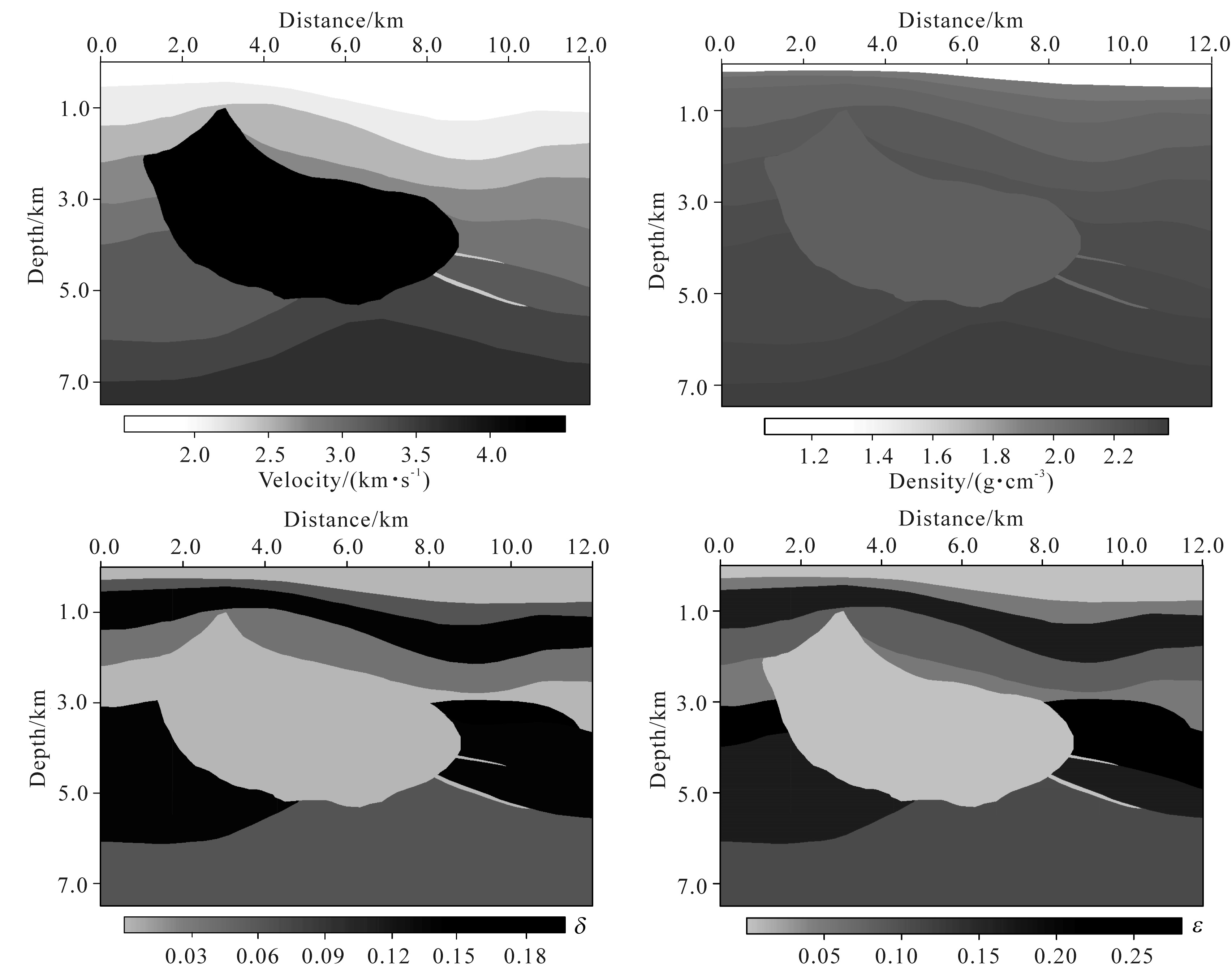
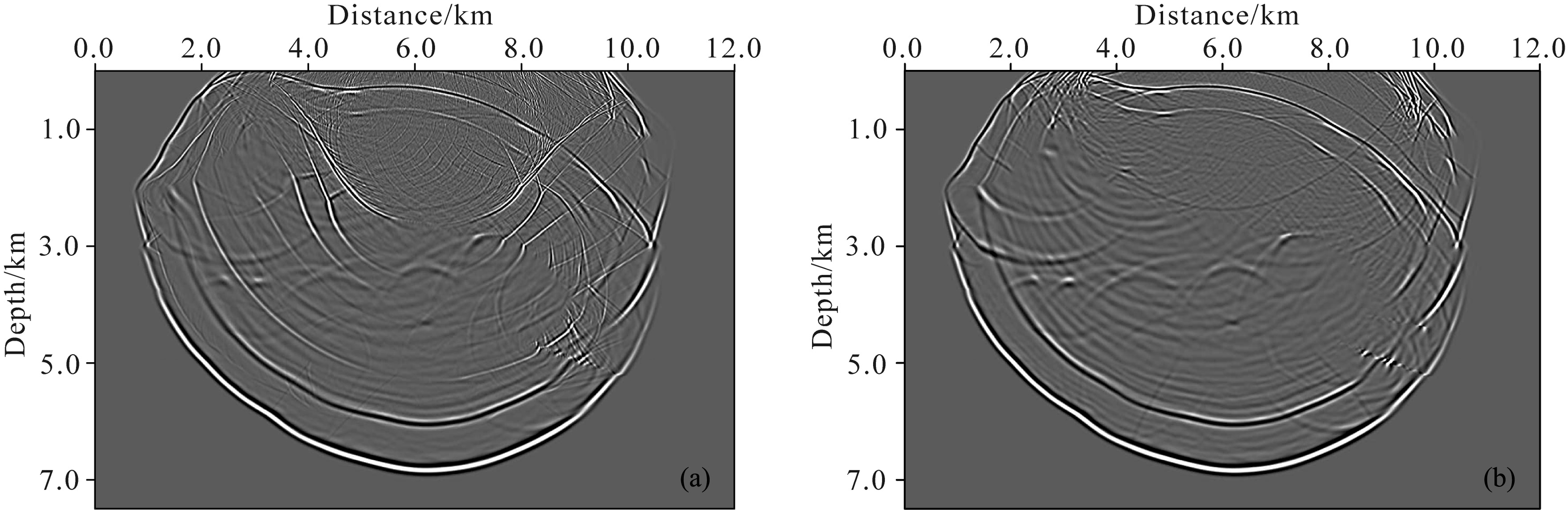
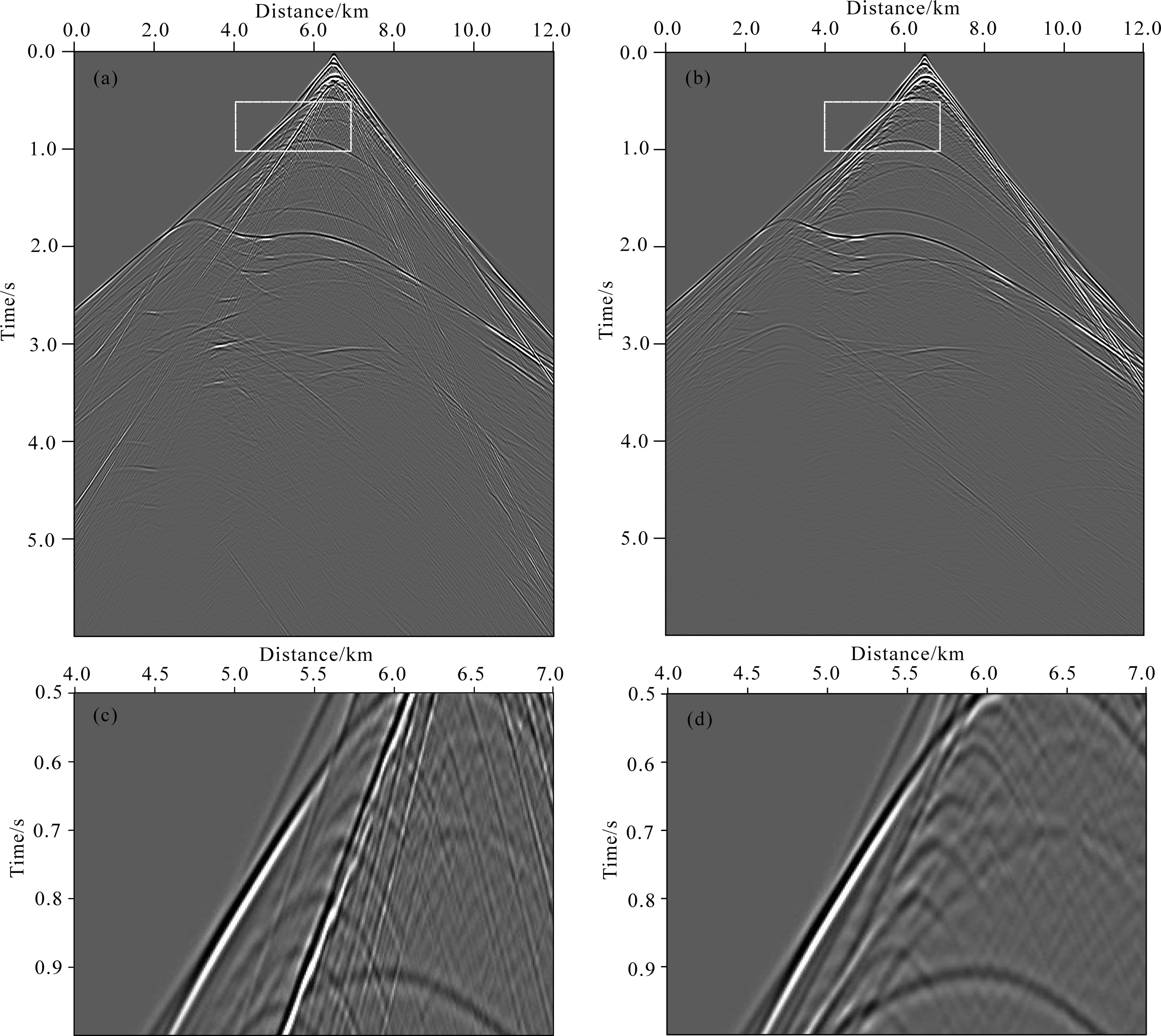
Next, we use a modified Hess VTI model(Fig. 10)with spatial variations in all model parameters to testthe robustness of the proposed method for complex anisotropic models. The model dimensions are nx = 1200 and nz = 750, with grid sampling step of 12.5 m in two directions. We again use the Ricker wavelet as the sourcewavelet with a peak frequency of 25 Hz. We put the source wavelet location at the position of(x, z)=(650, 50).The propagation time step is 1 ms. Fig. 11 shows the wavefield snapshots computed by(a)elastic equation and (b)first-order pure P-wave equation using staggered-grid hybrid PS/FD scheme. Fig. 12 is the correspondingcommon-source gathers. From the snapshots and gathers, we can see that even in such complex anisotropicmodel with sharp contrasts, first-order pure P-wave equation can also provide stable and accurate numericalresults. Table 1 shows the average time costs and memory requirements of three different equations. The twoacoustic approximation equations are close in computational costs and both more efficient than original elasticequation. In fact, the pure P-wave equation can use larger spatial sampling step since it doesn’t need to considerthe numerical dispersion caused by shear wave. Thus it can be more efficient further.
|
Fig.10 Modified Hess VTI model |
|
Fig.11 Wavefield snapshots of vertical components for Hess Model synthesized by (a) elastic wave equation and (b) pure P-wave equation |
|
Fig.12 Shot gathers generated from the modified Hess model: (a) Seismic profile with elastic wave equation; (b) Seismic profile with pure P-wave equation; (c) Zoom of rectangle area in (a); (d) Zoom of rectangle area in (b) |
| Table 1 The average time costs and memory requirements of three different equations |
Starting from the VTI exact phase velocity, the first-order pure P-wave equation is derived by using afirst-order Taylor series expansion to the radical. We adopt an efficient hybrid PS/FD scheme to solve the pureP-wave equation rather than using PS method alone. The stability condition of such scheme on central and staggered grids is investigated. Stability analysis shows that the hybrid scheme on a staggered grid is morestable than that on a central grid. To deal with the instability problem of the central-grid hybrid PS/FDscheme, we apply a low-pass filter to wavenumber operator. The kinetic and dynamic accuracy of the proposedequation is analyzed by comparison with original elastic equation and pseudo-acoustic equation. Synthetic2D examples demonstrate that the proposed first-order pure P-wave equation provides stable and kineticallyaccurate numerical results. In spite of its dynamic inaccuracy in heterogeneous media, the first-order pure Pwave equation is practically promising in anisotropic modeling and migration algorithms oriented to subsurfacestructures.
ACKNOWLEDGMENTSThis work was supported by the National Natural Science Foundation of China(41174100), Large-scaleOil & GasField and Coalbed Methane Development Major Projects(2011ZX05019-008-08), and China NationalPetroleum Corporation(2014A-3609). We are also grateful to the reviewers and the editor for their very detailed and constructive comments that significantly improve the original manuscript. We thank Professor ShuTingWang, Doctor Gang Fang and Dong Han for their useful suggestions. We would like to thank Hess for makingthe VTI model available.
Appendix The Relation Between Two Different Acoustic ApproximationsIn this appendix, we briefly discuss the relation between pseudo-acoustic equation and pure P-wave equation. The dispersion relation that Alkhalifah(2000)presented is as follows
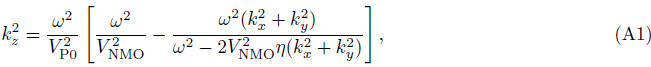
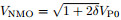 isthe small offset P-wave normal moveout velocity, η =(ε - δ)/(1 + 2δ)is effective anisotropy parameter, kx, ky and kz are spatial wavenumbers in x, y and z directions, respectively. After some algebraic manipulations, Eq.(A1)can be cast into the equivalent rational fractional form:
isthe small offset P-wave normal moveout velocity, η =(ε - δ)/(1 + 2δ)is effective anisotropy parameter, kx, ky and kz are spatial wavenumbers in x, y and z directions, respectively. After some algebraic manipulations, Eq.(A1)can be cast into the equivalent rational fractional form: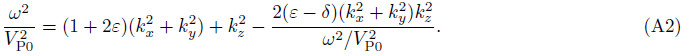
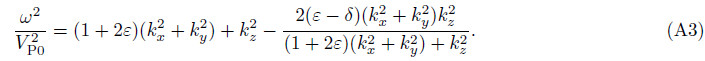

| [1] | Alkhalifah T, Tsvankin I. 1995. Velocity analysis for transversely isotropic media. Geophysics, 60(5): 1550-1566. |
| [2] | Alkhalifah T. 2000. An acoustic wave equation for anisotropic media. Geophysics, 65(4): 1239-1250. |
| [3] | Berenger J P. 1994. A perfectly matched layer for absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. |
| [4] | Zhan G, Pestana R C, Stoffa P L. 2013. An efficient hybrid pseudo-spectral/finite-difference scheme for solving the TTI pure P-wave equation. J. Geophys. Eng., 10(2): 025004. |
| [5] | Zhang Y, Zhang H Z, Zhang G Q. 2011. A stable TTI reverse time migration and its implementation. Geophysics, 76(3):WA3-WA11. |
| [6] | Zhou H, Zhang G, Bloor R. 2006. An anisotropic acoustic wave equation for VTI media. 68th EAGE Conference and Exhibition incorporating SPE EUROPEC 2006. |
| [7] | Carcione J M, Herman G C, Ten Kroode A P E. 2002. Seismic modeling. Geophysics, 67(4): 1304-1325. |
| [8] | Chu C L, Macy B K, Anno P D. 2011. An accurate and stable wave equation for pure acoustic TTI modeling. 81th Annual International Meeting. SEG, Expanded Abstracts, 179-184. |
| [9] | Chu C L, Macy B K, Anno P D. 2013. Pure acoustic wave propagation in transversely isotropic media by the pseudospectral method. Geophysical Prospecting, 61(3): 556-567. |
| [10] | Crawley S, Brandsberg-Dahl S, McClean J, et al. 2010. TTI reverse time migration using the pseudo-analytic method.The Leading Edge, 29(11): 1378-1384. |
| [11] | Dong L G, Ma Z T, Cao J Z. 2000. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation. Chinese J. Geophys.(in Chinese), 43(6): 856-864. |
| [12] | Duveneck E, Milcik P, Bakker P M, et al. 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration. 78th Annual International Meeting. SEG, Expanded Abstracts, 2186-2190. |
| [13] | Duveneck E, Bakker P M. 2011. Stable P-wave modeling for reverse-time migration in tilted TI media. Geophysics, 76(2):S65-S75. |
| [14] | Etgen J T, Brandsberg-Dahl S. 2009. The pseudo-analytical method: Application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation. 79th Annual International Meeting. SEG, Expanded Abstracts, 2552-2556. |
| [15] | Fletcher R P, Du X, Fowler P J. 2009. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics, 74(6): WCA179-WCA187. |
| [16] | Fowler P J, Du X, Fletcher R P. 2010. Coupled equations for reverse time migration in transversely isotropic media.Geophysics, 75(1): S11-S22. |
| [17] | Furumura T, Koketsu K, Wen K L. 2002. Parallel PSM/FDM hybrid simulation of ground motions from the 1999 Chi-Chi, Taiwan, earthquake. Pure Appl Geophys, 159(9): 2133-2146. |
| [18] | Grechka V, Zhang L B, Rector J W III. 2004. Shear waves in acoustic anisotropic media. Geophysics, 69(2): 576-582. |
| [19] | Hestholm S. 2009. Acoustic VTI modeling using high-order finite differences. Geophysics, 74(5): T67-T73. |
| [20] | Huang Y J, Zhu G M, Liu C Y. 2011. An approximate acoustic wave equation for VTI media. Chinese J. Geophys. (in Chinese), 54(8): 2117-2123, doi: 10.3969/j.issn.0001-5733.2011.08.019. |
| [21] | Klié H, Toro W. 2001. A new acoustic wave equation for modeling in anisotropic media. 71st Annual International Meeting. SEG, Expanded Abstracts, 1171-1174. |
| [22] | Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. |
| [23] | Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436. |
| [24] | Li B, Li M, Liu H W, et al. 2012. Stability of reverse time migration in TTI media. Chinese J. Geophys. (in Chinese), 55(4): 1366-1375, doi: 10.6038/j.issn.0001-5733.2012.04.032. |
| [25] | Liu F Q, Morton S A, Jiang S S, et al. 2009. Decoupled wave equations for P and SV waves in an acoustic VTI media. 79th Annual International Meeting. SEG, Expanded Abstracts, 2844-2848. |
| [26] | Moczo P, Kristek J, Bystricky E. 2000. Stability and grid dispersion of the P-SV 4th-order staggered-grid finite-difference schemes. Studia Geophysica et Geodaetica, 44(3): 381-402. |
| [27] | Mu Y G, Pei Z L. 2005. Seismic Numerical Modeling for 3-D Complex Media (in Chinese). Beijing: Petroleum Industry Press, 33-34. |
| [28] | Pestana R C, Ursin B, Stoffa P L. 2011. Separate P-and SV-wave equations for VTI media. 12th International Congress of the Brazilian Geophysical Society, 1227-1232. |
| [29] | Reshef M, Kosloff D, Edwards M, et al. 1988a. Three-dimensional acoustic modeling by the Fourier method. Geophysics, 53(9): 1175-1183. |
| [30] | Reshef M, Kosloff D, Edwards M, et al. 1988b. Three-dimensional elastic modeling by the Fourier method. Geophysics, 53(9): 1184-1193. |
| [31] | Thomsen L. 1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966. |
| [32] | Tsvankin I. 1996. P-wave signatures and notation for transversely isotropic media: An overview. Geophysics, 61(2): 467-483. |
| [33] | Virieux J. 1984. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. |
| [34] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. |
| [35] | Yan J, Sava P. 2009. Elastic wave-mode separation for VTI media. Geophysics, 74(5): WB19-WB32. |
| [36] | Zhan G, Pestana R C, Stoffa P L. 2011. An acoustic wave equation for pure P wave in 2D TTI media. 12th International Congress of the Brazilian Geophysical Society, 993-997. |
| [37] | Zhan G, Pestana R C, Stoffa P L. 2013. An efficient hybrid pseudo-spectral/finite-difference scheme for solving the TTI pure P-wave equation. J. Geophys. Eng., 10(2): 025004. |
| [38] | Zhang Y, Zhang H Z, Zhang G Q. 2011. A stable TTI reverse time migration and its implementation. Geophysics, 76(3):WA3-WA11. |
| [39] | Zhou H, Zhang G, Bloor R. 2006. An anisotropic acoustic wave equation for VTI media. 68th EAGE Conference and Exhibition incorporating SPE EUROPEC 2006. |
 2015, Vol. 58
2015, Vol. 58

