2. Research Center for Urban Safety and Security, Kobe University, Japan 6578501, China
In order to avoid miscellaneous background interferences, strain observation system has been moved from ground to deep underground in the United States, Japan, Germany, and China. As a result, borehole strain gauge system was applied on a large scale in the 1990 s and early 2000 s. Borehole strain gauge is a geophysical observation system with good prospects for its wide b and width and range of measurement. There are more than 40 stations engaged in 4-component borehole strain observation in China by now. These stations are equipped with two types of borehole strain gauges(YRY-4, RZB-3D)to observe the crustal strain by four evenly distributed observation lines. There are 81 stations of 4-component borehole strainmeters in the Plate Boundary Observatory(PBO)(Li, 2010; Chen et al., 2011)in the United States, equipped with the gauges improved from the 3-component borehole strain gauge invented by the Australian professor Gladwin(Gladwin, 1984). 4 observation lines are used in every station, including three evenly distributed observation lines, which are 60 degrees apart from each other, and the fourth line is at the angle bisectors of two adjacent lines. Observation data of these stations can be downloaded from the PBO website(http://pbo.unavco.org/).
Because there are so many 4-component borehole strain stations, related observations and studies should have been done. However, we found that the previous studies mostly focused on the analysis of borehole strain, such as Longbein et al., 2006; Chi et al., 2007; Johston et al., 2006; Zhang et al., 2010; Shi et al., 2013; Qiu et al., 2009, 2010; and Chi et al., 2013. Longbein(2006) and Chi(2007)mainly focused on coseismic signal analysis by strain observation; Johston(2006) and Zhang(2010)analyzed fault nucleation and response, earthquake forecasting by high precision continuous data of borehole strain and pore-pressure near epicenter; Shi(2013)studied the capability of 4-component borehole strain to record earthquake waves; Hart(1996)discussed the calibration of borehole strain gauges by theoretical tidal values, as well as how to remove the effect of small-scale inhomogeneity; Qiu(2009, 2010)studied precursory strain changes of Wenchuan earthquake by 4-component borehole strain observation in Guzan station; Chi(2013)described the borehole strain anomalies before Lushan Ms7.0 earthquake in April 2013. However, all of these studies did not include the calculation and analysis of strain invariants of 4-component borehole strain observations. Therefore, we perform calculation and analysis of strain invariants of the above-mentioned 3 types of 4-component borehole strain observation, and examine the reliability of the 4-component borehole strain observations and the consistency of strain invariants.
According to the theory of elastic mechanics, strain invariant is the coefficient of the characteristic polynomial of a tensor matrix(Wang et al., 2002; Qian et al., 1980), which is independent of the coordinate system. For the characteristic polynomial of a 2-dimensional strain tensor matrix, the first coefficient is the surface strain, which is a combined result of maximum and minimum principal strain. Another coefficient is the determinant of a tensor matrix, which is the cross product of maximum and minimum principal strain. Therefore, it does not contradict with the meaning of invariant in elasticity for us to take principal strain and its direction as invariants in this paper. Contrarily, it reveals the profound geometric characteristics of strain invariant. Jaeger(1964) and Heitz(1988)also defined the invariants in the same way. Expression of strain tensor matrix in different orthogonal curvilinear coordinates is different, and their conversion matrix is an orthogonal matrix, so strain tensor matrix in different coordinates is similarity matrix. It is proved that similar matrices have the same characteristic value and the characteristic polynomial in linear algebra(Yu et al., 2008). For strain tensor matrix, the characteristic value is the maximum and minimum principal strain; its corresponding direction called as principal direction, is also independent of coordinate system. In 4-component borehole strain observation, what are strain invariants? And what are their characteristics? How to derive the concise formula for computing the strain invariants when 4 observation lines of borehole strain do not overlap with the geographical rectangular coordinate axes? According to the elastic mechanics theory, strain invariant is unique in the isotropic medium. So strain invariant calculated by different combinations of 4-component borehole strain should be equal to each other. But actually, due to measurement errors, non-intact and heterogeneous bedrock, imperfect coupling between probe and borehole wall, flawed smoothness of borehole wall, and environmental interference, strain invariants may not be exactly equal with each other. Although they can’t be exactly equal, they should be close to each other anyway. How to test their consistency? Through the collected continuous observation data of 12 stations of YRY-4 type and 2 stations of RZB-3 type 4-component borehole strain in China, and 11 stations of improved Glodwin 4-component borehole strain in USA, we found that the 5 groups of maximum and minimum principal strain are close to each other, while the 5 groups of the principal direction are quite different from each other at most of the stations. What caused it and how to estimate the calculation error of borehole strain invariants? How to improve the mathematical model of data processing and calibration of strainmeter? The purpose of this paper is to explore above-mentioned problems.
2 METHOD OF CALCULATION FOR STRAIN INVARIANTSAccording to the previous researches(Jaeger, 1964; Means, 1982; Niu et al., 2005; Young et al., 2005), there will be two mutually orthogonal directions, in which the linear strain is called as maximum principal strain and minimum principal strain, and the corresponding shear strain is zero, called as principal direction. In orthogonal curvilinear coordinate system, maximum and minimum principal strain, principal direction are unique, and independent of coordinate system selection. Therefore, maximum and minimum principal strain, and principal direction are called strain invariants. Strain invariants cannot be directly measured, but it can be calculated from strains in three different directions on the same plane.
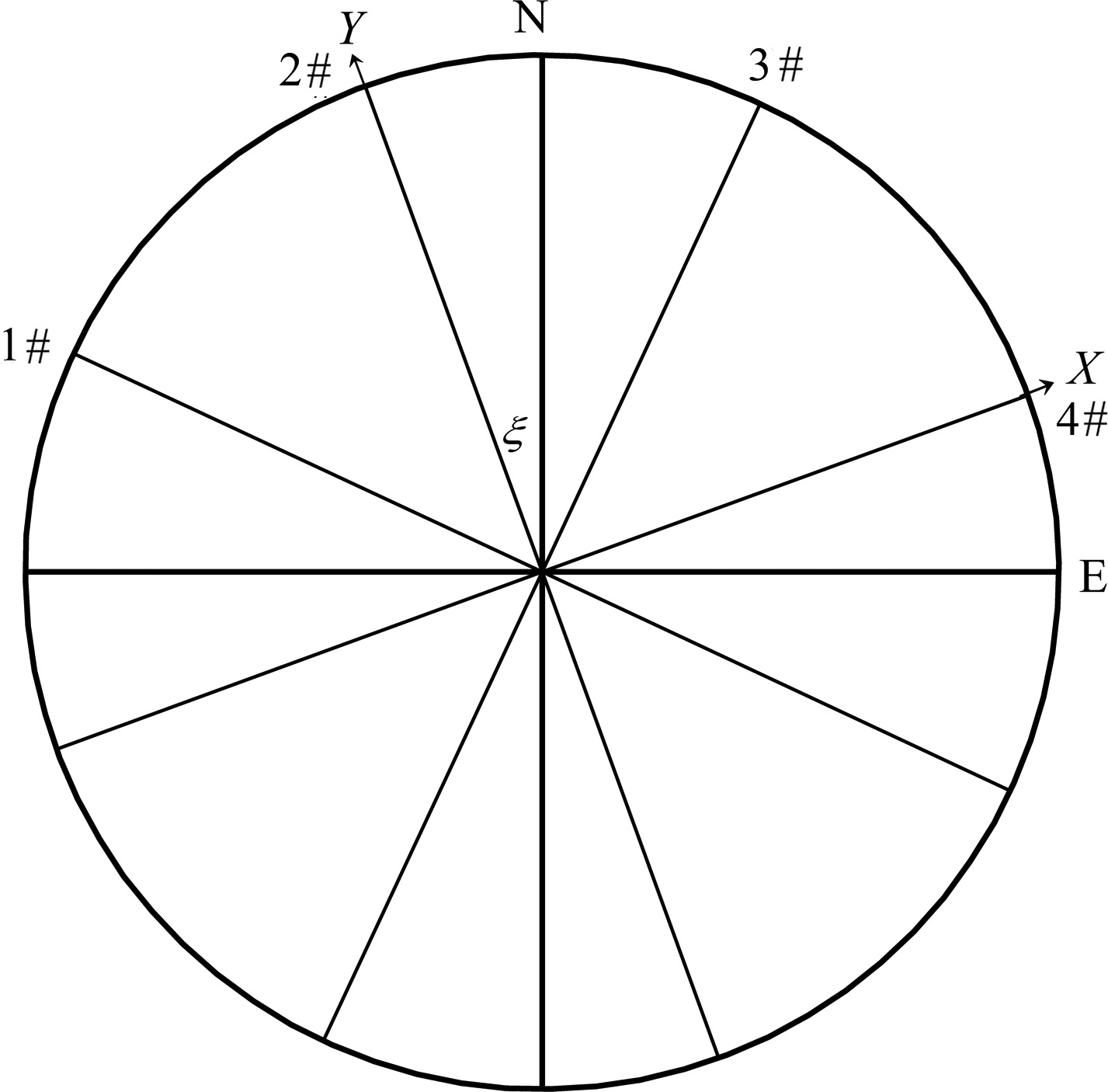
Figure 1 shows the distribution of four observation lines of 4-component borehole strain observation stations in China, which are 45° apart from each other. According to the elastic mechanics, assuming there is a cylinder in the interior of isotropic homogeneous rock, maximum principal strain η1, minimum principal strain η2 and principal direction ψ can be calculated from linear strains on three different directions with Mohr’s circle theorem:
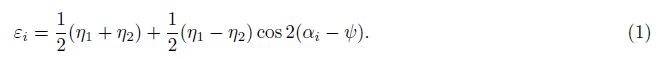
|
Fig.1 Distribution of 4-component borehole strain measurement of China |
Pan(1981)gives a general formula to compute the above-mentioned three strain invariants. But that formula is a transcendental equation, and its solution is very complex. Considering that principal strain and principal direction are independent of coordinate system, in this paper, we take strain observation line 2# as Y axis, and its orthogonal direction(strain observation line 4#)as X axis, the probe center as the origin of coordinate. The 4 strain observation lines are evenly distributed like symbol “*” on the end surface of a probe(Ouyang, 2009). $\hat \alpha $i is assumed to be the reference azimuth of the ith strain observation line in the XOY coordinate, and θ is assumed as the reference azimuth of principal direction. The reference azimuths of 4 strain observation lines are 0°, 45°, 90°, and 135° in the XOY coordinate, respectively.
In the XOY coordinate, formula(2)can be obtained from formula(1):
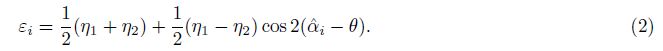
There are total 5 kinds of possible combinations, including 4 kinds which use only 3 strain observation lines, and 1 kind using all the 4 strain observation lines, to calculate maximum principal strain η1, minimum principal strain η2 and principal direction ψ .
Corresponding to the 5 kinds of possible combinations, there are 5 sets of formulae to calculate strain invariant according to formula(2).
The first possible combination(2#, 3#, 4#):
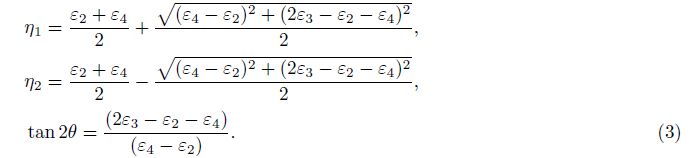
The second possible combination(2#, 4#, 1#):
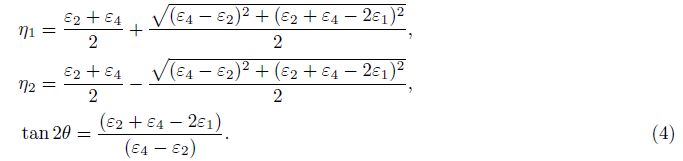
The third possible combination(3#, 4#, 1#):
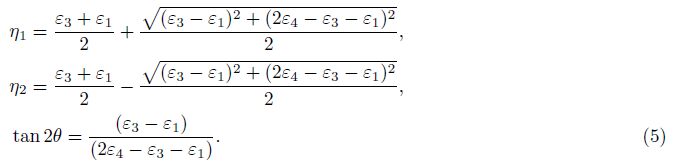
The fourth possible combination(2#, 3#, 1#):
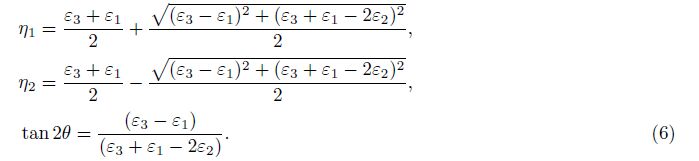
The fifth possible combination(1#, 2#, 3#, 4#):
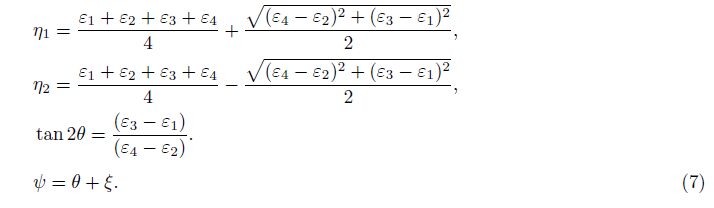
In these formulae, ζ is the azimuth of Y axis, also it is the azimuth of strain observation line 2#, ψ is the azimuth of maximum principal strain, called principal direction.
We show the distribution of four observation lines of the 4-component borehole strain stations in USA in Fig. 2. Assuming the observation line at the angle bisectors of two adjacent lines to be 1#, the rest observation lines is prescribed to be 2#, 3#, 4# in a clockwise direction. Taking the 1# line as the Y axis, line 3# as X axis, then the reference azimuths of 4 observation lines are 0°, 30°, 90°, and 150° in the XOY coordinate, respectively.

|
Fig.2 Distribution of 4-component borehole strain measurement in the United States |
We can get 5 sets of formulae to calculate strain invariant according to formula(2): The first possible combination(1#, 2#, 3#):

The second possible combination(1#, 2#, 4#):
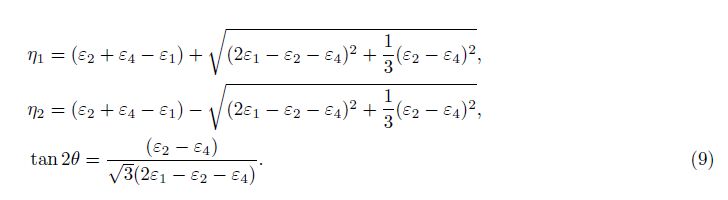
The third possible combination(3#, 4#, 1#):
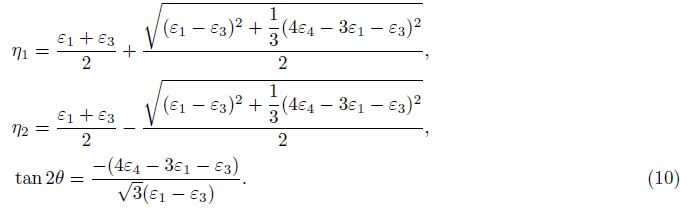
The fourth possible combination(2#, 3#, 4#):
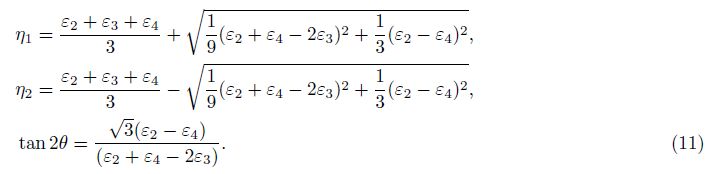
The fifth possible combination(1#, 2#, 3#, 4#):
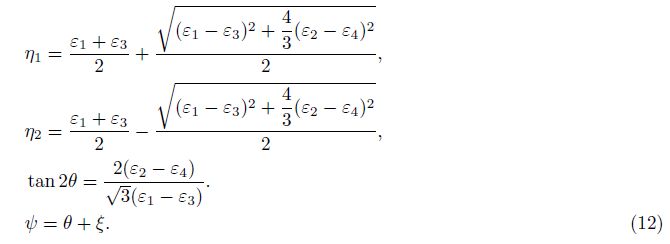
In these formulae, ζ is the azimuth of Y axis, also is the azimuth of strain observation line 1#, is the azimuth of maximum principal strain, called principal direction. Then, the areal strain and shear strain can be obtained from maximum principal strain η1, minimum principal strain η2 and principal direction ψ .
Actually, the observed strain at the borehole is not equal to the original strain when the borehole is not drilled. Therefore, the strain invariant cannot be obtained through Mohr’s circle theorem. It must use another model called coupling model(Pan, 1981)to calculate strain invariant:
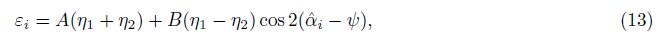
In the formula, A and B are two coupling coefficient, η1, η2 and ψ are the strain invariants.
After determining the value of A and B, we can get strain invariant by 5 sets of formulae similar to Mohr’s circle theorem. In formulae(3)-(6), the first denominator “2” in the right side of the equation should be replaced by “4A”, and the second denominator “2” should be replaced by “4B”. In formula(7), the first denominator is “8A” instead of “2”, the second denominator should be “4B” instead of “2”.
3 DATA SELECTION AND PROCESSINGSo far, there are more than 30 stations of YRY-4 type 4-component borehole strainmeter, and many stations of RZB-3D type 4-component borehole strain gauges in China; 81 stations of 4-component borehole strainmeter along the west coast of the San Andreas fault by PBO plan in USA. Because the data of 4-component borehole strainmeters in China is not open to public, it is difficult to collect the related data in China. Therefore, we only select 12 stations of YRY-4 type and 2 stations of RZB-3D type of borehole strainmeter to analyze. The data of 4-component borehole strainmeters in USA can be downloaded from the PBO website, and we r and omly select 11 evenly distributed stations to analyze. Considering the sampling rate and the length of observation data are much different from each other, we select the data of more than one year from each station for analysis. Some preprocessing of strain data should be done before analysis, such as removing large jump to reduce earthquake influences, deducting the strain value at start time from the hourly data to obtain the strain variation.
Because the 4-component borehole strain observation provides redundant observation, the quality of data can be self-checked. According to the elastic mechanics theory, once the strain observation on 3 different directions is obtained, the maximum, minimum principal strain and the principal direction are available. Now, if considering the redundant observation on the fourth direction, we can get 5 groups of solution for the maximum, minimum principal strain and the principal direction. If the adjustments of calibration on 4 component borehole strain observation lines are almost the same, i.e. the instrument and borehole are coupling well, and the rock around borehole is isotropic, the 5 groups of results should be consistent. To quantify the consistency of 5 groups of results(maximum, minimum principal strain and the principal direction), the results are analyzed with correlation and regression analysis method. The correlation coefficient shows the relationship of independent variable and dependent variable. If the correlation coefficient is close to 1, there is a strong correlation between dependent variable and independent variable. The regression coefficient shows dependence of independent variable and dependent variable. If the regression coefficient is close to 1, and constant term is close to 0, then dependent variable and independent variable are approximately equal to each other. That means the two groups of results are exactly equal to each other. If the regression coefficient is close to 1, and constant term is not close to 0, then two groups of results differ from each other by a constant value.
To evaluate the quality of the observation data, strain invariants of Chinese stations and American stations are analyzed. Then, the consistency of 5 groups of strain invariants is calculated, and the reason why 5 groups of strain invariants are not consistent with each other is also given in this paper.
Of course, we can evaluate the quality of the observation data with areal strain. For Chinese 4-component borehole strain, the areal strain is ε1 + ε3 = ε2 + ε4 = η1 + η2, and for American 4-component borehole strain, the areal strain is ε1 + ε3 = 2(ε2 + ε4 - ε1)= 2(ε2 + ε3 + ε4)/3 = η1 + η2.
4 RESULTS OF STRAIN INVARIANTS AND THEIR CONSISTENCYTable 1 shows 12 stations of 4-component borehole strain in China.
| Table 1 Information of 4-component borehole strain stations in China |
Table 2 shows 11 stations of 4-component borehole strain in USA.
| Table 2 Information of 4-component borehole strain stations in the United States |
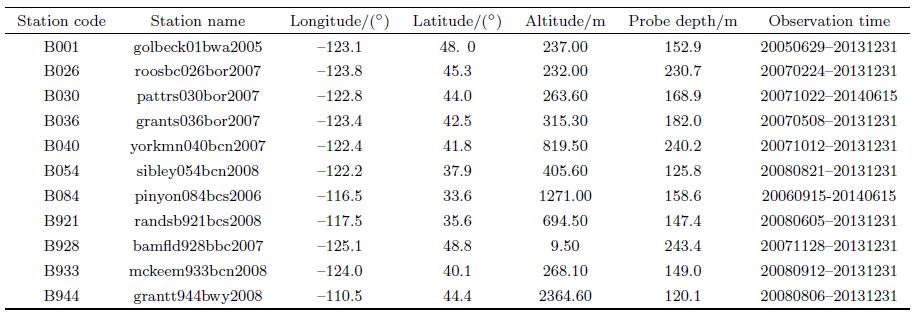
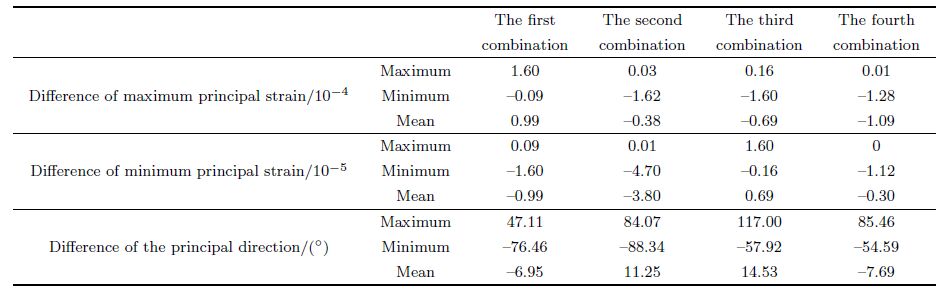
| Table 3 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in Gaotai station |
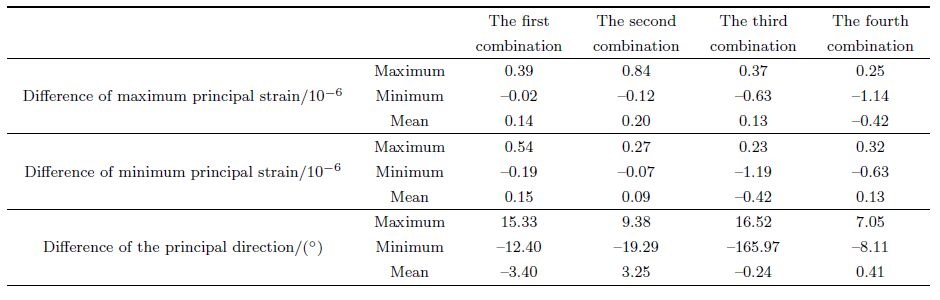
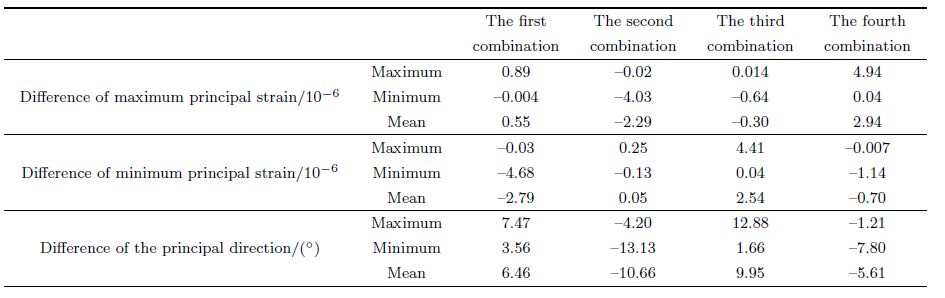
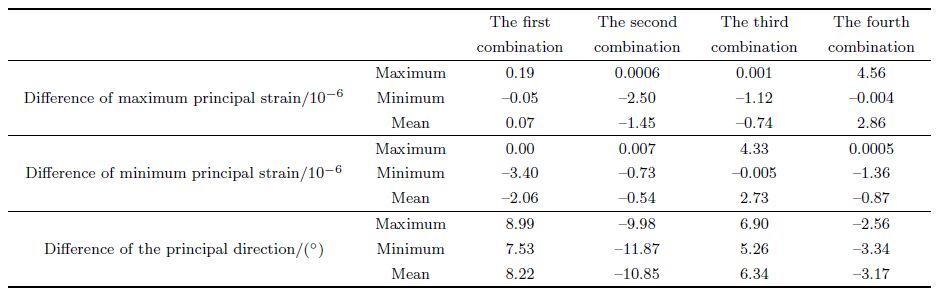
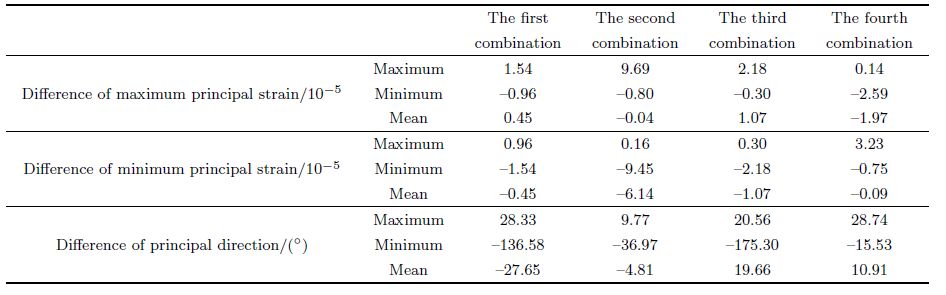
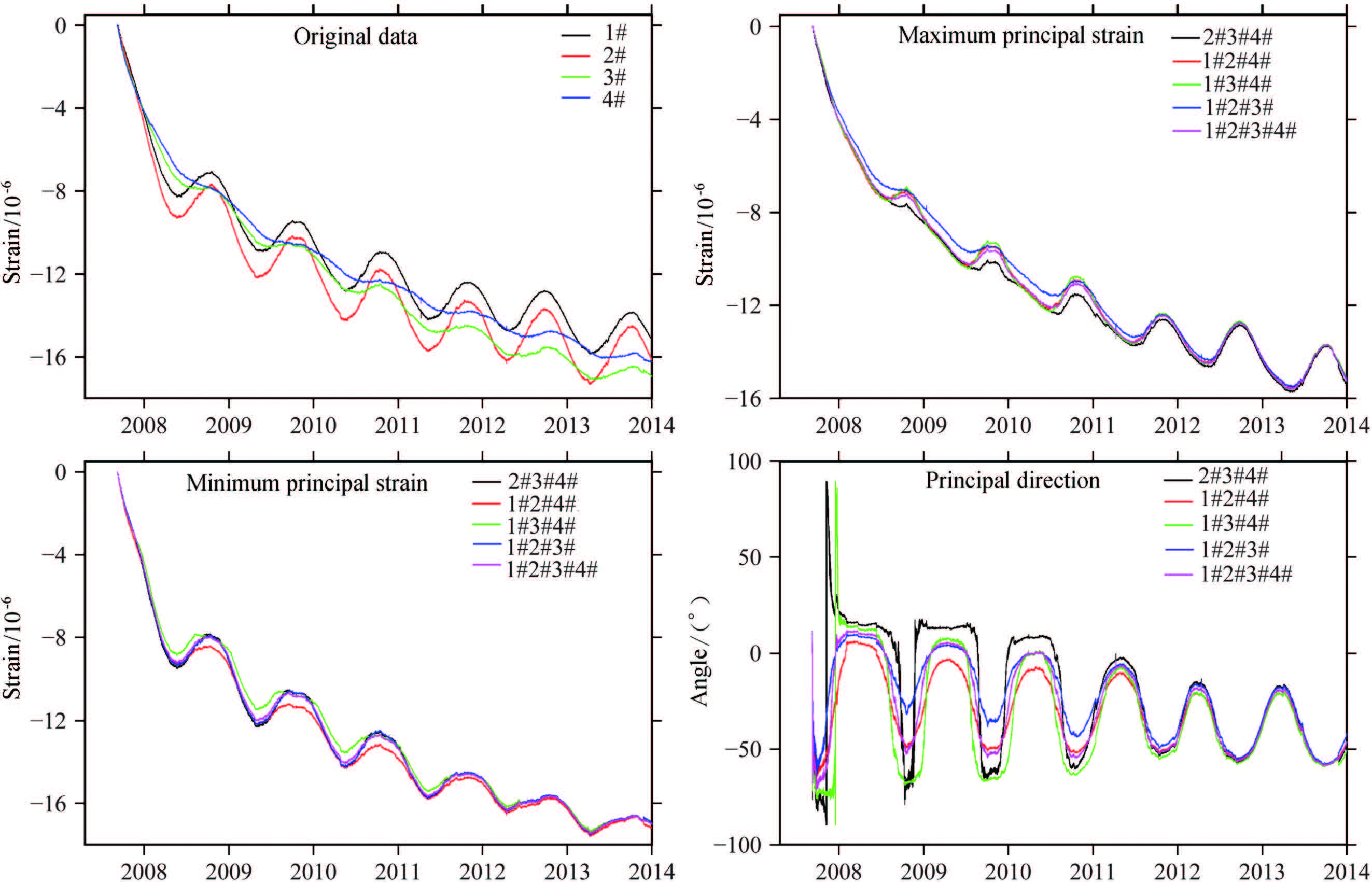
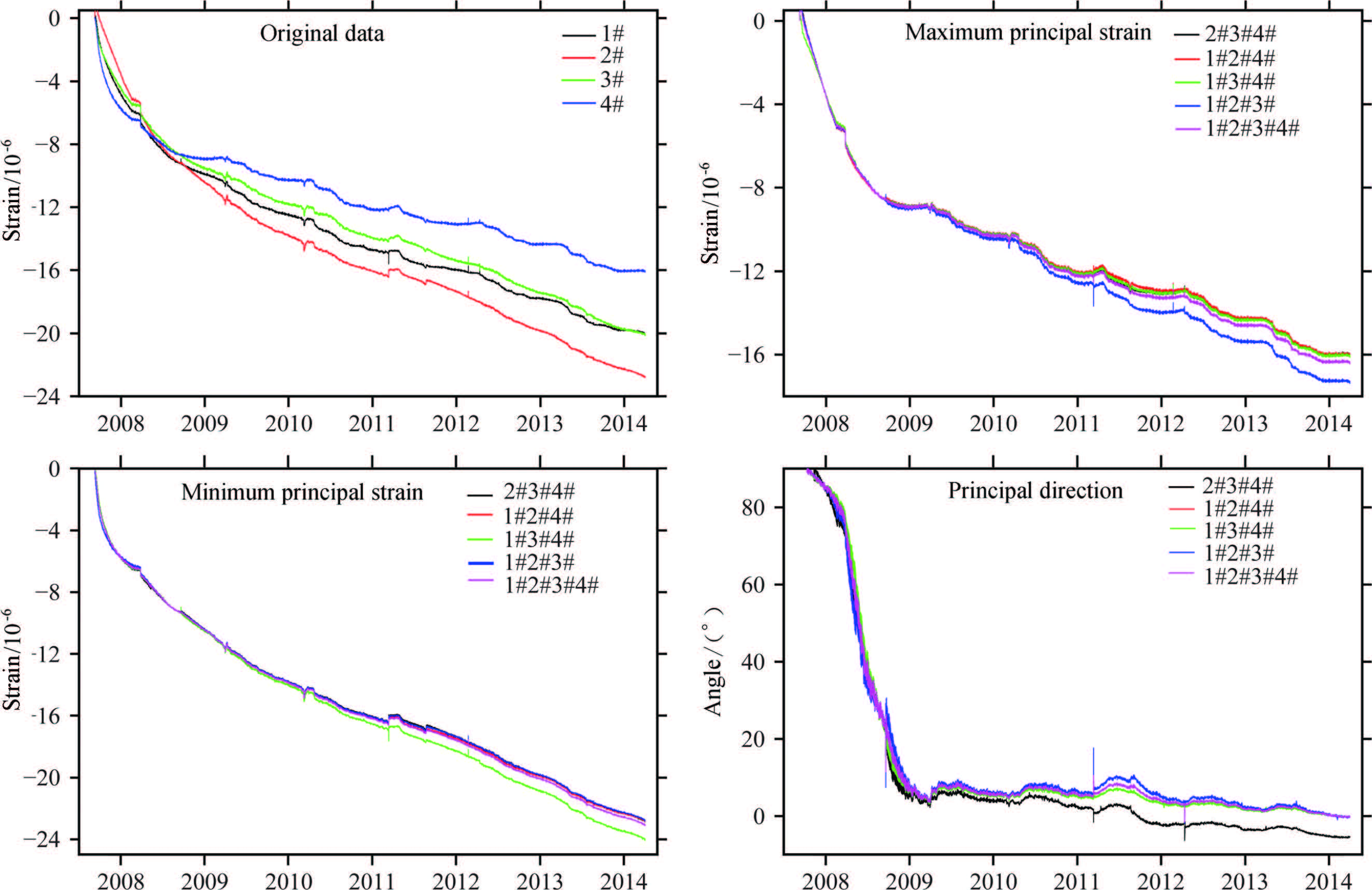
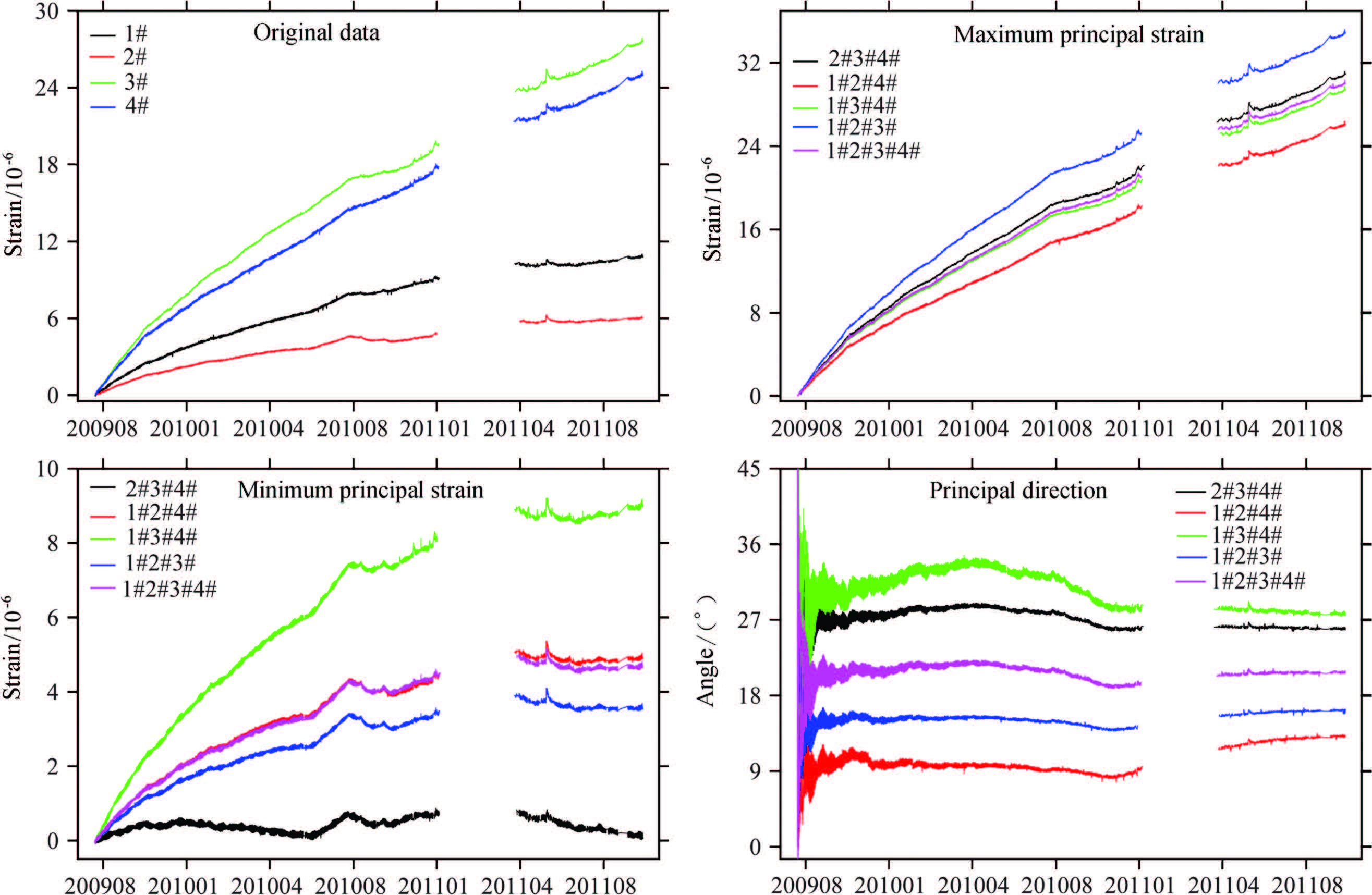
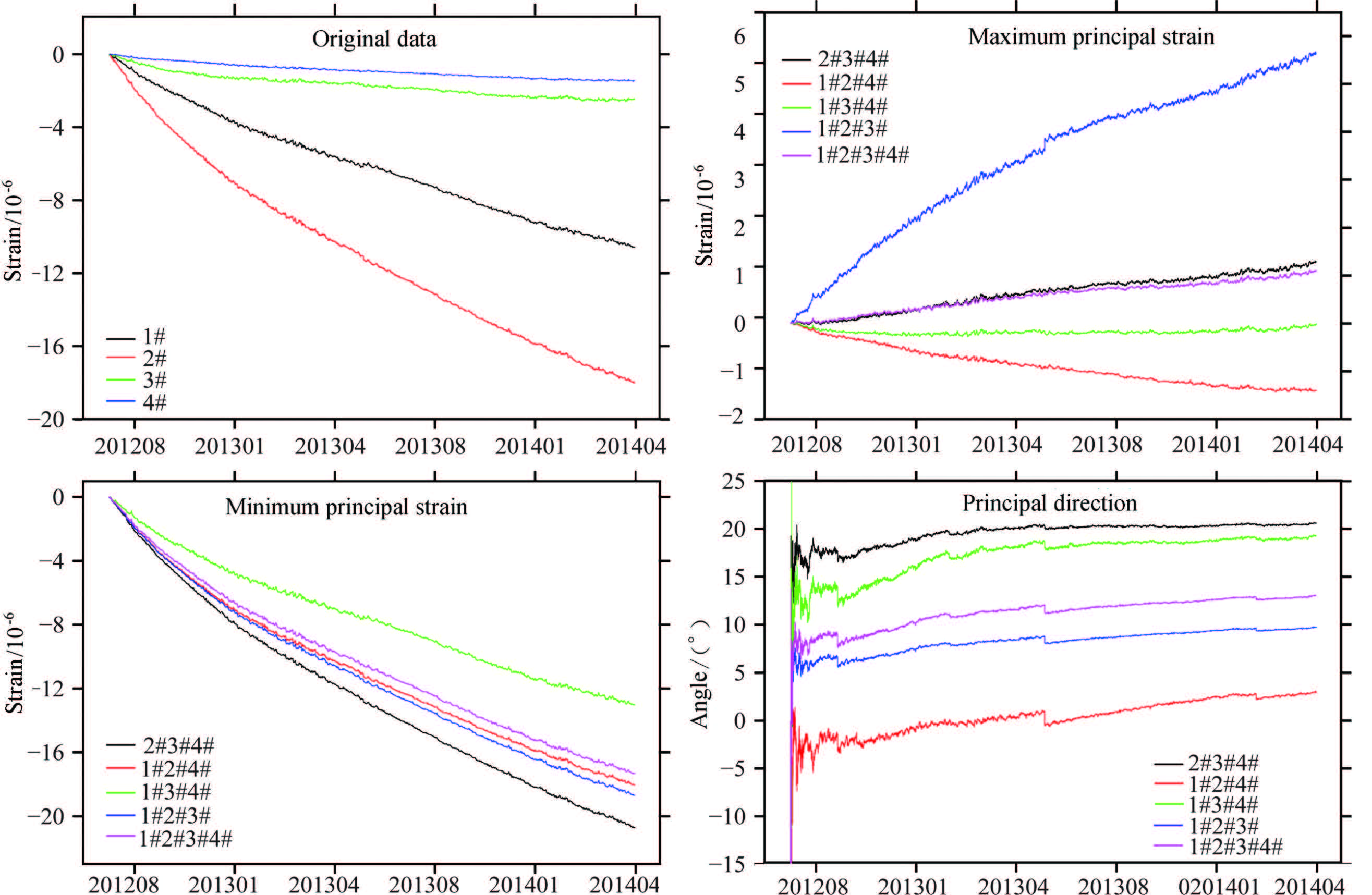
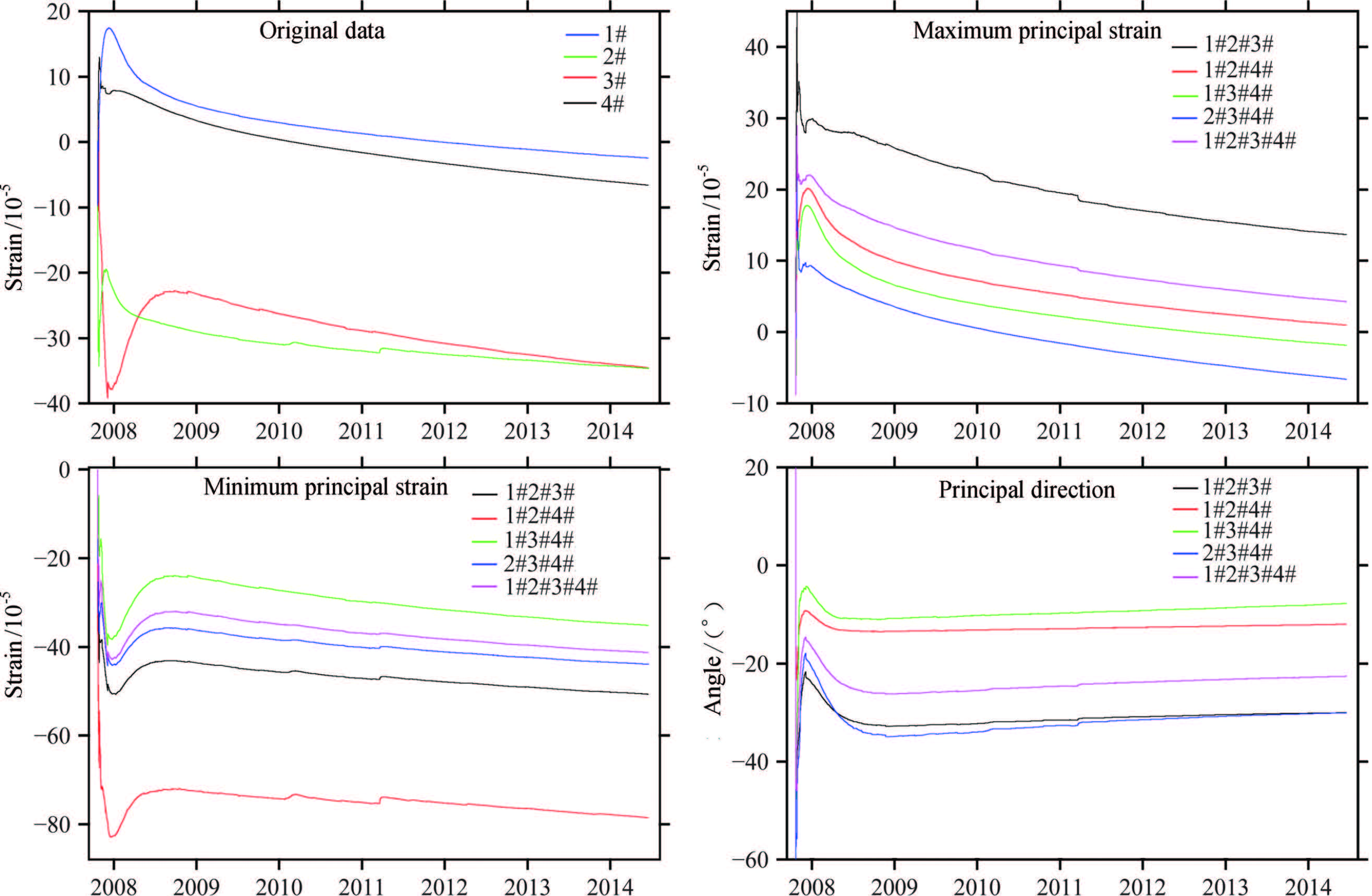
We show the results of 5 groups of strain invariants of two stations of YRY-4 type(Gaotai and Tonghua), two stations of RZB-3D type(Zhangzhou and Shanghai), two stations of American stations(B030, B084)in Figs. 3-8. The observation data of Gaotai and Tonghua stations are selected for they have the best quality in observation stations of YRY-4 type. Zhangzhou and Shanghai stations are selected for they are the only two stations of type RZB-3D that we can collect the data, and they are both deep well observation stations. The probe depth of Shanghai station is up to 463.6 m, and that of Zhangzhou station is 253m. B030 and B084 also are the two stations of best quality observation data in USA. The relevant charts and tables are given in more detail below.
|
Fig.3 Original data and calculated results of strain invariant of Gaotai station |
|
Fig.4 Original data and calculated results of strain invariant of Tonghua station |
|
Fig.5 Original data and calculated results of strain invariant of Zhangzhou station |
|
Fig.6 Original data and calculated results of strain invariant of Shanghai station |
|
Fig.7 Original data and calculated results of strain invariant of B030 station |

|
Fig.8 Original data and calculated results of strain invariant of B084 station |
| Table 4 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in Tonghua station |
| Table 5 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in Zhangzhou station |
| Table 6 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in Shanghai station |
In addition, there are other stations, such as Chinese stations Golmud, Huangyuan, Guiyang, Guzan, Delingha, Datong, and American stations B001, B036, B040, B054, B921, and B944 which also have good quality observation data. 5 groups of principal strain are very consistent to each other at these stations, but their principal directions are different from each other. The results of rest stations are worse than these stations. But overall, the consistency of the principal strain is better than that of the principal direction.
| Table 7 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in B030 station |
| Table 8 Difference value of maximum principal strain, minimum principal strain, and principal directions between fifth group and other groups in B084 station |
The continuous observation data of 4-component borehole strain of more than 20 stations are analyzed in this paper. Through the analysis, we can get some conclusions:
(1)In the initial period of observation, the principal strain of all Chinese stations and American stations change remarkably. In comparison, 5 groups of principal strain of Chinese YRY-4 type stations are consistent better than that of American stations. But the consistency of 5 groups of principal direction is worse than principal strain at all stations. After the initial period, 5 groups of principal strain are parallel with each other, and their values converge. The correlation coefficient and regression coefficient of principal strain of all stations are more and more close to 1. Principal strain and principal direction become more and more steady, but 5 groups of their values are still different from each other. The correlation coefficient and regression coefficient of principal direction of all stations differ more than expected.
(2)The principal strain of the stations in China and the United States shows a linear change trend to a different extent. Gaotai station in China is an example, its principal strain change is obviously linear, but the correlation coefficient and regression coefficient of its principal strain and principal direction is close to 1(almost equals to 1 for principal strain). There are obvious yearly periodic variations of principal strain and principal direction at Gaotai station. Five groups of principal strain and principal direction converges remarkably. Some other stations, such as Guiyang, Guzan, Delingha, have similar characteristics. The principal strain of American station B030 shows step changes of different magnitudes in March and April of 2010, 2011, 2012, and the amplitude of change reaches 10-5. The changes are not caused by the zero drift of the measuring instrument, and they may be caused by stress adjustment of the rock after instrument installation in deep well. It is normal that the performance of instrument is somehow unsatisfactory during installation, because borehole strain technology is different from other ground observations. Improvement of borehole strain observation must be carried out in deep well or drilled holes in rock. Therefore, it will take a long time to make borehole strain gauge become qualified scientific instrument through the process of invention, improvement and perfection.
(3)The maximum difference of principal strain of American stations is larger than that of Chinese stations. The maximum of American stations are mostly up to 10-5, but that of Chinese stations are mostly between 10-6 and 10-7. The differences between 5 groups of principal direction of Chinese stations are also smaller than that of American stations.
(4)The depth of deep well of YRY-4 type borehole strain station in China is shallower than that of American stations, and there are obvious annual variations at the five stations of YRY-4 type borehole strain. But in general, the correlation coefficient and regression coefficient of strain invariant of these stations are closer to 1 than that of American stations.
(5)The reading of 4-component borehole strain observation of Chinese stations is calibrated in laboratory experiments, but at American stations it is calibrated by theoretical value of solid Earth tide.
5 ERROR ESTIMATION FORMULAE FOR STRAIN INVARIANTSWhy the correlation coefficient and regression coefficient of principal strain are close to 1, but that of principal direction are far from the expected value? Is that attributed to the 5 sets of formulae? To make it clear, we calculated 5 groups of strain invariant with theoretical strain values of solid Earth tide instead of observations. The results show that the 5 groups of strain invariant are almost the same, and they are slightly different due to calculation error(the unit of solid Earth tide is 10-9). Why is there great difference between the results calculated from theoretical value of solid Earth tide and from the observed strain? We found that it is attributed to that the theoretical strain value of solid Earth tide does not have problems such as observation error, imperfectly coupled probe and borehole, orientation error, anisotropy of rock, and unsatisfactory quality of drilling, etc. Therefore, Mohr’s circle theorem(the formula(2))works well. According to the formula(2), we can prove that strain invariant calculated with 5 sets of formulae is completely equivalent. But for observations, because of the above errors, formula(2)is only approximate. Therefore, the 5 groups of strain invariant are not completely equivalent. It is very normal that 5 groups of principal strain and principal direction calculated from strain observations are different from each other. We consider that the observed strains are of equal weight, and the observation errors should be the same for 5 sets of formulae. However, why the 5 groups of principal strain are so close to each other, but principal directions have great discrepancy? We found that this is caused by the observation error propagation. According to the law of error propagation, the root mean square errors of maximum and minimum principal strain must have upper limit values, which are equal to each other, but there is no upper limit in the root mean square errors of principal direction, and they are different from each other.
Assuming that the root mean square error of borehole strain observation is m, the root mean square errors of maximum and minimum principal strain are ση1 and ση2, and the root mean square error of principal direction is σθ, we can get 5 groups of the root mean square error of strain invariants calculated with coupling model(13).
The first possible combination:
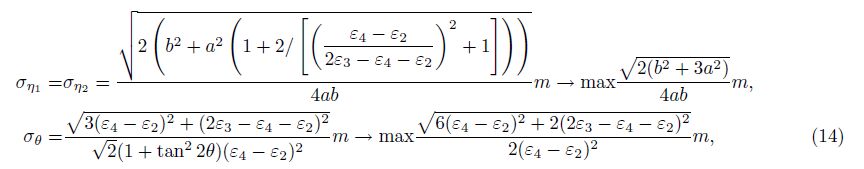
The second possible combination:
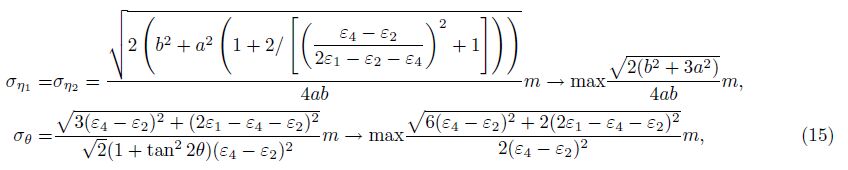
The third possible combination:

The fourth possible combination:
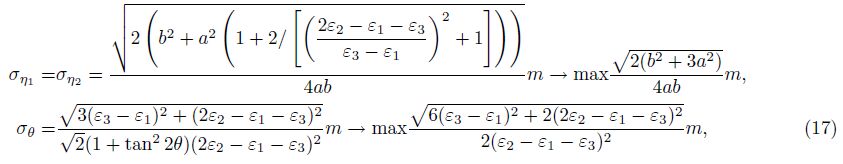
The fifth possible combination:

Because strain invariant is computed with Mohr’s circle theorem in this paper, so we can get 5 groups of the root mean square error of strain invariants by making a = b = 0.5 in formulae(14)-(18), the maximal root mean square error of principal strain is $\sqrt 2 $m, and the root mean square errors of principal direction are different from each other. This is caused by observation errors. Due to the observation errors, the denominator or numerator in the root mean square error of principal direction is possibly equal or close to 0, which shouldn’t happen. It may make the root mean square error of principal direction equal to 0, or infinite, or uncertain, that means that the calculated values of 5 groups of principal direction are obviously different from each other.
We can obtain the strain invariant error estimation from formulae(8)-(12)for the American borehole strain stations in the same way. As mentioned above, we can get 5 formulae to estimate the root mean square error of strain invariants according to the law of error propagation. It can be sure that the root mean square error of principal strain caused by the observation error is bounded, but the root mean square error of principal direction is unbounded.
There is a redundant observation in 4-component borehole strain, so it is possible to check the reliability of strain observation for users. This could be done not only by checking whether the areal strains calculated by different linear strain combinations are equal, but also by checking whether the 5 groups of principal strain and principal direction are equal to each other.
According to the elastic mechanics, the value of strain invariant is unique. It is derived from the elastic mechanics theorem, but the real situation is complicated. As said by the Australian philosopher Wittgenstein“It is not how things are in the world that is mystical, but that it exists”(Zhang, 2013), the results also shows that strain invariants calculated from observations are not unique in this paper. After gauge installation, there are many factors, such as the change of calibration value, inexactitude of strain observation line orientation, imperfectly coupled gauge and borehole, anisotropy of the fault or rock, environmental interference, and other observation errors, to make strain invariants different from each other. It is no doubt that the check is very critical, but now that 4-component borehole strain has been installed, we have to improve them to satisfy selfchecking requirements within the range of permissible error. As far as we know, if the adjustments of calibrated value of 4 strain observation lines are almost the same, and the instrument and borehole are coupling well, and rock around borehole is isotropic, then the 5 groups of results will be obviously close to each other. Gaotai station is a good example. The result of Gaotai station shows that the correlation coefficient of maximum and minimum principal strain are almost equal to 1, the minimum is 0.997; correlation coefficient of principal directions is a bit poor, but mostly between 0.98~0.81. The 5 groups of principal strain and principal direction are becoming closer to each other, and the difference of principal strain is on the order of 10-7; the regression coefficient of principal strain is close to 1, and that of principal directions is slightly worse. The result of B030 stations also shows that the 5 groups of principal strain are consistent with each other, the maximum difference is about 10-5, but the result of principal directions is somehow worse. There are many examples to demonstrate that strain invariant is unique according to the elastic mechanics, e.g., for most of the stations, the correlation coefficient and regression coefficient of principal strain is close to 1, and 5 groups of principal strain seem to be fairly smooth over approximately 1~2 years’ time after installation, and they become closer to each other. It shows that 4-component borehole strainmeter objectively observes the nominal strain of a drilling hole. It also shows that it is effective to calculate strain invariant with the Mohr’s circle theorem. We believed that the fifth possible combination using 4 linear strains is the best one, because it uses the entire information of strain observation. Besides, the root mean square error of principal strain is also smaller than that of other possible combinations.
In the 1960 s, China(according to Li Siguang, many departments are encouraged to separately install multiple borehole strain gauges) and United State(Sacks first invented the body strain gauge)began to explore the borehole strain observation technology. After half a century of research, practice and development, borehole strainmeter gradually meets the requirement for scientific observation. With the development of borehole strain gauge, China formed their own unique technology by absorbing the international technology and experience. Now, after the efforts of two generations, China approached the international frontier of borehole strain research, and some of the nucleus technologies become leading in the world. Technology of seismometer contributes significantly to investigate the interior structure of the Earth after a century of development; even if there are still special difficulties in borehole strain observation, many progresses were made after half a century of practice. The problems remained to be solved include how to reduce the differences of principal strains among 5 groups; how to improve lightning protection and prolong life of the instruments, and so on.
In an intact homogeneous elastic medium, we adopt 5 groups of formulae for strain invariants with Mohr’s circle theorem. For a borehole, we add the coupling model. According to error propagation law, the root mean square errors of principal direction are unlimited, and they are different from each other. It shows that there are still defects in calculating the principal strain and principal direction by the two models. Thus it should be improved. As we know, principal strain and principal direction are modulus and azimuth of characteristic vector, which are indispensable. Otherwise, it is impossible to determine the two characteristic vectors, and we cannot know on which direction the shear strain is 0. If the principal strain is reliable, then the size and shape of strain ellipse is sure. If the principal direction is not reliable, positioning of the strain ellipse is uncertain. When calculating principal direction, it will use arc tangent, which is nonlinear, and sometimes it is very sensitive to error. Maybe a small error may cause a big difference. So it should be improved. But it is confirmed that if adjustments of calibration value on 4 strain observation lines are almost the same, instrument and borehole are coupling well, and rock around borehole is isotropic, then 5 groups of results will be equal to each other. It is also illustrated by the examples in this paper. By now, we do not know how to calibrate after instrument was installed. We can only use the calibration value from laboratory experiments, or calibrate with earth tide theory. It is an urgent technical problem that needs to be solved. Qiu(2013)attempted to determine site relative calibration and absolute calibration by data processing method, but in fact is not feasible(Liu, 2013). Hart(1996)attempted to calibrate with solid tidal strain, which is also debatable, because theoretical value is not equal to borehole strain observations. It does not conform to the st and ard of relative scale calibration(Liu, 2013), and it is only an alternative method. The strain observation is not real strain in rock but a nominal strain. Construction of 4-component borehole observation station is systematical project, for we must be very careful in site selection, station construction, borehole drilling, development of instrument, orientation of strain observation line, coupling between probe and borehole, etc. Once the borehole strain gauge is installed in deep well, it is very difficult for inspection, maintenance and repairing. Therefore, it is especially important that the instrument can work reliably for long time. In practice, some stations have only given voltage value, failing to give calibration value; some stations have to stop observation because of instrument failure in less than 2-3 years after installation, which causes a great loss. In consideration of popularizing 4-component borehole strain by China Earthquake Administration, there are many aspects that need to be taken into consideration before construction of stations, such as site selection, equipment selection, instrument installation, observation precision, annual change of rock strain caused by air temperature, drilling depth, construction qualification, and so on. These factors need to be deeply analyzed and integrally balanced to obtain a high performance for observation and ensure the long term of stable operation of 4-component borehole strainmeter.
In research of two coefficients A and B in coupling model, the physical significance of two coefficients is discussed and theoretical formula of them is given by Zhang(2013). However this formula cannot be applied because the calculation of some parameters is quite complicated, and it needs to sample the rock core near the sensor which is hardly done in most Chinese 4-component borehole strain stations. For this reason, we calculate the strain invariant with Mohr’s circle theorem in this paper, offering 5 groups of strain invariant which are very close to each other. Among all of the stations, Gaotai station has the best calculated result. It may be due to that the site calibration value is very close to the originally calibrated value in laboratory; or correction coefficients of calibration value in every sensor are close to each other, which means a zoom-in or zoom-out of the same size, the instrument and borehole are coupling well, and rock around borehole is isotropic. The correlation coefficient and regression coefficient between 5 groups of strain invariant with coupling model should be more close to 1. It is too early to judge that the results of coupling model are better than that of Mohr’s circle theorem, until the formula given by Zhang is applied to calculate two coefficients A and B in the future. It is yet to be proved by further calculation.
ACKNOWLEDGMENTSThe observation data of 4-component borehole strain in China are downloaded from the network of China Earthquake Administration. The observation data of Shanghai station is provided by Earthquake Administration of Shanghai Municipality. The observation data of American stations are downloaded from PBO website. We thank them for sharing the data which are used in this study.
| [1] | Chen Q C, Li H, Liao C T, et al. 2011. An experimental study of the technique for in-situ stress measurement and monitoring:an introduction to the project SinoProbe-06. Acta Geoscientia Sinica (in Chinese), 32(Suppl. Ⅰ):113-124. |
| [2] | Chi S L, Wu H L, Luo M J. 2007. Discussion on strain tidal factor separation and anisotropy-Analysis of first data of borehole component strain-meter of China's digital seismological observational networks. Progress in Geophysics (in Chinese), 22(6):1746-1753. |
| [3] | Chi S L, Liu Q, Chi Y, et al. 2013. Borehole strain anomalies before the 20 April 2013 Lushan MS7.0 earthquake. Acta Seismologica Sinica (in Chinese), 35(3):296-303. |
| [4] | Gladwin M T. 1984. High-precision multi-component borehole deformation montoring. Rev. Sci. Instrum., 55(12):2011-2016. |
| [5] | Hart R H G, Gladsin M T, Gwgther R L, et al. 1996. Tidal calibration of borehole strain meters:Removing the effects of small-scale inhomogeneity. Journal of Geophysical Research, 101(B11):25553-25571. |
| [6] | Heitz S. 1988. Coordinates in Geodesy. Berlin Heidelberg:Springer. |
| [7] | Jaeger J C. 1964. Elasticity, Fracture and Flow. London:Methuen & Co., 54-58. |
| [8] | Johnston M J S, Borcherdt R D, Linde A T, et al. 2006. Continuous borehole strain and pore pressure in the near field of the 28 September 2004 M6.0 parkfield, California, earthquake:Implications for nucleation, fault response, earthquake prediction and tremor. Bulletion of the Seismological society of America, 96(4B):556-572. |
| [9] | Li H L, Li H. 2010. Status and developments of borehole strain observations in China. Acta Geologica Sinica (in Chinese), 84(6):895-900. |
| [10] | Liu X Y. 2013. Instrument site calibration can not be replaced by data processing. Journal of Geodesy and Geodynamics(in Chinese), 33(4):151-154. |
| [11] | Longbein J, Marray J R, Snyder H A. 2006. Coseismic and initial postseismic deformation from the 2004 Parkfield, Californica, earthquake, observed by global positioning system, electronic distance meter, greepmeter, and borehole strainmeters. Bulletin of the Seismological Society of America, 96(4B):S304-S320. |
| [12] | Means W D. 1982. Stress and Strain (in Chinese). Ding Z Y, Trans. Beijing:Science Press, 74-114. |
| [13] | Niu B H, Sun C Y. 2005. Solid Elastic Medium and Seismic Wave Transmit (in Chinese). Beijing:Geological Publishing House, 39-49. |
| [14] | Ouyang Z X, Zhang J, Chen Z, et al. 2009. New progress in multi-component observation of crustal deformation in deep boreholes. Recent Developments in World Seismology (in Chinese), (11):1-13. |
| [15] | Pan L Z. 1981. Derivation and discussion of several formulas on ground stress measurent.//China Geological Academy Geological Institute, Principles and applications of ground Stress measurement (in Chinese). Beijing:Geological Publishing House, 163-203. |
| [16] | Qian W C, Ye K Y. 1980. Elastic Mechanics (in Chinese). Beijing:Science Press, 27-34. |
| [17] | Qiu Z H, Tang L, Zhang B H, et al. 2013. In situ calibration of and algorithm for strain monitoring using. Four-gauge borehole strainmeters (FGBS). Journal of Geophysical Research, 118(4):1609-1618, doi:10.1002/jgrb.50112. |
| [18] | Qiu Z H, Zhou L S, Chi S L, et al. 2009. Study on precursory strain changes of Wenchuan earthquake with ORA method.Journal of Geodesy and Geodynamics (in Chinese), 29(4):1-4. |
| [19] | Qiu Z H, Zhang B H, Chi S L, et al. 2010. Precursory strain changes of Wenchuan earthquake. Science China:Earth Sciences (in Chinese):40(8):1031-1039. |
| [20] | Shi Y F, Shi J S, Cui Q G, et al. 2013. Research on the ability of borehole strainmeter in Guiyang seismic station to respond the earthquake. Recent Developments in World Seismology (in Chinese), (9):19-26. |
| [21] | Wang M Z, Wang W, Wu J K. 2002. The Course of Elastic Mechanics (in Chinese). Beijing:Peking University Press, 35-36. |
| [22] | Young W C, Budynas R G. 2005. Roark's Formulas for Strain and Stress (in Chinese). 7th ed. Yue Z F, Gao X S, Wang F H, et al., Trans. Beijing:Science Press, 9-26. |
| [23] | Yu Z G, Lu Z Q, Lin R L. 2008. Linear Algebra and Geometry (1) (in Chinese). Beijing:Tsinghua University Press, 217-221. |
| [24] | Zhang F. 2013. Features of western philosophy in the perspective of four philosophical sayings. Journal of CUPL (in Chinese), 22(4):142-148, 161. |
| [25] | Zhang J, Liu Q. 2010. Processing and analysis of four-component borehole strain observations. Journal of Geodesy and Geodynamics (in Chinese), 30(6):6-9. |
| [26] | Zhang L K, Niu A F. 2013. Component borehole strain observations coupling coefficients calculation. Chinese J. Geophys.(in Chinese), 56(9):3029-3037. |
 2014, Vol. 57
2014, Vol. 57