2. SINOPEC Geophysical Research Institute, Nanjing 210014, China
With the fast development of computer science and technology, it is viable for researchers to simulateglobal seismic wave propagation(Komatitsch et al., 2002; Yan et al., 2009; Zhang et al., 2009; Komatitsch et al., 2010; Long et al., 2010). Because of irregular interfaces and rugged free surface of the earth(Komatitsch and Tromp, 2002a, b), traditional finite difference method or pseudo-spectral method with regular grid is notable to correctly fit complex topography(Fornberg, 1987; Moczo et al., 2000; Magnoni et al., 2014). Classicalspectral element method(SEM)chooses GLL(Gauss-Lobatto-Legendre)interpolation points, and constructshigh-order polynomial in the form of Lagrange tensor product, which obtains lumped mass matrix and avoidssolving large scale linear equation system(Wang et al., 2012). Though classical SEM is highly efficient inmodeling seismic wave in global model, quadrilateral elements(hexahedron in 3D case)in SEM are not able toaccurately describe rough interfaces. Though a finer grid can well present boundary variation, computation costmay increase dramatically. SEM with triangular mesh(TSEM)can easily h and le complex geological structures, however it needs more interpolation nodes to obtain acceptable accuracy, as the accuracy of each Koornwinder-Dubiner polynomials is not the same, which leads to a huge global stiffness matrix and hinders the applicationof TSEM in large scale seismic wave simulations. Many optimized methods with satisfactory accuracy havebeen developed based on the traditional methods, such as nearly analytic discretized method(Yang et al, 2003, 2014), convolutional differentiator method(Li et al., 2012) and optimized coefficient finite difference method(Zhang and Yao, 2013), but these methods still suffer from some drawbacks of the traditional methods, such aslow accuracy in modeling surface wave and incapability h and ling rugged topography.
Classical finite element method(FEM)has the power of discretizing a geological model with a mesh ofarbitrary shape elements, however classical FEM with consistent mass matrix(CFEM)is confronted with huge computation costs as the inversion of consistent mass matrix is involved, which decreases the computationefficiency in practical applications. Using mass lumping technique and considering the acceleration in eachelement does not change obviously, we can lump the coupled inertial force to one node, and obtain the lumpedmatrix finite element method(LFEM), which leads to an explicit method. The numerical orders of LFEM and CFEM are the same. LFEM can gain comparable accuracy as CFEM under the condition that element sidelength is much shorter than wave length and numerical integration has sufficient accuracy, or the numericalaccuracy of LFEM may be very low. Marfurt(1984)proposed a new mass matrix(mixed mass matrix)(MFEM)by linearly combining consistent mass with lumped mass, and investigated its accuracy by analyzing its numericaldispersion in solving acoustic wave equation, however MFEM does not lead to an explicit method. In this article, we introduce a residual mass matrix to exp and the inverse of mixed mass matrix into a series based on Taylorexpansion. One can select the first several terms of the series to satisfy different precision requirements.
Few researchers have discussed dispersion properties of FEM with triangular mesh in the literature(Mullen, 1982), and the discussion of dispersion properties is mainly concentrated on square or quadrilateral element grid(Abboud and Pinsky, 1992; Mulder, 1999; Zyserman and Gauzellino, 2005; De Basabe and Sen, 2007, 2010;Zyserman and Santos, 2007; Seriani and Oliveira, 2008). The dispersion properties of TSEM are also paid littleattention for the scheme is hard to construct(Mazzieri and Rapetti, 2012; Liu et al., 2013). It is necessaryto conduct a comprehensive study about dispersion properties of FEM with triangular mesh, and find thedifferences among the above three types of mass matrix in modeling acoustic and elastic wave propagation. Thebehaviors of dispersion are also related to element shape, interpolation order and P- to S-wave speed ratio, and a quantitative discussion is useful for grid generation and parameter setting in practical simulations.
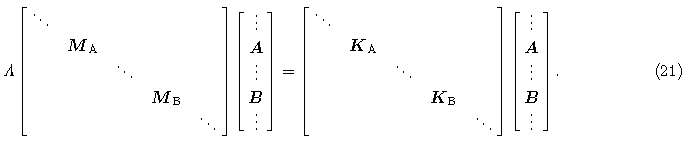
The basis functions along two orthogonal directions are decoupled for FEM with quadrilateral mesh, and the mass matrix can be decomposed into the tensor products of one dimensional mass matrix(Wang, 1993;Zhou et al., 1997). By analyzing the periodicity of mesh, the dispersion relations in 2D case can be expressedin the form of the combinations of dispersion relations in 1D case(De Basabe and Sen, 2007, 2010). The basisfunctions are coupled as area coordinates should satisfy a certain equality, so dispersion relations can not beobtained from 1D relations. Here we construct the generalized eigenvalue problem for FEM with triangularmesh, and analyzing the periodicity of the nodes in a regular mesh, and then infinite order eigenvalue problemcan be simplified to a finite order problem. We discuss the influence factors of dispersion properties, and presentthe dissipation of MFEM at the end of the paper.
2 DISCRETIZING ACOUSTIC AND ELASTIC EQUATIONS BY FEM 2.1 Classical Finite Element MethodThe media of the earth is extremely complex. For theoretical analysis and practical application, seismicwave propagation through the earth is usually described by acoustic or elastic equations(Ma et al., 2010, 2011).The acoustic wave equation in heterogeneous medium can be written as

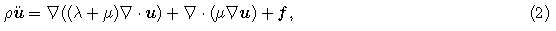
We need make some assumptions before dispersion analysis. First, exterior force is free; second, themedium is isotropic. Under these assumptions, Eq.(1)can be reduced to

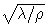 is acoustic wave velocity. Eq.(2)can be simplified as
is acoustic wave velocity. Eq.(2)can be simplified as 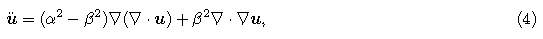
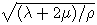 is the velocity of P-wave, and β =
is the velocity of P-wave, and β = 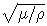 is the velocity of S-wave.
is the velocity of S-wave.
Discretizing Eq.(3)by FEM, multiplying Eq.(3)by an arbitrary test function v, and integrating in thefinite element domain, the following weak form of acoustic equation can be obtained by integration by parts and Green formula.
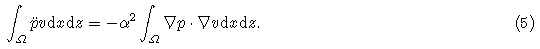
We discretize the spatial domain into N nonoverlappping triangular elements, choose n interpolationnodes in each element, and construct basis function Φi(i = 1, 2, · · ·, n). Then the value of pressure field can beapproximately expressed as


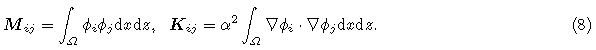
Various temporal schemes can be adopted to solve Eq.(7), such as Lax-Wendroff method with arbitraryeven order(Dablain, 1986; Chen, 2009; De Basabe and Sen, 2010), Runge-Kutta scheme(Chen et al., 2010), Newmark method(Komatitsch and Tromp, 2002a, b) and symplectic methods(Ma et al., 2011; Li et al., 2012;Wang et al., 2012; Liu et al., 2013a, b). Among these methods, central difference(i. e. second-order Lax-Wendroff method)is the most efficient scheme. In the paper, we mainly discuss the spatial discretization, so wesimply choose central difference to discretize Eq.(7), and the fully discretized form of Eq.(7)can be written as
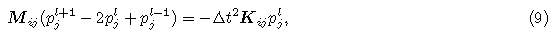
Multiplying elastic wave Eq.(4)by a test vector function, integrating over the finite element domain, and using integration by parts and Green formula, we obtain the following weak form equation
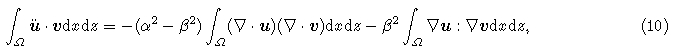
 AijBij, and A and B are both m-th order tensors. Eq.(10)can be discretized as
AijBij, and A and B are both m-th order tensors. Eq.(10)can be discretized as 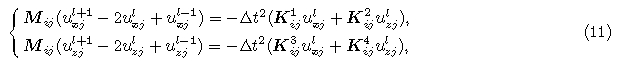
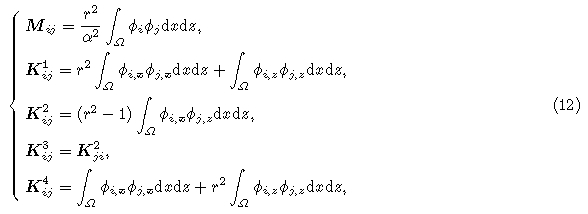
From Eqs.(9) and (11), we can find that classical FEM for modeling seismic wave propagation involvessolving a large linear equation system. In order to reduce computation costs, we often lump the mass matrixto form a diagonal mass matrix based on the assumption that acceleration does not change obviously in eachelement. From the basic theory of FEM, one can easily prove that the error order of this approximation isthe same as that of consistent mass matrix, so convergence rate of lumped mass matrix is nearly the same asthe consistent mass matrix(Fried and Malkus, 1975). But the accuracy of LFEM is inferior to that of CFEM(Mullen and Belytschko, 1982). Lumped mass matrix can be expressed as


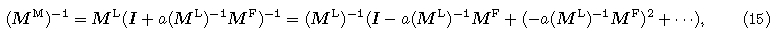
The dispersion property of acoustic and elastic propagation is related to analyzing the generalized eigenvalueproblem, which can be written as Eq.(17). In this section, we discuss the different factors that influencedispersion of FEM with triangular mesh. We can obtain the close form of dispersion relation when first-orderinterpolation is used. However, we can only obtain numerical results when high-order interpolation is employed.Let us consider the plane wave solution of a wave equation:

Inserting Eq.(16)into Eq.(9), we obtain the following generalized eigenvalue problem

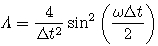 3.1 Dispersion Characteristics of Three Mass Matrix Types
3.1 Dispersion Characteristics of Three Mass Matrix Types
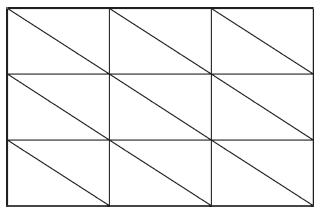
We use isosceles right triangular elements with both side being h to discretize finite element domain, whichis shown in Fig. 1, and we discuss the grid dispersion of the three types of mass matrix in Eqs.(8), (13) and (14).For first order interpolation, the dispersion relations on every node in figure 1 are the same, so the dispersionrelation of any node can represent the global dispersion property, which is proved in Appendix A. From Eqs.(16) and (17), the dispersion relation of CFEM, LFEM, and MFEM for acoustic wave modeling can be written as
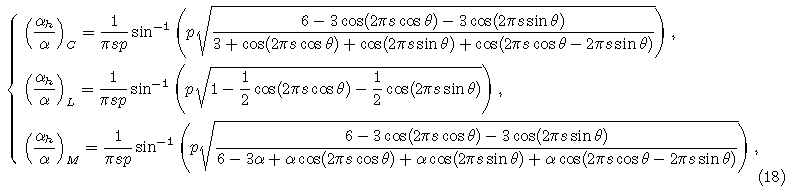
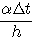 is stability parameter(Courant number).
is stability parameter(Courant number).
|
Fig. 1 Dispersion analysis of three types of mass matrix in isosceles right triangular mesh |
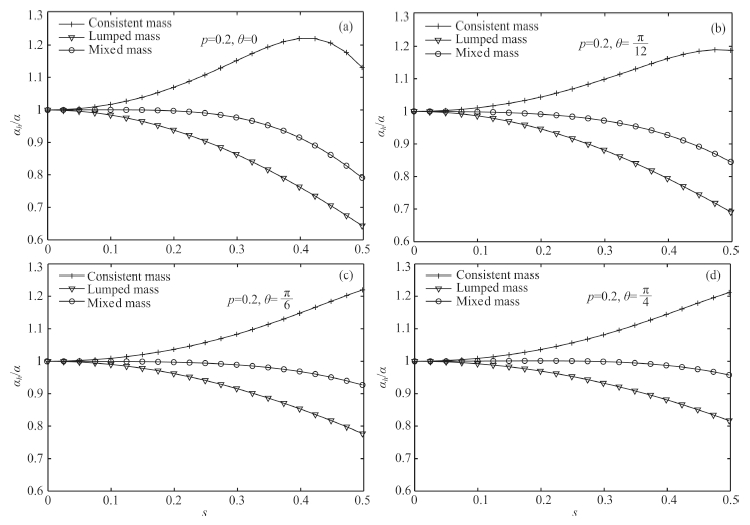
From Eq.(18), stability limits of CFEM, LFEM, and MFEM are 0.408248, 0.707107, and 0.577350, respectively.CFEM has the smallest stability range, while LFEM possessesthe largest stability range, and MFEM has a moderatestability range. Fig. 2 shows that three types of massmatrix FEM exhibit the largest numerical dispersion alongcoordinate axis, and smallest dispersion in the directionθ = 45°. In all directions, the numerical velocity of CFEMis larger than physics velocity, while the numerical velocitiesof LFEM and MFEM are both smaller than physicsvelocity. For the amplitude of numerical dispersion, LFEMsuffers from the most severe numerical dispersion, and amplitudeof CFEM is slightly smaller than that of LFEM, while the amplitude of MFEM is the smallest. To keep dispersion error less than 1%, it is suggested to use atleast five points per wavelength in practical simulations. In the following comparisons, we use MFEM to discussthe other influence factors.
|
Fig. 2 Numerical dispersion of three types of mass matrix in different directions; the stability parameter p is equal to 0.2; symbols +,▽ and ○ are corresponding to CFEM, LFEM and MFEM, respectively |
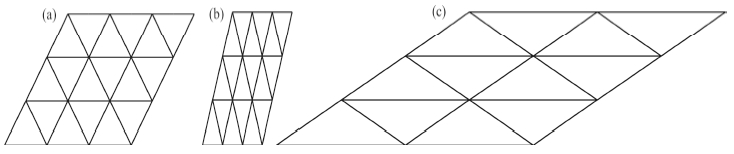
In the process of mesh generation, we need to know the different effects of different element shapes onnumerical dispersion so as to avoid distorted grids and get better numerical results. Besides the mesh in Fig. 1(T1), we choose additional three mesh types to discuss the numerical dispersion of MFEM, which is shown inFig. 3. Fig. 3a is the mesh with equilateral triangular elements(T2), while Fig. 3b and c are other two mesheswith isosceles triangular elements with vertex angle being 30°(T3) and 120°(T4), respectively. For linearinterpolation, we present the numerical dispersion of MFEM in the four meshes in Fig. 4.
|
Fig. 3 Triangle meshes of different shape are used for numerical dispersion analysis (a) Equilateral triangle; (b) Isosceles triangle with vertex angle being equal to 30°; (c) Isosceles triangle with vertex angle being equal to 120° |
|
Fig. 4 Numerical dispersion of MFEM in four triangle meshes in different directions The four curves of +, ▽, ○ and □ are corresponding to T1, T2, T3 and T4, respectively. |
We also obtain the stability limits for the three meshes, which are 0.645494, 0.203597, and 0.268643, respectively. The stability properties of MFEM in T1 and T2 are much better than that in T3 and T4. FromFig. 4, one can find that the numerical dispersion in T4 is the smallest when wave propagates along z axis.When the direction of propagation slightly deviates from z axis, the dispersion in T4 becomes very large. Whenpropagation angle equals 60°, the amplitude of dispersion exceeds 40%; the amplitude is larger than 70% whenpropagation angle equals 90°. The dispersion in T2 varies very intensively, especially when the sample rate issmall. The dispersion in T1 and T2 does not change intensively as wave propagating in different directions.During the process of mesh generation, the elements should be close to the isosceles right triangle or equilateral triangle and avoid triangles with small or large degrees of internal angle. Because the area of isosceles righttriangle is 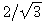 times as that of equilateral triangle, using right triangular elements to discretize the finiteelement domain generates fewer elements.
times as that of equilateral triangle, using right triangular elements to discretize the finiteelement domain generates fewer elements.
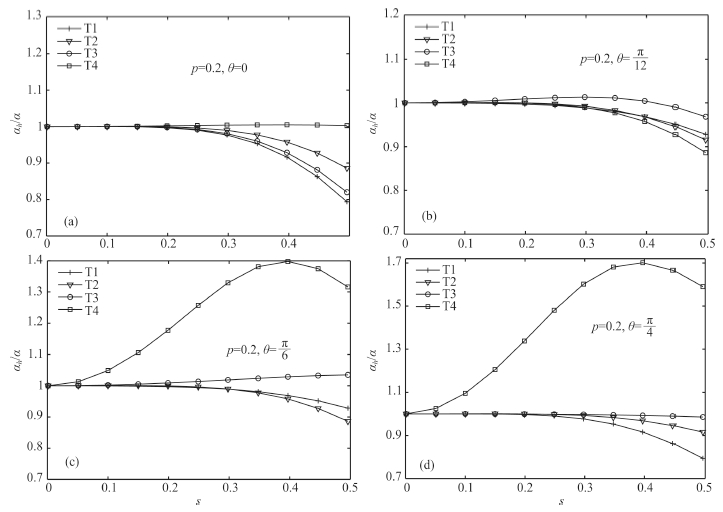
From Sections 3.1–3.2, we can find that MFEM with linear interpolation suffers from large numericaldispersion and anisotropy unless the sample rate is very small. In order to suppress numerical dispersion and anisotropy, high-order interpolations are often employed.In this section, we discuss the numericaldispersion of MFEM with second-order and thirdorderinterpolations in T1 mesh. Fig. 5 depicts theperiodic points for second-order interpolation(solidcircle) and third-order interpolation(empty circle), and one can find the four and nine points periodicallyappear in T1 for second- and third-order interpolations, respectively. Here we select the nine periodicalpoints to discuss the generalized eigenvalue problem.One group of 9 points(denoted as A)can be movedto another group(denoted as B)by a times translationalong x axis and b times translation along z axis. The generalized eigenvalue problem for A and B can be written as
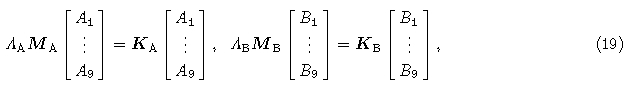

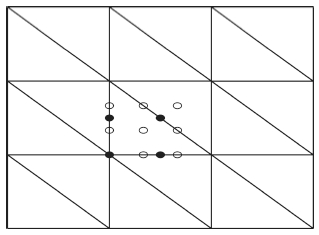
|
Fig. 5 Four points (solid circle) periodically occur in the mesh when second-order interpolation is used in each cell Nine points (empty circle) are corresponding to third-order interpolation. |
|
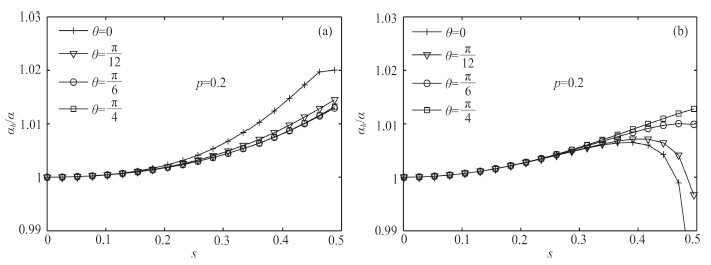
Fig. 6 Numerical dispersion of MFEM with second-order (a) and third-order (b) interpolation in each element Four curves under +, ▽, ○ and □ are corresponding to propagation angles in the direction 0, π/12, π/6 and π/4, respectively. |
Second- and third-order interpolation can successfully reduce numerical dispersion compared to linearinterpolation. When the sample rate is smaller than 1/3, the dispersion errors are less than 1% and 0.6% forsecond- and third-order interpolations, respectively. The numerical anisotropy of second-order interpolationis much less than that of linear interpolation. The numerical anisotropy of third-order interpolation can beneglected. The dispersion error is mainly controlled by sample rate, and the variation of dispersion errorin different directions is not obvious. From the discussion of this section, it is suggested to use third-orderinterpolation to reduce numerical dispersion.
3.4 The Effects of Wave Speed Ratio on Numerical DispersionIn Sections 3.1–3.3, we discussed the dispersion of acoustic wave propagation, and the above influencefactors on P- and S-wave in elastic media are nearly the same as acoustic wave, so we does not make a repeated discussion. In this section, we discuss another factor affecting P- and S-wave dispersions in elastic media, whichis wave speed ratio(r)or Poisson ratio. Fig. 7 presents dispersion properties of P- and S-wave when the stabilityparameter p = 0.2 and interpolation is third-order. The directions of P- and S-wave propagation are both alongz axis.
|
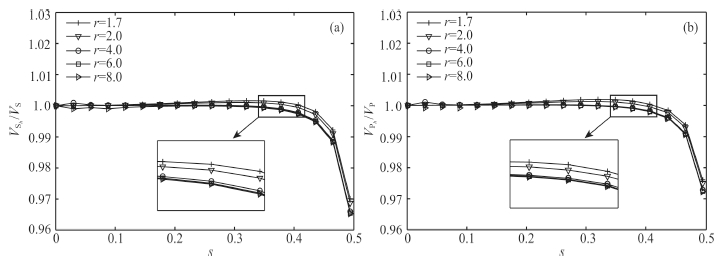
Fig. 7 Numerical dispersion of S (a) and P (b) wave corresponds to five P- to S-wave speed ratios when third-order interpolation in each cell is used Five curves under +, ▽, ○ , □ and right ▽ are corresponding to five wave speed ratios r=1.7, 2.0, 4.0, 6.0 and 8.0, respectively. |
From Fig. 7, we can see that the dispersion amplitude of both P- and S-wave increases as r increases. Theinfluence from r is very small, and the difference of dispersion amplitude between r = 1.7 and r = 8.0 is lessthan 0.5%. The dispersion error of S-wave is slightly larger than that of P-wave. We can also observe that theamplitudes of dispersion error are less than 3.6% and 2.8% for S- and P-wave, respectively, even if s reaches 0.5.
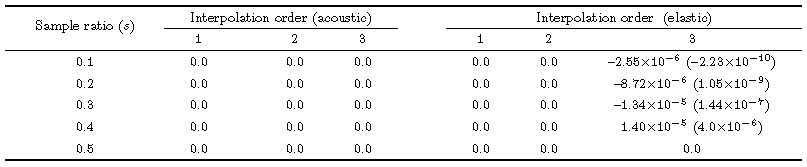
3.5 Numerical Dissipation of MFEMIn Eq.(16), if the characteristic frequency is a complex number by solving Eq.(17), the characteristicfrequency can be written as wh+iε, in which wh is numerical frequency. Substituting the characteristic frequencyinto Eq.(16), the imaginary part iε generates numerical dissipation, and the amplitude of plane wave at thenext time instance is e-ε△t times as that at current time instance. In this section, we present the dissipation ofMFEM using various sample ratios with stability parameter being 0.2 as wave propagating along z axis. Table 1 shows the numerical dissipation of MFEM modeling acoustic and elastic wave(r = 1.7)for different sampleratios and interpolation orders. From Table 1, one can see that MFEM does not show dissipation in acousticcase. For first- and second-order interpolation, MFEM still keeps nondissipative property, while for third-orderinterpolation, both P- and S-wave exhibit dissipation, and generally the dissipation increases as s increases.The dissipation of P-wave is larger than that of S-wave by one order of magnitude, however the " values areextremely small, which is nearly negligible. Here we can come to the conclusion that numerical errors are mainlyfrom numerical dispersion.
|
|
Table 1 The ε values of MFEM under various sample ratios and interpolation orders; the dissipation values of S-wave are presented in the brackets |
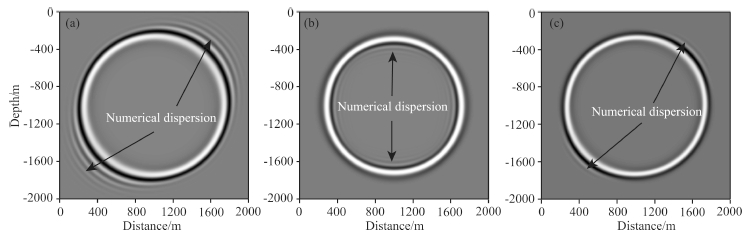
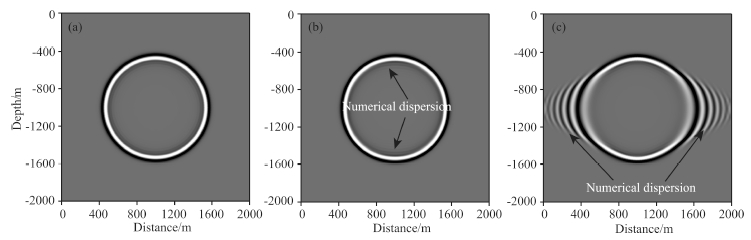
In this section, we conduct three numerical experiments to demonstrate the validity of the analysis above.The size of the first model is 2000 m×2000 m, and the velocity of acoustic wave is 2000 m·s-1. A source islocated at the center of the model, which is a Ricker wavelet with peak spectrum at 20 Hz. To minimize thedispersion from temporal discretization, we choose a relatively small temporal increment, which is 0.2 ms. Themodel is discretized by T1 mesh, the right angle side length is 10 m. Figs. 8(a–c)show the snapshots of wavefieldat 0.4 s, which are computed by CFEM, LFEM, and MFEM, respectively. In the direction 45° to z axis, strongnumerical dispersions occur in Fig. 8a, and numerical velocity is larger than the physical velocity. In the interiorof wave-front circle, very strong numerical dispersions appear in Fig. 8b. In the direction as that in Fig. 8a, thenumerical dispersions are very weak compared to those in Figs. 8a and b. From this experiment, we verify thatMFEM has great ability in suppressing numerical dispersion.
|
Fig. 8 Snapshots of acoustic wavefield at t=0.4 s modeled by three types of mass matrix (a) CFEM, (b) LFEM, and (c) MFEM. Arrows point at numerical dispersion |
The parameters of the second experiment are the same as the first experiment except the peak frequencyof Ricker being 35 Hz. We use T2, T3, and T4 meshes to discretize the second model. The snapshots at 0.3 sgenerated by MFEM in T2, T3, and T4 meshes are shown in Fig. 9. One can see that no obvious numericaldispersion occurs in Fig. 9a; in the vertical direction, some weak dispersions exist interior of the wave-frontcircle in Fig. 9b; extremely strong numerical dispersion appears along x axis in Fig. 9c. From the comparison, we conclude that when we generate a finite element mesh, the element shape should be close to regular shape and avoids the deformity shape.
|
Fig. 9 Snapshots of acoustic wavefield at t=0.3 s modeled by MFEM with three types of FEM mesh. (a) T2, (b) T3, and (c) T4 |
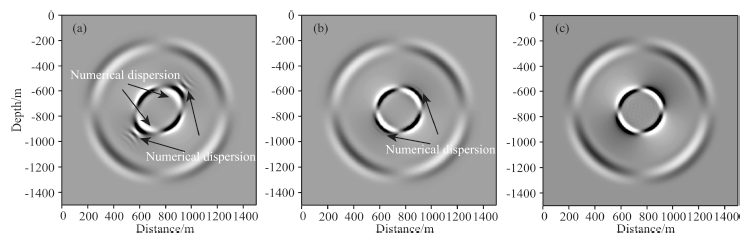
In the third experiment, we examine the dispersion behavior of MFEM modeling P-SV wave in elasticmedia with relatively large wave speed ratio. The size of the third model is 1500 m×1500 m. The velocityof P-wave is 3000 m·s-1, and the velocity of S-wave is 1000 m·s-1. The source is vertical force, which is aRicker wavelet with peak spectrum at 20 Hz. We choose T1 mesh to discretize this model. The right angle sidelength is 5 m, 10 m, and 15 m for first-, second-, and third-order interpolation, respectively, and the total nodesafter discretization are the same for different interpolations. The temporal interval is 0.2 ms. The snapshotsof elastic wavefield at 0.2 s are shown in Fig. 10. The shortest wavelength of S-wave is about 20 m, and thenumber of points per shortest wavelength is 4. The snapshot in Fig. 10a is generated by MFEM with first-orderinterpolation, and one can see that the shape of the wave-front of S-wave is an ellipse, and severe numericaldispersion exists in front of the wave-front of S-wave. First-order interpolation presents very bad results and the propagation of elastic wave is not well modeled. When the interpolation becomes second-order, very weaknumerical dispersion exists in front of the wave-front of S-wave in Fig. 10b, and the numerical anisotropy is not visible. When the interpolation becomes third-order, the propagation of P- and S-wave is correctly modeled. Inpractical seismic wave simulations, we suggest using third-order interpolation to suppress numerical dispersion.
|
Fig. 10 Snapshots of P-SV wavefield modeled by first- , second- , and third-order MFEM in elastic media with wave speed ratio r = 3 (a) First-order MFEM; (b) Second-order MFEM; (c) Third-order MFEM. |
In this article, we propose MFEM to model acoustic and elastic wave propagation. The dispersion propertyof MFEM is compared with that of CFEM and LFEM, and the analysis shows MFEM has great ability tosuppress numerical dispersion. Three typical influences on numerical dispersion are discussed when MFEMsimulates wave propagation. We suggest that element shape should be as regular as possible and third-orderinterpolation should be used for spatial approximation. We point out that numerical errors are mainly fromnumerical dispersion and numerical dissipation is negligible.
We adopt simple meshes with regular element for discussion. In practical seismic wave modeling, the meshmay be composed of very complex elements, and the discussion about numerical dispersion in this kind of meshmay be impossible. But we can use the conclusions of this paper to speculate the tendency of the numericaldispersion in a complex mesh.
Special thanks are given to Professor Zhang Huai for his constructive comments of the original manuscript.Valuable suggestions from the two anonymous reviewers are also acknowledged. We are grateful to editor HuSufang for her careful reading and finding the mistakes of the paper. This work was supported by the NationalNatural Science Foundation of China(41174047 and 40874024).
If we use a linear interpolation in Eq.(9) and transform the integration from physics element to referenceelement, the element consistent mass matrix and stiffness matrix can be written as
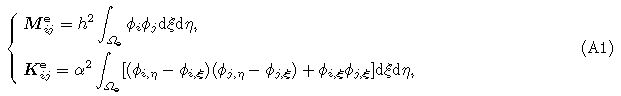
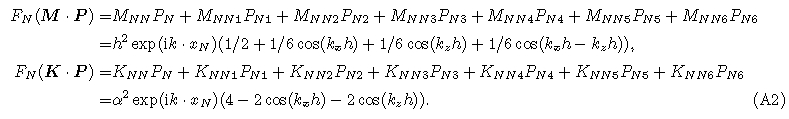
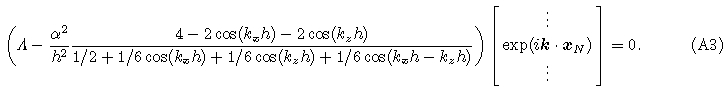
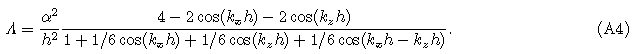
| [1] | Abboud N N, Pinsky P M. 1992. Finite element dispersion analysis for the three-dimensional second-order scalar wave equation. Int. J. Numer. Methods Eng., 35(6):1183-1218. |
| [2] | Chen J B. 2009. Lax-Wendroff and Nystrm methods for seismic modelling. Geophysical Prospecting, 57(6):931-941. |
| [3] | Chen S, Yang D H, Deng X Y. 2010. An improved algorithm of the fourth-order Runge-Kutta method and seismic wave-field simulation. Chinese J. Geophys. (in Chinese), 53(5):1196-1206. |
| [4] | Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1):54-66. |
| [5] | De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equation. Geophysics, 72(6):T81-T95. |
| [6] | De Basabe J D, Sen M K. 2010. Stability of the high-order finite elements for acoustic or elastic wave propagation with high-order time stepping. Geophys. J. Int., 181(1):577-590. |
| [7] | Fornberg B. 1987. The pseudospectral method:Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4):483-501. |
| [8] | Fried I, Malkus D S. 1975. Finite element mass matrix lumping by numerical integration with no convergence rate loss.Int. J. Solid. Structures, 11(4):461-466. |
| [9] | Komatitsch D, Tromp J. 2002a. Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys.J. Int., 149(2):390-412. |
| [10] | Komatitsch D, Tromp J. 2002b. Spectral-element simulations of global seismic wave propagation-II. Three-dimensional models, oceans, rotation and self-gravitation. Geophys. J. Int., 150(1):303-318. |
| [11] | Komatitsch D, Ritsema R, Tromp J. 2002. The spectral-element method, Beowulf computing, and global seismology.Science, 298(5599):1737-1742. |
| [12] | Komatitsch D, Erlebacher G, Gddeke D, et al. 2010. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster. J. Comp. Phys., 229(20):7692-7714. |
| [13] | Li X F, Wang W S, Lu M W, et al. 2012. Structure-preserving modelling of elastic waves:a symplectic discrete singular convolution differentiator method. Geophys. J. Int., 188(3):1382-1392. |
| [14] | Liu S L, Li X F, Liu Y S, et al. 2013a. Symplectic RKN schemes for seismic scalar wave simulations. Chinese J. Geophys.(in Chinese), 56(12):4197-4205. |
| [15] | Liu S L, Li X F, Wang W S, et al. 2013b. Optimal symplectic scheme and generalized discrete convolutional differentiator for seismic wave modeling. Chinese J. Geophys. (in Chinese), 56(7):2452-2462. |
| [16] | Liu T, Sen M K, Hu T Y, et al. 2012. Dispersion analysis of the spectral element method using a triangular mesh. Wave Motion, 49(4):474-483. |
| [17] | Liu Y S, Teng J W, Liu S L, et al. 2013. Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition. Chinese J. Geophys. (in Chinese), 56(9):3085-3099. |
| [18] | Long G H, Li X F, Jiang D H. 2010. Accelerating seismic modeling with staggered-grid Fourier Pseudo-spectral differentiation matrix operator method on graphics processing unit. Chinese J. Geophys. (in Chinese), 53(12):2964-2971. |
| [19] | Ma X, Yang D H, Zhang J H. 2010. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation.Chinese J. Geophys. (in Chinese), 53(8):1993-2003. |
| [20] | Ma X, Yang D H, Liu F Q. 2011. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophys. J. Int., 187(1):480-496. |
| [21] | Magnoni F, Casarotti E, Michelini A, et al. 2014. Spectral-element simulations of seismic waves generated by the 2009 L'Aquila Earthquake. Bull. Seism. Soc. Am., 104(1):73-94. |
| [22] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations.Geophysics, 49(5):533-549. |
| [23] | Mazzieri I, Rapetti F. 2012. Dispersion analysis of triangle-based spectral element methods for elastic wave propagation.Numer. Algor., 60(4):631-650. |
| [24] | Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes:stability and grid dispersion.Bull. Seism. Soc. Am., 90(3):587-603. |
| [25] | Mulder W A. 1999. Spurious modes in finite-element discretizations of the wave equation may not be all that bad. Appl.Numer. Maths., 30(4):425-445. |
| [26] | Mullen R, Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. International Journal for Numerical Methods in Engineering, 18(1):11-29. |
| [27] | Pasquetti R, Rapetti F. 2004. Spectral element methods on triangles and quadrilaterals:comparisons and applications.Journal of Computational Physics, 198(1):349-362. |
| [28] | Seriani G, Oliveira S P. 2007. Optimal blended spectral-element operators for acoustic wave modeling. Geophysics, 72(5):SM95-SM106. |
| [29] | Seriani G, Oliveira S P. 2008. Dispersion analysis of spectral element methods for elastic wave propagation. Wave Motion, 45(6):729-744. |
| [30] | Wang R Q. 1993. Stability analysis in wave equation migration using finite element method. OGP, 28(6):657-665. |
| [31] | Wang W S, Li X F, Lu M W, et al. 2012. Structure-preserving modeling for seismic wavefields based upon a multisymplectic spectral element method. Chinese J. Geophys. (in Chinese), 55(10):3427-3439. |
| [32] | Wu S R. 2006. Lumped mass matrix in explicit finite element method for transient dynamics of elasticity. Comput.Methods Appl. Engrg., 195(44-47):5983-5994. |
| [33] | Yan Z Z, Zhang H, Yang C C, et al. 2009. Spectral element analysis on the characteristics of seismic wave propagation triggered by Wenchuan Ms8.0 earthquake. Science in China Series D:Earth Sciences, 52(6):764-773. |
| [34] | Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2):882-890. |
| [35] | Yang D H, Wang M X, Ma X. 2014. Symplectic stereomodelling method for solving elastic wave equations in porous media. Geophys. J. Int., 196(1):560-579. |
| [36] | Zhang H, Zhou Y Z, Wu Z L, et al. 2009. Finite element analysis of seismic wave propagation characteristics in Fuzhou basin. Chinese J. Geophys. (in Chinese), 52(5):1270-1279. |
| [37] | Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broad-band seismic wave modeling. Geophysics, 78(1):A13-A18. |
| [38] | Zhou H, Xu S Z, Liu B, et al. 1997. Modeling of wave equations in anisotropic media using finite element method and its stability condition. Chinese J. Geophys. (in Chinese), 40(6):833-841. |
| [39] | Zyserman F I, Gauzellino P M. 2005. Dispersion analysis of a nonconforming finite element method for the threedimensional scalar and elastic wave equations. Finite Elements in Analysis and Design, 41(13):1309-1326. |
| [40] | Zyserman F I, Santos J E. 2007. Analysis of the numerical dispersion of waves in saturated poroelastic media. Comput.Methods Appl. Mech. Engrg., 196(45-48):4644-4655. |
 2014, Vol. 57
2014, Vol. 57