1 INTRODUCTION

Compared with relative positioning, PPP(Precise Point Positioning)can realize precise user positioning by using observation from one receiver, together with precise satellite orbit and clock products, thus is more flexible and widely used in geodesy(Bisnath et al., 2008; Kouba et al., 2001; Zumberge et al., 1997). During the application of real time PPP, a convergence time is required for the ambiguity parameter to achieve precise positioning results(Li et al., 2011). It takes about 10 minutes even if realizing PPP ambiguity resolution(Geng et al., 2011), which is much slower than relative positioning(Giorgi et al., 2012). When the environment is poor, precise positioning results cannot be achieved in a long period as the ambiguity parameter should be reinitialized due to signal obstruction or interruption. This would directly affect the application of PPP. Hence, it is of great necessity to find an effective way to solve the problem in this field.

Normally, the short time variation of satellite instrumental bias can be neglected(Zhang and Li, 2012). The variation of ambiguity(cycle slip)caused by signal interruption and others can be considered as an integer value. Provided that the cycle slip can be fixed, combining with the estimated results before the cycle slip, we can determine the new ambiguity precisely and the accurate user positioning results can be achieved rapidly(Shi and Gao, 2011; Li et al., 2013). Therefore, the key factor in realizing instantaneous re-initialization in real time PPP relies on the detection and determination of cycle slip to realize cycle slip fixing.

In general, the cycle slip detection and fixing methods can be divided into two categories when utilizing observation of one receiver only. One is applying cycle slip detection and fixing using various combinations of observations(Dai et al., 2008; de Lacy et al., 2008; Xu et al., 2011). The other is to estimate the ambiguity or cycle slip parameters as unknown and try to fix them into integers. Of them, Banville and Langley(2009)proposed to fix the cycle slip of wide-lane and geometry free combination separately. Geng et al.(2010)achieved instantaneous wide-lane ambiguity resolution by inputing predicted ionosphere information so as to accelerate PPP ambiguity resolution. While Zhang and Li(2012)estimated and fixed the cycle slip parameters using the epoch differenced observation, in which the ionosphere delay is corrected by the predicted results.

Concluded from the methods in the second category, it is an effective way to solve the problem by introducing ionosphere constraints to improve the accuracy of estimated parameters, together with success rate of cycle slip fixing. Nevertheless, the accuracy of ionosphere prediction will directly affect the performance of the method. As the ionosphere variation is strongly correlated with many factors, such as station position and solar activity, the ionosphere predicting accuracy varies significantly under different circumstances. Hence, when we input the ionosphere predicting value, the accuracy of results should be considered to improve the reliability and avoid the negative effect on parameter estimation.

In this paper, we propose an instantaneous re-initialization method in real time PPP through fully considering the accuracy of the ionosphere predicting value. Firstly, the observation model and data processing scheme in cycle slip fixing using GPS observation only are discussed. Secondly, we design an effective ionosphere predicting and weighting method. At last, the performances under different circumstances are evaluated using observations from different regions and periods.

2 OBSERVATION MODEL OF CYCLE SLIP FIXING

The raw GPS observation equation can be written as:

where p and m denote the receiver and satellite, respectively, f_i(i = 1, 2)represents the signal frequency, P_pi^m and L_pi^m are the pseudo-range and phase observables at L_i frequency, respectively, ρ_p^m is the geometrical distance between satellite and receiver, I_p1^m is the ionosphere delay in the first frequency, T_p^m denotes the troposphere delay, dtp and dt^m denote the clock error of receiver and satellite, respectively, w_pi denotes the phase wind up error at L_i frequency, λ_i represents the wavelength, Nmpi denotes the ambiguity at Li frequency, and ε_pi^m and δ_pi^m denote the r and om error of pseudo-range and phase, respectively. The other systematic errors, including the tidal error and phase center offset, are corrected directly using models.

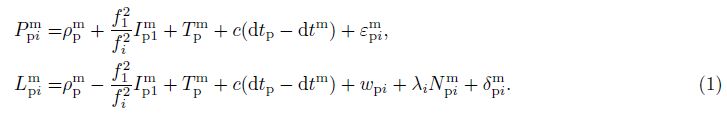
In real time kinematic PPP, satellite differencing is applied first to eliminate the phase wind up error of the receiver, which generates the following observation equation:

where m, n denote the satellites to be differenced.

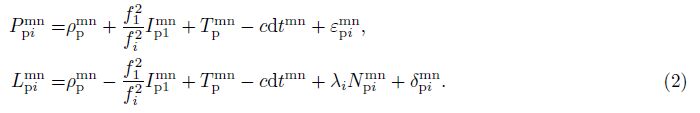
Suppose that the signals are continuous from epoch n₀ to n_t, and a cycle slip occurs in epoch n_t+j, we will apply epoch differencing between epoch n_t and n_t+j . In this process, the satellite orbit and clock error are fixed and the zenith wet delay is fixed to the latest results in real time PPP considering the small variation in a short time. Then the observation equation can be expressed as

where △ denotes epoch differencing, CS_pi^mn represents the cycle slip between satellites m, n in L_i frequency. It should be 0 if no cycle slip occurs in the two satellites. If we can obtain the fixed results of cycle slips, the re-initialization of ambiguities can be avoided.

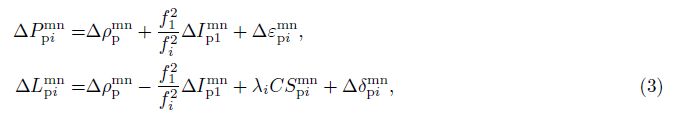
The float solutions of wide-lane combination of cycle slips based on Eq.(3)equal to the results based on MW combination. The accuracy of float results when using observations of a few epochs is lower, and difficult to fix into integers. Also, even if the wide-lane combination is successfully fixed, the narrow-lane combination is also difficult to fix to integers considering its shorter wavelength, since the accuracy of float results relies on the ionosphere free pseudo-range observations. Because of these reasons, the cycle slip fixing is not reliable based on Eq.(3)only. To solve this problem, many authors proposed to introduce other types of observations and surveying instruments to improve the accuracy(Carcanague, 2012; Du et al., 2012; Kim et al., 2012). Different from these methods, we will explore other constraints when using GPS observation only. Considering that the delay variation of ionosphere delay is regular in a certain time interval, we can construct an ionosphere prediction model and import the predicted results as constraints in parameter estimation to improve the accuracy of cycle slip parameters and the success rate of cycle slip fixing.

3 IONOSPHERE DELAY PREDICTION MODEL AND WEIGHTING STRATEGY

Based on Eq.(2), I_p1^mn can be written as

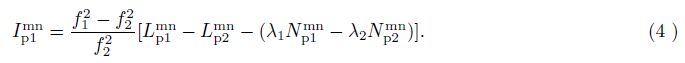
Up to now, Dai et al.(2003)has done much work on analyzing the time correlation of atmosphere delay, and proposed various prediction models. In this paper, we apply a linear model for short term ionosphere prediction, which can be expressed as

where I_p1^mn(t)represents the satellite differenced ionosphere delay at epoch t, and a and b are coefficients.

We compute the coefficients based on the ionosphere delay during one time interval(we select a period of 300 s in this paper) and predict the inonosphere delay variation, which will be imported to parameter estimation as virtual observations. The virtual observation equation can be written as

where △$\hat I$_p1^mn denotes the predicted results of ionosphere variation.

Since the accuracy under different circumstances varies significantly, the accuracy of virtual observation should be carefully considered to ensure the accuracy and reliability in parameter estimation. In this paper, we determine the st and ard deviation based on the equivalence of ionosphere prediction on both sides. Details can be depicted by Fig. 1.

Suppose that we fit based on the observation in(T₁, T₂) and predict for(T₂, T₂ + △t₂). Choose one epoch T₁ - △t₁ in which the real data is present, and the difference between △t₁ and △t₂ should be as small as possible, we can then predict the variation in(T₂, T₂+△t₂) and (T₁, t₁-△t₁). As the variation in(T₁, T₁-△t₁)can be computed from real observation, the external accuracy of △$\hat I$_p1^mn(T₁, T₁ - △t₁)can be approximately interpreted by the difference between the predicted and the observed values. In addition, we will consider the effect of predicting length and satellite elevation on the prediction accuracy. The following relationship can be obtained:

where p(E) represents the scaling factor of satellite elevation, which can be expressed as where E denotes the smallest value of elevation for the two satellites in the predicted time interval, p(τ_I0) represents the scaling factor of prediction length(Geng et al., 2010), which can be written as where τ denotes the prediction length in seconds. From Eq.(7), we can obtain the value of σ_I0 .

4 FILTERING MODEL AND DATA PROCESSING SCHEME

In real time cycle slip fixing, we apply Kalman filter in parameter estimation. Combining Eqs.(3) and (6), the linearized observation equation can be expressed as

where P, L, I₀ denote the corrected pseudo-range, phase and ionosphere prediction results, respectively; X, I, CS represent the unknown parameters, including station position, ionosphere variation and cycle slips; A, B are the coefficient matrix of P with respect to X, I;E is an identity matrix; O denotes zero matrix; M is the coefficient matrix of L with respect to CS, which equals to E when the cycle slips are occurred to all satellites, and Γ denotes the r and om error.

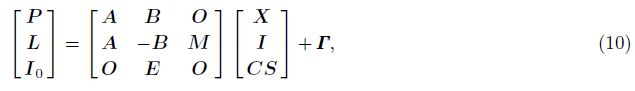
The state equation can be written as

where the variance of the process noise ε_X and ε_I areset to be infinity. The variance is set to be 0 for ε_CS if no cycle slip occurs and infinity otherwise.

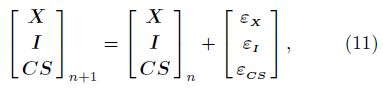
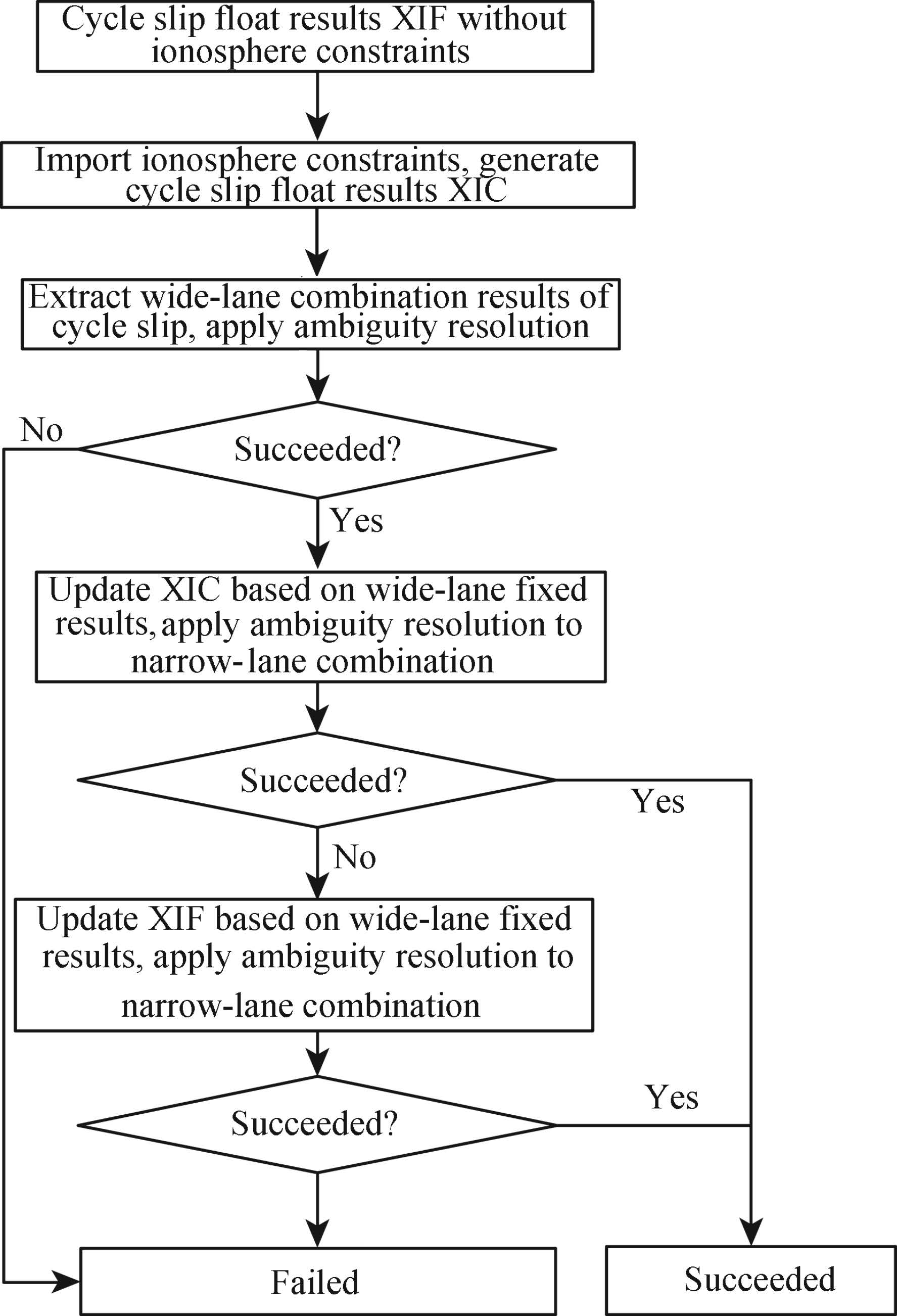
In this paper, we set the maximum continuous epoch number of cycle slip fixing to 3. When the number of epoch exceeds 3, the cycle slip fixing is failed, and a re-initialization process of real time PPP is started. At each epoch, we extract the float results of CS, apply ambiguity resolution and validation by the LAMBDA method(Teunissen, 1995) and ratio test(Wang et al., 1998), respectively. The limit of ratio test is set to be 2. The flow chart of cycle slip fixing and validation is shown in Fig. 2. Apply wide-lane ambiguity resolution first and exit if failed. Otherwise, update the float results of cycle slip parameters when the ionosphere constraints are applied or not using the fixed results of wide-lane combination, and apply ambiguity resolution to the narrow-lane combination under the two circumstances. If succeeding in one case, cycle slip at original frequencies can be determined based on the two combinations.

5 CASE ANALYSIS AND DISCUSSION 5.1 GPS Data

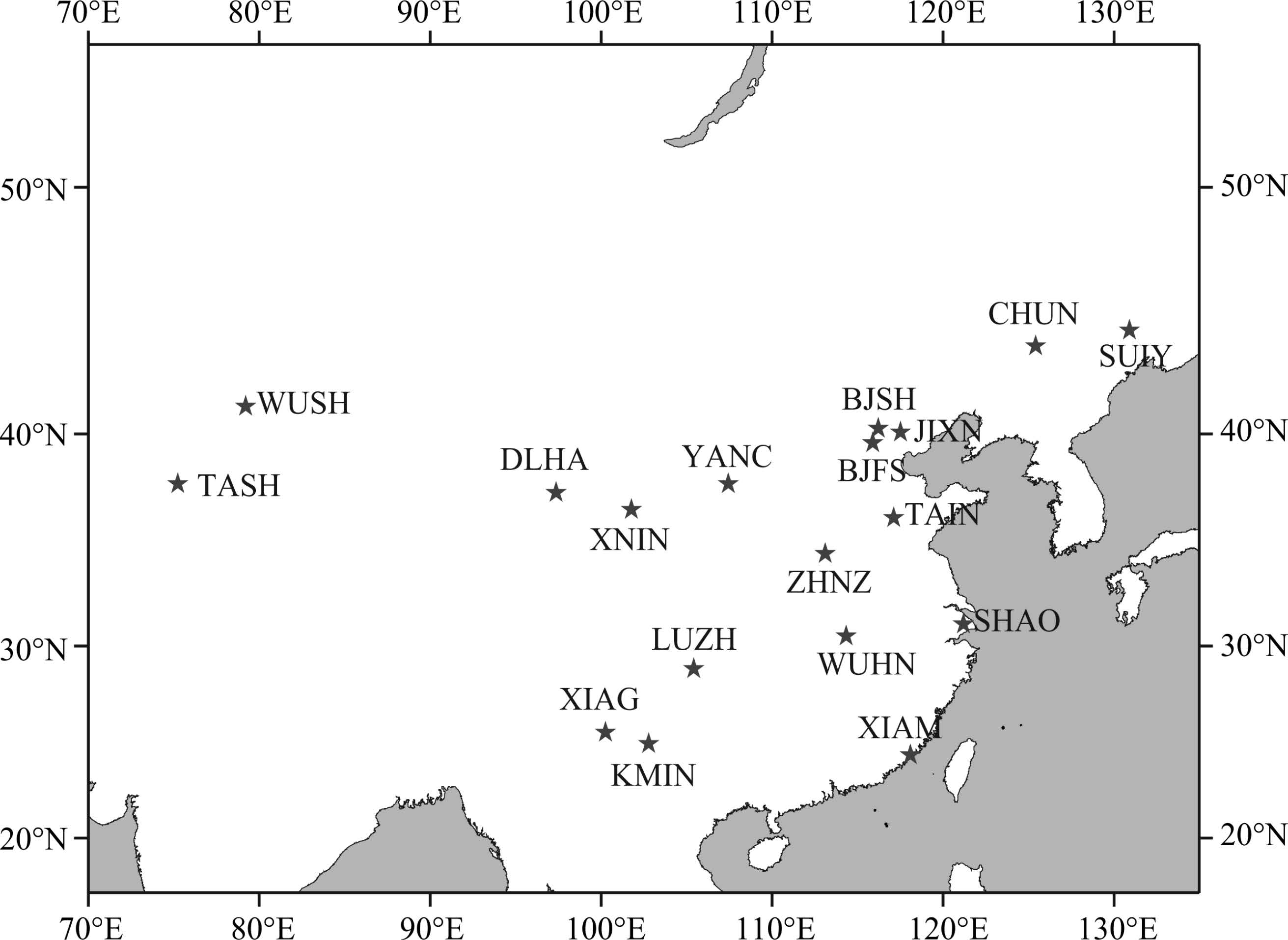
To analyze the performance of the above method in different regions and epochs, we select one GPS network in China and one IGS network in Europe according to the station distribution and data quality. In China, we select 18 stations from CMONOC(Crustal Movement Observation Network of China)(Fig. 3). According to their latitudes, the stations can be grouped into three regions(Table 1). In Europe, we select 24 IGS stations(Fig. 4). Among the stations, the latitudes of stations in Europe are higher(bigger than 45 degrees), while those in China have a wide range, lowering down to 25 degrees.

The sampling interval of observations is 30 s. The satellite orbit and clock products used in the analysis are IGS final products, which can be replaced by the real time products provided by relevant institutions(Ge et al., 2012; Zhang et al., 2007; Zhang et al., 2011). During the analysis, cycle slips to all satellites are simulated every 30 minutes(00 h 30 min, 01 h 00 min, · · ·)to analyze the performance under the worst circumstance. In addition, observations of several epochs are deleted to simulate different time latency. Here, we choose 30 s, 90 s, 150 s, 210 s and 270 s. To quantify the fixing performance, we count the success rate of the cycle slip fixing(the ratio between the successful and whole number of cycle slip fixing process) and the average epoch(average number of epoch used in cycle slip fixing). In addition, the RMS of ionosphere predicting error(IONO RMS)is summarized in this paper to analyze the correlation between the prediction error and the performance of the method.

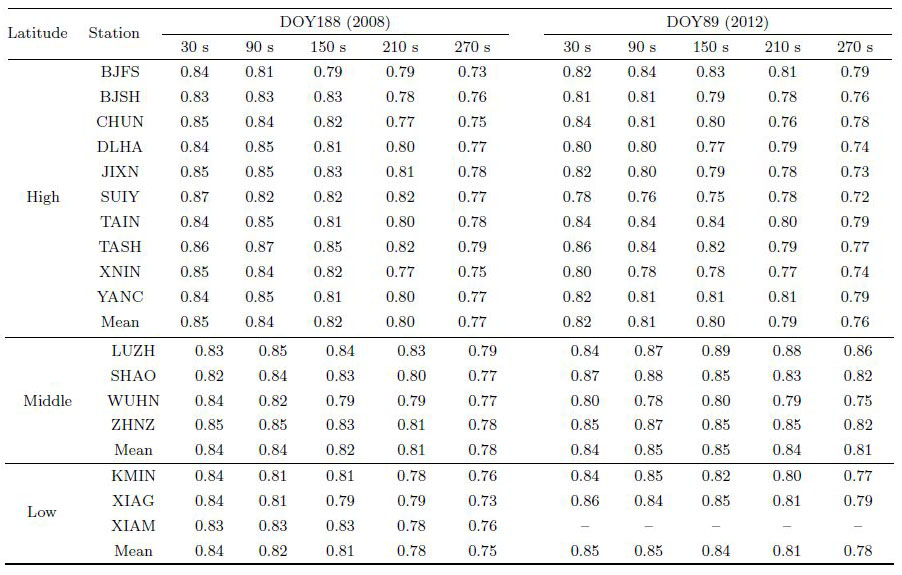
5.2 Analysis of Weighting Method

The weighting method plays a key role in the performance of cycle slip fixing. We use real observations of the 18 stations in China on DOY188, 2008 and DOY89, 2012 to evaluate the weighting method. Firstly, we compare the predicted and real ionosphere delay to obtain real accuracy of the predicted ionosphere delay. Secondly, the accuracy of the predicted value is calculated based on the method in paragraph 3 of this paper. Finally, we evaluate the accuracy of the weighting method by comparing the previous two results.

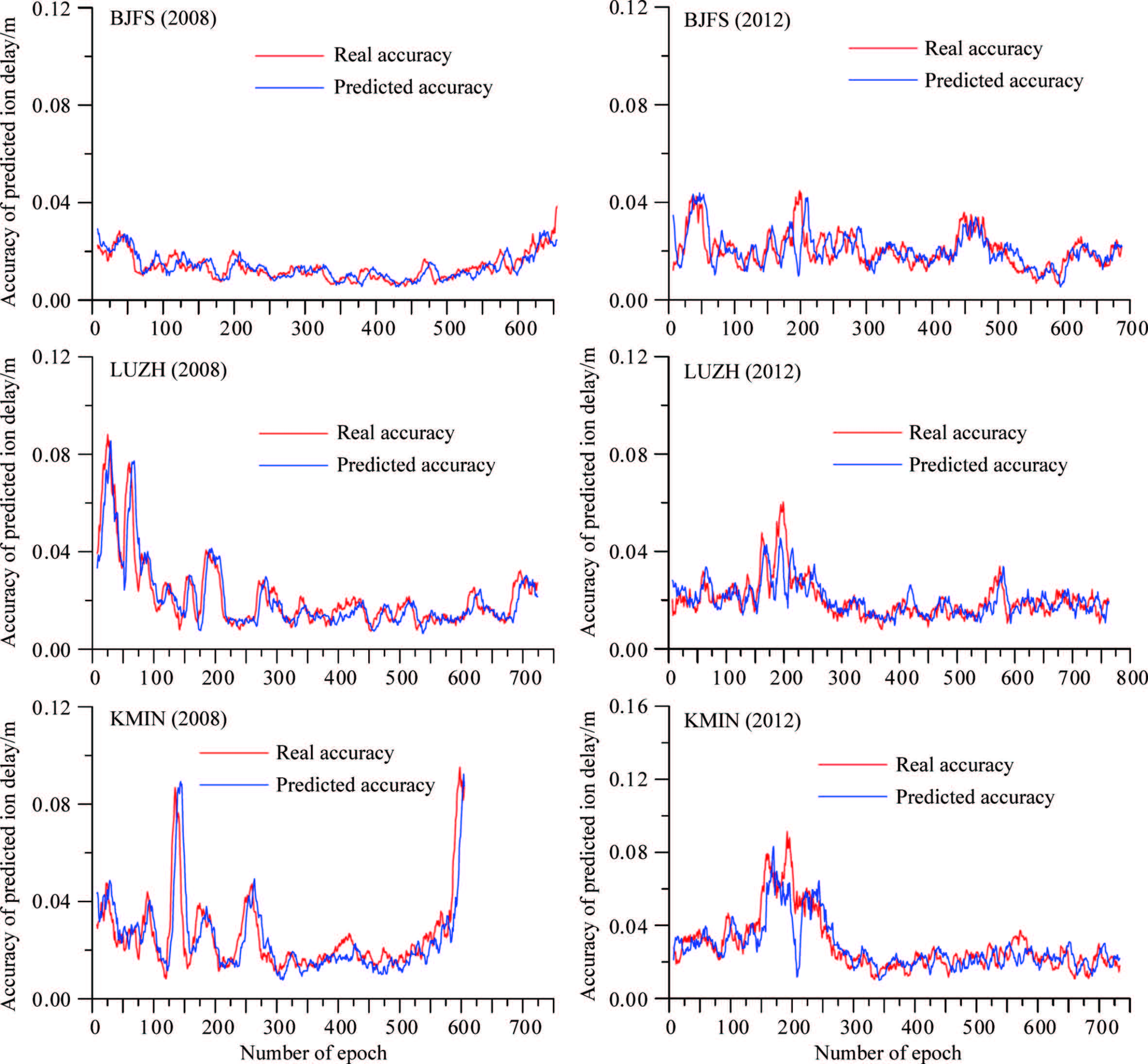
Figure 5 gives the predicted and real accuracies of the ionosphere prediction for PRN02 at stations BJFS, LUZH and KMIN when the length of time latency is set 30 s. The results in year 2008 and 2012 are shown in the left and right panels(Fig. 5), respectively. The accuracy is better than 10 cm at low latitudes and 5 cm at high latitude regions. The variance computed based on the weighting method can basically reflect the real accuracy generally, since it fully considers the real accuracy of the ionosphere prediction in the time interval(T₁, T₁ - △t1).

To further analyze the correlation between the two values of all satellites under different lengths of time latency, Table 2 gives the correlation coefficients for all stations. The predicted accuracy can represent the real accuracy more accurately when the correlation coefficient becomes bigger. We can conclude from the statistic results that the correlation coefficients at different latitudes are comparable, which means that the method proposed in paragraph 3 effectively takes into account the effect of ionosphere activity on the predicted accuracy. In other words, the predicted accuracy reflects the real accuracy of the ionosphere prediction. With the growth of time latency, the correlation coefficient becomes smaller, which is approximately 0.85 at 30s and 0.75 in 270 s. This phenomenon can be attributed to the declination of equivalence on both sides, which results in the declination of reliability in ionosphere prediction based on formula(7).

From these results, we can see that the predicted accuracy computed based on the method proposed can basically reflect the real accuracy. Thus, it is feasible to generate the a-priori information constraints on ionosphere variation to aid cycle slip fixing.

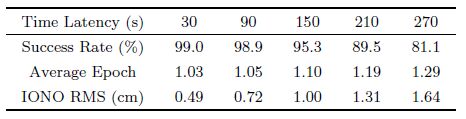
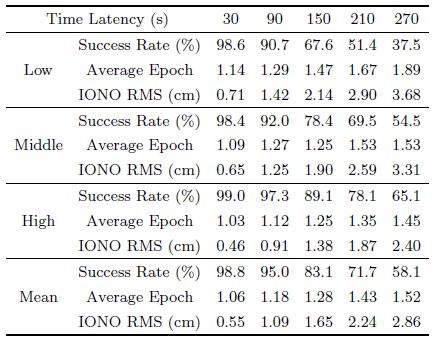
5.3 Comparison Analysis of Performance in Different

Regions In this section, we compare the difference of performance in different regions. By selecting the observations on DOY188, 2008 for simulation analysis, the statistic results in Europe and China are given in Tables 3 and 4, respectively.As shown in Table 3, almost all processes are fixed successfully when the time latency is 30 s and the success rate reaches 99.0%. In addition, observation of only one epoch is required in most cases, and the average number of epoch is 1.03. The success rate slightly decreases when prolonging the time latency. When the time latency increases to 150 s, the success rate is still above 95% and the average number of epoch is 1.10. These results show that the method proposed can effectively improve the accuracy of station’s position and cycle slip parameters, which increases the probability of ambiguity resolution in both wide-lane and narrowlane combinations. When the time latency reaches 270 s, the success rate and average epoch used further decrease along with the increasing ionosphere predicting error. Neglecting the influence of multi-path error, the ionosphere prediction error plays a key role in the reduction of the success rate. As the ionosphere activity is comparably quiet in Europe, the success rate can still be bigger than 80%, thus attesting to the performance of method in Europe.

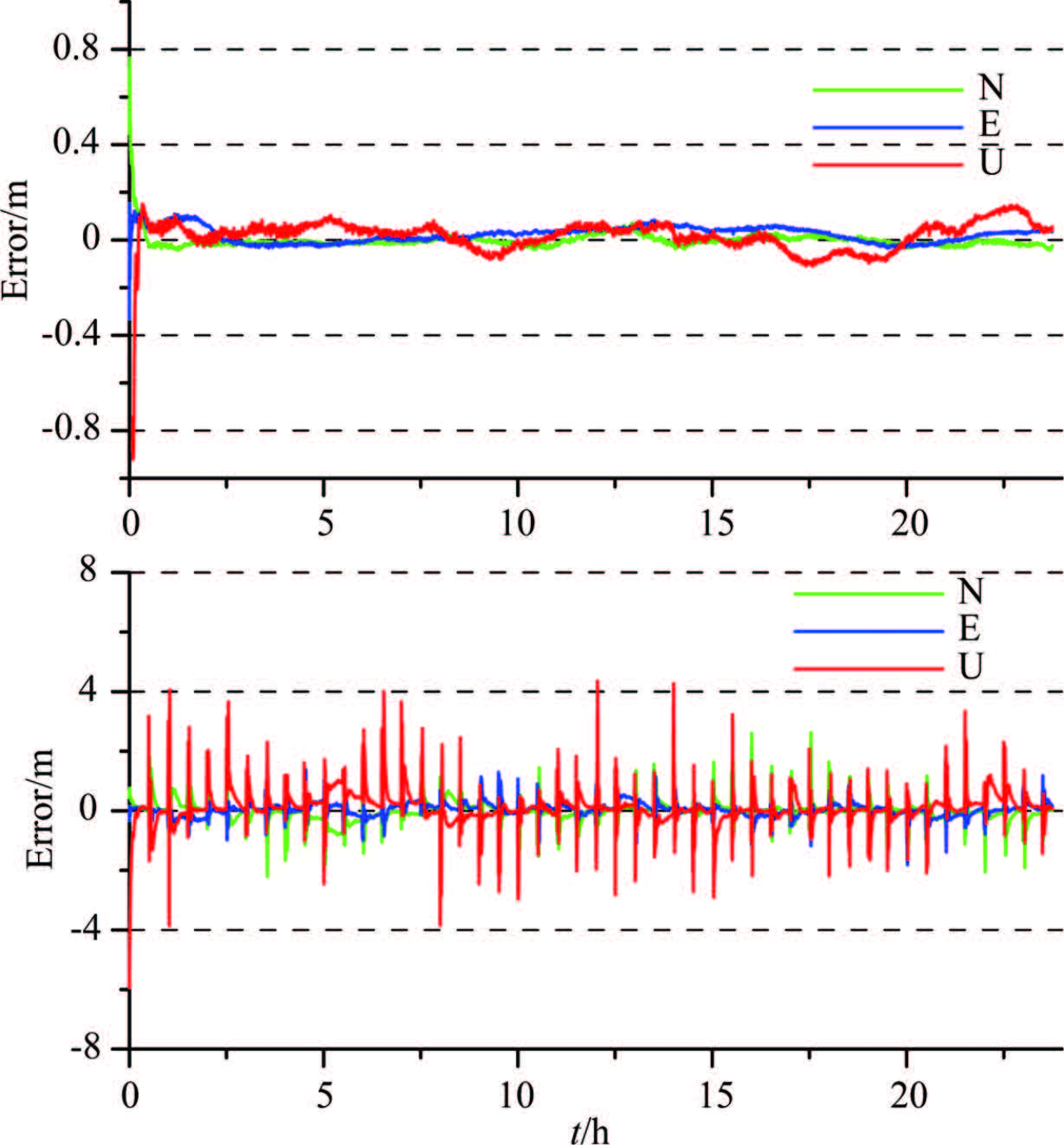
Meanwhile, we select station BOR1 as an example to present the improvement in real time positioning. The situation of other stations is similar to BOR1. Suppose that the time latency is 30 s, the real time positioning error is plotted in Fig. 6a when applying cycle slip fixing. As comparison, Fig. 6b plots the positioning error based on the st and ard PPP method. We can find that the cycle slip fixing is succeeded in all epochs using observation of one epoch and the user positioning accuracy remains at a high level after the convergence period. However, in the traditional mode, the re-initialization of real time PPP occurs frequently, and we cannot obtain precise positioning results in a long period, which obviously cannot fulfill the requirements of real application.

With respect to China, the success rates of stations in different regions are largely identical when the time latency is set 30 s, and the average number of epoch used increases with the declination of latitude. The number of average epoch is 1.14 in low-latitude regions, and 1.03 in high-latitude regions, which is same as that in Europe. The success rate decreases with the increasing time latency, and it is more obvious for stations in low-latitude regions. When the time latency prolongs to 90 s, the success rate decreases to 90% in middle and low latitude regions. However, it only shows a slight decrease in high latitude regions. Furthermore, the success rate becomes 37.5% and 65.1% for low and high latitude regions respectively when the time latency reaches 270 s. Thus, it can be concluded that the performance of cycle slip fixing is strongly correlated with station positions.

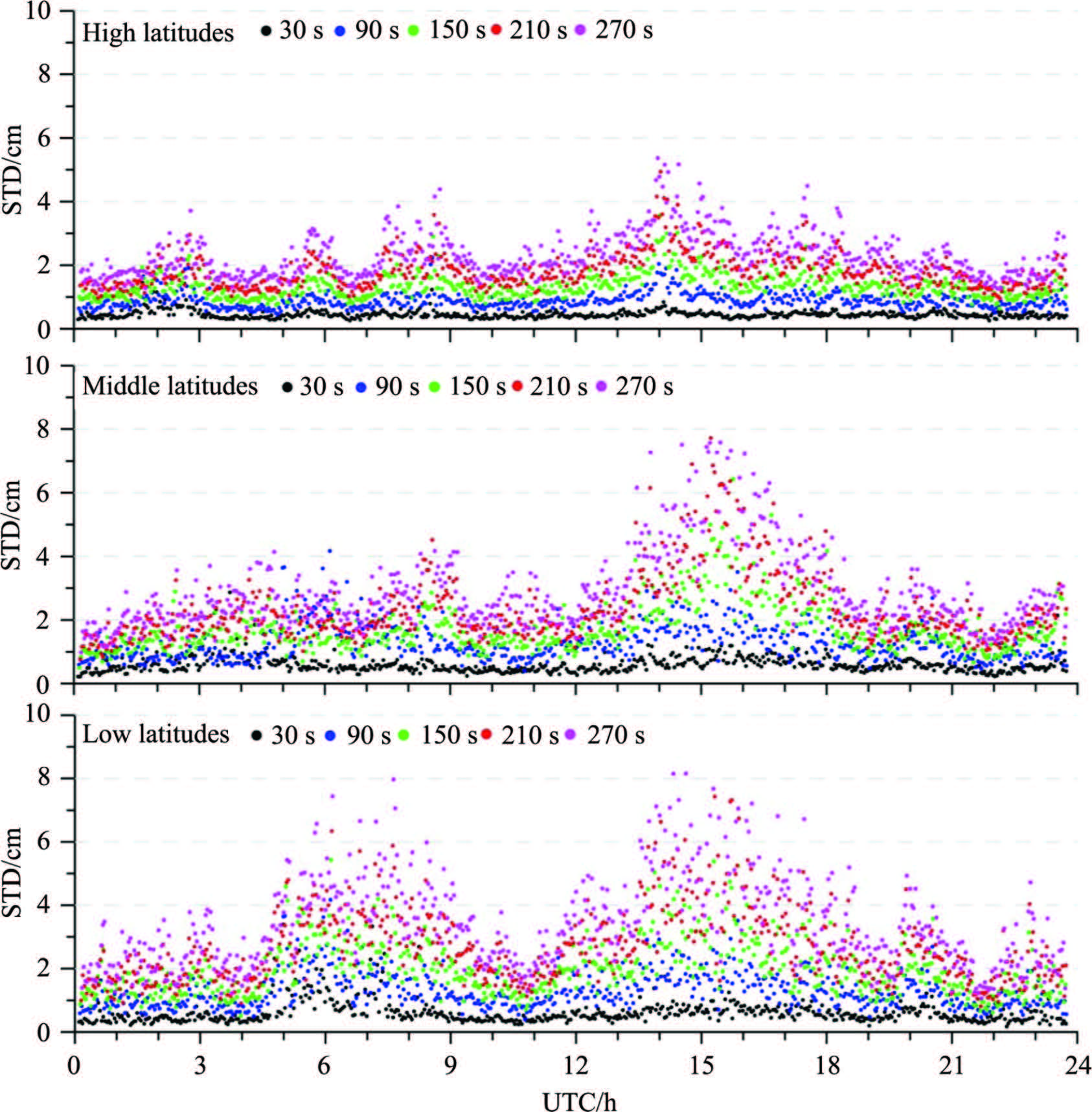
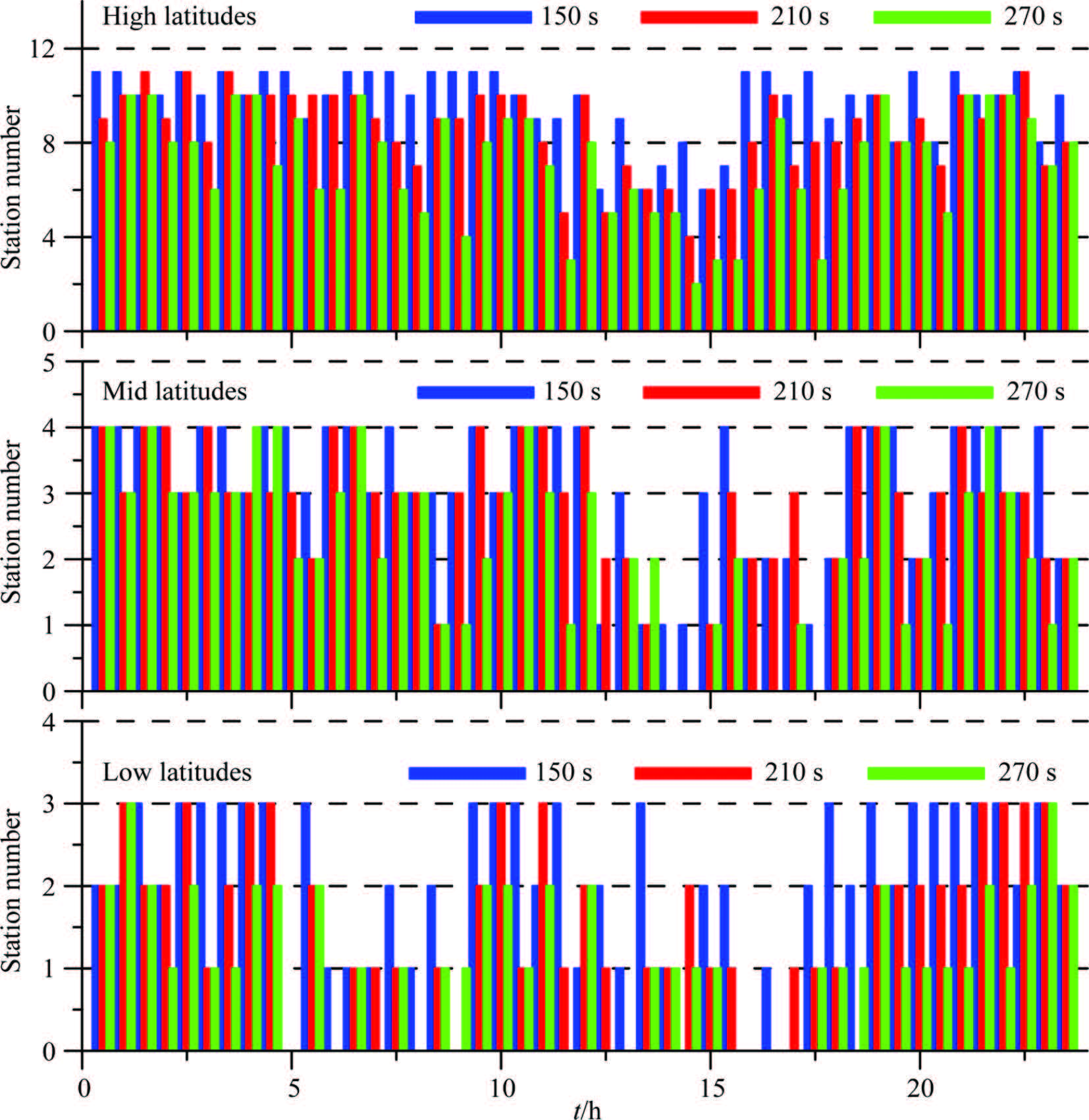
To clearly reflect the impact of ionosphere predicting error, we compute the accuracy of ionosphere prediction at different epochs(Fig. 7). Correspondingly, we count the number of stations succeeded at each epoch for different regions and time latency. The results for 150 s, 210 s and 270 s are plotted in Fig. 8. The ionosphere predicting error is overall very small during the whole day among stations in different regions when the time latency is set 30 s. Under this circumstance, on one h and , we can improve the accuracy of station’s position, together with the success rate of ambiguity resolution in wide-lane combination; on the other h and , the effect on the accuracy of narrow-lane combination is small, thus providing the probability of cycle slip fixing. When prolonging the time latency, the ionosphere predicting error grows significantly in two time intervals(UTC5:00~UTC9:00, UTC12:00~UTC18:00)for stations in low-latitude regions. It reaches 8 cm when the time latency is set 270 s. In this situation, the success rate of narrow-lane ambiguity resolution will be seriously affected even if the wide-lane combination is successfully fixed. It also can be seen from Fig. 8 that all stations are failed at some epochs within the time intervals. In middle-latitude regions, the ionosphere prediction error increases within only one time interval(UTC13:00~UTC17:00), in which the performance of the method decreases significantly. In high-latitude regions, the ionosphere predicting error shows a slightly increase at about UTC14:00 and the number of stations succeeded decreases. However, compared with stations in middle and low latitude regions, the effect is much smaller.

5.4 Analysis of Performance in Different Time Periods

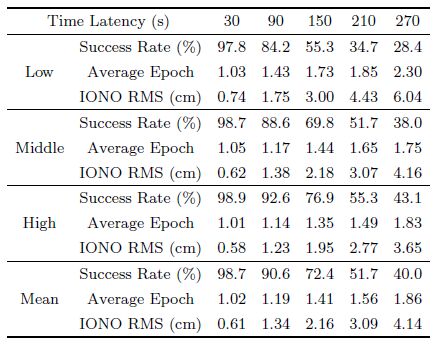
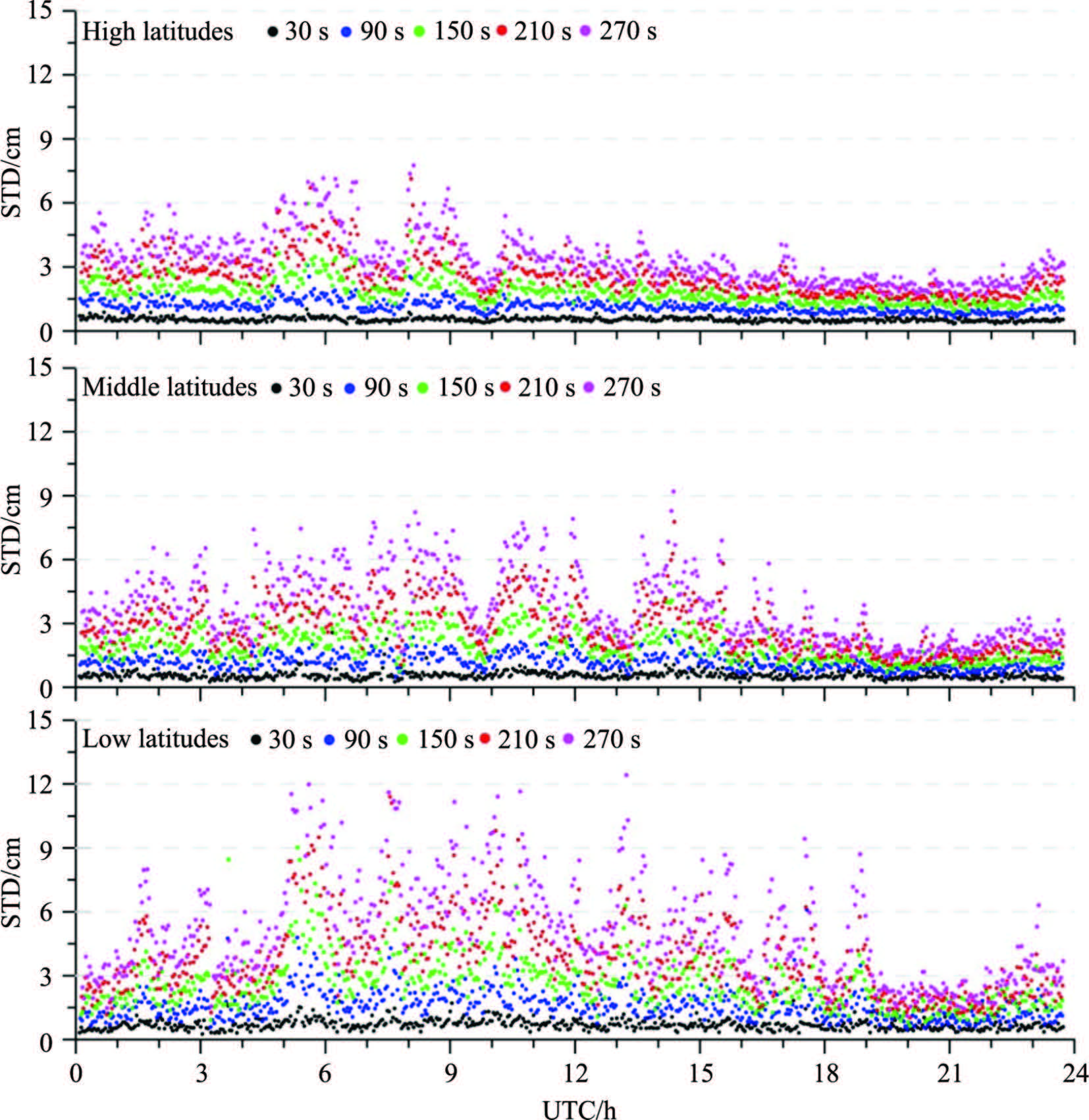
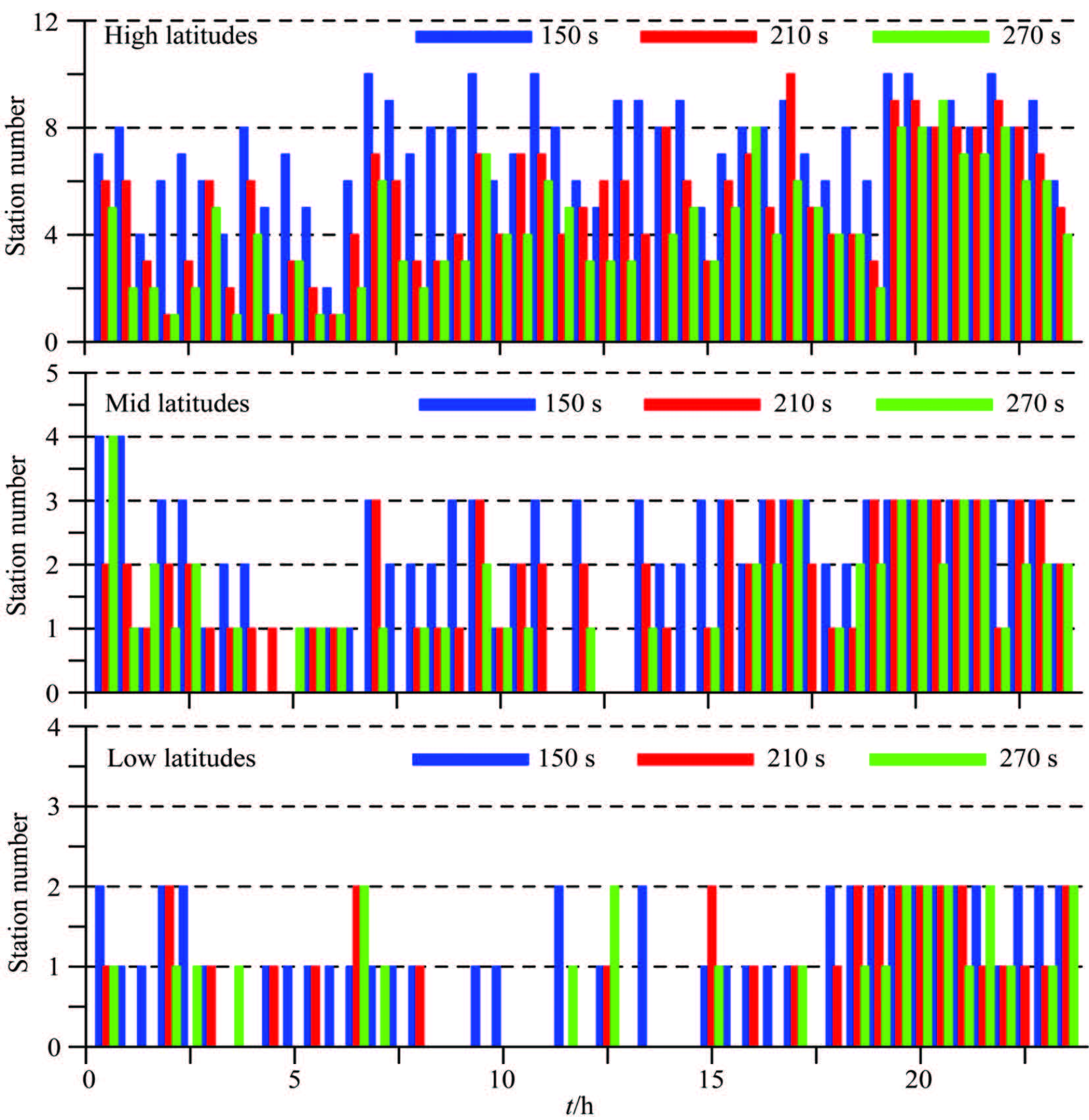
The variation of the ionosphere is strongly correlated with solar activity. The observation data analyzed in Section 5.3 is collected in quiet periods of solar activity. When the solar activity is severe, the ionosphere variation is less regular, and the prediction accuracy becomes lower. Table 5 gives the statistical results of observation data on DOY89, 2012 of stations in China. Also, we summarize the ionosphere predicting errors(Fig. 9) and the number of stations succeeded(Fig. 10)at each epoch.

Figure 9 and Table 5 show that the ionosphere predicting error is within 1.5 cm when the time latency is 30 s, and the success rate is bigger than 97%, which is nearly equivalent with that in the quiet period of solar activity. This result reveals that the performance of the method is less affected by the solar activity and nearly equal in different periods.

Compared with the quiet period of solar activity, the prediction accuracy decreases more rapidly when prolonging the time latency. Also, the predicting error is obviously big in a longer time interval within one day. This phenomenon becomes more obvious for stations in low-latitude regions where the predicting error is bigger than 4 cm during most of the time when the time latency is bigger than 150 s. Correspondingly, the success rate lowers down rapidly with the increasing time latency and decreasing latitude, which is about 80% and 55%, respectively in high- and low-latitude regions when the time latency reaches 150s.

6 CONCLUSIONS

We propose a method to solve the re-initialization problem in real time kinematic PPP caused by signal interruption and other causes. We design the ionosphere prediction model and proper weighting method of the predicted results to adaptively adjust the weighting of the predicted results. This method effectively takes into account the difference of ionosphere activity in different regions, which thus ensure the accuracy and reliability of the estimated results. Based on that, cycle slip parameters are estimated by combining epoch/satellite differenced observation through utilizing observations before and after cycle slip and the predicted ionosphere information, and then attempt is made to fix to realize instantaneous re-initialization of PPP.

We conduct analysis using observations from different regions and periods to comprehensively evaluate the performance of the method. Analysis results show that the method performs well under different circumstances when the time latency is small, thus proving that the method can effectively solve the re-initialization problem of real time kinematic PPP and exp and the real application of PPP. When prolonging the time latency, the performance under different circumstances varies significantly, and the success rate decreases with the decreasing latitude and increasing solar activity.

7 ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China(41174015, 41304034, 41231064). We thank CMONOC(Crustal Movement Observation Network of China)for providing the observation data. We also thank IGS for providing the observation data in Europe.