1 INTRODUCTION

The technology applications of the Satellite-to-Satellite Tracking(SST) and the Satellite Gravity Gradiometry(SGG)mark the beginning of a new epoch for improving the cognitive competences to the Digital Earth. The successful launches of the CHAllenging Minisatellite Payload(CHAMP)satellite, the Gravity Recovery and Climate Experiment(GRACE)satellite and the Gravity field and steady-state Ocean Circulation Explorer(GOCE)satellite, and the upcoming implementation of the next-generation GRACE Follow-On mission declare that we will usher in an unprecedented era of the satellite gravity measurement. Since CHAMP, GRACE and GOCE satellites respectively have its strong points, they are complementary rather than competitive. The CHAMP satellite is a forerunner for successfully implementing satellite gravity mission, the superiority of the twin GRACE satellites is inclined to detect the static and temporal signals of the Earth's gravitational field(2 ≤ L ≤ 120), and the GOCE mission is good at mapping the Earth's static gravitational field in the mediumshort- wavelength b and (120 < L ≤ 250)(Zheng et al., 2011a). Accordingly, the future Earth gravity field model with higher spatial and temporal resolution is propitious to being produced by the incorporation of the GRACE and GOCE observations. On account of having made a tremendous contribution to exploring the Earth's medium-long-wavelength static and long-wavelength time-varying gravitational field by the existing GRACE mission(Jekeli, 1999; Zhang et al., 2004; Shen et al., 2005; Tapley et al., 2005; Zheng et al., 2005, 2006, 2008, 2009a, 2009b, 2009c, 2011, 2012a, 2012b; Cheng and Xu, 2006; Zhou et al., 2006; Xu, 2008), the National Aeronautics and Space Administration(NASA)have proposed the next-generation GRACE Follow-On satellite gravity mission applied to precisely measure the Earth's medium-short-wavelength static and medium-long-wavelength time-varying gravitational field. The future twin GRACE Follow-On satellites plan to fly in an almost-circular, near-polar and low-Earth orbit, and precisely measure the intersatellite range and intersatellite range-rate by the Interferometric Laser Ranging(ILR)system, continuously track the low-orbiting twin satellites by the high-orbiting GPS(Global Positioning System)satellites, real-timely compensate the nonconservative force based on the Drag-Free Control System(DFCS), and accurately gain the three-dimensional attitudes using the Star Camera Assembly(SCA). Since the laser has some virtues consisting of the ultra-short and stable wavelength, etc., the measurement accuracy of the intersatellite range and intersatellite range-rate by the interferometric laser ranging system from GRACE Follow-On is at lowest 10 times higher than that by the K-B and Ranging(KBR)system from GRACE.

Up to now, many scientific institutions at home and abroad have carried out the requirements demonstration and gravity recovery around the future GRACE Follow-On mission based on the Satellite-to-Satellite Tracking in the High-Low/Low-Low(SST-HL/LL)principle(Stephens et al., 2006; Flechtner et al., 2009; Loomis, 2009, 2012; Zheng et al., 2009, 2010, 2012). Because the twin GRACE Follow-On satellites are equivalent to the one-dimensional horizontal gravity gradiometer with a intersatellite baseline of 50 km, how to accurately attain the medium-high-frequency signals of the Earth's gravitational field based on the GRACE Follow-On data is one of the research hotspots of the satellite gravity recovery at present. Rummel et al.(1993)measured the precision of the GRACE gravity gradiometer based on the torsion-balance principle. Keller and Heβ(1998)carried out the theoretical studies on the GRACE satellite gravity gradiometry measurement. Keller and Sharifi(2005)carried through the demonstration investigations on the GRACE satellite gravity gradiometry recovery from the aspects of the linear approximation, cube approximation, improved linear approximation, linear and cube approximation, and so on. However, they did not consider the influences of the conservative force and the non-conservative force on the twin GRACE satellites. Unlike the previous studies, we first acquire the second-order tensors of the geopotential by exp and ing the Earth's gravitational acceleration difference as a Taylor series, and precisely and rapidly recovered the Earth's gravitational field from GRACE Follow-On complete up to degree and order 120 through adding in the comprehensive effects of the conservative force and the non-conservative force in the observation equation of the satellite gravity gradiometry.

The advantages of the GRACE Follow-On satellite gravity gradiometry method are listed as follows: the SST-HL/LL mode chiefly aims to measure the medium-long-wavelength signals of the Earth's gravitational field, and the SGG mode is mainly sensitive to the Earth's gravitational field in the medium-short-wavelength b and . Hence, the GRACE Follow-On satellite gravity gradiometry method is propitious to further improving the recovery accuracy of the Earth's gravitational field by a combination of SST-HL/LL and SGG modes. The disadvantages are as below: since the future twin GRACE Follow-On satellites can not obtain the gravity gradient information in the cross-track and radial-track directions(Vyy and Vzz), but just in the along-track direction(Vxx), the sensitivity of the future GRACE Follow-On one-dimensional gravity gradiometer to the Earth's medium-high-frequency gravitational field is lower than that of the current GOCE satellite. To sum up, the GRACE Follow-On satellite gravity gradiometry method is helpful for making up the defects of the SST-HL/LL mode, and is hopeful to become an optimal approach for establishing the Earth gravity field model with higher spatial and temporal resolution.

2.1 Establishment of Observation Equation

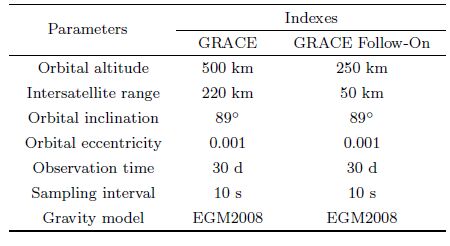
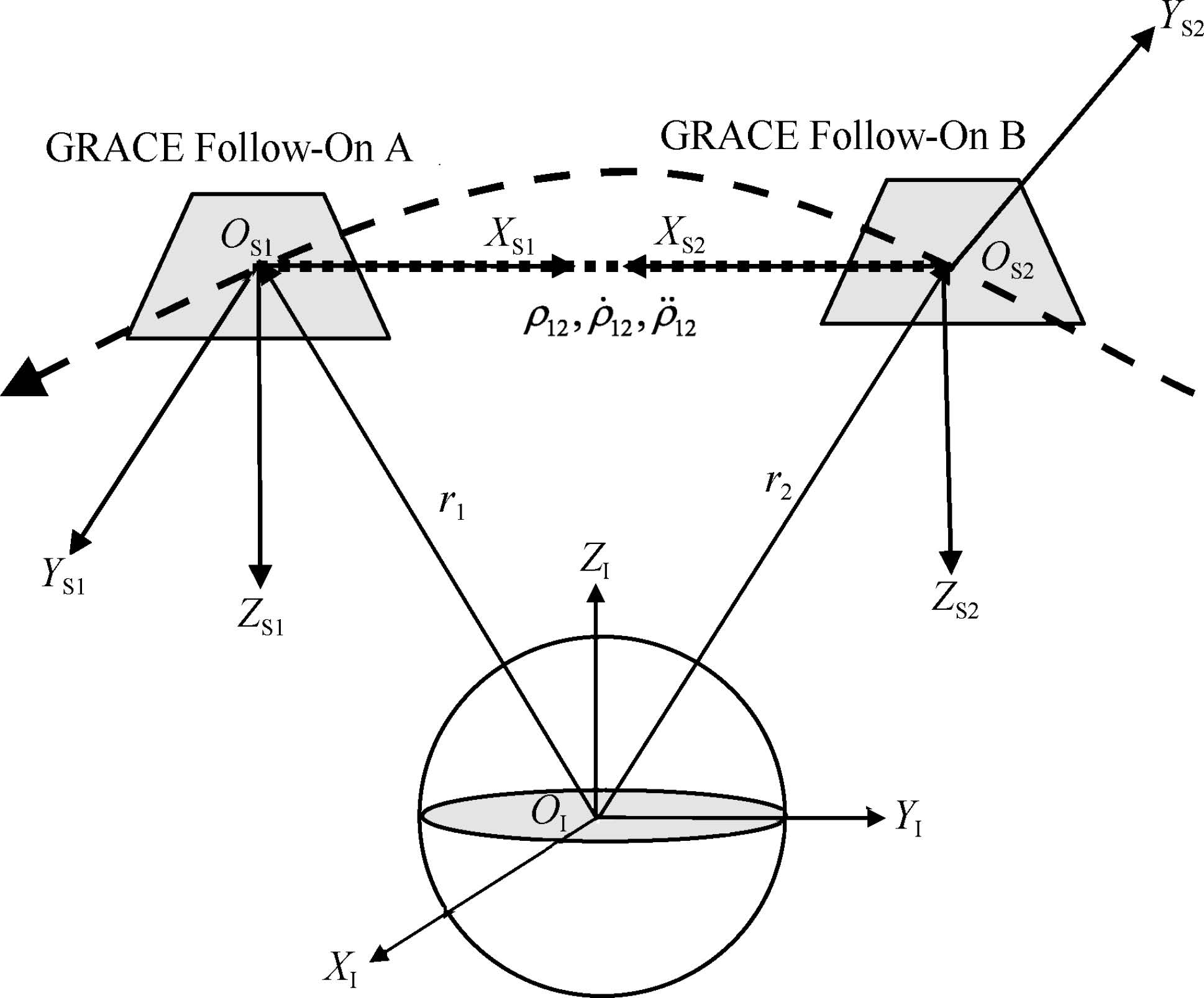
As illustrates in Fig. 1, O_I -X_IY_IZ_I denotes the Earth-Centered Inertial(ECI)frame, where the origin O_I lies in the Centre of Mass(COM)of the Earth, the positive directions of XI and ZI respectively point to the mean equinox and the North Pole of the Earth, and Y_I forms a right-h and ed triad with X_I and Z_I. O_S1(2) - X_S1(2)Y_S1(2)Z_S1(2) shows the Satellite Frame(SF), where the origins O_S1(2) are respectively located in the COM of the twin GRACE Follow-On-A/B satellites; X_S1(2)(Roll axis)is from the origin to target location of the phase center of the interferometric laser ranging system, and the positive directions of X_S1 and X_S2 are co-linear reversely; Z_S1(2)(Yaw axis)is normal to X_S1(2) and positive towards the satellite radiator; and Y_S1(2)(Pitch axis)forms a right-h and ed triad with X_S1(2) and Z_S1(2).

In the OI -XIYIZI frame, the intersatellite range ρ₁₂ from the GRACE Follow-On-A/B system is represented as

where r₁₂ = r₂ - r₁ is the relative orbital position vector, and r₁ and r₂ indicate the orbital position vectors of the twin GRACE Follow-On-A/B satellites. e₁₂ = r₁₂/|r₁₂| displays the unit vector identifying the direction to the GRACE Follow-On-B satellite from the GRACE Follow-On-A satellite.

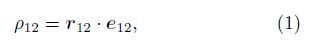
By the first-order derivatives of Eq.(1)with respect to t on both sides, the intersatellite range-rate $\dot \rho $₁₂ can be expressed as

where $\dot r$₁₂ = $\dot r$₂-$\dot r$₁ represents the relative orbital velocity vector of the twin GRACE Follow-On-A/B satellites, and $\dot e$₁₂ is a unit vector perpendicular to the line of sight. From r₁₂ · $ot e$₁₂= 0, Eq.(2)can be simplified as

Through the first-order derivatives of Eq.(4)on both sides with respect to t, the intersatellite rangeacceleration $\ddot \rho $₁₂ is denoted as

where $\ddot r$₁₂ is the relative orbital acceleration vector of the twin GRACE Follow-On-A/B satellites.

In Eq.(5), the particular form of $\ddot r$₁₂ is given by

where F₁₂^C= F₁₂^C- F₁^CFC1 represent the relative conservative forces except for the gravitational force of the Earth, including solar and lunar gravitation, Earth's solid tides, ocean tides, atmospheric tides, polar tide, etc.; f₁₂^N = f₂^N- f₁^N display the relative non-conservative forces, comprising atmospheric drag, solar radiation pressure, Earth's albedo, orbital altitude and attitude control forces, and so on; and g₁₂^o = g₂^o- g₁^o denote the relative geocentric gravitational forces: where GM represents the product of the Earth's mass M and gravitational constant G; express the geocentric radiuses of the twin GRACE Follow-On-A/B satellites, and x₁₍₂₎, y₁₍₂₎ and z₁₍₂₎ show three scalar components of the orbital position vectors r₁₍₂₎. g₁₂^T denotes the relative Earth's disturbing gravitational force acting on the twin GRACE Follow-On-A/B satellites where ▽T₁ and ▽T₂ are the gradients of the disturbing geopotential from the twin GRACE Follow-On-A/B satellites, respectively.

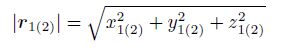
Exp and ing the gradients ▽T₂ of the disturbing geopotential as a Taylor series and keeping terms up to the first order yields

where ▽²T₁ shows the second-order gradients of the disturbing geopotential. O(▽T₁)is the infinitely small quantity starting from the third-order term. The numerical results show that because the magnitude of error of O(▽T₁)is smaller than 10-14 m·s^-2 and is at least 10 times lower than the measurement error of the key payloads(e.g. the space-borne accelerometer with a precision of 10-11 ~ 10-13 m·s^-2), the influences of the higher-order terms on the recovery accuracy of the Earth's gravitational field are able to be completely neglected.

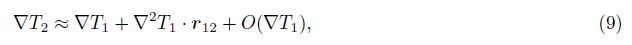
Substituting Eq.(9)into Eq.(8)yields

Combining Eqs.(1), (3), (5), (6), (7) and (10), the GRACE Follow-On observation equation of the satellite gravity gradiometry can be expressed as

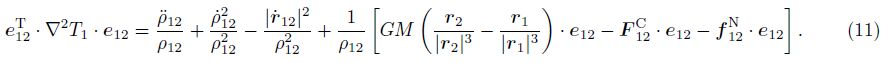
Eq.(11)can be accurately and rapidly solved based on the Pre-Conditioned Conjugate-Gradient(PCCG) approach(Zheng et al., 2011b). The PCCG approach is one of the most efficient iterative methods for solving the large-scale overdetermined system of linear equations at present. In addition, the research results by numerical simulation show: since the maximum degree of the spherical harmonic function is truncated at 120 in this study, the impacts of the ill-condition of the normal matrix on the recovery accuracy of the Earth's gravitational field are extremely small. Therefore, it has no need to suppress the high-frequency noises of the Earth's gravitational field determination by the regularization methods(e.g. Kaula, Tikhonov, etc.)in this study.

2.2 First-order Gradient of Disturbing Geopotential

The disturbing geopotential T(r, θ, λ)is defined as

where r displays the distance from the centroid of the satellite to the geocenter, θ and λ express respectively geocentric colatitude and geocentric longitude, R_e denotes the mean radius of the Earth, Plm(cos θ)shows the normalized Legendre polynomial of degree l and order m, and ${\bar C_{lm}}$, ${\bar S_{lm}}$ represent the estimated normalized geopotential coefficients.

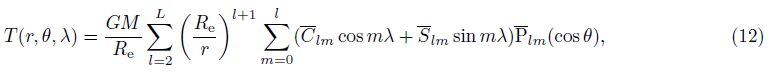
The conversion relationship of the disturbing geopotential gradient ▽T between the spherical coordinate system(r, θ, λ) and the Cartesian coordinate system(x, y, z)is displayed as

where ▽T_{r, θ, λ} is the partial derivatives of T with respect to(r, θ, λ) where the Legendre function ${\bar P_{lm}}$(cos θ)is denoted as(Koop, 1993) the initial values are represented as the coefficients are expressed as

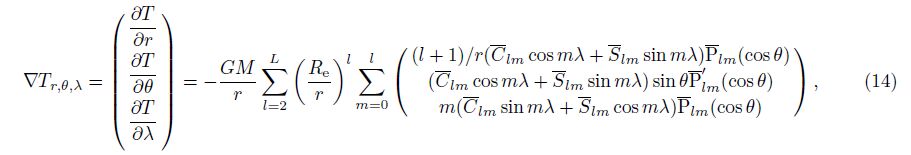
The first-order derivatives ${\bar P'_{lm}}$(cos θ)of the Legendre function are shown as

the starting values are displayed as

The J is the transformation matrix from ▽T_{r, θ, λ} to ▽T_{x, y.z}

2.3 Second-order Gradients of Disturbing Geopotential

The second-order gradients of the disturbing geopotential are defined as

where the second-order derivatives ${\bar P''_{lm}}$(cos θ)of the Legendre function are represent as the provisional values are denoted as

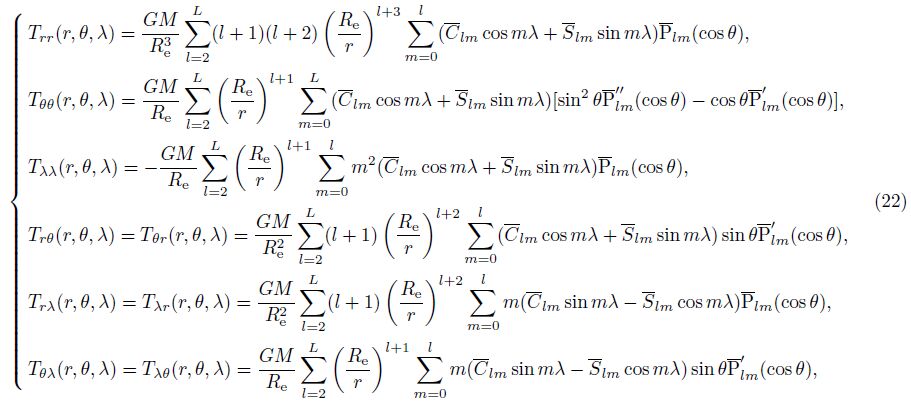
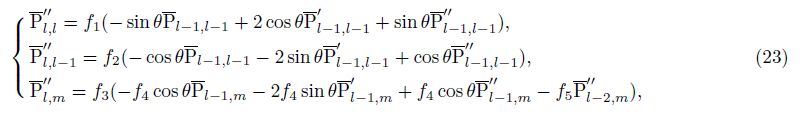
The Eq.(21)can be rewritten as

2.4 Intersatellite Range-Acceleration

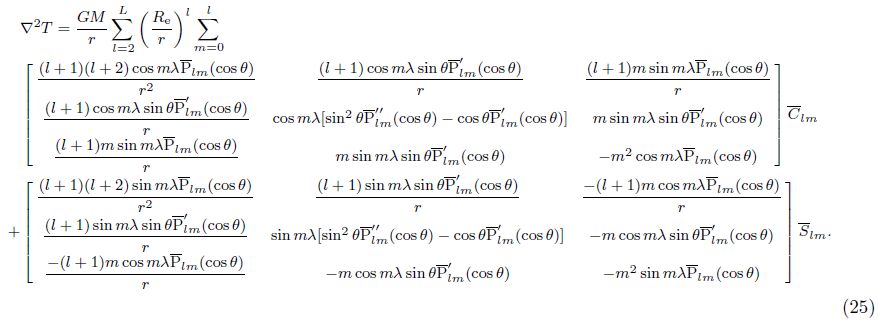
Based on the Newton-Gregory interpolating model, the Taylor series expansion of the intersatellite range ρ₁₂ is denoted as

where $\left({\begin{array}{*{20}{c}}q\\i\end{array}} \right)$ displays the binomial coefficients, q =$\frac{{t - {t_1}}}{{\Delta t}}$ t₁ indicates the initial time instant of interpolation, t denotes the time instant of computing point, and △t represents the sampling interval.△_1+(n-1)/2^n-1 =$\sum\limits_{i = 1}^n {{{(- 1)}^{n + i}}\left({\begin{array}{*{20}{c}}{n - 1}\\{i - 1}\end{array}} \right)} $ ρ₁₂(t_i)is the difference operator, and n shows the amount of interpolation points.

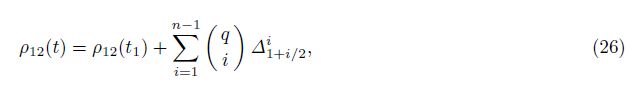
From the second-derivatives of Eq.(26)with respect to t on both sides, the intersatellite range-acceleration $\ddot \rho $₁₂ is given by

where the nine-point Newton-Gregory interpolation formula can be indicated as

3 RESULTS 3.1 Simulation of Satellite Orbit

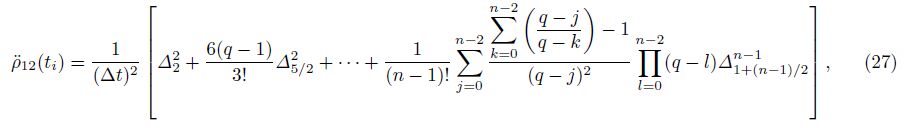
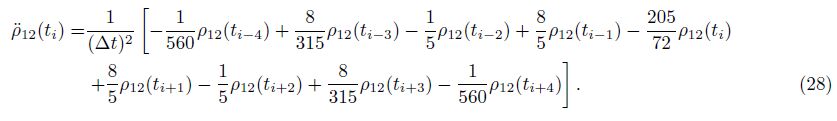
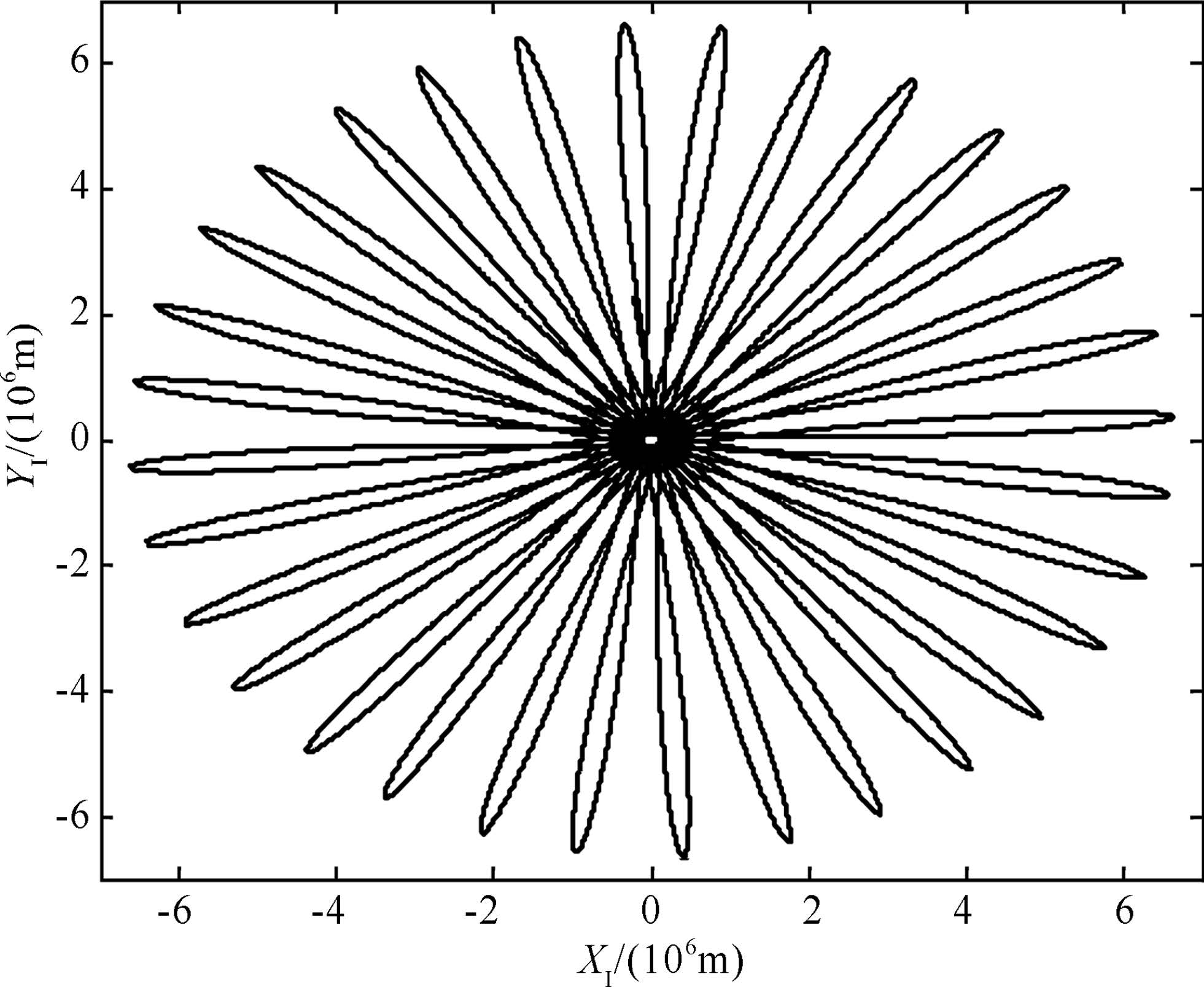
We precisely calculated the orbital positions and orbital velocities of the current twin GRACE-A/B satellites and the future twin GRACE Follow-On-A/B satellites through the numerical integration formulas of the 9th-order Runge-Kutta linear single-step method in combination with the 12th-order Adams-Cowell linear multi-step method by the numerical simulation. The simulation parameters of the satellite orbits are shown in Table 1. Fig. 2 illustrates the X_IY_I-plane projection of the GRACE Follow-On-A satellite orbit during one day in the O_I - X_IY_IZ_I frame.

3.2 Satellite Gravity Gradiometry Recovery

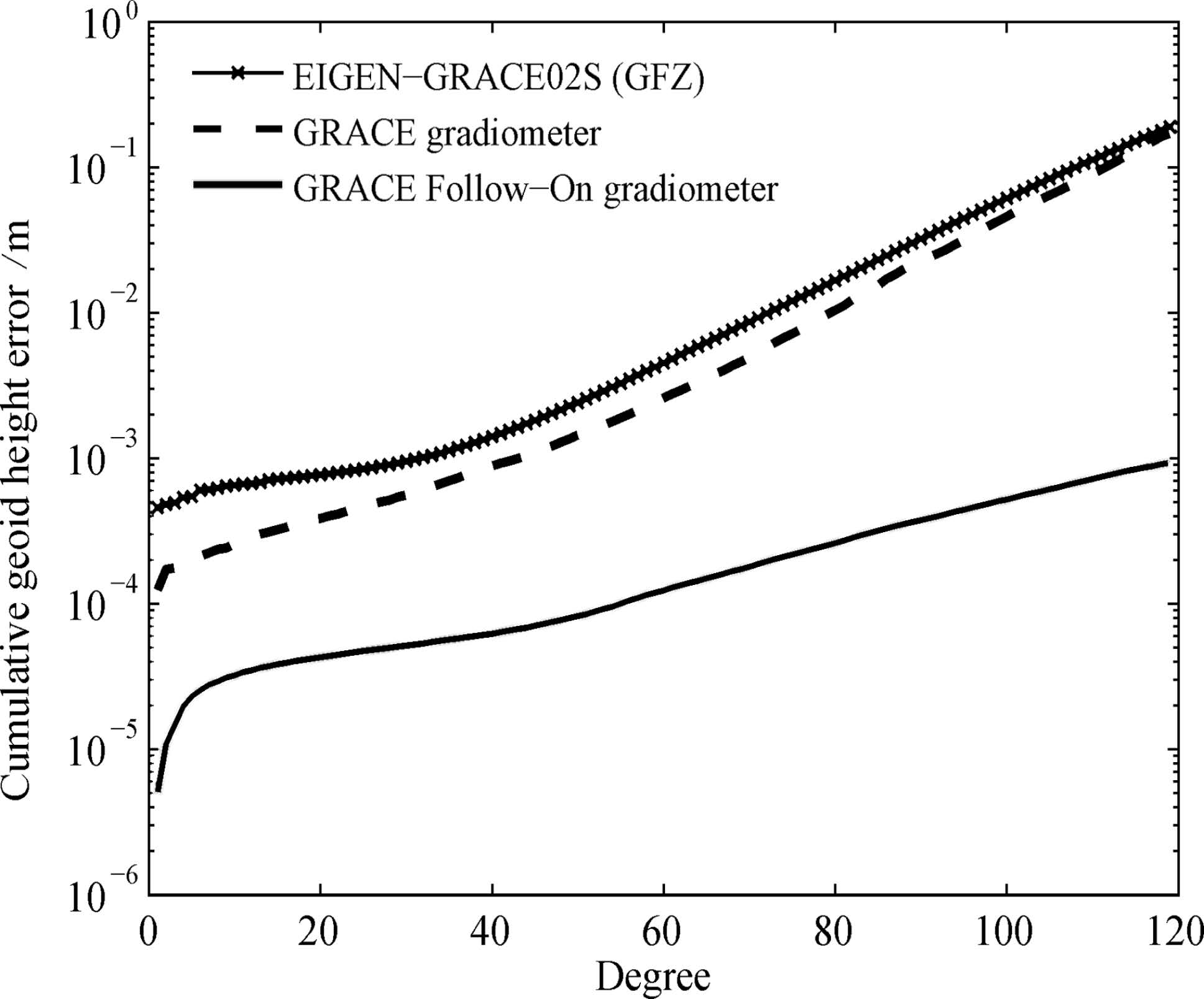
As displayed in Fig. 3, the line with crosses represents the real accuracy of the Earth gravity field model EIGEN-GRACE02S complete up to degree and order 120 released by the German Research Centre for Geosciences (GFZ) and the cumulative geoid height error is 1.893×10-1 m at degree 120; the dashed and solid lines respectively denote the simulation accuracies of the Earth's gravitational field recovery based on the GRACE and GRACE Follow-On satellite gravity gradiometry method using the orbital parameters of the satellite(Table 1) and the measurement precision of the space-borne instruments(Table 2) and the cumulative geoid height errors are 1.708×10^-1 m and 9.331×10^-4m at degree 120; and the statistical results of the cumulative geoid height errors are listed in Table 3. The research results are shown as follows.

Firstly, by a comparison of the cross and dashed lines in Fig. 3, the accuracy of the Earth's gravitational field recovery based on the GRACE satellite gravity gradiometry method is averagely improved by 72% as compared to that of the EIGEN-GRACE02S model in 120 degrees. The principal reasons are as below: for the dynamical method, energy conservation principle, acceleration method, and so on, the Earth's gravitational field from GRACE is recovered by the SST mode. However, for the GRACE satellite gravity gradiometry method, the Earth's gravitational field is determined through a combination of advantages between the SST mode and the SGG mode. Therefore, the recovery accuracy of the Earth's gravitational field is propitious to being further improved based on the GRACE satellite gravity gradiometry method.

Secondly, through a comparison of the cross line with solid line in Fig. 3, because the determination accuracy of the Earth's gravitational field based on the next-generation GRACE Follow-On mission is about 61 times higher than that based on the present GRACE mission, the GRACE Follow-On satellite gravity gradiometry method is a preferred selection for precisely producing the next-generation Earth gravity field model with higher spatial resolution. The main reasons are analyzed as follows:(1)the orbital altitude of the future twin GRACE Follow-On satellites(200~300 km)is lower than that of the current twin GRACE satellites(400~500 km). For the current GRACE mission, the non-conservative force is measured by the spaceborne accelerometer and is removed during the data post-processing step. Because the non-conservative force makes for being drastically increased with the decay of the orbital altitude of the satellite, it is highly difficult to substantially reduce the orbital altitude of the current twin GRACE satellites. For the future GRACE Follow-On mission, since the non-conservative force is able to be real-timely and accurately compensated by the drag-free control system, the orbital altitude of the satellite is helpful for being sufficiently decreased and the signal attenuation of the gravity field with increasing the orbital altitude is in favor of being efficiently mitigated. (2)The measurement precision of the space-borne instruments from the future GRACE Follow-On mission is higher than that from the current GRACE mission. The twin GRACE satellites measure the intersatellite range with a precision of 10 μm and intersatellite range-rate with a precision of 1 μm·s^-1 by the K-b and ranging system, and acquire the non-conservative force with a precision of 10^-10 m·s^-2 by the accelerometer. The twin GRACE Follow-On satellites obtain the intersatellite range with a precision of 10~1000 nm and intersatellite range-rate with a precision of 1~100 nm·s^-1 by the interferometric laser ranging system, and eliminate the non-conservative force with a precision of 10^-11 ~ 10^-13 m·s^-2 by the drag-free control system. (3)The intersatellite range of GRACE Follow-On is shorter than that of GRACE. The proper increase of the intersatellite range is propitious to improving the accuracy of the Earth's long-wavelength gravitational field, and appropriately decreasing the intersatellite range makes for enhancing the accuracy of the Earth's shortwavelength gravitational field. Because the intersatellite range of GRACE Follow-On(50~100 km)is shorter than that of GRACE(220 km), the accuracy of the medium-high-frequency Earth's gravitational field is able to be substantially improved by the future GRACE Follow-On mission.

4 CONCLUSION

In view of the outst and ing contributions of the current GRACE mission to the related interdisciplines (e.g. geodesy, geophysics, oceanography, hydrology, etc.) and the inherent limitations(e.g. higher orbital altitude of the satellite, lower measurement precision of the key payloads, and so on), many domestic and foreign researcher are actively demonstrating the next-generation satellite gravity mission with higher spatial and temporal resolution. Based on the above-mentioned causes, we precisely recovered the Earth's gravitational field from GRACE Follow-On complete up to degree and order 120 by a combination of the various observations consisting of intersatellite range, intersatellite range-rate, intersatellite range-acceleration and the second-order tensors of the geopotential. The study results indicate that the recovery accuracy of the Earth's gravitational field based on the future GRACE Follow-On mission is at least one order of magnitude higher than that based on the current GRACE mission. Consequently, the GRACE Follow-On satellite gravity gradiometry method is full of promise to establish the high-accuracy and high-resolution Earth gravity field model in future.

ACKNOWLEDGMENTS

We greatly appreciate the helpful suggestions from anonymous referees and editors. This work was supported by the Main Direction Program of Knowledge Innovation of Chinese Academy of Sciences for Distinguished Young Scholar(KZCX2-EW-QN114), the National Natural Science Foundation of China(41004006, 41202094, 41131067 and 11173049), the Merit-based Scientific Research Foundation of the State Ministry of Human Resources and Social Security of China for Returned Overseas Chinese Scholars(2011), the Open Research Fund Program of the Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, China (11-01-02), the Open Research Fund Program of the Key Laboratory of Geo-Informatics of National Administration of Surveying, Mapping and Geoinformation of China(201322), the Open Research Fund Program of the State Key Laboratory of Geo-information Engineering(SKLGIE2013-M-1-5), the Main Direction Program of Institute of Geodesy and Geophysics, Chinese Academy of Sciences(Y309451045), and the Research Fund Program of State Key Laboratory of Geodesy and Earth's Dynamics(Y309491050).