2. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China
Some hotspot volcano mountains are distributed in all the oceans,which are generated when a lithospheric plate moves over a mantle source,where magma rises from deep mantle and is stored in the form of the magma reservoir beneath the volcanoes,forming active volcano chains. Their trajectories are volcanic mountain ranges,and such volcanic sources are called hotspots. When the lithosphere plate moves to the top of a hotspot,a volcano center is generated. As the plate continues to move across the hotspot,the earlier-formed volcano is away from the hotspot,extinguishes gradually and becomes a dead volcano. And behind the hotspot formes a new volcano. Because the hotspot is fixed relative to the lower mantle,so the plate movement relative to the hotspots is relative to the lower mantle movement. The hotspot reference frame is relative to the lower mantle reference frame fixed,which has a clear geophysical significance,so the absolute plate motion model based on hotspot reference frame is adapted by many geophysical scholars.
The AM1 model,the first absolute plate motion model based on the hotspot reference frame,was established by Minste and Jordon in 1974[1] using the data of hotspot trends. Then,Chase[2] used hotspot data to derive the absolute plate motion model of P073 from the relative motion model of P071. With the increasing of hotspots observation data,using both the hotspot trend data of hot volcano ridges and hotspot rate data to establish the reference datum at the same time has become a tendency,just like the model AM1-2[3],HS2-NUVEL1[4] and HS3-NUVEL1A[5] etc. The AM1-2 model was used for analysis of satellite laser ranging data,the hotspot data used to build HS2-NUVEL1 and AM1-2 model are the same data set,i.e. 5 hotspot rates and 9 hotspot trends data,which are distributed in the Pacific plate,Cocos plate,Nazca Plate and the North American plate,So the plate motion speed relative to hotspots in HS2-NUVEL1 is largely similar to the AM1-2 model,the difference between them might be mainly in the relative motion model of NUVEL-1 and RM2[4, 6]. The HS3-NUVEL1A model was established by 2 hotspot rates and 11 hotspot trends data of Pacific (0~5.8 Ma) young hotspot volcano chain constraints to the relative motion model of NUVEL-1A,which gives 15 plate velocities relative to hotspots. There is little relative movement between the hotspots,but in the 95% confidence range,relative velocity is in 20 km/Ma to 40 km/Ma,and some even reaches ±145 km/Ma range. Plate relative motion speed uncertainty of HS3-NUVEL1A is smaller than HS2-NUVEL1,in which 9 of 14 Euler vectors are out of the HS3-NUVEL1A 95% confidence region; and all 14 Euler vectors of HS3-NUVEL1A are in the 95% confidence region of HS2-NUVEL1. Relative to the HS2-NUVEL1 datum,angular velocity vector of the Pacific plate in HS3-NUVEL1A is in the Pacific plate of the 95% confidence region,but in the 0~3 Ma periods,Wessel and Kroenke[7] estimation of the Pacific plate angular velocity is much outside the confidence interval. Relative to the HS3-NUVEL1A datum,angular velocity vector of the Pacific plate is different from the mean value before 47 Ma,but in the direction is roughly the same. In the Hawaii-the Emperor Range volcano chain,rotation rate of the Pacific plate (1.06±0.10°/Ma) is faster 50% than the average (0.70°/Ma) of 47Ma years[5]. Fig.1 shows the plate motion velocities relative to the hotspot reference frame HS3-NUVEL1A and HS2-NUVEL1,respectively,the thick arrows represent the plate motion velocities relative to hotspot reference frame in HS3-NUVEL1A,and thin arrows represent in HS2-NUVEL1. In HS3-NUVEL1A,the Pacific plate movement is faster than that in HS2-NUVEL1 by 8~9 km/Ma,and moving north to the West[5]; the vector difference of angular velocity relative to hotspots in HS3-NUVEL1A and HS2-NUVEL1 changes with the plate,the maximum vector difference (0.17°/Ma) is the Cocos plate; the smallest is 0.08°/Ma,located in the Pacific plate (see Fig.1 and Table1).
|
Fig.1 Plate velocities relative to HS2-NUVEL1 and HS3-NUVEL1A model[5] |
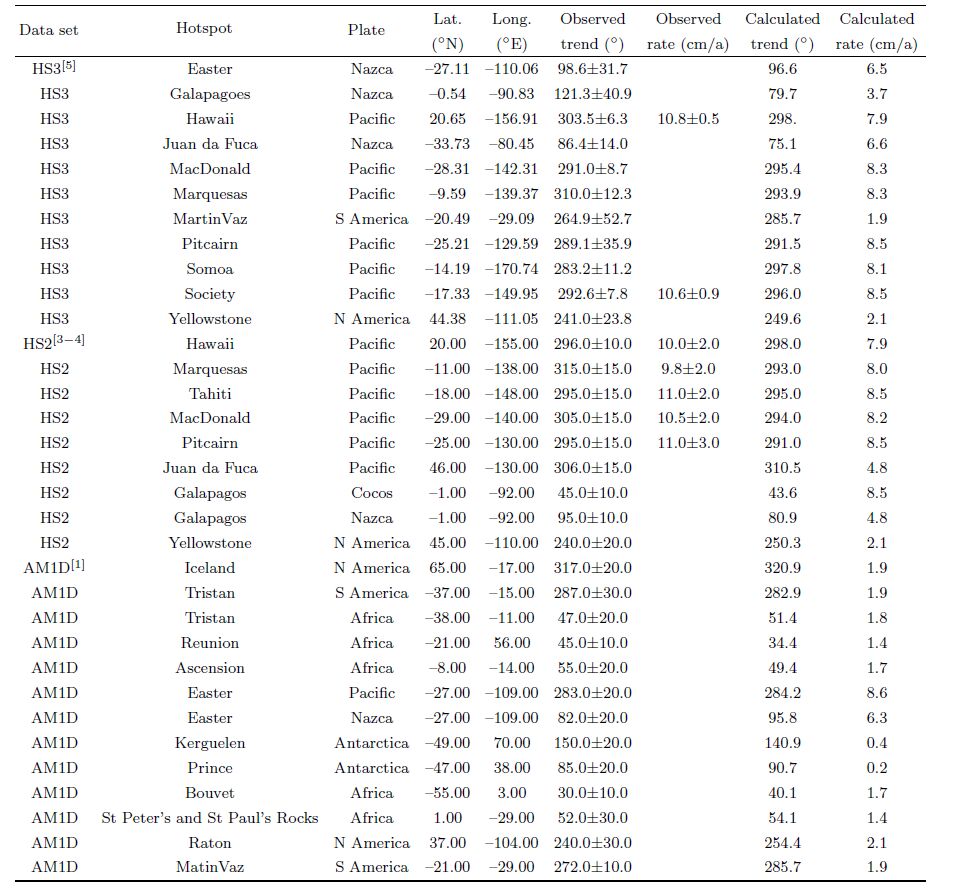
| Table 1 Data of hotspot trends and rates |
Jordan, using the relative plate motion Euler vectors in the ITRF2000VEL model, Jin et al.[9] derived the absolute plate motion model HS2-ITRF2000 based on hotspots, while which did not reflect the adjacent lithosphere of the Atlantic is affected by the spreading ridge in the Atlantic, and the hotspot data are not accurate, especially the speed error is large, also there is relative motion between hotspots, so that this model cannot accurately represent plate absolute motion. By using a group of recent (0~7.8 Ma) hotspot migration rates and trends of global distribution, combined with the plate motion model of NNR-NUVEL1A, Wei[10] established the absolute plate motion model APM2, which shows that, the lithosphere has a net rotation relative to the hotspots by 0.1983°±0.135°/Ma, with a pole at 49.423°S, 90.625°E with respect to the deep mantle. This model also shows that the Pacific hotspots were inconsistent with that in the Indo-Atlantic, which displays the Pacific hotspot motion is not consistent either. At the same time, Wei[10] also shows that the speed and direction of the same plate motion are different in different models. For example, some models give a clockwise rotation of the Eurasian plate,other models suggest an opposite result. Such case also occurs to the Africa plate and other plates. Perhaps it is related with the different hotspot data used by different authors. If the hotspots are relatively fixed,and the relative plate motion model is correct,the hotspots on a separate plate are enough to determine the absolute plate motion. However,the hotspots are actually not fixed relative to each other.
Some Chinese scholars had also done a lot of work in hotspot and hotspot reference frame. Sun[6] analyzed the hotspot hypothesis of Wilson-Morgan,discussed the differences and relations between the same data set of two reference frames HS2-NUVEL1 and AM1-2,aiming at that the hotspot reference frame and lithospheric nonet-rotation reference frame may have some problems,and put forward his own model,namely the Pacific ridge fixed reference frame PRF-NUVEL1,and analyzed the rationality and feasibility of this reference frame. Wang et al.[8] found that the widely used model HS2-NUVEL1 in previous work is not consisten with the hotspots outside of the Pacific region,so they used the relative plate motion model NUVEL-1A,by fitting 22 hot volcano trends distributed in 7 plates,got a new absolute plate motion model named T22A. This model was not only better in fitting the global hotspot data than the HS2-NUVEL1 model,but also reflected that the lower mantle as the hotspot origin is moving in an direction opposite to the lithospheric plate motion at a rate about 1/4 of the plate speed. This result denies hotspot fixed hypothesis which was widely used in the past decades,and infers the mantle viscosity structure consistent with the result from postglacial rebound data,therefore,it is of great significance to the study of mantle convection,reconstruction of ancient plate motion,true polar wander and the global reference system. According to hotspot observations and estimates provided by Minster and Jordan,using the relative plate motion Euler vectors in the ITRF2000VEL model,Jin et al.[9] derived the absolute plate motion model HS2-ITRF2000 based on hotspots,while which did not reflect the adjacent lithosphere of the Atlantic is affected by the spreading ridge in the Atlantic,and the hotspot data are not accurate,especially the speed error is large,also there is relative motion between hotspots,so that this model cannot accurately represent plate absolute motion. By using a group of recent (0~7.8 Ma) hotspot migration rates and trends of global distribution,combined with the plate motion model of NNR-NUVEL1A,Wei[10] established the absolute plate motion model APM2,which shows that,the lithosphere has a net rotation relative to the hotspots by 0.1983°±0.135°/Ma,with a pole at 49.423°S,90.625°E with respect to the deep mantle. This model also shows that the Pacific hotspots were inconsistent with that in the Indo-Atlantic,which displays the Pacific hotspot motion is not consistent either. At the same time,Wei[10] also shows that the speed and direction of the same plate motion are different in different models. For example,some models give a clockwise rotation
As to the hotspot reference frame,there may be questions in the following two aspects: (1) hotspot data is not accurate; (2) there is relative motion between hotspots. Whether the hotspot is stable with respect to the lower mantle,there is no unified conclusion. Molnar and Stock[11] showed that the hotspot relative motion about 1 cm/a along the southeast direction exists in the Pacific and the Atlantic. However,Steinberger[12] believed that the relative motion between hotspots were much smaller than that between plates,so the hotspot is often used as a reference framework for plate motion; Divenere and Kent[13] devoted to the fixity of hotspots in the Pacific and Indo-Atlantic,and considered there is also relative motion between hotspots in Hawaii-Emperor and Indo-Atlantic,with the magnitude approximately 2.5 cm/a. Gripp and Gordon[4] also analyzed the problem when constructing the HS3-NUVEL1A model. They believed that there was not big relative movement between the hotspots,but in the 95% confidence range,relative velocity is between 2 cm/a to 4cm/a. Tarduno et al.[14] thought that Hawaii hotspots moved at the speed greater than 4cm/a in 81~47 Ma. Wang[15] also considered that during the past 40 Ma,hotspots were in a state of systematically movement. Wei[10] also suggested that hotspots in the Pacific and Indo-Atlantic were inconsistent,showing that the Pacific hotspot motion was not consistent. Nevertheless,today’s state-of-arts force us to favor the hotspot reference frame to measure the absolute motion of plates even though it is merely a quasi-fixed reference frame. We believe the non-fixity of hotspots will not jeopardize the conclusions to be drawn. So,we still choose the hotspot reference frame as the basic reference frame[10].
In view of above,the idea of medial-hotspot (MHS) reference datum was proposed in this study,which means to choose the hotspot rates and trends data as much as possible,establish a rule,deduce average relative motion between hotspots,take the minimum total movement of hotspots relative to the lower mantle as the criterion,and establish the reference datum based on the medial-hotspots. Taking plate motion data relative to the hotspot as constraint,two absolute plate motion models designated as MHS-NUVEL1A and MHS-ITRF2005 have been developed using a set of hotspot data globally distributed in conjunction with plate motion models NNR-NUVEL1A and ITRF2005VEL,respectively. These two models were also compared and analyzed with other absolute plate motion models based on the hotspots reference frame. The lithosphere’s net rotation was discussed and compared at last.
2 DATATable1 gives the data sets used in the establishment of various hotspot models,of which,HS3 refers to the 11 trends data and 2 rates data used by Gripp and Gordon[5],which is from the Pacific region of the young volcano chain in 0~5.8 Ma. HS2 data set is also from the Pacific region,but time span was later than that of HS3,that is,volcano activity data in 0~10 Ma,both used in the model HS2-NUVEL1 of Gripp and Gordon[4] and AM1-2 of Minster and Jordan[3],which include 9 trends data and 5 rates data. AM1D refers to 13 trends data used in Minster et al.[1],which were from different plates,the time span was constrained in the past 40Ma volcano activities. These observation data were used to set up the model in this paper,contain 33 trends and 11 rates totally,with the time span 0~40 Ma of volcano activity.
The absolute plate motion is affected by hotspot rates and trends in different ways. Hotspot rates are sensitive to the plate velocity,while hotspot trends are sensitive to the plate moving direction,of course,utilizing rates and trends at the same time is better than using either data alone[10].
3 METHODAccording to the theory of plate tectonics,each plate obeys Euler law,i.e. Vi = Ω ×ri. If the plate motion speed or other motion data is known,the plate Euler vector could be inversed out. The inversion method of Euler vectors is: (1) assume that global relative plate motion model is known (such as NUVEL-1A); (2) solve any plate (usually the Pacific plate) Euler vector relative to hotspots; (3) add the absolute motion of this plate to the relative motion of the other plates relative to this plate,then the global absolute plate motion based on hotspots[6, 10] is obtained.
Using the line of thought,the absolute plate motion model based on hotspots can be established. Here,we put forward the criterion to establish the medial hotspot reference datum. As stated previously,although there is relative motion between hotspots,the average speed is no more than 2 cm/a. For example,the India ocean hotspot moving speed is only 1 cm/a,that between the Pacific and the Atlantic is 3 cm/a; while the speed of plate motion in general is about 2~10 cm/a. The observations of hotspot rates in the Pacific plate (Table1) show that the error of hotspot rates is between 2~3 cm/a,so taking hotspot as a reference point of the absolute plate motion is feasible. Wang[8] found that the lower mantle,from which hotspots are originated,is moving in a direction opposite to lithospheric plates at a rate about 1/4 of plate motion speed. We took this as foundation and established a constraint criterion of the medial-hotspot reference datum. From Table1,only the hotspots in the Pacific plate have movement rate data,then taking 1/4 of which as a constraint criterion and hotspot rates located in the Pacific plate were constrained to this criterion. Because hotspots move in the opposite direction to plates[8],so the constraint criterion is to subtract plate average rate’s 1/4 from the rate of hotspots which lie on this plate. This hotspot data constrained by the above criterion is used to construct the hotspot motion model and calculate its parameters by the following steps.
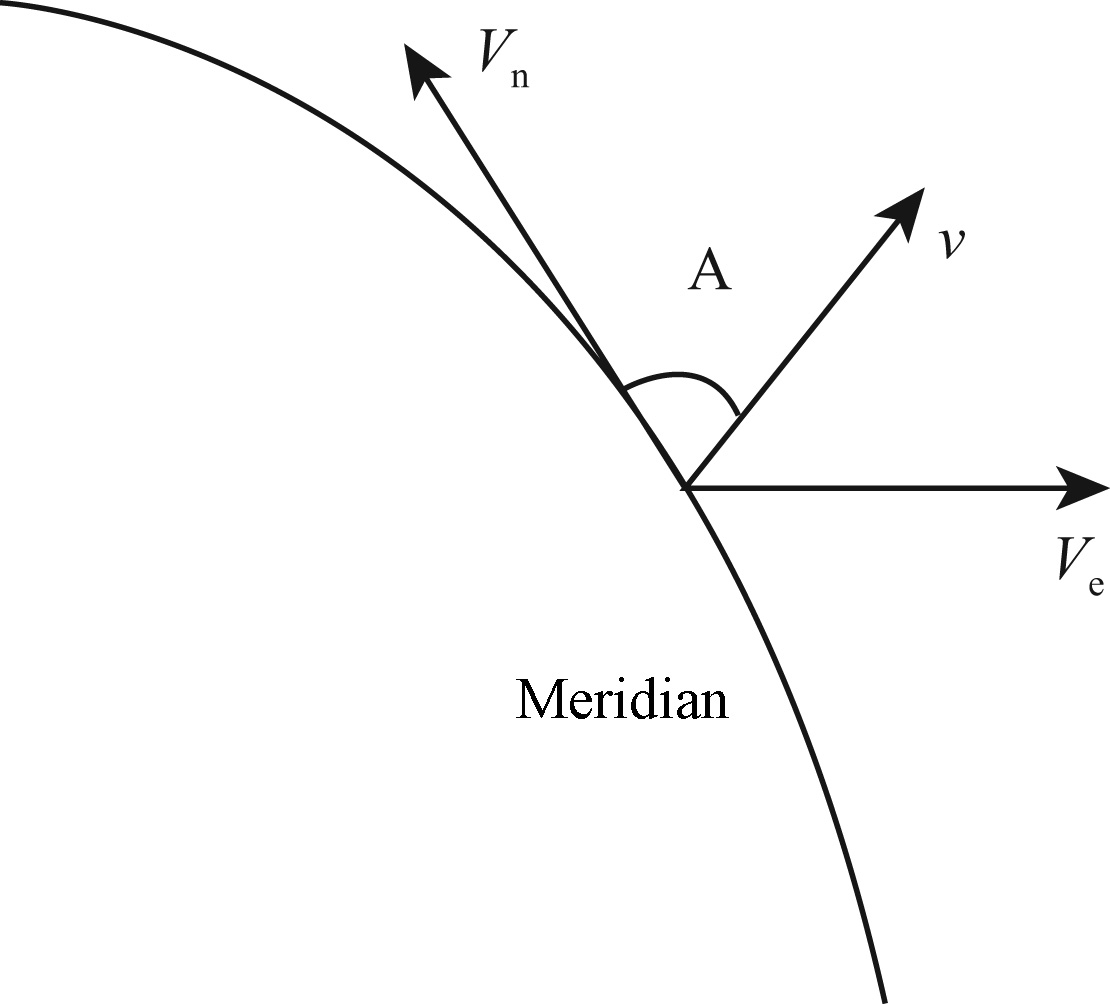
After data processing,the observation model of hot reference datum based on the above idea could be established. Let (ωx,ωy,ωz) represent the plate Euler vector,(r,Φ,λ) be a position vector of any point on the Earth. The velocity vector can be expressed by latitude component of Vn and longitude component of Ve because the relative velocity of any point on the earth surface is tangent to the sphere,which are shown in Fig.2. Then we have
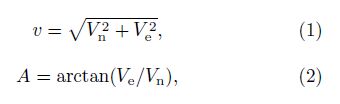
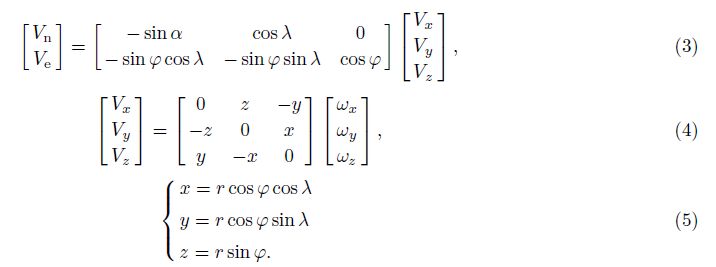
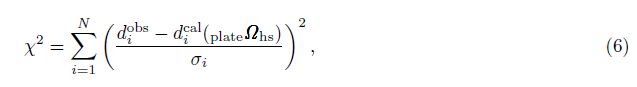
|
Fig.2 Schematic diagram of velocity components of a station |
According to the hotspot data in Table1,using the above method and constraint criterion,based on the geographical model NUVEL-1A[18] and measured model ITRF2005VEL[19],the geographical and measured absolute plate motion models MHS-NUVEL1A and MHS-ITRF2005 based on the medial-hotspot reference frame are established respectively,which are compared and analyzed with other absolute plate motion models based on hotspots.
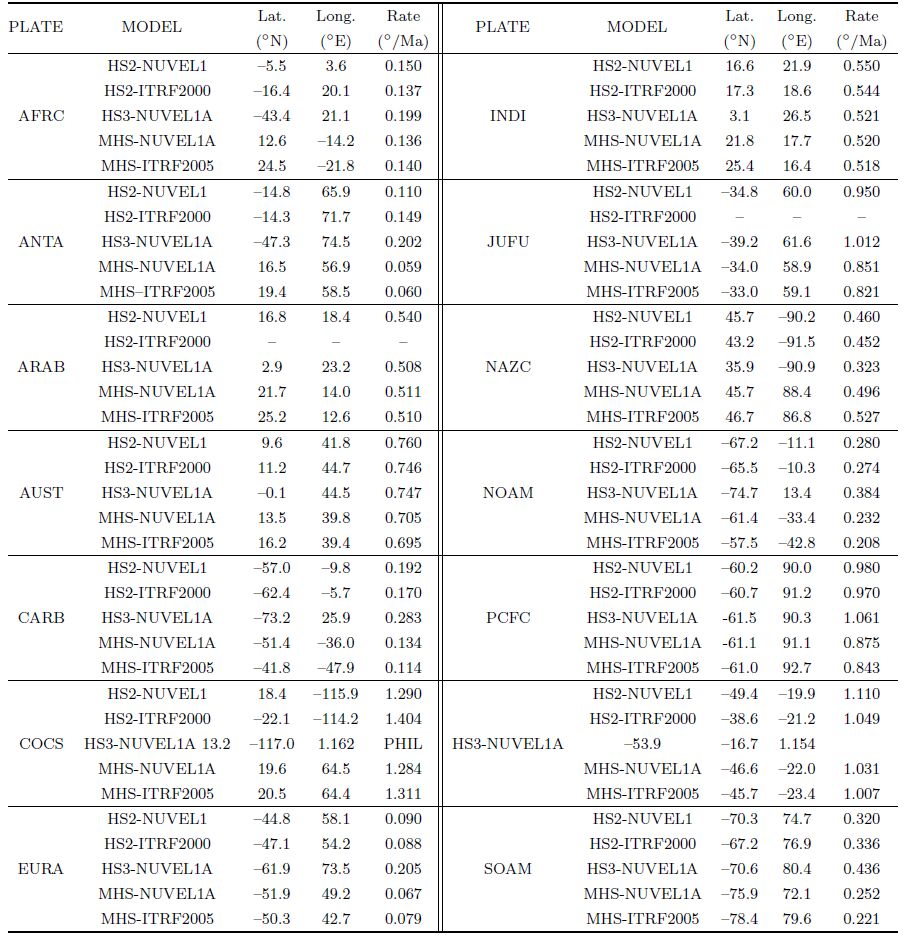
4 RESULTS AND ANALYSISComparison of several absolute plate motion models based on the hotspot reference frame is shown in Table2. Among them,the HS2-NUVEL1 model is from Gripp and Gordon[4]; HS2-ITRF2000[9] is an absolute plate motion model based on measured model ITRF2000VEL by Jin et al. using hotspot data from the HS2-NUVEL1 model; the HS3-NUVEL1A[5] model is based on the geological plate motion model NUVEL-1A and 11 trends and 2 rates; and the MHS-NUVEL1A and MHS-ITRF2005 models based on the medial-hotspot reference frame are established by this work using 33 azimuth (trends) and 11 rates on the basis of the geological model NUVEL-1A and measured model ITRF2005VEL,respectively.
| Table 2 Comparison of several absolute plate motion models based on hotspot reference frame |
Because the hotspot data used by HS2-ITRF2000 and HS2-NUVEL1 are same,the difference of which is that between ITRF2000VEL and NUVEL-1. On the whole,the absolute Euler vectors of the two models estimated,such as AUST,PHIL,NAZC and PCFC plates are relatively close,while that of NOAM,SOAM,AFRC and EURA plates differ much,even change in direction[9].
Similarly,MHS-ITRF2005 and MHS-NUVEL1A are also obtained from the same hotspot data. The difference is primarily that between ITRF2005VEL and NUVEL-1A models. On the whole,they have good consistency,small differences of Euler poles and rotation speeds for most plates. Only individual plates have differences. For example,in the CARB plate,the Euler poles and rotation rates estimated by the two models have some differences,especially the absolute value of the Euler pole position has an about 10° discrepancy.
While the HS3-NUVEL1A and MHS-NUVEL1A,the two absolute plate motion models are based different hotspot data,their constraint criteria are roughly same,i.e. through inverting their hotspot data respectively and making the relative velocity equal to the NUVEL-1A model. On the whole,there are obvious differences between the two models. Plate rotating speed in the HS3-NUVEL1A model is generally higher than that in the MHS-NUVEL1A: it is around 2%~17% with small difference among plates AUST,INDI,PHIL,JUFU and PCFC. In AFRC,CARB,NOAM and SOAM plates,this difference between two models is up to 30%~50%. Only the rotation rate of NAZC plate in the MHS-NUVEL1A model is higher than that in the HS3-NUVEL1A model by 35%,by about 10% in the COCS plate,and about 6% in the ARAB plate.
In addition,comparing the medial-hotspot reference datum MHS-ITRF2005 and MHS-NUVEL1A with models HS2-ITRF2000 and HS2-NUVEL1,the biggest difference lies in that the hotspot rate and trend data used in the MHS models are more than HS2,besides different constraint criteria applied. Hotspot rates are sensitive to the velocity of plate motion,while hotspot trends are sensitive to the plate movement direction. MHS-ITRF2005 and MHS-NUVEL1A use more hotspot trends data than HS2-ITRF2000 and HS2-NUVEL1. Therefore,some plates Euler pole positions are quite different in above models on the whole. For example,the AFRC plate Euler pole magnitude and direction are obviously different in the MHS and HS2 datum,longitude direction opposite in NAZC,latitude direction opposite in ANTA,longitude of Euler poles in NOAM and CARB differ much. In short,the hotspot trends data have obvious constraints on the Euler pole positions of plate motion.
From the results above we find that hotspot data have an important effect on the construction of hotspot reference datum,i.e. hotspot reference datum is determined by hotspots[10]. Therefore,collecting and collating the hotspot data more comprehensively and more precisely is a very important step. At the same time,eliminating some hotspot measurements with large errors,analyzing and processing the hotspot data,taking certain criterion to constrain hotspot relative movement,the hotspot reference datum established like this can be considered reliable to some extent.
5 WESTWARD DRIFT OF LITHOSPHEREFrom above results and analysis,the absolute plate motion model can be established by inversion of hotspot data,whose accuracy depends on the relative plate motion model chosen. While the establishment of the relative plate motion model is usually on the basis of No-Net-Rotation (NNR) criterion,the NNR reference itself is not fixed relative to the mean lithosphere,instead there exists the net rotation relative to the lithosphere,which is also known as the lithosphere drift. This drift magnitude can be calculated according to the plate stress model,also can be quantitatively estimated more accurately by the measured data of hotspot and plate motion model[6, 10, 17].
Assume that the vector of angular velocity in the hotspot reference datum of one plate is ωh,in NNR reference datum is ωn,the drift of lithosphere relative to the hotspot reference datum is ωnr,then the relationship of them is

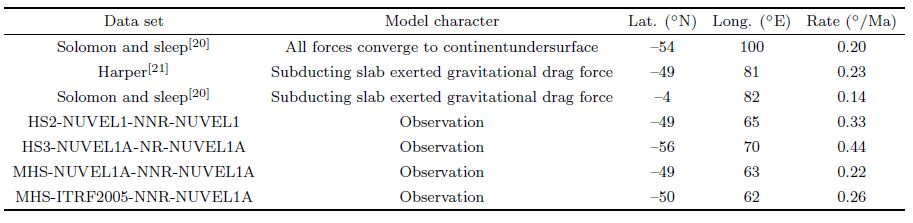
| Table 3 Comparison of the net rotation of the lithosphere in several models |
From the geophysical model MHS-NUVEL1A,there is a rotation rate of 0.2221°/Ma,with a pole of (48.7°S,62.7°E) in NNR-NUVEL1A,namely that the lithosphere has a same size of net rotation relative to the hotspot; which is similar to the first model taken by Solomon and Sleep[20] and Harper[21]. The latitudes of rotating polar are also very close,only the longitudes differ about 20°.
The MHS-ITRF2005 model based on measured hotspots is calculated by measured hotspot data and ITRF2005 velocity field,which shows that the NNR-NUVEL1A has a rotation of 0.2554°/Ma about 49.8°S,61.7°E,indicating the lithosphere has a net rotation of this magnitude. This result is awfully close to Harper (1986) and Argus and Gordon (1991) in rotation pole,while in rotation rate faster 11.5% than the Harper (1986) model and slower 21% than HS2-NUVEL1. It seems that the gravity drag torque exerted by the subducting slabs to the horizontal plate is the main source of plate force. At the same time,it also confirms the point of view of Richard[22]: the additional drag beneath continents is the main reason for the difference between the hotspot reference frame and the NNR reference frame. Of course,whether this view is correct or not also needs to be verified by more accurate hotspot data and measured plate motion.
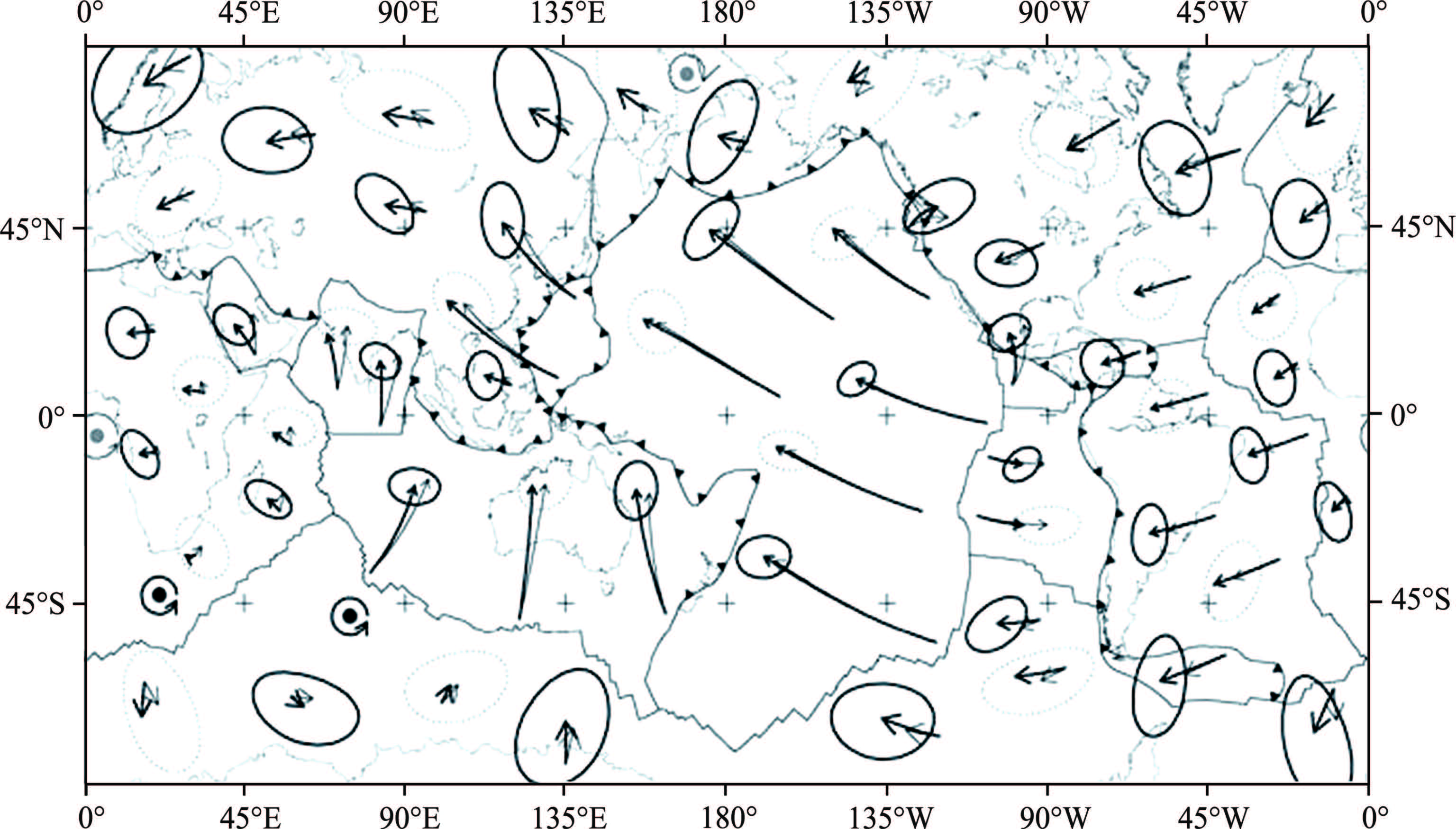
In addition,the westward drift of lithosphere has been studied by many scholars[4, 5, 18, 23, 24]. It can be seen from Fig.3 that the northern hemisphere lithospheric plate motion vector relative to the hotspot reference frame are all westward drift; while in the southern hemisphere,except the India ocean,the Atlantic and Africa are moving northward. The Pacific Ocean and the Atlantic ocean ridges,though dominated by the westward divergent movement on both sides,the motion vector on the ridge’s west is significantly greater than the east. Therefore,on the whole it can still be regarded as the westward drift in southern hemisphere. As westward drift amount of the northern hemisphere is larger than the southern hemisphere,there may be a north-south hemisphere relative torsion phenomenon near the equator. At present it has been generally accepted that the whole lithosphere is moving westward relative to the mantle[15].
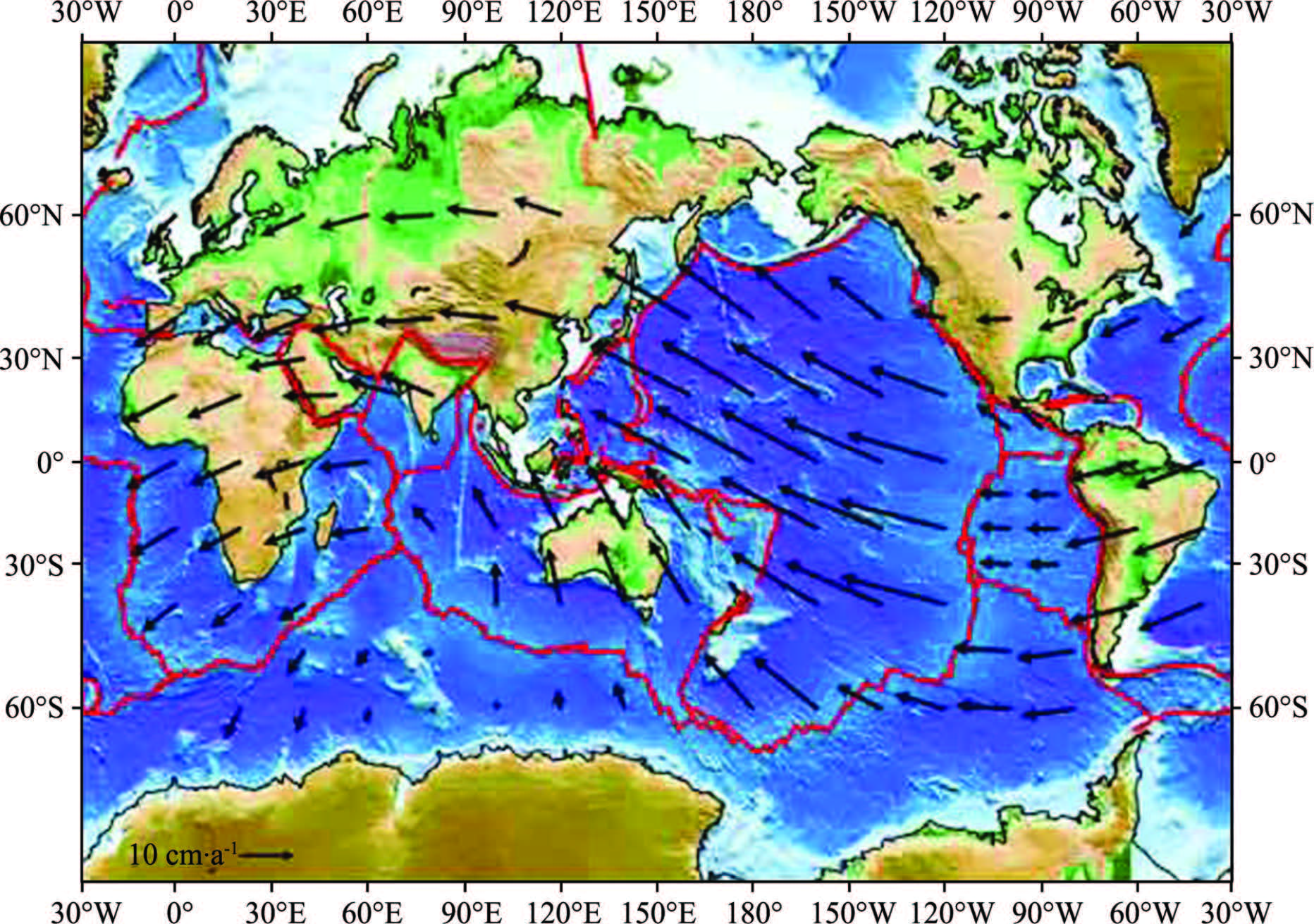
|
Fig.3 Present-day plate motions relative to the hotspot reference datum[24] |
Considering hotspot relative motion,a medial hotspot reference datum is put forward in this study by using more accurate hotspot data,and its constrain rule is given. Two absolute plate motion models designated as MHS-NUVEL1A and MHS-ITRF2005 are developed using a set of hotspot data globally distributed in conjunction with the plate motion models NNR-NUVEL1A and ITRF2005VEL,respectively,which are compared and analyzed with other absolute plate motion models based on the hotspot reference frame. The lithosphere’s net rotation is discussed and compared at last. The results show that the lithosphere has a net rotation relative to the hotspots of 0.26°/Ma,about a pole of 50°S,62°E with respect to the deep mantle,which is close to that from the plate forced model in direction,faster in the rate by 10%.
On the lithosphere westward drift and net rotation,there exist so many open basic questions,for example,what is the real velocity drift,how the drift and rotation are generated and so on. Because the large scale lithosphere mantle convection produces a stress field formed as a surface force which would cause deformation of the lithosphere itself,whether these questions are related with the inner lithosphere’s stress distribution[25] or not needs more measured data and more accurate models to clarify. With the rapid development of human cognitions and space observation technology,we have reasons to expect to solve these problems better in the future.
From above discussion,we find that the lithosphere’s net rotation is consistent in magnitude and direction with the hotspot reference frame and calculation according to the plate force model by geophysicists,which means that the MHS reference frame may be more in line with the actual situation. If we replace the current NNR reference frame IERS recommended by the new MHS reference frame,because of the net rotation between those two models,the velocity field to maintain the stability of the terrestrial reference frame (TRF) will have a big change,station displacement speed can reach 22 mm/a. In addition,the earth rotation parameter sequence will change remarkably. The NNR reference frame IERS recommended is defined as the horizontal motion reference frame of TRF,this is because the observation stations located on the earth’s crust,and this definition is self-consistent internally,which will not conflict with the previous results. If taking the new MHS reference frame instead,the earth rotation parameter sequence will not be continuous,and the terrestrial reference frame is not self-consistent. So,considering the history,status and user’s convenience,although the new MHS reference datum may be more accorded with the terrestrial reference system in theoretical definition,IERS still uses the NNR reference frame as the horizontal crustal movement reference frame. Because the hotspot reference frame can reflect more realistic situation of mantle convection,geophysicists studying mantle convection and plate motions favor to use the hotspot reference frame,while geodetic scientists tend to use the NNR reference frame.
ACKNOWLEDGMENTSSpecial thanks are extended Richard G. Gordon in Rice University and Wang Shi-Min in Missouri University for providing data and help to this study. We have benefited greatly from discussions with them. This work was supported by the National Natural Science Foundation of China (41074011) and State Key Laboratory of Geo-information Engineering Foundation of China (SKLGIE2013-M-1-4).
| [1] Minster J B, Jordan T H, Molnar P, et al. Numerical modelling of instantaneous plate tectonics. Royal Astronomical Society Geophysical Journal, 1974, 36(3): 541-576. |
| [2] Chase C. G. Plate kinematics: The Americas, East Africa, and the rest of the world. Earth Planet Sci. Lett., 1978, 37: 355-368. |
| [3] Minster J B, Jordan T H. Present-day plate motions. J. Geophys. Res., 1978, 83(B11): 5331-5354. |
| [4] Gripp A E, Gordon R G. Current plate velocities relative to the hotspots incorporating the NUVEL-1 global plate motion model. Geophys. Res. Lett., 1990, 17(8): 1109-1112. |
| [5] Gripp A E, Gordon R G. Young tracks of hotspots and current plate velocities. Geophysical Journal International, 2002, 150(2): 321-361. |
| [6] Sun F P. Research of Current Crustal Motions Based Upon Space Geodetic Techniques[Ph.D.thesis] (in Chinese). Shanghai: Shanghai Observatory, Chinese Academy of Sciences, 1994. |
| [7] Wessel P, Kroenke L. A geometric technique for relocating hotspots and refining absolute plate motions. Nature, 1997, 387(6631): 365-369. |
| [8] Wang S M, Wang R. Current plate velocities relative to hotspots: Implications for hotspot motion, mantle viscosity and global reference frame. Earth and Planetary Science Letters, 2001, 189(3-4): 33-140, doi:10.1016/S0012-821X (01)00351-X. |
| [9] Jin S G, Zhu W Y. Comparison and establishment of three absolute plate motion models. Annals of Shanghai Observatory Academa Sinica (in Chinese), 2002, (23): 21-27. |
| [10] Wei Z Q. Current absolute plate motions. Journal of Earth Sciences and Environment (in Chinese), 2009, 31(4): 331-343. |
| [11] Molnar P, Stock J. Relative motions of hotspots in the Pacific, Atlantic and Indian Oceans since late Cretaceous time. Nature, 1987, 327(6123): 587-591. |
| [12] Steinberger B. Motion of Hotspots and Changes of the Earth Rotation Axis Caused by a Convecting Mantle. Harvard: Harvard University, 1996. |
| [13] Divenere V, Kent D V. Are the Pacific and Indo-Atlantic hotspots fixed? Testing the plate circuit through Antarctica. Earth and Planetary Science Letters, 1999, 170(1-2): 105-117. |
| [14] Tarduno J A, Ducan R A, Scholl D W, et al. The Emperor Seamounts: Southward motion of the Hawaiian hotspot plume in Earth's mantle. Science, 2003, 301(5636): 1064-1069. |
| [15] Wang S M, Liu M. Moving hotspots or reorganized plates. Geology, 2006, 34(6): 465-468. |
| [16] http://baike.baidu.com/view/381613.htm. Plate motion. Baiduencyclopedia, 2012. |
| [17] Zhu X H, Sun F P, Wang R. Study on absolute plate motion based on different reference frame//5th Doctoral Proceedings of Surveying and Mapping Institute (in Chinese). Zhengzhou: Information and Engineering University, 2010: 85-89. |
| [18] Argus D F, Gordon R G. No-Net-Rotation model of current plate velocities incorporating plate motion model NUVEL-1. Geophys. Res. Lett., 1991, 18(11): 2039-2042. |
| [19] Zhu X H, Sun F P, Wang R. Global plate motion models based on ITRF2005. Progress in Geophysics (in Chinese), 2009, 24(3): 859-865. |
| [20] Solomon S C, Sleep N H. Some simple physical models for absolute plate motions. J. Geophys. Res., 1974, 79(17): 2557-2567. |
| [21] Harper J F. Mantle flow and plate motions. Geophys. J. Roy. Astron. Soc., 1986, 87(1): 155-171. |
| [22] Richard Y, Doglioni C, Sbedini R. Differential rotation between lithosphere and mantle: a consequence of lateral mantle viscosity variations. J. Geophys. Res., 1991, 96(B5): 8407-8415. |
| [23] DeMets C, Gordon R G, Argus D F, et al. Effect of recent revisions to the geomagnetic reversal time scale on estimates of current plate motions. Geophys. Res. Lett., 1994, 21(20): 2191-2194. |
| [24] Cuffaro M, Doglioni C. Global kinematics in deep versus shallow hotspot reference frame. Geological Society of America Special Papers, 2007, 430: 359-374. |
| [25] Wang J, Ye Z R. Effects of mantle flow on generation and distribution of global lithospheric stress field. Chinese J. Geophys. (in Chinese), 2005, 48(3): 584-590. |
 2013, Vol. 56
2013, Vol. 56