2. China Research Institute of Radiowave Propagation, Qingdao 266107, China
HF radio waves propagating through ionosphere have two characteristic modes, one is right hand circular polarized wave (X-mode wave for short), and the other is left hand circular polarized wave (O-mode wave for short). The theoretical[1, 2] and experimental results[3, 4, 5, 6] reported previously show that when the plasma is heated by O-mode electromagnetic waves, the processes of resonance and linear mode conversion occur between the upper hybrid resonance and reflection level of the heating waves, which lead to significant disturbances of electron temperature and density. Since X-mode waves are reflected below the plasma-resonance level, their effect on the ionosphere was considered to be limited to Ohmic heating of the plasma, so it was previously assumed that all these effects cause the generation of only a fairly weak artificial ionosphere turbulence. Therefore, they have received little attention of researchers and have not been analyzed in detail for a long time.
Since the 1990s, with the improvement of ionospheric heating device’s performance, high-power radiobeaming technology with X-mode has drawn continuous concerns in ionospheric heating experiments. The experiments[7] conducted in the period 1995-1997 with the “Sura” heating facility and additional ionospheric plasma heating by high-power X-mode waves show that such a heating significantly weakens the artificial turbulence excited by the high-power O-mode waves, particularly decreases the transverse scale of field-aligned irregularities. In these experiments, the heating facility transmits high-power X-mode waves and high-power O-mode waves with the same reflection height at the same time by satisfying the condition fHX = fHO +0.5fce, where fHO and fHX are heating frequency of O-mode and X-mode, respectively, and fce is electron gyrofrequency. Later, these phenomena have also been found in the experiments[8] conducted with the heating facility of HAARP (High Frequency Active Auroral Research Program).
Recently, the theoretical studies of ionosphere heating with high-power HF X-mode waves are focused on ELF/VLF radiation by modulated heating of the lower ionosphere[9, 10, 11, 12], whereas heating of the upper ionosphere using high-power X-mode waves is dominated by experiments. The experiments conducted by Lofas and Gustavsson[13, 14] indicate that electron temperature increases greatly in a large latitude interval, but there is no significant electron density modulation and ion temperature change. They have explained these experiments phenomena (electron temperature variation in the period of heating-on and heating-off and at different power levels) in theory. Considering these experiments and theoretical explanations, a theoretical model of under-dense heating by X-mode waves is constructed based on mechanisms of both electron cooling and heating in the ionosphere, and this model is tested by comparison to the known experimental results. Furthermore, we use this model to analyze the influences of heating parameters and ambient ionosphere on the heating effects.
2 THEORETICALMODEL OF UNDER-DENSE HEATING BY POWERFUL X-MODEWAVESWhen a high-power HF radio wave passing through the ionosphere, there are Ohmic heating due to nonzero HF-conductivity and associated collisional damping of the HF-waves along the entire wave propagation path. The Ohmic effect has been studied for over-dense conditions, in which most of the energy deposition in the F-region occurs just below the reflection altitude where heat is conducted up and down along the magnetic field. Due to a large number of possible wave-plasma processes acting in the vicinity of the reflection altitude, it is difficult to accurately separate the effects of Ohmic heating from the effects of nonlinear and resonant processes, unless one keeps the ERP low enough to make sure the peak E-field amplitude is below the threshold of the nonlinear processes. When transmitting X-mode waves at frequencies above the critical frequency fXF2, there is no standing wave and only limited beam swelling is present. Furthermore there is no altitude where the pump frequency is equal to the frequency of upper-hybrid fUH, or the plasma frequency fp, so no resonances processes are excited. Thus under-dense heating makes it possible to study the effects of Ohmic heating with large amplitude E-fields in a large altitude range. The experiments[8, 9] also indicate that there is no significant electron density modulation and ion temperature change during the under-dense heating process by X-mode waves. Based on these features, we only consider electron energy equation[5, 15, 16, 17]:
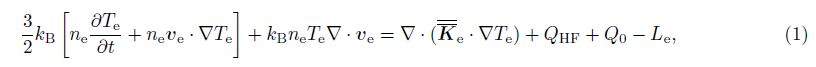
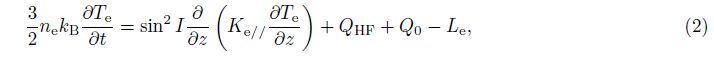

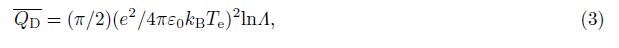
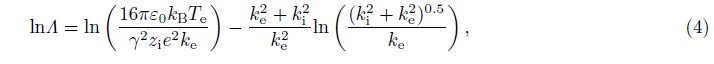

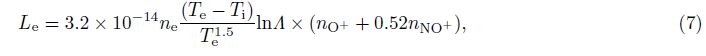
For under-dense conditions, HF pump wave energy deposition QHF contains Ohmic heating only, and which is the time average of the product between the pump wave electrical field and the induced current, which can be calculated[2] by



Due to heat convection up and down along the magnetic field, the relation between N±(z), σ±(z) and ε±(z) is[2]

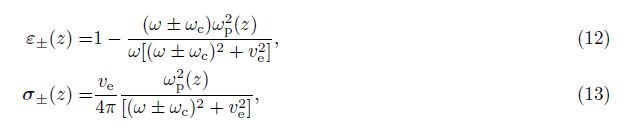
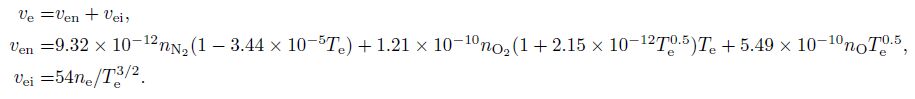
Based on known experimental results[6] and physical simulation models[1], in our calculations, with electron temperature being constant at the lower ionosphere border and the electron temperature gradient being constant at the upper ionosphere border, the time step dt=5 ms and the space step is dh = (1/ sin I) km, the pump wave absorption loss in lower ionosphere is about 4 dB, electron and ion temperatures in the background ionosphere are specified with the IRI-2012 model, and the atmosphere density and temperature are derived from the MSIS-90 model.
According to the above expressions (8)-(13), with the same heating parameters, the energy deposition profiles of O-mode and X-mode caused by under-dense heating are shown in Fig.1.

|
Fig.1 Comparison of energy deposition profiles of O-mode and X-mode caused by under-dense heating |
Comparison of energy deposition profiles of Omode and X-mode (Fig.1) indicates that the energy deposition of X-mode is about four times that of O-mode under the same conditions, so the electron temperature disturbance caused by under-dense heating with Xmode is considerably larger than that of O-mode. This is the reason why X-mode HF waves are commonly used in under-dense heating experiments.
3 ANALYSIS OF SIMULATION RESULTS 3.1 Comparison of Simulations with Experimental ResultsIn the first under-dense heating experiment by high-power X-mode waves with the EISCAT heating facility, Lofas et al.[13] observed that electron temperature was enhanced in the whole ionosphere F region and the maximum electron temperature variation was 300~400 K (Fig.2). In their experiment, heater radiated X-mode waves at frequency fHF=4.04 MHz with ERP=180 MW. During the experimental period, f0F2 varied from 2.1 MHz to 3.1 MHz, corresponding to fXF2 ranging from 3.0 MHz to 4.01 MHz. In order to verify the numerical model described in this paper, we use simulation heating parameters and background ionosphere parameters (f0F2=2.3 MHz, fXF2=3.1 MHz) same as those in the heating experiments. The comparison of simulation and experiment results is shown in Fig.2.
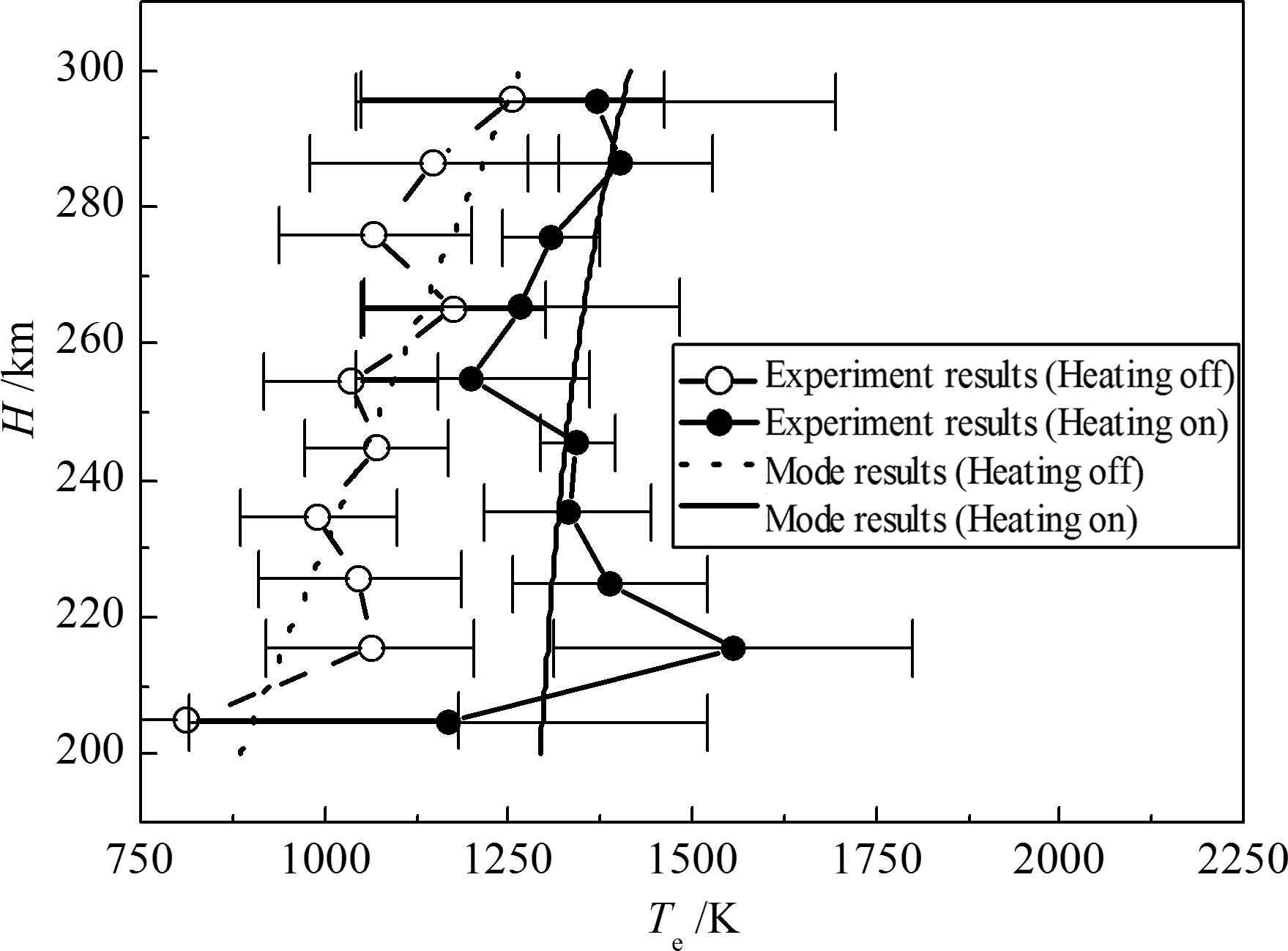
|
Fig.2 Comparison of simulation and experiment results |
It is found that the results of simulation are largely in agreement with that from experiment measurements, though with some differences. It may be that the experimental results presented in Fig.2 are the average values of electron temperature in a certain experimental period, and the relative error ranges of electron temperature in the period are also given. While the simulation results are within the error range given by experimental results. Meanwhile Fig.3 shows that the variation of electron temperature is about 400 K (40% relative increment) at 215 km altitude, the relative increment decreases with altitudes, and the simulation results are in accordance with the experimental results. In conclusion, the theoretical methods are validated and can be used in simulation of under-dense heating by X-mode waves.
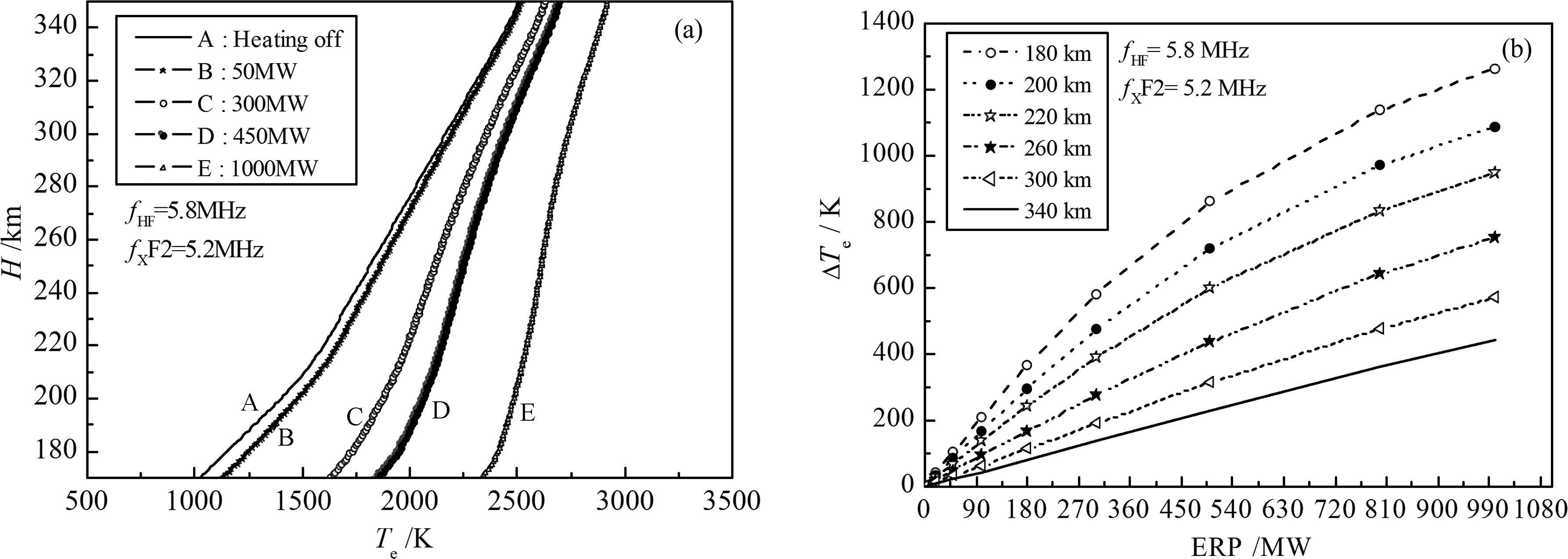
|
Fig.3 Influences of ERP on heating effects by X-mode (a) Height dependence of the electron temperature for different ERP; (b) Electronic temperature increase as a function of ERP. |
Influences of ERP on heating effects by X-mode are plotted in Fig.3. In our simulation, the heating place is Troms$\phi $, the X-mode critical frequency is 5.2 MHz, and pump frequency is 5.8 MHz.
As illustrated in Fig.3 the electron temperature variations at different altitudes rise as ERP increases but not in a linear relationship, e.g. electron temperature enhancements at 220 km altitude are 4%, 38% and 60%, respectively when ERP equals 50 MW, 500 MW and 1000 MW, respectively. This is because a larger ERP leads to more energy transfered into the ionosphere and thus causes a larger electron temperature disturbance. If the original ERP is low, an increase in ERP will lead to significant enhancement of the electron temperature, and there is a larger value at the lower altitude. For example, the electron temperature enhancement at 200 km altitude is about 300 K, and at 300 km altitude is about 100 K with an ERP of 180 MW, which are in accordance with the experimental results[9].
The background ionosphere is controlled by the solar activity and its critical frequencies vary in a large range in a day, especially during high solar activity. In order to investigate the influence of the ratio of fHF to fXF2 on heating effects and compare results under different pump frequency fHF, we keep fXF2 as a constant and change fHF. The heating effects at Troms$\phi $ with ERP of 300 MW are simulated. The results are plotted in Fig.4.
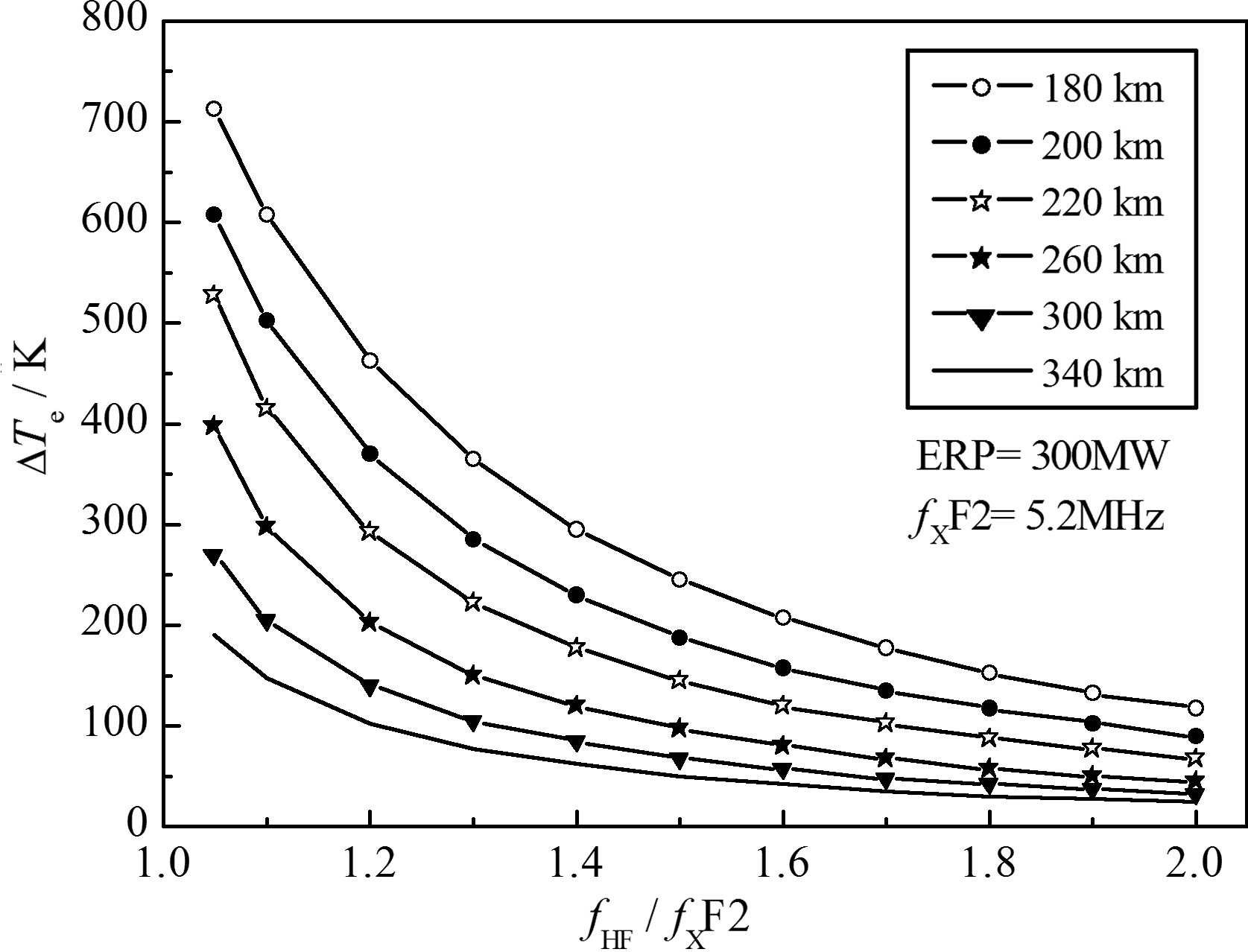
|
Fig.4 Influences of the ratio of fHF to f0F2 on electron temperature with a constant fHF and different values of f0F2 |
We can see from Fig.4, as fHF increases (hence the ratio fHF/fXF2 increases), electron temperature enhancements decrease. Furthermore electron temperature enhancements rapidly decrease as fHF/fXF2 approaches to 1, but which dicrease slowly as fHF/fXF2 is larger. The reason is that the heating effects are determined jointly with the collisional and transport processes under under-dense heating conditions, so they influence heating effects together. Whereas the ionospheric absorption loss decreases with the pump frequency increasing, thus there is less energy transferred into ionosphere, which results in a decrease in the electron temperature enhancement eventually.
3.3 Influences of Background Parameters on Heating EffectsComparison of Fig.2 and Fig.3 indicates that there are different electron temperature disturbances under the same ERP (180 MW) conditions and the same altitude 215 km, the former is about 400 K while the latter is about 300 K. The reason is that background ionosphere parameters (the electron density and temperature) are different in both cases.
The heating effects at Troms$\phi $ with ERP=300 MW and fXF2=5.2 MHz are simulated with different background electron density and temperature, and the results are plotted in Fig.5 and Fig.6, respectively. For different background electron densities and resultant different critical frequencies, in order to satisfy the same heating conditions, we take the same ERP and the same fHF/fXF2(=1.05). For different background electron temperatures, we take a pump frequency fHF=5.4 MHz.
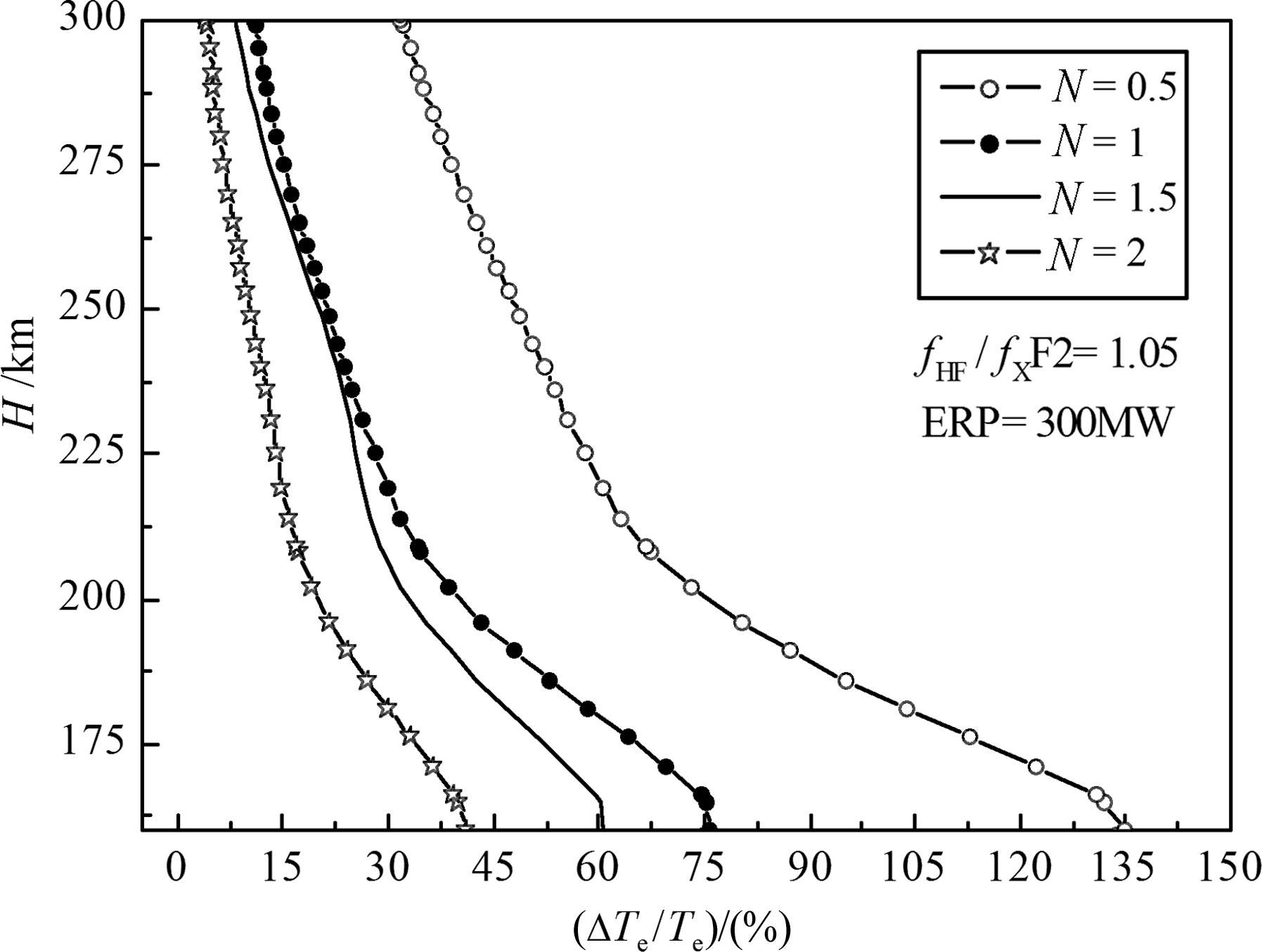
|
Fig.5 Influences of background electron density on heating effects |

|
Fig.6 Influences of background electron temperature on heating effects |
The parameter N in Fig.5 refers to the ratio of the background electron density to the reference electron density (N = 1) under different conditions. In the actual situation, the maximum value of N is 2 in our simulations. The calculating results show that the relative variation of the electron temperature increases from about 75% to 135% with N=0.5, but decreases from about 75% to 40% with N=2. It follows that a lower background density can leads to a better heating effect under an assumption of equivalent conditions. The parameter n in Fig.6 refers to the ratio of background electron temperature to reference electron temperature (n=1) under different conditions. For practical purposes, the maximum value of n is 3 in our simulations. The results showed that the relative variation of electron temperature increases from about 78% to 140% with n = 0.5, but decreases from about 78% to 3% with n = 3. It follows that a lower background temperature can leads to a better heating effect under an assumption of equivalent conditions.
Therefore, a larger electron density and a higher electron temperature of the background ionospheric F region leads to a weaker heating effect. The reason is that the energy absorption term Q0 and energy loss term Le increase with the electron density and temperature, but ERP is constant, so the electron temperature disturbance caused by heating is less. And when the background electron density and temperature are higher, their gradients are larger simultaneously; in this case, the electron temperature disturbance is smaller. So a better heating effect may be obtained when performing the heating experiments at night with a low electron density and temperature in the background ionosphere compared to the daytime.
3.4 Comparison of Simulation Results at Low and High LatitudesIn general the geomagnetic dips directly influence the magnitude of the heat conduction term (the second term on the right side of Eq.(2)), and the geomagnetic dips are different at different geographical locations. Consequently different heating effects are present at low and high latitudes. The profiles of background electron temperature and relative variation of electron temperature under equivalent conditions with ERP of 300 MW and fHF/fXF2=1.05 at Troms$\phi $, Qingdao, Guilin, and Arecibo are respectively plotted in Fig.7.
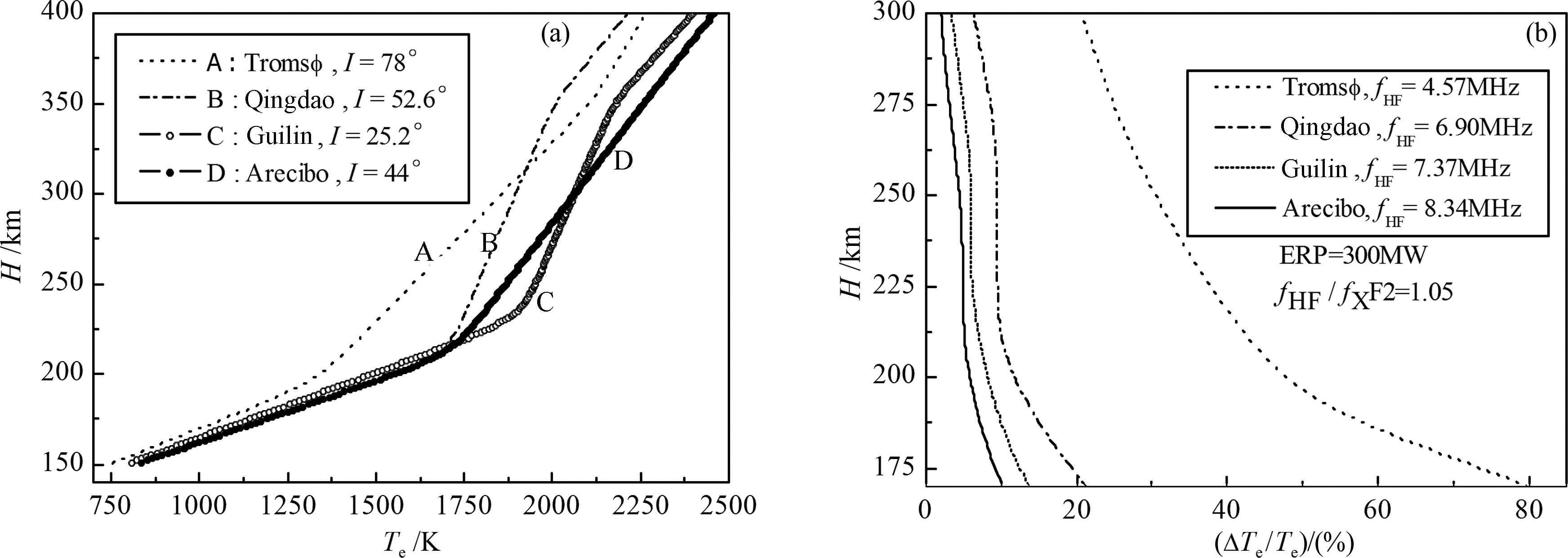
|
Fig.7 Heating effects at different localities (a) Background electron temperature; (b) Relative variation profiles of electron temperature caused by heating. |
Figure7a shows that the background electron temperatures are different in different regions, which are lower at high latitude (Troms$\phi $) than that at middle-low latitudes, but no so different in Guilin and Arecibo. The results in Fig.7b indicate that the heating effects at Troms$\phi $ is better than other regions under an assumption of equivalent conditions. Moreover, it must be pointed out that the critical frequency in Troms$\phi $ is the lowest of all, i.e. the least electron density; and the heating effects at Guilin is little stronger than Arecibo. This is because background electron density in Guilin is less than Arecibo. background electron density in Qingdao is medium, so its heating effect is also moderate. In conclusion, the under-dense heating effects caused by X-mode at high latitudes are better than middle-low latitudes.
4 CONCLUSIONS AND DISCUSSIONIn this paper, considering the features of under-dense heating ionosphere by high-power HF X-mode waves, and based on mechanisms of both electron cooling and heating in the ionosphere, a theoretical simulation model of under-dense heating by X-mode waves is constructed. And this model is verified by comparison to the experimental results. Furthermore, the analysis has been carried out on the influences of the background ionosphere parameters and heating parameters on heating effects.
(1) The heating effects are enhanced if the ERP increases. For example, under certain conditions, the electron temperature enhancement is about 4% with ERP of 50 MW, and 60% with ERP of 1000 MW.
(2) In the certain frequency intervals, the heating effects weaken with pump frequency increasing, Furthermore electron temperature enhancement rapidly decrease as fHF/fXF2 approaches to 1, but which dicrease slowly as fHF/fXF2 is larger.
(3) Under an assumption of equivalent conditions, a smaller electron density and lower electron temperature of the background ionospheric F region lead to a better ionospheric heating effect. And the heating effects at heigh latitudes are better than that at lower latitudes.
Theoretical and numerical modeling constructed in the paper can be used to estimate some relevant experimental results caused by under-dense heating by X-mode, and can also utilized as a reference to select the proper heating parameters. According to the simulation results in the paper, several measures can be taken to improve heating effects. For instance, we may increase the ERP of the heater to increase the incident power density of the heated volume, or select the proper pump frequency, or choose matched times with low ionosphere background and density (at dawn and dusk) to carry out experiments.
Under the under-dense heating conditions, the heating effects mainly occur in the region close to the reflection altitude, and it is difficult to accurately separate the effects of Ohmic heating from the effects of nonlinear and resonant processes, unless one keeps the ERP low enough to make sure the peak E-field amplitude is below the threshold for the nonlinear processes. So it is important to study the effect of Ohmic heating with large amplitude E-fields in a large altitude range by under-dense heating by X-mode. Moreover, it does not change background electron density, only increases background electron temperature, and this can be used for pre-heating the plasma to different initial temperatures for experiments investigating the temperature dependence of onset characteristics of resonant processes. For example, the precondition heating of the ionosphere by X mode waves may be performed to enhance the background electron temperature and thus increase the ratio of the electron and ion temperature, which may effectively enhance the generation of SEE in the following over-dense heating by O-mode experiments[22].
On the other hand, when the heater frequency is above the O-mode critical frequency but comparable with the X-mode critical frequency[23], the generation of the X-mode AFAIs (artificial field-aligned irregularities) is accompanied by electron temperatures up to 50% above the background level, but up to 33% by O-mode heating under the same conditions. Meanwhile, electron density increases greatly in a larger altitude interval. However, now there is no appropriate theory to explain this experimental phenomenon. Firstly, it satisfies the features of Ohmic heating (electron temperature enhancement in a larger altitude interval), and secondly it also meets characteristics of resonance heating (electron density increase). So this is a complex heating process with multiple mechanisms, and needs to develop a theory consistent with the process to direct the way of future investigations.
| [1] Hansen J D, Morales G J, Maggs J E. Large-scale HF-induced ionospheric modifications:theory and modeling. J. Geophys. Res., 1992, 97(A11):17019-17032. |
| [2] Shoucri M M, Morales G J, Maggs J E. Ohmic heating of the polar F region by HF pulses. J. Geophys. Res., 1984, 89(A5):2907-2917. |
| [3] Utlaut W F, Violette E J. A summary of vertical incidence radio observations of ionospheric modification. Radio Sci., 1974, 9(11):895-903. |
| [4] Inhester B, Das A C, Fejer J A. Generation of small-scale field-aligned irregularities in ionospheric heating experiments. J. Geophys. Res., 86(A11):9101-9106. |
| [5] Kuo S P, Lee M C. On the parametric excitation of plasma modes at upper hybrid resonance. Phys. Lett. A, 1982, 91(9):444-446. |
| [6] Hansen J D, Morales G J, Duncan L M, et al. Large-scale HF-induced ionospheric modifications-experiments. J. Geophys. Res., 1992, 97(A1):113-122. |
| [7] Frolov V L, Kagan L M, Sergeev E N, et al. Ionospheric observations of F region artificial plasma turbulence, modified by powerful X-mode radio waves. J. Geophys. Res., 1999, 104(A6):12695-12704. |
| [8] Hysell D L, Nossa E, McCarrick M. X-mode suppression of artificial E region field-aligned plasma density irregularities. Radio Sci., 2011, 46(2), RS2010, doi:10.1029/2010RS004551. |
| [9] Wang F, Zhao Z Y, Zhang Y N. Numerical modeling of ionospheric current artificial modulation at low latitude. Chinese J. Geophys. (in Chinese), 2009, 52(4):887-894, doi:10.3969/j.issn.0001-5733.2009.04.004. |
| [10] Chang S S, Zhao Z Y,Wang F. The downward ELF/VLF waves radiation excited by ionospheric artificial modulation. Chinese J. Geophys. (in Chinese), 2011, 54(10):2458-2467, doi:10.3969/j.issn.0001-5733.2011.10.003. |
| [11] Wang F, Zhao Z Y, Chang S S, et al. Radiation of ELF waves by ionospheric artificial modulation into a stratified ionosphere. Chinese J. Geophys. (in Chinese), 2012, 55(7):2167-2176, doi:10.6038/j.issn.0001-5733.2012.07.003. |
| [12] Stubbe P, Kopha H. Modulation of the polar electrojet by powerful HF waves. J. Geophys. Res., 1977, 82(16):2319-2325. |
| [13] Lofas H, Ivchenko N, Gustavsson B, et al. F-region electron heating by X-mode radiowaves in underdense conditions. Ann. Geophys., 2009, 27(6):2585-2592. |
| [14] Gustavsson B, Rietveld M T, Ivchenko N V, et al. Rise and fall of electron temperatures:Ohmic heating of ionospheric electrons from underdense HF radio wave pumping. J. Geophys. Res., 2010, 115(A12), A12332, doi:10.1029/2010JA15873. |
| [15] Meltz G L, Holway Jr H, Tomljanovich N M, et al. Ionospheric heating by powerful radio waves. Radio Sci., 1974, 9(11), 1049-1063. |
| [16] Deng F, Zhao Z Y, Zhou C, et al. Research of ionospheric instability excited in mid and low latitudes HF heating. Chinese J. Geophys. (in Chinese), 2010, 53(1):10-21, doi:10.3969/j.issn.0001-5733.2010.01.002. |
| [17] Wang Z G, Xu B, Xu Z W, et al. A comparison of numerical simulation and measurements during ionospheric heating. Chinese J. Geophys. (in Chinese), 2012, 55(3):751-759, doi:10.6038/j.issn.0001-5733.2012.03.004. |
| [18] Ni B B, Zhao Z Y, Xiang W, et al. Numerical modeling of ionospheric modificiation with powerful HF pump waves. Chinese Journal of Radio Science (in Chinese), 2004, 19(3):274-289. |
| [19] Schunk R W, Nagy A F. Electron temperatures in the F Region of the ionosphere:theory and observations. Rev. Geophys., 1978, 16(3):355-399. |
| [20] Bilitza D. International reference ionosphere-status 1995/96. Adv. Space. Res., 1997, 20(9):1751-1754. |
| [21] Banks P M, Kockarts G. Aeronomy, Part A and Part B. New York:Academic Press, 1973. |
| [22] Hussein A A, Scales W A. Simulation studies of parametric decay processes associated with ionospheric stimulated radiation. Radio Sci., 1997, 32(5):2099-2107. |
| [23] Blagoveshchenskaya N F, Borisova T D, Yeoman T K, et al. Artificial small-scale field-aligned irregularities in the high latitude F region of the ionosphere induced by an X-mode HF heater wave. Geophys. Res. Lett., 2011, 38(8):L08802, doi:10.1029/2011GL046724. |
 2013, Vol. 56
2013, Vol. 56

