2. 中山大学 管理学院,广东 广州 510275;
3. 广东金融学院 工商管理学院,广东 广州 510521
2. School of Business, Sun Yat-Sen University, Guangzhou 510275, China;
3. School of Business Administration, Guangdong University of Finance, Guangzhou 510521, China
随着社会的发展和进步,各个领域的关注焦点已经由早期的物质领域转向人的精神领域。正如2017年诺贝尔经济学奖获得者Richard Thaler提出的“心理账户”理论和“公平”理论一样,管理实践家认为在行为管理中人们也越来越多地关注自身的公平问题[1]。而公平的衡量则是通过与参照点相互比较判断得出,而参照点的设定由早期的固定点逐步转变为相对点[2]。在网络链条中,各节点成员往往将其他成员作为参照点,由此可知网络节点成员的决策不仅考虑自身收益最大化,还会考虑其他成员的收益:当其他成员的收益大于自身收益时,会产生厌恶心理,从而影响合作的态度;当其他成员收益小于自身收益时,会产生同情心理,甚至会牺牲自身利益来换取其他成员的公平[3]。这些非理性行为将影响网络中各节点成员的决策。
目前已有不少学者将这种非理性的偏好应用在商业、经济学和营销学等多个领域。其中Cui等[4]认为在营销渠道成员合作过程中应充分考虑成员的公平偏好,这有利于维持渠道的稳定。McCarthy[5]的研究表明供应商应该考虑的首要问题是渠道的公平性。Cox等[6]认为比起营销渠道,在拥有多成员的供应链中公平偏好的应用更加重要。Cachon等[7]认为通过成员之间的公平偏好协调供应链,可以实现供应链均衡,即没有成员愿意离开链条来打破这种均衡。
后续的学者多从批发价格契约角度分析公平偏好对供应链的影响。Cui等[4]在线性需求条件下构建了公平关切影响制造商和零售商之间契约交易的模型。杜少甫等[8]以Nash谈判解作为公平关切的参照点,研究两层供应链中供应商与零售商都有公平关切时的报童问题。Du等[9]进一步借用Nash讨价还价博弈思想构建相对公平关切效用体系,探讨了供应链中各成员的公平关切行为对系统决策与协调的影响。何丽红等[10]探讨了零售商公平关切对双渠道供应链合作广告决策的影响。舒亚东等[11]分析了公平关切程度对逆向供应链定价决策的影响。
马利军等[12]研究了幂函数需求形式下具有公平偏好的供应链的协调问题。李媛等[13]在总量限制交易和碳排放权交易为背景下研究了供应链成员关注公平偏好时批发价格契约对低碳化供应链协调性的影响。浦徐进等[14]等考虑市场需求为随机的两级供应链,研究了零售商的风险规避和公平关切特性对供应链运作的影响。李绩才等[15]考虑供应商与制造商均具有公平关切,分析了公平关切和供应链博弈结构对产品质量与零售定价优化决策的影响。赵婉鹛等[16]考虑供应商同时具有损失规避和公平关切行为,分析了多种行为偏好对运作的影响。王垒等[17]考虑横向公平的双渠道销售闭环供应链定价策略与协调研究。周艳菊等[18]从相对公平偏好的角度分析了广告合作契约及广告合作-减排成本分担契约对低碳供应链最优决策及协调性的影响。范如国等[19]对比研究了低碳企业具有公平偏好时,消费者低碳产品购买倾向和政府补贴对供应链企业决策的影响。
以上研究多是在考虑公平偏好的前提下,通过批发价格对供应链进行协调。对成员之间的合作效率未做明确的对比分析。王能民等[20]对供应链协调机制的选择与供应链绩效之间的关系研究作了综述,但涉及到具体函数的供应链协调与合作效率的分析较少。孙彩虹等[21]研究了5种价格需求函数下供应链成员合作动力差异问题,但未考虑随机需求下成员之间的公平偏好性。牟能冶[22]鉴于消费者公平关切和零售商信用下,考虑一个生产商通过2个电子零售商基于不同的契约售销产品的问题。覃燕红等[23]在指数函数需求下对零售商公平偏好信息动态演进进行了研究,并与线性需求条件下的研究结论进行了对比分析,但未考虑零售商、制造商同时公平偏好时的合作效率的对比分析问题。
因此,本文在考虑公平关切的条件下构建了批发价契约下的二级供应链,制造商和零售商之间进行Stackelberg博弈。通过对比随机需求函数下供应链的集中决策与公平关切下的分散决策,分别探讨仅零售商具有公平关切、仅制造商具有公平关切、制造商和零售商都具有公平关切3种情况下的供应链合作效率问题。
1 基础模型与假设本文研究基于单个制造商为主导,单个零售商为随从的两层供应链,以供应链合作效率作为研究对象,各变量的含义如下:
零售商面临的需求为线性随机函数D,
假设商品无滞销,产品销售量为
零售商的利润函数为
| $\qquad{\pi _{\rm{r}}} = (F - \alpha p)(p - w){\text{;}}$ | (1) |
制造商的利润函数为
| $\qquad{\pi _{\rm{m}}} = (F - \alpha p)(w - c){\text{;}}$ | (2) |
零售商的期望收益函数为
| $\qquad{\varPi _{\rm{r}}}(p) = E({\pi _{\rm{r}}}) = (f - \alpha p)(p - w){\text{;}}$ | (3) |
制造商的期望收益函数为
| $\qquad{\varPi _{\rm{m}}}(w) = E({\pi _{\rm{m}}}) = (f - \alpha p)(w - c){\text{。}}$ | (4) |
制造商和零售商构成一个虚拟体,该虚拟体做出使得虚拟体利益最大的决策,视为一个决策主体,集中决策下整条供应链的期望利润为
| $\qquad{\varPi _{{\rm{sc}}}}(p) = E({\pi _{{\rm{sc}}}}) = (f - \alpha p)(p - c){\text{。}}$ | (5) |
对
| $\qquad\frac{{\partial {\varPi _{{\rm{sc}}}}(p)}}{{\partial p}} = (\alpha c + f - 2\alpha p){\text{,}}$ |
| $\qquad\frac{{{\partial ^2}{\varPi _{{\rm{sc}}}}(p)}}{{\partial {p^2}}} = - 2\alpha{\text{<}} 0{\text{。}}$ |
由上式二阶导数小于零可以看出,式(5)为严格的凸函数,令一阶导数为零可得系统的最优零售价格
| $ \qquad{p^ * } = \frac{{f + \alpha c}}{{2\alpha }},{q^ * } = \frac{{f - \alpha c}}{2}{\text{。}} $ |
将
| $\qquad{\varPi _{{\rm{sc}}}}({p^ * }) = \frac{{{{(f - \alpha c)}^2}}}{{4\alpha }}{\text{。}}$ | (6) |
分散决策下,制造商是Stackelberg博弈的领导者,零售商是Stackelberg博弈的跟随者。可求得制造商的最优批发价为
| $ \qquad w_0^ * = \frac{{f + \alpha c}}{{2\alpha }},p_0^ * = \frac{{3f + \alpha c}}{{4\alpha }},q_0^ * = \frac{{f - \alpha c}}{4}{\text{。}} $ |
将
| $\qquad\varPi _{\rm{r}}(p_0^ * ) = \frac{{{{(f - \alpha c)}^2}}}{{16\alpha }}{\text{,}}$ |
| $\qquad\varPi _{\rm{m}}(w_0^ * ) = \frac{{{{(f - \alpha c)}^2}}}{{8\alpha }}{\text{,}}$ |
| $\qquad\varPi _{{\rm{sc}}}(p_0^ * ) = \frac{{3{{(f - \alpha c)}^2}}}{{16\alpha }}{\text{。}}$ |
公平关切通常是在效用函数中引入利润差异进行刻画,此处采用Cui等[4]的处理方法,通过引入参照点依赖来描述公平偏好效用函数。所以,具有公平关切的效用函数为
| $\qquad{U_i} = {\varPi _i} - \mu ({\varPi _j} - {\varPi _i}){\text{。}}$ | (7) |
式中,
如果零售商是公平关切者(在下标处增加r表示),除了关注自身获得的利润多少以外,还关注自己与制造商之间的利润差异,则零售商的效用函数为
| $\qquad U_{{\rm{rr}}} = {\varPi _{\rm{r}}}(p) - \lambda \left[ {{\varPi _{\rm{m}}}(w) - {\varPi _{\rm{r}}}(p)} \right]{\text{。}}$ | (8) |
当
零售商的决策问题可以描述为
| $\qquad U_{{\rm{rr}}} = E(\pi _{\rm{r}}) - \lambda \max \left\{ {\left[ {E(\pi _{\rm{m}}) - E(\pi _{\rm{r}})} \right],0} \right\}{\text{。}}$ | (9) |
其中,
| $\qquad\varPi _{\rm{m}}({w_{\rm{r}}}) = {E}(\pi _{\rm{m}}) = (f - \alpha {p_{\rm{r}}})({w_{\rm{r}}} - c){\text{,}} $ | (10) |
| $ \begin{split} &\qquad\varPi _{{\rm{rr}}}({p_{\rm{r}}}) = (1 + \lambda )(f - \alpha {p_{\rm{r}}})({p_{\rm{r}}} - {w_{\rm{r}}})- \lambda (f - \alpha {p_{\rm{r}}})\times \\&({w_{\rm{r}}} - c) {\text{。}} \end{split} $ | (11) |
对式(11)求
| $ \qquad\frac{{\partial \varPi _{{\rm{rr}}}}}{\partial {p_{\rm{r}}}} = - 2\alpha (1 + \lambda ){p_{\rm{r}}} + (1 + \lambda )f + (1 + 2\lambda )\alpha {w_{\rm{r}}} - \lambda \alpha c{\text{,}} $ |
| $\qquad\frac{{{\partial ^2}\varPi _{{\rm{rr}}}}}{{\partial {p_{\rm{r}}}^2}} = - 2\alpha \left( {1 + \lambda } \right) {\text{<}}0{\text{。}}$ |
显然,
| $\qquad{p_{\rm{r}}}({w_{\rm{r}}}) = \frac{{(1 + \lambda )f - \lambda \alpha c + (1 + 2\lambda )\alpha {w_{\rm{r}}}}}{{2\alpha (1 + \lambda )}}{\text{。}}$ | (12) |
将
| $ \qquad\varPi _{\rm{m}}({w_{\rm{r}}}) \!= \!\frac{{({w_{\rm{r}}} \!- \!c)}}{{2(1\! + \!\lambda )}}\left[(1 \!+\! \lambda )f \!+ \! {\lambda \alpha c\! -\! (1 + 2\lambda )\alpha {w_{\rm{r}}}} \right]{\text{。}} $ | (13) |
对上式求
| $\begin{split} &\qquad\frac{{\partial \varPi _{\rm{m}}({w_{\rm{r}}})}}{{\partial {w_{\rm{r}}}}} = \frac{1}{{2(1 + \lambda )}}\left[ { - 2\left( {1 + 2\lambda } \right)\alpha {w_{\rm{r}}}} +(1 + \lambda )f + \right.\\ &\left. { (1 + 3\lambda )\alpha c} \right]{\text{,}} \end{split} $ |
| $\qquad\frac{{{\partial ^2}\pi _{\rm{m}}({w_{\rm{r}}})}}{{\partial {w_{\rm{r}}^2}}} = - \frac{{(1 + 2\lambda )\alpha }}{{(1 + \lambda )}} {\text{<}} 0 {\text{。}}$ |
由上式可知
| $\qquad w_{\rm{r}}^ * = \frac{{(1 + \lambda )f + (1 + 3\lambda )\alpha c}}{{2\alpha (1 + 2\lambda )}}{\text{。}}$ |
进一步可得
将
| $\qquad\varPi _{\rm{r}}(p_{\rm{r}}^ * ) = \frac{{(1 + \lambda ){{(f - \alpha c)}^2}}}{{16\alpha }}{\text{,}}$ |
| $\qquad\varPi _{\rm{m}}(w_{\rm{r}}^ * ) = \frac{{(1 + \lambda ){{(f - \alpha c)}^2}}}{{8\alpha (1 + 2\lambda )}}{\text{,}}$ |
| $\qquad\varPi _{{\rm{sc}}}(p_{\rm{r}}^ * ) = \frac{{(1 + \lambda )(3 + 2\lambda ){{(f - \alpha c)}^2}}}{{16\alpha (1 + 2\lambda )}}{\text{。}}$ |
如果零售商是公平中性者,制造商是公平关切者(在下标处增加
| $\qquad U_{{\rm{mm}}} = E(\pi _{\rm{m}}) - \beta \max \left\{ {\left[ {E(\pi _{\rm{m}}) - E(\pi _{\rm{r}})} \right],0} \right\}{\text{。}}$ | (14) |
整理公式可得
| $ \begin{split} &\qquad \varPi _{{\rm{mm}}}({w_{\rm{m}}}) = (1 + \beta )(f - \alpha {p_{\rm{m}}})({w_{\rm{m}}} - c)- \beta (f - \alpha {p_{\rm{m}}})\times\\ & ({p_{\rm{m}}} - {w_{\rm{m}}}){\text{,}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (15) |
| $ \qquad \varPi _{\rm{r}}({p_{\rm{m}}}) = (f - \alpha {p_{\rm{m}}})({w_{\rm{m}}} - c){\text{。}} $ | (16) |
对式(16)求
| $\qquad \frac{{\partial \varPi _{\rm{r}}}({p_{\rm{m}}})}{{\partial {p_{\rm{m}}}}} = - 2\alpha {p_{\rm{m}}} + f + \alpha {w_{\rm{m}}}{\text{,}}$ |
| $\qquad \frac{{{\partial ^2}\varPi _{\rm{r}}({p_{\rm{m}}})}}{{\partial {p_{\rm{m}}}^2}} = - 2\alpha {\text{<}} 0{\text{。}}$ |
| $ \qquad {p_{\rm{m}}}({w_{\rm{m}}}) = \frac{{f + \alpha {w_{\rm{m}}}}}{{2\alpha }}{\text{。}} $ | (17) |
将式(17)代入式(15)可得
| $ \qquad \varPi _{{\rm{mm}}}({p_{\rm{m}}})= \frac{{(1 + \beta )}}{2}(f - \alpha {w_{\rm{m}}})({w_{\rm{m}}} - c)- \frac{\beta }{{4\alpha }}{(f - \alpha {w_{\rm{m}}})^2}{\text{。}} $ | (18) |
对式(18)求
| $ \qquad \frac{{\partial \varPi _{{\rm{mm}}}({w_{\rm{m}}})}}{{\partial {w_{\rm{m}}}}} = \frac{1}{2} \left[ { - (2 + 3\beta )\alpha {w_{\rm{m}}} + (1 + 2\beta )f + (1 + \beta )\alpha c} \right]{\text{,}} $ |
| $\qquad \frac{{{\partial ^2}\varPi _{{\rm{mm}}}({w_{\rm{m}}})}}{{\partial {w_{\rm{m}}}^2}} = - \frac{{(2 + 3\beta )\alpha }}{2} {\text{<}} 0{\text{。}}$ |
由
进一步可得
| $\qquad p_{\rm{m}}^* = \frac{{(3 + 5\beta )f + (1 + \beta )\alpha c}}{{2\alpha (2 + 3\beta )}}{\text{,}}$ |
| $\qquad q_{\rm{m}}^* = \frac{{(1 + \beta )(f - \alpha c)}}{{2(2 + 3\beta )}}{\text{。}}$ |
将
| $\qquad \varPi _{\rm{r}}(p_{\rm{m}}^*) = \frac{{{{(f - \alpha c)}^2}}}{{4\alpha {{(2 + 3\beta )}^2}}}{\text{,}}$ |
| $\qquad \varPi _{\rm{m}}(w_{\rm{m}}^ * ) = \frac{{{{(1 + \beta )}^2}{{(f - \alpha c)}^2}}}{{4\alpha (2 + 3\beta )}}{\text{,}}$ |
| $\qquad \varPi _{{\rm{sc}}}(p_{\rm{m}}^*) = \frac{{3{{(1 + \beta )}^3}{{(f - \alpha c)}^2}}}{{4\alpha {{(2 + 3\beta )}^2}}}{\text{。}}$ |
当制造商和零售商都是公平关切者时(相关变量在下标处增加
| $\qquad U_{{\rm{rmr}}} = E(\pi _{\rm{r}}) - \lambda \max \left\{ {\left[ {E(\pi _{\rm{m}}) - E(\pi _{\rm{r}})} \right],0} \right\}{\text{,}}$ | (19) |
| $\qquad U_{{\rm{mmr}}} = E(\pi _{\rm{m}}) - \beta \max \left\{ {\left[ {E(\pi _{\rm{m}}) - E(\pi _{\rm{r}})} \right],0} \right\}{\text{。}}$ | (20) |
对上述期望函数组合进行整理得
| $ \begin{split} &\qquad \varPi _{{\rm{rmr}}}({p_{{\rm{mr}}}}) = (1 + \lambda )(f - \alpha {p_{{\rm{mr}}}})({p_{{\rm{mr}}}} - {w_{{\rm{mr}}}})- \lambda (f -\\ & \alpha {p_{{\rm{mr}}}})({w_{{\rm{mr}}}} - c){\text{,}} \end{split} $ | (21) |
| $\begin{split} & \qquad \varPi _{{\rm{mmr}}}({w_{{\rm{mr}}}}) =(1 + \beta )(f - \alpha {p_{{\rm{mr}}}})({w_{{\rm{mr}}}} - c) - \beta (f - \alpha {p_{{\rm{mr}}}})\times\\ &({p_{{\rm{mr}}}} - {w_{{\rm{mr}}}}){\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (22) |
利用逆向递归求解法求解得
| $ \begin{split} &\qquad w_{{\rm{mr}}}^ * = \frac{{(1 + 2\beta ){{(1 + \lambda )}^2}f - {\lambda ^2}\beta \alpha c}}{{\alpha (1 + 2\lambda )[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}}+\\ &\frac{{(1 + \lambda )(1 + 3\lambda )(1 + \beta )\alpha c}}{{\alpha (1 + 2\lambda )[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}}{\text{,}} \end{split}$ |
| $ \qquad p_{{\rm{mr}}}^ * = \frac{{[3(1 + \lambda ) + (5 + 4\lambda )\beta ]f + (1 + \lambda + \beta )\alpha c}}{{2\alpha [2(1 + \lambda ) + (3 + 2\lambda )\beta ]}}{\text{,}} $ |
| $ \qquad q_{{\rm{mr}}}^ * = \frac{{(1 + \lambda + \beta )(f - \alpha c)}}{{2[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}}{\text{。}} $ |
将
| $\qquad \varPi _{\rm{r}}(p_{{\rm{mr}}}^*) = \frac{{(1 + \lambda ){{(1 + \lambda + \beta )}^2}{{(f - \alpha c)}^2}}}{{4\alpha {{[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}^2}}}{\text{,}}$ |
| $ \qquad \varPi _{\rm{m}}(w_{{\rm{mr}}}^*) = \frac{{{{(1 + \lambda + \beta )}^2}{{(f - \alpha c)}^2}}}{{4\alpha (1 + 2\lambda )[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}}{\text{,}} $ |
| $ \qquad \varPi _{{\rm{sc}}}(p_{{\rm{mr}}}^*) = \frac{{(3 + 2\lambda ){{(1 + \lambda + \beta )}^3}{{(f - \alpha c)}^2}}}{{4\alpha (1 + 2\lambda ){{[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}^2}}}{\text{。}} $ |
供应链的效率决定了供应链成员间的合作空间。供应链的效率越高,合作空间就越大,成员的合作意愿越强;反之,合作空间越小,合作意愿也越弱。
基于上述假设函数分别讨论以下4种情况下的供应链合作效率(e)。
1) 零售商和供应商均为公平中性时,
| $\qquad {e_0} = \frac{{\varPi _{{\rm{sc}}}(p_0^ * )}}{{{\varPi _{{\rm{sc}}}}({p^ * })}} = \frac{{3{{(f - \alpha c)}^2}4\alpha }}{{16\alpha {{(f - \alpha c)}^2}}} = 75\% {\text{。}}$ |
2) 仅零售商为公平关切者时,
| $\qquad {e_{\rm{r}}} = \frac{{\varPi _{{\rm{sc}}}(p_{\rm{r}}^ * )}}{{{\varPi _{{\rm{sc}}}}({p^ * })}} = \frac{{(1 + \lambda )(3 + 2\lambda )}}{{4(1 + 2\lambda )}}{\text{。}}$ |
对上式方程进行推导求解
| $ \begin{align} &\qquad \frac{{\partial e_{\rm{r}}(\lambda )}}{{\partial {\lambda }}} = \frac{{(4{\lambda ^2} + 4\lambda - 1)}}{{4{{(1 + 2\lambda )}^2}}}{\text{,}}\\ & \qquad \frac{{{\partial ^2}e_{\rm{r}}(\lambda )}}{{\partial {\lambda ^2}}} = \frac{2}{{{{(1 + 2\lambda )}^3}}}{\text{>}} 0{\text{。}}\end{align} $ | (23) |
由二阶导数大于零,可知
因此,在
3) 仅供应商为公平关切者时,
| $\qquad {e_{\rm{m}}} = \frac{{\varPi _{{\rm{sc}}}(p_{\rm{m}}^*)}}{{{\varPi _{{\rm{sc}}}}({p^ * })}} = \frac{{3{{(1 + \beta )}^3}}}{{{{(2 + 3\beta )}^2}}}{\text{。}}$ | (24) |
对上式进行推导运算如下
| $\qquad \frac{{\partial e_{\rm{m}}(\beta )}}{{\partial {\beta }}}{\rm{ = }}{\left(\frac{{3 + 3\beta }}{{2 + 3\beta }}\right)^2} \times \frac{\beta }{{(2 + 3\beta )}}{{ {\text{>}} 0}}{\text{。}}$ | (25) |
由于
4) 零售商和供应商均为公平关切者时,
| $ \qquad {e_{\rm{mr}}} = \frac{{\varPi _{{\rm{sc}}}(p_{\rm{mr}}^*)}}{{{\varPi _{{\rm{sc}}}}({p^ * })}} = \frac{{(3 + 2\lambda ){{(1 + \lambda + \beta )}^3}}}{{(1 + 2\lambda ){{[2(1 + \lambda ) + (3 + 2\lambda )\beta ]}^2}}}{\text{。}} $ |
这种情况比较复杂,将借助图形进行分析。
3.2 数值分析由上述分析可以看出,在零售商和供应商同时是公平中性时在线性情况下,供应链的合作效率为一固定常数75%;在零售商和供应商存在公平关切行为时,供应链的效率则与相应的参数有关。为了更好地区分各种情况,需要对各参数赋值分析。
1) 零售商和供应商均为公平中性。
不论参数
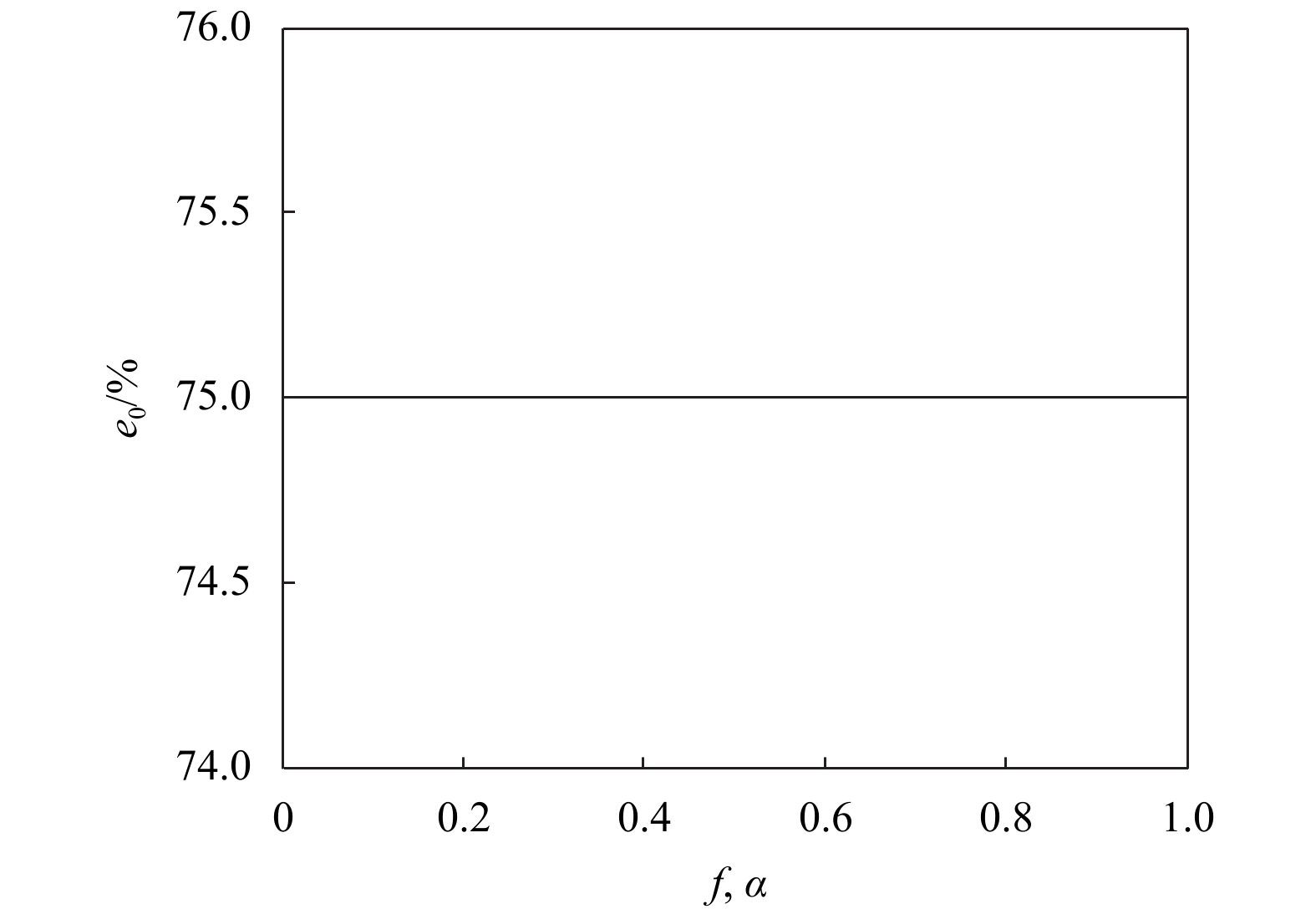
|
图 1 |
2) 仅零售商存在公平关切。
依据3.1中分析可知
|
表 1 |
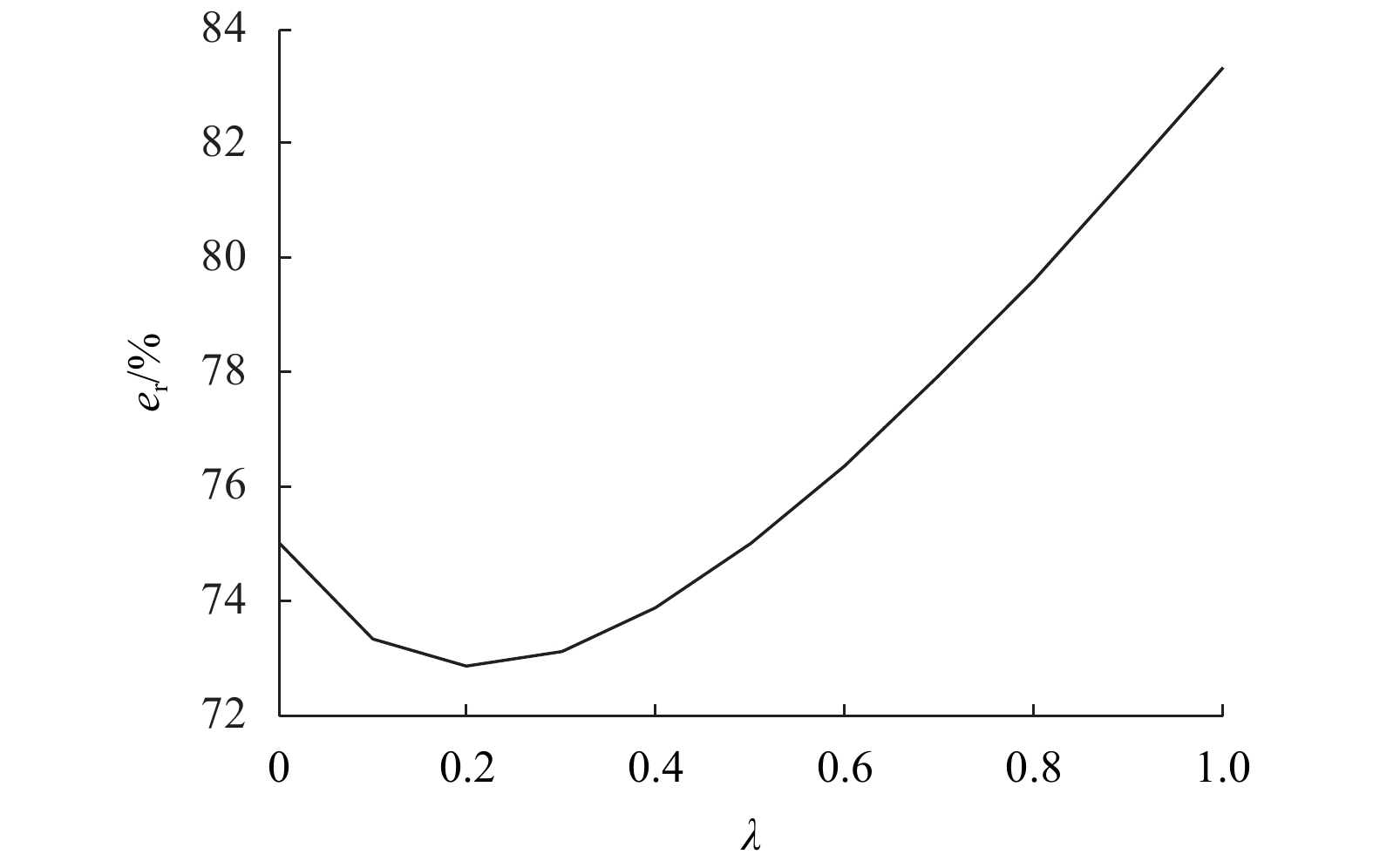
|
图 2 |
3) 仅制造商存在公平关切。
依据3.1的分析可知,
|
表 2 |
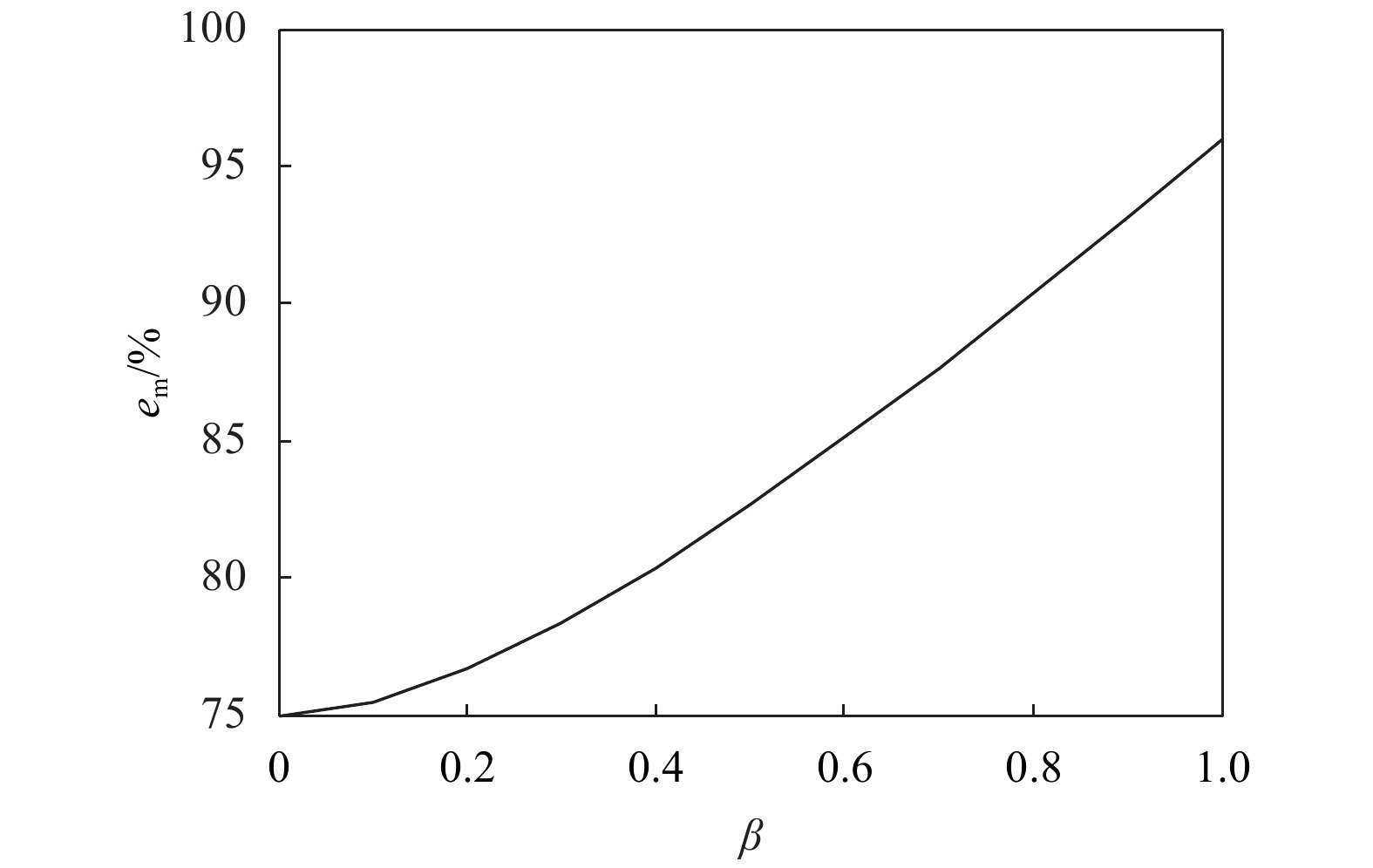
|
图 3 |
4) 零售商和供应商均为公平关切者。
| $\qquad {e_{\rm{mr}}}{\rm{ = }}\frac{{(3 + 2\lambda ){{({\rm{1 + }}\lambda {\rm{ + }}\beta )}^3}}}{{(1 + 2\lambda ){{[2(1 + \lambda ) + ({\rm{3 + 2}}\lambda )\beta ]}^2}}}{\text{。}}$ |
由公式可知
|
表 3 |
|
表 4 |
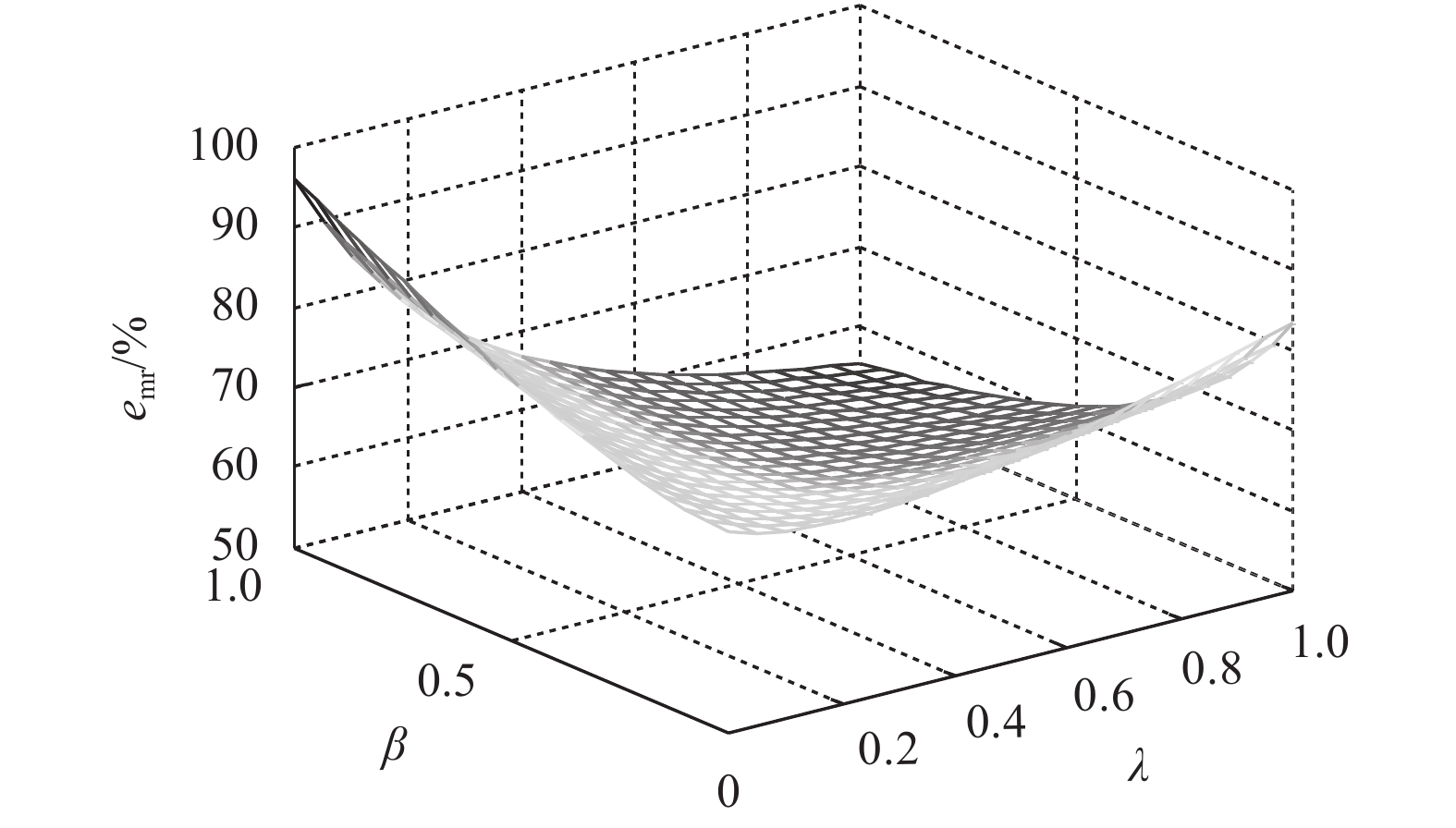
|
图 4 |
结论1:当
结论2:当
为进一步证明结论2,根据公平偏好的系数取值,当
情形1 当
供应链的合作效率变化如图5所示,当
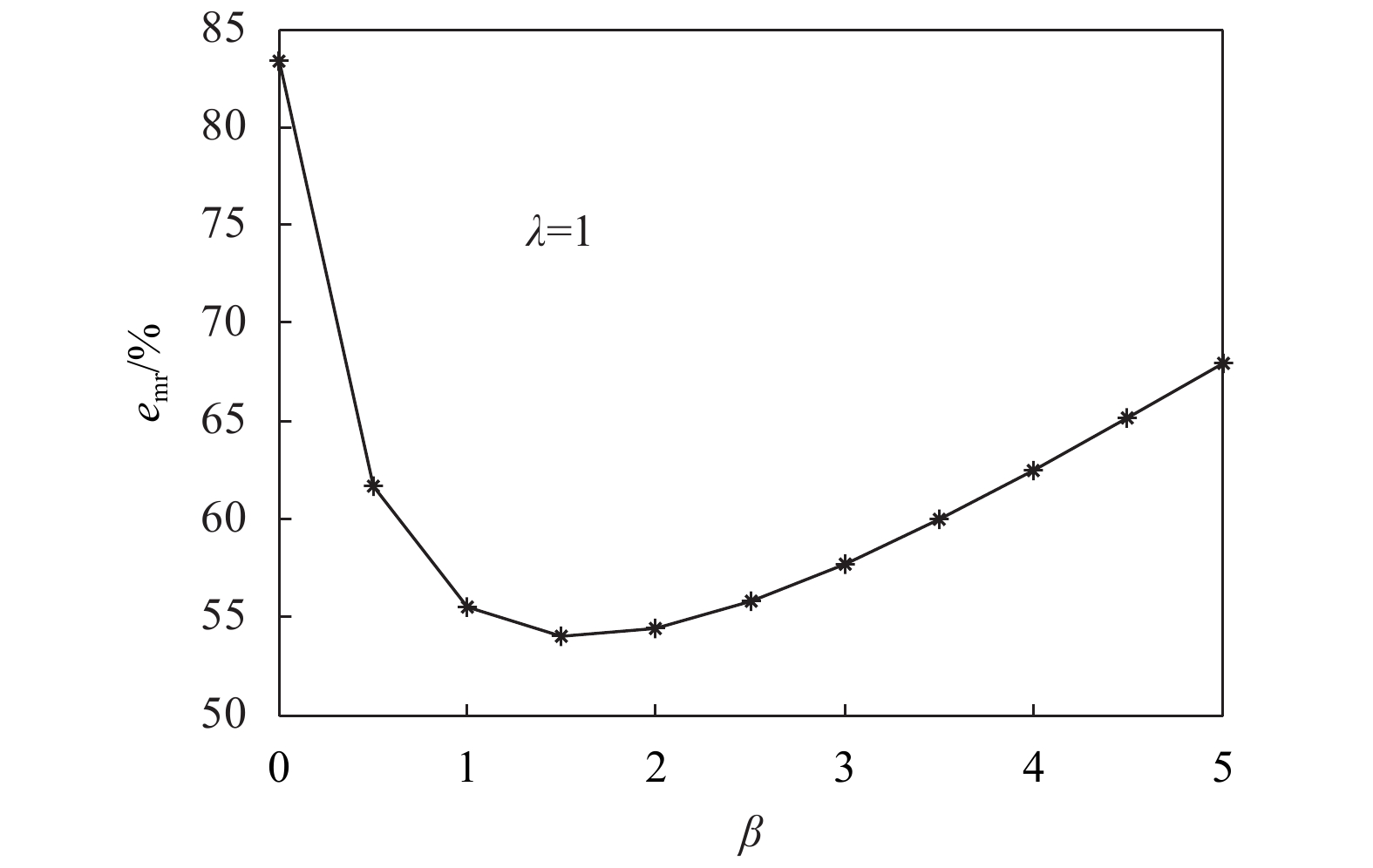
|
图 5 |
情形2 当
| $\qquad {e_{\rm{mr}}} = \frac{{(3 + 2\lambda ){{(2 + \lambda )}^3}}}{{(1 + 2\lambda ){{(5 + 4\lambda )}^2}}}{\text{。}}$ |
供应链的合作效率变化如图6所示,当
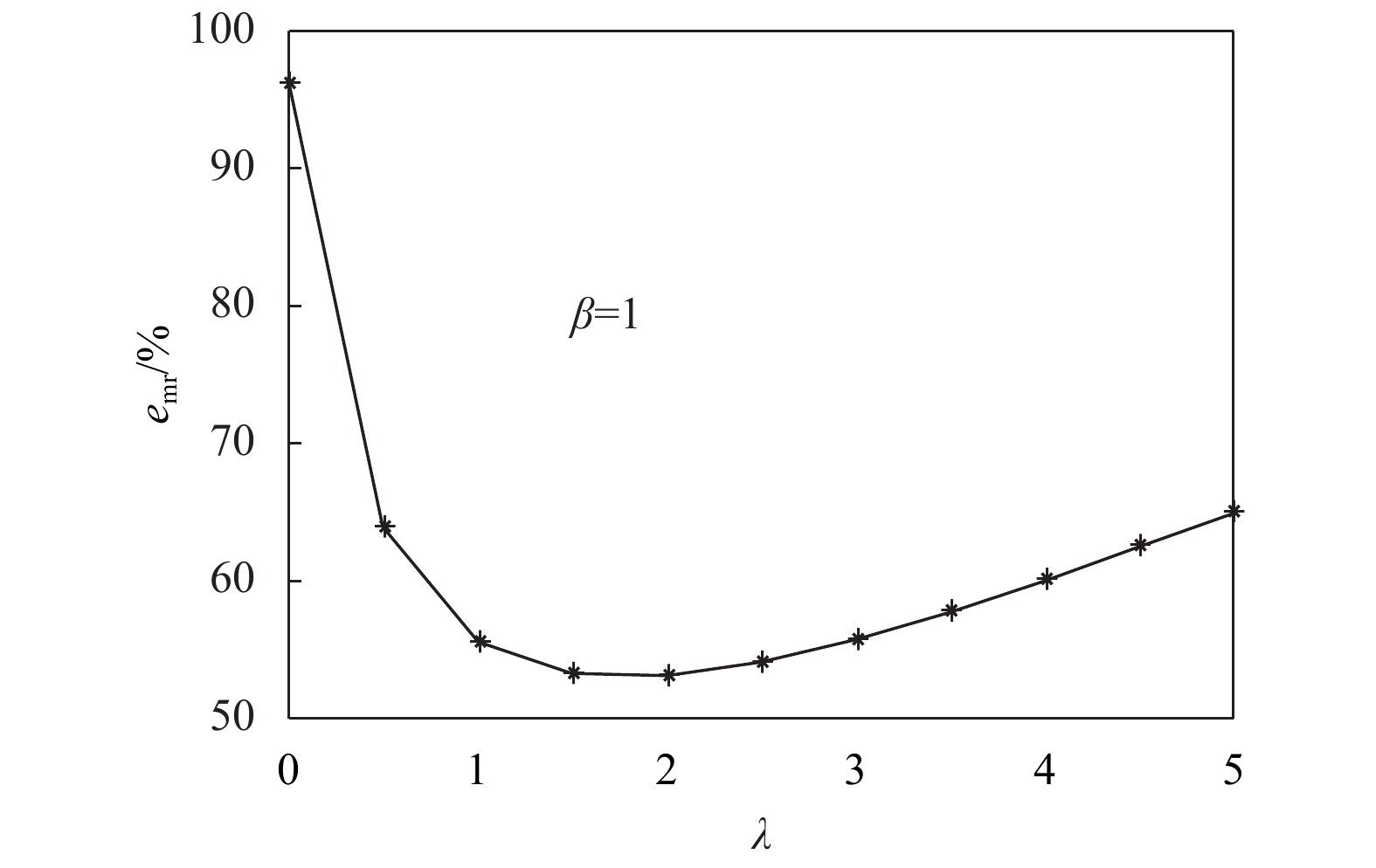
|
图 6 |
在现实的决策中,由于供应链成员认知和心理偏差的存在,导致成员在决策时,不仅仅关注自身收益,也关注其他成员的收益,这种决策会影响到供应链的运行效率和成员之间的合作效率。本文在线性随机需求下考虑两级供应链成员在单一存在公平关切和双方公平关切下成员的合作效率。通过与双方公平中性下的运行效率对比,得出以下结论。
1) 仅零售商具有公平关切时,合作效率随公平关切系数的增加先下降后上升,公平关切系数大于0.5时,合作效率相比公平中性会增强。因此,在二级供应链合作过程中,零售商应将公平关切系数设为大于0.5,以增强合作效率。同时需关注制造商的态度。
2) 仅制造商具有公平关切时,合作效率随公平关切系数的增加而上升,公平关切系数大于0时,合作效率会增强。制造商单方面采取公平策略,会使合作效率增强,但要关注零售商的态度。
3) 零售商和制造商同时具有公平关切时,双方公平关切系数差异越大,随着系数的增大合作效率会增强。反之,公平关切系数相同时,取值越大,合作效率越小。当制造商和零售商同时具有公平关切时,各成员需要考虑公平各自公平关切系数的差异性,在一定差异范围内有助于提高合作效率。
因此,当信息对称时,供应链可根据以上3点结论调整公平关切系数来增强成员的合作效率,提高供应链的运行效率。
本文仅考虑成员的绝对公平偏差,没有考虑相对公平的因素。另外,决策是在供应链成员信息对称时作出的,未考虑信息私有化的问题,这些将是后续的研究方向。
| [1] |
FEHR E, SCHMIDT K M. A theory of fairness, competition and cooperation[J].
Quarterly Journal of Economics, 1999, 114(3): 817-868.
DOI: 10.1162/003355399556151. |
| [2] |
MUSSWEILER T. Comparison processes in social judgment: mechanisms and consequences[J].
Psychological Review, 2003, 110(3): 472.
DOI: 10.1037/0033-295X.110.3.472. |
| [3] |
KUMAR N. The power of trust in manufacturer-retailer relationships[J].
Harvard Business Review, 1996, 74(6): 92-106.
|
| [4] |
CUI H, RAJU J, ZHANG Z. Fairness and channel coordination[J].
Management Science, 2007, 53(8): 1303-1314.
DOI: 10.1287/mnsc.1060.0697. |
| [5] |
MCMARTHY R. How to handle channel conflict?[J].
High-Tech Marketing, 1985(7): 31-35.
|
| [6] |
COX J C, FRIEDMAN D, GJERSTAD S. A tractable model of reciprocity and fairness[J].
Games and Economic Behavior, 2007, 59(1): 17-45.
DOI: 10.1016/j.geb.2006.05.001. |
| [7] |
CACHON G, GERARD P. Supply chain coordination with contracts[M/OL].(2003-12). https://doi.org/10.1016/s0927-0507(03)11006-7.
|
| [8] |
杜少甫, 杜婵, 梁樑. 考虑公平关切的供应链契约与协调[J].
管理科学学报, 2010, 13(11): 41-48.
DU Shaofu, DU Chan, LIANG Liang. Supply chain coordination considering fairness concerns[J]. Journal of Management Sciences in China, 2010, 13(11): 41-48. |
| [9] |
DU S F, NIE T F, CHU C B, et al. News vendor model for a dynamic supply chain with Nash bargaining fairness concerns[J].
International Journal of Production Research, 2014, 54(17): 5070-5085.
|
| [10] |
何丽红, 李政道. 考虑零售商公平关切的双渠道供应链合作广告决策分析[J].
工业工程与管理, 2017, 22(4): 107-114.
HE Lihong, LI Zhengdao. Analysis of cooperative advertising strategy in a dual- channel supply chain with a fairness concerns of the retailer[J]. Industrial Engineering and Management, 2017, 22(4): 107-114. |
| [11] |
舒亚东, 代颖, 马祖军. 基于Shapley值公平参考框架的回收商竞争逆向供应链定价决策[J].
工业工程与管理, 2017(6): 121-127.
SHU Yadong, DAI Ying, MA Zujun. Pricing decisions for a reverse supply chain with competitive recyclers based on Shapley value fairness concerns[J]. Industrial Engineering and Management, 2017(6): 121-127. |
| [12] |
马利军, 曾清华, 邵新建. 指数函数需求模式下具有公平偏好的供应链协调[J].
系统工程理论与实践, 2013, 33(12): 3009-3019.
MA Lijun, ZENG Qinghua, SHAO Xinjian. Channel coordination with fairness concerns under power-form demand[J]. SystemsEngineering-Theory&Practice, 2013, 33(12): 3009-3019. DOI: 10.12011/1000-6788(2013)12-3009. |
| [13] |
李媛, 赵道致. 考虑公平偏好的低碳化供应链契约协调研究[J].
管理工程学报, 2015, 29(1): 156-16.
LI Yuan, ZHAO Daozhi. Low Carbonization supply chain coordination with contracts considering fairness preference[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(1): 156-16. DOI: 10.3969/j.issn.1004-6062.2015.01.021. |
| [14] |
浦徐进, 诸葛瑞杰, 包含. 零售商风险规避和公平关切对供应链运作的影响研究[J].
中国软科学, 2014, 28(7): 76-81.
PU Xujin, ZHUGE Ruijie, BAO Han. Research on supply chain operation mechanisms with the considering of risk aversion and fairness preference of retailers[J]. China Soft Science, 2014, 28(7): 76-81. |
| [15] |
李绩才, 周永务, 李昌文. 考虑公平关切的供应链产品质量与零售定价博弈决策分析[J].
中国软科学, 2017, 31(3): 139-144.
LI Jicai, ZHOU Yongwu, LI Changwen. Quality and retail pricing decision in a supply chain with fairness concerns[J]. China Soft Science, 2017, 31(3): 139-144. |
| [16] |
赵婉鹛, 叶春明. 考察供应商具有双重行为偏好特征的供应链契约与协调[J].
工业工程与管理, 2018, 23(1): 23-29.
ZHAO Wanmei, YE Chunming. Study on the contracts and coordination of supply chain with the supplier’s dual behavior preference[J]. Industrial Engineering and Management, 2018, 23(1): 23-29. |
| [17] |
王垒, 曲晶, 刘新民. 考虑横向公平的双渠道销售闭环供应链定价策略与协调研究[J].
工业工程, 2018, 21(3): 21-31.
WANG Lei, QU Jing, LIU Xinmin. Pricing strategy and coordination of closed-loop supply chain considering horizontal fairness under dual channel sales[J]. Industrial Engineering Journal, 2018, 21(3): 21-31. DOI: 10.3969/j.issn.1007-7375.2018.03.003. |
| [18] |
周艳菊, 鲍茂景, 陈晓红. 基于公平关切的低碳供应链广告合作-减排成本分担契约与协调[J].
中国管理科学, 2017, 25(2): 121-128.
ZHOU Yanju, BAO Maojing, CHEN Xiaohong. Co-op advertising and emission reduction cost sharing contract and coordination in low-carbon supply chain based on fairness concerns[J]. Chinese Journal of Management Science, 2017, 25(2): 121-128. |
| [19] |
范如国, 沈文英. 公平偏好下低碳供应链企业博弈及其仿真研究[J].
中国地质大学学报, 2017, 15(5): 18-29.
FAN Ruguo, SHEN Wenying. Analysis and simulation of game in low –carbon supply chain enterprises considering fairness preferences[J]. Journal of China University of Geosciences (Social Sciences Edition), 2017, 15(5): 18-29. |
| [20] |
王能民, 汪应洛, 杨彤. 供应链协调机制选择与绩效关系研究综述[J].
管理科学, 2007, 20(1): 22-29.
WANG Nengmin, WANG Yingluo, YANG Tong. Literature review and some issues on the relationship between supply chain coordination and performance[J]. Journal of Management Sciences, 2007, 20(1): 22-29. DOI: 10.3969/j.issn.1672-0334.2007.01.005. |
| [21] |
孙彩虹, 田真真, 于辉. 价格需求函数的供应链合作动力对比分析[J].
工业工程, 2015, 18(4): 58-65.
SUN Caihong, TIAN Zhenzhen, YU Hui. Comparative analysis of supply chain's collaborative motivation under different price-dependent demand functions[J]. Industrial Engineering Journal, 2015, 18(4): 58-65. DOI: 10.3969/j.issn.1007-7375.2015.04.009. |
| [22] |
牟能冶. 多契约下基于消费者公平关切和零售商信用的供应链定价策略[J].
工业工程与管理, 2017, 22(2): 28-36.
MU Nengye. Pricing strategies of supply chain based on consumers’ fairness concern and retailers’ credit under multi-contracts[J]. Industrial Engineering and Management, 2017, 22(2): 28-36. |
| [23] |
覃燕红, 徐丹丹, 陈戈. 指数函数需求下供应链公平偏好信息动态演进研究[J].
经济数学, 2017, 34(2): 1-9.
QIN Yanhong, XU Dandan, CHEN Ge. Dynamic evolution of supply chain fairness information under exponential demand[J]. Journal of Quantitative Economics, 2017, 34(2): 1-9. DOI: 10.3969/j.issn.1007-1660.2017.02.002. |
 2019, Vol. 22
2019, Vol. 22

