A Multi-objective Robust Optimization Model for Site-selection of Construction Waste Facilities under Uncertainty
近几十年来,快速的城市化进程推动着国民经济的发展。与此同时,大规模的城市建设和拆除产生了数量庞大的建筑废弃物[1]。据研究估计,中国每年约产生23.6 亿建筑废弃物 [2], 占城市固体废弃物排放总量的30%~40%[3]。目前国内对建筑废弃物的处理仍以填埋为主,资源化率不足5%,且高昂的处理成本与运输成本滋生出大批非法倾倒行为,导致建筑废弃物围城现象在各大城市日益严重,对城市环境,市民健康以及后续处理造成了巨大困扰。因此,合理的消纳设施选址以及较优的废弃物分配方案为政府、市民、建筑废弃物产生方以及运营方都能带来更好的环境与效益。
设施选址及分配问题通常是战略性问题,固定成本高,决策期长,因此建筑废弃物所面临的环境存在诸多不确定,如对建筑废弃物产生量估算的误差,对建筑废弃物非法倾倒量的未知,以及成本的波动等。不确定性下的优化问题主要分为2类:随机优化和鲁棒优化。随机优化的一个基本假设是已知不确定性参数的概率分布,然而现实问题中,不确定性参数的概率分布却较难获知。近年来,鲁棒优化被广泛应用于各个领域[4-5]。在鲁棒优化中,不确定性参数采用离散的情景或连续的区间范围来描述,其目的是找到一个最优解,使它对任意的不确定性参数观测值不敏感,而不仅仅强调数学期望值[6]。
目前,国内学者对建筑废弃物的研究与日俱增[7],但有关建筑废弃物设施选址方面的研究大多仅考虑单一处理设施,且考虑环境不确定性的研究仍较少。吕新福等[8]采用两阶段Tabu搜索启发式算法研究城市固体废弃物MSW(municipal solid waste)回收中转站的选址和废弃物运输路线。Dosal等[9]运用多标准分析(multicriteria analysis,MCA)综合考虑经济、环境和社会3方面指标对建筑废弃物回收设施的选址进行了分析。Eiselt等[10]以成本和污染为目标函数,对MSW系统中的填埋场和转运站进行选址以及废弃物分配。Habibi等[11]在Eiselt的基础上增加温室气体(greenhouse gas,GHG)污染目标函数,充分考虑可回收废弃物与不可回收废弃物的人均产生量的不确定性,采用El Aghezzaf等[12]所提出的鲁棒优化模型,通过情景集对不确定性参数进行描述,以此对MSW系统展开选址及分配。
有效的建筑废弃物管理应集中于经济、环境、社会3项绩效指标的均衡发展[13]。经济方面,建筑废弃物设施的建设固定成本、运营成本以及建筑废弃物的运输成本是影响选址分配的重要因素;环境方面,渣土车运输大量建筑废弃物的过程中所排放的有害气体对空气造成污染的同时也加剧了温室效应;社会方面,现实中的填埋场与资源化工厂虽然尽量避免在人口密集区选址,但由于建筑废弃物消纳设施(填埋场与资源化工厂)占地面积较广,所消纳废物污染较大,其对周边居民的影响仍不容忽视。因此,本文对成本、GHG排放与视觉污染进行最小化控制,建立多目标混合整数规划模型,并将建筑废弃物产生量、成本、建筑废弃物资源化率等参数的不确定性考虑其中,运用Ben-Tal[14]和Pishvaee [15]所提出的鲁棒优化方法,在各种不确定性水平下对建筑废弃物填埋场与资源化工厂进行选址以及废弃物分配,决策者可根据项目风险偏好选择适用方案,以合理平衡项目目标与风险。
1 确定性模型
1.1 问题描述
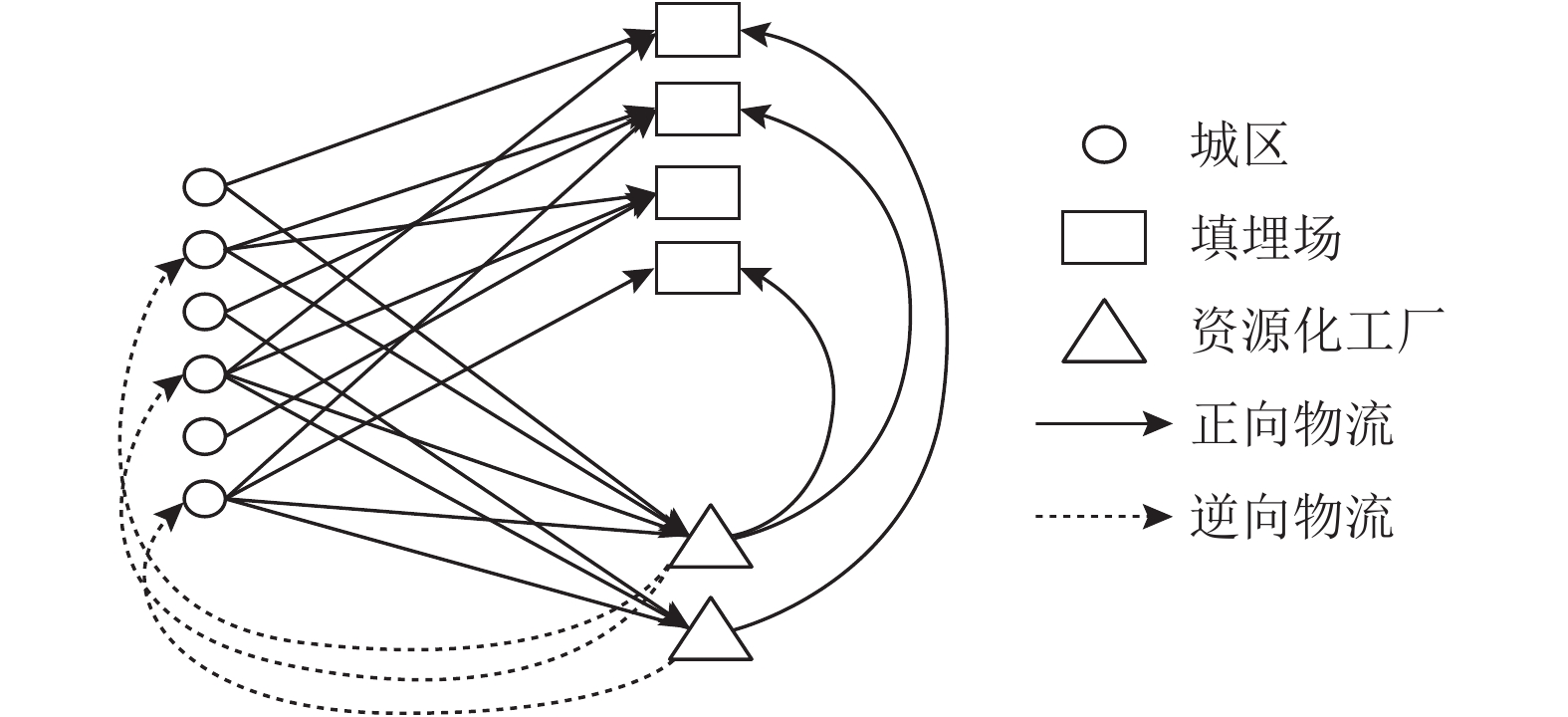
目前,建筑废弃物主要按以下3种方式处理:填埋、回收利用、非法倾倒。鉴于非法倾倒并非合法的处置方式,且数据零碎,无法获取,本文仅考虑填埋与回收利用,并将非法倾倒量考虑在废弃物产生量的不确定集合中。如图1所示,以某城市各城区为单位个体,各城区所产生的建筑废弃物可运往一个或多个填埋场和资源化工厂,各消纳设施(填埋场和资源化工厂)可接收来自一个或多个城区的建筑废弃物,废弃物经由资源化工厂处理后,再将资源化产品销往各城区,废渣则被运至填埋场处理。
1.2 符号变量
为方便描述,参数定义如下:
$I$
为城区集合(
$i = 1,2, \cdots ,I$
);
$J$
为填埋场候选点集合(
$j = 1,2, \cdots ,J$
);
$K$
为资源化工厂候选点集合(
$k = 1,2, \cdots ,K$
);
$Q$
为填埋场消纳规模集合(
$q = 1,2, \cdots ,Q$
);
$P$
为资源化工厂处理规模集合(
$p = 1,2, \cdots ,P$
);
$S$
为运输车排放污染物种类集合(
$s = 1,2, \cdots ,S$
);
${P_i}$
为i城区的年常住人口;
${W_i}$
为i城区建筑废弃物产生量;
$\gamma $
为各城区运往资源化工厂的建筑废弃物比率;
h为资源化工厂处理建筑废弃物的综合利用率;
$\lambda $
为资源化工厂处理建筑废弃物的综合废弃率;
$f_{jq}^{\rm{L}}$
为在j处修建q规模的填埋场的建设固定成本;
$f_{kp}^{\rm{P}}$
为在k处修建p规模的资源化工厂的建设固定成本;
$c_{ij}^{\rm{L}}$
为来自i城区的建筑废弃物在j填埋场的单位处理成本;
$c_{ik}^{\rm{P}}$
为来自i城区的建筑废弃物在k资源化工厂的单位处理成本;
$c_{kj}^{\rm{R}}$
为来自
$k$
资源化工厂的废渣在j填埋场的单位处理成本;
${\rm{pr}}_{ki}$
为由k资源化工厂生产的资源化产品在i城区的单位销售价格;
$a$
为单位运输车的起步价格;
$b$
为运输车的单位运输价格;
$d_{ij}^{\rm{L}}$
为i城区与j填埋场之间的距离(
$d_{ik}^{\rm{P}}$
、
$d_{kj}^{\rm{R}}$
、
$d_{ki}^{{\rm{RP}}}$
定义同理);
${\pi _s}$
为运输车所排放污染物s的单位距离排放量;
${\nu ^{\rm{T}}}$
为运输车的额定载重量;
$V_{jq}^{\rm{L}}$
为规模为q的j填埋场的年最大处理量;
$V_{kp}^{\rm{P}}$
为规模为p的k资源化工厂的年最大年处理量;
${\phi ^{\rm{L}}}$
与
${\phi ^{\rm{P}}}$
分别为填埋场与资源化工厂的视觉污染系数。
决策变量定义如下:
$\varpi _i^{\rm{L}}$
为i城区需填埋处理的建筑废弃物量;
$\varpi _i^{\rm{P}}$
为i城区需回收利用的建筑废弃物量;
$w_{ij}^{\rm{L}}$
为i城区运往j填埋场的建筑废弃物量;
$w_{ik}^{\rm{P}}$
为i城区运往k资源化工厂的建筑废弃物量;
$w_{kj}^{\rm{R}}$
为k资源化工厂运往j填埋场的建筑废弃物量;
$w_{ki}^{{\rm{RP}}}$
为k资源化工厂销往i城区的资源化产品数量;
$t_{ij}^{\rm{L}}$
为由i城区开往j填埋场的渣土车数量(
$t_{ik}^{\rm P}$
、
$t_{kj}^{\rm R}$
定义同理);
$t_{ki}^{{\rm{RP}}}$
为由k资源化工厂开往i城区的资源化产品运输车数量;
${L_{jq}}$
为在j候选点修建规模q的填埋场时为1,否则为0;
${R_{kp}}$
为在k候选点修建规模p的资源化工厂时为1,否则为0。
1.3 模型建立
本部分模型包括式(1)—式(3) 3个目标函数,式(1)为最小化总成本,包括填埋场建设固定成本、运营成本,资源化工厂建设固定成本、运营成本,资源化产品购买成本、废渣处理成本以及运输成本。
|
$ \begin{split} &\qquad {\rm{min}}\;{{\rm{Z}}_{\rm{c}}} = \sum\limits_j {\sum\limits_q {f_{jq}^{\rm{L}}{L_{jq}}} } + \sum\limits_i {\sum\limits_j {c_{ij}^{\rm{L}}w_{ij}^{\rm{L}}} {\rm{ + }}\sum\limits_i {\sum\limits_j {t_{ij}^{\rm{L}}(a + } } } \\ & bd_{ij}^{\rm{L}}) + \displaystyle\sum\limits_k {\displaystyle\sum\limits_{\rm{p}} {f_{kp}^{\rm{P}}{R_{kp}}} } + \displaystyle\sum\limits_i {\displaystyle\sum\limits_k {c_{ik}^{\rm{P}}w_{ik}^{\rm{P}}} } + \displaystyle\sum\limits_i {\displaystyle\sum\limits_k {t_{ik}^{\rm{P}}(a + b d_{ik}^{\rm{P}})} } + \\ & \displaystyle\sum\limits_k {\displaystyle\sum\limits_i {{\rm{p}}{{\rm{r}}_{ki}}w_{ki}^{{\rm{RP}}}} } + \displaystyle\sum\limits_k {\displaystyle\sum\limits_i {t_{ki}^{{\rm{RP}}}(a + b d_{ki}^{{\rm{RP}}})} } + \displaystyle\sum\limits_k {\displaystyle\sum\limits_j {c_{kj}^{\rm{R}}w_{kj}^{\rm{R}}} } {\rm{ + }}\\&\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {t_{kj}^{\rm{R}}(a + b d_{kj}^{\rm{R}}} } ){\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $
|
(1) |
式(2)为最小化运输车所排放的GHG,GHG排放量为车辆每公里污染物排放量与总里程数的乘积。
|
$ \begin{array}{l} \qquad \min\;{Z_{\rm{g}}} = \displaystyle\sum\limits_s {{\pi _s}\left( {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {t_{ij}^{\rm{L}}} } d_{ij}^{\rm{L}} + \displaystyle\sum\limits_i {\displaystyle\sum\limits_k {t_{ik}^{\rm{P}}d_{ik}^{\rm{P}}} } + } \right.} \\ \left. { \displaystyle\sum\limits_k {\displaystyle\sum\limits_i {t_{ki}^{{\rm{RP}}}d_{ki}^{{\rm{RP}}}} } +\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {t_{kj}^{\rm{R}}d_{kj}^{\rm{R}}} } } \right){\text{。}} \end{array} $
|
(2) |
式(3)为最小化填埋场与资源化工厂对周边居民造成的视觉污染,j填埋场的建筑废弃物总量为
$\displaystyle\sum\limits_{i'} {w_{i'j}^{\rm{L}}} + \displaystyle\sum\limits_k {w_{kj}^{\rm{R}}} $
,
$k$
资源化工厂的建筑废弃物总量为
$\displaystyle\sum\limits_{i'} {w_{i'k}^{\rm{P}}} $
,其中i'取值范围同i。假设视觉污染与消纳设施接收的建筑废弃物总量成正比,与距离的平方成反比[8]。
|
$ \begin{split} \min\; {Z_{\rm{v}}}\! =\! \sum\limits_i {{P_i}\left[ {\sum\limits_j {\frac{{{\phi ^{\rm{L}}}(\displaystyle\sum\limits_{i'} {w_{i'j}^{\rm{L}}} \! +\! \displaystyle\sum\limits_k {w_{kj}^{\rm{R}}} )}}{{{{(d_{ij}^{\rm{L}} \!+\! \varepsilon )}^2}}} \!+ \!\!\!} } \right.} \left. {\sum\limits_k {\frac{{{\phi ^{\rm{P}}}(\displaystyle\sum\limits_{i'} {w_{i'k}^{\rm{P}}} )}}{{{{(d_{ik}^{\rm{P}} \!+\! \varepsilon )}^2}}}} } \right]{\text{。}} \end{split} $
|
(3) |
约束条件如下
|
$ \qquad{W_i} = \varpi _i^{\rm{L}} + \varpi _i^{\rm{P}},{\rm{ }}\forall i{\text{;}} $
|
(4) |
|
$ \qquad\varpi _i^{\rm{L}} = \left( {1 - \gamma } \right){W_i},{\rm{ }}\forall i{\text{;}} $
|
(5) |
|
$ \qquad\varpi _i^{\rm{P}} = \gamma {W_i},{\rm{ }}\forall i{\text{;}} $
|
(6) |
|
$ \qquad\varpi _i^{\rm{L}} = \sum\limits_j {w_{ij}^{\rm{L}}}; {\rm{ }}\forall i{\text{;}} $
|
(7) |
|
$ \qquad \varpi _i^{\rm{P}} = \sum\limits_k {w_{ik}^{\rm{P}}},{\rm{ }}\forall i{\text{;}} $
|
(8) |
|
$ \qquad h\sum\limits_i {w_{ik}^{\rm{P}}} = \sum\limits_{i'} {w_{ki}^{{\rm{RP}}}} ,{\rm{ }}\forall k{\text{;}} $
|
(9) |
|
$ \qquad \lambda \sum\limits_i {w_{ik}^{\rm{P}}} = \sum\limits_j {w_{kj}^{\rm{R}}}, {\rm{ }}\forall k{\text{;}} $
|
(10) |
|
$ \qquad{\nu ^{\rm{T}}}t_{ij}^{\rm{L}} {\text{≥}} w_{ij}^{\rm{L}},{\rm{ }}\forall i,j{\text{;}} $
|
(11) |
|
$ \qquad{\nu ^{\rm{T}}}t_{ik}^{\rm{P}}{\text{≥}}w_{ik}^{\rm{P}},{\rm{ }}\forall i,k{\text{;}} $
|
(12) |
|
$ \qquad{\nu ^{\rm{T}}}t_{ki}^{{\rm{RP}}} {\text{≥}} w_{ki}^{{\rm{RP}}},{\rm{ }}\forall i,k{\text{;}} $
|
(13) |
|
$ \qquad{\nu ^{\rm{T}}}t_{kj}^{\rm{R}}{\text{≥}} w_{kj}^{\rm{R}},{\rm{ }}\forall j,k{\text{;}} $
|
(14) |
|
$ \qquad\sum\limits_i {w_{ij}^{\rm{L}}} + \sum\limits_k {w_{kj}^{\rm{R}}} {\text{≤}} \sum\limits_q {V_{jq}^{\rm{L}}{L_{jq}}}, {\rm{ }}\forall j{\text{;}} $
|
(15) |
|
$ \qquad\sum\limits_i {w_{ik}^{\rm{P}}} {\text{≤}}\sum\limits_q {V_{kp}^{\rm{R}}{R_{kp}}}, {\rm{ }}\forall k{\text{;}} $
|
(16) |
|
$ \qquad\sum\limits_q {{L_{jq}}} {\text{≤}} 1,{\rm{ }}\forall j{\text{;}} $
|
(17) |
|
$ \qquad\sum\limits_p {{R_{kp}}} {\text{≤}} 1,{\rm{ }}\forall k{\text{;}} $
|
(18) |
|
$ \qquad{L_{jq}},{R_{kp}} \in \{ 0,1\} ,{\rm{ }}\forall j,k,q,p{\text{;}} $
|
(19) |
|
$ \begin{split} &\qquad\varpi _i^{\rm{L}},\varpi _i^{\rm{P}},w_{ij}^{\rm{L}},w_{ik}^{\rm{P}},w_{kj}^{\rm{R}},w_{ki}^{{\rm{RP}}} {\text{≥}} 0{\text{且}}{\rm{ }}\forall i,j,k{\text{;}}\\ & t_{ij}^{\rm{L}},t_{ik}^{\rm{P}},t_{kj}^{\rm{R}},t_{ki}^{{\rm{RP}}} {\text{≥}} 0{\text{且为整数}},{\rm{ }}\forall i,j,k{\text{。}} \end{split} $
|
(20) |
其中,式(4)表示各城区分别运往填埋场与资源化工厂的建筑废弃物量等于该城区建筑废弃物总产生量;式(5)表示各城区采取填埋处理的建筑废弃物占总量的
$1 - \gamma $
;式(6)表示各城区回收利用的建筑废弃物占总量的
$\gamma $
;式(7)与式(8)分别表示各城区运往各填埋场、各资源化工厂的总量与该城区采取填埋处理、回收利用的总量相等;式(9)表示由各城区运往k资源化工厂的建筑废弃物回收利用后生产的资源化产品与该工厂销往各城区的资源化产品总量保持质量守恒;式(10)表示由各城区运往k资源化工厂的建筑废弃物回收利用后的废渣总量等于从该工厂运往各填埋场的总废渣量;式(11)为将建筑废弃物由i城区运往j填埋场所需的渣土车数量(式(12),式(13),式(14)同理);式(15)表示每年由各城区、各资源化工厂运往j填埋场的建筑废弃物总量不得超过该填埋场的年最大处理量;式(16)表示由各城区运往k资源化工厂的建筑废弃物总量不得超过该工厂的年最大处理量;式(17)表示各填埋场候选点仅能建至多一种消纳规模的填埋场,式(18)表示各资源化工厂候选点仅能建至多一种处理规模的资源化工厂;式(19)为对决策变量的0−1约束;式(20)为对决策变量的非负约束。
1.4 目标函数的处理
上述确定性模型为多目标混合整数规划问题,为求得模型的Pareto解,引入线性加权法,将多目标转化为单一目标进行求解,各分目标权重系数分别为
${\tau _{\rm{c}}}$
、
${\tau _{\rm{g}}} $
、
${\tau _{\rm{v}}} $
。模型中3个目标分别为成本、GHG排放量以及视觉污染,均为不同量纲不同量级,需无量纲化后再进行线性加权。
|
$ \begin{split} \qquad \min \;Z \!=\! 100\left[ {{\tau _{\rm{c}}}\left( {\frac{{{Z_{\rm{c}}} \!-\! Z_{\rm{c}}^*}}{{Z_{\rm{c}}^*}}} \right) \!+\! {\tau _{\rm{g}}}\left( {\frac{{{Z_{\rm{g}}} \!-\! Z_{\rm{g}}^*}}{{Z_{\rm{g}}^*}}} \right)\! +\!\!\! } \right. \left. {{\tau _{\rm{v}}}\left( {\frac{{{Z_{\rm{v}}} \!-\! Z_{\rm{v}}^*}}{{Z_{\rm{v}}^*}}} \right)} \right]{\text{。}} \end{split} $
|
(21) |
其中,
$Z_{\rm{c}}^*$
、
$Z_{\rm{g}}^*$
和
$Z_{\rm{v}}^*$
分别为确定模型下的最小成本、最小GHG排放量和最小视觉污染。
2 鲁棒优化模型
线性规划问题一般形式如下。
|
$ \qquad \left\{ \begin{array}{l} \min\; {{cx}} + {{d}}{\text{。}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\;\;{{Ax}} {\text{≤}} {{b}} {\text{。}} \end{array} \right. $
|
(22) |
传统的线性规划问题中,参数c、d、A、b的基本假设都是确定性的,而在鲁棒优化中,充分考虑数据的不确定性,不确定性参数在既定的不确定性集合U中变化。
|
$ \qquad \left\{ \begin{array}{l} \min \;{\rm{ }}{{cx}} + {{d}}{\text{。}}\\ {\rm{s}}{\rm{.t}}{\rm{. }}\;{{Ax}} {\text{≤}} {{b}}{\text{;}} {{c}},{{d}},{{A}},{{b}} \in U{\text{。}} \end{array} \right. $
|
(23) |
若向量x满足来自不确定性集合U的约束的所有实现,则向量
${{x}}$
是问题(23)的鲁棒可行解。Ben-Tal 等[16]将问题(23)的鲁棒相对(robust counterpart,RC)定义如下
|
$ \qquad\min \;\left\{ {\widehat {{c}}(x) \!=\! \mathop {\sup }\limits_{(c,d,A,b \in U)} [{{cx}} \!+\! {{d}}]\!:\!{{Ax}} {\text{≤}} {{b}}{\rm{ }}\forall {{c}},{{d}},{{A}},{{b}} \in U} \right\}{\text{。}} $
|
(24) |
问题(24)的最优解是问题(23)的鲁棒最优解,此解满足数据的所有可能实现的约束并且保证最优的目标函数值不差于
$\widehat {{c}}({{{x}}^*})$
。问题(24)为一半定线性优化问题且较难计算,但对于紧凑的、凸不确定集,RC是容易求解的(多项式可解的)凸数学问题。
为便于陈述,将上述确定性模型简化如下。
|
$ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\min \;{\rm{ }}{{fy}} + {{cx}}{\text{。}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;{{Hx}} = {{d}}, \\ \qquad {{Nx}} = 0 , \\ \qquad {{Ar}} {\text{≥}} {{Vx}}, \\ \qquad {{Bx}} {\text{≤}} {{Cy}} , \\ \qquad {{Gy}} {\text{≤}} {{m}} , \\ \qquad {{y}} \in \left\{ {0,1} \right\},{{x}} \in {{\bf{R}} ^ * },{ r} \in {{\bf{N}}^ * } {\text{。}} \end{array} \right. $
|
(25) |
模型(25)中,向量f、c、d、m分别代表消纳设施建设固定成本、消纳设施单位处理成本(及资源化产品销售价格)、各城区建筑废弃物产生量和设施选址的数量约束;矩阵H、N、A、V、B、C、G为约束的系数矩阵;y是消纳设施选址的0~1变量;x包含所有连续决策变量;r是运输车数量的决策变量。
本文将消纳设施建设固定成本,单位处理成本(及资源化产品销售价格),各城区建筑废弃物产生量以及废弃物资源化率定为不确定性参数,对应模型(25)中的f、c、d、假设各不确定性参数在一特定的有界闭空间内变化
|
$ \qquad{u_{\rm{{Box}}}} = \left\{ {{{\vartheta}} \in {R ^n}:\left| {{\vartheta _t} - \overline {{\vartheta _t}} } \right| {\text{≤}} \rho {G_t},t = 1, \cdots ,n} \right\}{\text{。}} $
|
(26) |
其中,
${\overline \vartheta _t}$
是向量
${{\vartheta}} $
第
$t$
个参数
${\vartheta _t}$
的标称值;正数
${G_t}$
代表不确定性范围;
$\rho {\text{>}}0$
,表示不确定性水平;当
${G_t} = {\overline \vartheta _t}$
时,
${\vartheta _t}$
与标称值
${\overline \vartheta _t}$
的相对偏差则为
$\rho $
。综上,模型(25)的RC可表示如下。
|
$ \qquad\min \; {\textit{z}}{\text{。}} $
|
(27) |
|
$ {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;\;{{fy}} + {{cx}} {\le} {\textit{z}},{\rm{ }}\forall {{f}} \in u_{{\rm{Box}}}^{\rm{f}},{\rm{ }}\forall c \in u_{{\rm{Box}}}^{\rm{c}}{\text{;}} $
|
(28) |
|
$ \qquad{{Hx}} = {{d}},\;\forall d \in u_{{\rm{Box}}}^{\rm{d}}{\text{;}} $
|
(29) |
|
$ \qquad{{Nx}} = 0{\text{;}} $
|
(30) |
|
$ \qquad{{Ar}} {\text{≥}} {{Vx}}{\text{;}} $
|
(31) |
|
$ \qquad{{Bx}} {\text{≤}} {{Cy}}{\text{;}} $
|
(32) |
|
$ \qquad{{Gy}} {\text{≤}} {{m}}{\text{;}} $
|
(33) |
|
$ \qquad{{y}} \in \left\{ {0,1} \right\},x \in {{\bf{R}} ^ * },r \in {{\bf{N}}^ * }{\text{。}} $
|
(34) |
根据式(26),式(28)等同于
|
$ \begin{split} &\qquad {{fy}} + {{cx}} {\text{≤}} {\textit{z}},{\rm{ }}\forall {{f}} \in u_{{\rm{Box}}}^{\rm{f}}|u_{{\rm{Box}}}^{\rm{f}} = \left\{ {{{f}} \in {R ^{{n_f}}}:\left| {{f_l} -} \right. }\left. {{{\overline f }_l}} \right| {\text{≤}} \right.\\ &\left. {{\rho _{\rm{c}}}G_l^{\rm{f}},l = 1, \cdots ,{n_{\rm{f}}}} \right\} {\text{;}} \\ &\qquad \forall {{c}} \in u_{{\rm{Box}}}^{\rm{c}}|u_{{\rm{Box}}}^{\rm{c}}\! =\! \left\{ {{{c}} \in {R ^{{n_c}}}\!:\!\left| {{c_t} \!-\! {{\overline c }_t}} \right| {\text{≤}} {\rho _{\rm{c}}}G_t^{\rm{c}},t \!=\! 1, \cdots ,{n_{\rm{c}}}} \right\}{\text{。}} \\ \end{split} $
|
(35) |
不等式(35)的左侧均为不确定性参数的向量,因此,上述半定不等式的易处理形式如下,其中
$\eta $
为非负实数
|
$ \quad\quad\left\{ \begin{array}{l} \displaystyle\sum\limits_t {\left( {{c_t}{x_t} + \eta _t^{\rm{c}}} \right)} + \displaystyle\sum\limits_l {\left( {{f_l}{y_l} + \eta _l^{\rm{c}}} \right)} {\text{≤}} {\textit{z}} {\text{;}}\\ {\rho _{\rm{c}}}G_t^c{x_t} {\text{≤}} \eta _t^{\rm{c}},{\rm{ }}\forall t \in \left\{ {1, \cdots ,{n_{\rm{c}}}} \right\} {\text{;}} \\ {\rho _{\rm{c}}}G_t^c{x_t} {\text{≥}} - \eta _t^{\rm{c}},{\rm{ }}\forall t \in \left\{ {1, \cdots ,{n_{\rm{c}}}} \right\}{\text{;}} \\ {\rho _{\rm{f}}}G_l^f{y_l} {\text{≤}} \eta _l^{\rm{c}},{\rm{ }}\forall l \in \left\{ {1, \cdots ,{n_{\rm{f}}}} \right\}{\text{;}} \\ {\rho _{\rm{f}}}G_l^f{y_l} {\text{≥}} - \eta _l^{\rm{c}},{\rm{ }}\forall l \in \left\{ {1, \cdots ,{n_{\rm{f}}}} \right\}{\text{。}} \\ \end{array} \right. $
|
(36) |
同理,对式(29)转换后,本文确定性模型的鲁棒相对的易处理模型如下。
|
$ \quad\quad\min\; {Z_{\rm{c}}}, $
|
(37) |
|
$ \begin{split} &\qquad\min \;{Z_{\rm{g}}} = \sum\limits_s {{\pi _s}\left( {\sum\limits_i {\sum\limits_j {t_{ij}^{\rm{L}}} } d_{ij}^{\rm{L}} + \sum\limits_i {\sum\limits_k {t_{ik}^{\rm{P}}d_{ik}^{\rm{P}}} } + } \right.} \\ &\left. {\sum\limits_k {\sum\limits_i {t_{ki}^{{\rm{RP}}}d_{ki}^{{\rm{RP}}}} } + \sum\limits_k {\sum\limits_j {t_{kj}^{\rm{R}}d_{kj}^{\rm{R}}} } } \right), \end{split} $
|
(38) |
|
$ \qquad\min \;{Z_{\rm{v}}} \!=\! \sum\limits_i {{P_i}\left[ {\sum\limits_j {\frac{{{\phi ^{\rm{L}}}(\sum\limits_{i'} {w_{i'j}^{\rm{L}}} \!\! +\!\! \sum\limits_k {w_{kj}^{\rm{R}}} )}}{{{{(d_{ij}^{\rm{L}} \!\!+\!\! \varepsilon )}^2}}} \!\!+\!\! \sum\limits_k {\frac{{{\phi ^{\rm{P}}}(\sum\limits_{i'} {w_{i'k}^{\rm{P}}} )}}{{{{(d_{ik}^{\rm{P}}\! \!+\!\! \varepsilon )}^2}}}} } } \right]} {\text{。}} $
|
(39) |
|
$ \begin{split} &{\rm{s}}.{\rm{t}}.\\ &\qquad \sum\limits_j {\sum\limits_q {\left( {\overline {f_{jq}^{\rm{L}}} {L_{jq}} \!+\! \eta _{jq}^{{\rm{fL}}}} \right)} } \!+\!\!\sum\limits_i {\sum\limits_j {\left( {\overline {c_{ij}^{\rm{L}}} w_{ij}^{\rm{L}} \!+\! \eta _{ij}^{{\rm{cL}}}} \right)} } \!+\! \\ &\sum\limits_k {\sum\limits_p {\left( {\overline {f_{kp}^{\rm{P}}} {R_{kp}} \!+\! \eta _{kp}^{{\rm{fP}}}} \right)} } \!+\!\!\sum\limits_i {\sum\limits_k {\left( {\overline {c_{ik}^{\rm{P}}} w_{ik}^{\rm{P}} \!+\! \eta _{ik}^{{\rm{cP}}}} \right)} } \!+\!\!\sum\limits_i {\sum\limits_j {t_{ij}^{\rm{L}}\left( {a \!+\! } \right.} } \\ &\left. {bd_{ij}^{\rm{L}}} \right) \!+\!\!\sum\limits_i {\sum\limits_k {t_{ik}^{\rm{P}}(a \!+\! bd_{ik}^{\rm{P}})} } \!+\!\!\sum\limits_k {\sum\limits_i {\left( {\overline {{\rm{p}}{{\rm{r}}_{ki}}} w_{ki}^{{\rm{RP}}} \!+\! \eta _{ki}^{{\rm{pr}}}} \right)} } \!+\! \\ &\sum\limits_k {\sum\limits_i {t_{ki}^{{\rm{RP}}}(a \!+\! bd_{ki}^{{\rm{RP}}})} } \!+\!\!\sum\limits_k {\sum\limits_j {\left( {\overline {c_{kj}^{\rm{R}}} w_{kj}^{\rm{R}} \!+\! \eta _{kj}^{{\rm{cR}}}} \right)} } {\rm{ \!+\! }}\\ &\sum\limits_k {\sum\limits_j {t_{kj}^{\rm{R}}(a \!+\! b} } d_{kj}^{\rm{R}}) {\text{≤}} {Z_{\rm{c}}} {\text{;}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $
|
(40) |
|
$ \qquad{\rho _{{\rm{fL}}}}G_{jq}^{{\rm{fL}}}{L_{jq}} {\text{≤}} \eta _{jq}^{{\rm{fL}}},{\rm{ }}\forall j,q{\text{;}} $
|
(41) |
|
$ \qquad{\rho _{{\rm{fL}}}}G_{jq}^{{\rm{fL}}}{L_{jq}} {\text{≥}} - \eta _{jq}^{{\rm{fL}}},{\rm{ }}\forall j,q{\text{;}} $
|
(42) |
|
$ \qquad{\rho _{{\rm{fP}}}}G_{kp}^{{\rm{fP}}}{R_{kp}} {\text{≤}} \eta _{kp}^{{\rm{fP}}},{\rm{ }}\forall k,p{\text{;}} $
|
(43) |
|
$ \qquad{\rho _{{\rm{fP}}}}G_{kp}^{{\rm{fP}}}{R_{kp}} {\text{≥}} - \eta _{kp}^{{\rm{fP}}},{\rm{ }}\forall k,p{\text{;}} $
|
(44) |
|
$ \qquad{\rho _{{\rm{cL}}}}G_{ij}^{{\rm{cL}}}w_{ij}^{\rm{L}} {\text{≤}} \eta _{ij}^{{\rm{cL}}},{\rm{ }}\forall i,j{\text{;}} $
|
(45) |
|
$ \qquad{\rho _{{\rm{cL}}}}G_{ij}^{{\rm{cL}}}w_{ij}^{\rm{L}} {\text{≥}} - \eta _{ij}^{{\rm{cL}}},{\rm{ }}\forall i,j{\text{;}} $
|
(46) |
|
$ \qquad{\rho _{{\rm{cP}}}}G_{ik}^{{\rm{cP}}}w_{ik}^{\rm{P}} {\text{≤}} \eta _{ik}^{{\rm{cP}}},{\rm{ }}\forall i,k{\text{;}} $
|
(47) |
|
$ \qquad{\rho _{{\rm{cP}}}}G_{ik}^{{\rm{cP}}}w_{ik}^{\rm{P}} {\text{≥}} - \eta _{ik}^{{\rm{cP}}},{\rm{ }}\forall i,k{\text{;}} $
|
(48) |
|
$ \qquad{\rho _{{\rm{pr}}}}G_{ki}^{{\rm{pr}}}w_{ki}^{{\rm{RP}}} {\text{≤}} \eta _{ki}^{{\rm{pr}}},{\rm{ }}\forall k,i{\text{;}} $
|
(49) |
|
$ \qquad{\rho _{{\rm{pr}}}}G_{ki}^{{\rm{pr}}}w_{ki}^{{\rm{RP}}} {\text{≥}} - \eta _{ki}^{{\rm{pr}}},{\rm{ }}\forall k,i{\text{;}} $
|
(50) |
|
$ \qquad{\rho _{{\rm{cR}}}}G_{kj}^{{\rm{cR}}}w_{kj}^{\rm{R}} {\text{≤}} \eta _{kj}^{{\rm{cR}}},{\rm{ }}\forall k,j{\text{;}} $
|
(51) |
|
$ \qquad{\rho _{{\rm{cR}}}}G_{kj}^{{\rm{cR}}}w_{kj}^{\rm{R}} {\text{≥}} - \eta _{kj}^{{\rm{cR}}},{\rm{ }}\forall k,j{\text{;}} $
|
(52) |
|
$ \qquad{\overline W _i} + {\rho _{\rm{W}}}G_i^{\rm{W}} = \varpi _i^{\rm{L}} + \varpi _i^{\rm{P}},{\rm{ }}\forall i{\text{;}} $
|
(53) |
|
$ \qquad\varpi _i^{\rm{L}} = \left( {1 - \gamma \left( {1 + {\rho _\gamma }} \right)} \right)\left( {{{\overline W }_i} + {\rho _{\rm{W}}}G_i^{\rm{W}}} \right),{\rm{ }}\forall i{\text{;}} $
|
(54) |
|
$ \qquad\varpi _i^{\rm{P}} = \gamma \left( {1 + {\rho _\gamma }} \right)\left( {{{\overline {\rm{W}} }_i} + {\rho _{\rm W}}G_i^{\rm{W}}} \right),{\rm{ }}\forall i{\text{;}} $
|
(55) |
|
$ \qquad\eta _{jq}^{{\rm{fL}}},\eta _{kp}^{{\rm{fP}}},\eta _{ij}^{{\rm{cL}}},\eta _{ik}^{{\rm{cP}}},\eta _{ki}^{{\rm{pr}}},\eta _{kj}^{{\rm{cR}}} {\text{≥}} 0,{\rm{ }}\forall i,j,k,p,q{\text{。}} $
|
(56) |
其余约束条件与确定性模型中式(7)—式(20)同,其中变量
${\eta _*}$
为非负实数。
3 案例分析
以北京市为例,本文采用建筑面积估算法(见式(57))对北京市各城区建筑废弃物产生量进行估计,建筑废弃物包括新建垃圾、拆除垃圾、装修垃圾以及工程槽土,市政及其他工程暂不考虑,有关建筑结构对废弃物产生量的影响暂时忽略。
|
$ \qquad{W_i} = {A_i} \times {\rm{WGR}}{\text{。}} $
|
(57) |
式中,
${A_i}$
为城区i的年房屋建筑面积,
${\rm{WGR}}$
为废弃物产生量指标,
${W_i}$
为城区
$i$
的建筑废弃物产生量。对于新建工程,可由北京统计年鉴查得当年房屋建筑竣工面积,废弃物产生量指标为550 t/hm2;装修工程建筑面积借鉴当年房屋面积成交量,废弃物产生量指标0.13 t/m2;拆除面积取年施工面积的10 %,废弃物产生量指标为1.3 t/m2[17]。
北京市2010年—2016年常住人口、房屋施工面积、竣工面积及销售面积等相关数据可由北京市统计局官方网站[18]查得,根据式(57),历年来全市建筑废弃物总产生量如表1和图2所示。由图2可知,近年来北京市建筑废弃物产生量呈较平稳的上升趋势,然而北京市处理建筑废弃物的能力远没能跟上逐年增长的废弃物量,从而导致非法倾倒与垃圾围城等现象,因此,建筑废弃物消纳设施的合理选址以及废弃物的合理分配显得至关重要。
表 1(Tab. 1)
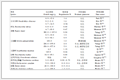
表 1 北京市2010年—2016年建筑废弃物产生量
Tab. 1 The amount of waste generation in Beijing in 2010−2016
| 年份 |
装修垃圾 |
拆除垃圾 |
新建垃圾 |
工程槽土 |
合计 |
| 2010 |
2 131 350 |
2 0243 730 |
2 149 620 |
9 471 580 |
33 996 280 |
| 2011 |
1 872 000 |
2 3484 760 |
2 218 260 |
10 987 984 |
38 563 004 |
| 2012 |
2 526 810 |
2 6059 020 |
2 047 925 |
12 192 421 |
42 826 176 |
| 2013 |
2 474 030 |
2 7983 800 |
2 194 335 |
13 092 982 |
45 745 147 |
| 2014 |
1 896 700 |
2 8181 010 |
2 732 125 |
13 185 252 |
45 995 087 |
| 2015 |
2 021 110 |
2 6011 830 |
2 293 610 |
12 170 342 |
42 496 892 |
| 2016 |
2 177 630 |
2 9537 820 |
1 976 535 |
13 820 073 |
47 512 058 |
|
表 1 北京市2010年—2016年建筑废弃物产生量
Tab. 1 The amount of waste generation in Beijing in 2010−2016
|
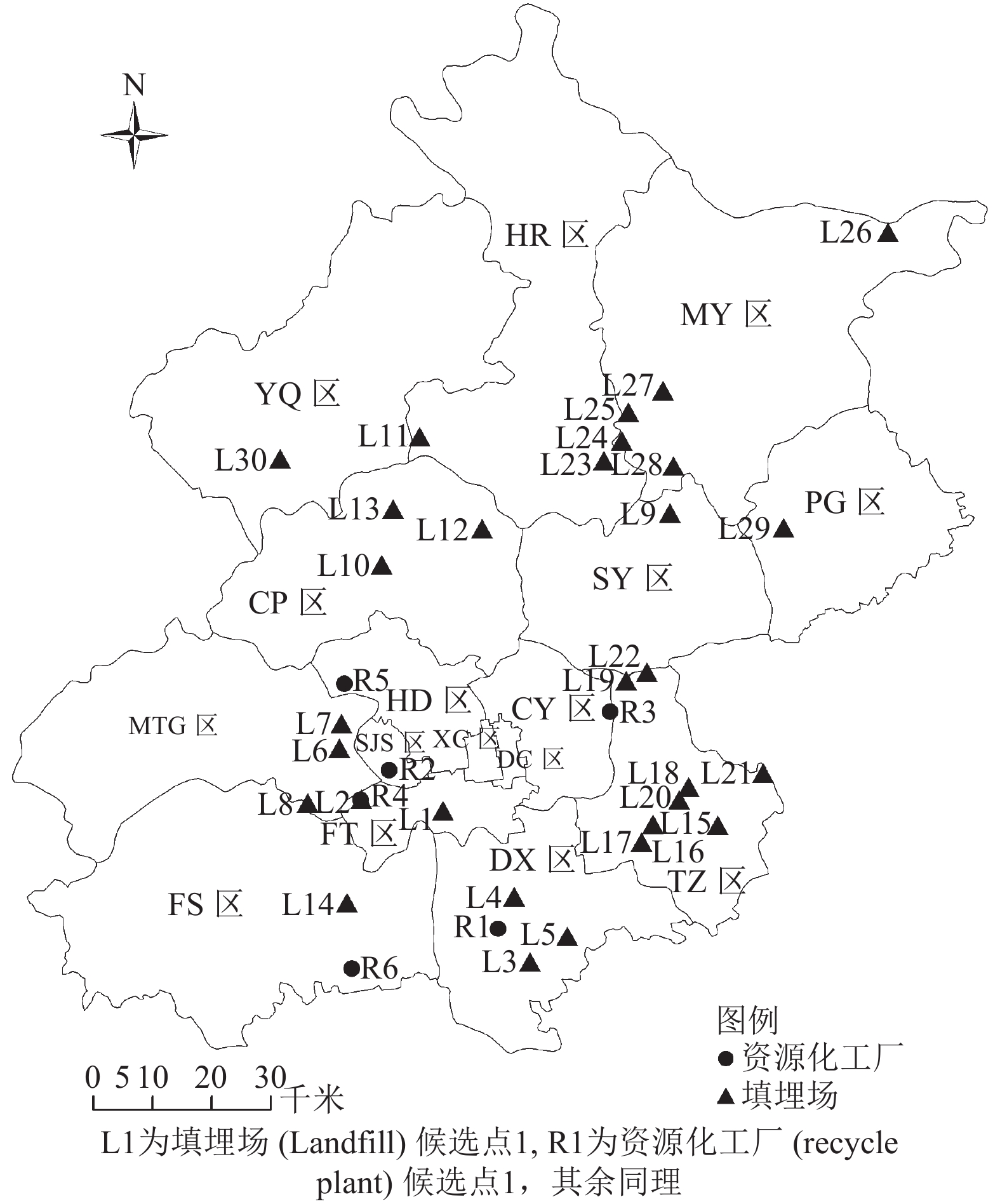
据北京市建筑垃圾综合管理及循环利用信息共享平台统计[19],目前北京市共有30多处经营性建筑废弃物填埋场,6处建筑废弃物资源化工厂,详细分布见图3。本文选取北京市2016年各城区建筑废弃物产生量,以现有消纳设施为候选点,运用上述鲁棒优化模型对北京市建筑废弃物消纳设施进行选址及废弃物分配。由《北京区域统计年鉴2017》[20]可查得各城区2016年相关数据。根据式(57),各城区废弃物产生量见表2。
表 2(Tab. 2)

表 2 北京市2016年各城区建筑废弃物产生量
Tab. 2 The amount of waste generation in Beijing in 2016
| 城区 |
装修垃圾 |
拆除垃圾 |
新建垃圾 |
工程槽土 |
合计 |
| DC区 |
0.085 8 |
2.510 3 |
0.041 8 |
1.174 5 |
3.812 4 |
| XC区 |
0.161 2 |
1.937 0 |
0.166 7 |
0.906 3 |
3.171 1 |
| CY区 |
2.111 2 |
42.585 4 |
2.730 2 |
19.924 7 |
67.351 5 |
| FT区 |
1.849 9 |
24.534 9 |
1.197 4 |
11.479 3 |
39.061 5 |
| SJS区 |
0.724 1 |
5.452 2 |
0.602 3 |
2.550 1 |
9.329 5 |
| HD区 |
0.795 6 |
25.576 2 |
1.212 8 |
11.966 5 |
39.551 1 |
| FS区 |
2.346 5 |
19.626 1 |
1.555 4 |
9.182 6 |
32.710 6 |
| TZ区 |
2.552 0 |
60.318 7 |
2.178 6 |
28.221 7 |
93.271 0 |
| SY区 |
2.620 8 |
21.365 5 |
1.422 9 |
9.996 4 |
35.405 6 |
| CP区 |
2.077 4 |
26.527 8 |
3 267 0 |
12.411 8 |
44.284 0 |
| DX区 |
3.273 4 |
38.252 5 |
3.071 8 |
17.897 5 |
62.495 1 |
| MTG区 |
1.185 6 |
11.373 7 |
0.577 5 |
5.321 5 |
18.458 3 |
| HR区 |
0.232 7 |
4.286 1 |
0.418 6 |
2.005 4 |
6.942 7 |
| PG区 |
0.999 7 |
4.791 8 |
0.642 4 |
2.242 0 |
8.675 9 |
| MY区 |
0.553 8 |
4.243 2 |
0.458 2 |
1.985 3 |
7.240 5 |
| YQ区 |
0.206 7 |
1.995 5 |
0.224 4 |
0.933 7 |
3.360 3 |
|
表 2 北京市2016年各城区建筑废弃物产生量
Tab. 2 The amount of waste generation in Beijing in 2016
|
假设有4种规模填埋场和2种规模资源化工厂,在各候选点建设不同规模的填埋场、资源化工厂的填埋场候选点建设固定成本如表3所示;表4为各点之间的距离;表5为资源化工厂候选点固定成本;表6为与模型相关的其他参数设定;货车排放的尾气中包括
${\rm{HC}}$
、
${\rm{CO}}$
、
${\rm{N}}{{\rm{O}}_x}$
、
${\rm{P}}{{\rm{M}}_{30}}$
等有害气体,由EmfacHKV34计算得运输车各类GHG排放量如表7所示。
表 3(Tab. 3)

表 3 填埋场候选点建设固定成本
Tab. 3 The fixed cost of landfill candidates
| 候选点 |
规模Q1 |
规模Q2 |
规模Q3 |
规模Q4 |
| L1 |
1.00 |
1.80 |
2.20 |
3.00 |
| L2 |
0.90 |
1.70 |
2.10 |
2.90 |
| L3 |
0.65 |
1.30 |
1.60 |
2.40 |
| L4 |
0.70 |
1.40 |
1.80 |
2.60 |
| L5 |
0.70 |
1.45 |
1.70 |
2.50 |
| L6 |
0.80 |
1.50 |
1.90 |
2.70 |
| L7 |
0.90 |
1.60 |
2.00 |
2.80 |
| L8 |
0.70 |
1.40 |
1.80 |
2.60 |
| L9 |
0.70 |
1.30 |
1.70 |
2.30 |
| L10 |
0.80 |
1.50 |
1.90 |
2.60 |
| L11 |
0.65 |
1.20 |
1.60 |
2.20 |
| L12 |
0.75 |
1.40 |
1.80 |
2.45 |
| L13 |
0.75 |
1.40 |
1.80 |
2.40 |
| L14 |
0.60 |
1.00 |
1.20 |
2.20 |
| L15 |
0.70 |
1.50 |
1.70 |
2.40 |
| L16 |
0.80 |
1.55 |
1.90 |
2.70 |
| L17 |
0.85 |
1.60 |
2.00 |
2.80 |
| L18 |
0.80 |
1.55 |
1.95 |
2.70 |
| L19 |
0.90 |
1.70 |
2.10 |
2.90 |
| L20 |
0.80 |
1.55 |
1.90 |
2.70 |
| L21 |
0.70 |
1.50 |
1.70 |
2.40 |
| L22 |
0.85 |
1.60 |
2.00 |
2.80 |
| L23 |
0.65 |
1.20 |
1.60 |
2.20 |
| L24 |
0.60 |
1.10 |
1.50 |
2.10 |
| L25 |
0.60 |
1.10 |
1.40 |
2.00 |
| L26 |
0.50 |
1.00 |
1.00 |
1.80 |
| L27 |
0.60 |
1.10 |
1.35 |
1.90 |
| L28 |
0.65 |
1.20 |
1.50 |
2.10 |
| L29 |
0.60 |
1.10 |
1.40 |
2.00 |
| L30 |
0.60 |
1.10 |
1.30 |
1.90 |
| 年处理量/106t
|
0.50 |
1.00. |
2.00 |
3.50 |
|
表 3 填埋场候选点建设固定成本
Tab. 3 The fixed cost of landfill candidates
|
表 5(Tab. 5)

表 5 资源化工厂候选点建设固定成本
Tab. 5 The fixed cost of recycled plant candidates
| 候选点 |
规模P1 |
规模P2 |
| R1 |
2.17 |
4.20 |
| R2 |
2.35 |
4.50 |
| R3 |
2.66 |
5.20 |
| R4 |
2.44 |
5.01 |
| R5 |
3.60 |
6.10 |
| R6 |
1.90 |
3.80 |
| 年处理量/106t
|
1.00 |
2.00 |
|
表 5 资源化工厂候选点建设固定成本
Tab. 5 The fixed cost of recycled plant candidates
|
表 4(Tab. 4)

表 4 各点之间的距离
Tab. 4 Distance between points
| 候选点 |
DC区 |
XC区 |
CY区 |
FT区 |
SJS区 |
HD区 |
FS区 |
TZ区 |
SY区 |
CP区 |
DX区 |
MTG区 |
HR区 |
PG区 |
MY区 |
YQ区 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
| L1 |
32 |
26 |
29 |
7 |
14 |
27 |
27 |
60 |
71 |
63 |
27 |
25 |
103 |
106 |
104 |
104 |
22 |
12 |
33 |
14 |
28 |
31 |
| L2 |
37 |
30 |
40 |
22 |
18 |
31 |
19 |
86 |
88 |
63 |
44 |
17 |
95 |
139 |
114 |
105 |
32 |
7 |
45 |
0 |
20 |
29 |
| L3 |
54 |
50 |
56 |
52 |
60 |
60 |
54 |
58 |
88 |
114 |
22 |
74 |
108 |
121 |
127 |
147 |
8 |
41 |
45 |
40 |
58 |
31 |
| L4 |
41 |
38 |
40 |
32 |
44 |
51 |
39 |
48 |
76 |
87 |
9 |
56 |
96 |
111 |
118 |
128 |
6 |
31 |
36 |
31 |
47 |
31 |
| L5 |
48 |
52 |
45 |
43 |
53 |
57 |
49 |
53 |
80 |
106 |
21 |
71 |
102 |
112 |
122 |
155 |
12 |
42 |
39 |
43 |
58 |
37 |
| L6 |
37 |
29 |
41 |
29 |
18 |
27 |
31 |
65 |
82 |
48 |
46 |
5 |
88 |
109 |
108 |
85 |
44 |
11 |
46 |
13 |
7 |
42 |
| L7 |
35 |
31 |
37 |
31 |
20 |
29 |
32 |
67 |
74 |
41 |
48 |
7 |
81 |
111 |
101 |
85 |
44 |
11 |
46 |
13 |
7 |
42 |
| L8 |
42 |
36 |
44 |
33 |
24 |
36 |
30 |
67 |
81 |
61 |
49 |
18 |
101 |
119 |
114 |
102 |
39 |
15 |
54 |
9 |
21 |
30 |
| L9 |
60 |
69 |
55 |
84 |
83 |
70 |
100 |
45 |
20 |
62 |
94 |
92 |
19 |
38 |
17 |
94 |
77 |
65 |
36 |
72 |
63 |
96 |
| L10 |
42 |
44 |
46 |
52 |
52 |
39 |
67 |
72 |
49 |
5 |
77 |
42 |
48 |
100 |
65 |
43 |
66 |
35 |
47 |
41 |
21 |
70 |
| L11 |
79 |
83 |
84 |
89 |
83 |
74 |
102 |
88 |
60 |
30 |
102 |
76 |
40 |
95 |
66 |
64 |
86 |
58 |
58 |
63 |
45 |
92 |
| L12 |
47 |
54 |
50 |
68 |
69 |
55 |
85 |
65 |
33 |
19 |
81 |
63 |
30 |
78 |
50 |
73 |
69 |
45 |
38 |
51 |
36 |
79 |
| L13 |
54 |
53 |
53 |
62 |
58 |
49 |
77 |
83 |
56 |
12 |
77 |
52 |
52 |
97 |
71 |
36 |
74 |
45 |
51 |
50 |
31 |
79 |
| L14 |
54 |
47 |
56 |
34 |
35 |
48 |
11 |
76 |
92 |
72 |
33 |
34 |
112 |
135 |
124 |
113 |
26 |
24 |
56 |
18 |
38 |
11 |
| L15 |
47 |
53 |
44 |
58 |
67 |
66 |
75 |
26 |
53 |
87 |
50 |
81 |
79 |
72 |
99 |
138 |
42 |
57 |
27 |
61 |
69 |
67 |
| L16 |
42 |
49 |
40 |
53 |
62 |
60 |
62 |
21 |
50 |
87 |
34 |
69 |
70 |
77 |
89 |
126 |
32 |
46 |
21 |
50 |
58 |
57 |
| L17 |
38 |
43 |
34 |
43 |
51 |
52 |
55 |
25 |
60 |
77 |
29 |
66 |
80 |
87 |
98 |
121 |
29 |
45 |
23 |
49 |
58 |
54 |
| L18 |
44 |
47 |
42 |
53 |
62 |
58 |
70 |
16 |
52 |
80 |
53 |
76 |
74 |
62 |
76 |
124 |
41 |
51 |
19 |
56 |
62 |
66 |
| L19 |
30 |
37 |
29 |
52 |
55 |
42 |
69 |
11 |
18 |
57 |
53 |
63 |
38 |
54 |
54 |
102 |
48 |
44 |
6 |
50 |
48 |
68 |
| L20 |
44 |
50 |
40 |
54 |
64 |
60 |
71 |
17 |
44 |
82 |
48 |
78 |
67 |
70 |
87 |
125 |
38 |
50 |
19 |
55 |
61 |
63 |
| L21 |
53 |
59 |
51 |
64 |
73 |
70 |
81 |
26 |
48 |
89 |
59 |
87 |
75 |
61 |
75 |
135 |
53 |
64 |
28 |
69 |
73 |
78 |
| L22 |
35 |
42 |
34 |
55 |
55 |
44 |
72 |
13 |
17 |
58 |
58 |
67 |
44 |
53 |
53 |
103 |
51 |
47 |
9 |
54 |
52 |
72 |
| L23 |
59 |
66 |
62 |
78 |
78 |
67 |
100 |
63 |
27 |
48 |
98 |
87 |
6 |
62 |
21 |
87 |
83 |
65 |
43 |
72 |
59 |
98 |
| L24 |
63 |
70 |
66 |
84 |
84 |
71 |
118 |
67 |
32 |
54 |
100 |
92 |
11 |
62 |
15 |
96 |
87 |
69 |
47 |
76 |
63 |
102 |
| L25 |
68 |
75 |
71 |
89 |
109 |
79 |
123 |
72 |
38 |
68 |
110 |
98 |
15 |
69 |
13 |
95 |
92 |
74 |
52 |
81 |
68 |
107 |
| L26 |
138 |
145 |
141 |
169 |
156 |
146 |
186 |
142 |
107 |
138 |
180 |
168 |
77 |
74 |
50 |
162 |
137 |
126 |
95 |
133 |
121 |
157 |
| L27 |
82 |
87 |
83 |
107 |
122 |
88 |
137 |
79 |
41 |
72 |
123 |
110 |
25 |
56 |
10 |
105 |
97 |
81 |
56 |
88 |
74 |
113 |
| L28 |
62 |
74 |
62 |
94 |
94 |
77 |
111 |
65 |
29 |
61 |
104 |
99 |
18 |
45 |
9 |
100 |
85 |
72 |
44 |
79 |
68 |
103 |
| L29 |
76 |
82 |
74 |
102 |
100 |
83 |
112 |
67 |
36 |
68 |
111 |
110 |
43 |
14 |
36 |
124 |
85 |
79 |
43 |
86 |
80 |
106 |
| L30 |
93 |
90 |
101 |
95 |
91 |
83 |
109 |
115 |
89 |
42 |
119 |
84 |
82 |
139 |
103 |
10 |
89 |
57 |
71 |
60 |
40 |
89 |
| R1 |
41 |
35 |
46 |
33 |
41 |
42 |
33 |
56 |
85 |
80 |
13 |
53 |
113 |
116 |
124 |
121 |
- |
- |
- |
- |
- |
- |
| R2 |
26 |
20 |
27 |
16 |
7 |
21 |
26 |
51 |
64 |
49 |
32 |
9 |
79 |
105 |
98 |
90 |
- |
- |
- |
- |
- |
- |
| R3 |
22 |
29 |
22 |
45 |
49 |
36 |
62 |
10 |
30 |
55 |
48 |
60 |
49 |
65 |
65 |
99 |
- |
- |
- |
- |
- |
- |
| R4 |
36 |
33 |
38 |
21 |
21 |
34 |
16 |
57 |
76 |
55 |
36 |
16 |
95 |
113 |
114 |
96 |
- |
- |
- |
- |
- |
- |
| R5 |
46 |
42 |
53 |
41 |
31 |
28 |
45 |
65 |
64 |
30 |
58 |
20 |
70 |
114 |
89 |
70 |
- |
- |
- |
- |
- |
- |
| R6 |
66 |
53 |
68 |
45 |
45 |
55 |
23 |
83 |
100 |
84 |
39 |
46 |
113 |
142 |
135 |
125 |
- |
- |
- |
- |
- |
- |
|
表 4 各点之间的距离
Tab. 4 Distance between points
|
表 6(Tab. 6)

表 6 其他相关参数
Tab. 6 Other related parameters
|
$c_{ij}^{\rm{L}}$
/(元·t−1)
|
$c_{ik}^{\rm{P}}$
/(元·t−1)
|
${\rm{p}}{{\rm{r}}_{ki}}$
/(元·t−1)
|
$c_{kj}^{\rm{R}}$
/(元·t−1)
|
a/元
|
b/(元·t−1)
|
γ
|
h
|
λ
|
${\phi ^{\rm{L}}}$
/(hm2·t−1)
|
${\phi ^{\rm{R}}}$
/(hm2·t−1)
|
${\nu ^{\rm{T}}}$
/t
|
| 10 |
22 |
24 |
10 |
150 |
10 |
0.05 |
0.95 |
0.05 |
10.0 |
2.5 |
25 |
|
表 6 其他相关参数
Tab. 6 Other related parameters
|
表 7(Tab. 7)

表 7 运输车GHG排放量
Tab. 7 The amount of GHG emission of the trucks
|
${\rm{HC}}$
|
${\rm{CO}}$
|
${\rm{N}}{{\rm{O}}_x}$
|
${\rm{P}}{{\rm{M}}_{30}}$
|
| 0.090 7 |
1.496 0 |
5.368 4 |
0.130 2 |
|
表 7 运输车GHG排放量
Tab. 7 The amount of GHG emission of the trucks
|
本文假设
${\tau _{\rm{c}}} = 0.5$
,
${\tau _{\rm{g}}} = 0.3$
,
${\tau _{\rm{v}}} = 0.2$
,且各不确定性参数的不确定性水平均相同,即
${\rho _{\rm{{fL}}}} = {\rho _{\rm{fP}}} = {\rho _{\rm{cL}}}=$
$ {\rho _{\rm{cP}}} = {\rho _{\rm{pr}}} = {\rho _{\rm{cR}}} = {\rho _{\rm{W}}} = {\rho _\gamma }$
。根据上述数据,采用CPLEX 12.6.1软件包进行求解,计算结果如表8所示,
$\rho = 0$
时即为确定性模型,总目标函数值随着
$\rho $
的增加而不断增大。
表 8(Tab. 8)

表 8 不同不确定性水平下的目标函数值
Tab. 8 Objective value under each uncertainty level
|
$\rho $
|
0 |
0.1 |
0.3 |
0.5 |
0.7 |
0.9 |
1 |
| 目标函数值 |
27.76 |
32.29 |
46.36 |
61.92 |
73.35 |
89.88 |
95.61 |
|
表 8 不同不确定性水平下的目标函数值
Tab. 8 Objective value under each uncertainty level
|
表9、图4为
$\rho = 0$
、
$\rho = 0.1$
、
$\rho = 0.3$
与
$\rho = 0.5$
时的选址结果。由表9可知,随着不确定性水平的增大,填埋场与资源化工厂的设施数量及其规模也逐渐增加;由图4可知,消纳设施的选址大多集中在废弃物产生量较大的城区附近。现实中,较偏远候选点虽建设固定成本较小,对居民所产生视觉污染较少,但其地理劣势也将造成运输成本以及GHG排放的增加。因此,在3个目标函数的相互约束下,选址结果更为均衡,各城区建筑废弃物分配至就近消纳设施,仅少数城区运至较远消纳设施。如
$\rho =$
0.3时,为保证更远城区的废弃物消纳,CY区建筑废弃物则运至L15、L17、R1和R2,并未选择就近的L16和R3。
表 9(Tab. 9)

表 9 不同不确定性水平下的消纳设施选址
Tab. 9 Location of construction waste facilities under each uncertainty level
| 不确定性水平
$\rho $
|
填埋场 |
资源化工厂 |
| 0 |
L2(Q4),L3(Q4),L5(Q4),L7(Q4),L8(Q4),L9(Q4),L11(Q2),L12(Q4),L14(Q4),L16(Q4),L17(Q4),L18(Q4),L20(Q4),L21(Q3),L24(Q1), L25(Q1),L27(Q1),L29(Q2),
L30(Q1)
|
R2(P1),R3(P1), R6(P1) |
| 0.1 |
L2(Q4),L3(Q4),L5(Q4),L7(Q4),L8(Q4),L9(Q4),L11(Q2),L12(Q4),L14(Q4),L15(Q4),L17(Q4),L18(Q4),L20(Q4),L21(Q2),L24(Q1), L25(Q2),L29(Q2),L30(Q1) |
R2(P1),R3(P1),R6(P1) |
| 0.3 |
L2(Q4),L3(Q4),L5(Q4),L7(Q4),L8(Q4),L9(Q4),L11(Q2),L12(Q4),L14(Q4),L15(Q4),L16(Q4),L17(Q4),L18(Q4),L20(Q4),L24(Q1), L25(Q1),L27(Q1),L29(Q2),
L30(Q1)
|
R1(P1),R2(P1), R3(P1), R6(P1) |
| 0.5 |
L2(Q4),L3(Q4),L4(Q1),L5(Q4),L7(Q4),L8(Q4),L9(Q4),L11(Q3),L12(Q4),L14(Q4),L15(Q4),L16(Q4),L17(Q4),L18(Q4),L20(Q4),L22(Q1),L24(Q1),L25(Q1),L27(Q1),L29(Q2),L30(Q1) |
R1(P1),R2(P2), R3(P1),R6(P1) |
|
表 9 不同不确定性水平下的消纳设施选址
Tab. 9 Location of construction waste facilities under each uncertainty level
|
随后,在各不确定性水平下,在相应的不确定性集合中均匀生成5个随机实现(例如:~[标称值−
${\rho _ \bullet }G_ \bullet ^*$
,标称值+
${\rho _ \bullet }G_ \bullet ^*$
])用于评估所构建的确定性模型与鲁棒模型所获得的解的性能,计算结果见表10。如表10所示,在所有不确定性水平下,鲁棒模型所获得的解相较于确定模型所获得的解,总目标函数值更大但标准差更小,因此在处理参数不确定的情况下,本文所构建的鲁棒模型具有较好的稳定性。
表 10(Tab. 10)

表 10 各随机实现下的计算结果
Tab. 10 Summary of results under five realizations
| 不确定性水平
$\rho $
|
标称值下的目标函数值 |
|
随机实现目标函数的均值 |
|
随机实现目标函数的标准差 |
|
各随机实现的目标函数值 |
| 确定模型 |
鲁棒模型 |
|
确定模型 |
鲁棒模型 |
|
确定模型 |
鲁棒模型 |
|
确定模型 |
鲁棒模型 |
| 0.1 |
27.76 |
32.29 |
|
27.98 |
32.61 |
|
0.272 7 |
0.267 2 |
|
28.21 |
32.75 |
|
|
|
|
|
|
|
|
|
|
27.52 |
32.17 |
|
|
|
|
|
|
|
|
|
|
27.85 |
32.76 |
|
|
|
|
|
|
|
|
|
|
28.25 |
32.92 |
|
|
|
|
|
|
|
|
|
|
28.09 |
32.43 |
| 0.3 |
27.76 |
46.36 |
|
28.01 |
46.36 |
|
1.120 2 |
0.869 7 |
|
26.84 |
45.89 |
|
|
|
|
|
|
|
|
|
|
30.06 |
48.03 |
|
|
|
|
|
|
|
|
|
|
27.32 |
45.81 |
|
|
|
|
|
|
|
|
|
|
27.58 |
45.68 |
|
|
|
|
|
|
|
|
|
|
28.24 |
46.40 |
| 0.5 |
27.76 |
61.92 |
|
28.17 |
62.05 |
|
1.056 5 |
0.877 2 |
|
29.98 |
62.43 |
|
|
|
|
|
|
|
|
|
|
28.41 |
63.44 |
|
|
|
|
|
|
|
|
|
|
26.75 |
61.20 |
|
|
|
|
|
|
|
|
|
|
27.94 |
61.03 |
|
|
|
|
|
|
|
|
|
|
27.75 |
62.13 |
|
表 10 各随机实现下的计算结果
Tab. 10 Summary of results under five realizations
|
4 结论与展望
建筑废弃物设施的合理选址及废弃物分配受到一系列外部环境不确定因素(比如:废弃物产生量、资源化率、成本等)的影响,而如何在充分考虑外部环境不确定性下综合控制成本、GHG排放和视觉污染等主要目标的最小化是实现建筑废弃物设施合理选址及废弃物分配的关键。本文先后围绕此问题建立确定性模型和综合考虑参数不确定性的鲁棒优化模型,并以北京市为算例,运用CPLEX 12.6.1进行模型求解与分析。结果显示:鲁棒模型的总目标函数值随着不确定性水平的增加而不断增大;与确定性模型相比,鲁棒模型所获得的解更加稳定,具有较强的鲁棒性,证明了所构建鲁棒模型的有效性。本文为建筑废弃物设施选址与废弃物分配的相关决策提供了有效实现工具,决策者可根据项目实际和风险偏好选择合适的不确定性水平,以合理平衡项目目标与风险水平。
本文研究未来可作进一步拓展:首先,若站在政府视角考虑处理非法倾倒建筑废弃物的惩罚成本,可将非法倾倒量定为不确定性参数,用上述鲁棒模型进行求解;其次,目标函数式(2)仅考虑了运输车的GHG排放,有关建筑拆除废弃物生命周期内的碳排放可参考Wang等[21]的研究来予以完善;最后,Bertsimas等[22]所提出的离散鲁棒优化也可用于处理参数的不确定性,未来可综合鲁棒优化与GIS[23](geographic information system)进行设施选址与废弃物分配。


 2019, Vol. 22
2019, Vol. 22