双边装配线多应用于汽车、装载机等大型产品的装配生产中^[1]。该类装配线的投产成本很大，在正式投产之前，设计一条高效、低成本的装配线是节约成本的有效措施之一。而当前双边装配线平衡问题的研究集中于简单的双边装配线平衡问题(two-sided assembly line balancing problem，TALBP)的求解。相对而言，一般双边装配线平衡问题(general two-sided assembly line balancing problem，GTALBP)的研究比较少^[2]。而一般装配线平衡问题往往会考虑更多实际的因素和约束，比如：作业时间不确定、U型/并行装配线、混合模型，作业间的调整时间或其他约束等。

装配生产过程中，调整时间可能产生于：1) 不同作业间走动的时间；2) 取材料的时间；3) 作业之间换工具的时间；4) 其他因素，比如旋转或者等待冷却时间。调整时间对装配效率的影响是不容忽视的，但带有顺序相关调整时间(setup time，ST)的一般装配线平衡问题相关研究较少。文献[3]以作业不兼容的分配约束来简化调整时间的约束，文献[4-5]用数学模型描述了带有ST的装配线平衡问题(assembly line balancing problem with sequence-dependent setup time，ALBPS)，并提出了用启发式算法来求解。文献[6]在文献[5]的基础上，区分了前向ST和后向的ST，并提出了启发式算法和数学模型。此后，不同的元启发式算法涌现，包括SA^[7]、PSO^[8]通过优化作业间的相互顺序，最大程度地降低ST对装配效率的影响，从而大大提高生产率。

此外，针对带有顺序相关调整时间的双边装配线平衡问题(two-sided assembly line balancing problem with sequence-dependent setup time，TALBPS)的研究更少，文献[9]提出了混合整数规划模型和一种2-COMOSOAL/S启发式算法。但该文献假定前向ST和后向ST一样，而本文对ST作了区分。此外，2-COMOSOAL/S算法虽编程简单，但搜索性能有限，尤其是针对大规模算例。因此，本文提出一种变邻域搜索算法来对该问题进一步寻优。

虽然变邻域搜索算法(variable neighborhood search algorithm，VNS)已经被广泛应用于生产排程、汽车排序、位置问题等各种组合优化问题^[10]，但在装配线平衡问题优化中却被忽略。VNS具备编程简单、参数少等优点。本文利用VNS来求解TALBPS的大规模算例问题，来证明该算法在装配线平衡问题中的有效性。

双边装配线顾名思义就是将装配线分为左边和右边。由于装配作业属性的制约，只能分配给装配线左边/右边(left-L/right-R)的作业为L-type/R-type作业，而可以分配给任一边(Either-E)的作业为E-type作业。在装配线的一个位置的左右相对的2个区域内，操作工人分别独立、并行地进行作业。这一个位置对应的工作站称为工作站组。在工作站组中相对的2个工位互称为伴随工位。为了说明双边装配线的特征，如图1所示，箭头的方向是物料流动的方向，物料首先经过工作站组1，而工位1、2在工作站组1中，且互为伴随工位。

图 1(Fig. 1)

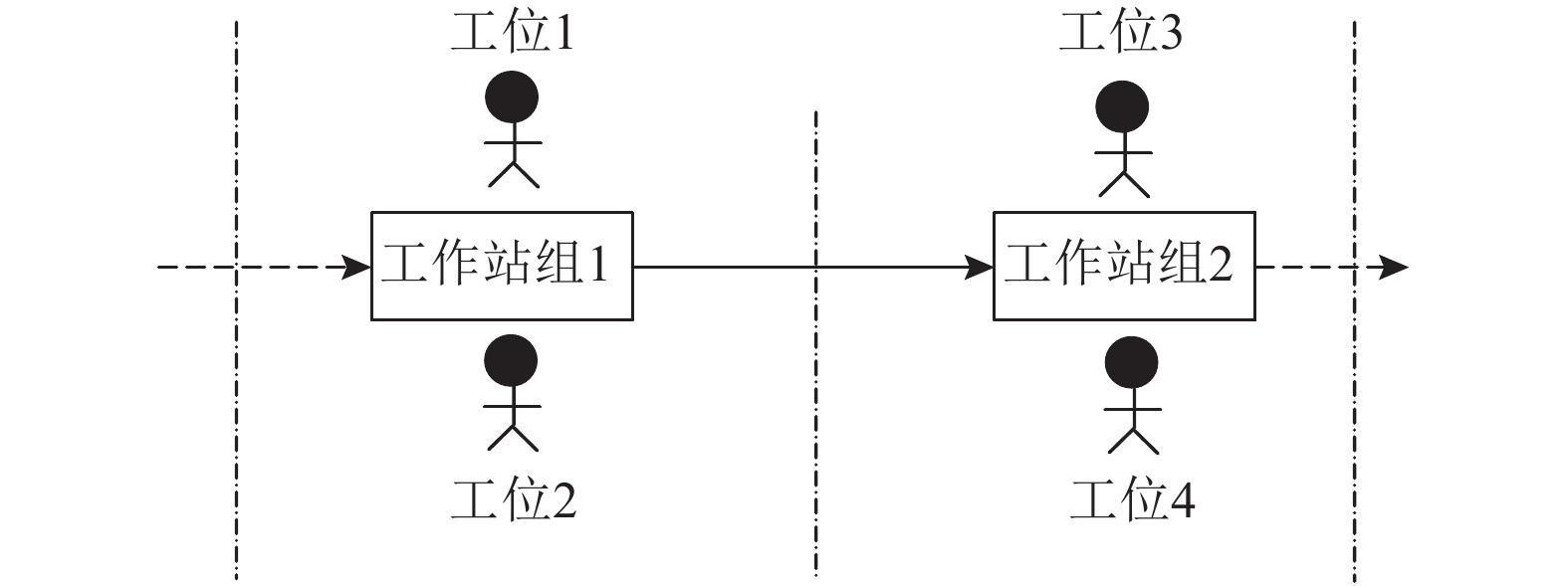
图 1 双边装配线示例 Fig. 1 An example of two-sided assembly line

相较于单边装配线，双边装配线具有以下优点：装配线长度更短，物料搬运成本更低，人员的移动时间更少。但在双边装配线中，由于来自伴随工位的前序作业的影响，作业必须等到前序作业完成才能开始，该等待时间称为序列相关空闲时间。如图2所示，作业1使作业3产生序列相关空闲时间。因此，为了有效减少序列相关空闲时间对装配效率的影响，TALBPS致力于寻找更合理的作业序列。

图 2(Fig. 2)

图 2 序列相关调整时间示例 Fig. 2 An example of sequence-dependent setup times

在实际生产中，调整时间是不可避免的一种非生产时间。而在双边装配线平衡问题中，若在一个工作站组j，工位k中，一个作业i被分配在另一个作业r的紧前位置，则可能会产生前向的调整时间；若在工作站组j，工位k中，一个作业p被分配在第一个位置，另一个作业h被分配在工位k的最后一个位置，则可能产生后向的调整时间。如图2所示：作业1、2之间可能产生前向的调整时间Fst₁₂，由于工位是按节拍周期作业，作业2、1之间可能有后向调整时间Bst₂₁，作业3则可能产生后向调整时间Bst₃₃。

本文选取标准算例中作业数量为9的算例(P9^[9]，如图3所示)来说明调整时间对工位的影响。图4表示在节拍为5的情况下，有调整时间和无调整时间问题的2种不同的最优分配结果。在分配1中，共开启2个工作站组和4个工位。而在分配2中，共开启3个工作站组和5个工位，其中工位4为空闲工位。由此可知，调整时间对装配效率的影响不容忽略。

图 3(Fig. 3)

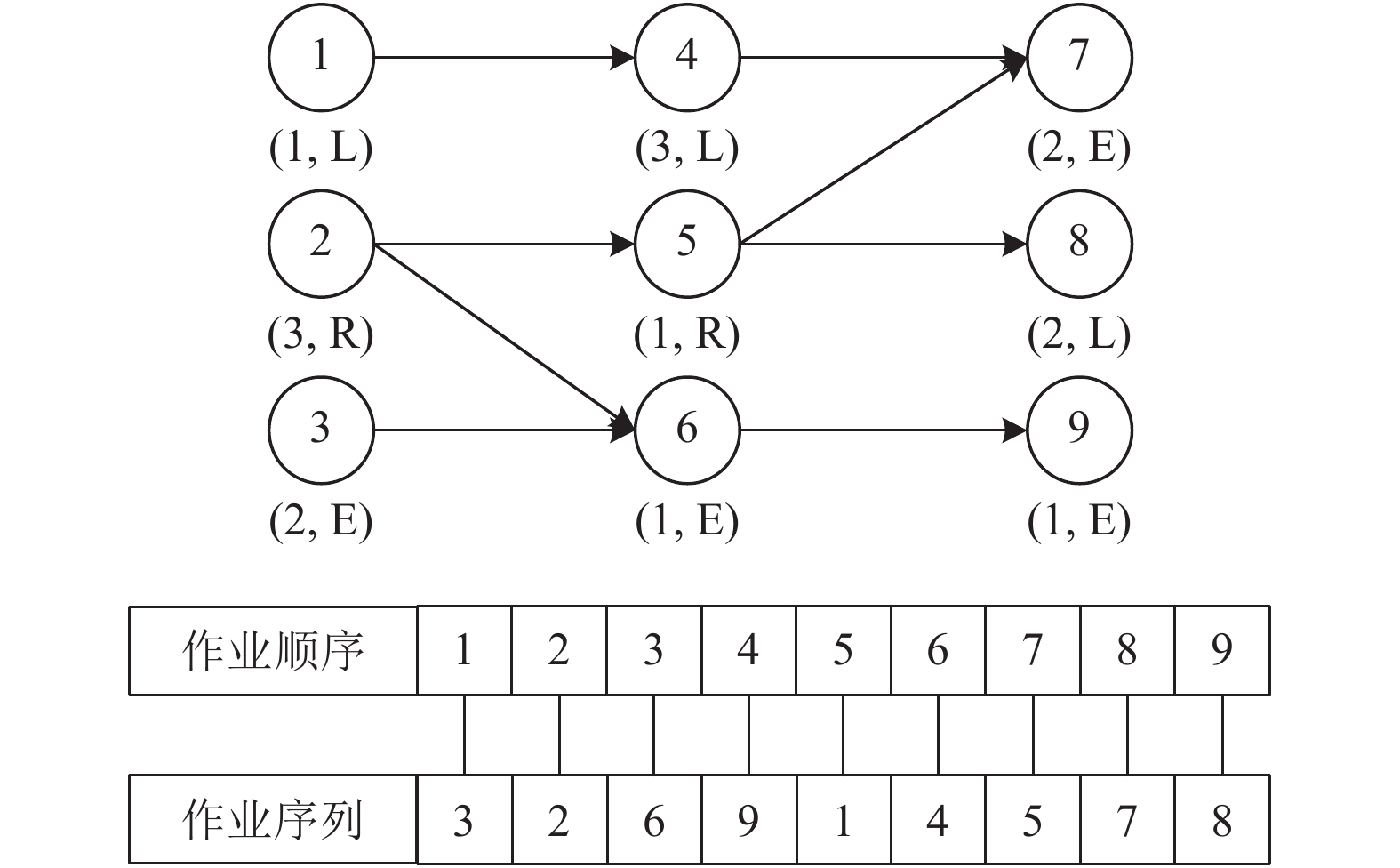
图 3 编码的示例 Fig. 3 An example of encoding method

图 4(Fig. 4)

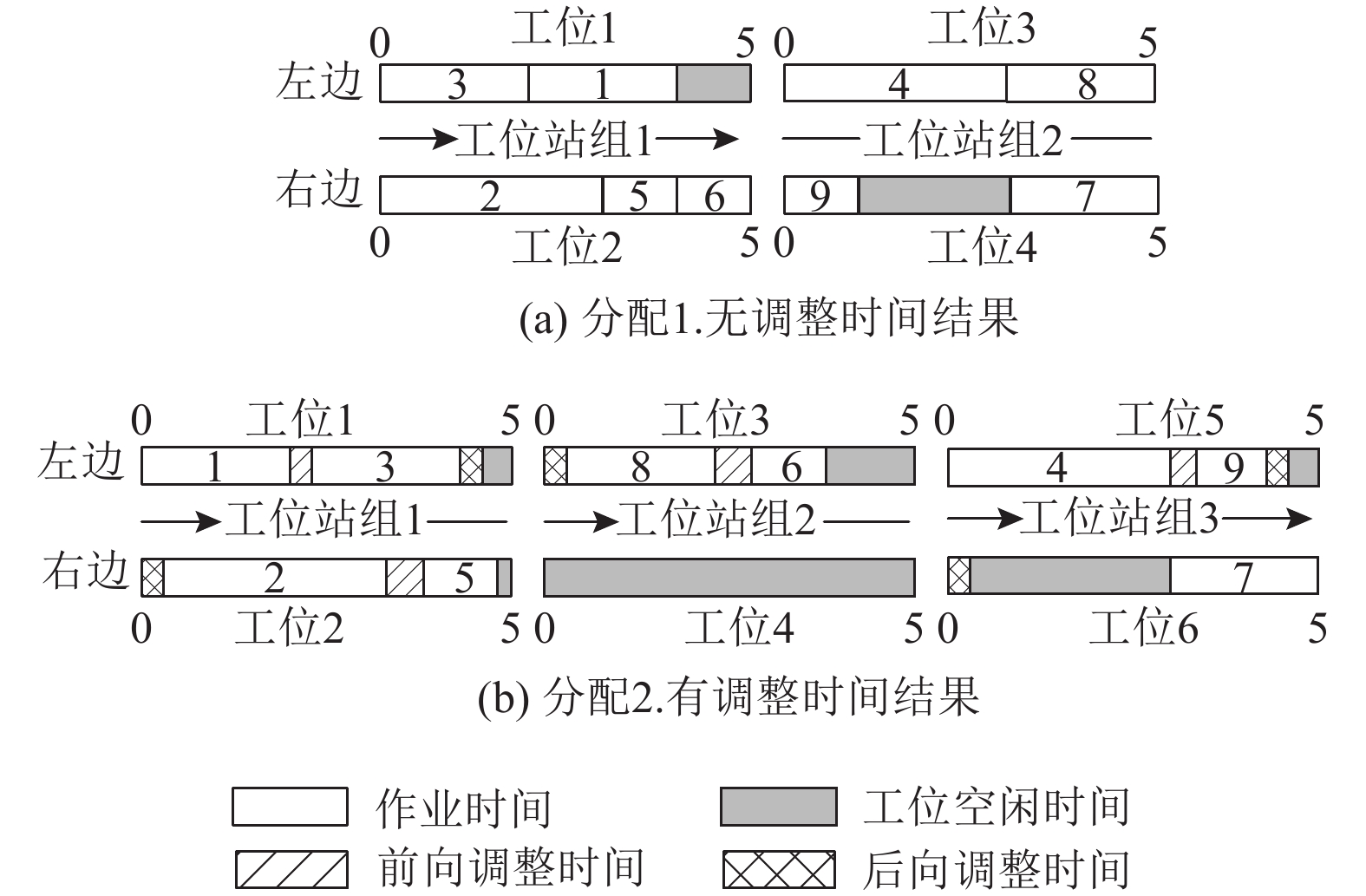
图 4 P9问题的2种分配结果 Fig. 4 An example of MIP results of P9

总之，TALBPS不仅要最大程度避免产生序列相关空闲时间，而且要充分利用序列相关空闲时间来处理ST，从而降低ST对装配效率的影响，因此TALBPS比TALBP更复杂。针对区分前向和后向带有顺序相关的调整时间的双边装配线平衡问题的复杂性，本文提出一种基于变邻域搜索的算法。

针对双边装配线平衡问题，文献[11]比较了不同编码解码的优劣及适用范围。由于第一类双边装配线平衡的工位数量未知，不适合采用基于工位的编码方式，因此，本文采用基于操作序列的编码方式。该序列为1到N的一个序列，且序列顺序满足作业间的优先关系约束，序列中第i个位置的值代表第i个被分配的作业元素。作业数量为9的示例(P9)^[9]如图3所示，编码序列为[3，2，6，9，1，4，5，7，8]，该序列满足优先约束，可称为可行序列。

针对提出的编码方式，解码方式设计如下：根据编码序列，依次选择作业分配，若作业为L-type或者R-type，则分配给当前工作站组的左边/右边；若作业为E-type，则优先选择作业可以最早开始的工位；如果一样，则随机选择。具体流程如图5所示。作业详细分配过程参考文献[9]。

图 5(Fig. 5)

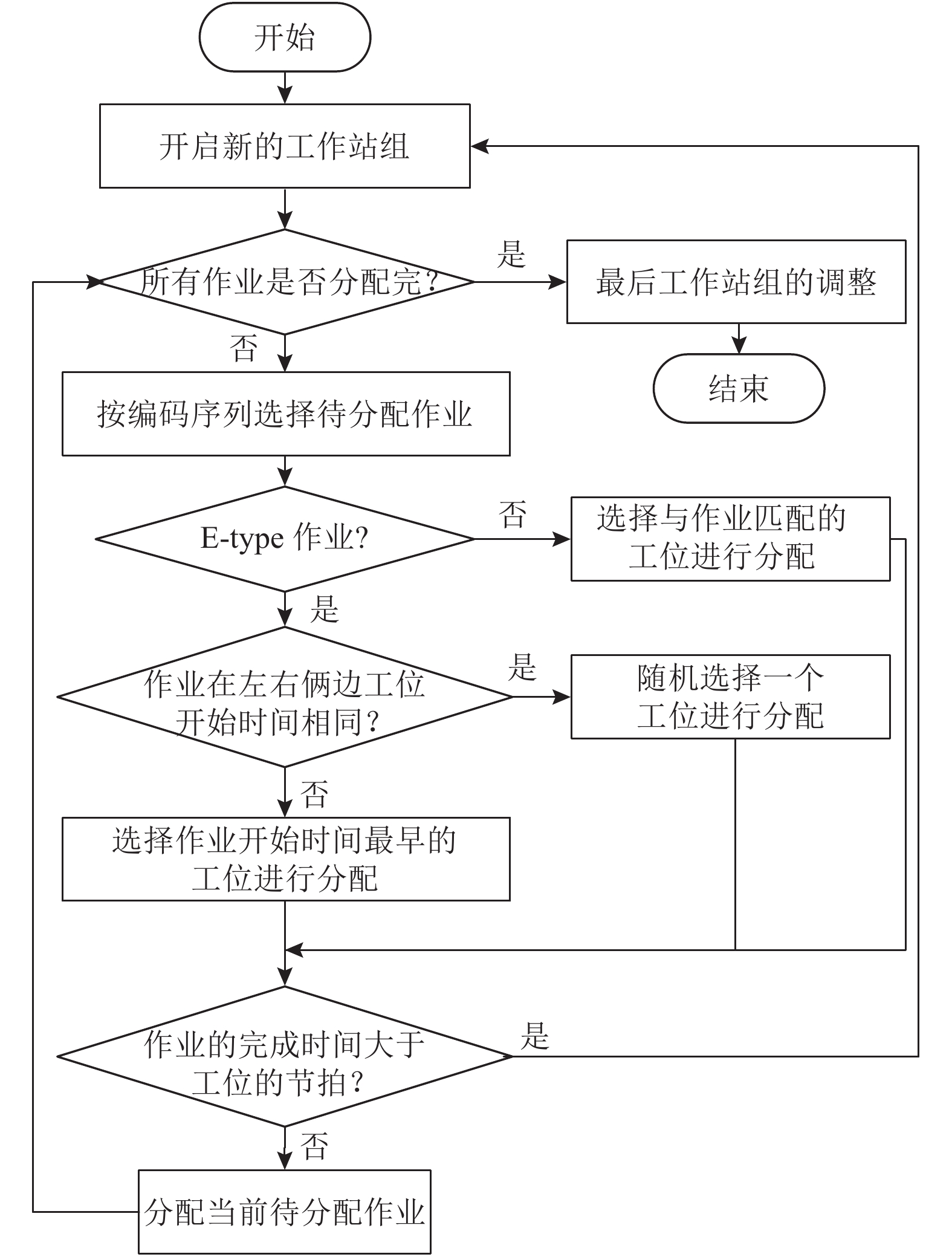
图 5 解码方式 Fig. 5 The decoding method procedure

本文的目标即在给定节拍的情况下，以最小化工作站组数量(线长)为第一目标，以最小化工位数量(工人数量)为第二目标。若仅以上述函数为目标，可能导致算法收敛过慢，因此，本文提出式(1)和式(2)所示的辅助函数来加快收敛速度。式(1)旨在减少工位末端空闲时间，式(2)旨在减少工位的序列相关的空闲时间。此外，若装配线前端工位空闲时间越少，则末端开启的工位数越少。基于这一点，给前端工位的空闲时间一个更大的权重，从而得到辅助函数y₁和y₂。综上所述，适应值函数由3部分组成，第1部分为最小化工作站组数量(NM)，权重为ω₁，设定为10；第2部分为最小化工作站数量(NS)，权重为ω₂，设定为1；第3部分则是辅助函数y₁。权重ω₃设定如式(3)所示，而整个适应值函数如式(4)所示。

式中，CT为节拍；W为工位的上界；k为某工作站组的左边或右边的工位；j为某个工作站组；f_jk为(j，k)工位最后一个作业的完成时间；s_jk为(j，k)工位的负荷。

变邻域算法是基于系统的变换邻域结构来进行局域搜索的元启发式算法。局域搜索算法的缺点为存在大量的不必要的邻域搜索，而变邻域算法仅在少数有希望的邻域结构中搜索，从而避免算法早熟。本文针对TALBPS问题设计了4种比较有效的邻域结构，依次为考虑优先关系约束的交换、插入、交叉和变异等算子。4种邻域的特点为：搜索过程中，仅在可行解的范围内搜索，从而保证邻域解的可行性；4个邻域结构的搜索空间依次增大，从而大大增强算法的搜索能力。

装配线平衡问题算法初始解的生成方式有2种，一种是启发式算法生成，一种是随机生成。本文采用随机法，即随机生成一个数量为N的作业序列，该序列的每一个值在[1，N]中，且各不相同。然后基于矩阵编码方式^[12]，将该随机序列可行化，如图6所示。首先为示例P9随机生成一个初始序列为[5，1，2，3，6，7，4，8，9]，接着从头到尾扫描该随机序列，一旦找到不违背作业优先关系约束的作业，则分配给可行初始序列。其中，先找到作业1，接着作业2，从而得到可行初始序列[1，2，5，3，6，4，7，8，9]。

图 6(Fig. 6)

图 6 初始解可行化示例 Fig. 6 An example of generating feasible initial solution

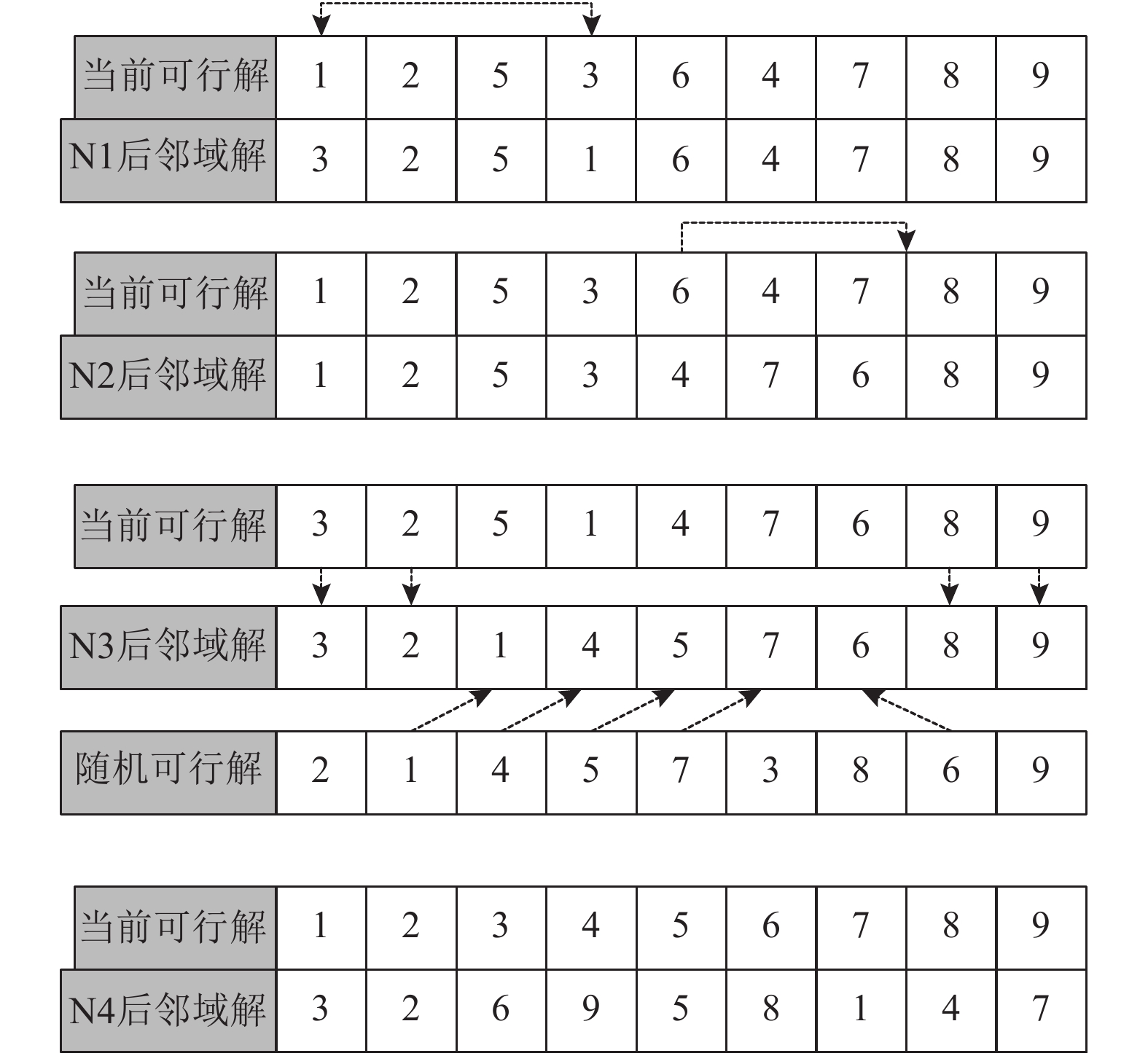
邻域结构的设计如图7所示。N1和N2的操作均为常见的邻域结构，即交换和插入操作。在本文中，序列在进行交换和插入操作时，需要额外考虑优先关系约束，因此N1和N2描述如下。

图 7(Fig. 7)

图 7 变邻域算法的4个邻域结构示例 Fig. 7 An example of four neighborhood structure of VNS

若执行N1，则在序列中随机选择一个作业i，根据优先关系，决定能与作业i交换的作业集合S₁，若S₁不为空，则在S₁中随机选择一个作业j与之交换，得到新的序列；否则，重新随机选择一个作业。其中，S₁集合中的任一作业应满足和作业i交换之后得到的序列仍可行。若执行N2，则在序列中随机选择一个作业i，根据优先关系，决定作业i能插入的位置集合S₂，若S₂不为空，则在S₂中随机选择一个位置j插入当前作业，得到新的序列；否则，重新随机选择一个作业。其中，S₂集合中的位置应满足作业i插入该位置后得到的序列仍可行。

N3的操作基于遗传算法中PMX的交叉算子。N4则基于遗传算法中的变异算子。在本文中，序列在交叉和变异时，均需要考虑优先关系约束，因此，N3和N4描述如下。若执行N3，则在原序列FS₁中随机选择2个位置r₁、r₂(r₁＜r₂)，保留序列中1到r₁以及r₂+1到末尾位置的值，将r₁+1到r₂位置的值删除，同时随机生成一个可行序列FS₂；然后从头到尾搜索FS₂的值，设定count=r₁+1.若搜索到的值已经在FS₁中，则继续搜索下一个位置；否则将该值赋值给FS₁[count]，count=count+1；若count＞r₂或者FS₂序列搜索到最后一个位置，则结束。由此可知，若FS₁和FS₂均可行，则生成的邻域解也是可行的。因为新的邻域解的作业顺序一部分继承自FS₁，而另一部分则继承自FS₂，而且2个序列均满足优先约束。此外，若执行N4，生成一个随机可行序列。针对P9的4个邻域结构如图8所示。从上到下依次为N1—N3。N4为生成随机可行解来作为邻域解，可参考图6。

图 8(Fig. 8)

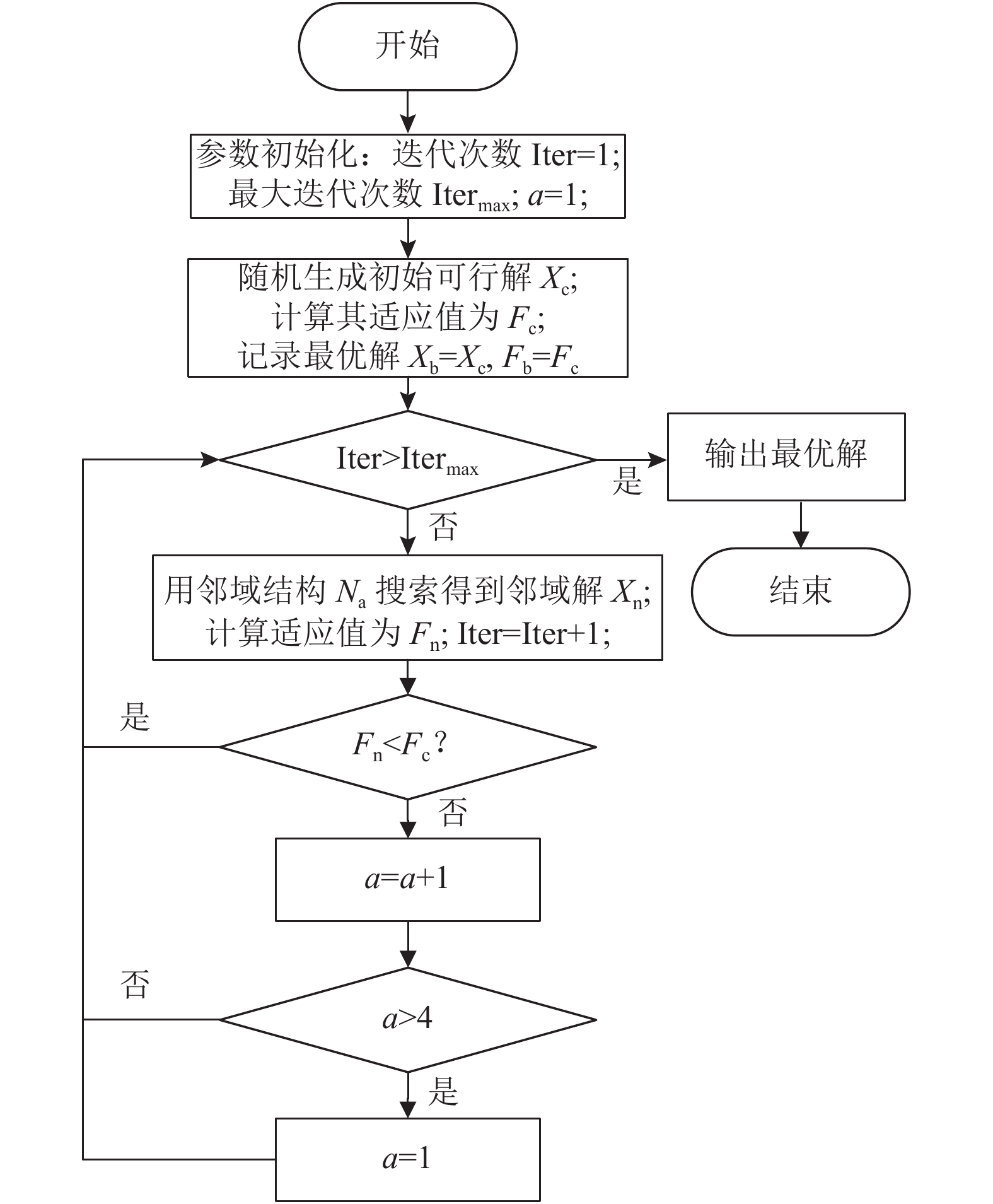
图 8 变邻域搜索算法的流程图 Fig. 8 The flow chart of the VNS algorithm

变邻域搜索算法的具体流程如图8所示。

为了验证VNS算法在求解双边装配线平衡问题的有效性，首先将VNS算法用于求解不带顺序相关调整时间的双边装配线平衡的第一类问题，即TALBP-1问题。该问题已经有大量的算法可供对比。其中，包括文献[13]中的改进蚁群算法(p-ACO)、蚁群算法(ACO)以及禁忌算法(TS)。为了验证算法在大规模问题的有效性，选取作业数量为65的算例(P65)^[14]，作业数量为148的算例(P148)^[1]，以及作业数量为205的算例(P205)^[15]等数据集来进行测试对比，结果如表1所示。由表1可知，在求解TALBP-1问题时，VNS算法在17个测试数据集中，在找到其他算法均搜索到的最优解的基础上，更新了其中4个算例的最优解。表1中带*表示搜索到的更优解，P表示测试问题。由此可见，VNS算法在求解不带ST的TALBP-1时的搜索优越性。

表 1(Tab. 1)

表 1 TALBP-1实验结果对比 Tab. 1 Comparison results of TALBP-1 P CT 最优解 ACO TS p-ACO VNS P65 381 8 8 8 7* 435 7 7 7 7 490 6 6 6 6 544 6 6 5 5 P148 357 9 8 8 8 408 8 7 7 7 459 7 6 6 6 510 6 6 6 6 P205 1 322 11 11 11 10* 1 510 10 9 9 9 1 699 8 9 8 8 1 888 8 8 8 7* 2 077 7 7 7 6* 2 266 7 7 7 6* 2 454 6 6 6 6 2 643 5 6 5 5 2 832 5 6 5 5

表 1 TALBP-1实验结果对比 Tab. 1 Comparison results of TALBP-1

为了验证VNS算法在带ST的TALBPS问题的有效性，将该算法与2-COMOSOAL/S的结果进行比较。VNS算法运用Matlab R2016a进行编程实现，在 Windows 7系统下 Intel Core 3.4 GHz CPU、4 GB RAM的计算机上多次运行。测试的算例包括P65、P148和P205。低水平前向调整时间设置为 $U[ 0,\lceil 0.25 $ $ {\mathop {\min }\limits_{\forall i \in I}}{t_i} \rceil ]$ ，高水平前向调整时间设置为 $U[ 0,\lceil 0.75 $ $ {\mathop {\min }\limits_{\forall i \in I}}{t_i} \rceil ]$ ，而低水平后向调整时间设定为 $ U[ 0,\lceil 1.15 \cdot $ $0.25 \cdot {\mathop {\min }\limits_{\forall i \in I}}{t_i} \rceil ]$ ；高水平后向调整时间设定为 $U[ 0,\lceil 1.15 \cdot $ $ 0.75 \cdot {\mathop {\min }\limits_{\forall i \in I}}{t_i} \rceil ]$ 。此外，对于不同规模问题的最大迭代次数设定如下：P65为10 000次，P148为25 000次，P205为40 000次。每一个算例迭代10次，结果记录最佳的工作站组数(NM)和工位数(NS)。如表2所示，其中，LB为TALBPS的下界^[9]；G是NS和下界之间的差值百分比， $ G = \dfrac{{{\rm NS} - {\rm LB}}}{{\rm NS}} \times 100\% $ ；Avg是G的平均值；Time1和Time2分别为2COMSOAL/S算法和VNS算法的平均收敛时间。

表 2(Tab. 2)

表 2 TALBPS实验结果对比 Tab. 2 Comparison results of TALBPS P CT LB 低水平调整时间 高水平调整时间 Time1 Time2 2COMSOAL/S VNS 2COMSOAL/S VNS NM [NS] G/% NM [NS] G/% NM [NS] G/% NM [NS] G/% P65 326 16 9[18] 11.1 9[17]* 5.88 9[18] 11.1 9[18] 11.1 13 27 381 14 8[15] 6.67 8[15] 6.67 8[16] 12.5 8[15]* 6.67 12 18 435 12 7[13] 7.69 7[13] 7.69 7[14] 14.3 7[13]* 7.69 12 9 490 11 6[12] 8.33 6[12] 8.33 6[12] 8.33 6[12] 8.33 13 3 544 10 6[11] 9.09 5[10]* 0.00 6[11] 9.09 6[11] 9.09 15 35 P148 255 21 11[22] 4.55 11[21]* 0.00 11[22] 4.55 11[22] 4.55 239 59 306 17 10[19] 10.5 9[18]* 5.56 10[19] 10.5 9[18]* 5.56 261 176 357 15 8[16] 6.25 8[15]* 0.00 8[16] 6.25 8[15]* 0.00 306 45 408 13 7[14] 7.14 7[13]* 0.00 7[14] 7.14 7[14] 7.14 281 20 459 12 7[13] 7.69 6[12]* 0.00 7[14] 14.3 6[12]* 0.00 268 132 510 11 6[12] 8.33 6[11]* 0.00 6[12] 8.33 6[11]* 0.00 279 9 P205 1 133 21 12[24] 12.5 12[23]* 8.70 12[24] 12.5 12[23]* 8.70 1 044 59 1 322 18 11[21] 14.3 10[20]* 10.0 11[22] 18.2 10[20]* 10.0 1 063 110 1 510 16 9[18] 11.1 9[18] 11.1 10[19] 15.8 9[18]* 11.1 1 047 65 1 699 14 8[16] 12.5 8[16] 12.5 9[17] 17.7 8[16]* 12.5 1 029 40 1 888 13 8[15] 13.3 7[14]* 7.14 8[16] 18.8 7[14]* 7.14 1 013 97 2 077 12 7[14] 14.3 6[12]* 0.00 7[14] 14.3 7[13]* 7.69 1 087 450 2 266 11 7[13] 15.4 6[12]* 8.33 7[13] 15.4 6[12]* 8.33 1 113 36 2 454 10 6[12] 16.7 6[11]* 9.09 6[12] 16.7 6[12] 16.7 995 27 2 643 9 6[11] 18.2 5[10]* 10.0 6[12] 25.0 5[10]* 10.0 1 110 34 2 832 9 5[10] 10.0 5[10] 10.0 6[11] 18.2 5[10]* 10.0 1 112 390 Avg/% 10.7 5.76 13.3 7.73

表 2 TALBPS实验结果对比 Tab. 2 Comparison results of TALBPS

由表2可知，与2-COMOSOAL/S算法相比，在高/低水平调整时间配置下的21个算例中，VNS算法分别更新了其中15/15个算例的更优解。尤其是针对P205的高调整时间下，VNS算法更新了2-COMOSOAL/S算法在10个算例中的9个更优解。以上证明相较于2-COMOSOAL/S算法，VNS算法搜索结果更优。

此外，在低/高水平设置水平的调整时间下搜索到的Avg中，变邻域搜索算法分别比2-COMOSOAL/S算法的低4.6和5.57。这意味着总体来说，VNS算法比2-COMOSOAL/S算法找到了更多更接近下界的解。综上所述，VNS算法在求解TALBPS-1问题中，尤其是针对大规模算例时，比2-COMOSOAL/S算法更优。此外，在2个算法的结果中均发现，高水平调整时间配置下的Avg比低水平调整时间配置下的Avg要高几个百分点，由此可以说明，调整时间越大，装配所需的工位/工作站组更多。

最后，由表2的Time1和Time2可知，虽然在P65算例计算中，VNS算法的收敛时间比2-COMOSOAL/S长，但是在针对P148和P205的算例中，VNS算法均比2-COMOSOAL/S算法收敛更快，由此可知，VNS算法的收敛性能更优。

本文针对带有顺序相关设置时间的双边装配线平衡的第一类问题，提出了变邻域搜索算法。该算法设计了4个有效的考虑优先关系约束的邻域结构，并通过大规模算例验证，证明VNS在TALBPS-1问题中比2-COMOSOAL/S算法更优，且其易于编码和实现，可以将其应用于其他的一般装配线平衡问题的求解。此外也证明了调整时间的大小对最终工位数的影响是不容忽略的。但本文只针对第一类问题进行研究，下一步可以考虑第二类问题。此外，本文仅考虑了生产单一模型的双边装配线，下一步可研究带调整时间的混流双边装配线平衡问题。最后，VNS算法在装配线平衡中的优越性在本文得到进一步证明，