随着全球制造业多样化个性化市场的扩大,生产制造系统逐渐由刚性的批量生产向柔性多品种小批量生产方式转变,其转变方式的柔性主要体现在面向订单的变批量生产方面。另外,车间内以机器设备和操作人员为代表的不同制造资源的效率也存在着差异,有限的制造资源同时也制约着企业对订单的合理安排。随着绿色制造理念的提出,可持续的生产制造方式逐步提上了日程,并影响着企业长远的发展。在此种生产情景下,如何对客户的订单进行合理的安排是保证企业综合效益最大化的首要前提,是企业保持市场竞争力的关键。
本文绿色制造和外协方式视角下的订单安排问题,是以综合成本最小、绿色指标最优为决策目标,得出多品种订单在不同周期内的生产量和外协量。目前,国内外学者对该问题的研究主要集中在订单生产品种和生产量的接受或拒绝方面。1969年,Miller[1]利用马尔科夫决策方法解决订单选择问题;而后Lippman等[2]在Miller研究的基础上利用半马尔科夫决策过程进行建模,得到订单安排问题的最优决策。而考虑企业的有限生产能力,以利润最大化为决策目标从大量订单中选择性生产则是在20世纪90年代由De等[3]及Slotnick等[4]提出的;其团队成员Ghosh[5]则证明了这是一个基于订单排序的整数规划问题,并提出了一种集束算法来解决这一NP-hard问题。后来随着计算机的普遍应用,Slotnick等[4]和Luo等[6]提出使用遗传算法、模拟退火和禁忌搜索等算法来对订单安排问题进行优化求解。除此之外,Lewis等[7]针对多个阶段订单的安排问题,提出用动态规划方法解决此类订单安排问题。继Slotnick的研究之后,其团队成员Rom等[8]提出采用分批策略,考虑了新增订单的插入情况完善这一方法模型。近几年,Shi等[9]在解决这一问题的混合整数规划模型中加入价格决策等变量解决订单安排问题,并且利用数值方法对模型的正确性进行检验。Li等[10]以拖期惩罚成本为目标,利用最大化产出模型解决这一问题。
国内的研究中,郭源生[11]提出以顾客满意度为目标的规划模型,用于指导中小型企业的订单选择。张欣等[12]以制造能力和产出缓存为约束,构建订单接受决策模型。张人千[13]利用时间序列关联规则,并考虑不同生产周期订单之间的时间序列关联。曹俊杰等[14]针对企业制造能力有限的情形下,利用其改良的遗传算法求解,通过对比研究验证了方法的实用性。肖依永等[15]构建较为复杂的多个节点订单排序优化模型,利用模拟退火算法,给出较为详细的最优解搜索策略。吴红等[16]以订单指向型企业为研究背景,提出了一种基于订单排序的蚁群算法,较好地解决此类企业的实际问题。李艳茹[17]以目标客户的满意度为目标设计了遗传算法进行求解。何晓漩[18]主要针对MTO企业的订单接受问题进行研究,得出需求产品的最优库存量要受到其余产品库存水平的制约等结论。宋栓军等[19]在研究满足交货期的基础上,以供应链企业利润最大化为目标构建优化模型。李娟等[20]利用分支定界方法构建针对MTO企业的数学模型,并对研究结果进行验证。庄晓霞等[21]研究流程型企业订单的生产排序问题,构建以利润最大化为目标的规划模型,其研究结果被证明能够对产能规划起到关键作用。
综上所述,在制造资源有限的情况下,保证企业利益最大化,拒绝部分订单以使多个订单生产平衡的研究是国内外学者的主要方向,目前取得了一些成果。然而,从制造业长远的利益考虑,拒绝订单将会使得企业损失客户源。另外鲜有文献考虑生产制造的绿色性,所建立的模型都仅考虑企业的成本的单周期订单安排。
基于以上分析,针对当前研究的不足,本文考虑多品种小批量企业的制造能力和多周期的可持续性制造,主要探讨以下几个问题:1) 针对多周期的客户订单,如何协调不同周期订单安排才可以使得企业综合效益最优?2) 考虑现代制造业的可持续发展,如何合理地配置制造资源才能使得生产对环境的影响最小?3) 考虑生产能力和外协等成本,如何在不拒绝客户订单情况下合理安排订单生产?
1 问题描述及模型假设本文构建的订单安排模型考虑了多周期的绿色制造以及多成本约束,其问题描述如下:假设多品种小批量制造企业配备有M台机器设备,P位操作人员,第h个周期需要完成的每个种类的生产数量为Dih(i=1, 2,
模型满足以下假设条件:
1) 每个生产周期内必须满足一人一机操作;
2) 生产周期内工人工时不变,机器设备加工能力不变,所有的机器设备和操作人员在任一时刻都可用;
3) 工序的加工时间与机器设备和操作人员有关,工序加工时间不变,不同种类产品工序间切换时间被考虑在加工时间内;
4) 周期内工件各项单位库存成本不变,生产周期内工人工资采取固定工资加单件提成工资的形式。
2 考虑绿色制造和外协方式的多周期订单安排模型的构建 2.1 决策变量Xijmh是第h周期i产品j工序在设备m上加工,取1;否则,取0。
Ylmh是第h周期操作人员l操作设备m,取1;否则,取0。
Qijmh是第h周期i产品j工序在设备m上加工的加工量。
Sih是第h周期i产品需外协的数量。
Cijh是第h周期i产品j工序的库存量。
2.2 参数设置H为计划生产周期数;
N为客户订单的产品种类总数;
Oi为第i类产品工序总数;
P为可用设备操作人员总数;
M为生产周期内可用设备总数;
tijm为第i类产品的第j工序在设备m的操作时间;
tpm为操作人员p操作设备m时间;
Tm为周期内设备m的可用时间;
Rih为产品i在第h周期的客户订单需求量;
Zijm为设备m操作i产品j工序的操作成本;
Wp为人员p的单件提成工资;
Ki为产品i的单位库存成本;
αi为i产品的单位外协成本;
Lijm为设备m操作i产品j工序的噪声值;
Tp为周期内操作人员可用总工时。
2.3 模型构建根据实际生产情况,选择与企业综合效益相关的指标作为模型的优化目标。根据Jovane等[22]在CIRP上提出的竞争性可持续制造(competitive sustainable manufacturing)的构想,本文应用这一思想,将模型的优化指标分为包括各项制造成本和外协成本的竞争性指标,以及包括机器噪声和设备能耗的绿色性指标。
1) 竞争性指标:本文考虑包括制造成本(设备成本、人工成本、库存成本)和外协成本在内的多成本约束竞争性指标。制造成本和外协成本越低,企业的竞争力就越强。
| $\qquad\mathop f\nolimits_1 = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {\sum\limits_{m = 1}^M {\mathop X\nolimits_{ijmh} \mathop Q\nolimits_{ijmh} t_{ijm}^{} \mathop Z\nolimits_{ijm} } } } }, $ | (1) |
| $\qquad\mathop f\nolimits_2 = \sum\limits_{h = 1}^H {\sum\limits_{p = 1}^P {\sum\limits_{m = 1}^M {\left[ {\mathop Y\nolimits_{pmh} \mathop W\nolimits_p \cdot (\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {\mathop X\nolimits_{ijmh} \cdot \mathop Q\nolimits_{ijmh} )} } } \right]} } } ,$ | (2) |
| $\qquad\mathop f\nolimits_3 = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^N {\mathop K\nolimits_i {C_{i\mathop O\nolimits_i h}}} }, $ | (3) |
| $\qquad\mathop f\nolimits_{\rm{4}} = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^N {\mathop \alpha \nolimits_i {S_{ih}}} } {\text{。}}$ | (4) |
2) 绿色性指标:研究表明,同一设备操作不同工序的设备能耗是不同的,选择合理设备加工产品能够减少能源负荷,机器噪声在生产过程中对人员也会造成较大危害;绿色制造正是考虑将这种有危害的指标指数降到最低,以实现企业的可持续性发展。
| $\qquad\mathop f\nolimits_{\rm{5}} = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {\sum\limits_{m = 1}^M {\mathop X\nolimits_{i\!jmh} \mathop Q\nolimits_{i\!jmh} t_{i\!jm} \mathop \delta \nolimits_m } } } }, $ | (5) |
| $\qquad\mathop f\nolimits_{\rm{6}} = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {\sum\limits_{m = 1}^M {10\lg (\frac{{{{10}^{{L_{i\!jm}}}}}}{{t_{i\!jm}^{}}})\mathop {{X_{i\!jmh}} Q}\nolimits_{i\!jmh} } } } } {\text{。}}$ | (6) |
s.t.
| $\qquad \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {X_{i\!jmh} Q_{i\!jmh} t_{i\!jm}} } {\text{≤}} T_m,\forall m,h{\text{;}}$ | (7) |
| $\qquad\sum\limits_{m = 1}^M {\left[ {{Y_{lmh}}t_{pm}^{} \cdot (\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{O_i}} {{\rm{ }}{X_{i\!jmh}} \cdot {\rm{ }}{Q_{i\!jmh}})} } } \right]} {\text{≤}} T_p^{},\;\forall p,h{\text{;}}$ | (8) |
| $\qquad\sum\limits_{p = 1}^P {\mathop Y\nolimits_{pmh} } {\text{≤}} 1,\forall m,h{\text{;}}$ | (9) |
| $\qquad\sum\limits_{m = 1}^M {\mathop Y\nolimits_{pmh} } {\text{≤}} 1,\forall p,h{\text{;}}$ | (10) |
| $\qquad C_{i\!jh} = C_{i\!j(h - 1)} + Q_{i\!jh} - {Q_{i(j + 1)h}},\forall h{\text{;}}$ | (11) |
| $\qquad C_{i n_i h} = C_{i n_i (h - 1)} + {S_{ih}} + Q_{i n_i h} - R_{ih} ,\forall h{\text{;}}$ | (12) |
| $\qquad C_{i\!j(h - 1)} + Q_{i\!jh} {\text{≥}} Q_{i(j + 1)h} ,\forall h{\text{;}}$ | (13) |
| $\qquad\mathop {{S\!_{ih}} + C}\nolimits_{i n _i h} {\text{≥}} \mathop R\nolimits_{ih} ,\forall h{\text{;}}$ | (14) |
| $\qquad\mathop X\nolimits_{i\!jmh} ,\mathop Y\nolimits_{lmh} \in \{ 0,1\} ,{Q_{i\!jmh}},{C_{i\mathop O\nolimits_i h}} \in N{\text{。}}$ | (15) |
该多周期订单安排模型的优化目标为竞争性指标中的式(1)设备成本、式(2)人工成本、式(3)库存成本、式(4)外协成本,以及绿色性指标中的式(5)设备能耗和式(6)噪声指标。该模型以期在实现订单安排最优情况下使得各项成本最小,设备能耗和噪声影响最低。在模型的约束方面,式(7)和(8)表示制造资源能力约束,式(7)表示每周期内每台设备不能超过给定的总可用时间,式(8)表示每周期内的每位工作人员都是有工时限定的,安排其操作设备的总时间不能多于可用总工时;式(9)—(15)表示生产过程的逻辑约束,其中式(9)和(10)表示生产中的一人一机限定,式(11)表示每周期的生产过程中在制品库存应满足的等量关系,式(12)表示为完成订单要求,每周期的生产量和外协量需满足的等式关系,式(13)表示在制品的生产量和库存量的前后约束,式(14)表示如期完成订单时,每周期的外协量、生产量和订单需求的关系,式(15)表示该模型决策变量应该满足的数值约束。
3 求解算法的设计本节以多品种变批量制造企业制造成本和绿色性指标最优为模型的优化目标,但因为两种目标度量的不统一可能会造成求解的偏差,故将多个目标涉及的输入参数归一化。相关研究表明,优化目标的成本指标权重和绿色性指标权重之比为2∶1,故将
该订单安排问题的模型为非线性混合整数规划模型,其求解的变量均为包括0-1变量在内的整数变量。考虑到输入参数的离散性及模型求解的复杂性,一般的求解方法可能会使模型陷入局部最优。而遗传算法求解此类非线性混合整数规划模型具有较好的收敛性,其按一定的概率随机选择初始种群适合输入参数的随机性。故而本节在模型求解方法的选择上,选用较为成熟的遗传算法。算法的核心分为初始种群构建、基因交叉、基因复制以及基因变异4个部分。
1) 初始种群构建:按照本模型所设定的决策变量Xijmh、Ylmh、Qijmh和Sih,此初始种群包括4个染色体。根据决策变量的实际意义编码4条染色体上的基因,而后随机生成
2) 基因交叉:生成
3) 基因复制:将新种群每条染色体对应的值代入模型的目标函数F,而F值就作为新种群的适应度。计算每个种群的适应度后,选择数值最小的
4) 基因变异:对于每个种群,当经过交叉复制生成种群的概率值rand超过设定的变异概率
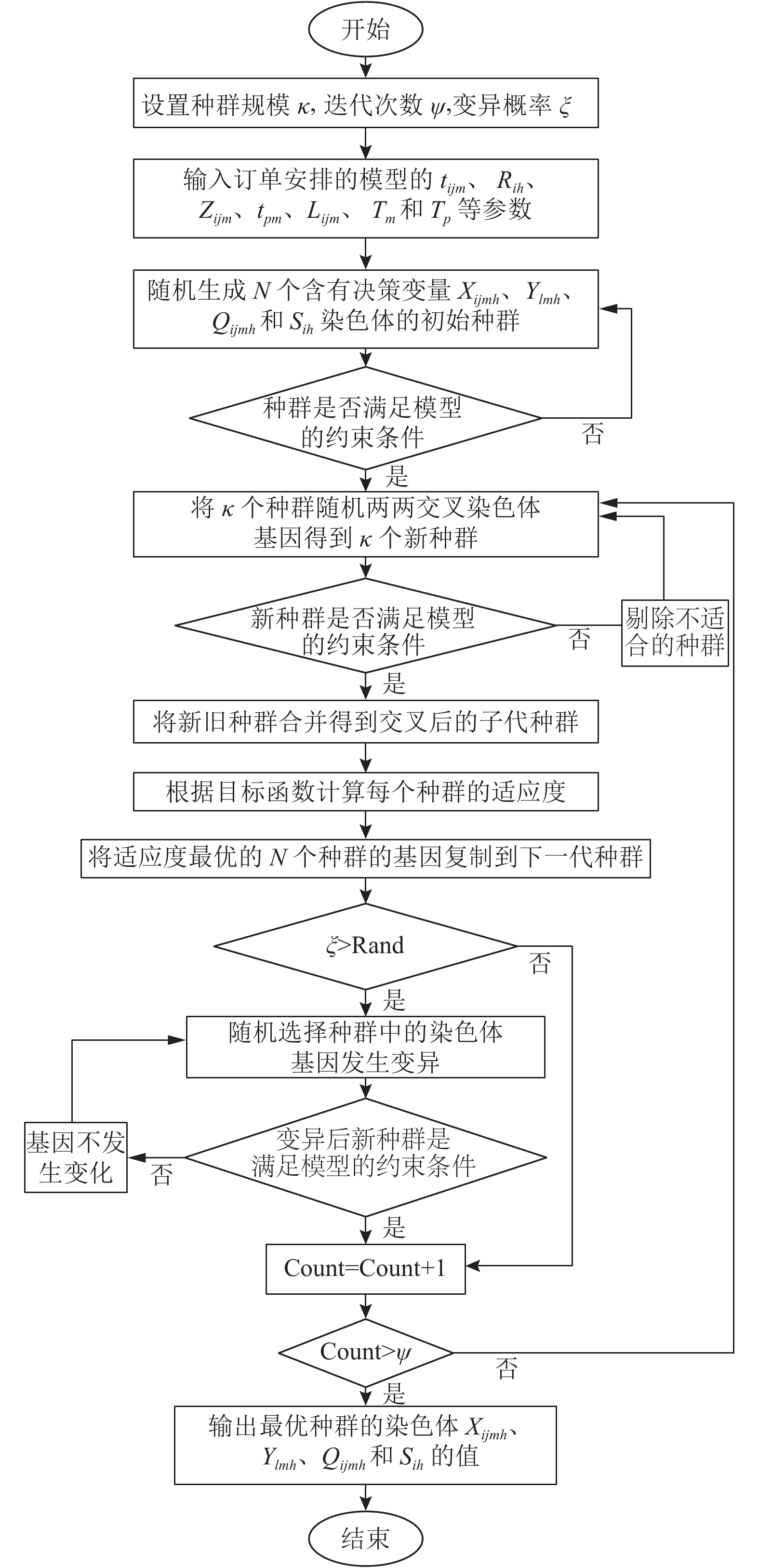
经过基因交叉复制变异的过程,在多次循环计算后种群的适应度值F则会趋于稳定,此时对应染色体Xijmh、Ylmh、Qijmh和Sih的决策变量值即为所求。求解订单安排模型的算法流程图如图1所示。
|
图 1 模型求解的算法流程图 Fig. 1 Algorithm flowchart for model solving |
根据上述构建的多周期订单安排模型,现以某订单拉动为主要生产方式的多品种变批量制造企业的订单安排问题为例,验证本文所构建模型和算法的有效性及实用性,并为该企业合理安排多周期的订单提供最优参考方案。
4.1 算例数据该多品种变批量制造企业目前接到H1—H4一共4个周期的订单,每周期都有N1—N3 3类生产品种,且每周期共6 d,每周期产品订单量各不相同,每种产品的工艺路线和工序也不相同,各工序在生产过程中产生的库存成本各不相同。每类产品的需求量及相关成本的具体数据见表1。企业共有加工这些产品的M1—M6 6台设备以及操作这些设备的P1—P6 6位操作工人,并且对应设备操作产品工序的成本、时间、能耗以及噪声指标各有不同,具体数据见表2和表3。每位工人可操作的设备不同,每位工人每天工作10 h,且操作的熟练程度也有所差异,具体数据见表4。
| 表 1 订单的周期需求量、库存成本和外协成本 Tab. 1 Cycle demand, inventory costs, and foreign co-costs for orders |
| 表 2 某工序在具体设备上的操作时间和操作成本 Tab. 2 Operating time and costs of a process on a specific device |
| 表 3 某工序在具体设备上的噪声影响和能耗成本 Tab. 3 Noise impact and energy consumption cost of a process on a specific device |
| 表 4 工人操作具体设备时间 Tab. 4 Time for workers to operate specific equipment |
基于上述考虑绿色制造的多周期订单安排问题模型及其算法,结合某多品种变批量企业生产数据,运用Matlab软件实现该问题的求解算法,当迭代次数为350,种群规模为100时可得本案例的多周期订单安排最优结果(表5)。
| 表 5 多周期订单安排模型下的最优方案 Tab. 5 Optimal scheme under the multi-cycle order scheduling model |
1) 考虑绿色制造的必要性。
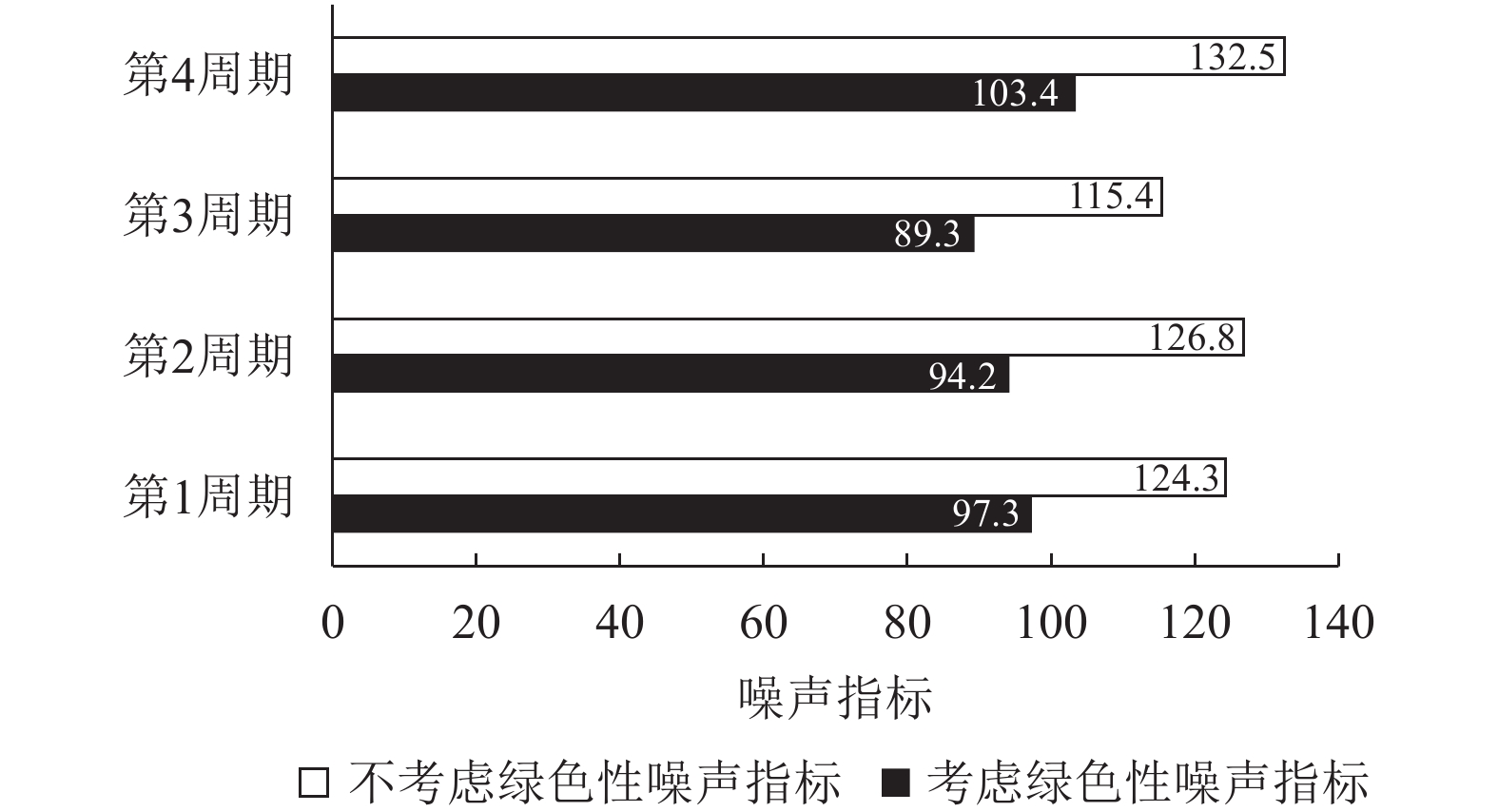
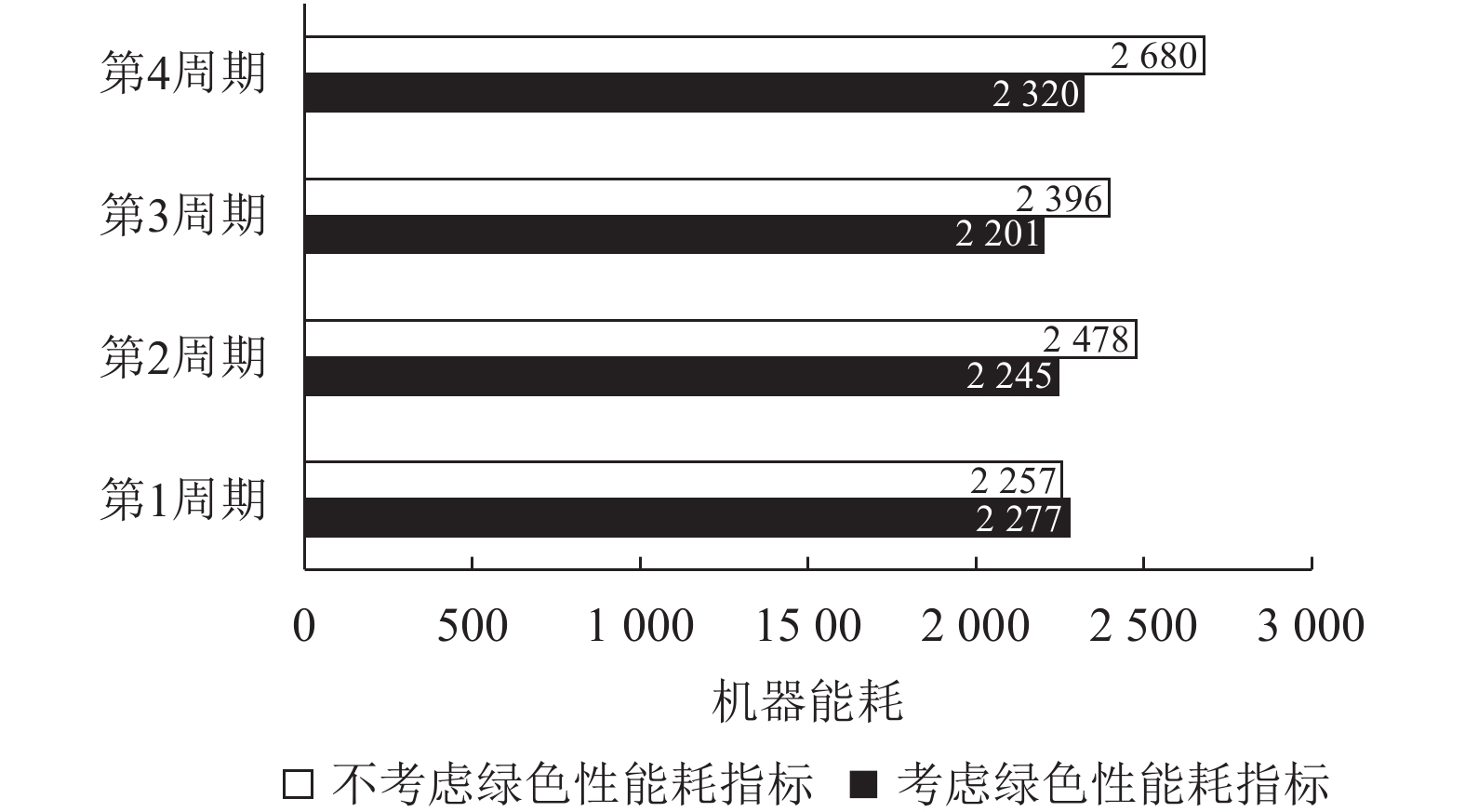
按照本文所构建的订单安排模型和求解算法,只考虑企业生产成本和外协成本最小,不考虑绿色性优化指标的情况下,生产过程中产生的噪声指标和能耗指标对比见图2和图3。
|
图 2 考虑绿色性时机器噪声指标对比 Fig. 2 Comparison of machine noise index when considering green |
|
图 3 考虑绿色性时机器能耗指标对比 Fig. 3 Comparison of machine energy consumption index considering green |
由图中对比可以看出,相对于仅以生产效益最优为目标的订单安排方案,考虑绿色性指标可以使得各个周期内噪声指标和能耗指标都有所下降,从而说明考虑生产周期绿色性的订单安排方式对环境的副作用最小、资源利用率最优。这种订单安排方式综合考虑环境和资源的影响,与企业制造过程的经济效益和社会效益协调发展,满足工业可持续制造发展理念,符合企业的长远利益需求。
2) 考虑订单外协方式的多周期制造资源的协调作用。
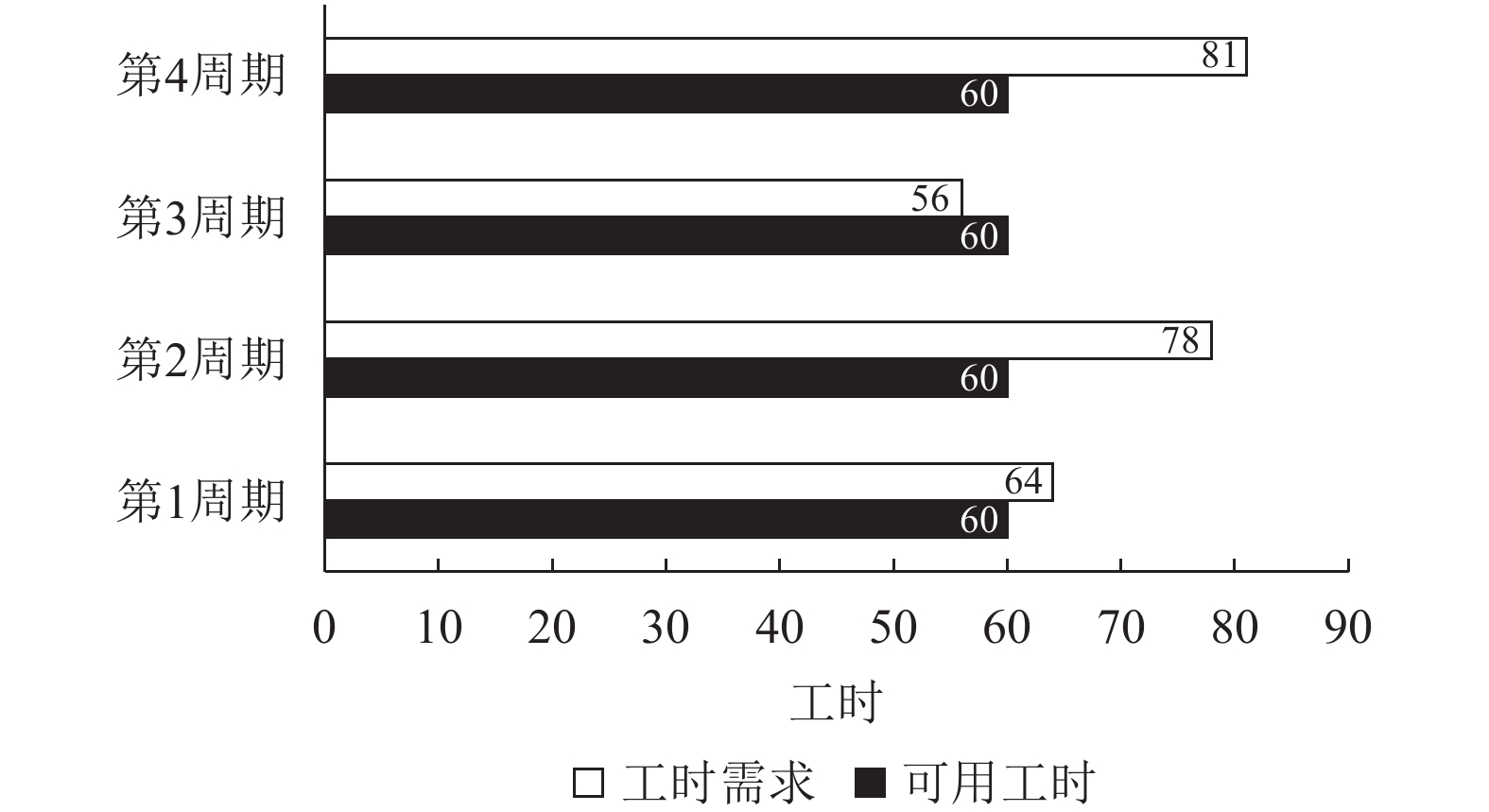
按照客户要求,接单后的每个周期的订单都需在一周以内交货,在一周内操作人员的最大工作时间为6 d,共60 h。如果6 d内无法完成,企业就只有支付拖期罚单或组织加班两种选择。
按照该企业生产这批订单的工艺流程,可以计算出在没有外协情况下,完成每周期订单的操作时间,见图4。由表中的无外协需求时间和实际可用操作时间对比可以看到,在不能够延迟订单交货下,依靠企业自身的生产能力无法完成除第3周期外的订单生产,所以需要依靠订单外协和多周期的制造资源协调分配以缓解订单无法按时交货的压力。
|
图 4 各周期可用工时和实际工时对比 Fig. 4 Comparison of available hours and actual work for each cycle |
与此同时,企业还可以选择组织员工加班的方式完成生产,各周期订单均依靠此方式完成生产的成本,见图5。由采取工人加班的无外协方式完成生产和依靠外协完成生产的各周期总成本对比可知,采取外协完成各个周期订单生产的这种方式,不仅可以完成客户订单不承担大额拖期罚单,而且不会因为工人的长时间劳作产生生产效率低下等现象,更重要的是,实现了生产周期内企业总成本最小,保证综合效益最优。
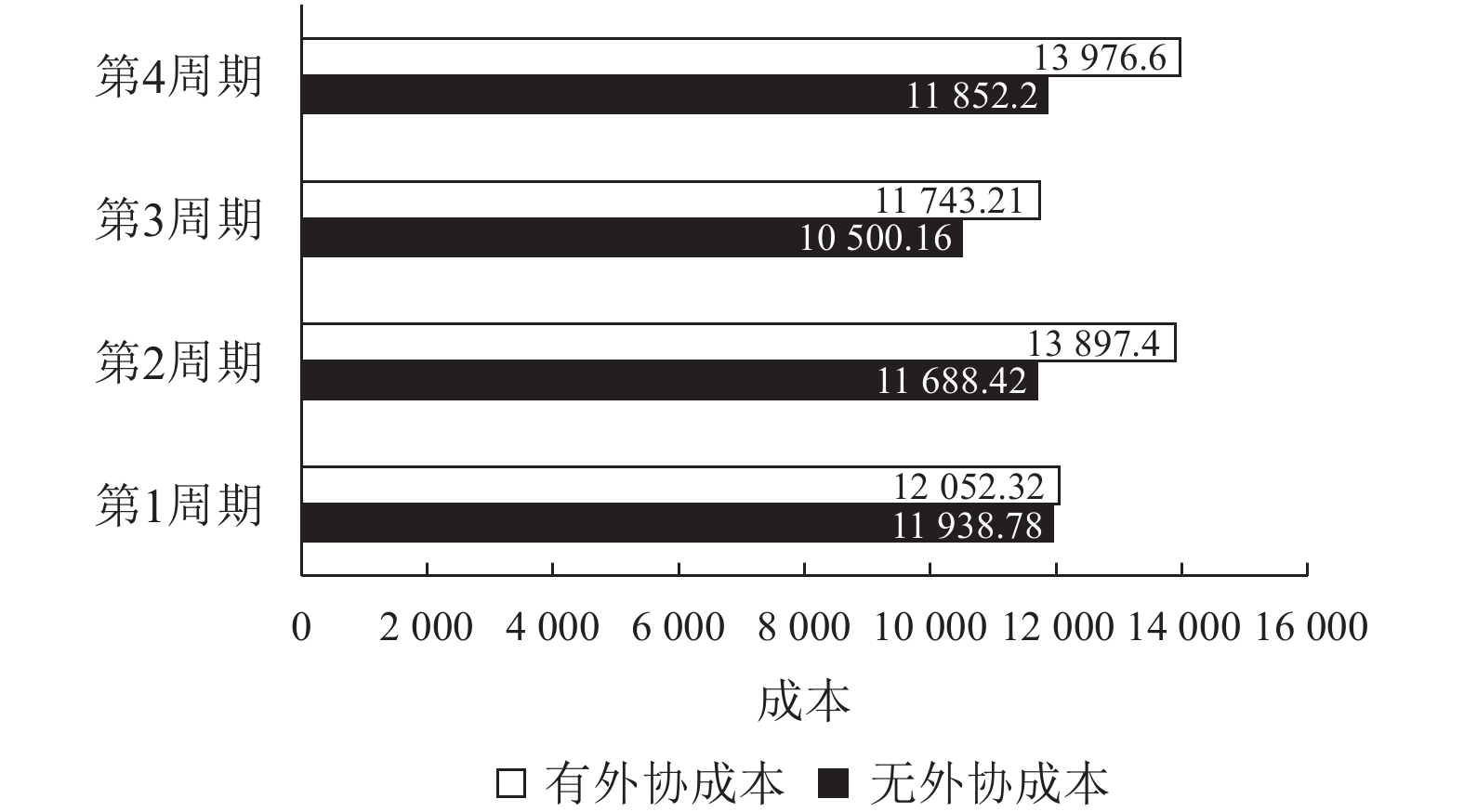
|
图 5 有无外协完成生产各周期成本对比 Fig. 5 Comparison of production cycle cost if there is foreign association |
为解决多品种小批量企业多周期订单的协同安排问题,本文提出了一种基于绿色制造和外协方式的订单安排模型以及求解算法,并通过案例分析验证了该方法的有效性和实用性。通过研究本文得到如下结论。
1) 在最小化企业综合成本的基础上,考虑生产过程中的绿色制造,理论上可以保证企业综合效益最优,并使客户订单得到合理配置。
2) 在订单安排问题的实际研究中,为保证企业市场信誉,可以采用订单外协方式而不是拒绝订单的方式完成订单的合理安排,这样也可以最大化企业综合效益。
3) 为保证订单安排的协调性,可采用这种多周期动态制造资源分配的方式,以成本视角为企业的制造资源提供合理的分配方案,既不会造成订单延期,也可提高资源的利用率,并有利于有效的指导实际生产。
4) 可从绿色制造的角度考虑企业的长远利益,并结合订单外协、资源合理配置等方式在保证企业利益最大化基础上提高企业自身生产制造的绿色制造能力,以一种前瞻性眼光应对工业制造2025。
在实际应用中,随着订单种类越来越繁杂,任务数量越来越多,多品种小批量向多品种变批量生产方式转变,这将对算法的效率有着更高的要求,因此在面对大规模数据时如何改进现有模型的求解算法将是本文未来的研究工作之一。
| [1] |
MILLER B L. A queueing reward system with several customer classes[J].
Management Science, 1969, 16(3): 234-245.
DOI: 10.1287/mnsc.16.3.234. |
| [2] |
LIPPMAN S A, ROSS S M. The streetwalker’s dilemma: a job shop model[J].
SIAM Journal on Applied Mathematics, 1971, 20(3): 336-342.
DOI: 10.1137/0120036. |
| [3] |
DE P, GHOSH J B, WELLS C E. Job selection and sequencing on a single machine in a random environment[J].
European Journal of Operational Research, 1993, 70(3): 425-431.
DOI: 10.1016/0377-2217(93)90252-I. |
| [4] |
SLOTNICK S A, MORTON T E. Selecting jobs for heavily loaded shop with lateness penalties.[J].
Computers & Operations Research, 1996, 23(2): 131-140.
|
| [5] |
GHOSH J B. Job selection in a heavily loaded shop[J].
Computers and Operations Research, 1997, 24(2): 141-145.
DOI: 10.1016/S0305-0548(96)00045-7. |
| [6] |
LUO X, CHU C. A branch-and-bound algorithm of the single machine schedule with sequence-dependent setup times for minimizing maximum tardiness.[J].
Applied Mathematics & Computation, 2007, 183(1): 575-588.
|
| [7] |
LEWIS H F, SLOTNICK S A. Multi-period job selection: planning work loads to maximize profit[J].
Computers & Operations Research, 2002, 29(8): 1081-1098.
|
| [8] |
ROM W O, SLOTNICK S A. Order acceptance using genetic algorithms[J].
Computers & Operations Research, 2009, 36(6): 1758-1767.
|
| [9] |
SHI C T, LI T, LIU Y Z. A heuristic algorithm for integrated surplus inventory matching problem in steel enterprises[J].
Applied Mechanics and Materials, 2013, 423-426: 2178-2183.
DOI: 10.4028/www.scientific.net/AMM.423-426. |
| [10] |
LI Z, HUANG R, PENG B, et al. A divide-conquer heuristic search algorithm for cutting surplus steel plates of steel & iron companies[J].
International Journal of Innovative Computing Information & Control, 2015, 11(1): 363-374.
|
| [11] |
郭源生. 基于顾客满意度的客户订单选择[J].
西安电子科技大学学报(社会科学版), 2007, 17(6): 36-40.
GUO Yuansheng. Options of customer orders based on customer satisfaction[J]. Journal of Xidian University(Social Science Edition), 2007, 17(6): 36-40. DOI: 10.3969/j.issn.1008-472X.2007.06.007. |
| [12] |
张欣, 马士华. 基于有限生产能力和产出缓存的订单接受策略[J].
工业工程与管理, 2008, 13(2): 34-38.
ZHANG Xin, MA Shihua. Order acceptance with limited capacity and finite output buffers in MTO environment[J]. Journal of Industrial Engineering and Management, 2008, 13(2): 34-38. DOI: 10.3969/j.issn.1007-5429.2008.02.008. |
| [13] |
张人千. 考虑时间序列关联的订单选择决策比较研究[J].
管理科学学报, 2009, 12(3): 44-55.
ZHANG Renqian. A comparative study of order selection decisions considering time series associations[J]. Journal of Management Science, 2009, 12(3): 44-55. DOI: 10.3321/j.issn:1007-9807.2009.03.005. |
| [14] |
曹俊杰, 侍洪波. 资源受限多订单选择计划模型及其改进遗传优化决策方案[C/OL]. [2018-07-01] http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGXC200910001052.htm.
CAO Junjie, SHI Hongbo. Resource restricted multi-order selection planning model and its improved genetic optimization decision scheme[C/OL]. [2018-07-01] http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGXC200910001052.htm. |
| [15] |
肖依永, 常文兵, 张人千. 基于模拟退火算法的多节点订单排序模型[J].
计算机应用研究, 2009, 26(2): 460-463.
XIAO Yiyong, CHANG Wenbing, ZHANG Renqian. Multi-node order sorting model based on simulated annealing algorithm[J]. Computer Application Research, 2009, 26(2): 460-463. DOI: 10.3969/j.issn.1001-3695.2009.02.016. |
| [16] |
吴红, 王远世, 陈光聪, 等. 基于奇偶蚁群算法的印刷厂订单排序方法研究[J].
现代计算机(专业版), 2010(7): 9-12.
WU Hong, WANG Yuanshi, CHEN Guangcong, et al. Research on sorting orders in printing house based on odd-even ant algorithm[J]. Modern Computer (Professional Edition), 2010(7): 9-12. |
| [17] |
李艳茹. 基于遗传算法的订单拣货实时排序问题研究[J].
包装工程, 2011, 32(13): 97-101.
LI Yanru. Research on real-time sorting of order picking based on genetic algorithm[J]. Packaging Engineering, 2011, 32(13): 97-101. |
| [18] |
何晓璇. 基于收益管理理论的两级装配系统最优控制策略研究[D]. 长春: 吉林大学, 2011.
HE Xiaoxuan. Research on optimal control strategy of two-stage assembly system based on revenue management theory[D]. Changchun: Jilin University, 2011. |
| [19] |
宋栓军, 王宁, 赵小惠. 产能和产出缓存有限的BTO供应链订单接受策略研究[J].
天津工业大学学报, 2013, 32(1): 84-88.
SONG Shuanjun, WANG Ning, ZHAO Xiaohui. Research on BTO supply chain order acceptance strategy with limited capacity and output caching[J]. Journal of Tianjin University of Technology, 2013, 32(1): 84-88. DOI: 10.3969/j.issn.1671-024X.2013.01.020. |
| [20] |
李娟, 王军. 基于外包的流程型生产订单选择问题研究[J].
物流科技, 2014(2): 68-70.
LI Juan, WANG Jun. Research on process type production order selection based on outsourcing[J]. Logistics Technology, 2014(2): 68-70. DOI: 10.3969/j.issn.1002-3100.2014.02.022. |
| [21] |
庄晓霞, 王军. 流程型生产企业订单选择问题及方法研究[J].
物流科技, 2016, 39(3): 24-27.
ZHUANG Xiaoxia, WANG Jun. Research on order selection problems and methods of process-oriented production enterprises[J]. Logistics technology, 2016, 39(3): 24-27. DOI: 10.3969/j.issn.1002-3100.2016.03.007. |
| [22] |
JOVANE F, YOSHIKAWA H, ALTING L, et al. The incoming global technological and industrial revolution towards competitive sustainable manufacturing[J].
CIRP Annals - Manufacturing Technology, 2008, 57(2): 641-659.
DOI: 10.1016/j.cirp.2008.09.010. |
 2019, Vol. 22
2019, Vol. 22