2. 宁夏理工学院 经济管理学院,宁夏 石嘴山 753000;
3. 宁夏理工学院 理学与化学工程学院,宁夏 石嘴山 753000
2. School of Economics and Management, Ningxia Institute of Science and Technology, Shizuishan 753000, China;
3. School of Science and Chemical Engineering, Ningxia Institute of Science and Technology, Shizuishan 753000, China
随着市场竞争的增加,现实中制造商和零售商面临的不确定因素和盈利压力也随之加大,在考虑利益的同时,不得不考虑风险承受能力。Rockafeller等[1-2]提出用条件风险价值(CVaR)度量风险。很多学者对如何选择有效的度量风险的方法进行了广泛的研究[3-5],通过多种契约机制组合研究供应链是近年来的研究热点。文献[6-9]分别考察和研究了回购契约、收益共享契约和成本分摊契约等多种契约的定价和订货策略机制。文献[10-13]基于CVaR准则研究了风险规避对供应商和零售商决策行为的影响。黄晶等[14]讨论了基于CVaR和供应商承诺回购的供应链决策模型,指出通过设计合理的供应链契约,存在最优回购率和最优银行贷款利率,以此缓解供应链的资金约束。
然而,作为度量方法,CVaR在一定程度上克服了VaR方法的缺点,但CVaR准则仅度量了低于分位数收益的平均值,而忽略了高于分位数的部分收益,使得决策者预期收益也有所降低[15]。文献[16]采用均值–CVaR方法,通过建立批发价格契约模型,研究了不同价格契约对供应链收益的影响。陈宇科等[17]运用均值–CVaR方法,构建成本分摊契约模型,讨论了闭环供应链的协调问题,指出均值–CVaR方法更能提高供应链渠道的最优决策水平。
近年来,资源环境问题日益突出,有关供应链的社会责任问题和供应链协同创新问题受到广泛关注。朱庆华[18]从传统企业、再生企业以及整条供应链3个角度对可持续供应链协同管理与创新的研究进行了梳理,并提出可持续供应链创新的研究方向。影响供应链创新机制的因素较复杂,消费者的消费偏好,产品生命周期的缩短,替代产品的多元化以及市场的不确定性等都会使企业为了保持供应链竞争优势,不断地进行技术创新投入。学术界从企业、供应链和利益相关者3个层次开展研究,取得了有价值的结果。Gilbert等[19]考察研究了供应商机会主义行为与销售商创新投入对供应链策略的影响。Gupta等[20]通过建立上游制造商创新投入补偿模型,研究了使供应链产品成本降低的策略机制。田巍等[21]利用CVaR度量准则研究了零售商不同风险偏好下混合渠道供应链创新协作策略。
基于此,本文推广了Gilbert等[19]的创新模型。针对传统的零售渠道,在文献[16-17]的基础上采用均值–CVaR方法来度量风险规避的零售商,构建在随机需求下回购契约供应链创新模型。虽然本文的研究是建立在上述文献的基础上,但却有着很大不同,具体表现如下。1) 文献[16-17]运用均值–CVaR的方法,通过定价和订货策略研究了价格契约供应链和成本分摊供应链。本文建立了制造商创新投入的供应链模型,运用均值–CVaR的方法探讨了回购契约供应链的最优订购量和协调性。结果表明,均值–CVaR方法比CVaR度量准则更能提高零售商的订货量,同时指出零售商的风险规避程度影响供应链的创新和需求,当零售商喜好风险,将增大制造商的创新投入度,供应链渠道的总需求增加。2) 由于标准的回购契约会导致零售商有过度订购的风险,考虑到供应链的实际运营情况,通过对回购商品数量有条件地限制改进标准的回购契约供应链,采用CVaR风险度量准则和均值–CVaR方法联合度量风险规避的零售商。研究表明,在一定条件下,改进的制造商创新投入回购契约能使供应链达到协调。本文给出了制造商创新投入的回购契约供应链决策者在分散决策和联合决策时最优决策的解析表达式,最后结合数值算例验证了回购契约供应链创新协调机制的有效性。
1 模型假设与风险度量准则 1.1 基本假设和符号说明1) 考虑由一个制造商与一个零售商构成的二级供应链。制造商供给单位产品成本为
2) 商品的市场需求
3) 供应链使用回购契约进行协调,零售商只有一次订购机会,设其订购量为
4) 考虑制造商风险中性,追求期望收益最大化,零售商风险规避,其风险价值用“均值–CVaR”方法度量。
1.2 制造商技术创新假设为了刺激消费者的需求,实现利润最大化,制造商往往在生产过程中会进行技术改进和创新。考虑到制造商为降低生产运营成本,提高产品竞争力,通过技术改进和创新投入,降低单位产品生产成本,本文主要关注零售商的风险偏好对制造商创新投入力度的影响。参考文献[19-21],利用幂函数构造制造商创新投入函数。假设制造商每投资
根据上述假设,在制造商创新投入后供应链系统、零售商和制造商的利润函数分别为
| $\qquad\pi (q,t) = (p - c + ts)q - p{(q - x)^ + } - k{t^2},$ | (1) |
| $\qquad{\pi _{\rm r}}(q) = (p - w)q + (b - p){(q - x)^ + },$ | (2) |
| $\qquad{\pi _{\rm{m}}}(q,t) = (w - c + ts)q - b{(q - x)^ + } - k{t^2}{\text{。}}$ | (3) |
其中,符号
CVaR是对风险度量和控制的准则,由VaR度量准则发展而来,Rockafller等[1]证明了CVaR良好的运算特性。CVaR度量了低于
| $ \begin{split} &\qquad{\rm{CVaR}}({\pi _{\rm{r}}}( \cdot )) = E[{\pi _{\rm r}}( \cdot )|{\pi _{\rm r}}( \cdot ) {\text{≤}} {\rm{VaR}}({\pi _{\rm r}}( \cdot ))] = \\ &\dfrac{1}{\beta }\int_{{\pi _{\rm r}}( \cdot ) {\text{≤}} {\rm VaR}({\pi _{\rm r}}( \cdot ))} {{\pi _{\rm r}}} ( \cdot )f(x){\rm d}x{\text{。}}\end{split}$ | (4) |
其中,
| $\qquad{\rm{CVaR}}({\pi _{\rm{r}}}( \cdot )) = \mathop {\max \{ }\limits_{v \in R} v + \frac{1}{\beta }E[\min \{ {\pi _{\rm r}}( \cdot ) - v,0\} ]{\rm{\} }}{\text{。}}$ | (5) |
根据CVaR的定义,不难得出CVaR准则会使决策者的目标过于保守。因为在CVaR准则下,当
| $\qquad G(\pi ( \cdot )) = \lambda E(\pi ( \cdot )) + (1 - \lambda ){\rm{CVaR}}(\pi ( \cdot )){\text{。}}$ | (6) |
其中,
在集权决策下,假设制造商作为供应链系统的核心,它以实现整个供应链系统收益最大化为目标支配双方决策。供应链系统面临的问题是选择最优订购量和最佳创新投入度实现供应链系统期望收益的最大化,即
| $\begin{split} &\qquad \mathop {\max }\limits_{q,t} E(\pi (q,t)) = \mathop {\max }\limits_{q,t} \left[ {(p - c + ts)q - k{t^2} - p\int_0^q ( q - } \right. \\ &. {x)f(x){\rm{d}}x} ] {\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (7) |
因为
| $ \qquad \frac{{{{\partial} ^2}E(\pi) }}{{{\partial} {q^2}}} \!=\! -\! pf(q),\frac{{{{\partial} ^2}E(\pi) }}{{{\partial} {t^2}}}\! = \! - \!2k, \frac{{{{\partial} ^2}E(\pi) }}{{{\partial} q \partial t}} \!= \!\frac{{{\partial ^2}E(\pi) }}{{\partial t\partial q}} \!=\! s{\text{。}} $ |
因此供应链系统期望收益函数
| $ \begin{split} \qquad{ H}{\rm{ = }}\left( {\begin{array}{*{20}{c}} {\dfrac{{{\partial ^2}}}{{\partial {q^2}}}E\left( \pi \right)}&{\dfrac{{{\partial ^2}}}{{\partial q\partial t}}E\left( \pi \right)}\\ {\dfrac{{{\partial ^2}}}{{\partial t\partial {{q}}}}E\left( \pi \right)}&{\dfrac{{{\partial ^2}}}{{\partial {t^2}}}E\left( \pi \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - pf\left( q \right)}&s\\ s&{ - 2k} \end{array}} \right){\text{。}}\end{split} $ |
又因为
| $ \qquad{q^ * } = {F^{ - 1}}\left(\frac{{p - c + ts}}{p}\right),{t^ * } = \frac{{sq}}{{2k}}{\text{。}} $ | (8) |
式(8)表明,联合决策下的最优决策
在现实中,由于制造商创新投入要先期进行,制造商首先确定批发价
根据CVaR的定义,风险规避的零售商的目标函数为
| $ \begin{split} &\qquad\mathop {\max }\limits_q \;\{ {\rm{CVaR}}({\pi _{\rm{r}}}(q))\} = \mathop {\max }\limits_q \mathop {\max }\limits_{v \in {\rm{R}}} {\rm{\{ }}v +\frac{1}{\beta }E[\min \{ {\pi _{\rm{r}}}(q)- \\ &v,0\} ]\}{\text{。}} \end{split}$ |
根据参考文献[1-2]的求解方法,可得零售商基于CVaR度量准则的最优订购量为
| $\qquad{q_1} = {F^{ - 1}}\left(\beta \frac{{p - w}}{{p - b}}\right){\text{。}}$ | (9) |
将式(9)代入式(3),得到制造商的期望利润函数为
| $ \qquad E({\pi _{\rm m}}(q,t)) = (w - c + ts){q_1} - k{t^2} - b\int_0^{{q_1}} {({q_1} - x)f(x){\rm d}x} {\text{。}} $ |
上式对
| $\qquad{t_1} = \frac{{s{q_1}}}{{2k}}{\text{。}}$ | (10) |
从而风险规避零售商基于CVaR度量准则下的期望利润函数为
| $\qquad{E_1}({\pi _{\rm r}}({q_1})) = (p - w){q_1} + (b - p)\int_0^{{q_1}} {({q_1} - x)f(x){\rm d}x} {\text{。}}$ |
式(9)和式(10)表明,基于CVaR准则下的最优决策
根据Gan等[22]的供应链契约协调理论,要实现供应链协调,要求分权供应链系统应该达到集权供应链系统运作的绩效,因此,分散决策时零售商的最优订购量与联合决策时供应链系统的最优订购量相同且各自利润大于等于零。结合式(8)—式(10)可知,实现供应链渠道协调,要求
推论1 当
根据均值–CVaR的定义,可得零售商的目标函数
| $\qquad G({\pi _{\rm r}}(q)) = \lambda E({\pi _{\rm r}}(q)) + (1 - \lambda ){\rm CVaR}({\pi _{\rm r}}(q)){\text{。}}$ | (11) |
命题1 在分散决策下,基于均值–CVaR方法的最优订购量
| $ \begin{split} \qquad& t_1^ * \!\!\!=\!\!\! \dfrac{{sq_1^ * }}{{2k}},\\ &\;q_1^ * \!\!\!=\!\!\! \left\{ \begin{array}{l} {F^{ - 1}}\left( {\dfrac{{p \!-\! w}}{{(p - b)\left(\lambda \!+\! \dfrac{{1 - \lambda }}{\beta }\right)}}} \right),q \!{\text{<}}\! {F^{ - 1}}(\beta ){\text{;}} \\ {F^{ - 1}}\left( {1 - \dfrac{{w - b}}{{\lambda (p \!-\! b)}}} \right),q {\text{≥}} {F^{ - 1}}(\beta ){\text{。}} \\ \end{array} \right. \end{split} \!\!\!\!\!\!\!$ | (12) |
推论2 由命题1可得出以下结论。
1) 当
2) 对任意
3) 对于任何固定
证明:显然,当
推论2表明:1) 对任意
推论3 对于由风险中性制造商和均值–CVaR方法度量的零售商构成的供应链系统,在制造商创新投入的回购契约下,
1) 当
2) 当
证明:要实现供应链协调,必须满足
回购契约存在过度订购的潜在风险,CVaR准则使决策目标过于保守,因此,制造商与零售商达成如下回购契约安排:零售商的订购量小于
| $\qquad{\pi _{\rm r}} = \left\{ \begin{array}{l} (p - w)q + (b - p){(q - x)^ + },q {\text{≤}} {q_1}{\text{;}} \\ (p - w)q + (b\theta - p){(q - x)^ + },q {\text{>}} {q_1}{\text{。}} \\ \end{array} \right.$ | (13) |
| $\qquad{\pi _{\rm m}} \!\!=\!\! \left\{ \begin{array}{l} (w - c + ts)q - b{(q - x)^ + } - k{t^2},q {\text{≤}} {q_1}{\text{;}} \\ (w - c + ts)q - b\theta {(q - x)^ + } - k{t^2},q {\text{>}} {q_1}{\text{。}} \\ \end{array} \right.$ | (14) |
命题2 在分散决策时,基于CVaR和均值–CVaR联合度量方法下的最优订购量
| $ \qquad t_2^ * = \frac{{sq_2^ * }}{{2k}},$ |
| $ \qquad q_2^ * \! =\! \left\{\!\!\!\! \begin{array}{l} {F^{ - 1}}\left(\beta \dfrac{{p - w}}{{p - b}}\right),q {\text{≤}} {q_1}{\text{;}} \\ {F^{ - 1}}\left(\! {\dfrac{{p - w}}{{(p\! - \!b\theta )\left(\lambda \! + \!\dfrac{{1\! -\! \lambda }}{\beta }\right)}}} \!\right),{q_1} \!{\text{<}}\! q \!{\text{<}}\! {F^{ - 1}}(\beta ){\text{;}} \\ {F^{ - 1}}\left( {1 - \dfrac{{w - b\theta }}{{\lambda (p - b\theta )}}} \right),{F^{ - 1}}(\beta ) {\text{≤}} q{\text{。}} \\ \end{array} \right.\!\!\!\!\!\! $ | (15) |
式(15)表明,当
推论4 对于由风险中性制造商和风险规避的零售商构成的供应链系统,在改进的制造商创新投入的回购契约下,有如下结论。
1) 当
2) 当
3) 当
推论4刻画了改进的制造商创新投入的回购契约供应链协调满足的条件。结果表明通过对回购商品数量有条件地限制改进标准的回购契约供应链,采用CVaR风险度量准则和均值–CVaR方法联合度量风险规避的零售商,在满足一定条件下,改进的制造商创新投入回购契约能使供应链达到协调。
限于篇幅,命题1、命题2以及推论4的证明略。
5 数值算例下面通过算例分析说明风险规避因子
假设产品市场需求
1) 基于CVaR度量准则下的最优决策。

|
图 1 分散决策下
|

|
图 2 分散决策下
|
从图1和图2可以看出,订货量
2) 基于CVaR和均值–CVaR的决策分析。

|
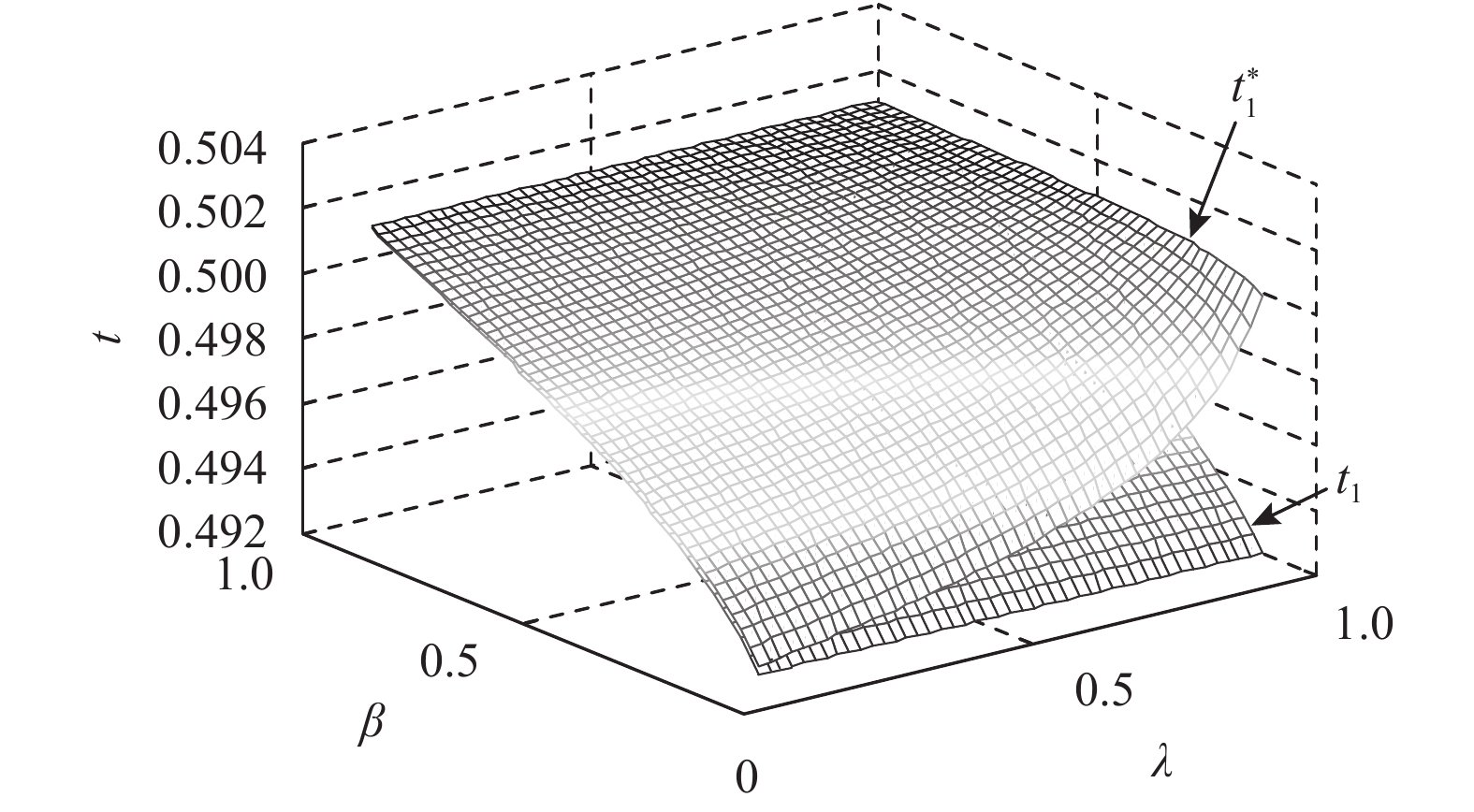
图 3 2种度量方法下
|
|
图 4 2种度量方法下
|
从图3和图4可以看出,2种准则下,供应链系统的最优决策水平受风险规避因子
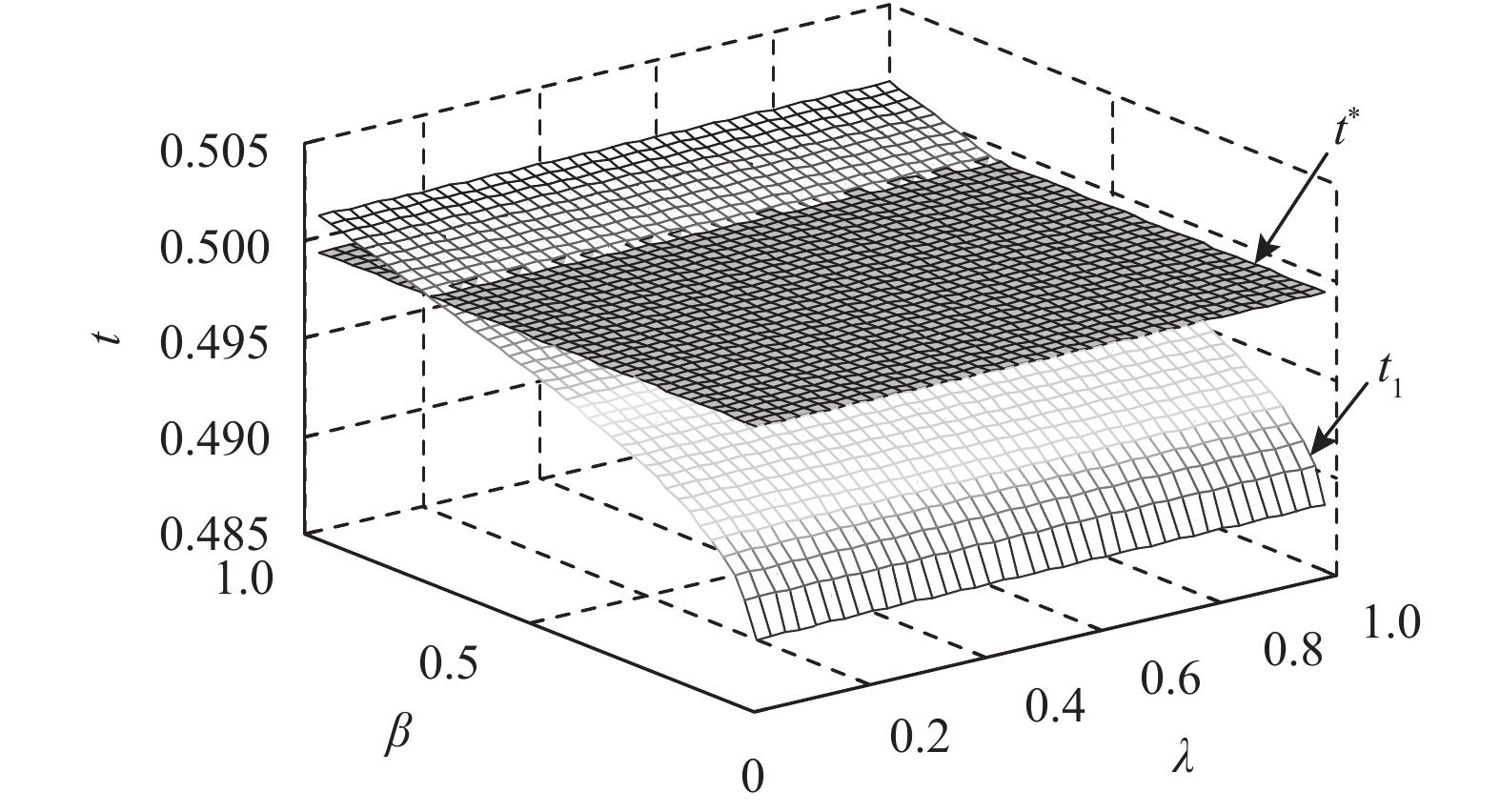
3) 基于CVaR和均值–CVaR下的供应链协调。
|
图 5 CVaR方法下
|
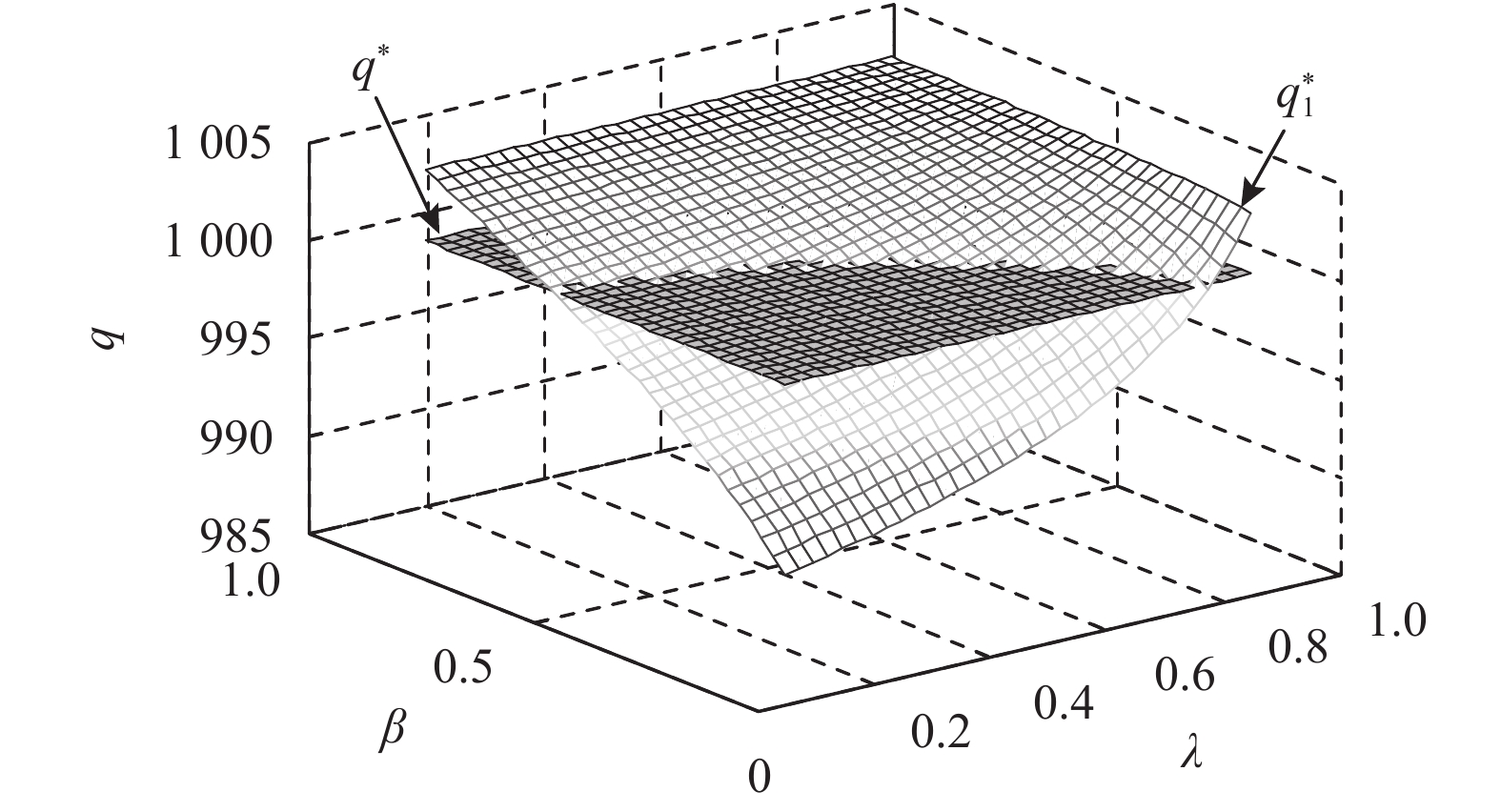
|
图 6 均值–CVaR方法下
|
从图5可以得出,在CVaR度量准则下,存在
本文运用均值–CVaR的方法研究了回购契约供应链创新协调问题。运用CVaR度量准则和均值–CVaR的方法分别构建风险规避零售商的利润函数,分析指出CVaR准则使决策目标过于保守,相比较CVaR度量准则,风险规避的零售商在均值–CVaR方法下的最优订购量更多,说明权重能加大零售商的订购量。研究表明,零售商的风险规避程度影响供应链的创新和需求,当零售商喜好风险,将使制造商的创新投入度增大,供应链渠道的总需求增加。
从供应链的运营实际来看,回购契约虽可以消除规避效应,但零售商面临市场需求不确定导致过度订购的风险,制造商面临盲目创新投入和大量回购而导致期望收益减少的风险。通过对回购商品数量的限制改进回购契约供应链创新模型,采用CVaR风险度量准则和均值–CVaR方法联合度量风险规避的零售商。结果表明,对回购数量的限制能够约束零售商过度订购的风险,而且在一定条件下改进的回购契约能够协调供应链。
本文研究结果表明,回购的比例和零售商风险偏好的程度对供应链的优化和协调问题有一定的影响,选择合适的回购比例和适当的评估供应链成员的风险追求水平对提高供应链的效率有很大帮助,这也为决策者考虑回购契约决策时提供了参考依据。然而,随着技术的进步和消费者对产品要求的提高,传统的销售渠道已不能满足销售需求,网络直销对传统销售产生很大冲击,与此同时,新产品的研发和替代产品的多元化缩短了产品寿命周期,使得制造商面临现金流短缺的问题,因此多渠道供应链的融资模式成为进一步的研究方向。
| [1] |
ROCKAFELLAR R T, URYASEV S. Conditional value-at-risk for general loss distributions[J].
Journal of Banking and Finance, 2002, 26(7): 1443-1471.
DOI: 10.1016/S0378-4266(02)00271-6. |
| [2] |
ROCKAFELLAR R T, URYASEV S. Optimization of conditional value-at-risk[J].
Journal of Risk, 2000, 2(3): 21-41.
DOI: 10.21314/JOR.2000.038. |
| [3] |
CACHON G P, FISHER M. Supply chain inventory management and the value of shared information[J].
Management Science, 2000, 46(8): 1032-1048.
DOI: 10.1287/mnsc.46.8.1032.12029. |
| [4] |
CACHON G P. Supply chain coordination with contracts[M]// de Kok A G, Graves S C. Handbooks in Operations Research and Management Science: Supply Chain Management. Amsterdam: Elsevier, 2003: 229-239.
|
| [5] |
CHEN J, BELL P C. Coordinating a decentralized supply chain with customer returns and price-dependent stochastic demand using a buyback policy[J].
European Journal of Operational Research, 2011, 212(2): 293-300.
DOI: 10.1016/j.ejor.2011.01.036. |
| [6] |
CHIU C H, CHOI T M, Tang C S. Price, rebate, and returns supply contracts for coordinating supply chains with price-dependent demands[J].
Production and Operations Management, 2011, 20(1): 81-91.
DOI: 10.1111/poms.2010.20.issue-1. |
| [7] |
SEYEDESFAHANI M M, BIAZARAN M, GHARAKHANI M. A game theoretic approach to coordinate pricing and vertical co-op advertising in manufacture-retailer supply chains[J].
European Journal of Operational Research, 2011, 211(2): 263-273.
DOI: 10.1016/j.ejor.2010.11.014. |
| [8] |
CACHON G P, LARIVIERE M A. Supply chain coordination with revenue-sharing contracts: strengths and Limitations[J].
Management Science, 2005, 51(1): 30-44.
DOI: 10.1287/mnsc.1040.0215. |
| [9] |
DONOHUE K L. Efficient supply contracts for fashion goods with forecast updating and two production modes[J].
Management Science, 2000, 46(11): 1391-1411.
|
| [10] |
SU X. Consumer returns policies and supply chain performance[J].
Manufacturing & Service Operations Management, 2009, 11(4): 595-612.
|
| [11] |
KRISHNAN H, KAPUSCINSKI R, BUTZ D A. Coordinating contracts for decentralized supply chains with retailer promotional effort[J].
Management Science, 2004, 50(1): 48-63.
DOI: 10.1287/mnsc.1030.0154. |
| [12] |
代建生, 孟卫东. 基于CVaR的供应链联合促销的回购契约协调研究[J].
中国管理科学, 2014, 22(7): 43-51.
DAI Jiansheng, MENG Weidong. Buy-bacy contracts for a supply chain with a risk-neutral supplier and a risk-averse retailer who take joint promotion actions based on CVaR[J]. Chinese Journal of Management Science, 2014, 22(7): 43-51. |
| [13] |
张新鑫, 侯文华, 申成霖. 顾客策略行为下基于CVaR和回购契约的供应链决策模型[J].
中国管理科学, 2015, 23(2): 82-91.
ZHANG Xinxin, HOU Wenhua, SHEN Chenglin. Decision models for supply chain based on CVaR and buyback contract under strategic consumer behavior[J]. Chinese Journal of Management Science, 2015, 23(2): 82-91. |
| [14] |
黄晶, 杨文胜. 基于CVaR和供应商承诺回购的供应链决策模型[J].
管理学报, 2016, 13(8): 1250-1256.
HUANG Jing, YANG Wensheng. Supply chain decision model based on supplier CVaR and buy-back commitments[J]. Chinese Journal of Management, 2016, 13(8): 1250-1256. DOI: 10.3969/j.issn.1672-884x.2016.08.016. |
| [15] |
WAN Yang, CLUTTER M L, MEIC B, et al. Assessing the role of U. S. timberland assets in a mixed portfolio under the mean-conditional value at risk framework[J].
European Journal of Operational Research, 2015, 50(1): 118-126.
|
| [16] |
慕永国, 麦强, 冯英浚. 供应链价格契约的均值-CVaR模型[J].
哈尔滨工业大学学报, 2009, 41(12): 298-300.
MU Yongguo, MAI Qiang, FENG Yingjun. Mean-CVaR models of price-only contracts of supply chain[J]. Journal of Harbin Institute of Technology, 2009, 41(12): 298-300. DOI: 10.3321/j.issn:0367-6234.2009.12.066. |
| [17] |
陈宇科, 熊龙, 董景荣. 基于均值-CVaR的闭环供应链协调机制[J].
中国管理科学, 2017, 25(2): 68-77.
CHEN Yuke, XIONG Long, DONG Jingrong. Closed-loop supply chain coordination mechanism based on mean-CVaR[J]. Chinese Journal of Managment Science, 2017, 25(2): 68-77. |
| [18] |
朱庆华. 可持续供应链协同管理与创新研究[J].
管理学报, 2017, 14(5): 775-780.
ZHU Qinghua. A study of sustainable supply chain coordinated management and innovation[J]. Chinese Journal of Management, 2017, 14(5): 775-780. DOI: 10.3969/j.issn.1672-884x.2017.05.016. |
| [19] |
GILBERT S M, CVSA V. Strategic commitment to price to stimulate downstream innovation in a supply chain[J].
European Journal of Operational Research, 2003, 150(3): 617-639.
DOI: 10.1016/S0377-2217(02)00590-8. |
| [20] |
GUPTA S, LOULOU R. Process innovation, product differentiation, and channel structure: strategic incentives in a duopoly[J].
Marketing Science, 1998, 17(4): 301-316.
DOI: 10.1287/mksc.17.4.301. |
| [21] |
田巍, 陈思源, 黄晗. 零售商不同风险偏好下混合渠道供应链创新协作策略[J].
工业工程与管理, 2017, 22(6): 114-120.
TIAN Wei, CHEN Siyuan, HUANG Han. Mixed channel supply chain innovation collaboration strategy under retailer’s different risk preferences[J]. Industrial Engineering and Management, 2017, 22(6): 114-120. |
| [22] |
GAN X H, SETHI S P, YAN H. Coordination of supply chain with risk-averse agents[J].
Production and Operations Management, 2004, 13(2): 135-149.
|
 2019, Vol. 22
2019, Vol. 22