由于资源枯竭压力和大众环境保护意识的不断提高,绿色供应链的概念在全世界得到了广泛的传播和重视,绿色供应链管理也已经逐渐成为世界领先企业实现可持续发展的重大战略[1]。世界上许多国家和地区积极响应绿色供应链号召,为推行绿色供应链管理作出了贡献,如2002年11月,欧盟通过了《废电机电子设备指令》及《电机电子设备限用有害物质指令》等[2]。近些年来,由于我国的生态环境日益恶化,消费者的环境保护意识在逐渐提高并开始倾向于购买绿色产品,我国政府也已经实施了相关政策对实施环保策略的企业和购买绿色产品的消费者进行财政补贴,并开展了诸如“节能产品惠民工程”等一系列针对节能绿色产品的财政补贴活动,这些政策措施在鼓励企业绿色经营及消费者购买绿色产品方面取得了一定成效。但当消费者绿色偏好及政府的绿色补贴达到何种程度时制造商和零售商才会倾向于采取绿色营销策略尚不明确,所以探讨消费者绿色偏好及政府绿色补贴达到何种程度才能最有效地促进制造商和零售商均采取绿色营销模式具有重要的现实意义。
到目前为止,国内外学者已经对绿色供应链进行了较为深入的研究,通过梳理以往文献,发现国内外学者们主要从以下角度对绿色供应链进行了研究。1) 影响因素。如Walker等[3]研究得到组织、客户、监管、政府和竞争对手是驱动绿色供应链实施的主要因素。Brik等[4]研究了新兴经济体的绿色供应链驱动因素。朱庆华[5]通过实证研究得出,企业意识与能力、财务绩效和成本、供应链影响和政府法规是制约中国企业实施绿色供应链管理的影响因素。张璇等[6]通过元分析法得出影响企业实施绿色供应链管理的因素可以划分为社会系统、生产系统、消费系统、环境系统。刘玫[7]运用解释结构模型法研究了影响绿色供应链管理实施效果的因素,并探讨了各因素之间的层级关系。张荣兰等[8]运用因子分析和结构方程模型研究了影响钢铁企业实施绿色供应链管理的因素,得出绿色供应链总效益是主要动因,政府支持推动是主要外因。2) 绩效。如方陈承等[9]利用元分析法研究了绿色供应链管理对企业绩效的影响。黄国青等[10]运用模糊综合评价法对绿色供应链绩效进行了评价研究。3) 供应链成员间的博弈及协调。如杨渠等[11]考虑制造商和零售商的风险规避行为,基于博弈理论探讨了两者的最优决策问题。何彬斌等[12]研究了基于消费者绿色偏好的供应链纵向演化博弈。白春光等[13]构建了3种博弈模型,研究了供应链成员在合作和非合作情况下供应链成员绩效和利润的变化情况。江世英等[14]建立了4种绿色供应链博弈模型,比较了这4种模型下的产品价格、绿色度等,并进一步构建了收益共享契约下的博弈模型。白世贞等[15]在产品绿色化程度和销售努力共同影响市场需求的情况下,建立了批发价格下的收益共享契约。4) 包含第三方(如政府机构)的绿色供应链博弈。如朱庆华等[16]构建了考虑产品绿色度和政府补贴的3阶段博弈模型。张艳丽等[17]运用博弈理论探讨了政府财政干涉对绿色供应链销售渠道的影响问题。
由于目前有关绿色供应链博弈方面的研究大多是在保证制造商和零售商或政府监督方获利的前提下探讨绿色供应链的制度设计或契约协调问题,却很少有文献在消费者具有绿色偏好且政府对绿色营销企业进行补贴的情况下探讨供应链不同成员的营销策略选择情况。鉴于此,为进一步丰富理论研究成果,揭示政府不同补贴水平和消费者不同绿色偏好水平对供应链成员营销策略选择的影响机理,本文建立了多种博弈模型并利用演化博弈理论进行了深入分析,所得结论可以为政府相关部门和供应链成员制定科学决策提供有益参考。
1 问题描述和基本假设本文以仅包含一个制造商和一个零售商的两级供应链为研究对象,制造商作为博弈的主导者首先以批发价格
1) 制造商和零售商受到政府政策和市场因素的影响时只会采取两种不同的策略,即制造商采取或不采取绿色生产策略、零售商采取或不采取绿色销售策略。
2) 制造商采取绿色营销策略意味着制造商将在企业内部进行环境管理,并对产品进行绿色设计,从而生产出环境友好型绿色产品,用绿色度
3) 零售商采取绿色营销策略意味着零售商将对绿色产品进行宣传,以吸引消费者购买绿色产品。为方便研究,假设零售商不进行绿色营销时的营销成本忽略不计,进行绿色营销时的绿色投入为固定值,且零售商进行绿色营销时的总成本与其绿色投入成二次方关系[19],即总成本为
4) 假设市场需求函数为线性函数[18],产品的市场需求受价格、消费者绿色偏好共同影响,且消费者倾向于购买绿色度高、绿色宣传程度高且价格低廉的产品,所以产品的市场需求函数分为以下4种情况。
当制造商采取绿色生产且零售商采取绿色销售策略时,产品市场需求为
当制造商采取绿色生产策略而零售商不采取绿色销售策略时,产品市场需求为
当制造商不采取绿色生产策略而零售商采取绿色销售策略时,产品市场需求为
当制造商不采取绿色生产且零售商不采取绿色销售策略时,产品市场需求为
其中
设
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma g + \gamma c} \right) - \frac{1}{2}{\eta _1}{g^2}{\text{,}}$ | (1) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma g + \gamma c} \right) - \frac{1}{2}{\eta _2}{c^2}{\text{。}}$ | (2) |
当制造商采取绿色生产策略而零售商不采取绿色销售策略时
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma g} \right) - \frac{1}{2}{\eta _1}{g^2}{\text{,}}$ | (3) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma g} \right){\text{。}}$ | (4) |
当制造商不采取绿色生产策略而零售商采取绿色销售策略时
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma c} \right){\text{,}}$ | (5) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma c} \right) - \frac{1}{2}{\eta _2}{c^2}{\text{。}}$ | (6) |
当制造商不采取绿色生产且零售商不采取绿色销售策略时
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p} \right){\text{,}}$ | (7) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p} \right){\text{。}}$ | (8) |
由于该博弈为制造商主导的两阶段斯坦伯格博弈,故将采用逆向归纳法求最优解。
首先,当制造商采取绿色生产且零售商采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad {\pi _{{\rm{M}}1}} = \frac{{{{\left( {\alpha + \gamma g + \gamma c} \right)}^2}}}{{8\beta }} - \frac{1}{2}{\eta _1}{g^2},$ | (9) |
| $\qquad {\pi _{{\rm{R}}1}} = \frac{{{{\left( {\alpha + \gamma g + \gamma c} \right)}^2}}}{{16\beta }} - \frac{1}{2}{\eta _2}{c^2}{\text{。}}$ | (10) |
同理,当制造商采取绿色生产策略而零售商不采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad {\pi _{{\rm{M}}2}} = \frac{{{{\left( {\alpha + \gamma g} \right)}^2}}}{{8\beta }} - \frac{1}{2}{\eta _1}{g^2},$ | (11) |
| $\qquad {\pi _{{\rm{R}}2}} = \frac{{{{\left( {\alpha + \gamma g} \right)}^2}}}{{16\beta }}{\text{。}}$ | (12) |
当制造商不采取绿色生产策略而零售商采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad {\pi _{{\rm{M}}3}} = \frac{{{{\left( {\alpha + \gamma c} \right)}^2}}}{{8\beta }},$ | (13) |
| $\qquad {\pi _{{\rm{R}}3}} = \frac{{{{\left( {\alpha + \gamma c} \right)}^2}}}{{16\beta }} - \frac{1}{2}{\eta _2}{c^2}{\text{。}}$ | (14) |
当制造商不采取绿色生产且零售商不采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad {\pi _{{\rm{M}}4}} = \frac{{{\alpha ^2}}}{{8\beta }},$ | (15) |
| $\qquad {\pi _{{\rm{R}}4}} = \frac{{{\alpha ^2}}}{{16\beta }}{\text{。}}$ | (16) |
通过对以上4种情况的分析,可以得到如表1所示的制造商和零售商在不同策略选择下的博弈支付矩阵。
| 表 1 制造商和零售商营销策略支付矩阵 Tab. 1 The payoff matrix of marketing strategy for the manufacturer and retailer |
假设在有限理性条件下,有一个企业群体,制造商群体中采取绿色生产策略所占比例为
| $ \begin{split} &\qquad \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = x\left( {{U_{\rm{G}}} - \overline {{U_{\rm{M}}}} } \right) = x\left( {1 - x} \right) \left[ {y\left( {{\pi _{{\rm{M}}1}} - {\pi _{{\rm{M}}3}}} \right) + \left( {1 - y} \right) \times }\right.\\ &\left. {\left( {{\pi _{{\rm{M}}2}} - {\pi _{{\rm{M}}4}}} \right)} \right]{\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (17) |
同理,采用绿色销售策略的零售商的期望收益为
| $ \begin{split} &\qquad \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = y\left( {{U_{\rm{G}}} - \overline {{U_{\rm{R}}}} } \right) = y\left( {1 - y} \right) \left[ {x\left( {{\pi _{{\rm{R}}1}} - {\pi _{{\rm{R}}2}}} \right) + \left( {1 - x} \right) \times}\right.\\ &\left. {\left( {{\pi _{{\rm{R}}3}} - {\pi _{{\rm{R}}4}}} \right)} \right]{\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (18) |
由式(17)和(18)可得到一个二维动力系统,如下所示。
| $ \begin{split} \qquad \left\{ \begin{array}{l} \dfrac{{{\rm{d}}x}}{{{\rm{d}}t}} = x\left( {{U_{\rm{G}}} - \overline {{U_{\rm{M}}}} } \right) = x\left( {1 - x} \right)[ y\left( {{\pi _{{\rm{M}}1}} - {\pi _{{\rm{M}}3}}} \right) +\\ \left( {1 - y} \right)\left( {{\pi _{{\rm{M}}2}} - {\pi _{{\rm{M}}4}}} \right) ] {\text{,}}\\ \dfrac{{{\rm{d}}y}}{{{\rm{d}}t}} = y\left( {{U_{\rm{G}}} - \overline {{U_{\rm{R}}}} } \right) = y\left( {1 - y} \right)[ x\left( {{\pi _{{\rm{R}}1}} - {\pi _{{\rm{R}}2}}} \right) +\\ \left( {1 - x} \right)\left( {{\pi _{{\rm{R}}3}} - {\pi _{{\rm{R}}4}}} \right) ] {\text{。}} \end{array} \right. \end{split}$ |
容易判断该系统的平衡点为(0,0)、(0,1)、(1,0)、(1,1),但是由复制者动态方程得到的平衡点不一定是系统的演化稳定策略(ESS),根据Friedman[20]提出的方法,演化均衡点的稳定性可以从该系统的雅可比(Jacobian)矩阵(记为J)的局部稳定分析导出。
| $ \begin{split} &\qquad {{J}} = \left( {\begin{array}{*{20}{c}} {\dfrac{{{\text{δ}} x}}{{{\text{δ}} x}}}&{\dfrac{{{\text{δ}} x}}{{{\text{δ}} y}}} \\ {\dfrac{{{\text{δ}} y}}{{{\text{δ}} x}}}&{\dfrac{{{\text{δ}} y}}{{{\text{δ}} y}}} \end{array}} \right) =\\ &\left( {\begin{array}{*{20}{c}} {\left( {1 \!-\! 2x} \right)\left( {{\pi _{{\rm{M}}2}}\! - \!{\pi _{{\rm{M}}4}}\! +\! y\Delta p} \right)}&{x\left( {1 - x} \right)\Delta p} \\ {y\left( {1 - y} \right)\Delta q}&{\left( {1 \!- \!2y} \right)\left( {{\pi _{{\rm{R}}3}}\! - \!{\pi _{{\rm{R}}4}} \!+\! x\Delta q} \right)} \end{array}} \right){\text{。}} \end{split}$ |
上式中,
计算雅克比矩阵
| 表 2 系统平衡点局部稳定性分析 Tab. 2 Local stability analysis of system equilibrium points |
1) 当
2) 当
3) 当
为了更加直观地体现消费者绿色偏好对供应链中制造商和零售商营销策略选择的影响,在参考相关研究的基础上将相应参数赋值为
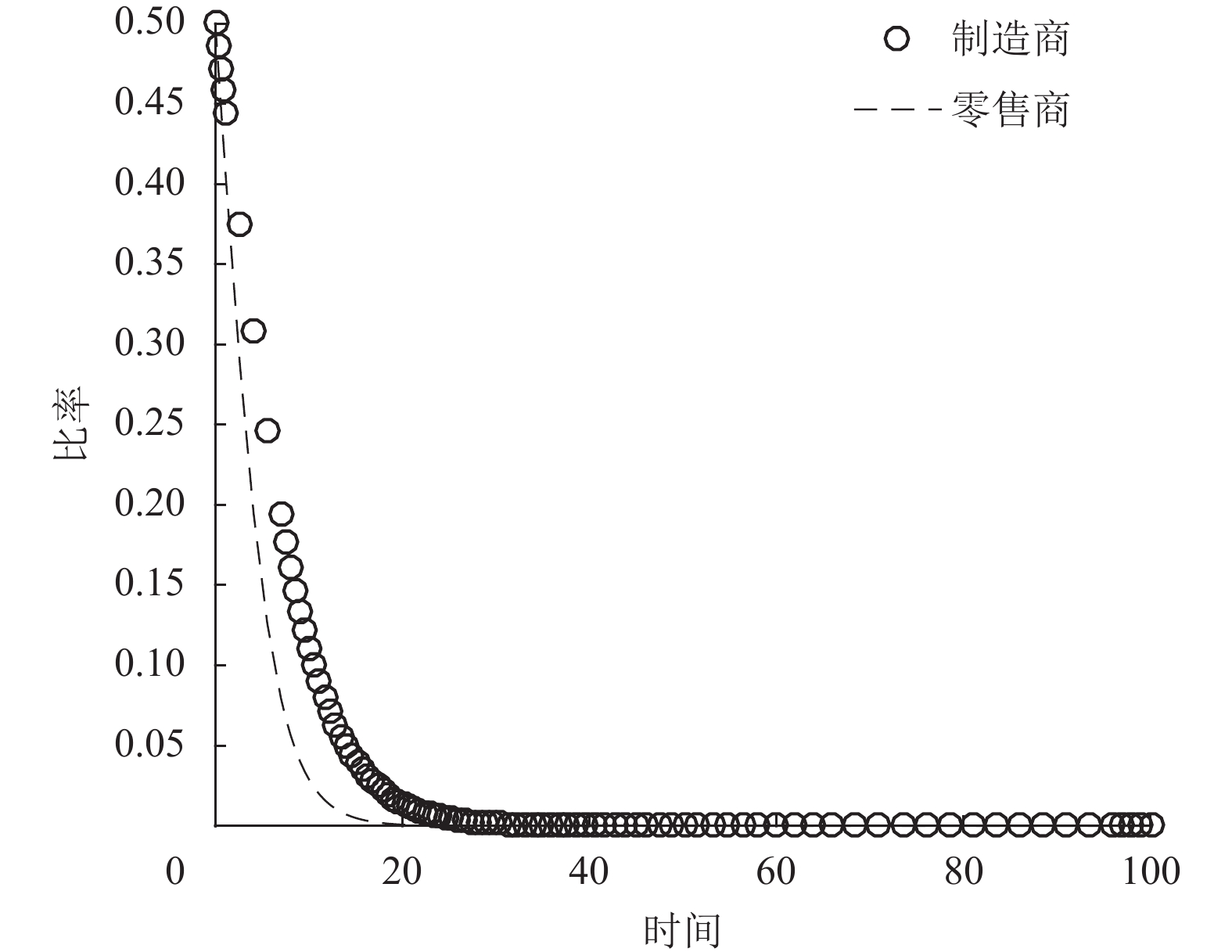
|
图 1 γ = 0.5时的演化轨迹 Fig. 1 Evolutionary trajectories when γ = 0.5 |
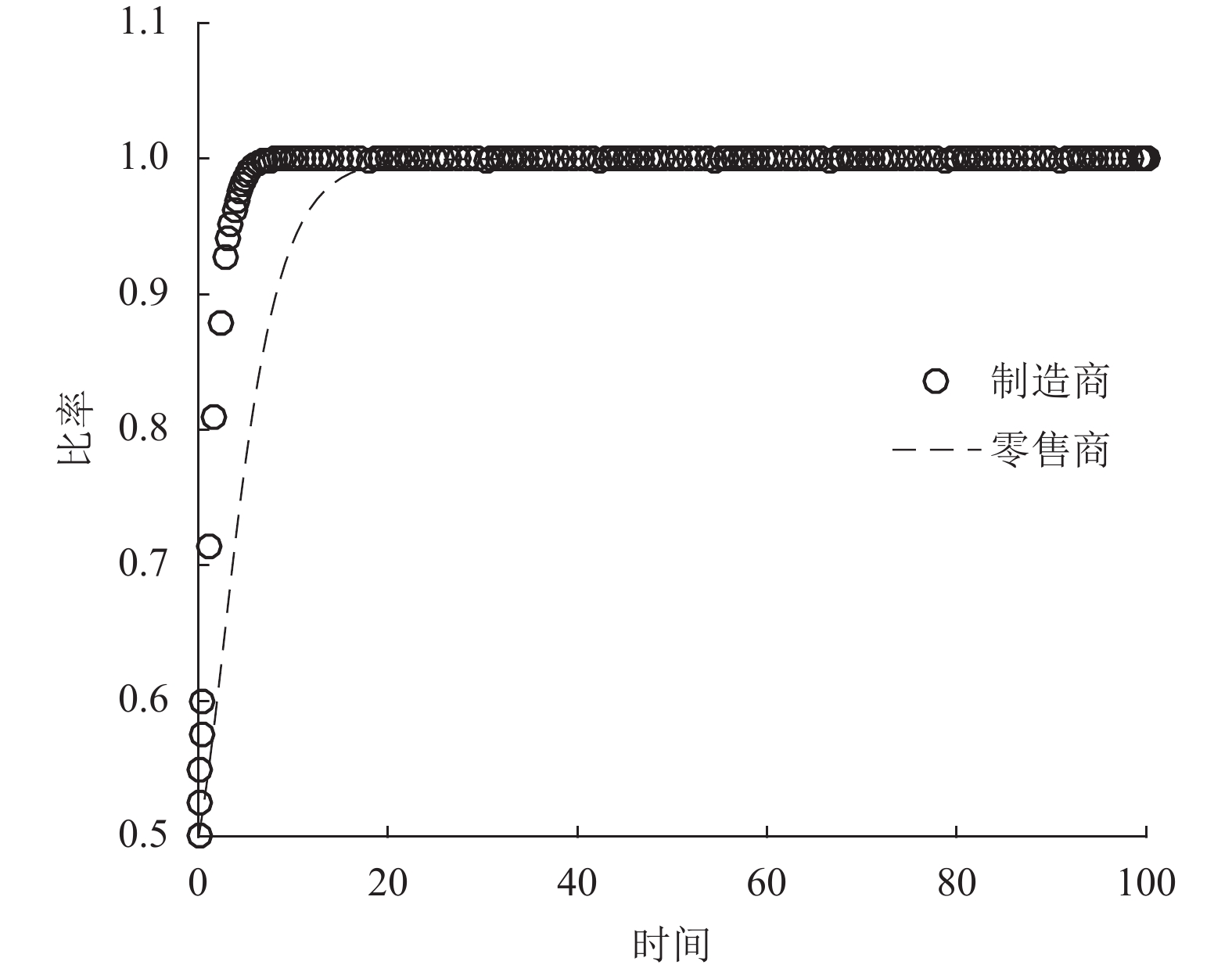
|
图 3 γ = 1.5时的演化轨迹 Fig. 3 Evolutionary trajectories when γ = 1.5 |
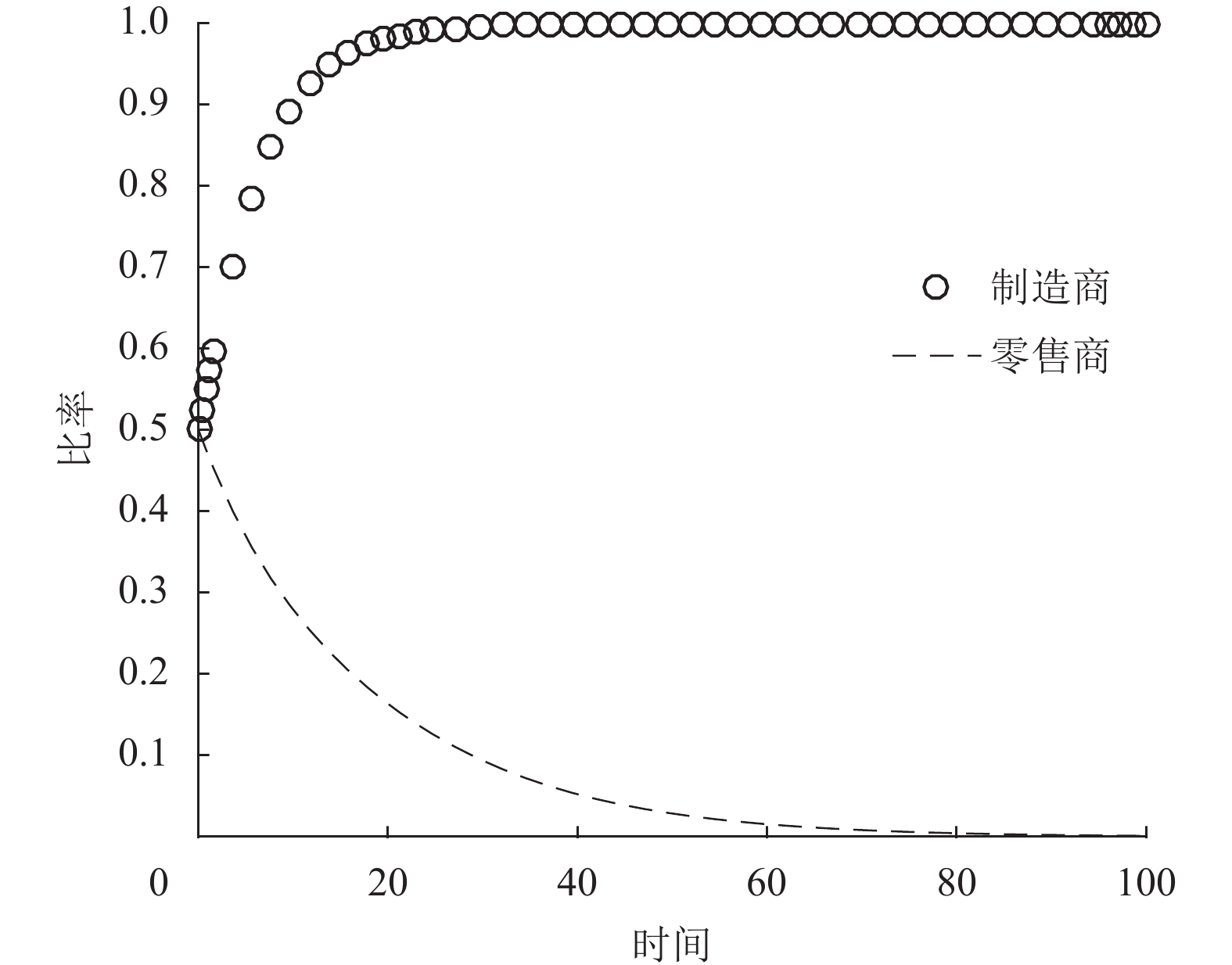
|
图 2 γ = 1时的演化轨迹 Fig. 2 Evolutionary trajectories when γ = 1 |
由系统平衡点局部稳定性分析的结果和Matlab的仿真图可以得到如下结论。
1) 当消费者的绿色偏好水平较低时(取
2) 当消费者的绿色偏好水平较低时(取
3) 由消费者绿色偏好的取值范围可以看出,其取值与制造商和零售商的绿色营销投入存在正向关系,说明随着制造商和零售商采取绿色营销策略投入成本的逐渐上升,促使双方采取绿色营销策略所需要的消费者绿色偏好水平也会逐渐上升。
3 同时考虑消费者绿色偏好和政府绿色补贴的营销策略演化分析经过上文的探讨,发现当
设
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma g + \gamma c} \right) - \frac{1}{2}{\eta _1}{g^2} + M,$ | (19) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma g + \gamma c} \right) - \frac{1}{2}{\eta _2}{c^2} + M{\text{。}}$ | (20) |
当制造商采取绿色生产策略而零售商不采取绿色销售策略时,制造商和零售商的利润分别为
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma g} \right) - \frac{1}{2}{\eta _1}{g^2} + M,$ | (21) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma g} \right){\text{。}}$ | (22) |
当制造商不采取绿色生产而零售商采取绿色销售策略时,制造商和零售商的利润分别为
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p + \gamma c} \right),$ | (23) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p + \gamma c} \right) - \frac{1}{2}{\eta _2}{c^2} + M{\text{。}}$ | (24) |
当制造商不采取绿色生产且零售商不采取绿色销售策略时,制造商和零售商的利润分别为
| $\qquad {\pi _{\rm{M}}} = w\left( {\alpha - \beta p} \right),$ | (25) |
| $\qquad {\pi _{\rm{R}}} = \left( {p - w} \right)\left( {\alpha - \beta p} \right){\text{。}}$ | (26) |
当制造商采取绿色生产且零售商采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad \pi _{{\rm{M}}1}^* = \frac{{{{\left( {\alpha + \gamma g + \gamma c} \right)}^2}}}{{8\beta }} - \frac{1}{2}{\eta _1}{g^2} + M,$ | (27) |
| $\qquad \pi _{{{\rm{R}}1}}^* = \frac{{{{\left( {\alpha + \gamma g + \gamma c} \right)}^2}}}{{16\beta }} - \frac{1}{2}{\eta _2}{c^2} + M{\text{。}}$ | (28) |
当制造商采取绿色生产策略而零售商不采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad \pi _{{\rm{M}}2}^* = \frac{{{{\left( {\alpha + \gamma g} \right)}^2}}}{{8\beta }} - \frac{1}{2}{\eta _1}{g^2} + M{\text{,}}$ | (29) |
| $\qquad \pi _{{\rm{R}}2}^* = \frac{{{{\left( {\alpha + \gamma g} \right)}^2}}}{{16\beta }}{\text{。}}$ | (30) |
当制造商不采取绿色生产而零售商采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad \pi _{{\rm{M}}3}^* = \frac{{{{\left( {\alpha + \gamma c} \right)}^2}}}{{8\beta }}{\text{,}}$ | (31) |
| $\qquad \pi _{{\rm{R}}3}^* = \frac{{{{\left( {\alpha + \gamma c} \right)}^2}}}{{16\beta }} - \frac{1}{2}{\eta _2}{c^2} + M{\text{。}}$ | (32) |
当制造商不采取绿色生产且零售商不采取绿色销售策略时,制造商和零售商的最优利润分别为
| $\qquad \pi _{{\rm{M}}4}^* = \frac{{{\alpha ^2}}}{{8\beta }}{\text{,}}$ | (33) |
| $\qquad \pi _{{\rm{R}}4}^* = \frac{{{\alpha ^2}}}{{16\beta }}{\text{。}}$ | (34) |
同理可建立一个二维动力系统
| $ \begin{split} \qquad \left\{ \begin{array}{l} \dfrac{{{\rm{d}}x}}{{{\rm{d}}t}} = x\left( {1 - x} \right)\left[ {y\left( {\pi _{{{\rm{M}}1}}^* - \pi _{{{\rm{M}}3}}^*} \right) + \left( {1 - y} \right)\left( {\pi _{{\rm{M}}2}^* - \pi _{{\rm{M}}4}^*} \right)} \right] {\text{,}}\\ \dfrac{{{\rm{d}}y}}{{{\rm{d}}t}} = y\left( {1 - y} \right)\left[ {x\left( {\pi _{{{\rm{R}}1}}^* - \pi _{{{\rm{R}}2}}^*} \right) + \left( {1 - x} \right)\left( {\pi _{{\rm{R}}3}^* - \pi _{{\rm{R}}4}^*} \right)} \right] {\text{。}} \end{array} \right. \end{split}$ |
雅可比(Jacobian)矩阵为
| $ \begin{split} &\qquad {{J}} = \left( {\begin{array}{*{20}{c}} {\dfrac{{{\text{δ}} x}}{{{\text{δ}} x}}}&{\dfrac{{{\text{δ}} x}}{{{\text{δ}} y}}} \\ {\dfrac{{{\text{δ}} y}}{{{\text{δ}} x}}}&{\dfrac{{{\text{δ}} y}}{{{\text{δ}} y}}} \end{array}} \right) = \\ &\left( {\begin{array}{*{20}{c}} {\left( {1 - 2x} \right)\left( {\pi _{_{{\rm{M}}2}}^* - \pi _{_{{\rm{M}}4}}^* + y\Delta p} \right)}&{x\left( {1 - x} \right)\Delta p} \\ {y\left( {1 - y} \right)\Delta q}&{\left( {1 - 2y} \right)\left( {\pi _{{\rm{R}}3}^* - \pi _{_{{\rm{R}}4}}^* + x\Delta q} \right)} \end{array}} \right){\text{。}} \end{split}$ |
上式中,
| 表 3 系统平衡点局部稳定性分析 Tab. 3 Local stability analysis of system equilibrium points |
1) 当
2) 当
3) 当
同样将相应参数赋值为
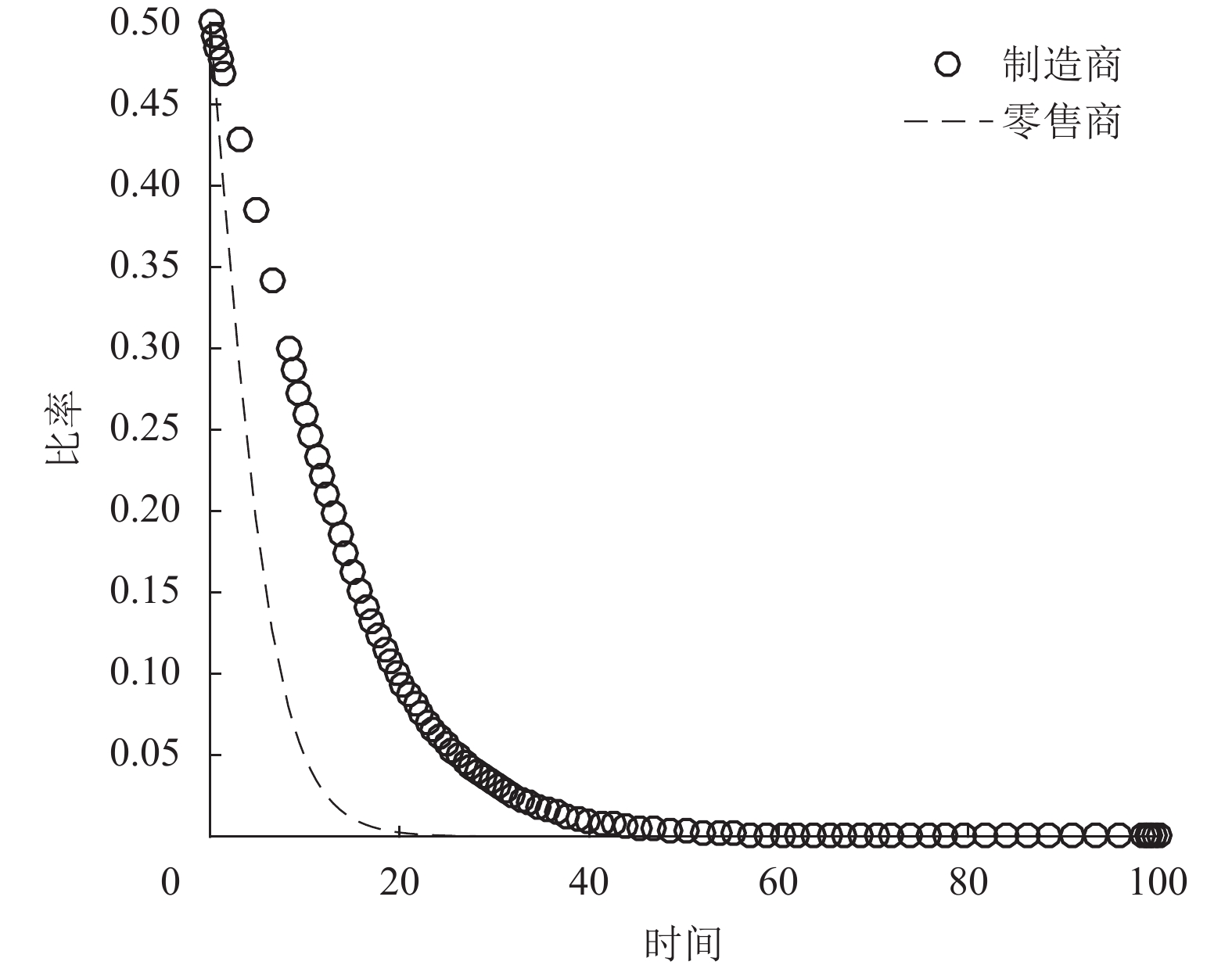
|
图 4 M = 0.1时的演化轨迹 Fig. 4 Evolutionary trajectories when M = 0.1 |
|
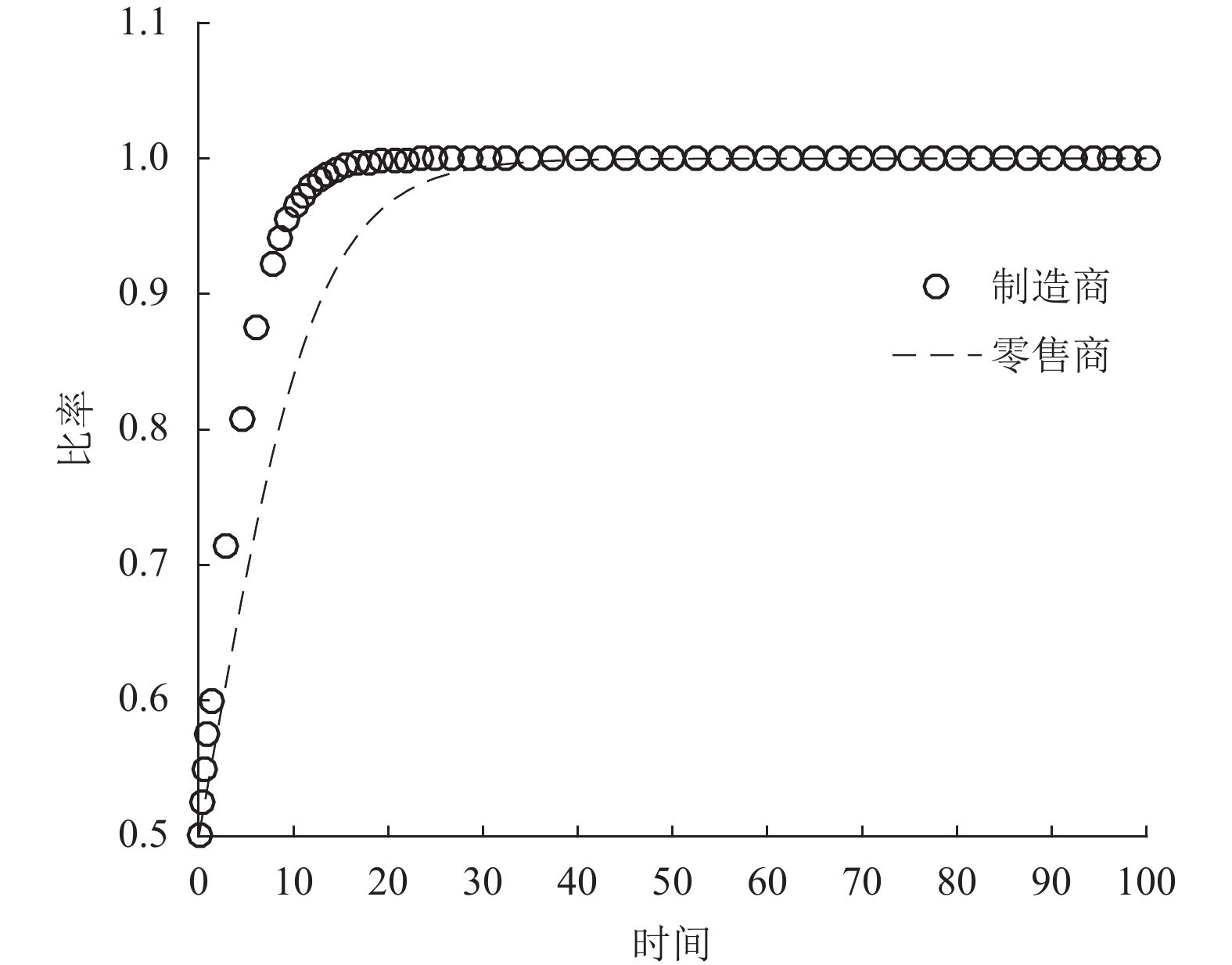
图 6 M = 0.5时的演化轨迹 Fig. 6 Evolutionary trajectories when M = 0.5 |
|
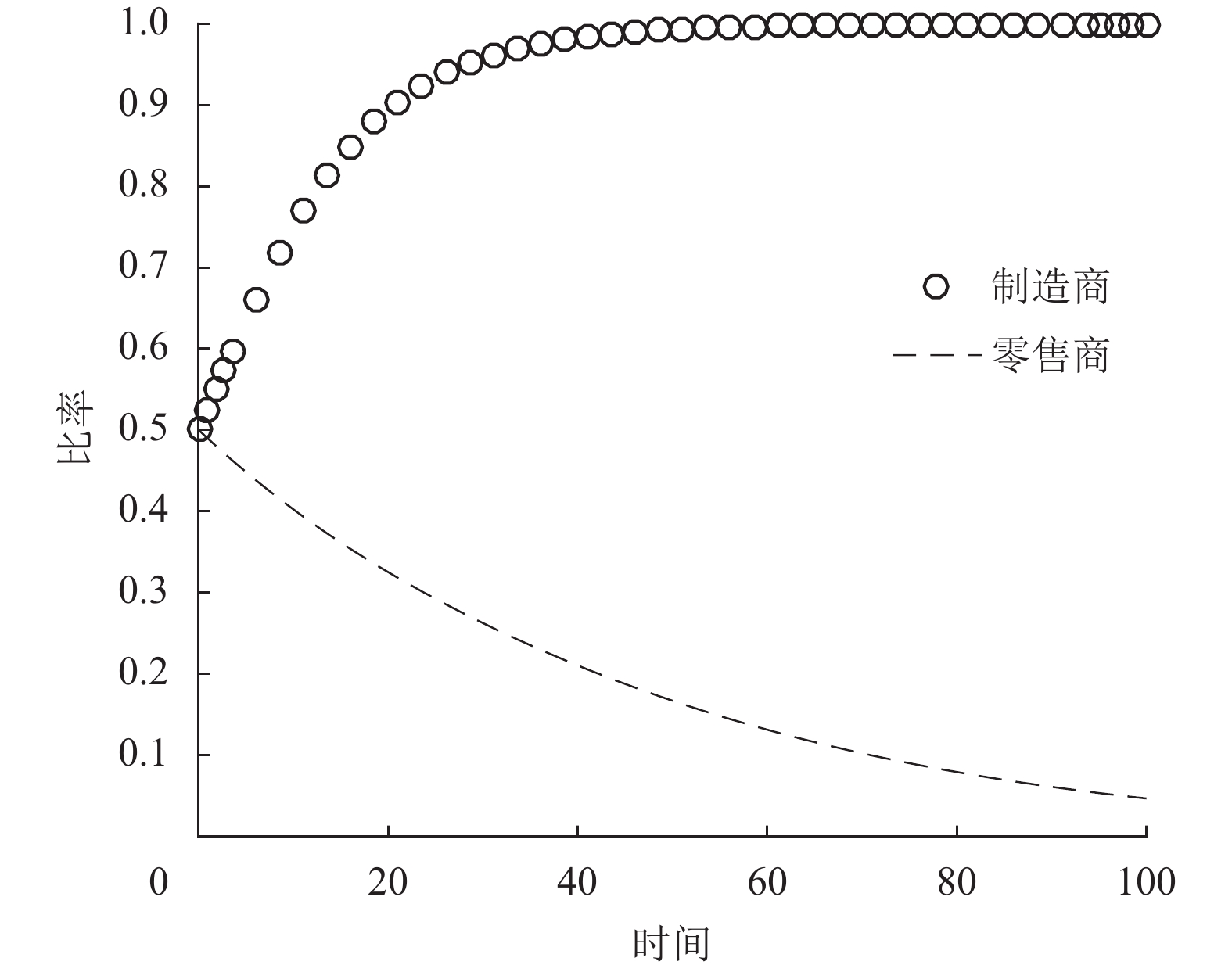
图 5 M = 0.3时的演化轨迹 Fig. 5 Evolutionary trajectories when M = 0.3 |
由系统平衡点局部稳定性分析的结果和Matlab的仿真图可以得到如下结论。
1) 当政府补贴水平较低时(取
2) 当政府补贴水平较低时(取
3) 由政府绿色补贴的取值范围可以看出,其取值与消费者的绿色偏好水平存在负向关系,说明随着市场上消费者绿色偏好水平的不断上升,促使双方采取绿色营销策略所需要的政府补贴水平将会逐渐下降。
4 总结本文针对消费者具有绿色偏好以及政府推行绿色补贴的市场环境,运用演化博弈理论与方法深入探讨了消费者绿色偏好及政府绿色补贴对制造商和零售商营销策略选择的影响。研究有以下发现。1) 消费者的绿色偏好会对双方的营销策略选择产生显著影响,但是只有当消费者的绿色偏好达到一定水平时才能最有效地促进制造商和零售商采取绿色营销策略。2) 目前我国绿色供应链管理水平较低,政府的资金支持是激励制造商和零售商采取绿色营销模式的重要手段,但是只有当政府补贴达到一定水平时,政府的补贴政策才能发挥最有效的作用。3) 在消费者绿色偏好和政府补贴保持同等水平条件下,制造商相较于零售商更易于采取绿色营销策略,特别当消费者绿色偏好或政府补贴处于较低水平时,零售商往往会通过搭便车的方式分享制造商绿色营销所带来的市场收益。4) 随着制造商和零售商采取绿色营销投入成本的不断上升,促使双方采取绿色营销策略所需要的消费者绿色偏好水平也会不断上升;随着市场上消费者整体绿色偏好水平的不断上升,促使双方采取绿色营销策略所需要的政府补贴水平将会不断下降。
根据上述结论,提出如下建议。1) 为有效促进绿色供应链在我国的推行,一方面必须进行绿色环保宣传,提高公众的环保意识,另一方面各级政府部门必须对采取绿色营销的企业进行适当补贴,但是为从根本上促进企业采取绿色营销模式,各级政府部门应该广泛开展绿色宣传活动,营造绿色消费理念,鼓励消费者进行绿色消费,而不能仅仅依靠为企业提供补贴。2) 各级政府部门在制定补贴标准时应充分考虑制造和零售企业经营模式的不同,并依据双方的实际经营情况对制造和零售企业提供绿色补贴,且为鼓励零售企业积极进行绿色宣传,扩大绿色产品市场需求,提高绿色供应链整体效益,可适当给予零售企业额外补贴。
本文研究仍存在不足之处,有待进一步补充和完善,如只考虑了制造商主导的供应链,未来可进一步在其他权利结构下开展相关研究。
| [1] |
朱庆华, 耿勇. 中国制造企业绿色供应链管理实践类型及绩效实证研究[J].
数理统计与管理, 2006, 25(4): 392-399.
ZHU Qinghua, GENG Yong. Statistics analysis on types of Chinese manufacturers based on practice of green supply chain management and their performance[J]. Application of Statistics and Management, 2006, 25(4): 392-399. DOI: 10.3969/j.issn.1002-1566.2006.04.003. |
| [2] |
朱庆华, 窦一杰. 绿色供应链中政府与核心企业进化博弈模型[J].
系统工程理论与实践, 2007(12): 85-89.
ZHU Qinghua, DOU Yijie. An evolutionary model between governments and core-enterprises in green supply chains[J]. Systems Engineering-Theory & Practice, 2007(12): 85-89. DOI: 10.3321/j.issn:1000-6788.2007.12.013. |
| [3] |
WALKER H, DI SISTO L, MCBAIN D. Drivers and barriers to environmental supply chain management practices: lessons from the public and private sectors[J].
Journal of Purchasing & Supply Management, 2008, 14(1): 69-85.
|
| [4] |
BRIK A B, MELLAHI K, RETTAB B. Drivers of green supply chain in emerging economies[J].
Thunderbird International Business Review, 2013, 55(2): 123-136.
DOI: 10.1002/tie.v55.2. |
| [5] |
朱庆华. 影响企业实施绿色供应链管理制约因素的实证分析[J].
中国人口·资源与环境, 2009, 19(2): 83-87.
ZHU Qinghua. An empirical study on barriers for implementing green supply chain management in manufacturers[J]. China Population Resources and Environment, 2009, 19(2): 83-87. DOI: 10.3969/j.issn.1002-2104.2009.02.015. |
| [6] |
张璇, 马志军, 田东红, 等. 企业绿色供应链管理实践的影响因素研究——基于元分析方法的探索[J].
中国人口·资源与环境, 2017, 27(12): 183-195.
ZHANG Xuan, MA Zhijun, TIAN Donghong, et al. Meta-analysis on the affecting factors of green supply chain management practices[J]. China Population Resources and Environment, 2017, 27(12): 183-195. |
| [7] |
刘玫. 基于解释结构模型法的绿色供应链影响因素分析[J].
科技管理研究, 2011(12): 192-194.
LIU Mei. Influencing factors analysis of green supply chain based on the ISM[J]. Science and Technology Management Research, 2011(12): 192-194. DOI: 10.3969/j.issn.1000-7695.2011.12.050. |
| [8] |
张荣兰, 路世昌. 钢铁企业绿色供应链影响因素测度研究[J].
环境科学与技术, 2015, 38(1): 188-194.
ZHANG Ronglan, LU Shichang. Study on influencing factors measurement of green supply chain management in iron and steel enterprises[J]. Environmental Science & Technology, 2015, 38(1): 188-194. |
| [9] |
方陈承, 张建同. 绿色供应链管理对企业绩效的影响—一项元分析研究[J].
科技管理研究, 2017(24): 234-240.
FANG Chencheng, ZHANG Jiantong. Impact of green supply chain management on firm performances: a meta analysis[J]. Science and Technology Management Research, 2017(24): 234-240. DOI: 10.3969/j.issn.1000-7695.2017.24.035. |
| [10] |
黄国青, 华凤燕. 绿色供应链绩效评价的模型研究[J].
工业工程, 2007, 10(1): 116-121.
HUANG Guoqing, HUA Fengyan. Research model of performance evaluation of green supply chain[J]. Industrial Engineering Journal, 2007, 10(1): 116-121. DOI: 10.3969/j.issn.1007-7375.2007.01.027. |
| [11] |
杨渠, 窦祥胜. 基于风险规避的绿色供应链定价研究[J].
工业工程, 2018, 21(5): 40-49.
YANG Qu, DOU Xiangsheng. A research on green supply chain pricing based on risk aversion[J]. Industrial Engineering Journal, 2018, 21(5): 40-49. DOI: 10.3969/j.issn.1007-7375.2018.05.006. |
| [12] |
何彬斌, 刘芹. 基于消费者绿色偏好的供应链纵向合作演化博弈[J].
统计与决策, 2018(13): 39-43.
HE Binbin, LIU Qin. Analysis on evolutionary game of vertical cooperation in supply chain considering consumer′s green preference[J]. Statistics & Decision, 2018(13): 39-43. |
| [13] |
白春光, 唐家福. 制造—销售企业绿色供应链合作博弈分析[J].
系统工程学报, 2017, 32(6): 818-828.
BAI Chunguang, TANG Jiafu. Manufacturing-marketing green supply chain cooperative game analysis[J]. Journal of Systems Engineering, 2017, 32(6): 818-828. |
| [14] |
江世英, 李随成. 考虑产品绿色度的绿色供应链博弈模型及收益共享契约[J].
中国管理科学, 2015, 23(6): 169-176.
JIANG Shiying, LI Suicheng. Green supply chain game models and revenue sharing contract with product green degree[J]. Chinese Journal of Management Science, 2015, 23(6): 169-176. |
| [15] |
白世贞, 阮雨璐, 吴雪艳. 供应链视角下绿色产品定价及协调[J].
商业经济研究, 2018(8): 27-30.
DOI: 10.3969/j.issn.1002-5863.2018.08.009. |
| [16] |
朱庆华, 窦一杰. 基于政府补贴分析的绿色供应链管理博弈模型[J].
管理科学学报, 2011, 14(6): 86-95.
ZHU Qinghua, DOU Yijie. A game model for green supply chain management based on government subsidies[J]. Journal of Management Sciences in China, 2011, 14(6): 86-95. |
| [17] |
张艳丽, 胡小建, 杨海洪. 基于政府财政干涉的绿色供应链销售渠道模型[J].
工业工程, 2015, 18(5): 27-33.
ZHANG Yanli, HU Xiaojian, YANG Haihong. Distribution channel models of green supply chain based on government financial intervention[J]. Industrial Engineering Journal, 2015, 18(5): 27-33. DOI: 10.3969/j.issn.1007-7375.2015.05.005. |
| [18] |
SWAMI S, SHAH J. Channel coordination in green supply chain management[J].
Journal of the Operational Research Society, 2013, 64(3): 336-351.
DOI: 10.1057/jors.2012.44. |
| [19] |
JOGRENSEN S, ZACCOUR G. Channel coordination over time: incentive equilibria and credibility[J].
Journal of Economic Dynamics & Control, 2003, 27(5): 801-822.
|
| [20] |
FRIEDMAN D. Evolutionary game in economics[J].
Econometrica, 1991, 59(3): 637-666.
DOI: 10.2307/2938222. |
 2019, Vol. 22
2019, Vol. 22