多元统计过程控制是制造业中必不可少的环节,针对多维正态数值型数据的控制图发展已十分成熟,最受欢迎的是Hotelling T2控制图[1]、多元累积和(MCUSUM)控制图[2]和多元指数加权移动平均(MEWMA)控制图[3]。然而,这3类控制图都存在一定的应用局限性,都无法处理非正态型的数据。非参数控制图的出现为这一问题提供了解决方案。Bakir[4]通过设计秩统计量,打破了原有控制图在变量分布上的限制。Graham等[5]建立了一种非参数的EWMA控制图,并且证明了其在受控过程中的鲁棒性。Qiu[6]使用对数线性模型建立了不限分布的多变量CUSUM控制图。除此之外,Zou等[7]通过一种自启动算法也实现了对非正态变量的有效监测。
然而,在实际应用中,需要监测的数据可能不仅仅只有数值型变量,往往还包括顺序型类别变量。例如,在钻石的品控环节中不仅要考虑钻石的克拉数,也要考虑切割分级、颜色分级、杂质分级这类带有明显等级特征的顺序型类别变量。在这种情况下,混合型数据监测控制图应运而生。Ning等[8]提出了一种可以有效处理混合型数据的基于密度的控制图,将类别型变量转化成数值型变量,然后结合LOF算法[9]来考量数据的异常程度,并且将该控制图与非参数的simplicial depth方法[10]进行对比,证明了该控制图的有效性。Ding等[11]采用等级排名数来代替顺序型数据这一方法,结合MEWMA控制图进行数据监测。然而,这类控制图大多使用自定义的数值来代替顺序性变量,将混合型数据转化为纯数值型数据,最后利用纯数值型控制图进行监测。而随着数据复杂性和维度的提高,这类自定义数值转化的方法明显存在设计上的主观性和不合理性。因此,如何处理好顺序型类别数据且有效利用数据间的相关关系,是多维混合型数据监测领域的重要挑战之一。
Copula函数是将变量的联合分布函数与它们各自的边缘分布函数连接在一起的函数,可以有效地描述变量间的相关关系[12],为混合型数据建模提供了新的突破口。Song等[1 3]使用二元Gaussian Copula构建了一个含有离散和连续型变量的双变量模型。Fatahi等[14]提出了基于Copula的零膨胀泊松模型,实现了对罕见事件的监测。Sukparungsee等[15]将5种二元Copula函数应用于Hotelling T2 控制图,比较了各类Copula在不同均值偏移量和不同变量相关性情况下的表现。当问题从二元延伸到多元时,二元Copula被多元Copula结构所代替[16]。Verdier[17]提出了一种基于非参数核密度估计方法的多元Copula控制图,证明了其相对于Hotelling T2控制图和DDMA控制图[18]在监测多维非正态数据上的优势。Kosmidis等[19]使用多元Copula混合模型也成功建立了一个三维聚类模型。然而,随着数据维度和变量类型的增加,使用二元Copula将会因为函数中的参数估计问题而导致巨大的计算负担,而多元Copula函数种类又极少,且在描述多元变量之间相关性时,缺乏灵活性和通用性[20-22]。
Vine Copula模型的出现解决了上述问题:它将高维Copula函数分解为多个二元Copula函数的结合,大大提高了模型的拟合度。其中,不同的分解方式代表不同的Vine Copula结构。在众多Vine Copula结构中,最早被提出的是R-Vine结构[23]。但是这种结构不固定,没有被广泛应用。随后在R-Vine基础上,Aas等[24]推出了D-Vine和C-Vine模型,这两种模型结构较简单,常常被用于多维数据建模。Zilko等[25]使用D-Vine Copula模型,建立了一个含有5个离散型变量和3个连续型变量的多变量模型,并且与多元正态Copula模型对比,证明了其在描述伯努利分布数据上更高的覆盖性。Kim等[26]和郑文静等[27]使用混合D-Vine Copula模型完成了对多维数据的建模。然而,D-Vine和C-Vine模型的结构相对固定,无法拟合更复杂的相关性结构。为了增加Vine Copula模型的灵活性,Dissmann等[28]将最大生成树的算法应用于R-Vine结构中,简化了原有R-Vine结构的选择过程,设计出了一种简洁、高效的多维数据建模方法。该方法在金融领域已经被广泛使用[29],然而由于起步较晚,在控制图领域还鲜少被涉及。
Vine Copula通过利用多个种类丰富且成熟的二元Copula函数来描述变量两两之间不同的相关性结构,从而灵活地建立多元变量之间的相关性模型。本文将在混合型数据监测过程中引入Vine Copula模型,建立一种基于R-Vine Copula的多维混合型数据控制图。通过实例研究比较R-Vine Copula控制图(RVC)和现有多维混合型数据控制图表现,证明该控制图在混合型数据监测过程的优势。
1 Vine Copula模型 1.1 Copula函数简介Copula 模型最早由Sklar于1959年提出,它利用各个变量的边缘分布函数和一个Copula函数的组合来描述多维变量的联合分布,这个Copula函数的选择取决于变量之间的相关关系。一般地,对于一个n维随机变量
| $ \qquad F\left( {{x_{1,}}{x_{2,}} \cdots ,{x_n}} \right) = C\left( {{u_{1,}}{u_{2,}} \cdots ,{u_n}} \right){\text{。}} $ | (1) |
其中ui是第i个变量xi的边缘累计分布函数,C表示多元Copula函数。在众多Copula函数中,二元Copula函数的种类最为丰富。对于两个随机变量X、Y,边缘分布函数为F(x)、F(y),边缘概率密度函数为f(x)、f(y)。此时,随机变量X、Y的联合分布函数H(x,y)和联合概率密度函数f(x,y)可以表示为:
| $ \qquad H\left( {x,y} \right) = C\left( {u,v;\theta} \right) = C\left( {F\left( x \right),F\left( y \right);\theta} \right), $ | (2) |
| $ \qquad{{f}}\left( {x,y} \right) = f\left( x \right)f\left( y \right)c\left( {u,v;\theta } \right){\text{。}} $ | (3) |
其中,θ是Copula函数的参数,u= F(x),v= F(y),且u、v均服从[0,1]上的均匀分布。c(u,v;θ)是C(u,v;θ)的密度函数。由此,两个变量的联合概率密度函数就可以由每个变量的边缘概率密度函数和Copula密度函数共同来表示。对于已知边缘分布的两个变量,只要选择合适的Copula函数来描述其相依结构,就可以得到其联合概率密度函数,完成对数据的建模。
常用的二元Copula函数可以分为椭圆族和阿基米德族。椭圆族中包括Gaussian、Student-t等,都是由多元椭圆分布推导而来。阿基米德族中包括Clayton、Gumbel、Frank等,这类函数具有一些代数特征,如次序性等。除了这几种常用的二元Copula函数,还有一些其他的二元Copula函数,比如概率密度为1的独立Copula函数(Independence Copula),以及基于各类二元Copula函数衍生出的生存Copula函数(Survival Copula)、旋转Copula函数(Rotated Copula)。不同Copula函数在描述变量相关性上差别很大,但也正因为这样,才能使得Copula函数在面对不同场景下的适用性更强,数据建模能力更强。当变量维度从二维延伸到多维时,二元Copula函数也延伸为多元Copula函数,常见的如多元Gaussian Copula函数、多元Student-t Copula函数等。但是这类多元Copula函数只适用于变量之间具有相同相关性结构的场景,在使用过程中有很大的局限性。为了解决这个问题,Joe[30]提出了Pair Copula的概念,通过条件概率公式将高维变量的联合分布分解成多个二元Copula的乘积,对应的分解方法也被称为Vine Copula。
假设有n维变量
| $ \begin{split} &\qquad f\left( {{x_1}, \cdots ,{x_n}} \right) = {f_1}\left( {{x_1}} \right) \times f\left( {{x_2}|{x_1}} \right) \times f\left( {{x_3}|{x_1},{x_2}} \right) \times\cdots \times\\ & f\left( {{x_n}|{x_1}, \cdots ,{x_{n - 1}}} \right){\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (4) |
根据条件概率和式(3)可得
| $ \begin{split} &\qquad f\left( {{x_n}|{x_1}, \cdots ,{x_{n - 1}}} \right) = \dfrac{{f\left( {{x_n},{x_{n - 1}}|{x_1}, \cdots ,{x_{n - 2}}} \right)}}{{f\left( {{x_{n - 1}}|{x_1}, \cdots ,{x_{n - 2}}} \right)}}=\\ & \dfrac{{c\left( {F\left( {{x_n}|{x_1},\! \cdots\! ,\!{x_{n\! -\! 2}}} \right) \!\times \!F\left( {{x_{n \!-\! 1}}|{x_1}, \!\cdots\! ,{x_{n \!-\! 2}}} \right)} \right) \times f\left( {{x_n}|{x_1},\! \cdots \!,{x_{n\! -\! 2}}} \right) \times f\left( {{x_{n \!-\! 1}}|{x_1}, \!\cdots\! ,{x_{n\! -\! 2}}} \right)}}{{f\left( {{x_{n \!-\! 1}}|{x_1}, \!\cdots\! ,{x_{n\! -\! 2}}} \right)}}\!= \! c\left( {F\left( {{x_n}|{x_1}, \!\cdots \!,{x_{n \!-\! 2}}} \right)\times F\left( {{x_{n\! -\! 1}}|{x_1}, \!\cdots \!,{x_{n\!-\! 2}}} \right)} \right) \times\\ & f\left( {{x_n}|{x_1}, \!\cdots\! ,{x_{n \!- \!2}}} \right){\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (5) |
令
| $ \begin{split} &\qquad f\left( {{x_n}|{x_1}, \cdots ,{x_{n - 1}}} \right) ={c_{n,n - 1|1, \cdots ,n - 2}} \times f\left( {{x_n}|{x_1}, \cdots ,{x_{n - 2}}} \right) = \\ &{c_{n,n - 1|1, \cdots ,n - 2}}\times {c_{n,n - 1|1, \cdots ,n - 3}}\times f\left( {{x_n}|{x_1}, \cdots ,{x_{n - 3}}} \right) = \\ &{f_{{n}}}\left( {{x_{{n}}}} \right)\prod\limits_{i = 1}^{n - 2} {{c_{n,n - i|1, \cdots ,n - i + 1}}} {\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (6) |
由此可得式(4)的联合概率密度函数最终可以由数个
R-Vine Copula[23]也被称为正则藤(Regular Vine),它通过一种树形的嵌套结构来描述高维变量联合分布的分解过程。图1展示了一个五维的R-Vine结构,从图中可以看出该结构共有4层树,每两个结点之间有一条边相连,上层数的边构成了下层树的结点,且只有相邻的边才可以在下一层树中作为结点相连。每一层树的结构可以基于最大生成树算法来确定[28]。以五维变量为例,其R-Vine结构构造过程如下。

|
图 1 一个五维的R-Vine结构 Fig. 1 A five-dimensional R-Vine structure |
1) 计算两两变量之间的Kendall系数,根据最大生成树算法选择令Kendall系数绝对值总和最大的结构,确定第1层的结构。
2) 确定每条连接边对应的Pair Copula函数类型,完成Pair Copula函数的参数估计。Pair Copula函数类型的选择有3种选择标准,分别是赤池信息量准则(Akaike information criterion, AIC)[31],consistent AIC(CAIC)[32]和贝叶斯信息准则(Bayesian information criterion,BIC)[33]。AIC准则是以熵的概念为基础来衡量模型的复杂度和数据拟合度,在衡量模型优良性上效果较好。本文也将依据AIC准则来进行Pair Copula函数的选择。同时,采用极大似然估计(maximum likelihood estimate,MLE)对选中的Pair Copula的参数进行估计。
3) 基于Pair Copula得到条件变量分布,将各Pair Copula的估计结果代入下一层,重新根据最大生成树算法和AIC准则分别确定下一层的结构及Pair Copula函数,对各Pair Copula模型进行参数估计。
4) 重复步骤3),进行第3层及其他层的结构构造,直到结点数只有2个,完成R-Vine结构构造。
对于一个已知的n维R-Vine的结构,共有n−1层树结构。每一层的树结构的连接边集合为
| $ \begin{split} &\qquad f\left( {{x_1}, \cdots ,{x_n}} \right) = \prod\limits_{k = 1}^n {{f_k}} \left( {{x_k}} \right)\prod\limits_{i = 1}^{n - 1} {\prod\limits_{e \in {E_i}} {{c_{{S_{e,a}},{S_{e,b}}|{D_e}}}} } \times \\ &\left( {{F_{{S_{e,a}}|{D_e}}}\left( {{x_{{S_{e,a}}}}{\rm{|}}{x_{{D_e}}}} \right),{F_{{S_{e,b}}|{D_e}}}\left( {{x_{{S_{e,b}}}}{\rm{|}}{x_{{D_e}}}} \right)} \right){\text{。}} \end{split} $ | (7) |
其中,fk(xk)表示各变量的边缘概率密度函数。e表示连接结点a、b的边,Se,a、Se,b表示结点a、b上所有非条件变量的变量集合,De表示边e上所有条件变量的集合。
本文选用R-Vine Copula对受控状态下的混合型数据建模,根据测试数据的概率密度分位数来确定控制界限。该控制图构建主要步骤如下。
1) 将受控样本点分为训练用受控数据和测试用受控数据两个部分,确定模型的训练集和测试集。
2) 确定训练集中各变量的边缘概率密度函数。对于计数型变量,使用概率质量函数来表示边缘概率密度。对于连续型变量,使用核密度估计方法[34]来确定其边缘概率密度函数。假设一个连续型变量中有n个独立同分布的样本点
| $ \qquad {\hat f_h}\left( x \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{K_h}} \left( {x - {x_i}} \right) = \frac{1}{{nh}}\sum\limits_{i = 1}^n K \left( {\frac{{x - {x_i}}}{h}} \right){\text{。}} $ | (8) |
其中,K为核函数,可选的种类有“Gaussian” “Epanechnikov[35]” “Rectangular”“Triangular”“Biweight”“Cosine”“Optcosine”等等。h是一个平滑参数,也被称作带宽(bandwidth),它决定了核密度估计函数的平滑程度。在RVC控制图的设计中使用高斯核函数作为核密度估计方法的核函数,带宽的选择遵循Silverman经验法则[36],具体计算方法为
| $ \qquad h = {\left( {\frac{{4{{\hat \sigma }^5}}}{{3n}}} \right)^{\frac{1}{5}}} \approx 1.06\hat \sigma {n^{ - \frac{1}{5}}}{\text{。}} $ | (9) |
其中,
3) 对训练数据进行秩标准化处理,计算训练数据下变量间的Kendall系数。根据最大生成树算法完成R-Vine Copula的逐步构建,结合各变量的边缘概率密度函数,得到混合模型的联合概率密度函数,确定控制图的统计量。
4) 确定控制图的控制界限H。根据联合概率密度函数计算测试受控数据的概率密度函数值,根据设置的第一类错误值得到相应的静态概率密度分位数,以该值作为控制图的控制界限H。
5) 计算监测数据的统计量。对于当前的监测数据,计算该数据的联合概率密度值。
6) 判断是否发出异常信号。如果其对应的概率密度值大于或等于H,表示没有检测到异常状态,继续监测下一个测试数据;如果其对应概率密度函数值小于H,则表示监控系统失控,然后发出报警信号。
3 算例分析本文将通过实际算例来比较RVC控制图和现有的控制图在监测含顺序型变量的混合型数据时的表现。以钻石质量数据集[37]为案例背景,分别使用RVC控制图、多元Copula控制图[17]和基于密度的控制图[8]进行监测,然后比较这三类控制图对多维混合型数据的监测效果。
钻石质量数据集共有5万条数据,每条数据记录了一颗钻石的信息。该信息由克拉数、切工分级、颜色分级、净度分级、宽高比((冠部高度/平均直径)×100%)、台宽比((台面宽度/平均直径)×100%)、价格、长、宽、高等属性组成。钻石的价值由多个属性决定,即使在克拉数一定的情况下,不同钻石的价值也各不相同。本算例选取了同为0.3克拉的2 604条钻石数据作为实验数据,研究在克拉数固定情况下,钻石质量的控制方案。钻石的质量可以由钻石的价格反映,将价格前90%的钻石视为正常品质钻石,即控制图中的受控数据。价格后10%的钻石划分为低品质钻石,即控制图中的失控数据。在构建控制图的过程中,对受控数据进行随机划分,选取75%的数据作为控制图的训练集,剩余25%的作为测试集。该算例数据为8维混合型数据,包含5个数值型变量(宽高比、台宽比、长、宽、高)和3个顺序型变量(切工分级、颜色分级、净度分级)。其中,3个顺序型变量的具体信息见表1。
| 表 1 顺序型变量的属性值信息 Tab. 1 The Attribute information of ordinal variables |
首先根据测试数据构建一个8维的R-Vine模型,构建好的模型结构图见图2。其中1、2、3、4、5、6、7、8为不同的变量,分别代表切工分级、颜色分级、净度分级、宽高比、台宽比、长、宽、高。
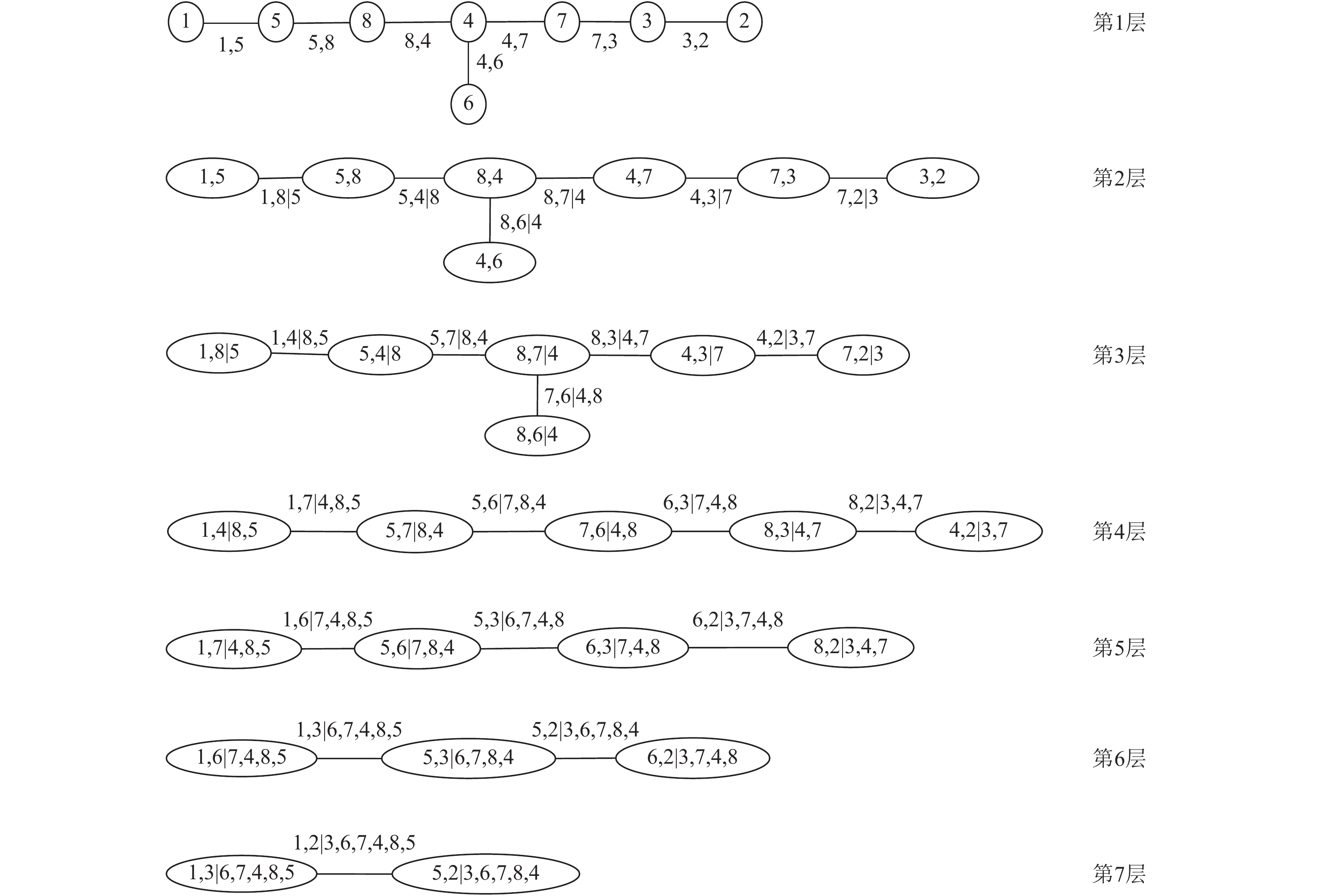
|
图 2 钻石质量数据的R-Vine Copula结构图 Fig. 2 The R-Vine Copula structure of diamond quality dataset |
每一个层级不同的连接边结构以及其对应的Pair Copula函数类型和参数见表2。有些Pair Copula函数只有一个参数,如Gaussian函数、Frank Copula函数。有些Pair Copula函数有两个参数,如Student-t Copula函数。
| 表 2 R-Vine Copula模型的参数估计结果 Tab. 2 The estimated parameters of R-Vine Copula model |
为了深入比较不同Vine Copula模型的拟合效果,本文同样基于钻石质量数据建立了C-Vine Copula和D-Vine Copula模型。表3列出了3种Vine Copula模型的拟合优度对比。从表中可以看出,R-Vine Copula的对数似然值最大,且其AIC和BIC的值最小,这也证明了R-Vine Copula相对于其他Vine Copula模型在数据拟合方面的优势。
| 表 3 不同Vine Copula模型拟合结果对比 Tab. 3 The Comparison of different Vine Copula models in fitting parameters |
根据训练数据建立了R-Vine模型后,基于测试数据确定控制图的控制界限,完成了RVC控制图的设计。同时构造了基于密度的控制图、多元Gaussian Copula控制图和多元Student-t Copula控制图,测试这4类控制图监测表现。图3展示了这4种控制图的ROC(receiver operating characteristic)[38]曲线。从图中可以看出,在钻石质量案例中,在第一类错误值较小时,相比基于密度的控制图、多元Gaussian Copula控制图以及多元Student-t Copula控制图,RVC控制图有明显的监测优势。这4种控制图的综合表现由好到差依次为:RVC控制图>多元Gaussian Copula控制图>基于密度的控制图>Student-t Copula控制图。
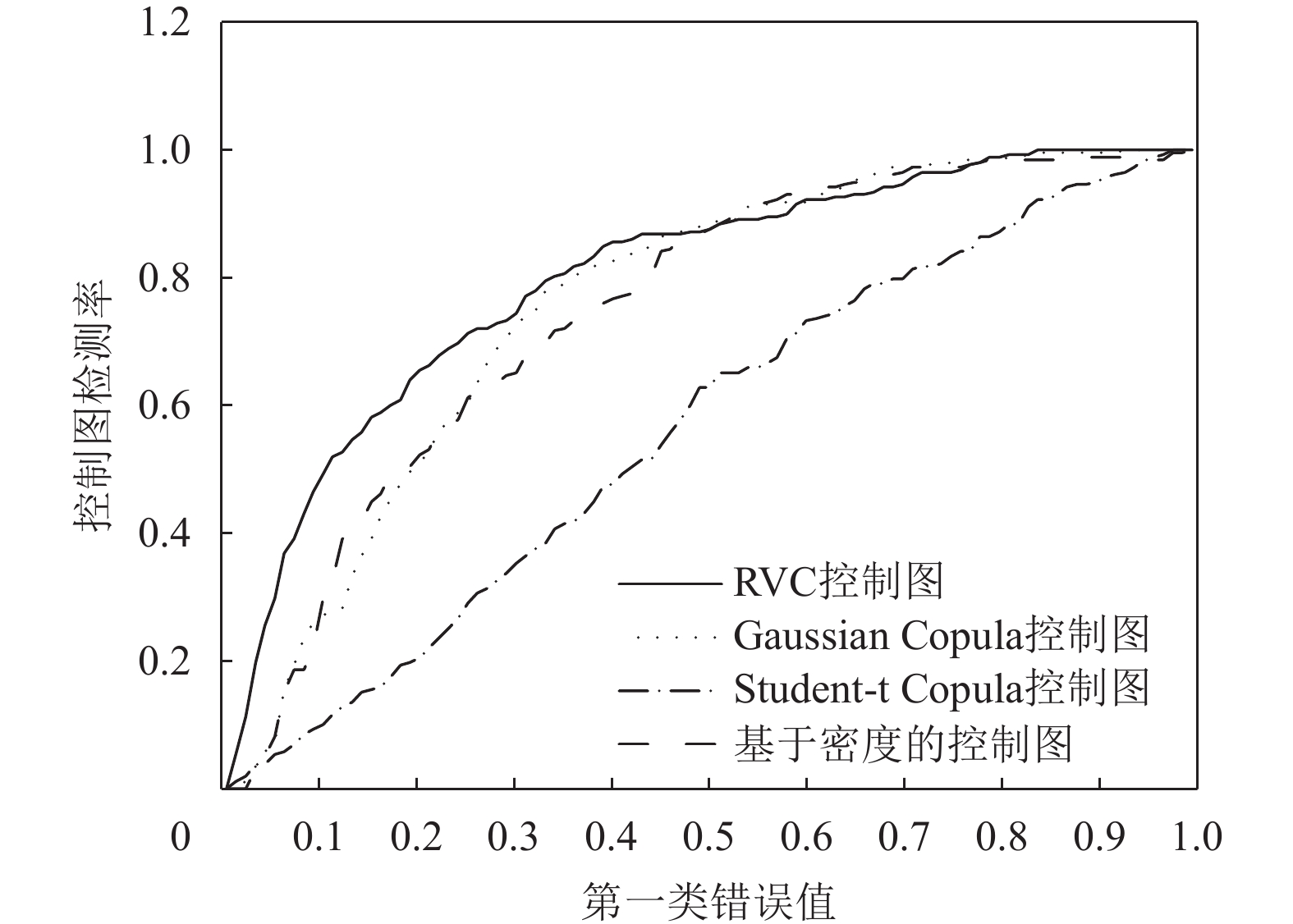
|
图 3 RVC控制图与其它控制图的ROC曲线 Fig. 3 The ROC curve of RVC control chart and other control charts |
本文在混合型数据监测过程中引入了R-Vine Copula结构,完成了RVC控制图的设计。该控制图充分利用了数据间的秩相关性,可以有效地处理含有顺序型变量的混合型数据。利用钻石质量数据集将RVC控制图与基于密度的控制图和多元Copula控制图进行了对比,证明了新控制图的有效性。在未来,关于混合型数据监测,还有以下几个方面值得研究。1) 引入含时变性的Vine Copula结构,提升模型对含时变性数据的监测效果。2) 研究含名义型变量的混合型数据处理方法,扩展控制图的应用性。3) 将控制图与降维方法相结合,解决更高维混合型数据的监测问题。
| [1] |
HOTELLING H. Multivariate quality control by air testing of sample bombsights//Eisenhart C, Hastay M W, Wallis W A. Techniques of statistical analysis[M]. New York: McGraw,1947.
|
| [2] |
WOODALL W H, NCube M M. Multivariate CUSUM quality-control procedures[J].
Technometrics, 1985, 27(3): 285-292.
DOI: 10.1080/00401706.1985.10488053. |
| [3] |
LOWRY C, WOODALL W, CHAMP C, et al. A multivariate exponentially weighted moving average control chart[J].
Technometrics, 1992, 34(1): 8.
|
| [4] |
BAKIR S. Distribution-free quality control charts based on signed-rank-like statistics[J].
Communications in Statistics, 2006, 35(4): 15.
|
| [5] |
GRAHAM M A, CHAKRABORTI S, HUMAN S W. A nonparametric EWMA sign chart for location based on individual measurements[J].
Quality Engineering, 2011, 23(3): 227-241.
DOI: 10.1080/08982112.2011.575745. |
| [6] |
QIU P. Distribution-free multivariate process control based on log-linear modeling[J].
IIE Transactions, 2008, 40(7): 664-677.
DOI: 10.1080/07408170701744843. |
| [7] |
ZOU C, WANG Z, TSUNG F. A spatial rank-based multivariate EWMA control chart[J].
Naval Research Logistics (NRL), 2012, 59(2): 91-110.
DOI: 10.1002/nav.v59.2. |
| [8] |
NING X, TSUNG F. A density-based statistical process control scheme for high-dimensional and mixed-type observations[J].
IIE Transactions, 2012, 44(4): 301-311.
DOI: 10.1080/0740817X.2011.587863. |
| [9] |
BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density-based local outliers[C/OL]. (2000-05-16). https://www.researchgate.net/publication/221214719_LOF_Identifying_Density-Based_Local_Outliers.
|
| [10] |
LIU R Y. Control charts for multivariate processes[J].
Publications of the American Statistical Association, 1995, 90(432): 1380-1387.
DOI: 10.1080/01621459.1995.10476643. |
| [11] |
DING D, TSUNG F, LI J. Rank-based process control for mixed-type data[J].
IIE Transactions, 2016: 673-683.
|
| [12] |
SKLAR M. Fonctions de repartition à n dimensions et leurs marges[J].
Publication de 1’Institut de Statistique de 1’Universite de Paris, 1959, 8: 229-231.
|
| [13] |
SONG P X, LI M, YUAN Y. Joint regression analysis of correlated data using Gaussian Copulas[J].
Biometrics, 2009, 65(1): 60-68.
DOI: 10.1111/j.1541-0420.2008.01058.x. |
| [14] |
FATAHI Amir Afshin, NOOROSSANA Rassoul, DOKOUHAKI Pershang, et al. Copula-based bivariate ZIP control chart for monitoring rare events[J].
Communications in Statistics, 2012, 41(15): 18.
|
| [15] |
SUKPARUNGSEE S, KUVATTANA S, BUSABABODHIN P, et al. Bivariate Copulas on the Hotelling's T2 control chart[C/OL]. (2017-12-18). https://www.tandfonline.com/doi/abs/10.1080/03610918.2016.1228958.
|
| [16] |
TRIVEDI P K, ZIMMER D M, TRIVEDI P K, et al. Copula modeling: an introduction for practitioners//Foundations and Trends® in Econometrics[M].Boston: Now Publishers, 2005.
|
| [17] |
VERDIER G. Application of Copulas to multivariate control charts[J].
Journal of Statistical Planning & Inference, 2013, 143(12): 2151-2159.
|
| [18] |
LIU R Y, SINGH K, TENG J H. DDMA-charts: nonparametric multivariate moving average control charts based on data depth[J].
Allgemeines Statistisches Archiv, 2004, 88(2): 235-258.
DOI: 10.1007/s101820400170. |
| [19] |
KOSMIDIS I, KARLIS D. Model-based clustering using Copulas with applications[J].
Statistics & Computing, 2016, 26(5): 1079-1099.
|
| [20] |
MIN A, CZADO C. Bayesian inference for multivariate Copulas using Pair-Copula constructions[J].
Journal of Financial Econometrics, 2010, 8(4): 511-546.
DOI: 10.1093/jjfinec/nbp031. |
| [21] |
BRECHMANN E C, SCHEPSMEIER U. Modeling dependence with C- and D-vine Copulas: the R package CDVine[J].
Journal of Statistical Software, 2013, 52(3): 1-27.
|
| [22] |
SCHMIDL D, CZADO C, HUG S, et al. A Vine-Copula based adaptive MCMC sampler for efficient inference for dynamic systems[J].
Bayesian Analysis, 2013, 8(1): 1-22.
DOI: 10.1214/13-BA801. |
| [23] |
BEDFORD T, COOKE R M. Vines: a new graphical model for dependent random variables[J].
Annals of Statistics, 2002, 30(4): 1031-1068.
DOI: 10.1214/aos/1031689016. |
| [24] |
AAS K, CZADO C, FRIGESSI A, et al. Pair-Copula constructions of multiple dependence[J].
Insurance: Mathematics and Economics, 2009, 44(2): 182-198.
DOI: 10.1016/j.insmatheco.2007.02.001. |
| [25] |
ZILKO A A, KUROWICKA D. Copula in a multivariate mixed discrete–continuous model[J].
Computational Statistics & Data Analysis, 2016, 103: 28-55.
|
| [26] |
KIM D, KIM J M, LIAO S M, et al. Mixture of D-Vine Copulas for modeling dependence[J].
Computational Statistics & Data Analysis, 2013, 64(4): 1-19.
|
| [27] |
郑文静, 李绍军, 蒋达. D-vine copulas混合模型及其在故障检测中的应用[J].
化工学报, 2017, 68(7): 2851-2858.
ZHENG Wenjing, LI Shaojun, JIANG Da. Mixture of D-vine copulas model and its application in fault detection[J]. CIESC Journal, 2017, 68(7): 2851-2858. |
| [28] |
DISSMANN J, BRECHMANN E C, CZADO C, et al. Selecting and estimating regular vine Copula and application to financial returns[J].
Computational Statistics & Data Analysis, 2013, 59: 52-69.
|
| [29] |
FINK H, KLIMOVA Y, CZADO C, et al. Regime switching vine Copula models for global equity and volatility indices[J].
Econometrics, 2017, 5(1): 3.
DOI: 10.3390/econometrics5010003. |
| [30] |
JOE H. Families of m-variate distributions with given margins and m (m-1)/2 bivariate dependence parameters[J].
Lecture Notes-Monograph Series, 1996: 120-141.
|
| [31] |
AKAIKE H. Information theory and an extension of the maximum likelihood principle// Springer series in statistics book series[M]. New York: Springer, 1973.
|
| [32] |
Bozdogan H. Model selection and Akaike's information criterion (AIC): the general theory and its analytical extensions[J].
Psychometrika, 1987, 52(3): 345-370.
DOI: 10.1007/BF02294361. |
| [33] |
Schwarz G. Estimating the dimension of a model[J].
The annals of statistics, 1978, 6(2): 461-464.
DOI: 10.1214/aos/1176344136. |
| [34] |
LIEBSCHER E. Semiparametric density estimators using Copulas[J].
Communication in Statistics- Theory and Methods, 2005, 34(1): 59-71.
DOI: 10.1081/STA-200045883. |
| [35] |
EPANECHNIKOV V A. Non-parametric estimation of a multivariate probability density[J].
Theory of Probability & Its Applications, 1969, 14(1): 153-158.
|
| [36] |
SILVERMAN B W. Density estimation for statistics and data analysis[M]. UK: Routledge, 2018.
|
| [37] |
DUA, D, GRAFF, C. UCI machine learning repository[DB/OL]. [2018-11-01]. http://archive.ics.uci.edu/ml.
|
| [38] |
FAWCETT T. An introduction to ROC analysis[J].
Pattern recognition letters, 2006, 27(8): 861-874.
DOI: 10.1016/j.patrec.2005.10.010. |
 2019, Vol. 22
2019, Vol. 22