随着现代物流业的崛起，物流园区这一基础设施和公共服务平台也得到空前发展。由于物流园区包含多个功能区，集仓储、加工、展示、交易等功能于一体，功能复杂，为使园区运营更加有效，对物流园区的规划就显得十分必要。如何将资源要素合理利用进行物流园区规划就成了政府、企业以及学界关注的焦点问题。近年来，随着高铁事业的迅速发展，铁路运力被充分释放出来，铁路在国民经济发展的地位日渐突出。铁路是物流园区不可或缺的一部分，考虑铁路分割线因素可以为园区带来极大的便利。一方面可以减少地域限制，更好地符合周围环境条件；另一方面可以节约建设成本，提高园区运营效率。目前，一些学者已经对物流园区的建设进行了相关研究。邢虎松^[1]通过对我国物流园区建设的前期过程进行分析，借鉴外国经验，提出了相应的改进思路。张得志等^[2]在考虑市场特征后分别运用RO (real options)和NPV (net present value)法对物流园区的建设情况进行了研究，并将2种方法进行比较。为了获取物流园交通小区的最佳分类结果，温惠英等^[3]首先对物流园区进行定性划分，之后通过聚类分析确定了最佳分类数。而针对物流园区布局的研究主要集中于选址布局和功能区布局2个方面。其中，赵旭等^[4]主要利用复杂系统理论通过园区截流量来建立选址模型并通过算例进行验证。陶经辉等^[5]考虑与城市经济的协同发展，应用系统动力学构建“工业−物流”联动模型，并进行仿真验证。陶经辉等^[6]考虑总成本和碳减排因素，对物流、产业园区协调选址进行了研究。还有部分学者如张得志等^[7]对动态物流节点的布局模型和求解算法进行了深入研究。Wang等^[8]围绕建设低碳物流园区的目标，提出了功能区划分和布局方法。

对于物流园区功能区布局问题，国内外学者大多采用系统布置设计法(SLP)来解决。SLP法是由理查德·缪瑟(Richard Muther)等人在20世纪60年代首先提出的。该方法将定性分析与定量分析相结合，综合考虑各功能区块之间的物流与非物流关系，是一种被广泛认可的设施布局方法。但由于SLP存在较多局限，目前大多学者都使用启发式算法进行模型求解。如冯芬玲等^[9]设计改进SLP法应用遗传算法进行布局问题求解。Xiao等^[10]提出基于低碳的SLP改进方法来对布局场所进行规划设计，改善了作业场所的物流状况。Zhang等^[11]提出了一个解决区域物流网络设计问题的模型并运用启发式算法求解。孙焰等^[12]利用遗传算法求解考虑园区交通网络的布局问题，以及刘景发等^[13]运用Wang-Landau抽样算法求解动态布局问题。

另外一些学者引入辅助技术，如Chong^[14]利用GIS技术等进行布局研究。Chen等^[15]应用切片结构技术来确定所有不规则功能区域的最终布局，以及孙刘诚等^[16]基于栅格数据结构对不规则物流园区的布局进行了深入分析。

以往的研究基本采用遗传算法等单一的启发式算法进行求解，但遗传算法等往往容易导致局部最优的现象发生。铁路物流基地的建设会对周边的交通环境产生重大影响，包括交通网络的重新构建、交通流量的重新分配等^[17]，其根本原因是铁路的建设导致了有效运力和需求的重新分配^[18]。然而以往的布局往往忽略铁路对布局的影响，或者将铁路设为外部固定设施。但在实际情况下，铁路是物流园区不可或缺的一部分，且服务于园区的铁路从园区内部横穿而过，既可以为园区日常运作带来极大的便利，又可有效节约建设成本，减少地域限制。

综上所述，本文在合理划分各功能区的基础上，考虑铁路分割线对物流园区布局的影响，利用改进的SLP法建立各功能区的相关关系，以总搬运费用最低和综合关系最大化为目标函数建立数学模型，并利用粒子群算法搜索速度快的特点，结合模拟退火算法进行求解，最终得到最优的布局方案。

1 考虑铁路分割线的物流园区布局规划模型建立 1.1 物流园区功能区块的划分

物流园区是物流节点集中组织和管理的场所，利用先进的物流设施，对各类物流活动进行综合管理，其功能应满足商品流转流通的需要，因此应当具备以下主要功能区。

1) 大宗散货仓储区。主要负责各类散货材料或者商品的储存管理。仓储区可用于存储原材料和产成品等。企业可将用于出售或出口的材料或者商品堆放至物流园区的仓储区内，由园区管理方进行统一管理。同时，在园区中进行加工后的半成品可从加工区转移至仓储区，等待进一步的加工或者运送至其他地方。

2) 集装箱仓储区。主要用于储存园区中的集装箱，货物采用装箱形式通过铁路运送至园区，之后通过加工再装箱转运至目的地。

3) 流通加工区。主要负责原材料的加工或者商品的精加工。为了充分发挥物流园区的核心功能，除了负责商品储存外，还可以通过园区对材料进行加工，同时企业还可以选择在园区中直接对产品进行包装从而进行销售，减少商品流动，节约商品加工成本。

4) 分拣区。运送至园区的货物种类繁多，需要通过分拣后进行分区储存。同时，也可将仓储区的货物进行进一步分拣加工后运送至其他目的地。

5) 综合办公区。该功能区包括2个部分，一部分是保证园区正常运作的办公区，主要负责日常的行政工作；另一部分则是综合交易区，负责园区与企业的合作事宜以及企业与客户的交易活动。

6) 铁路装卸区。为了保证货物能够高效、低价运输，铁路是最佳的交通工具选择，因此铁路有时会穿过园区，这时需要设置铁路分割线为装卸区，保障货物装卸的高效进行。

为了保障物流园区工作的有效进行，还需设置一些辅助功能区。

1) 后勤区。主要负责园区安保、设备维护等活动。

2) 停车区。园区内的车辆包括外来车辆和园区工作车辆，设置停车区可对这些车辆进行有效管理，同时具备车辆检修维护的功能。

3) 生活服务区。除为员工提供餐饮、娱乐等服务外，还可为外来办公人员提供所需服务。

1.2 物流园区布局规划的原则

1) 距离最优原则。物流园区规划过程中应尽量使各功能区块距离最短，从而减少人员、设施、货物等的移动距离，提高物流园区的整体运作效率。

2) 流程性原则。运送至物流园区的货物需要经过入库、存储、出库等功能，有时还需要进行再一次的加工，因此各功能区块的布局应尽量按流程进行规划，从而减少工作转移所耗费的时间。

3) 协调性原则。各功能区块间具有相关关系，在布局规划时要使各功能区块相关关系最大化，且不会影响其他区块间的正常运作。

4) 安全性原则。为了确保物流园区在以后的运营过程中能够高效运作，必须在设计过程中考虑安全因素，对于一些有危险性的设施应当单独安置。

5) 实用性原则。物流园区的设置应能够充分发挥其作用。首先其地点设置应满足各企业客户需求；其次，物流园区中存在着多个企业，这些企业的产品服务应满足消费者需求，设施应满足生产销售要求。

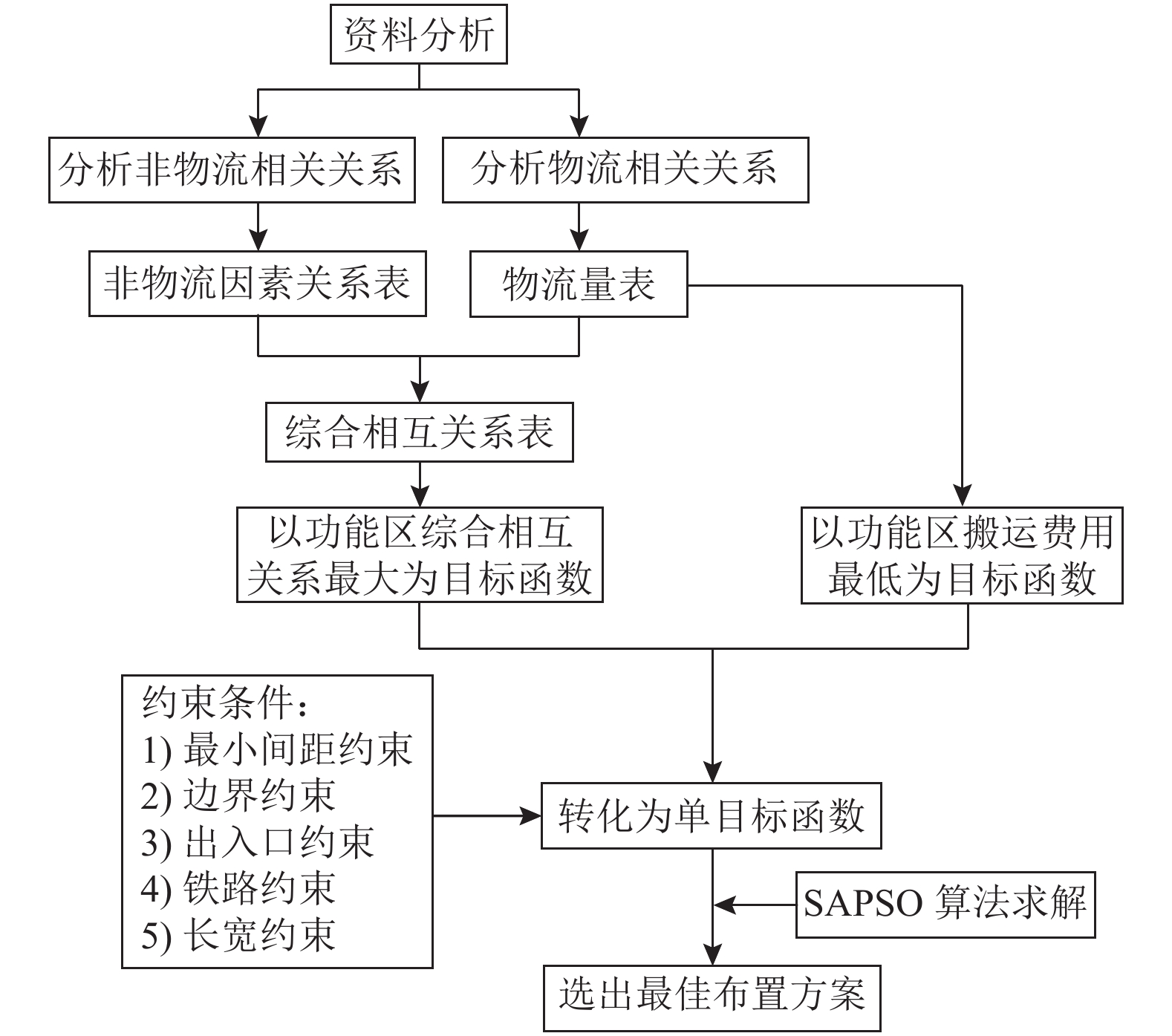
1.3 方法的实现

近年来，SLP法一直应用于布局规划问题，但其仍然存在着诸多局限：在应用过程中，各作业单元之间的密切程度需要由专业人士进行分析确定，具有较强的主观性；在评价可供选择的方案时，需要通过专家进行讨论，工作量巨大等一系列问题。所以，为了弥补这些不足，本文采用改进的SLP法进行布局设计，在确定各功能区的相互关系后，建立以搬运总费用最低和综合相互关系最大为目标函数的模型，采用数学方法求解。粒子群算法具有搜索速度快的特点，但其容易陷入局部最优，因此，引入了模拟退火算法，模拟退火算法能够有效改善粒子群算法过早收敛的缺点。将二者相结合，形成SAPSO算法，并根据当地的实际情况得到最终布局。改进后的SLP法如图1所示。

1.4 考虑铁路分割线的物流园区规划布局数学模型 1.4.1 模型假设

基于方便求解物流园区规划布局模型的目标，现作出以下假设。

1) 各功能区形状为长宽已知的矩形，其边界均与园区边界相互平行，且面积、数量均为已知。

2) 各功能区的中心均位于其几何中心，物流量均从其中心处产生。

3) 各功能区之间需要有道路界限，且道路距离一定。

4) 铁路横穿园区，铁轨所穿2个边界垂直，且铁路宽度一定，同时车辆可在没有火车时穿越铁路线。将铁路分割线设定为一个功能区，为铁路装卸功能区。

5) 园区存在一个出口和一个入口，门口均位于园区边界上，以保障车辆进出的方便性。

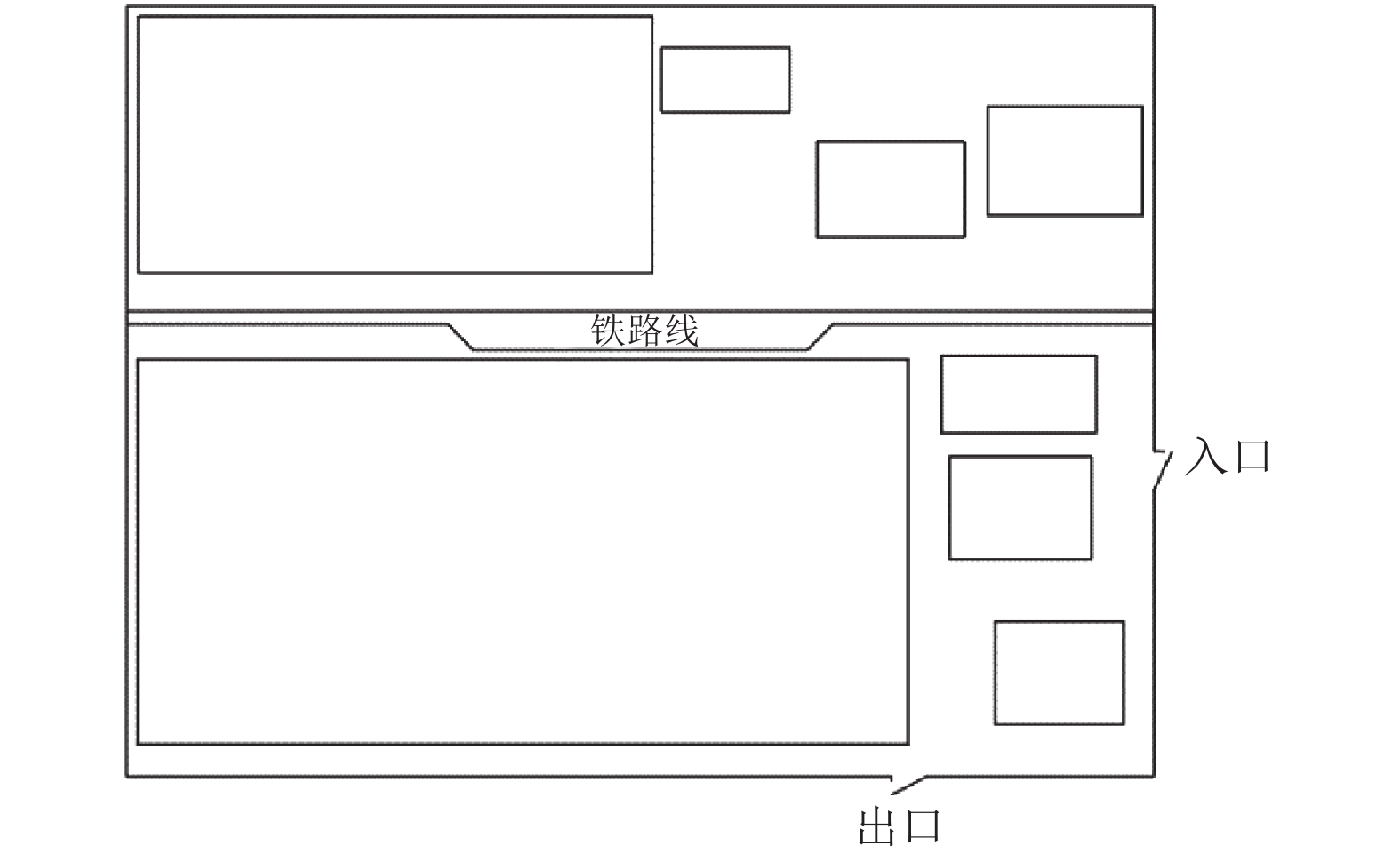
铁路示意图如图2所示。

1.4.2 模型构建

1) 目标函数。该布局模型共包含总搬运费用最低( $G_1$ )和综合相互关系最大( $G_2$ )2个目标函数，分别为

$\qquad\min\; G_1 = \sum\limits_{j = 1}^{n - 1} {\sum\limits_{i = j + 1}^n {e_{ij}p_{ij}d_{ij}} } ,$

(1)

$\qquad\max\; G_2 = \sum\limits_{j = 1}^{n - 1} {\sum\limits_{i = j + 1}^n {M_{ij}k_{ij}} } {\text{。}}$

(2)

其中， $n$ 为物流园区的功能区块数； $i$ 、 $j$ 为功能区块 $i$ 和 $j$ ； $G_1$ 为运输总成本； $G_2$ 为功能区块相互综合关系之和； $e_{ij}$ 为功能区 $i$ 、 $j$ 之间单位距离每吨货物的运输成本； $p_{ij}$ 为功能区 $i$ 、 $j$ 之间的年平均货流量； $d_{ij}$ 表示功能区 $i$ 、 $j$ 之间的货物搬运距离，本文假设各功能区之间的流量均从中心产生，因此 $d_{ij} = |x_i - x_j| + |y_i - y_j|$ ； $M{_{ij}}$ 为功能区 $i$ 、 $j$ 之间的综合相关性系数； $k_{ij}$ 表示功能区 $i$ 、 $j$ 之间的邻近值，可根据 $d_{ij}$ 转化得到，具体值如表1^[9]所示。

为了方便运算，需要将以上2个目标函数转化成单目标函数，即进行归一化处理。

$ \qquad\min \;G = \mu _1\alpha _1\sum\limits_{j \!=\! 1}^{n \!-\! 1} \!{\sum\limits_{i = j \!+\! 1}^n \!{e_{ij}p_{ij}d_{ij}} } \!-\! \mu _2\alpha _2\!\sum\limits_{j = 1}^{n \!-\! 1} \!{\sum\limits_{i = j\! +\! 1}^n\! {M_{ij}k_{ij}} }{\text{。}}\!\!\!\!\!\!\!\! $

(3)

其中， $\mu _1$ 和 $\mu _2$ 为归一化因子，且 $\mu _1 = {1}\Big/{ \displaystyle\sum\limits_{j = 1}^{n - 1} \times}\Big.$ $ {\displaystyle\sum\limits_{i = j + 1}^n {e_{ij}p_{ij}d_{m{\rm{ax}}}} } $ ， $\mu _2 = {1}\Big/{\displaystyle\sum\limits_{j = 1}^{n - 1} {\displaystyle\sum\limits_{i = j + 1}^n {M_{ij}} } }\Big.$ ； $d_{\max} $ 为物流园区规划区域长边与宽边的长度之和； $\alpha _1$ 和 $\alpha _2$ 为权重系数，且 $\alpha _1 + \alpha _2 = 1$ 。

2) 约束条件。

(1) 最小间距约束。在进行物流园区布局规划时，除了要保证各功能区的边界在各个方向上不重叠以外，还需满足最小间距要求，即

$\qquad\; \left| {x_i \!-\! x_j} \right|\!-\! (a_i \!+\! a_j)/2 {\text{≥}} S_{ij}; \left| {{{y}}_{{i}} \!- \!{{y}}_{{j}}} \right| \!-\! (b_i \!+\! b_j)/2 {\text{≥}} S_{ij}{\text{。}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$

(4)

其中， $x_i$ 、 $x_j$ 为功能区 $i$ 、 $j$ 的质心横坐标， $y_i$ 、 $y_j$ 为功能区 $i$ 、 $j$ 的质心纵坐标， $a_i$ 、 $a_j$ 为功能区 $i$ 、 $j$ 的长(横向坐标轴方向)， $b_i$ 、 $b_j$ 为功能区 $i$ 、 $j$ 的宽(纵向坐标轴方向)， $\mathop S\nolimits_{ij} $ 为功能区 $i$ 、 $j$ 之间的最小间距。

(2) 边界约束。所有功能区均不得超出园区边界，即

$ \qquad a_i/2 {\text{≤}} x_i {\text{≤}} A - a_i/2; b_i/2 {\text{≤}} y_i {\text{≤}} B - b_i/2{\text{。}} $

(5)

其中，A、B分别为物流园区的长度和宽度。

(3) 出入口约束。由于园区包含一个出口和一个入口，因此应将这2个门口放置在园区边界，其坐标设置为 $x_k = [0,A]$ ， $y_k = 0$ ；或者 $x_k = 0$ ， $y_k = $ $ [0,B]$ ；或者 $x_k = A$ ， $y_k = $ $ [0,B]$ ；或者 $x_k = [0,A]$ ， $y_k = B$ 。由于铁路横穿园区，且有最小边距限制，因此可保证出入口与铁路不重叠。

(4) 铁路约束。将铁路视为园区的一个实体功能区，由于横穿整个园区，且与园区的水平方向平行，因此可将其横坐标设置为 $A/2$ 。

(5) 长宽约束。为了防止除铁路以外的功能区过长或者过窄，对其长宽之比进行如下约束，即

$ \qquad 1/\beta {\text{≤}} a_i/b_i {\text{≤}} \beta{\text{。}} $

(6)

其中， $\beta $ 为最大长宽比，此处取值为6。

1.4.3 模型求解

粒子群算法(particle swarm optimization，PSO)是由Kennedy等人在1995年依据鸟群捕食开发的一种新算法，而模拟退火算法(simulated annealing algorithm，SA)最早是由Metropolis提出的，该方法的思想源于固体退火原理，而将二者相结合的SAPSO法，既汲取了PSO法收敛速度快的特点，又可利用SA法来抑制过早收敛。改进后的SAPSO法求解过程如下。

1) 参数初始化。设置群体规模N，最大迭代次数H，最大速度 $V_{\max} $ ，学习因子 $c_1$ 、 $c_2$ ，惯性权重ω以及模拟退火算法中的初始温度T等。

2) 适应度计算。根据适应度公式计算每个粒子的适应度。本文的适应度计算公式为

$\qquad f \!=\! 1/(\mu _1\alpha _1\sum\limits_{j = 1}^{n \!-\! 1} {\sum\limits_{i= j\! +\! 1}^n {e_{ij}p_{ij}d_{ij}} } \! -\! \mu _2\alpha _2\sum\limits_{j = 1}^{n \!-\! 1} {\sum\limits_{i = j\! + \!1}^n {M_{ij}k_{ij}} } ){\text{。}}\!\!\!\!\!\!\!\!\!\!$

(7)

3) 个体最优更新。将每一个粒子的适应度值 $f$ 与当前个体极值 $p_{\rm best}$ 对比，如若 $f{\text{＞}} f(p_{\rm best})$ ，则将该粒子代替 $p_{\rm best}$ ，否则仍取原值。

4) 全局最优更新。将每一个粒子的适应度值 $f$ 与当前全局极值 $g_{\rm best}$ 对比，如若 $f {\text{＞}} f(g_{\rm best})$ ，则将该粒子代替 $g_{\rm best}$ ，否则仍取原值。

5) 当 $p_{\rm best} = g_{\rm best} = x_i$ ，第 $i$ 个粒子停止进化，用模拟退火算法进化生成 $x_i$ 。

6) 更新粒子。在找到2个最优值后，采用下列公式对粒子的速度和位置进行更新：

$\qquad v_{id} = \omega {{v}_{{id}}} + c_1\gamma _1(p_{id} - x_{id}) + c_2\gamma _2(p_{{\rm g}d} - x_{id}),$

(8)

$\qquad x_{id} = x_{id} + v_{id}{\text{。}}$

(9)

其中， $ \omega $ 为惯性因子，其值为非负数，通过调整 $ \omega $ 的大小，可以对全局寻优性能和局部寻优性能进行调整。 $v_{id}$ 、 $x_{id}$ 分别为第 $i$ 个粒子在第 $d$ 维上的速度和位置， $p_{id}$ 为第 $i$ 个粒子个体极值的第 $d$ 维， $p_{{\rm g}d}$ 为全局最优的第 $d$ 维， $\gamma _1$ 和 $\gamma _2$ 为2个 $\left[ {0,1} \right]$ 之间的随机数。

7) 结束运算。当粒子足够优或者达到最大迭代次数时停止运算，获得最优解。

2 算例验证 2.1 参数确定

某地政府计划建设一个尺寸为800 m×600 m的物流园区。由于地理位置限制，现要求在原有铁路两侧进行建设，同时可对原有铁路进行适当改建。在经过对该物流园区的物流量进行预测以及作业流程分析后，依据国家有关要求，现规定该园区的功能区划分以及尺寸如表2所示。

其中，入口和出口均位于园区边界，且不与铁路线重叠。

该园区各功能区之间年均货流量矩阵P和最短距离矩阵S如式(10)和式(11)所示：

$\qquad {{P}} = \left[ \begin{array}{*{20}{r}} 0 \!\! &\!\! 100 \!\! &\!\! 35 \!\! &\!\! 70 \!\! &\!\! 0 \!\! &\!\! 90 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 150 \\ 80 \!\! &\!\! 0 \!\! &\!\! 40 \!\! &\!\! 85 \!\! &\!\! 0 \!\! &\!\! 100 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 50 \!\! &\!\! 0 \!\! &\!\! 160 \\[1.5pt] 30 \!\! &\!\! 50 \!\! &\!\! 0 \!\! &\!\! 15 \!\! &\!\! 0 \!\! &\!\! 60 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 40 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 70 \!\! &\!\! 80 \!\! &\!\! 35 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 95 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 50 \!\! &\!\! 0 \!\! &\!\! 130 \\[1.5pt] 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 95 \!\! &\!\! 95 \!\! &\!\! 50 \!\! &\!\! 70 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 150 \\[1.5pt] 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 0 \!\! &\!\! 50 \!\! &\!\! 60 \!\! &\!\! 10 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 120 \!\! &\!\! 130 \!\! &\!\! 60 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 150 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] \end{array} \right],$

(10)

$\qquad{{S}} = \left[\begin{array}{*{20}{r}} 0 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 0 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 0 \!\! &\!\! 10 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 0 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 0 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 0 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 0 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 0 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 8 \\[1.5pt] 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 0 \!\! &\!\! 10 \!\! &\!\! 10 \\[1.5pt] 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 0 \!\! &\!\! 10 \\[1.5pt] 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 8 \!\! &\!\! 10 \!\! &\!\! 10 \!\! &\!\! 0 \\[1.5pt] \end{array} \right]{\text{。}}$

(11)

为了方便计算，本文认为物流和非物流关系的重要性相等。通过对各功能区的物流及非物流关系进行分析，依据物流及非物流关系的密切程度计算表(表3)，得到该园区中各功能区之间的密切关系系数M_ij的矩阵M，如式(12)所示。同时，本文中将各功能区之间的搬运成本设定为0.05元/(t·m)。

$\qquad{{M}} = \left[\begin{array}{*{20}{r}} 0 \!\! &\!\! 2 \!\! &\!\! 2 \!\! &\!\! 3 \!\! &\!\! - 1 \!\! &\!\! 2 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 4 \\[1.5pt] 2 \!\! &\!\! 0 \!\! &\!\! 3 \!\! &\!\! 3 \!\! &\!\! - 1 \!\! &\!\! 2 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 4 \\[1.5pt] 2 \!\! &\!\! 3 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 0 \\[1.5pt] 3 \!\! &\!\! 3 \!\! &\!\! 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 2 \\[1.5pt] - 1 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 3 \!\! &\!\! 2 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! - 1 \\[1.5pt] 2 \!\! &\!\! 2 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 4 \\[1.5pt] - 1 \!\! &\!\! - 1 \!\! &\!\! - 1 \!\! &\!\! - 1 \!\! &\!\! 3 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 3 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 2 \!\! &\!\! 0 \!\! &\!\! 3 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! - 1 \\[1.5pt] 0 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 0 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] 4 \!\! &\!\! 4 \!\! &\!\! 0 \!\! &\!\! 2 \!\! &\!\! - 1 \!\! &\!\! 4 \!\! &\!\! 0 \!\! &\!\! - 1 \!\! &\!\! 0 \!\! &\!\! 0 \!\! &\!\! 0 \\[1.5pt] \end{array} \right]{\text{。}}$

(12)

2.2 SAPSO算法求解

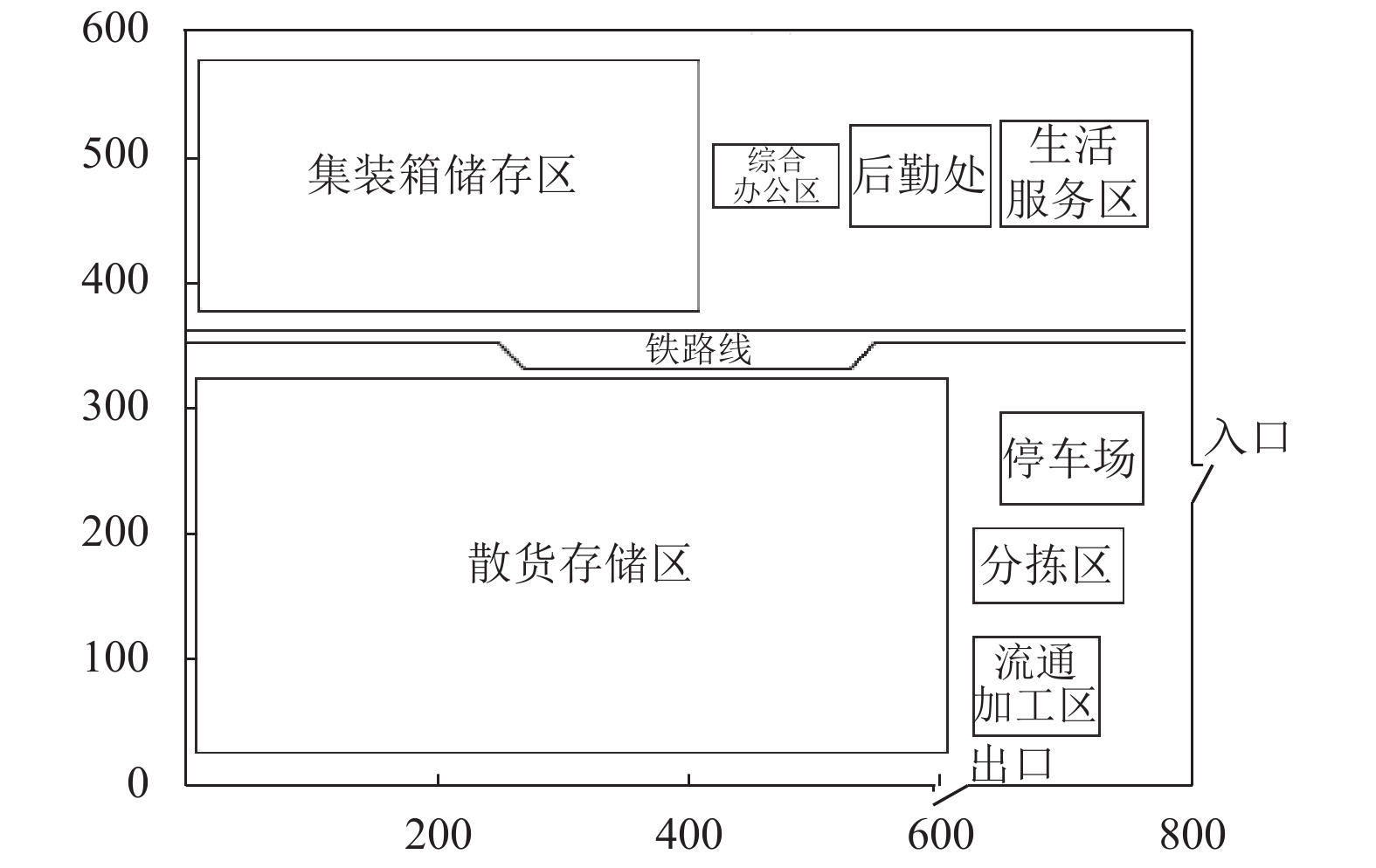
设种群规模N=200，最大迭代数 $H$ =150，模拟退火温度T=100，学习因子 $c_1 = c_2 = 2$ ，惯性系数 $\omega $ =1。经过多次求解得到最优粒子为{(309.603 3，176.518 4)，(210.691 3，476.743 5)，(680.236 4，77.874 6)，(688.942 0，174.856 1)，(471.309 6，485.395 4)，(687.211 4，260.432 0)，(585.933 8，485.188 8)，(707.995 2，487.029 6)，(800.000 0，223.091 6)，(621.726 1，0.000 0)，(400.000 0, 346.742 7)}，其示意图如图3所示。

通过图3可以看到布局规划结果基本符合实际需求，可通过AutoCAD进行进一步的修饰和调整，从而使结果更加契合实际。

3 结论与展望

本文提出将铁路作为园区内部一个实体功能区的布局方式，划分了包括出入口在内的11个功能区，经过有关专家分析后，确定了各功能区的面积、年平均物流流量、物流以及非物流关系，通过改进的SLP法确定各功能区之间的相互密切程度，引入粒子群算法和模拟退火算法相结合的SAPSO算法对模型进行求解，减少了人为主观因素对布局结果的影响，最终得到最优的功能区坐标，验证了该布局方式的可行性，为铁路物流园区的布局提供了一定的借鉴。本文假设物流园区及各功能区均为标准矩形，但有些物流园区由于技术及当地自然条件的限制无法完全做到矩形，因此，在以后的的研究中可加强对不规则物流园区和不规则功能区相关方面的研究，同时依据当地实际条件对结果进行进一步的优化，不断丰富布局理论。