代码混淆技术作为一类重要的软件保护方法,常用于现代工业工程中的控制与调度软件保护领域,基本思想是对代码在功能等价的前提下进行转换,令转换后的代码更难于阅读和理解软件功能的设计与算法[1]。在代码混淆效果的度量方面,Collberg等[2]提出了4个评价标准:健壮性、弹性、隐蔽性和执行代价。其中健壮性是指混淆算法对程序增加的复杂度,例如程序长度复杂度、圈复杂度、嵌套复杂度、数据结构复杂度、数据流复杂度和扇出/扇入复杂度等;执行代价是指由代码转换带来的系统开销,包括内存空间和运行时间等。在一定程度上,各项复杂度可以作为混淆效果的直观反映。然而,某些复杂度之间可能会存在冲突。例如应用压扁控制流技术进行代码混淆时,会在增大圈复杂度的同时可能降低嵌套复杂度。因此,采用多目标优化进化算法(multi-objective evolutionary algorithms,MOEAs)成为解决此问题的方法之一。基于快速非支配排序和精英策略的多目标优化遗传算法NSGA-II (fast and elitist non-dominated sorting in genetic algorithms)[3]是多目标优化算法中的经典算法,目前被广泛地运用在各行各业以寻找最优方案,例如多目标电网规划[4]、水资源优化配置[5]和航空运输优化[6]等应用场合。Martinez[7]、Bertholon等[8]曾经提出运用多目标优化遗传算法解决代码混淆问题,但对遗传算法的部分核心操作进行了简化,例如省略了极其重要的交叉操作,并且实验使用的代码混淆技术对目标函数影响较小而导致复杂度增减速率过慢。
在实际应用中,往往需要反复调用代码混淆技术获得具有理想的复杂度的程序以尽量保证足够安全。本文从工业工程实践的角度,应用NSGA-II算法解决在多次、多种调用代码混淆技术过程中的复杂度冲突问题,从代码健壮性和执行代价这两方面的多项复杂度作为优化目标,运用树形编码设计,完整实现选择、变异和交叉操作,最终获得较优的代码混淆技术调用序列作为可行解。
1 基于NSGA-II的代码混淆问题算法设计 1.1 多目标优化代码混淆问题的数学模型多目标代码混淆问题可以描述为:对于原代码P,存在代码混淆技术集合Τ,多次应用ti∈Τ作用于P,直至得到满足代码复杂度指标集合C的混淆后代码P'。即
| $ \begin{split} &\qquad f(C) = \max \left\{ {{f_{\rm{h}}}\left( {{c_{\rm{h}}}} \right),{f_{\rm{c}}}\left( {{c_{\rm{c}}}} \right),{f_{\rm{n}}}\left( {{c_{\rm{n}}}} \right),{f_{{\rm{ds}}}}\left( {{c_{{\rm{ds}}}}} \right)} ,{f}_{\rm{d}\rm{f}}\left({c}_{\rm{d}\rm{f}}\right),\right.\\ &{f}_{\rm{f}}\left({c}_{\rm{f}}\right),{f}_{\rm{m}}\left({-c}_{\rm{m}}\right), {f}_{\rm{t}}\left({-c}_{\rm{t}}\right)\}{\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (1) |
式(1)中,
程序长度复杂度ch ch = η1 + η2,η1为程序P中不同运算符的个数,η2为程序P中不同操作数的个数。
圈复杂度cc cc = E – ω + 2,E为控制流图中的边数,ω为控制流图中的节点数。
嵌套复杂度cn cn=λ−1,λ为程序P中代码块的最大嵌套深度。
数据结构复杂度cds 为方便计算并且不影响评估效果,将cds简化定义为
数据流复杂度cdf
扇入扇出复杂度cf cf=finfout,fin为程序P中扇入总次数,fout为程序P中扇出总次数。
内存空间复杂度cm cm=k1+k2+k3,k1、k2和k3分别为程序P中对象头占用字节数、实例数据占用字节数和对齐填充占用字节数。
时间复杂度ct ct=t2−t1,t1为程序P开始运行时时间节点,t2为程序P运行结束时的时间节点。
1.2 NSGA-II与代码混淆的适配为设计将NSGA-II适配于求解代码混淆问题的算法框架,首先给出以下定义。
定义1(个体):由类、类属性、类方法以及类外部属性所组成的一份完整可运行的程序代码,记作I;当表示第n代个体时,记作In(n=1, 2, ···)。
定义2(原始个体):对原代码使用一次代码混淆技术所得到的代码,也称作初代个体,记作I0。
定义3(种群):由多个相同进化代数的个体I组成的集合,记作
定义4(退化个体):当I具有以下情况之一时,称为退化个体。退化个体记作Ierr:
1) 不能通过编译器编译;
2) 编译后程序执行出错;
3) 对于同一输入,其输出与源代码的输出不一致。
定义5(变异操作):在第n代中任意选择
定义6(交叉操作):在第n代中任意选择
定义7(选择操作):令
定义8(个体验证):对
定义9(个体评价):通过代码复杂度指标集合C进行衡量I的质量。本文设
基于NSGA-II解决代码混淆问题的算法设计框架如图1所示,主要步骤如下。
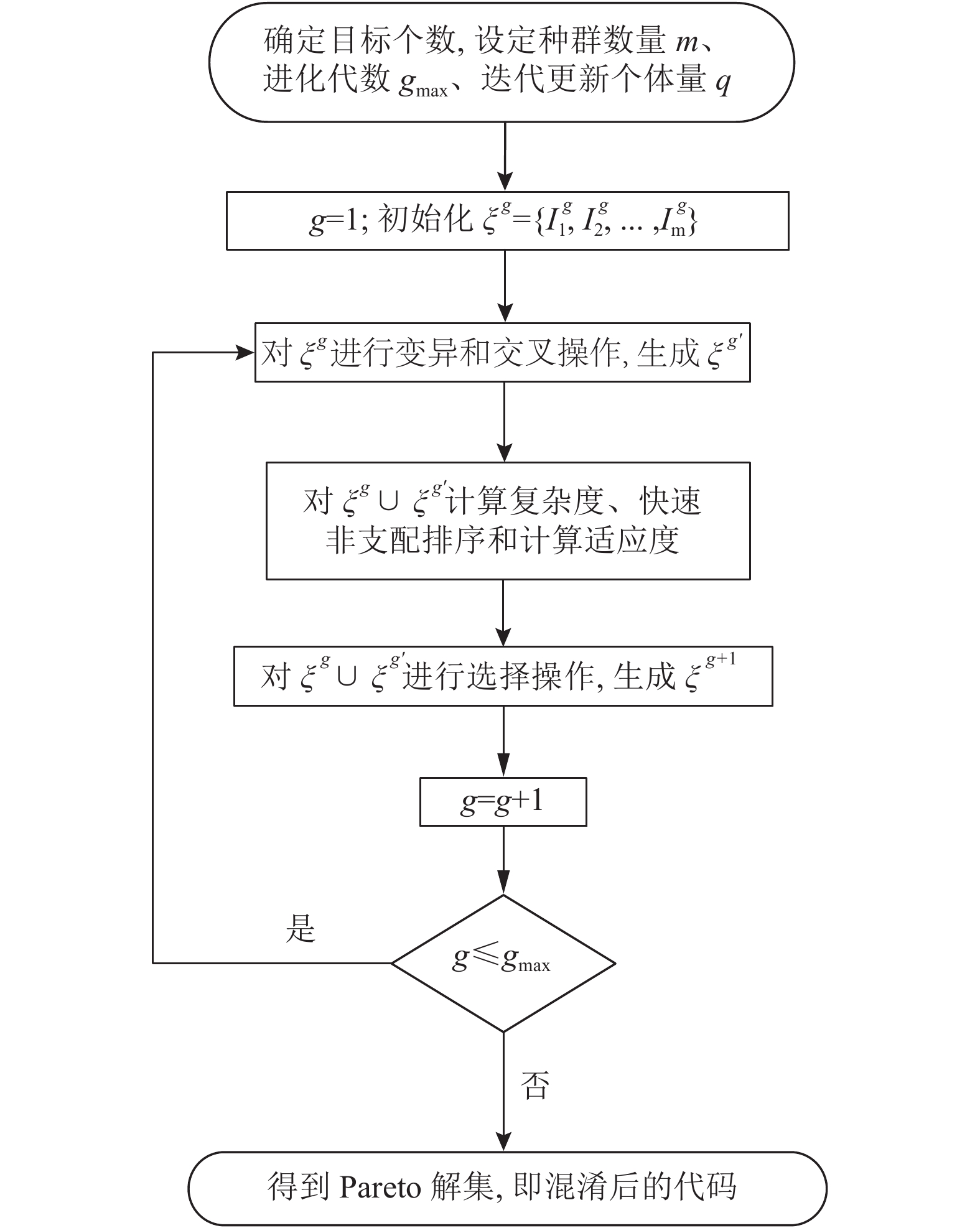
|
图 1 适配代码混淆问题的NSGA-II算法框架 Fig. 1 Framework of NSGA-II adapted to code obfuscation |
Step1 设定软件复杂度目标函数及其他参数,包括确立目标函数集合C、种群数量m、最大进化代数gmax和迭代更新个体量q。
Step2 初始化原始个体的种群。令g=1,对原代码P多次执行τ操作,得到若干个个体组成初代种群
Step3 种群进化。在第g代种群
Step4 判断是否满足NSGA-II结束条件。若g≤gmax,则返回Step3,否则退出。
Step5 根据Pareto解集获取可行解,即混淆后代码集合。
1.3 树形结构编码设计采用二叉树结构编码的遗传算法,最终能收敛到全局最优解,该结论可推广至一般树形结构编码的遗传算法。因此采用抽象语法树(abstract syntax tree, AST)[9]结构对个体基因进行编码,以描述代码如何从文法的初始符号开始推导出任意句子。在AST中,从左到右依次联结所有叶子节点则可生成该树所表示的代码。
定义10(基因):使用AST结构描述I。AST中的每个结点都为I的基因。基因分为2类:语句基因和文法基因。AST中的叶子结点属于语句基因,是保存代码语句信息的遗传因子;非叶子结点属于文法基因,是保存子结点文法信息的遗传因子。
定义11(染色体):染色体由基因组成。用A → X1. X2.
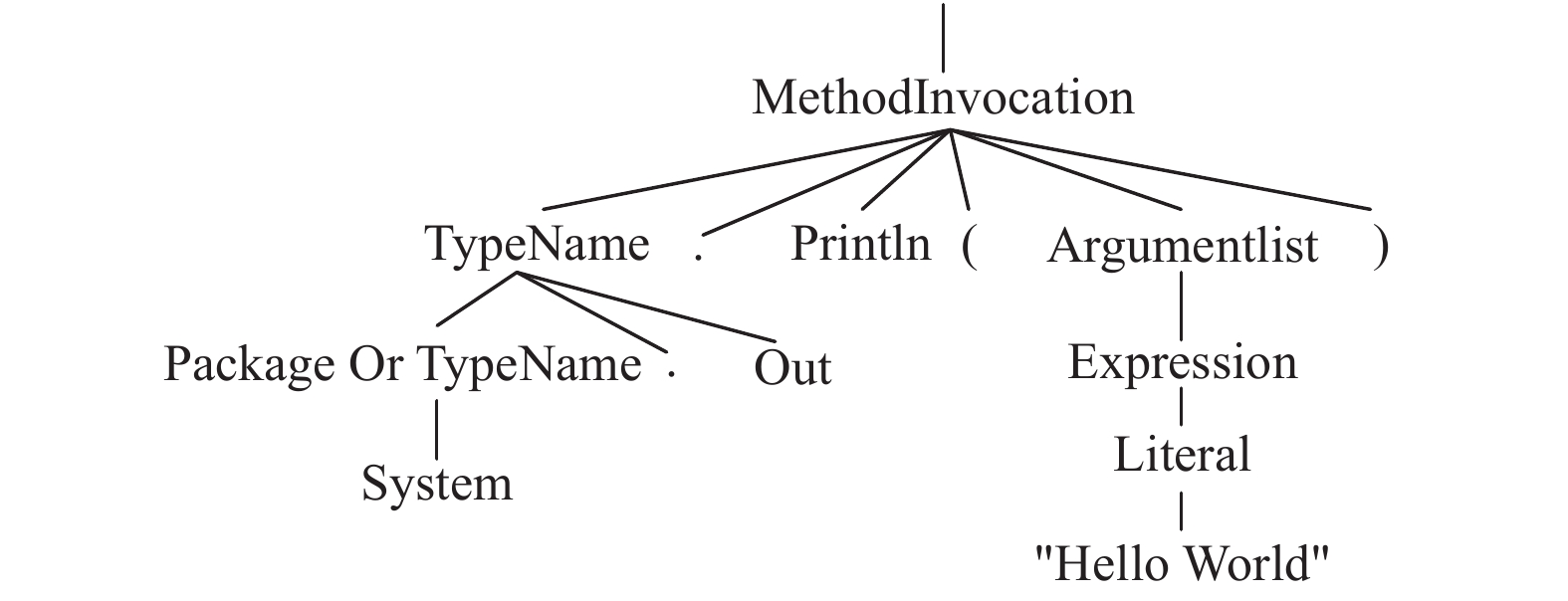
|
图 2 AST示例图 Fig. 2 Example of AST |
树型结构可采用Common LISP语言[10]中的前置标识表达式来描述成字符串,如下所示
| $ \begin{split} & \qquad T\left( {\chi ,A} \right) = \left( {{\chi _1}\left( {{\chi _2}\left( { \cdots \left( { \cdots {A_1}} \right) \cdots } \right) \cdots } \right.} \right. \left. {\left. {{\chi _n}\left( { \cdots \left( { \cdots {A_n}} \right) \cdots } \right)} \right)} \right),\\ & \;\;{n \in {N^ + }} {\text{。}} \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (2) |
式(2)中,Ai代表叶子节点(语句基因),χi代表非叶子节点(文法基因)。
在进行结构编码时,源点总是根结点,在S式中位于第一个“(”之后;父结点与子结点以一对括号相隔;兄弟结点位于同一对括号内;左右括号总是成对出现。例如,图2可用S式表示为T = (MethodInvocation (TypeName (PackageOrTypeName System) (.) (out)) (.) (println) (“(“) (argumentList (expression (literal “Hello World”))) (“)”))。
采用AST进行代码的编码具有明显优势:
1) 当需要对某种类型的代码进行定位时,可通过文法基因迅速找到所有的代码位置;
2) 当进行染色体突变或互换时,可直接在AST的子树上修改或嫁接。
2 NSGA-II算法中的关键操作 2.1 变异算子操作策略变异操作是个体中的染色体发生突变产生新个体的过程,可分为变量/常量变异和方法变异。
1) 变量/常量变异。指携带变量/常量基因的染色体发生突变,例如字符串加密混淆技术可把字符串常量加密成密文;改变变量存储方式混淆技术可将所有变量改用数组存储。
2) 方法变异。在一般情况下,代码中的一个方法包含有多条染色体。例如,压扁控制流代码混淆技术会改变程序结构,导致基因重组成新的染色体,从而达到方法变异的目的。图3展示了个体I中的某方法fun(其结点产生路径为···χ1χ4)的变异过程。首先对方法fun应用某种代码混淆技术得到功能等价的fun′;然后将fun′替换fun,此时个体I演变为I′。I′仍然需要通过个体验证方可加入种群。
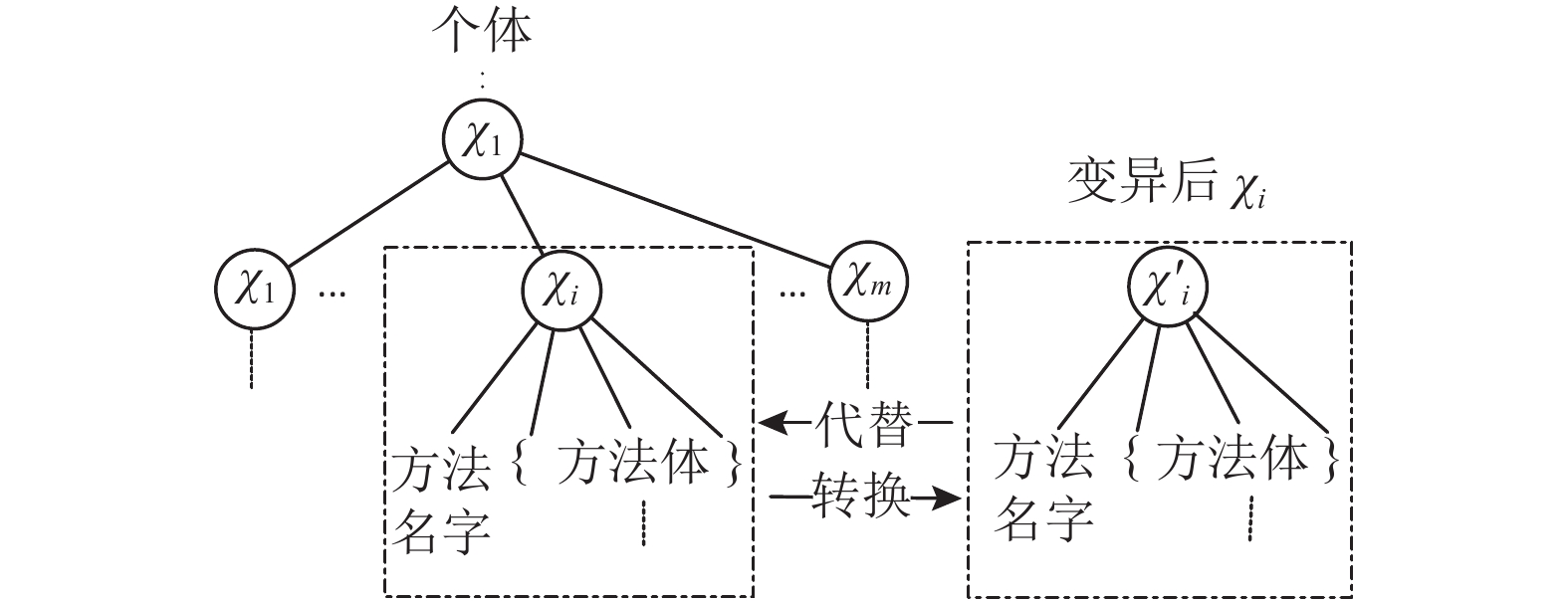
|
图 3 针对方法的变异操作示意图 Fig. 3 Mutated operation of method |
然而需要注意,对于一份待混淆代码,可使用的混淆技术大致上可分为3大类:可任意重复应用的技术、混淆技术之间存在制约关系的技术[11]和仅可应用一次的技术。变异操作需要注意保持多样性和进化效率之间的平衡:过于强调保持多样性,即为了获得较大的搜索范围,则有可能导致进化方向性不够集中,导致收敛速度慢;过于强调进化效率,即过于“贪婪”则收敛速度快,但容易陷入局部最优。所以,注重种群多样性的策略搜索能力强但进化效率往往较低;注重进化效率的策略搜索能力则速度快但往往多样性保持不佳。
在多目标优化算法执行周期中,应当根据混淆技术的特征,在周期的各个阶段调用各种混淆技术时有所侧重:在初期阶段,应当尽量多调用可重复应用的混淆技术,尽可能少用仅能应用一次的混淆技术;在中期阶段,可能适当增大调用混淆技术之间存在制约关系的混淆技术的概率;在后期则可以考虑使用仅能调用一次的混淆技术。多目标优化算法执行周期的分段会影响算法的性能,应当尽量保证算法在初期可以获得较大的搜索范围,而在后期可以快速收敛至全局最优。
本文通过计算迭代过程中相关决策方案的匹配概率,使用轮盘赌策略进行自适应选择,并分配决策执行相关代码混淆的方案。定义代码混淆的解决方案域solution={D1,D2,D3}为3个元素的非空有限集合,表示决策方案的属性集,分别为可重复应用的技术、混淆技术之间存在制约关系的技术、仅可应用一次的技术。
决策方案D1当前决策匹配概率Η1的计算如下
| $ \qquad {H}_{1}\left(x\right)={H}_{0}{\rm{e}}^{-\theta x}{\text{。}} $ | (3) |
式中,H0、θ分别为区间[0,1]上的非0系数,而x∈[0,xmax],x为当前迭代次数,xmax为最大的迭代次数,随着迭代次数的增加,H1(x)单调递减。
决策方案D2当前决策匹配概率H2的计算如下
| $ \qquad {H}_{2}\left(x\right)={\rm{e}}^{-\frac{{(x-\mu )}^{2}}{2{\varepsilon }^{2}}}-0{\text{。}} $ | (4) |
式中,μ、ε分别为区间[0,1]上的非0系数,而μ∈[0,xmax/2],而x∈[0,xmax]。当x=μ时,H1(x)取最大值,H1(μ)=1,为使匹配概率均衡,则ε与μ数量级相同。
决策方案D3当前决策匹配概率H3的计算如下
| $ \qquad {H_3}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\!\!\!1 - {H_1}\left( x \right) - {H_2}\left( x \right),} & {{H_1}\left( x \right) + {H_2}\left( x \right) {\text{<}} 1};\\ {0,} & {{H_1}\left( x \right) + {H_2}\left( x \right) {\text{≥}} 1}{\text{。}} \end{array}} \right. $ | (5) |
式(5)中,H1和H2分别是当前决策方案D1和D2的匹配概率,D1、D2、D3决策方案的当前匹配概率相加为1。
2.2 基于树型编码的PMX交叉算子交叉操作是指将两个个体之间的部分染色体进行互换。在代码混淆问题中,则是指选择两份代码,把两份代码内部中具备相同功能的代码块进行交换,从而产生两份新的源代码。本文采用部分映射交叉(partially-mapped crossover,PMX)算子[12],通过建立两份代码的常量、变量和方法的映射关系,必要时修改与交叉内容相关的基因值以解决常量、变量、方法交换后无法正常运行代码的问题。在交叉过程中,以AST树为具体的操作对象,采用节点交叉的策略,将AST的子树作为一个整体进行交叉,即在两个父代个体中选择可对应的交叉点,以交叉点作为根结点的子树进行交换,生成两棵新的AST树,即两个新个体。例如选择两份代码中用途相同但名字不同的常量进行交叉,需先建立常量名之间的映射关系,在两个常量交换后再根据映射关系修改所有使用到这两个常量名的代码。
在采用PMX算子时,需要先对父代作常规的两点交叉,再根据交叉区域内各基因值之间的映射关系来修改交叉区域之外的各个基因座的基因值。通过映射关系修改交叉区域外的染色体可确保个体的结构完整性,提高交叉后的存活率。本文中个体采用的树型基因编码会发生染色体长度不一的情况,因此不可采用传统PMX算子中相同长度染色体下基因一一映射的方式,而是应当根据染色体中的代码语句功能是否相同来确定是否进行映射,例如,I1和I2中的交叉区域同时包含变量名的语句基因即可进行映射。本文提出基于树型编码的PMX交叉算子,实施步骤如下。
Step1 对选定的个体I1和I2,确定I1和I2中的交叉点r1和r2,分别以r1和r2为根结点的子树为待交叉区域,要求子树包含的代码为变量、常量声明语句或方法。
Step2 交换I1和I2的交叉区域,如图4所示。
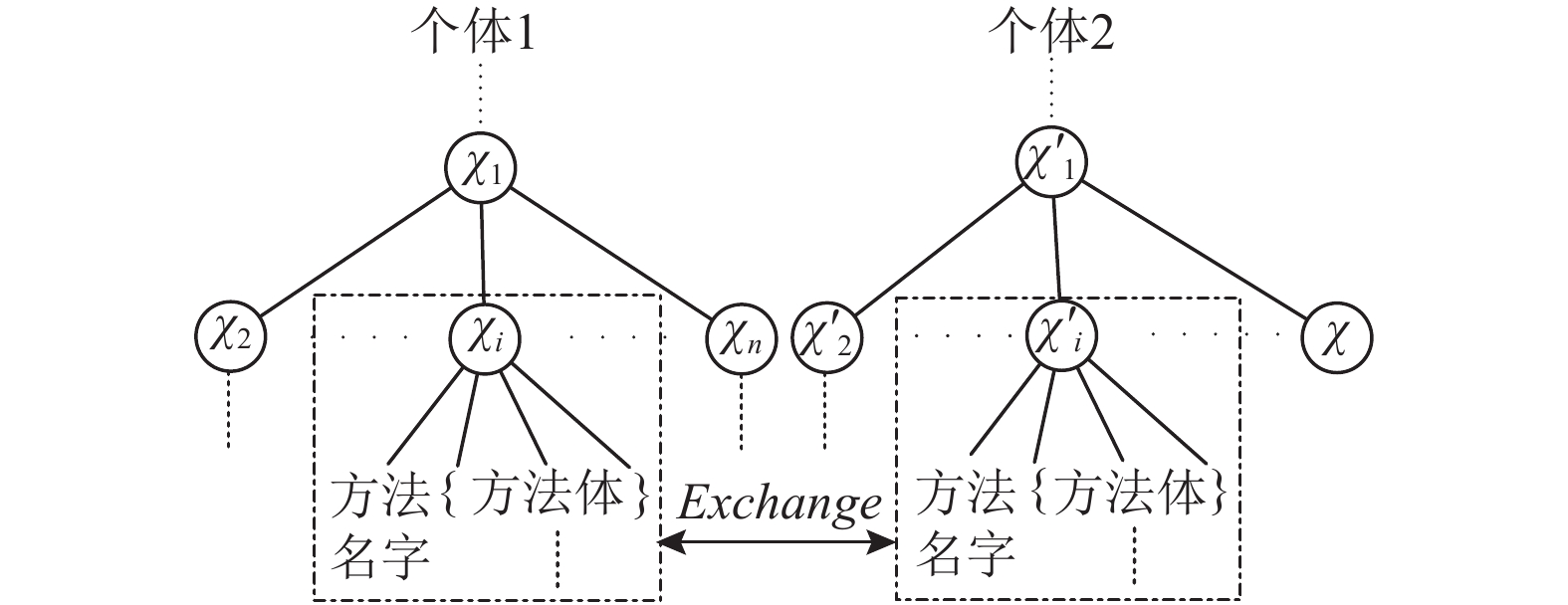
|
图 4 交换操作示意图 Fig. 4 Crossover operation |
Step3 根据交叉区域建立变量或常量映射关系并修改。把交叉区域中具有相同功能但名字不同的变量或常量χ1、χ2节点建立映射关系,通过映射关系把I1所有操作χ1语句中的χ1修改成χ2,同理对I2操作。
Step4 扇出检测。检查I1交叉区域中所调用的某些方法是否存在产生的子代中,如果不存在,则嫁接该方法的子树至子代中,以确保子代能够正常运行。
加入扇出检测改进后的PMX算子的搜索空间更广,局部搜索能力得到增强,更容易跳出局部最优。对于多目标优化来说,在Pareto前沿的完整性、均匀分布性和收敛性上都会有显著改善。
将基于树型编码的PMX算子引入NSGA-II算法避免了因搜索范围扩大,导致局部最优以及进化过程不稳定的问题,使Pareto最优解能均匀地扩展到整个Pareto域,提高Pareto最优解的质量,并将此算法应用于代码混淆问题中,可提供尽可能多的具有代表性的非劣解,而且有利于获得更合理的混淆方案。
2.3 交叉率pσ和变异率pτ的确定遗传算法在进化过程中,进化进程与交叉率和变异率的取值有很大关系,pσ取值越大,新个体产生的速度越快;但当pσ取值过小时会使搜索过程缓慢甚至停滞。当变异概率pτ取值过小时,不易产生新的结构;当pτ取值过大时,遗传算法就会变成纯粹的随机搜索算法。本文采取自适应的遗传算法[13]。根据交叉率和变异率对遗传算法群体进化过程中的影响,设计如下公式进行自适应调整。
| $ \qquad {p_{\text{σ}}} = \left\{ {\begin{array}{*{20}{c}} {{p_{{{\text{σ}}_{\rm{1}}}}} - {p_{{{\text{σ}}_{\rm{2}}}}}\dfrac{{{\rm{fi}}{{\rm{t}}_{\rm{c}}} - {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}}}{{{\rm{fi}}{{\rm{t}}_{{\rm{max}}}} - {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}}},}\\ {{p_{{{\text{σ}}_1}}},} \end{array}} \right.\;\;\;\;\;\begin{array}{*{20}{c}} \!\!\!\!\!{{\rm{fi}}{{\rm{t}}_{\rm{c}}} {\text{≥}} {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}};}\\ {{\rm{fi}}{{\rm{t}}_{\rm{c}}} {\text{<}} {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}{\text{。}}} \end{array} $ | (6) |
| $ \qquad {P_{\text{τ}}} = \left\{ {\begin{array}{*{20}{c}} {{P_{{{\text{τ}}_1}}} - {P_{{{\text{τ}}_2}}}\dfrac{{{\rm{fi}}{{\rm{t}}_{\rm{c}}} - {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}}}{{{\rm{fi}}{{\rm{t}}_{{\rm{max}}}} - {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}}}},\\ {{P_{{{\text{τ}}_1}}}}, \end{array}} \right.\;\;\begin{array}{*{20}{c}} {{\rm{fi}}{{\rm{t}}_{\rm{c}}} {\text{≥}} {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}};}\\ \;\;\;{{\rm{fi}}{{\rm{t}}_{\rm{c}}} {\text{<}} {\rm{fi}}{{\rm{t}}_{{\rm{avg}}}}{\text{。}}} \end{array} $ | (7) |
式中,fitc为两个交叉父代个体中适应度值较大的个体;fitavg为每一代群体的平均适应度值;fitmax为群体中适应度值最大的个体。
当个体的适应度值小于平均值时,采用较高的pσ和pτ,使个体进化成为优秀个体的概率增大;当个体的适应度值大于平均适应度值时,采用较低的pσ和pτ,这样可以确保优秀个体的结构不容易被改变。
2.4 基于锦标赛制的选择操作采用二元锦标赛选择法进行选择操作。通过τ、σ产生的子代记作
Step1 对ξn∪ξn'进行非支配排序。利用I的多个复杂度进行比较,其中ch、cc、cn、cds、cdf、cf数值较大的I支配数值较小的I;对于cm,则数值小的I支配数值大的I。计算每一维的支配数Oi与被支配数Ki,得到
Step2 计算ξn∪ξn'的适应度。在8种代码复杂度中可选择一种作为适应度,本文选择ct作为适应度,因为只有ct在合理的范围中,才能被称作“生存能力”强的个体。
Step3 选择比较个体。在ξn∪ξn'中,不以个体中的支配等级、适应度、复杂度作比较,使用随机选择算法选出Iin和Ijn,
Step4 选出列入ξn+1的I。在Iin和Ijn中使用锦标赛制比较,以支配等级和适应度作为比较指标,指标高的
本文实验验证选取了一份具有含类、方法、全局变量、局部变量、静态变量、for循环结构、while循环结构、if条件结构和switch结构的典型源代码作为混淆前原代码。为使实验结果更具代表性,选用4种对各项代码复杂度影响较大、应用较为广泛的代码混淆技术:插入垃圾代码(Ttrash)、字符串加密(Tencrypt)、不透明谓词[14](Topaque)和压扁控制流[15](Tchenxify)。实验分为3组,分别为包含ch&ct和cdf&cm的两目标方案组、cc&cdf&cm和cds&cdf&cm的三目标方案组和cc&ch&cn&cds&cdf&cf&cm的七目标方案组。通过两目标实验方案可在平面上观察Pareto最优解集在图的分布;利用两目标和三目标实验方案的典型性,可把目标函数推广至3个以上,再最后实现七目标实验方案。在实验过程中设定如下参数:种群规模为20;每代种群产生的新个体数为10;种群进化代数上限为20。
在实验目标选择的复杂度组合中,由于各目标在进化过程中会产生冲突,所以在实验结果中根据某一代的种群数据绘制出Pareto曲面图,其中,横纵坐标轴所表示的是目标复杂度的倒数,通过绘制其倒数图使数据在图中更好地展示结果,且不影响最终Pareto曲面。
测试用例源代码的原各项复杂度如表1所示。本文进行了两目标、三目标和七目标等多种组合的实验,选取部分有代表性的结果进行描述。
| 表 1 源代码各项复杂度 Tab. 1 Source code complexity |
为了不失一般性,本文分别选取了ch&ct和cdf&cm两种两目标方案的结果进行展示。
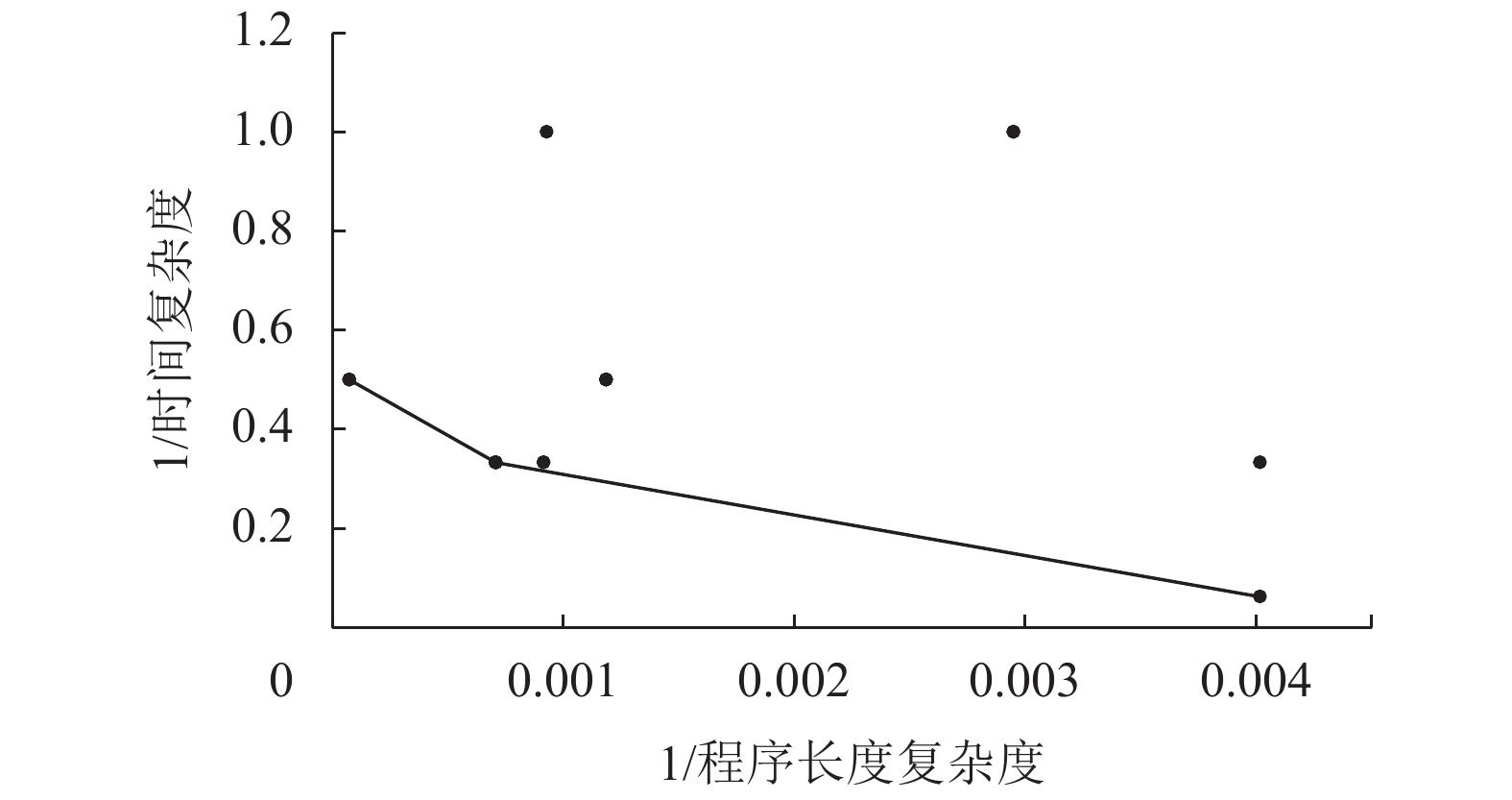
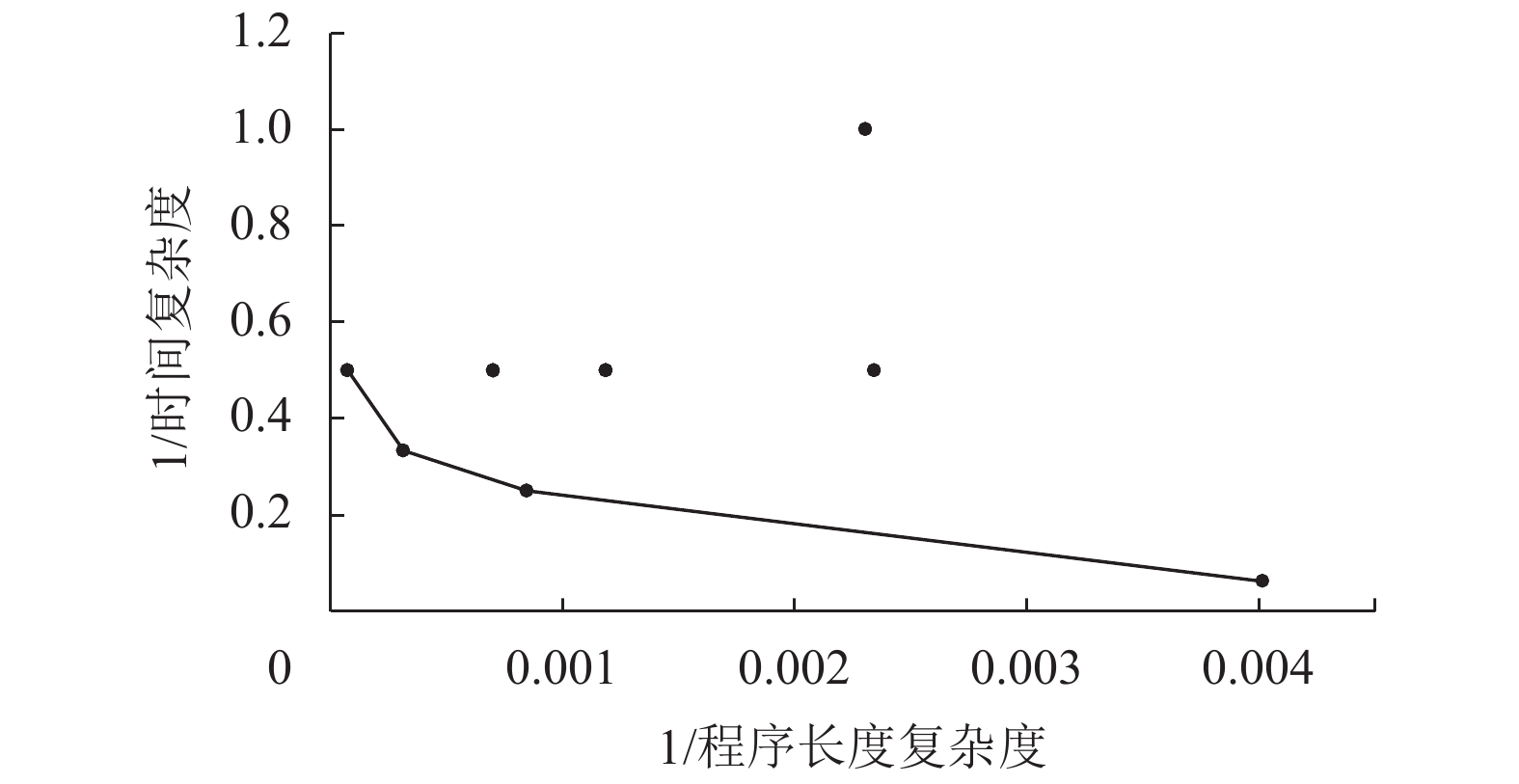
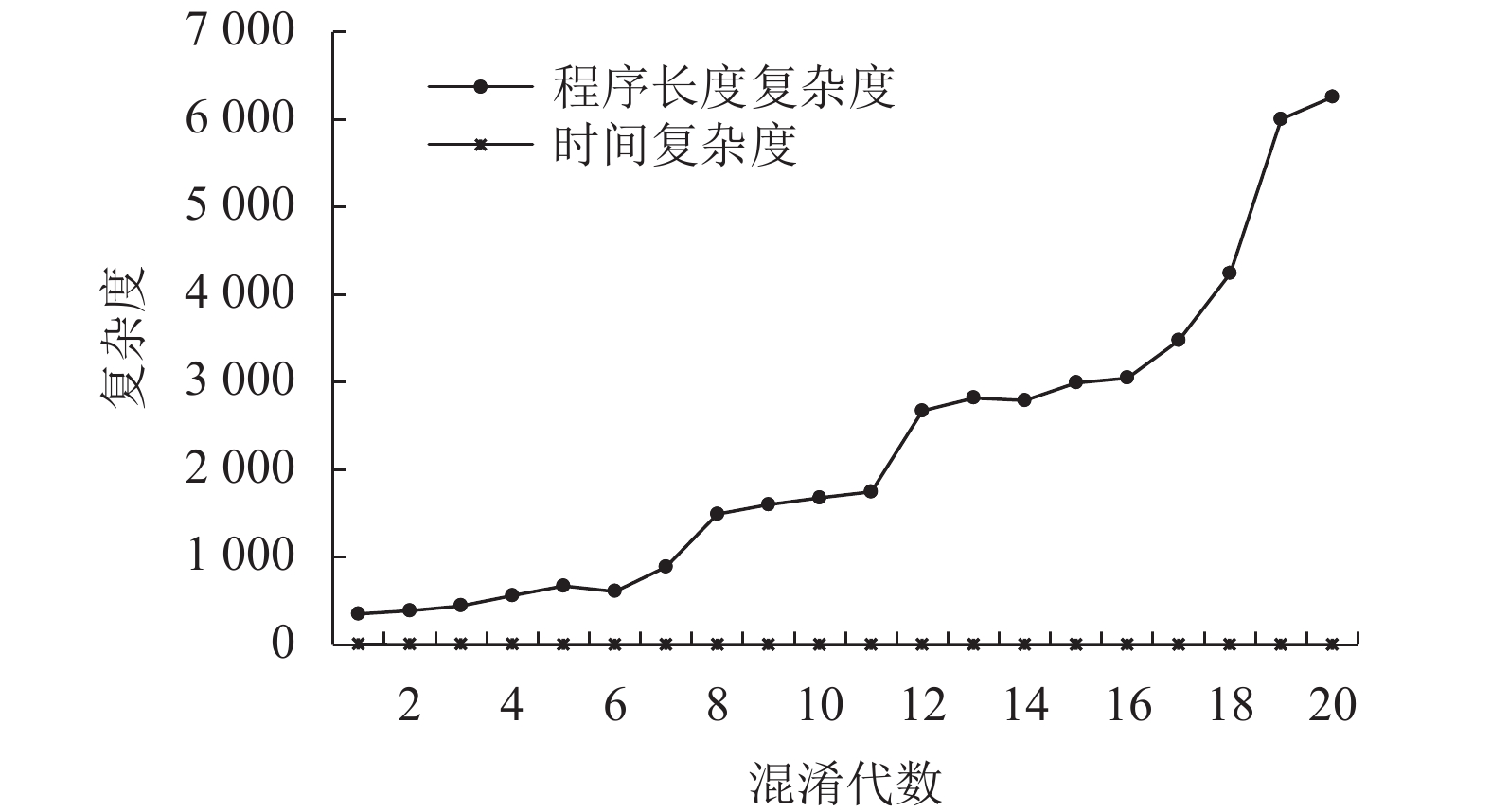
3.1.1 ch & ct实验1比较了ch和ct的数据,其中,图5、图6展示了第13代、第16代的Pareto曲面,将复杂度取倒数构造更便于观察Pareto曲面图。图中线相连的个体即为Pareto最优解集,可发现进化代数越高最优的解集会更多,说明更多的个体在逼近最优解。图7展示了第1代—第20代种群的平均ch和平均ct,由于程序复杂度数值较大,难以和时间复杂度清晰地展示在同一张图,因此,图7的平均ch数据是原有数值上缩小100倍所得。ch和ct的总体趋势是越来越大,但也会有局部下降,是因为由于目标冲突而产生了无效个体会被抛弃,所以图7中第5代—第6代数据有减少。
|
图 5 两目标ch&ct实验组中第13代的Pareto曲面 Fig. 5 The 13th generation Pareto surface in the two-target experimental group with ch & ct |
在本次实验结果中选择第20代中ch为6 077、ct为3的个体展示其混淆技术应用序列[16],即Ttrash→Tchenxify→Ttrash→Tencrypt→Topaque→Tencrypt→Topaque→Ttrash →Tchenxify→Tencrypt→Ttrash →Topaque→Tchenxify→Topaque。
|
图 6 两目标ch&ct实验组中第16代的Pareto曲面 Fig. 6 The 16th generation Pareto surface in the two-target experimental group with ch & ct |
|
图 7 两目标ch&ct实验组中第1代—第20代种群的平均复杂度 Fig. 7 Average complexity of the 1st to 20th generation populations in the two-target experimental group with ch & ct |
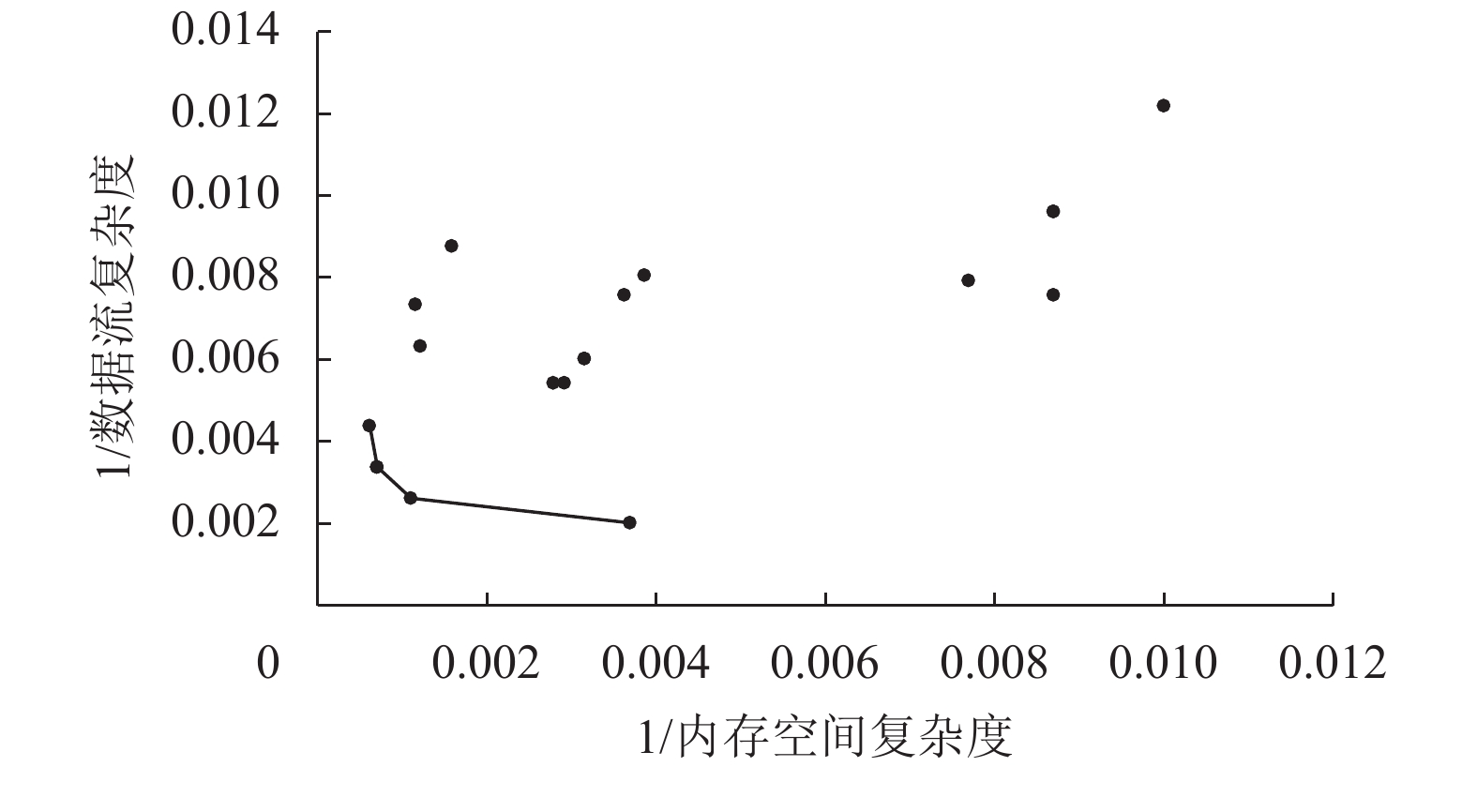
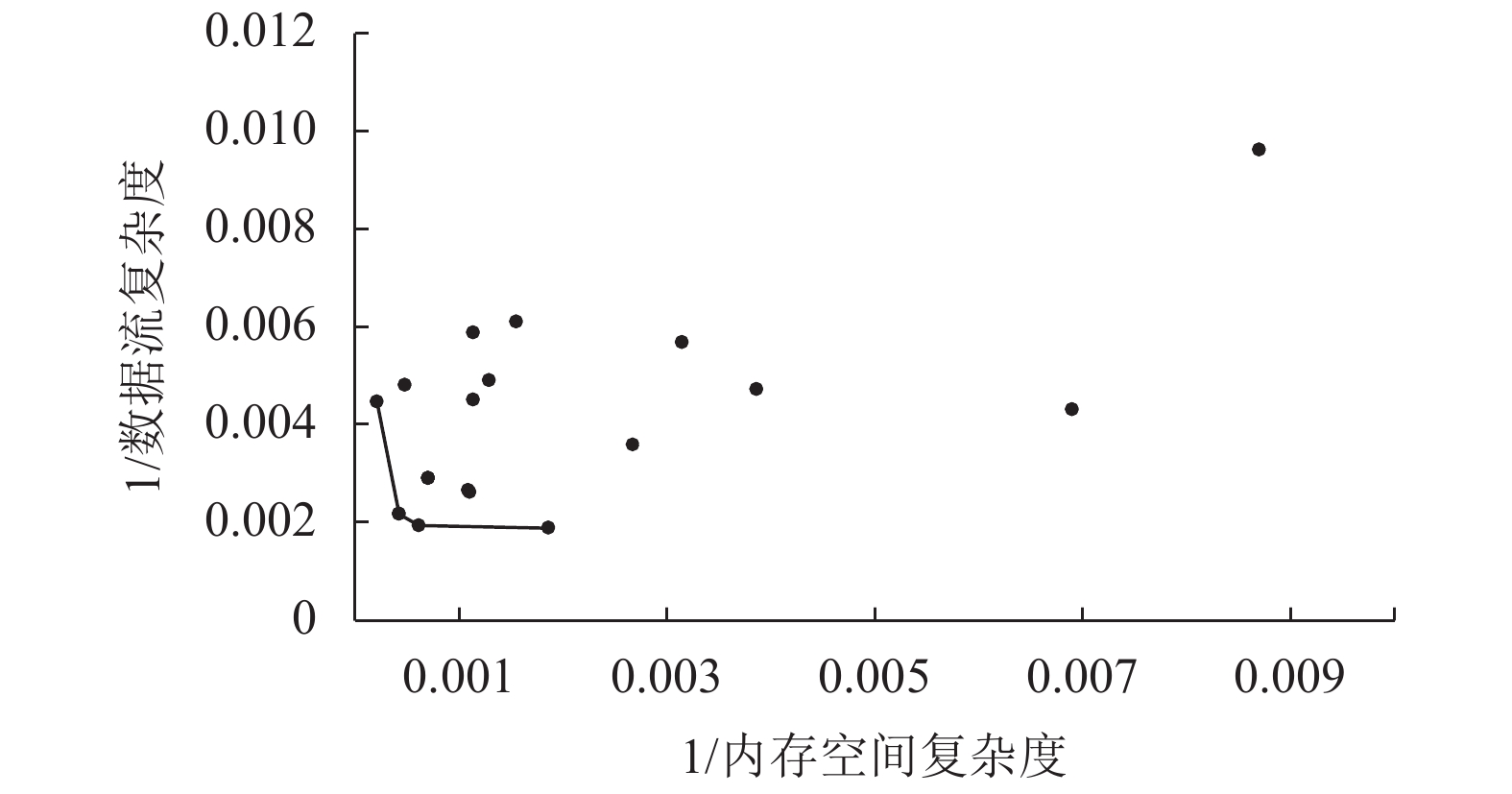
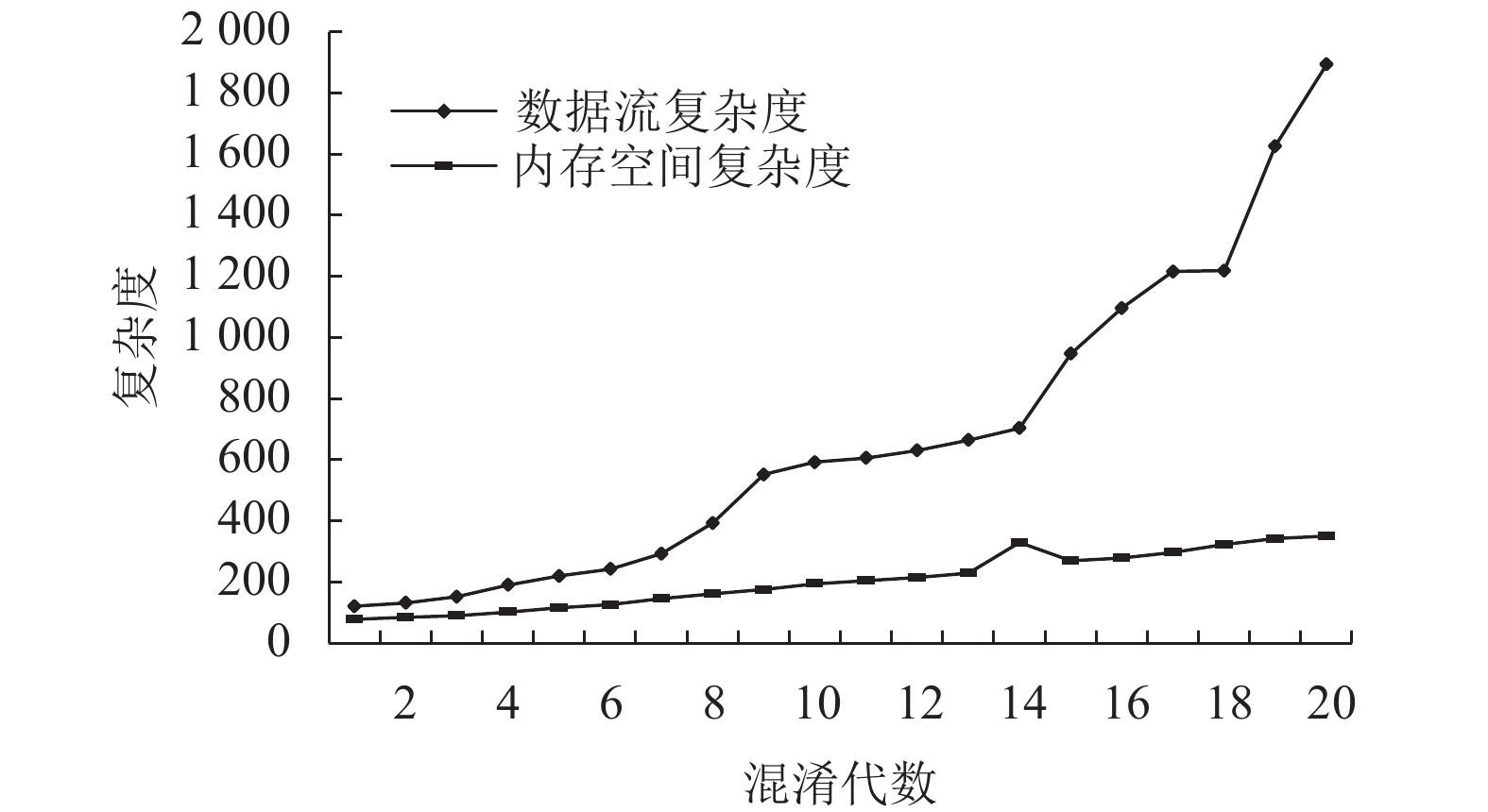
实验2比较了cdf和cm的数据,其中图8、图9显示了第10代、第17代的Pareto曲面图,实验2收敛的速度比实验1更快,在第10代中已经产生了4个最优解,并且在进化至17代的过程中更逼近限定的目标范围。图10展示了个体进化过程中平均cdf和平均cm的数据图,可以发现每次执行代码混淆技术都提高了代码的复杂度,因此图10的总体趋势是上升的。
在本次实验结果中选择第20代中cdf为2 388、cm为482的个体展示其混淆技术应用序列,即Tencrypt→Ttrash→Tencrypt→Tchenxify→Ttrash→Ttrash→Topaque→Ttrash→Topaque→Ttrash→Tencrypt→Topaque→Ttrash→Tchenxify→Ttrash→Topaque→Ttrash→Tencrypt→Ttrash。
通过两组两个目标的数据,可以发现个体在进化的过程中可产生Pareto最优解集,解集中包含多个个体,可作为当代的最优个体;在种群进化过程中,目标值的趋势是越来越大,但也会产生一些超过目标函数范围的无效个体。最终求解的结果是一个解集,选择的个体仅仅展示了最优解集中的其中一个有效解。由此证明运用NSGA-II算法解决在限定的两个目标下确定最优代码混淆技术调用序列问题的可行性。
|
图 8 两目标cdf&cm实验组中第10代的Pareto曲面 Fig. 8 The 10th generation Pareto surface in the two-target experimental group with cdf & cm |
|
图 9 两目标cdf&cm实验组中第17代的Pareto曲面 Fig. 9 The 17th generation Pareto surface in the two-target experimental group with cdf & cm |
|
图 10 两目标cdf&cm实验组中第1代—第20代种群的平均复杂度 Fig. 10 Average complexity of the 1st to 20th generation populations in the two-target experimental group with cdf & cm |
三目标实验组选取了cc & cdf & cm和cds & cdf & cm两种方案。
3.2.1 cc & cdf & cm实验结果展示了个体进化过程中平均cc和平均cdf、平均cm的数据图,如图11所示;并选择第20代中cc为160、cdf为11 172、cm为520的个体展示其混淆技术应用序列,即Ttrash →Ttrash →Tchenxify→Ttrash→Tencrypt→Tencrypt→Tencrypt→Ttrash→Tencrypt→Topaque→Topaque→Ttrash→Tencrypt→Tencrypt→Tencrypt→Tchenxify→Ttrash→Tencrypt→Tencrypt→Tchenxify。
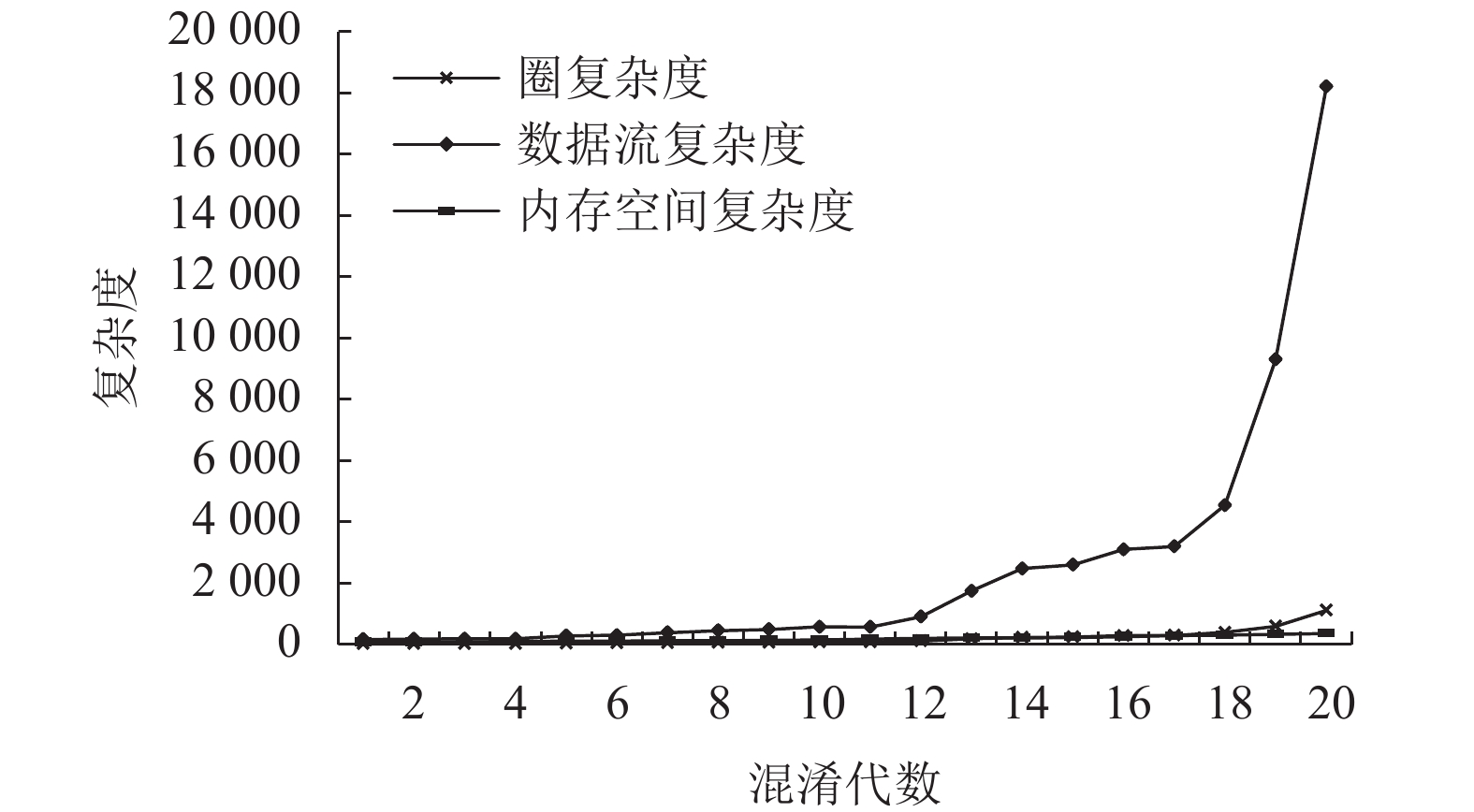
|
图 11 三目标cc&cdf&cm实验组中第1代—第20代种群的平均复杂度 Fig. 11 Average complexity of the 1st to 20th generation populations in the three-target experimental group with cc & cdf & cm |
实验结果展示了个体进化过程中平均cds和平均cdf、平均cm的数据图,如图12所示;并选择第20代中cds为337、cdf为5 567、cm为416的个体展示其混淆技术应用序列,即Ttrash→Tencrypt→Topaque→ Tchenxify→Tencrypt→Tencrypt→Ttrash→Tchenxify→Topaque→Ttrash→Tchenxify→Ttrash→Tencrypt→Topaque。
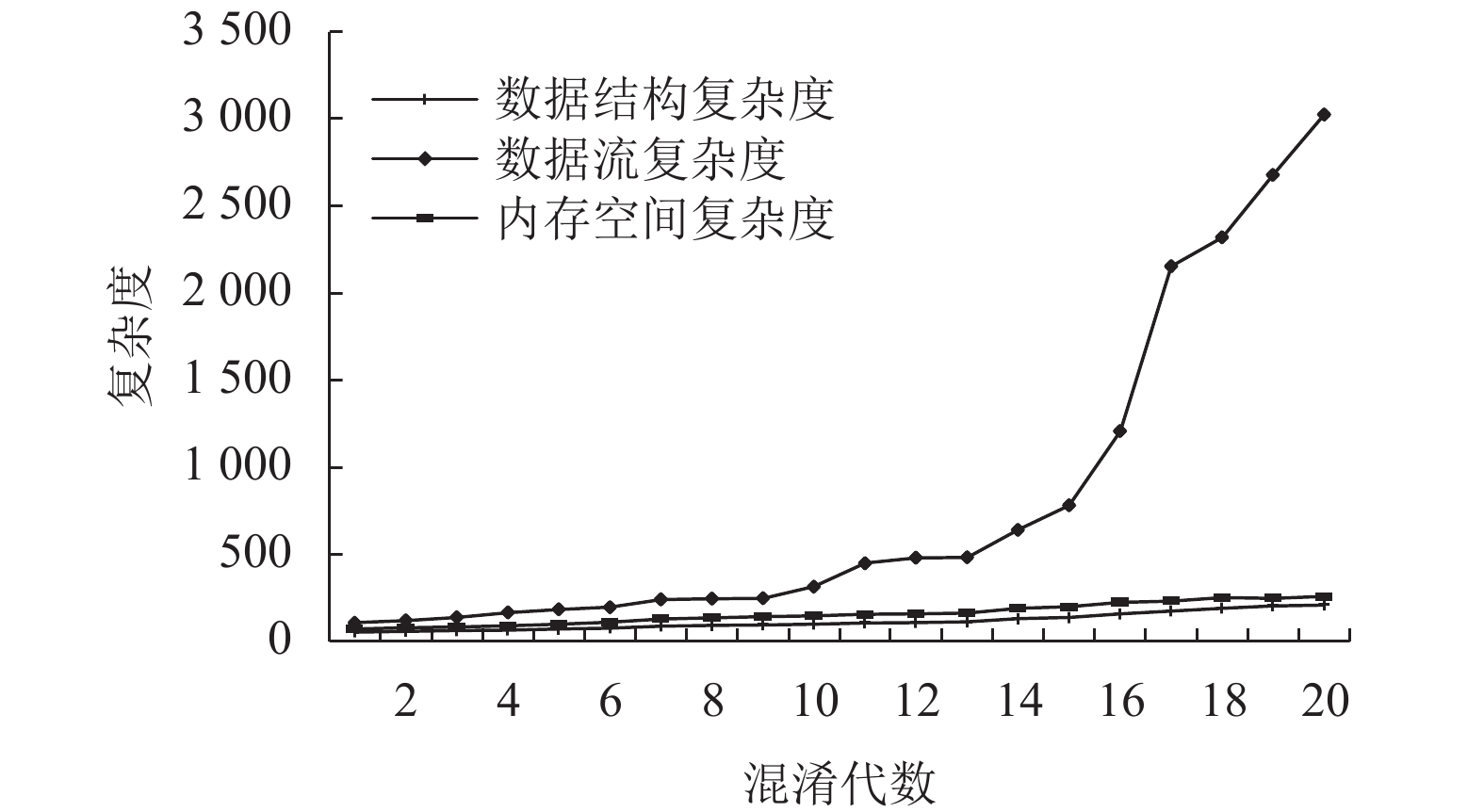
|
图 12 三目标cds&cdf&cm实验组中第1代—第20代种群的平均复杂度 Fig. 12 Average complexity of the 1st to 20th generation populations in the three-target experimental group with cds & cdf & cm |
选取cc & ch & cn & cds & cdf & cf & cm作为七目标实验组方案,实验结果展示了个体进化过程中平均cc、平均ch、平均cn、平均cds、平均cdf、平均cf和平均cm的数据图,如图13所示。当7个目标同时评价的时候可以发现虽然数据上升的趋势依然是越来越大,但增加的幅度没有两个或3个目标大;图中16和17代也因多目标冲突而发生数据下降的趋势;显然限定7个目标去确定代码混淆技术调用序列更具有有效性。
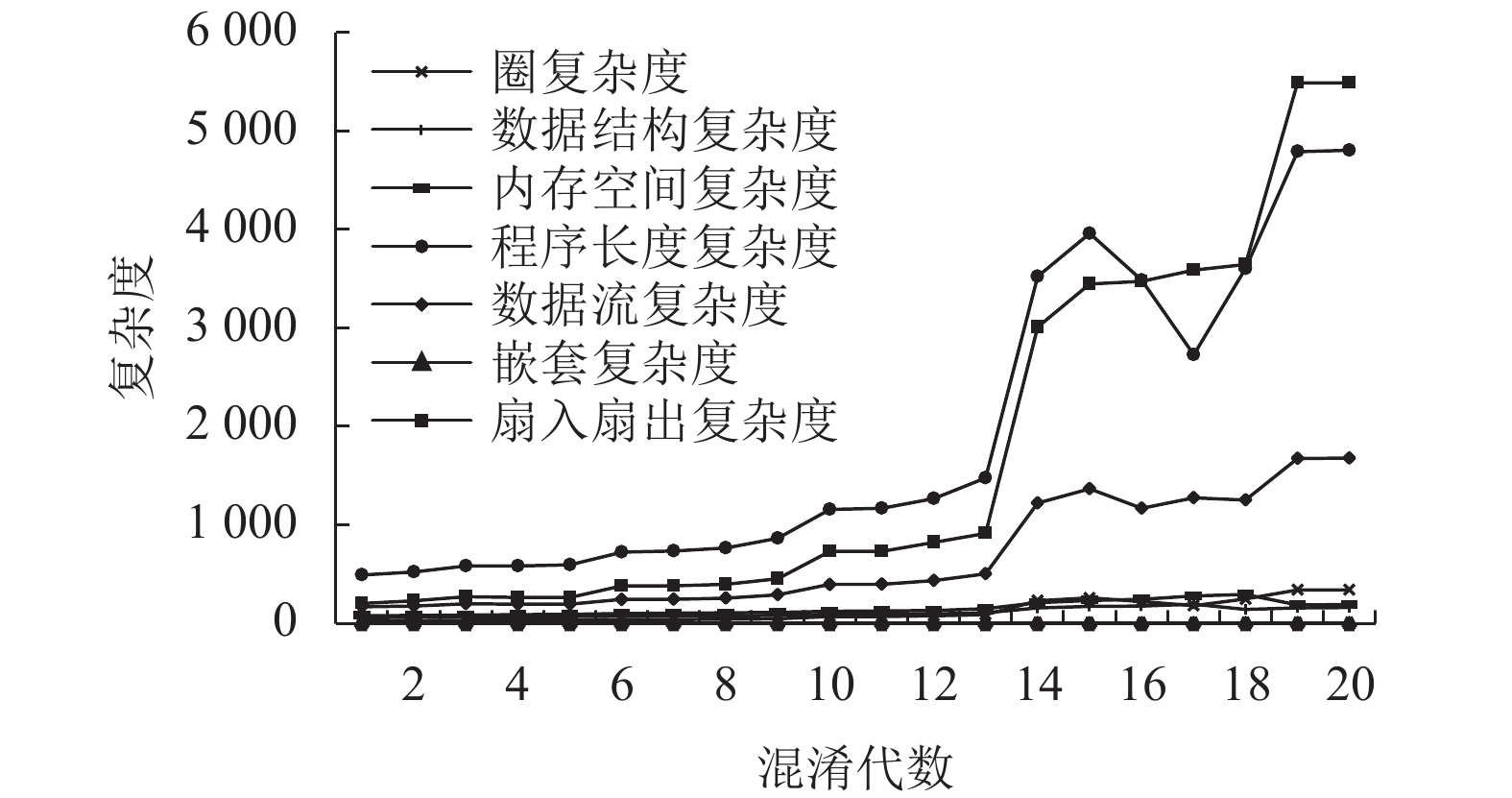
|
图 13 七目标cc&ch&cn&cds&cdf&ccf&cm实验组中第1代—第20代种群的平均复杂度 Fig. 13 Average complexity of the 1st to 20th generation populations in the seven-target experimental group with cc & ch & cn & cds&cdf & ccf & cm |
本文从工程实践的角度去解决代码混淆应用的问题,结合NSGA-II算法,设计了一个面向多目标的代码混淆模型,针对该模型提出基于AST的树型基因编码,完善了交叉、变异和选择操作,应用8种代码复杂度指标作适应度评估,并设计不同目标种类和个数的实验方案进行了验证。实验结果表明,利用基于NSGA-II算法思想设计的代码混淆模型可以在确定代码混淆技术应用序列的基础上,最终获得质量较理想的混淆代码。未来的工作将会利用此模型继续展开研究,考虑不同的角度评价代码质量以及增加更多的代码混淆技术完善应用工具,深入关于生成最优混淆代码的方法研究。
| [1] |
VITICCHIÉ A, REGANO L, TORCHIANO M, et al. Assessment of source code obfuscation techniques[C/OL]. (2016-11-20). https://ieeexplore.ieee.org/abstract/document/7781792.
|
| [2] |
COLLBERG C, THOMBORSON C, LOW D. A taxonomy of obfuscating transformations[R/OL]. [2018-11-19]. https://researchspace.auckland.ac.nz/handle/2292/3491.
|
| [3] |
LIU T, GAO X, YUAN Q. An improved gradient-based NSGA-Ⅱ algorithm by a new chaotic map model[J].
Soft Computing, 2016, 21(23): 1-15.
|
| [4] |
姜惠兰, 安星, 王亚微, 等. 基于改进NSGA2算法的考虑风机接入电能质量的多目标电网规划[J].
中国电机工程学报, 2015, 35(21): 5405-5411.
JIANG Huilan, AN Xing, WANG Yawei, et al. Improved NSGA2 algorithm based multi-objective planning of power grid with wind farm considering power quality[J]. Proceedings of the CSEE, 2015, 35(21): 5405-5411. |
| [5] |
刘士明, 于丹. 基于第二代非支配排序遗传算法(NSGA-Ⅱ)的水资源优化配置[J].
水资源与水工程学报, 2013, 24(5): 185-188.
LIU Shiming, YU Dan. Optimal allocation of water resources based on non-dominated sorting genetic algorithm - Ⅱ[J]. Journal of Water Resources & Water Engineering, 2013, 24(5): 185-188. DOI: 10.11705/j.issn.1672-643X.2013.05.041. |
| [6] |
李瑞阳, 孙景明, 卢厚清, 等. 基于改进NSGA2的航空运输优化[J].
解放军理工大学学报(自然科学版), 2017, 18(1): 74-80.
LI Ruiyang, SUN Jingming, LU Houqing, et al. Optimization of air transport based on improved NSGA2[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2017, 18(1): 74-80. |
| [7] |
MARTINEZ S. Source code obfuscation by mean of evolutionary algorithms[DB/OL]. (2012-08-24). https://dumas.ccsd.cnrs.fr/dumas-00725330.
|
| [8] |
BERTHOLON B, VARRETTE S, BOUVRY P. JShadObf: A JavaScript obfuscator based on multi-objective optimization algorithms[C/OL]. [2018-11-19]. https://www.lrde.epita.fr/wiki/Publications/newton.17.els.
|
| [9] |
黄松, 黄玉, 惠战伟. 基于JavaCC的抽象语法树的构建与实现[J].
计算机工程与设计, 2016, 37(4): 938-943.
HUANG Song, HUANG Yu, HUI Zhanwei. Construction and realization of abstract syntax tree based on JavaCC[J]. Computer Engineering and Design, 2016, 37(4): 938-943. |
| [10] |
NEWTON J, VERNA D, COLANGE M. Programmatic manipulation of common lisp type specifiers[C/OL]. (2017-02-06). https://www.lrde.epita.fr/wiki/Publications/newton.17.els.
|
| [11] |
王怀军, 房鼎益, 董浩, 等. 白盒环境中防动态攻击的软件保护方法研究[J].
电子学报, 2014, 42(3): 529-537.
WANG Huaijun, FANG Dingyi, DONG Hao, et al. Research on software protection defending dynamic atackin white-box environment[J]. Acta Electronica Sinica, 2014, 42(3): 529-537. DOI: 10.3969/j.issn.0372-2112.2014.03.017. |
| [12] |
WIDIARTHA I B K, ANJARWANI S E, BIMANTORO F. Traveling salesman problem using multi-element genetic algorithm[C/OL]. (2017-10-26). https://ieeexplore.ieee.org/abstract/document/8272917.
|
| [13] |
XU M, LI S, GUO J. Optimization of multiple traveling salesman problem based on simulated annealing genetic algorithm[DB/OL]. [2018-11-19]. https://www.researchgate.net/publication/315106266_Optimization_of_Multiple_Traveling_Salesman_Problem_Based_on_Simulated_Annealing_Genetic_Algorithm.
|
| [14] |
苏庆, 孙金田. 基于混沌不透明表达式的不透明谓词混淆技术研究[J].
计算机科学, 2017, 44(12): 114-119.
SU Qing, SUN Jintian. Research on opaque predicate obfuscation technique based on chaotic opaque expression[J]. Computer Science, 2017, 44(12): 114-119. DOI: 10.11896/j.issn.1002-137X.2017.12.022. |
| [15] |
吴伟民, 林水明, 林志毅. 一种基于混沌不透明谓词的压扁控制流算法[J].
计算机科学, 2015, 42(5): 178-182.
WU Weimin, LIN Shuiming, LIN Zhiyi. Chaotic-based opaque predicate control flow flaten algorithm[J]. Computer Science, 2015, 42(5): 178-182. DOI: 10.11896/j.issn.1002-137X.2015.05.036. |
| [16] |
苏庆, 何凡, 伍乃骐. 基于带抑止弧的Petri网的软件保护技术应用序列构建方法[J].
工业工程, 2017, 20(6): 77-83.
SU Qing, HE Fan, WU Naiqi. A method of constructing sequence of software protection technologies based on Petri Net with inhibitor Arcs[J]. Industrial Engineering Journal, 2017, 20(6): 77-83. DOI: 10.3969/j.issn.1007-7375.e17-4137. |
 2019, Vol. 22
2019, Vol. 22

