随着客户需求的升级，消费类电子产品更新换代频繁，面对移动通讯市场激烈的竞争，缩短产品制造周期以提高市场占有率至关重要。手机中框及后盖制造企业多采用典型的大批量生产模式。这种模式在一段特定的时间内只生产同一类型的工件，其自动化程度高、生产节拍快、换产时间长。AGV小车是智能车间重要的物流运输资源，能否将物料按时送达加工单元将影响系统生产资源的利用率。因此，如何快捷高效地调度有限的AGV小车，使得车间的生产效率最高是智能车间生产的重要环节。

针对AGV调度优化问题，表1为近年来国内外学者所展开的部分研究。通过分析这些研究，有以下发现。

1) 大多数学者都是针对柔性制造系统 (flexible manufacturing system，FMS)或作业车间(job shop)，以最小化时效指标(如：最大完工时间(makespan)、机器等待时间、任务拖期时间等)和小车搬运距离为优化目标或多目标考虑多AGV的调度优化问题。本文针对具有非同等并行单元的单工序、环形轨道、多AGV小车调度问题进行了研究，而文献[15]仅考虑具有同等并行单元的单AGV调度问题，且其AGV运行路径为线型。

2) 绝大多数学者采用智能优化算法进行静态调度方案的求解，然而本文研究的是在动态调度环境下，寻找高效的求解算法(算法运行时间要求达到毫秒级)，而规则类算法较之智能算法具有更高的时效性。因此，本文采用规则类算法对该问题进行求解。

综上所述，本文针对具有非同等并行单元的单工序、环形轨道、多AGV小车调度问题，以最小化最大完工时间为优化目标，提出了7种基于规则类的调度算法，并通过设计仿真实验对算法的有效性进行了分析和验证。

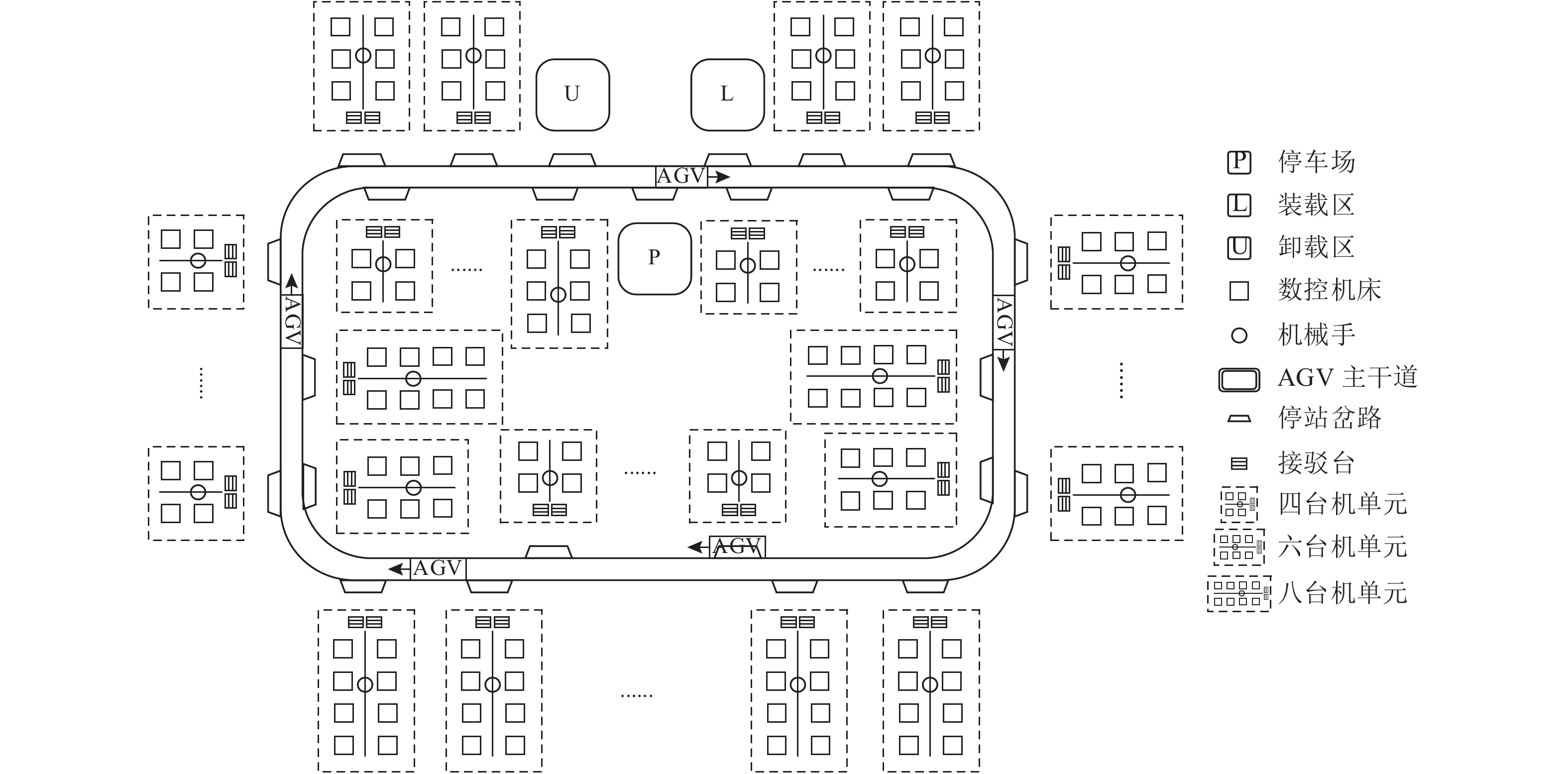
1 问题描述

手机中框及后盖的加工过程包含若干道工序，每道工序都在一个智能车间加工完成后流向下一个智能车间，本文主要针对某道典型工序的智能车间进行研究。图1是智能车间制造系统简图，智能车间包含自动化物料储运系统和若干个自动化制造单元2部分，其中自动化物料储运系统包括轨道(环形主干道和停站岔路)和若干辆AGV小车；自动化制造单元包含1个搬运机械手和若干台数量不等的数控机床。工件由车间的任意一个自动化制造单元内的任意一台数控设备加工处理。车间采用单回路导引系统，自动化制造单元绕回路排布，每个单元的接驳台(PD口)前是与主干道连接的用于单元上下料的停站岔路，单回路和停站岔路的设计，极大减少了交通堵塞、车辆干扰、死锁等的发生概率。

工件在加工前到达装载区，等待AGV小车将其搬入机器人制造单元进行加工。单元采用双箱系统，接驳台是容量为2个托盘的工件缓存区，当其中1个托盘上的工件加工完成后，单元缺料向系统发送物料搬运申请。其中AGV上下料任务可描述为：首先，空闲AGV响应申请，从停车场出发，绕主干道单向运动，到装载区搬运待加工托盘；接着，AGV行驶到对应目标单元的停站岔路，和单元的接驳台完成已完工托盘和未加工托盘的交换；最后，上下料完成后AGV运载已完工托盘绕环形轨道到卸载区卸料，AGV继而回到停车场。

对本文研究的智能车间AGV调度问题做以下约束和假设。

1) 智能车间设施布局以及AGV可行走的路径轨道已确定；

2) 每辆AGV都相同，且在同一时间段只执行一个任务，每个任务只能被一辆AGV执行；

3) 不考虑AGV的加减速，忽略电池电量对运行速度的影响，且在负载时的速度与空载时相同；

4) 每辆AGV在运行中不会发生碰撞。

由于单元的搬运需求频率不一，同一时段内可能会出现多个单元同时呼叫小车，如何对有限的物流运输资源进行调度，确定适当的配送小车，将固定时间内的运输任务分配给有限的AGV，使物料准时送达单元，加工设备利用率最高，是本文需要解决的问题。

2 仿真模型的建立

根据图1所示的智能车间简图和实际工作场景，搭建了基于Tecnomatix Plant Simulation 14软件的仿真模型用于研究智能车间AGV调度方法。图2为智能车间仿真模型。

2.1 仿真系统模型的参数设置

根据调研企业的车间尺寸和设施布局，给出模型主要仿真参数的设置。系统共有254台加工设备，41个自动化制造单元，其中，四台机单元(Cell-4)有11个，六台机单元(Cell-6)15个，八台机单元(Cell-8)15个，托盘装载量为8；自动化制造单元采用双箱系统，接驳台是容量为2的托盘缓存区，工件的加工时间为11 min，机械手运行速度为1.5 m/s，机械手对工件的上料/下料各需8 s。

AGV参数的设置：AGV对单元的上料/下料各需15 s；运行速度是1.5 m/s；每天轮班16 h，执行完搬运任务时在停车站待命；每天轮休8 h，其中充电6 h，冷却2 h，当AGV处于冷却状态时，可启用应急调度。

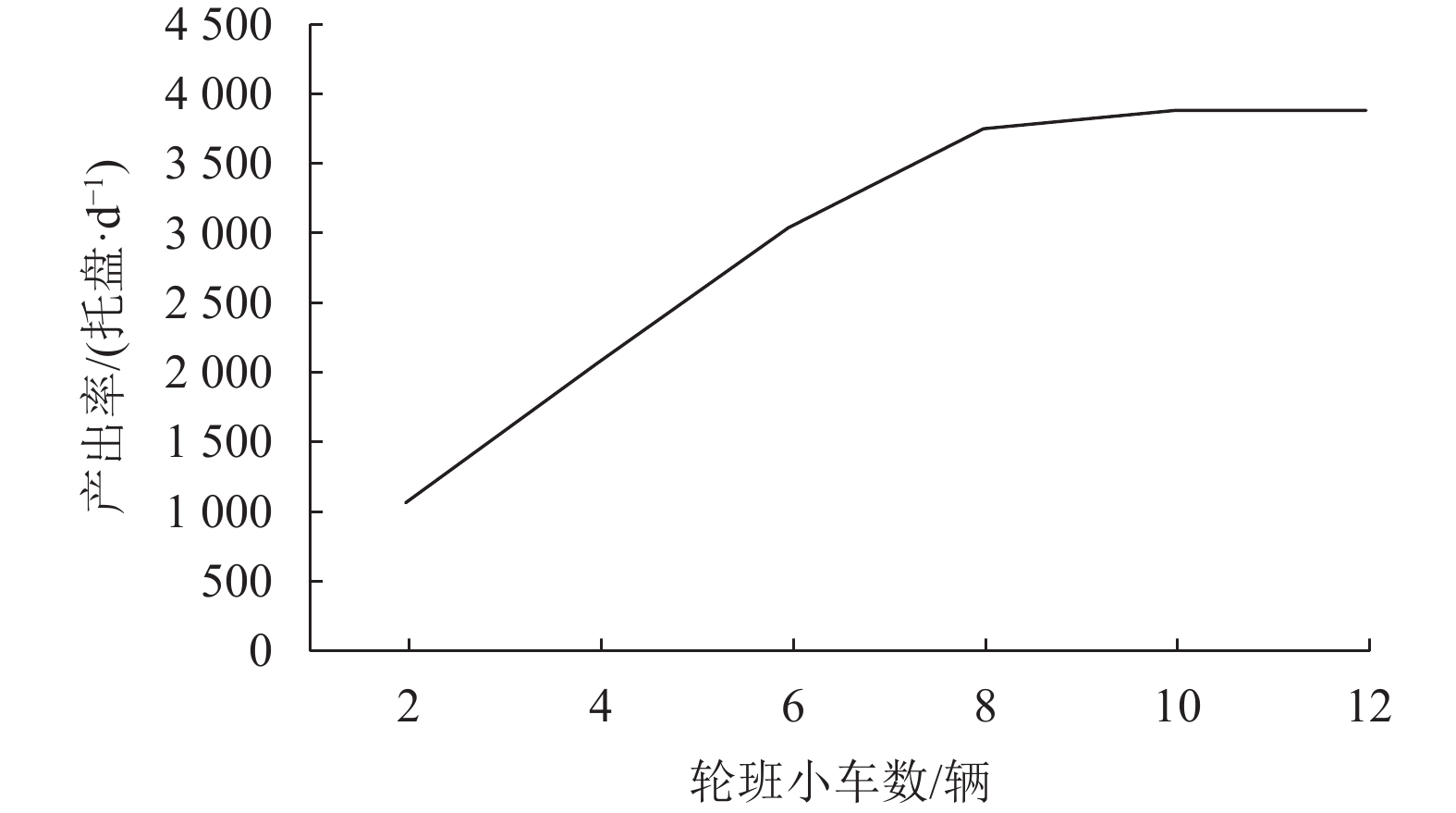
AGV数量的设置：AGV的数量将直接影响各机器人单元的运行效率，假定AGV调度遵循先提申请先服务规则进行仿真，得到AGV数量与产出率的关系如图3所示。随着AGV数量的增加，系统的产出率由显著提升到趋于平稳。这是由于此时制约系统产能的瓶颈不再是运输能力，更多运输能力的输入也无法增大系统的产出率。可见，增加AGV的数量可有效提升系统产出率，但存在一个较优的AGV数量，当超过这个数值时，AGV数量的增加造成浪费，且不利于制造系统的流畅和稳定。因此，考虑AGV的成本和堵塞问题，配置轮班AGV小车的数量为8，即系统共配置12辆AGV。

2.2 仿真系统模型的运行机制

任务触发机制 　AGV搬运任务由自动化单元触发。本文提出2种任务触发机制：1) 当AGV搬运一个未完工托盘到接驳台时，判断另一个托盘位是否为空，若为空，单元触发搬运任务申请；2) 当接驳台其中一个托盘上的工件加工完成后，单元缺料向系统发送物料搬运申请，任务将记录在任务表中。

任务响应机制 　系统根据调度规则每隔15 s扫描一次任务表并对任务表排序，继而判断停车站是否有待命小车。若有，等待时间最长的AGV执行任务；若无，判断充电站是否有充满电且处于冷却状态的小车，若有，AGV进入应急调度状态执行任务。本文启用应急调度策略的条件为当任务表的任务数大于5个，停车站无空闲小车，充电站有充满电且处于冷却状态的小车。

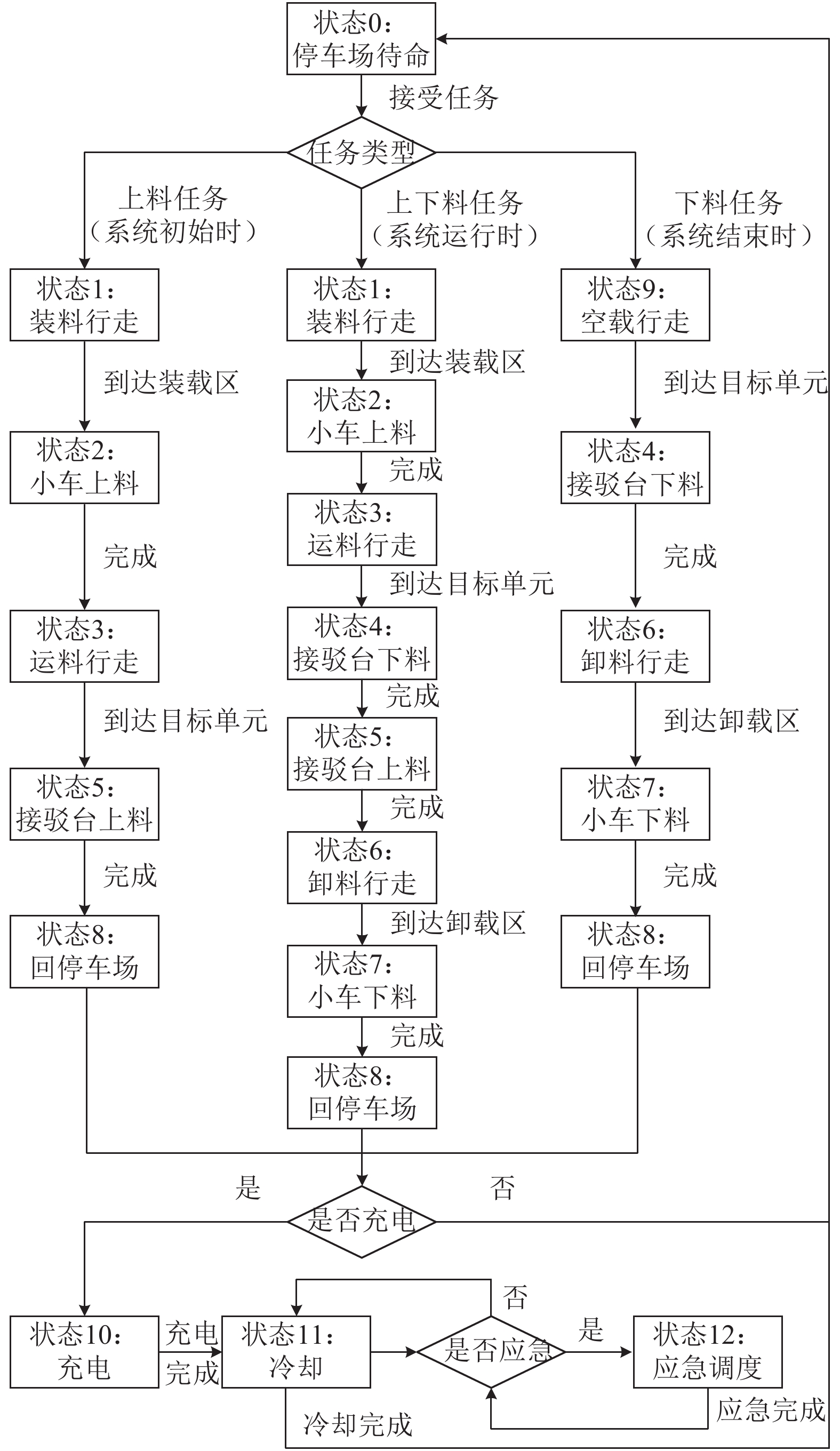
AGV运行机制 　当AGV电池容量消耗到预定值时会发出请求信息，系统将安排AGV回到停车场的充电站进行充电，并在未完成任务之前，遵循任务优先原则。根据上述运行规则可得到AGV状态跃迁图(图4)，其中状态1~9是AGV轮班时段的状态，状态10~12是AGV轮休时段的状态。

AGV调度规则 　AGV调度规则用于当多个机器人单元有托盘搬运需求时，或多辆AGV小车等待搬运托盘时，决定完成各托盘搬运任务的最佳先后顺序并选择合适的AGV小车进行搬运。本文统一采用先到达停车站待命的小车先指定任务的AGV任务分派策略。从智能车间实际系统的复杂性、规模性和可操作性角度考虑，对调度算法的实时性和有效性要求更高，因此合理选择适用于实际车间环境的调度规则尤为重要。本文提出7种AGV调度规则，分别如下。

1) FCFS规则：优先服务先提搬运申请的机器人单元。

2) Random规则：随机服务机器人单元。

3) SPT规则：优先服务设备数多的机器人单元，优先级为Cell-8＞Cell-6＞Cell-4。

4) ESD规则：优先服务越早停工的机器人单元。

5) Nearest规则：优先服务距离装载区近的机器人单元。

6) Farthest规则：优先服务距离装载区远的机器人单元。

7) Window规则：优先服务时间窗下限越早的机器人单元。

其中，前6种规则是较为常见的AGV调度规则，都基于某个单一指标，而Window规则综合考虑了机器人单元加工能力和距离的差异性。在Window规则中，本文定义了软时间窗概念 $\left[ {{\rm{E}}{{\rm{T}}_i},{\rm{L}}{{\rm{T}}_i}} \right]$ ，其中，i为任务下标， ${\rm{E}}{{\rm{T}}_i}$ 为搬运任务i的最早开始时间； ${\rm{L}}{{\rm{T}}_i}$ 为搬运任务i的允许最晚开始时间。软时间窗指AGV不一定在指定时间段 $\left[ {{\rm{E}}{{\rm{T}}_i},{\rm{L}}{{\rm{T}}_i}} \right]$ 开始服务，但在规定时间段以外，服务将导致机器人单元停工待料，生产效率下降。 ${\rm{E}}{{\rm{T}}_i}$ 和 ${\rm{L}}{{\rm{T}}_i}$ 的定义分别为

$ \qquad{\rm{E}}{{\rm{T}}_i} = {R_i}{\text{，}} $

(1)

$ \qquad{\rm{L}}{{\rm{T}}_i} = {S_i} - H_i^c - 3{{{L}}_i}{\text{。}} $

(2)

其中， ${R_i}$ 是单元提搬运申请的时间，即单元内有托盘上的工件全部加工完成，触发运料申请； ${S_i}$ 是单元因等待物料而有设备停工的时间点； $H_i^c$ 为AGV从响应任务i开始至到达机器人单元c的运输时间； ${L_i}$ 是单元的上下料时间。

AGV从响应任务到物料送达进行了3次上/下料。调度目标是使AGV响应搬运任务的时间尽量在运料时间窗 $\left[ {{\rm{E}}{{\rm{T}}_i},\;{\rm{L}}{{\rm{T}}_i}} \right]$ 内，尽可能在单元有设备停工待料前将物料送达加工单元，即物料送达时间点 ${T_i}$ 小于单元的停工时间点 ${S_i}$ ；或使单元停工时间最短，即停工时间点与物料运达时间点之间的时间差最小，当 ${T_i} {\text{＞}} {S_i}$ 时， $\displaystyle \min \;\sum\limits_{i = 1}^n {\left( {{T_i} \;- \;{S_i}} \right)} $ ，n为搬运任务总数。

本文研究的智能制造系统属于离散事件系统，这类系统仿真是由事件来驱动的，事件表按事件发生时间先后顺序安排事件。由于仿真钟推进方法为事件调度法，即按下一最早发生事件的发生时间推进，因此不能得到准确的未发生事件的发生时间。因此，实现软时间窗调度规则的关键在于，当搬运任务i发生时，如何较准确地预测时间窗 $\left[ {{\rm{E}}{{\rm{T}}_i},{\rm{L}}{{\rm{T}}_i}} \right]$ 的下限 ${\rm{L}}{{\rm{T}}_i}$ ，即在机器人单元提搬运申请的时刻预测单元的停工时间点 ${S_i}$ 。仿真模型中，实现Window规则算法步骤如下。

步骤1 　根据仿真历史数据，计算当AGV速度为1.5 m/s时，从响应任务开始至到达各机器人单元的运输时间 ${H^c}$ ；

步骤2 　记录托盘上的第一个工件开始加工的发生时间 ${\rm{B}}{{\rm{P}}^p}$ ，p为托盘编号( $1 {\text{≤}} p {\text{≤}} {\text{托盘总数}}$ )，其中，托盘总数为对订单量除以托盘装载量的值向上取整；

步骤3 　在单元提搬运申请的事件发生时，记录搬运任务i的发生时间 ${R_i}$ ；

步骤4 　结合步骤1，判断搬运任务i对应的机器人单元，得到 $H_i^c$ ；

步骤5 　判断搬运任务i的触发机制，针对第1种和第2种任务触发机制， ${S_i}$ 的预测分别为式(3)、式(4)；

步骤6 　计算搬运任务i的时间窗下限 ${\rm{L}}{{\rm{T}}_i}$ ；

步骤7 　搬运任务列表按 ${\rm{L}}{{\rm{T}}_i}$ 升序排列，AGV优先服务时间窗下限越早的机器人单元。

$ \qquad{S_i} = {R_i} + {\rm{CT}}_2^k, $

(3)

$ \qquad{S_i} = {\rm{BP}}_i^p + {\rm{CT}}_{14}^k \cdot {r_k}{\text{。}} $

(4)

式中， ${\rm{CT}}_2^k$ 、 ${\rm{CT}}_{14}^k$ 分别表示 $k\left( {k = 4,6,8} \right)$ 类单元在轮班AGV数量为2和14时的单元生产周期，指该托盘从投入单元开始，到托盘上所有工件加工完成为止的全部时间，即托盘流经单元的时间； ${\rm{BP}}_i^p$ 是触发任务i的托盘p的开始加工的时间； ${r_k}$ 为 $k$ $\left( {k = 4,6,8} \right)$ 类单元相应的修正系数。经过多次仿真实验，发现当 ${r_4} = 1,{r_6} = 0.8,{r_8} = 0.8$ 时Window规则有最好的表现。表2是系统轮班AGV数为2和14时，3种类型单元生产周期的仿真统计数据。AGV数为2时，认为系统运输能力紧张；AGV数为14时，认为系统运输能力松弛。由表2可以看出，AGV数量充足时，单元加工1个托盘工件的时间较长。原因在于设备加工完成时有足够的原料供机械手抓取去和成品交换，而AGV不足时单元原料也不足，机械手只需完成成品的卸载即可。

3 仿真结果分析 3.1 设备及AGV利用率分析

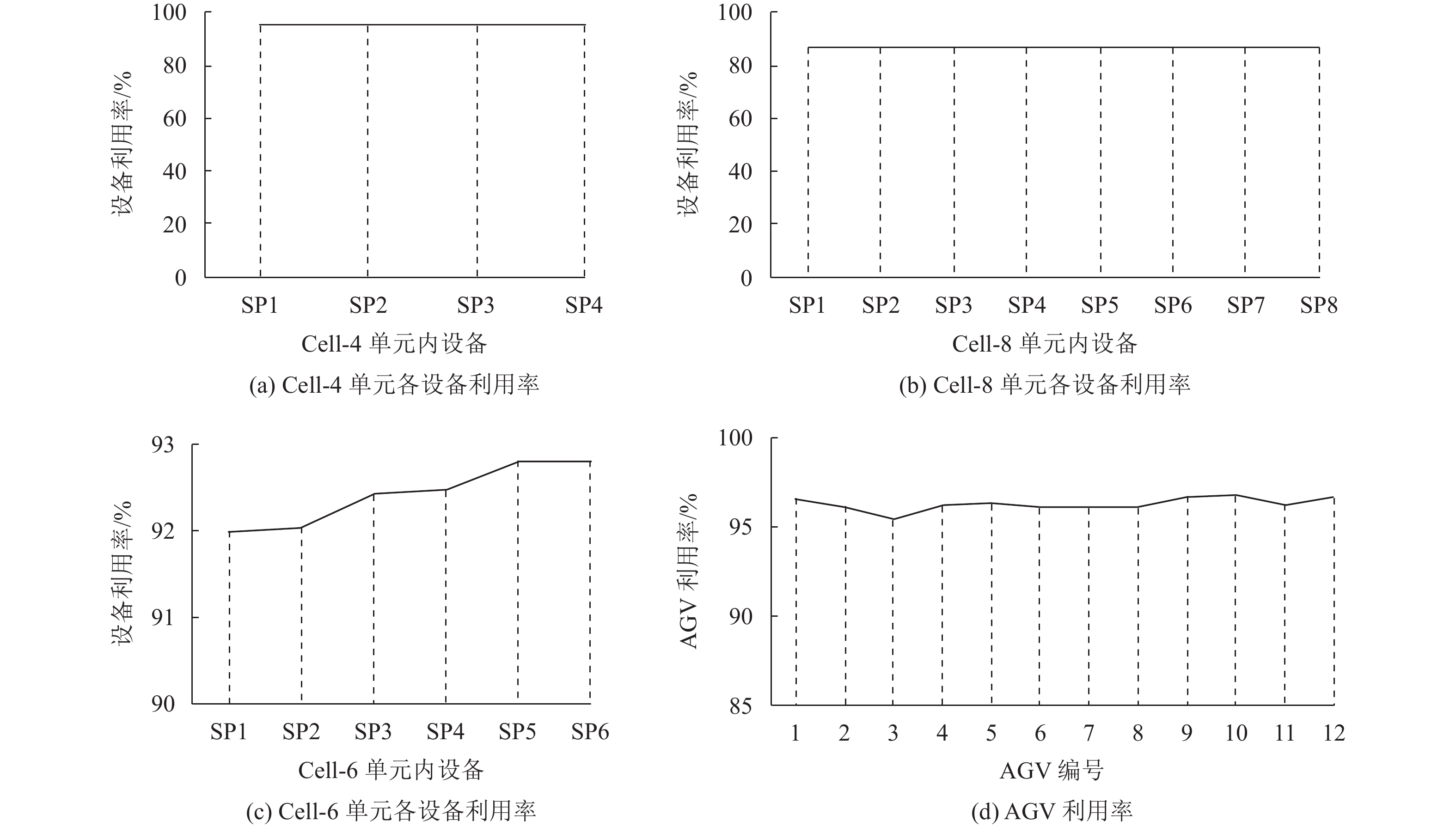
设置仿真模型参数，系统配置12辆AGV，输入订单数32 000个工件，以系统最后一个工件的完工时间作为仿真结束条件进行仿真实验。通过仿真分析，各调度规则下机器及AGV的利用率趋势相似。以FCFS规则的仿真数据为例，统计各种类型单元的设备平均利用率、各AGV利用率，其中AGV利用率为AGV轮班时的利用率，忽略轮休时参与应急调度的工作时间。由于托盘装载量为8个工件，四台机单元和八台机单元内的设备加工工件数量相同，因此单元内的设备平均利用率相同，如图5(a)、图5(b)所示。六台机单元内设备的平均利用率如图5(c)所示，SP1和SP2、SP3和SP4、SP5和SP6的利用率相近，且呈现上升趋势。这是由于单元内机械手的调度策略采用优先服务距PD口远的设备，而距离近的设备在加工完等待机械手服务时提高了设备的堵塞率。仿真模型采用的AGV任务分派策略为在停车站等待时间越长的小车优先指定任务，此任务分派策略使得各AGV的任务量得以均衡，利用率如图5(d)所示。

3.2 常用调度规则的特征分析

1) Random调度规则。基于Random调度规则的模型进行仿真实验，在置信度为95%的条件下观察10次，仿真结果由10组相同参数独立随机仿真试验的结果求平均值得到。选取3个性能指标输出值进行评估分析，结果如表3所示，3个性能指标的标准差和极差都较大，尤其是产出率的结果极不稳定，说明Random规则随机服务机器人单元引起较大的性能波动。

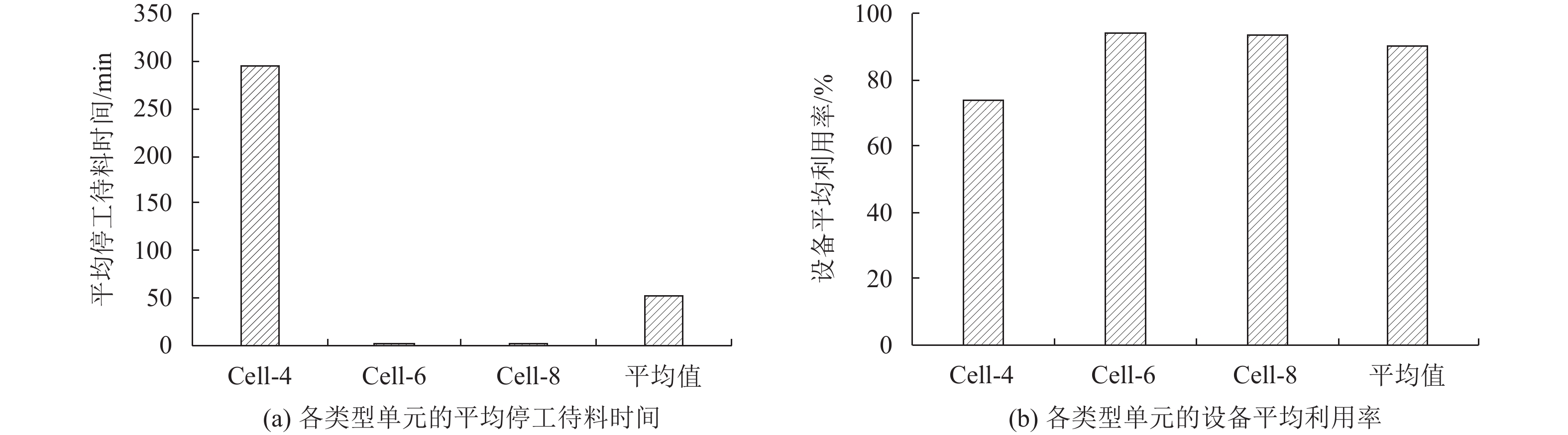
2) SPT调度规则。系统有3种类型的机器人单元，主要表现在单元加工能力不同，SPT规则优先服务设备数多的机器人单元。对基于SPT调度规则的模型进行仿真，结果表明Cell-4的单元类型平均停工待料时间远高于另外2种单元类型，各类型单元的平均利用率不均衡，如图6(a)和图6(b)所示。

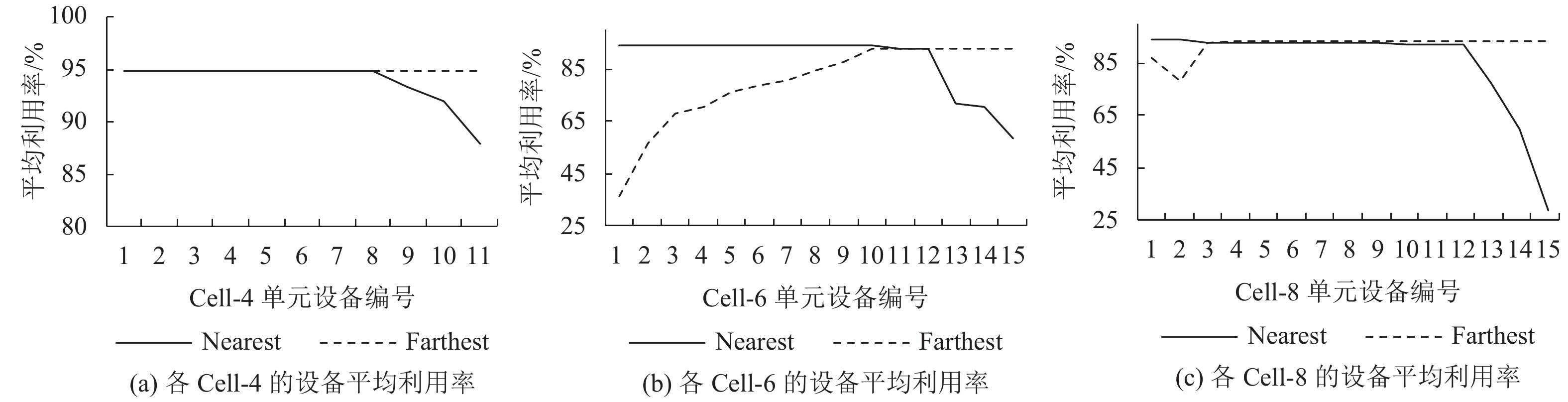
3) Nearest规则和Farthest规则。Nearest规则和Farthest规则基于运料距离的远近调度AGV。Nearest规则是较为常见的AGV调度规则，然而数据分析表明，随着距离的增加，单元的平均利用率呈现下降的趋势。因此，基于距离的规则优先级较高的单元设备利用率高，如图7所示，具体的利用率数值还与智能车间单元的布局有关。此种考虑单一指标的、用优先级定义搬运任务顺序的规则易导致单元利用率不均衡，不利于设备的使用寿命。

3.3 AGV调度规则的比较

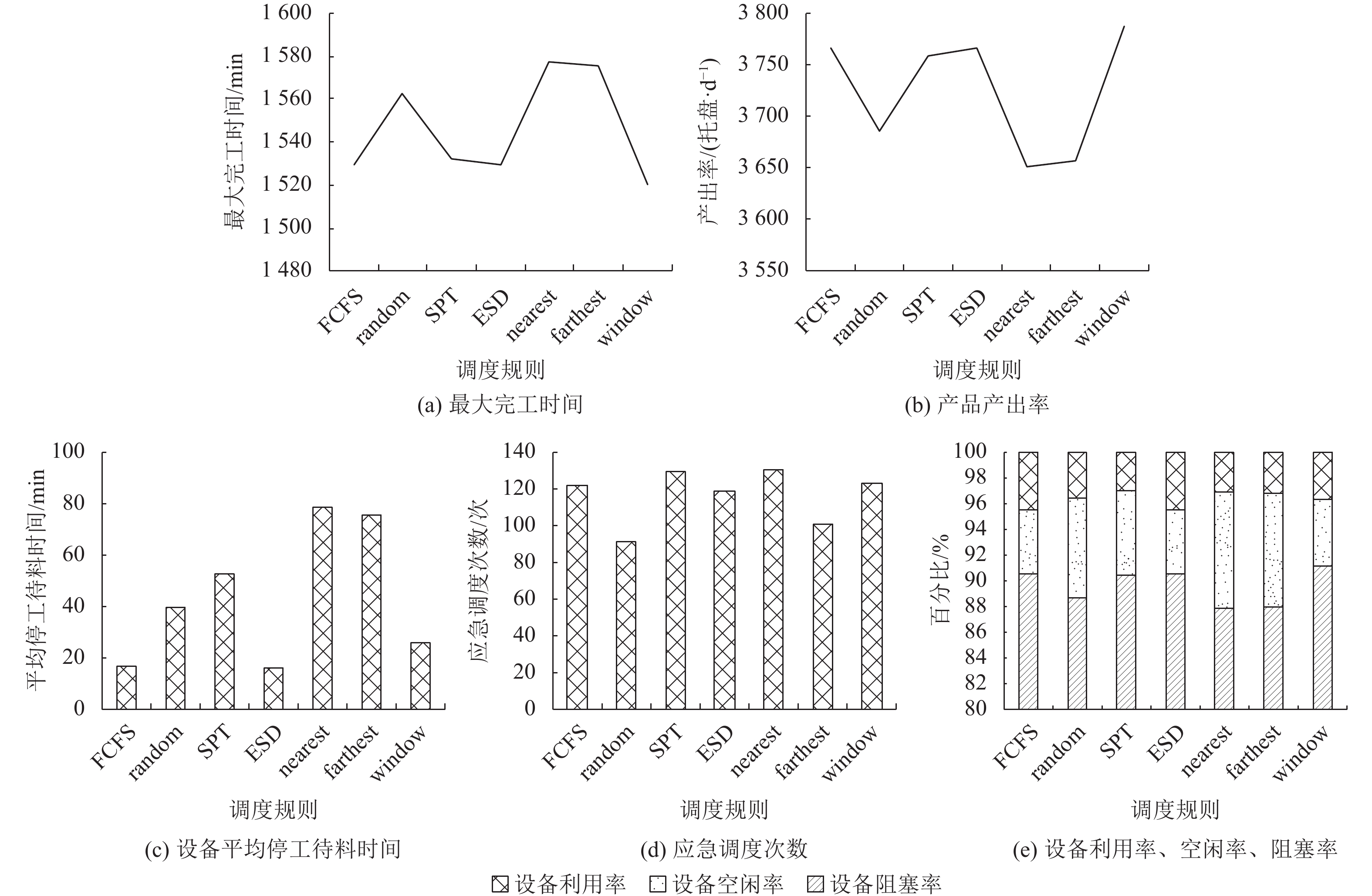
图8为7种调度规则不同性能指标对比分析图。由图可知，Nearest规则和Farthest规则完成订单的最大完工时间最大、产出率最小，且设备平均停工待料时间最长，设备利用率不均衡且利用率低。Random规则较其他规则而言，最大完工时间和产出率的表现较差，由于随机因素的存在，系统稳定性较差。SPT规则的生产效率指标表现良好，但由于SPT规则基于产能这一单一指标，优先服务加工能力强的制造单元，势必造成单元之间的利用率不均衡。

FCFS规则、ESD规则和Window规则的生产效率指标具有较好的表现，体现在最大完工时间小、产出率高、设备因待料而停工的平均时间短、设备利用率高等。其中，ESD规则是在FCFS的基础上对AGV进行调度的，即当有单元停工时，优先服务缺料时间长的单元，其余时间采用先提申请的单元优先服务的策略，可以认为是对FCFS规则的优化。仿真结果表明，ESD规则相比较于FCFS规则，设备平均停工待料时间略低，设备平均利用率略高、应急调度次数略低，但两者的最大完工时间和产出率表现几乎无异，说明优先服务先提申请的单元已经足够保证先停工的单元优先得到运料响应。

备选调度规则集中，基于软时间窗的Window规则综合表现最佳，这是因为此规则是基于多个指标的复合规则，而不是用单一指标去定义搬运任务的优先级，其综合考虑了单元提申请的时间点、单元将停工时间点，以及物料运达时间点。FCFS规则简单易实现、计算复杂度低，且有较优的性能指标表现，而基于软时间窗的Window规则在此种车间配置和调度环境下综合表现最佳。

4 结束语

本文以手机中框及后盖制造企业智能车间为研究背景，对具有有限物流运输能力的智能车间AGV调度算法展开研究。首先，搭建了基于Plant Simulation软件的仿真模型，并给出了模型中的参数设置和仿真模型的运行机制，其中针对AGV调度规则，提出了6种经典的调度规则和一种基于运料软时间窗的Window规则；最后，通过仿真实验对上述7个调度规则进行了分析和比较，得出各种AGV调度方法在不同调度环境下的求解效果。本文的研究成果对3C产品智能车间的运作具有重要的参考意义，同时可为企业配置AGV小车及选择AGV调度规则提供一种有效的方法，保证了车间的生产效率。然而，本文研究的单工序确定性模型，未考虑加工时间、产品合格率等参数的随机性对系统性能的影响。考虑随机因素的多工序智能车间AGV调度方法是进一步研究的方向。