2. 中山大学 管理学院,广东 广州 510275
2. School of Business, Sun Yat-sen University, Guangzhou 510275, China
在当前激烈的市场竞争中,企业越来越关注成本、质量、柔性和服务。准时生产在降低成本和快速反应客户方面具有很强的优势。它的基本思想是零库存、零故障和零缺陷。为实现零缺陷管理,企业必须建立完善的维护机制。条件维护操作不仅可以提高设备的性能,还会对生产批量决策有一定的影响。经典的生产批量模型假设生产过程是完备的,这与企业的实际生产并不相符。因此,研究不完备生产与条件维护策略下的生产批量问题具有很强的理论和实际意义。
条件维护策略是指根据设备可靠性的监测和诊断技术,判断设备异常的检修方式。Grall等[1]考虑了一个基于单组件劣化系统的条件维护模型,求解了模型的最优替换阈值和最优维护策略。Asadzadeh等[2]考虑了一个条件维护优化模型,模型中还考虑了人为因素导致的可靠性问题,提出了2个联合斐波那契算法,并最终求解了模型的最优解,同时还进行了敏感性分析。Chen等[3]建立了一个基于逆高斯退化的条件维护模型,求解了模型的最优检查策略并证明了单调控制极限策略为最优策略,并深入研究了最优替换策略的结构。Cherkaoui等[4]研究了条件维护策略下的鲁棒性,给出了2种不同的维护策略,通过比较研究了影响鲁棒性的关键因素,并给出了相关的建议。Liu等[5]研究了一个劣化系统下的条件维护问题,求解了最优方案和证明了最优维护策略为单调控制极限策略,比较了传统模型和条件维护模型之间的成本差异。Olde Keizer等[6]对多组件下的条件维护进行了综述,并通过实例对该问题进行了分析。范体军等[7]基于企业设备维护流程维度和时间维度,提出了设备维护外包策略。
维护决策不仅与设备有关,还直接影响到生产批量决策,因此,国内外学者越来越关注条件维护策略下的生产批量研究。邵校等[8]研究了多级产品质量体系下劣化设备的生产与维护联合决策。金垚等[9]研究了基于条件维护与生产批量联合决策模型,为了实现单位时间内的期望总成本,通过算法求解了最优维护策略。张博文等[10]研究了系统可靠性的生产与维护计划联合决策。Radhoui等[11]研究了基于备件和条件维护策略的生产批量决策模型,考虑备件对于决策模型的影响,采用基于仿真的优化算法求解了最优生产批量和最优维护阈值,并通过实例对决策过程进行了说明。Chouikhi等[12]研究了过度劣化环境和条件维护下的生产批量模型,利用Nelder-Mead算法求解了期望总成本下的最优解。Do Van等[13]研究劣化系统中基于条件维护的生产批量问题,比较了多种不同的情况,求解了最优维护策略,通过数值算例证明了本模型的可行性。Lee等[14]研究了劣化生产系统中条件维护和生产批量联合优化模型,利用马尔科夫决策过程求解了最优解。Compare等[15]研究了不确定环境下的条件维护问题,采用遗传算法比较了不同方案下的维护优化结果,其中,不确定的适应度用累积分布函数表示,最后采用遗传算法对条件维护策略进行了算例分析。Lu等[16]研究了劣化系统中条件维护和生产批量问题,建立了质量改善下的数学模型,求解了最优维护阈值和最优生产批量,最后通过数值算例证明了模型的有效性。Jafari等[17]研究了条件维护策略下的生产批量问题,构建了一个条件维护下允许缺货和检测的数学模型,其中,通过马尔科夫决策过程来评估设备的隐藏状态。Keizer等[18]研究了多组件的条件维护与生产批量的联合优化问题,考虑了备件在决策模型中的影响,采用马尔科夫决策过程建立了多组件下的联合优化模型。Cheng等[19]研究了多组件系统中条件维护和生产批量联合决策问题,考虑了组件随着使用逐步劣化的因素,建立了基于联合成本最小化的数学模型,求解了最优生产批量和最优维护阈值,最后通过一个实例证明了模型的最优性。
综上所述,虽然国内外已经有一些关于不完备生产下的最优生产批量决策的研究文献,但是这些文献中设备可靠性都不具有退化性。因此,本文在文献研究基础上探讨设备可靠性具有退化情况下的生产批量决策,从理论和实践上都有一定的意义。
1 基本模型 1.1 问题描述与基本假设为了方便模型的建立,给出的符号和假设如下。生产率为P,需求率为D,其中P>D。生产准备成本为s,库存成本为h。设备的可靠性阈值为R*。可靠性函数为r(t),其取值为[0,1]。失效率函数为λ(t)。生产批量为Q。条件维护的成本为Cp,最小维护的固定成本为c,最小维护的增量系数为a。一个周期内的第i次进行条件维护的时刻为
模型的目标是通过不完备生产下的生产批量和条件维护等决策来使得期望平均总成本最小化。总成本包括生产准备成本、库存成本、最小维护成本和条件维护成本。
根据可靠性函数与失效率函数之间的关系
命题1 若每次设备可靠性从初始值达到固定阈值R*所需要的时间为t1, t2, t3,
证明 根据
| $ \qquad{r_1}(t) = {{\rm{e}}^{ - {{\left(\dfrac{t}{{{v_1}}}\right)}^u}}}{\text{。}} $ | (1) |
而在[t1, t1+t2]的条件维护间隙,设备的可靠性函数
| $ \qquad{t_2} = \left( {{v_2}/{v_1}} \right){t_1}{\text{。}} $ | (2) |
以此类推,在[t1+t2+
| $ \qquad{t_m} = \left( {{v_m}/{v_1}} \right){t_1}{\text{。}} $ | (3) |
综上,t1, t2, t3,
命题2 由于设备具有退化性,当设备达到条件维护阈值时,进行条件维护,如图1所示。条件维护的阈值R*与条件维护操作次数m*之间的关系为,当R*增加时,m*也增加,反之亦然。
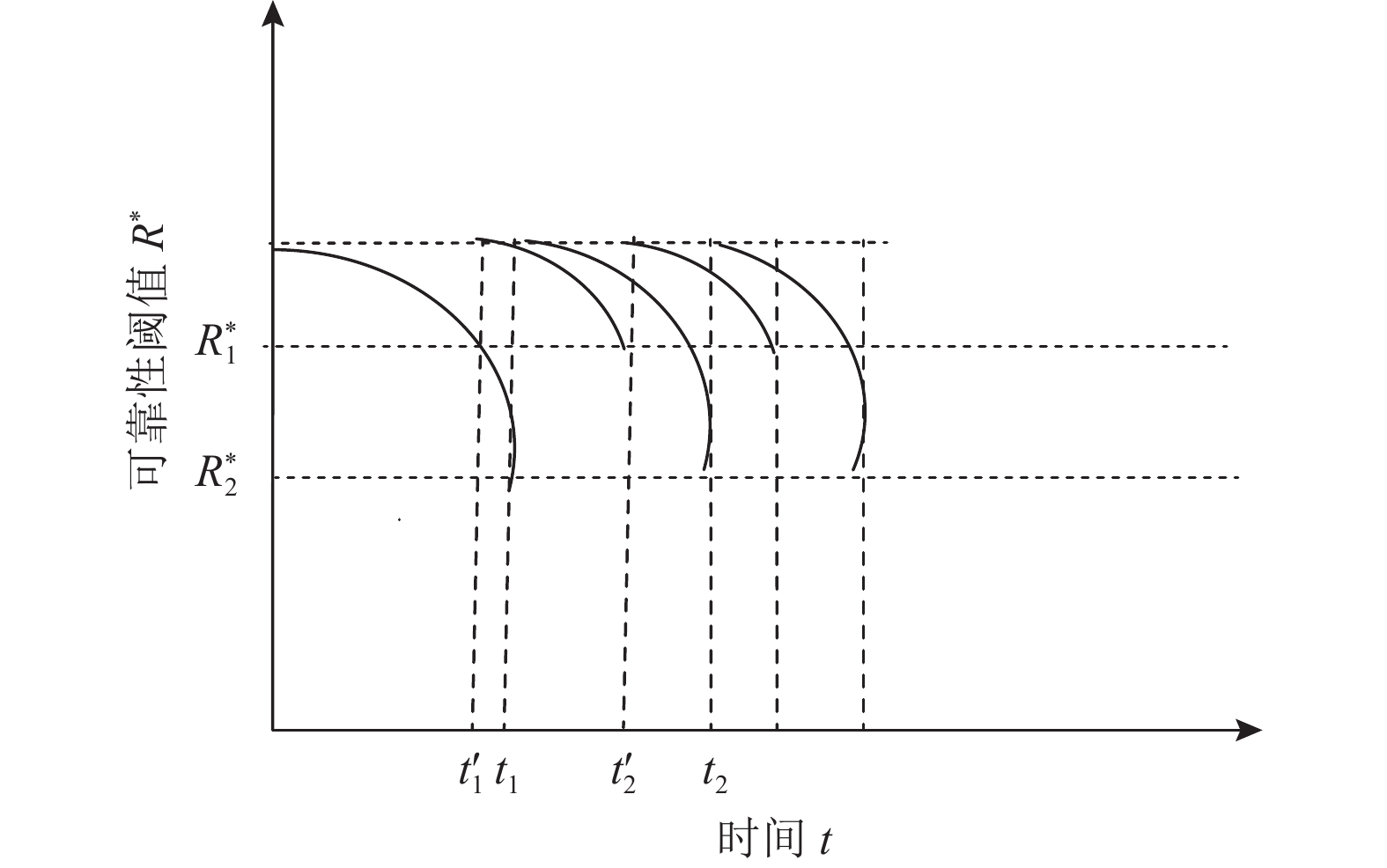
|
图 1 条件维护阈值和维护次数对应图 Fig. 1 Graph between conditional maintenance threshold and maintenance times |
证明 如图1所示,当条件维护阈值为
根据命题1可知,当条件维护阈值为
若Tm=Tn,则当
针对在2次条件维护之间出现的设备故障,将采取最小维护操作进行处理。关于最小维护操作成本,得到命题3。
命题3 在相邻2次条件维护之间采取最小维护操作,若最小维护操作是按照递增法则计算,则一个生产周期内最小维护操作的总成本为
证明 令
| $ \qquad{\mathit{\Lambda} } ({t_i}) = \int_0^{{t_i}} {\lambda (s){\rm{d}}s}{\text{。}} $ | (4) |
其中,
命题4 一个生产周期内,采取条件维护操作,同时在2次条件维护之间采取最小维护操作,最小维护操作按照递增法则计算,则一个生产周期内最小维护操作的总成本为
| $ \qquad{\mathit{\Lambda} } ({t_1})mc +\dfrac{{{\mathit{\Lambda} } ({t_1})(1 +{\mathit{\Lambda} } ({t_1}))}}{2}ma{\text{。}}{\text{其中}}{\text{,}}c {\text{>}} 0,a {\text{≥}} 0{\text{。}} $ |
证明 由于
| $ \begin{split} &\qquad \sum\limits_{i = 1}^m {\sum\limits_{k = 1}^{{\mathit{\Lambda} } ({t_i})} {{c_k}} } =m\sum\limits_{k = 1}^{{\mathit{\Lambda} } ({t_1})} {{c_k}} =m\sum\limits_{k = 1}^{{\mathit{\Lambda} } ({t_1})} (c +ka) ={\mathit{\Lambda} } ({t_1})mc +\\ & \frac{{{\mathit{\Lambda} } ({t_1})(1 +{\mathit{\Lambda} } ({t_1}))}}{2}ma{\text{。}} \end{split} $ |
综上,在相邻2次条件维护间隙内采取最小维护操作,每一次条件维护操作间隙ti内设备发生故障的平均时间比上一次条件维护操作间隙ti−1内设备发生故障的平均时间要短。证毕。
在一个生产周期内发生的其他各项成本:生产准备成本为s,库存成本为
| $ \qquad{\rm{ETC}} = \frac{{Ph}}{2}\left(\frac{P}{D} - 1\right){\left(\sum\limits_{i = 1}^m {{t_i}}\right)^2}{\rm{ +}}m{C_{\rm p}}{\rm{ +}}s{\rm{ +}}\sum\limits_{i = 1}^m {\sum\limits_{k = 1}^{{\mathit{\Lambda} } ({t_i})} {{c_k}} } {\text{。}} $ | (5) |
根据更新报酬理论[21],期望平均总成本为
| $ \begin{split} &\qquad{\rm{EAC}} = \mathop {\lim }\limits_{t \to \infty } \dfrac{{{\rm{ETC}}(t)}}{t} = \dfrac{{{\rm{ETC}}(m,{t_i})}}{T} =\\ &\dfrac{{\dfrac{{Ph}}{2}\left(\dfrac{P}{D} - 1\right){{\left(\displaystyle\sum\limits_{i = 1}^m {{t_i}}\right)}^2}{\rm{ +}}m{C_{\rm{p}}}{\rm{ +}}s{\rm{ +}}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{k = 1}^{{\mathit{\Lambda} } ({t_i})} {{c_k}} } }}{{\dfrac{P}{D}\displaystyle\sum\limits_{i = 1}^m {{t_i}} }}{\text{。}} \end{split} $ | (6) |
把命题1中ti=(vi/v1) t1代入式(6),整理,可得期望平均总成本为
| $ \begin{split} &\qquad{\rm{EAC}} = \\ &\dfrac{{\dfrac{{Ph}}{2}\left(\dfrac{P}{D} - 1\right){{\left[ {\displaystyle\sum\limits_{i = 1}^m {{v_i}} {{(\! -\! \ln {R^*})}^{\dfrac{1}{u}}}} \right]}^2}{\rm{ +}}m{C_{\rm{p}}}{\rm{ +}}s{\rm{\! +\!}}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{k = 1}^{\int_0^{{t_i}} {\lambda (s){\rm{d}}s} } {(c \!+\!ka} })}}{{\dfrac{P}{D}\displaystyle\sum\limits_{i = 1}^m {{v_i}} {{( \!-\! \ln {R^*})}^{\dfrac{1}{u}}}}}{\text{。}} \end{split} $ | (7) |
当v为等比数列时,式(7)可变为式(8)。这里,假设vi+1/vi=q,其中,0<q<1, i=1, 2,
| $ \qquad\qquad{\rm{EAC}} =\dfrac{{\dfrac{{Ph}}{2}\left(\dfrac{P}{D} - 1\right){{\left[ {\dfrac{{(1 - {q^m})}}{{1 - q}}{v_1}{{( - \ln {R^*})}^{\dfrac{1}{u}}}} \right]}^2}{\rm{ +}}m{C_{\rm{p}}}{\rm{ +}}s{\rm{ +}}{\mathit{\Lambda} } ({t_1})mc +\dfrac{{{\mathit{\Lambda} } ({t_1})(1 +{\mathit{\Lambda} } ({t_1}))}}{2}ma}}{{\dfrac{{P{v_1}}}{D}\dfrac{{(1 - {q^m})}}{{1 - q}}{{( - \ln {R^*})}^{\dfrac{1}{u}}}}}{\text{。}} $ | (8) |
此时最优生产批量为
| $ \qquad{Q^*} = P{v_1}\frac{{(1 - {q^m})}}{{1 - q}}{( - \ln {R^*})^{\frac{1}{u}}} $ | (9) |
当v为等差数列时,式(7)可变为式(10)。这里,假设vi+1-vi=d,其中,d<0,i=1, 2,
| $ \qquad\qquad{\rm{EAC}} =\dfrac{{\dfrac{{Ph}}{2}\left(\dfrac{P}{D} - 1\right){{\left\{ {\left[ {\dfrac{{md(m - 1)}}{2} +m{v_1}} \right]{{( - \ln {R^*})}^{\dfrac{1}{u}}}} \right\}}^2}{\rm{ +}}m{C_{\rm p}}{\rm{ +}}s{\rm{ +}}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{k = 1}^{\int_0^{{t_i}} {\lambda (s){\rm{d}}s} } {(c +ka} })}}{{\dfrac{P}{D}\left[ {\dfrac{{md(m - 1)}}{2} +m{v_1}} \right]{{( - \ln {R^*})}^{\dfrac{1}{u}}}}}{\text{。}} $ | (10) |
此时,最优生产批量为
| $ \qquad{Q^{\rm{*}}}=P\left[ {\frac{{md(m - 1)}}{2} +m{v_1}} \right]{( - \ln {R^*})^{\dfrac{1}{u}}}{\text{。}} $ | (11) |
由于该模型比较复杂,不能求得解析解。为求解模型的最优解,构造如下的求解步骤。
步骤1 令EAC**表示内循环最优解,EAC*表示模型的最优解,并把它们的初始值都赋值为一个较大的数,把设备的可靠性阈值R的初始值赋值为0.01,m**的初始值赋值为1;
步骤2 当R≤1时,进入下一步,否则,退出外循环,转到步骤11;
步骤3 利用式(6)或式(8)求出当m= 1时的期望平均总成本EAC**=EAC(R, 1);
步骤4 令条件维护次数m=2;
步骤5 当m≤10 000时,进入下一步,否则,转到步骤9;
步骤6 利用式(6)或式(8)求出当条件维护次数为m时的期望平均总成本EAC(R,m);
步骤7 比较EAC(R, m)和EAC**的值,当EAC(R, m)<EAC**时,令EAC**= EAC(R, m),同时m**=m, R**=R,否则跳出内循环,转到步骤9;
步骤8 令m=m+1,转到步骤5;
步骤9 比较EAC*和EAC**的值,当EAC*>EAC**时,令EAC*= EAC**,同时R*= R**,m*= m**;
步骤10 令
步骤11 当执行完以上步骤后,此时,条件维护次数的最优解为m*,可靠性阈值的最优解为R*,对应的期望平均最小总成本为EAC*。
算法的流程如图2所示。
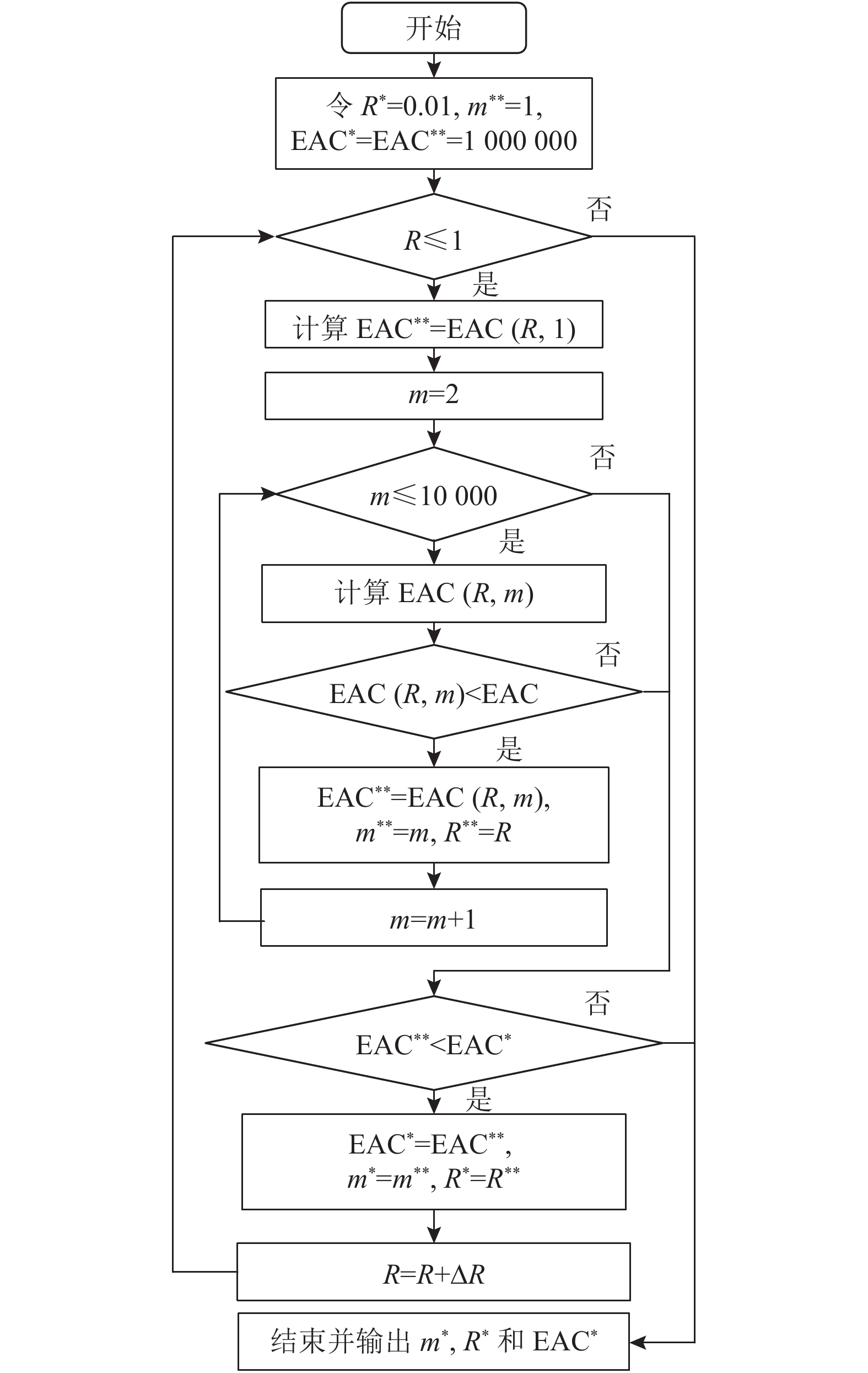
|
图 2 算法流程图 Fig. 2 Flow chart of algorithm |
为了检验上文所构造的模型,本节将通过以下具体的数值算例来对上面的求解过程作出说明。本模型参数的数据如下。P=300个/h,D=100个/h,s=$100/次,h=$1/h,Cp =$5/次,c=$50,a=$10,u1=2,v1=0.7,q=0.9,d=−0.1。
3.1 最优解求解算例1 v为等比数列
通过上一节中提供的求解步骤进行计算,模型求解的相关结果如图3所示。
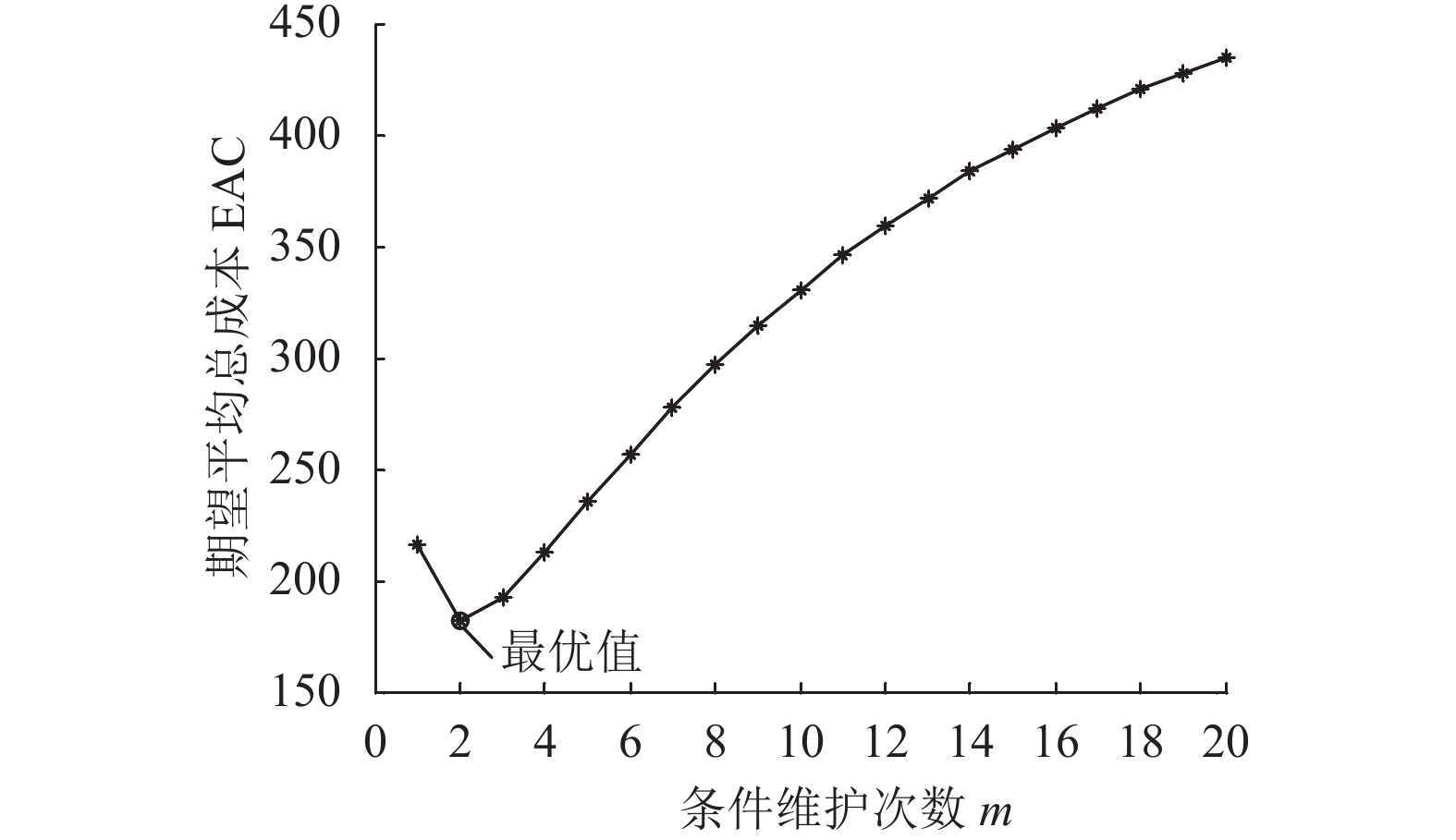
|
图 3 算例1中EAC和m的关系图 Fig. 3 Correlation between EAC and m in case 1 |
从图3可以看出,当条件维护阈值为R*时,EAC关于m先单调递减再单调递增。模型的最优解为m*=2,R*=0.91,Q*=121.02,
设备不具有退化性条件下期望平均总成本模型可简化为
| $ \qquad\qquad{\rm{EAC}} =\dfrac{{\dfrac{{Ph}}{2}\left(\dfrac{P}{D} - 1\right){{\left[ {m{v_1}{{( - \ln {R^*})}^{\dfrac{1}{u}}}} \right]}^2}{\rm{ +}}m{C_{\rm{p}}}{\rm{ +}}s{\rm{ +}}{\mathit{\Lambda} } ({t_1})mc +\dfrac{{{\mathit{\Lambda} } ({t_1})(1 +{\mathit{\Lambda} } ({t_1}))}}{2}ma}}{{\dfrac{{Pm{v_1}}}{D}{{( - \ln {R^*})}^{\dfrac{1}{u}}}}}{\text{。}} $ | (12) |
金垚等[9]的模型只是本模型的一种特殊情形。根据表1,可知当其他参数均相同的情况下,EAC*高于设备不具有退化性的EAC*。前者的R*、Q*和m*比后者的都要少。
| 表 1 等比数列时具有退化性的设备与非退化性的设备的对比 Tab. 1 Comparison of deterioration with geometric progression and no-deterioration equipment |
算例2 v为等差数列
同样通过上一节中提供的求解步骤计算模型的相关结果,如图4所示。从图4可以看出,当条件维护阈值为R*时,EAC关于m先单调递减再单调递增。通过上节给出的算法,求解了最优生产批量。其中m*
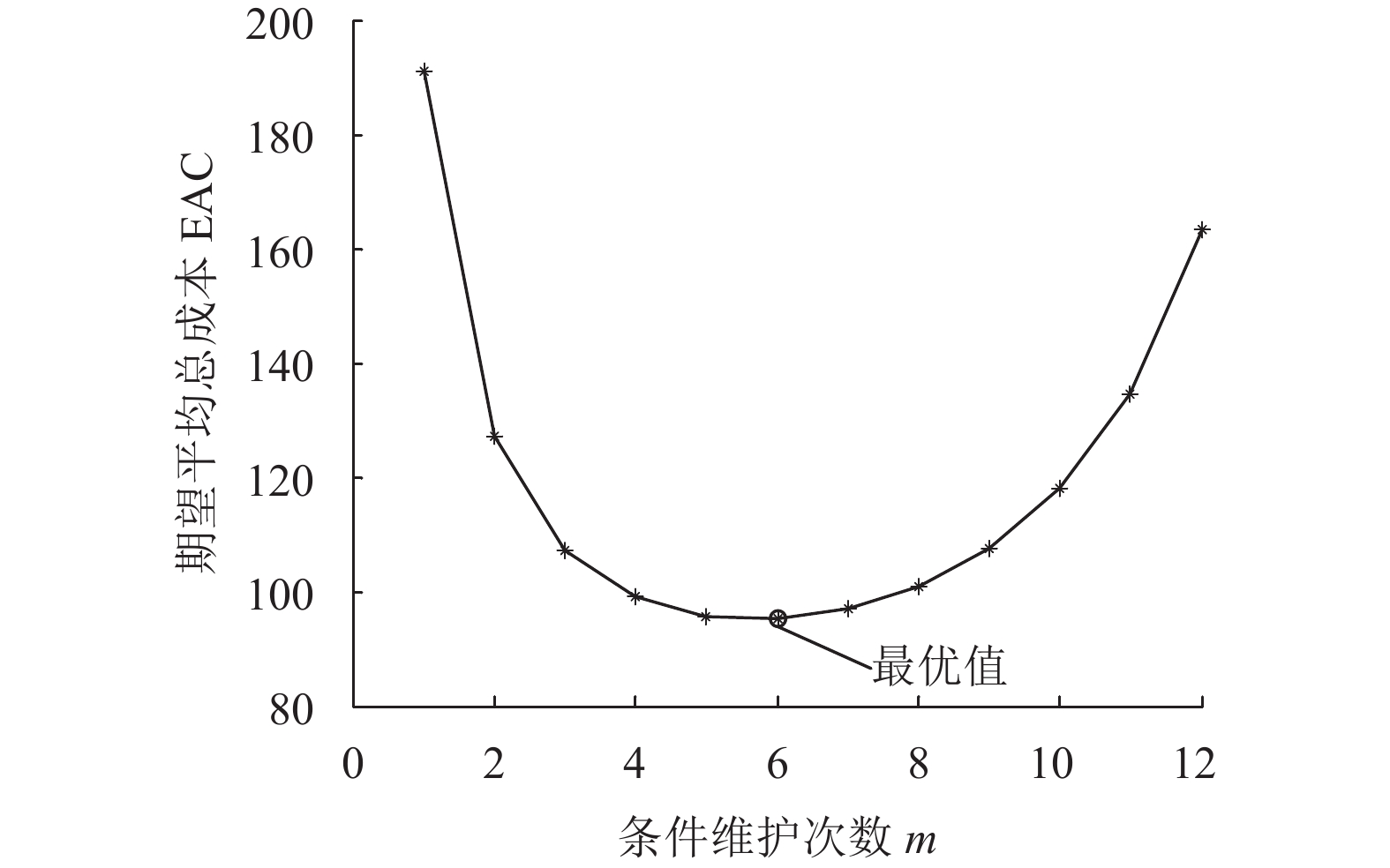
|
图 4 算例2中EAC和m的关系图 Fig. 4 Correlation between EAC and m in case 2 |
根据表2,通过对比具有退化性的设备与非退化性的设备在相同参数情况下的数据得到以下结论。EAC*总体要低于设备不具有退化性的EAC*。前者的条件维护的阈值比后者的少,而前者的m*和Q*均比后者的多。在这里,设备不具有退化性条件下模型依然采用式(12)的模型。
| 表 2 等差数列时具有退化性的设备与非退化性的设备的对比 Tab. 2 Comparison of deterioration with arithmetic progression and no-deterioration equipment |
算例1 v为等比数列
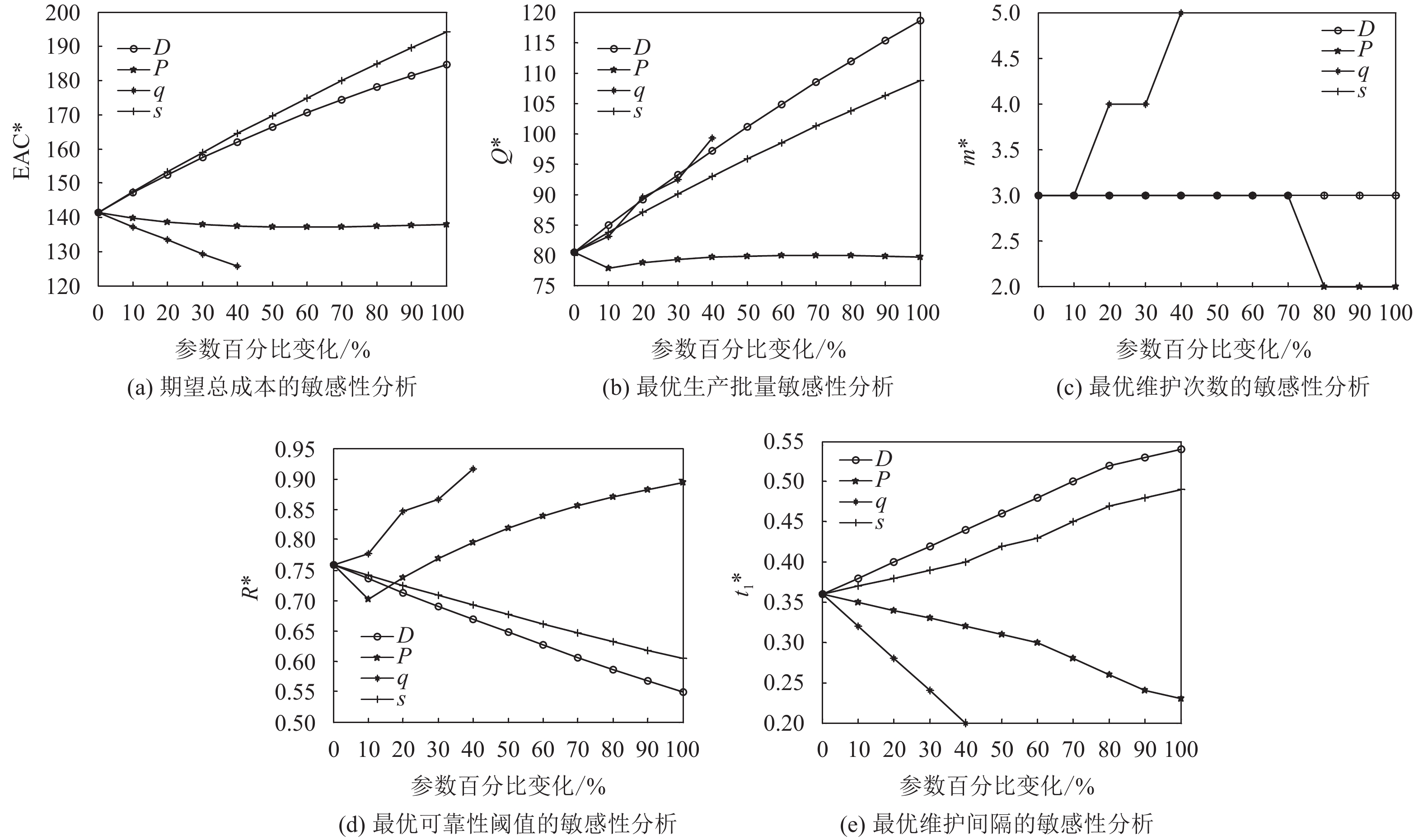
对D、P、q和s这4个重要的参数进行了敏感性分析。每个参数均以10%的速度增长。它们对EAC*、Q*、m*、R*和
|
图 5 算例1中各参数敏感性分析
Fig. 5 Sensitivity analyses of EAC*, Q*, m*, R* and
|
1) 随着D的增加,EAC*从141.46增加至184.76(图5a),Q*从80.48增加至118.65(图5b),m*基本稳定(图5c),R*从0.75减少至0.54(图5d),
2) 随着P的增加,EAC*从141.46减少至137.82(图5a),Q*从80.48减少至79.70(图5b),m*从3减少至2(图5c),R*从0.75增加至0.89(图5d),
3) 随着q的增加,EAC*从141.46减少至125.77(图5a),Q*从80.48增加至99.23(图5b),m*从3增加至5(图5c),R*从0.75增加至0.91(图5d),
4) 随着s的增加,EAC*从141.46增加至194.25(图5a),Q*从80.48增加至108.72图5(b),m*保持稳定(图5c),R*从0.75降低至0.60(图5d),
EAC*对P不太敏感,对D和s敏感,而对q非常敏感。总体而言,EAC*随着D和s的增加而增加,而随着P和q的增加而减少(图5a)。基于此,关注公比系数的变化有利于提高管理者对设备劣化水平的管控能力。Q*对P不敏感,对s敏感,对D和q非常敏感。总体而言,Q*随着D,q和s的增加而增加,而随着P的增加而减少(图5b)。因此D和q是影响Q*的最重要因素。m*对P 和q敏感,对D和s敏感。总体而言,m*随着P增加而减少,随着q的增加而增加(图5c)。因此,公比是影响最优维护次数最重要的因素,特别关注公比的变化是控制好最优维护次数的有效手段之一。R*对于P,q和s敏感,对于D非常敏感。总体而言,R*随着s和D增加而减少,随着P和q的增加而增加(图5d)。因此,关注需求的变化是控制可靠性阈值的一种有效手段。
算例2 v为等差数列
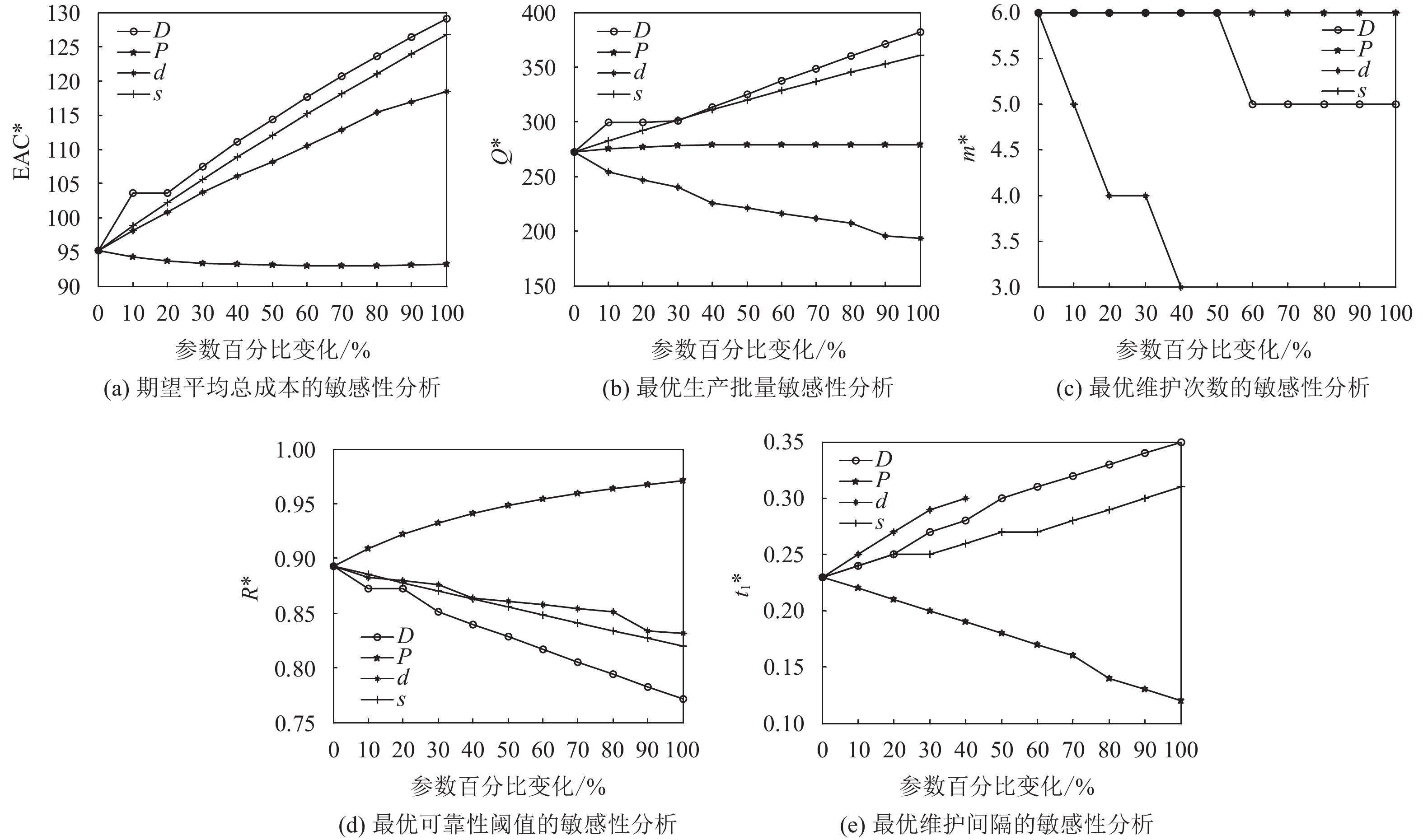
当v为等差数列时,本文对D、P、d和s这4个重要的参数进行了敏感性分析。这4个重要参数对EAC*、Q*、m*、R*和
|
图 6 算例2中期望平均总成本的敏感性分析
Fig. 6 Sensitivity analyses of EAC*, Q*, m*, R* and
|
1) 随着D的增加,EAC*从95.19增加至129.14(图6a),Q*从272.35增加至381.99(图6b),m*从6减少至5(图6c),R*从0.89减少至0.77(图6d),
2) 随着P的增加,EAC*从95.19减少至93.16(图6a),Q*从272.35增加至278.87(图6b),m*保持稳定(图6c),R*从0.89增加至0.97(图6d),
3) 随着d的增加,EAC*从95.19增加至118.46(图6a),Q*从272.35降低至193.30(图6b),m*从6降低至3(图6c),R*从0.89降低至0.83(图6d),
4) 随着s的增加,EAC*从95.19增加至126.76(图6a),Q*从272.35增加至361.05(图6b),m*保持稳定(图6c),R*从0.89降低至0.81(图6d),
EAC*对P不太敏感,对d和s敏感,而对D非常敏感。总体而言,EAC*随着D,d和s增加而增加,随着P的增加而减少(图6a)。基于此,决策者应特别关注需求的变化,提高对市场需求的预测水平。Q*对P不敏感,对D和s敏感,而对d非常敏感。总体而言,Q*随着D和s的增加而增加,而随着d的增加而减少(图6b)。因此,d是影响Q*的最重要因素,控制好公差系数将会有助于企业的生产运作。m*对D和d敏感,对P和s不敏感。总体而言,m*随着D和d增加而减少(图6c)。因此,公差是影响最优维护次数最重要因素,特别关注公差的变化是控制好最优维护次数的有效手段之一。R*对P,d和s敏感,对D非常敏感。总体而言,R*随着d,s和D增加而减少,随着P的增加而增加(图6d)。因此,需求是影响条件维护的可靠性阈值最重要的因素,特别关注需求的变化是管理好可靠性阈值的有效手段之一。
本文考虑了一个设备退化和条件维护策略下的生产批量决策模型。考虑等比和等差2种模型,并求解了生产批量的最优决策。当v为等比数列时,EAC*对P不太敏感,对D和s敏感,对q非常敏感。决策者应特别关注公比系数的变化,提高对设备劣化水平的管控能力。当v为等差数列时,Q*对P不敏感,而对d非常敏感。决策者控制好公差系数将会有助于企业的生产运作。需求是影响条件维护可靠性阈值最重要的因素。特别关注需求的变化是管理好可靠性阈值的有效手段之一。公比和公差是影响最优维护次数和最优维护间隔的最重要因素。因此,关注公比和公差的变化是控制好最优维护间隔和最优维护次数的有效手段之一。
本文下一步研究工作可以考虑需求不确定情况下的设备可靠性退化对于生产批量决策的影响,还可以拓展为多级供应链的情况,研究具有设备退化的制造商对上下游决策的影响。
| [1] |
GRALL A, BÉRENGUER C, DIEULLE L. A condition-based maintenance policy for stochastically deteriorating systems[J].
Reliability Engineering & System Safety, 2002, 76(2): 167-180.
|
| [2] |
ASADZADEH S M, AZADEH A. An integrated systemic model for optimization of condition-based maintenance with human error[J].
Reliability Engineering & System Safety, 2014, 124: 117-131.
|
| [3] |
CHEN N, YE Z S, XIANG Y, et al. Condition-based maintenance using the inverse Gaussian degradation model[J].
European Journal of Operational Research, 2015, 243(1): 190-199.
DOI: 10.1016/j.ejor.2014.11.029. |
| [4] |
CHERKAOUI H, HUYNH K T, GRALL A. On the assessment of performance and robustness of condition-based maintenance strategies[J].
IFAC-Papers Online, 2016, 49(12): 809-814.
DOI: 10.1016/j.ifacol.2016.07.874. |
| [5] |
LIU B, WU S M, XIE M, et al. A condition-based maintenance policy for degrading systems with age- and state-dependent operating cost[J].
European Journal of Operational Research, 2017, 263(3): 879-887.
DOI: 10.1016/j.ejor.2017.05.006. |
| [6] |
OLDE KEIZER M C A, FLAPPER S D P, TEUNTER R H. Condition-based maintenance policies for systems with multiple dependent components: a review[J].
European Journal of Operational Research, 2017, 261(2): 405-420.
DOI: 10.1016/j.ejor.2017.02.044. |
| [7] |
范体军, 陈荣秋, 崔南方. 设备维护外包策略分析[J].
中国管理科学, 2003, 11(4): 47-53.
FAN Tijun, CHEN Rongqiu, CUI Nanfang. Strategic analysis of equipment maintenance outsourcing[J]. Chinese Journal of Management Science, 2003, 11(4): 47-53. DOI: 10.3321/j.issn:1003-207X.2003.04.010. |
| [8] |
邵校, 陈志祥. 多级产品质量体系下劣化设备的生产与维护联合决策[J].
管理学报, 2017, 14(12): 1862-1869.
SHAO Xiao, CHEN Zhixiang. Joint decision of production and maintenance for deteriorating equipment under multi-grade product quality system[J]. Chinese Journal of Management, 2017, 14(12): 1862-1869. DOI: 10.3969/j.issn.1672-884x.2017.12.015. |
| [9] |
金垚, 王莹, 潘尔顺. 基于可靠度限制的PM与EPQ整合模型[J].
工业工程与管理, 2010, 15(5): 66-69.
JIN Yao, WANG Ying, PAN Ershun. Research on integrated model of economic production quantity and preventive maintenance strategy based on system reliability[J]. Industrial Engineering and Management, 2010, 15(5): 66-69. DOI: 10.3969/j.issn.1007-5429.2010.05.013. |
| [10] |
张博文, 陆志强, 张岳君. 基于系统可靠性的生产与维护计划联合决策[J].
计算机集成制造系统, 2015, 21(8): 2079-2088.
ZHANG Bowen, LU Zhiqiang, ZHANG Yuejun. Joint model of production and maintenance planning based on system reliability[J]. Computer Integrated Manufacturing Systems, 2015, 21(8): 2079-2088. |
| [11] |
RADHOUI M, REZG N, CHELBI A. Integrated model of preventive maintenance, quality control and buffer sizing for unreliable and imperfect production systems[J].
International Journal of Production Research, 2009, 47(2): 389-402.
DOI: 10.1080/00207540802426201. |
| [12] |
CHOUIKHI H, KHATAB A, REZG N. A condition-based maintenance policy for a production system under excessive environment degradation[J].
IFAC Proceedings Volumes, 2012, 45(6): 956-962.
DOI: 10.3182/20120523-3-RO-2023.00112. |
| [13] |
DO VAN P, BÉRENGUER C. Condition-based maintenance with imperfect preventive repairs for a deteriorating production system[J].
Quality and Reliability Engineering International, 2012, 28(6): 624-633.
DOI: 10.1002/qre.v28.6. |
| [14] |
LEE S, NI J. Joint decision making for maintenance and production scheduling of production systems[J].
International Journal of Advanced Manufacturing Technology, 2013, 66(5-8): 1135-1146.
DOI: 10.1007/s00170-012-4395-6. |
| [15] |
COMPARE M, MARTINI F, ZIO E. Genetic algorithms for condition-based maintenance optimization under uncertainty[J].
European Journal of Operational Research, 2015, 244(2): 611-623.
DOI: 10.1016/j.ejor.2015.01.057. |
| [16] |
LU B, ZHOU X, LI Y. Joint modeling of preventive maintenance and quality improvement for deteriorating single-machine manufacturing systems[J].
Computers & Industrial Engineering, 2016, 91(1): 188-196.
|
| [17] |
JAFARI L, MAKIS V. Optimal lot-sizing and maintenance policy for a partially observable production system[J].
Computers & Industrial Engineering, 2016, 93(3): 88-98.
|
| [18] |
OLDE KEIZER M C A, TEUNTER R H, VELDMAN J. Joint condition-based maintenance and inventory optimization for systems with multiple components[J].
European Journal of Operational Research, 2017, 257(1): 209-222.
DOI: 10.1016/j.ejor.2016.07.047. |
| [19] |
CHENG G Q, ZHOU B H, LI L. Joint optimization of lot sizing and condition-based maintenance for multi-component production systems[J].
Computers & Industrial Engineering, 2017, 110: 538-549.
|
| [20] |
BOLAND P J, PROSCHAN F. Optimum replacement of a system subjected to shocks[J].
Operations Research, 1983, 31(4): 697-704.
DOI: 10.1287/opre.31.4.697. |
| [21] |
ROSS S M. Introduction to probability models [M]. 5th Edition. New York: Academic Press, 1993.
|
 2019, Vol. 22
2019, Vol. 22