快递配送作为物流配送的重要分支,与传统的物流配送概念略有区别:传统物流配送包括“配货”与“送货”2个主要阶段,快递配送进行商品分散销售,所以在“配货”阶段,减少了拣选、加工、包装、组配等环节;而且快递配送更加侧重于“送货”阶段,在“送货”阶段重点提供由寄件方到收件方的门对门的商品配送运输服务。根据国家标准相关规定,快递配送系统的含义为:“快递配送企业从寄件方准确无误地收集货物及相关信息,通过各种交通工具,将商品准时完好无损地送达收件方,并取得满意评价的过程”[1]。随着互联网经济的快速发展,网购逐渐成为大众消费的首要选择,而作为连接电商与消费者之间的重要渠道——快递行业,也日益受到政府与消费者的关注。但由于我国快递行业起步较晚,快递企业普遍存在现代化程度不高,专业人员培训不足等问题,导致快递配送行业饱受消费者投诉。根据2017年09月份国家邮政局公布的关于邮政业消费者投诉数据显示:快递服务问题171 882件,占总体投诉数量的95.5%,其中配送不可靠导致的快递投诉、寄件延误、寄件丢失、寄件毁坏排名前4,分别达到41.6%、27.4%、17.5%、9.6%[2]。在可预见的未来,随着网购规模的增长,配送服务需求将越来越大,而快递配送系统的可靠性,直接影响快递配送服务质量。所以对快递配送系统的影响因素和作用机制进行分析,寻找有效的方法对影响因素进行评估并提出切实有效的措施已成为快递配送可靠性管理领域亟待解决的难题。
目前,国内外学者关于快递配送的研究主要集中于配送路径[3]、配送选址[4-5]等方向,涉及快递配送可靠性的研究较少。国外学者Munoz-Villamizar等[6]从运输网络可靠性角度,对交通运输进行研究,提出车辆协作战略,以降低供应过程的总成本,提高城市物流系统的效率和可靠性。而Kutanoglu等[7]从第三方物流运营商的角度,详细分析配送过程中各个环节(接收、中转、运输)对配送系统可靠性的影响。许振宇等[8]研究了不确定条件下应急供应链的可靠性问题,主要从保障机制、信息系统、网络结构、运作流程等5个方面构建可靠性评价模型。在网络结构上,供应链系统与配送系统具有一定相似性,但他们对快递配送可靠性的研究大多只关注于单个可靠性指标,未考虑整个系统的可靠性。在研究方法方面,已有部分国内学者开始将GO法与供应链系统进行结合,如张根保等[9]将GO法引入到供应链的可靠性诊断中,通过对供应链重要因素进行详细分析,以三级供应链为研究对象,构建供应链可靠性诊断的GO模型。蔡鉴明等[10]则运用GO法对供应链系统进行建模,将供应链系统转化为GO图,通过GO运算,求解供应链中消费点的等效可靠度。胡思涛等[11]将GO法运用于生鲜农产品供应链的可靠性评价中,提出可靠度评价等级划分标准,识别供应链中的薄弱环节。但他们都是在各个单元互相独立的假设前提下,采用GO法中的概率公式进行定量分析,而现实中的快递配送系统单元之间具有复杂相关性,如果继续使用GO法概率公式进行运算,会出现计算过程复杂繁琐且容易出错等缺点。因此有必要采用新的推理方法,来简化GO法的运算过程。
贝叶斯网络(Bayesian network,BN)是目前不确定知识表达和推理领域最有效的理论模型,具有良好的分析推理能力。刘林林等[12]2015年首次提出贝叶斯-GO综合算法,该算法利用了贝叶斯网络的推理能力,简化了GO法的运算过程,同时又具有GO法易于建模和模拟多状态的优点。由于贝叶斯-GO算法提出时间较短,现有的相关研究还比较少,主要集中于电力输送系统、油气管道运输系统的可靠性分析。例如,田录林等[13]将改进贝叶斯-GO法运用于高压直流输电系统可靠性评估中,提高了可靠性计算的精度和速度;陈洁等[14]使用贝叶斯-GO法对油气管道运输环节中深水关井的可靠性分析,运用贝叶斯网络的向前向后推理特性,得到工作流程中的薄弱环节及其不同工况下的成功概率。已有的研究结果表明贝叶斯-GO算法可以通过多次贝叶斯网络推理直接计算等效单元可靠性特征量,不需要考虑复杂的共有信号问题,还可利用贝叶斯网络寻找系统中可靠性薄弱环节,降低了复杂系统可靠性分析的计算复杂度。本文提出将贝叶斯-GO法引入快递配送系统可靠性评估当中,解决了传统GO法在快递配送系统可靠性研究中的运算复杂繁琐的问题,综合考虑了快递配送系统对时间、品质、服务可靠性的要求,建立快递配送系统故障与影响因素指标,同时在时间可靠性指标中引入提前状态,与以往研究中二态进行对比分析。最后通过实际案例,验证了贝叶斯-GO法对快递配送系统可靠性评估、故障推理和影响因素敏感度分析上的高效准确性,相比于GO法更加适合工程人员实际操作运用。
1 贝叶斯-GO综合方法与故障树等传统风险分析方法相比,贝叶斯-GO法可较为简捷地解决对多状态、多时序复杂系统可靠性评估问题。整个贝叶斯-GO法分析过程,包括系统分析、建立GO图、模型映射和贝叶斯推理计算等步骤,文献[15]给出了建立GO图的详细步骤,本文不做赘述,具体分析步骤,如图1所示。

|
图 1 Bayesian-GO法分析流程图 Fig. 1 Bayesian-GO analysis flow chart |
贝叶斯网络是一种基于概率推理的图形化因果关系网络,已广泛应用于复杂电力、机械、管道设备的故障分析和可靠性评估中。它由2部分构成:有向无环图(directed acyclic graph,DAG)和节点条件概率表(conditional probability table,CPT)。根据有向图的条件独立性假设,所有变量节点的联合概率分布可以表示为
| $ \qquad P\left( {{V_1},{V_2}, \cdots ,{V_n}} \right){\rm{ = }}\prod\limits_{{{i = 1}}}^n {{ P}\left( {{V_i}{\rm{|}}{\rm P}{\rm{arent}}\left( {{{{V}}_i}} \right)} \right)} {\text{。}} $ | (1) |
其中,Parent(Vi)表示Vi的父节点集合。贝叶斯网络的节点计算基于父节点的状态概率和节点本身的CPT进行。当知道其中部分节点的变量状态,就能通过推理算法得出其相关的节点状态概率。在贝叶斯-GO法中,对GO模型映射得到的贝叶斯网络进行故障诊断时,首先对模型中的特定节点进行故障注入,即将特定节点故障状态作为证据注入,然后使用贝叶斯反向推理算法分别计算各个节点的后验概率分布,其计算公式为
| $ \qquad P({O_i}|{F_j}) = \frac{{P({O_i})P({F_j}|{O_i})}}{{\displaystyle\sum\limits_{i \in ||O||} {P({O_i})P({F_j}|{O_i})} }}{\text{。}} $ | (2) |
式中,Oi为观察节点i的状态,Fj为故障节点j的状态,||O||为观察节点的数量。
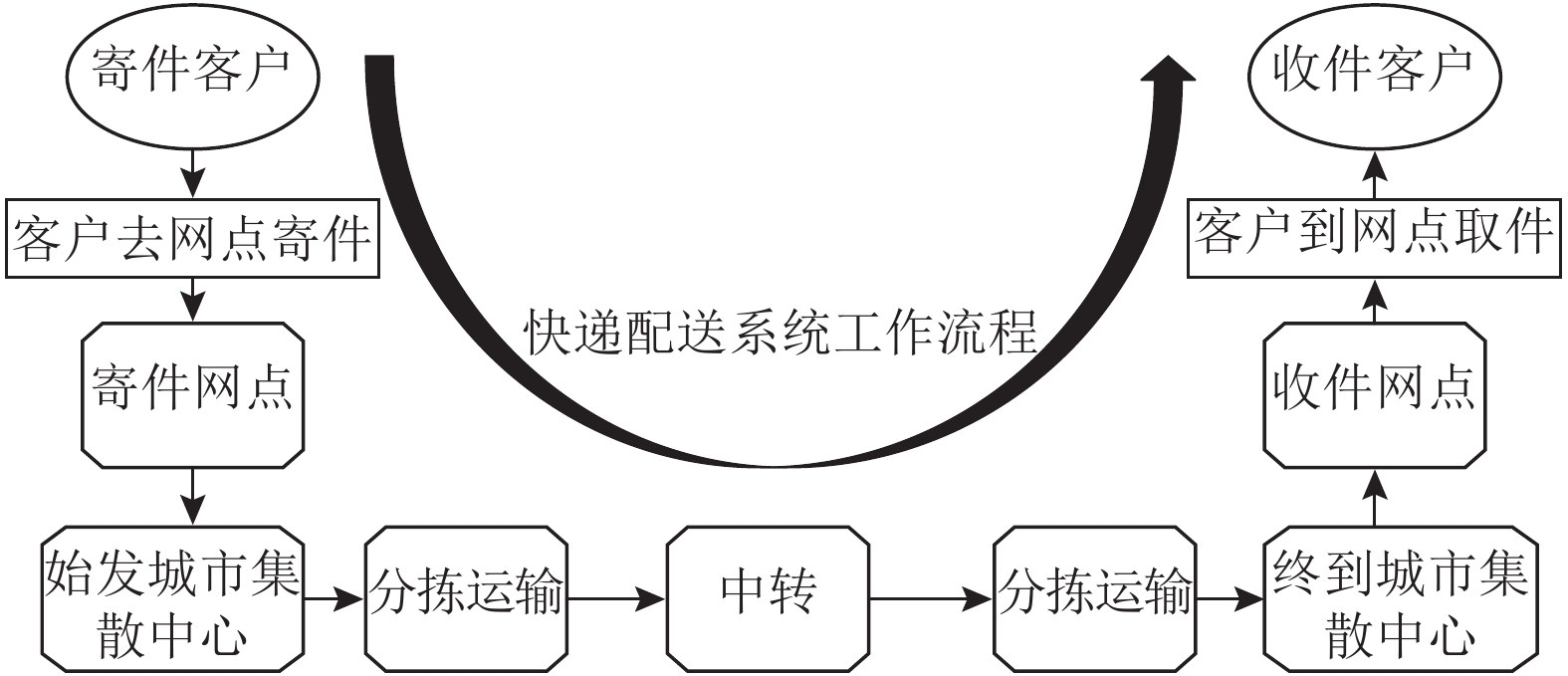
2 贝叶斯-GO法的快递配送系统可靠性分析 2.1 快递配送系统GO模型 2.1.1 快递配送工作流程分析快递配送一般是指快递公司收取客户的寄件,在约定的时间内运送至规定位置的收件地点并由收件人接受签收的过程,具有很强的时效性以及服务对象分散等特点[16]。快递配送与一般配送过程不同,快递配送主要进行商品分散配送,大多数商品由厂家或者寄件方自行进行配货,快递配送企业无需进行二次配货,取而代之的是集货和送货过程,其中集货过程包括从不同寄件网点收集寄件物品,送货过程则是快递配送企业提供的由寄件人到收件人的门对门配送服务。整个快递配送系统工作流程如图2所示。
|
图 2 快递配送系统工作流程图 Fig. 2 Express delivery system work-flow chart |
与一般的物流配送活动不同,网购背景下的快递配送具有客户群体分散、订单频次高、配送路线重复等特点,而且影响其系统可靠性的因素复杂多样[17-18]。之前的研究者大多是基于单个可靠性指标,如时间可靠性、品质可靠性、服务可靠性[19-20]等对快递配送系统进行研究。但是对于快递配送企业而言,在快递配送系统可靠性评估时,仅考虑单个可靠性指标是不合适的。本文在文献研究和专家访谈的基础上,按照快递配送流程,将其划分为寄件、集散、中转、分拣、收件5个子系统。综合考虑快递配送系统对时间、品质和服务可靠性方面的要求,将快递配送系统可靠性影响因素分为时间、品质、服务3个方面,分别列出各个子系统成功运营的影响因素,如表1所示。
| 表 1 快递配送系统可靠性影响因素 Tab. 1 Factors affecting the reliability of express delivery systems |
按文献[15]中GO法分析步骤,将子系统的影响因素作为系统输入信号,各个子系统按照GO法操作符规则转换为快递配送系统GO模型,其中子系统与影响因素之间通过信号流连接,所有子系统均为故障维修、正常工作的二态部件。各子系统影响因素之间通过与门连接,当任意一个影响因素发生故障,整个子系统就需要故障维修。寄件子系统与集散中心通过M取K门连接,代表快递配送集货过程。本文以3取2门来表示,说明至少2个寄件网点正常工作,集散中心才能正常运行,否则集散中心处于故障状态,等待足够货物才能恢复正常工作。同时按照影响因素的分类,之前的研究者对时间可靠性指标,大多数取故障、正常2种状态,但是实际配送过程中,由于交通畅通状态的不同,一般具有提前、正常、延时3种情况。本文考虑交通状态情况,将时间可靠性指标取提前、正常、故障3种状态,其他的品质、服务可靠性指标取故障、正常2种状态,利用GO法对多时序、多状态建模的优势,建立快递配送系统GO模型,如图3所示。

|
图 3 快递配送系统GO图 Fig. 3 Express delivery system GO map |
图3中三角形代表信号发生器,圆圈中连线前数字代表不同操作符的类型编码,连线后的数字代表快递配送系统中的顺序编号。具体含义如表2所示。
| 表 2 快递配送系统GO图操作符数据 Tab. 2 Courier delivery system GO map operator data |
操作符和信号流是GO法的2大要素,而操作符贝叶斯网络映射是贝叶斯-GO算法的核心。文献[12]中给出了GO法的17种操作符的贝叶斯网络映射规则,而快递配送系统GO图中涉及的操作符类型包括第1、5、6、10、11类。本文主要针对这些操作符进行映射转换,得到的操作符对应贝叶斯网络图及其CPT表,其中S表示输入信号,C表示操作符,R表示贝叶斯网络节点,0/1分别表示故障、正常状态,P表示各个状态下的概率。
1) 第1类操作符。
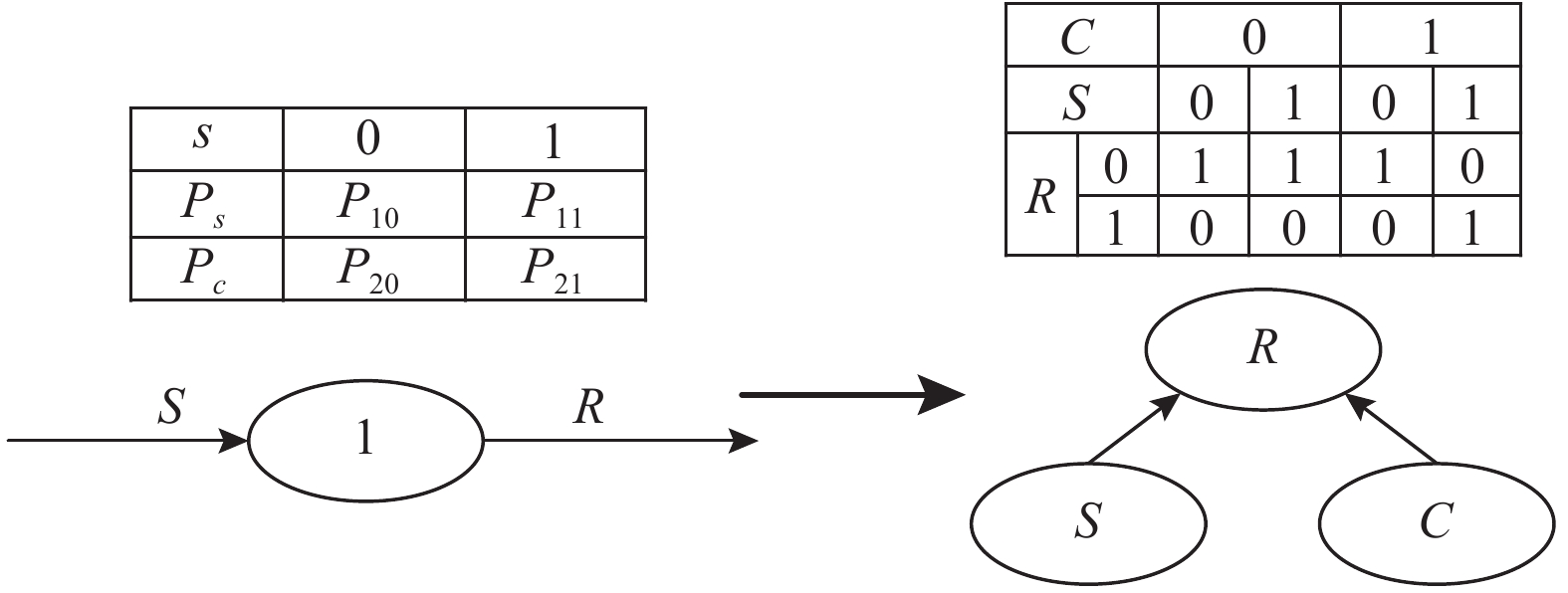
类型1操作符为两状态单元,只有正常工作和故障维修2个状态。在快递配送系统中,用于模拟寄件子系统。类型1操作符的输入信号、操作符本身都具有不同状态,在映射到贝叶斯网络时,不仅输入信号需要映射为根节点,操作符本身也要映射为根节点,得到的贝叶斯网络如图4所示。
|
图 4 第1类操作符及对应的贝叶斯网络 Fig. 4 Class 1 operator and corresponding bayesian network |
2) 第5类操作符。
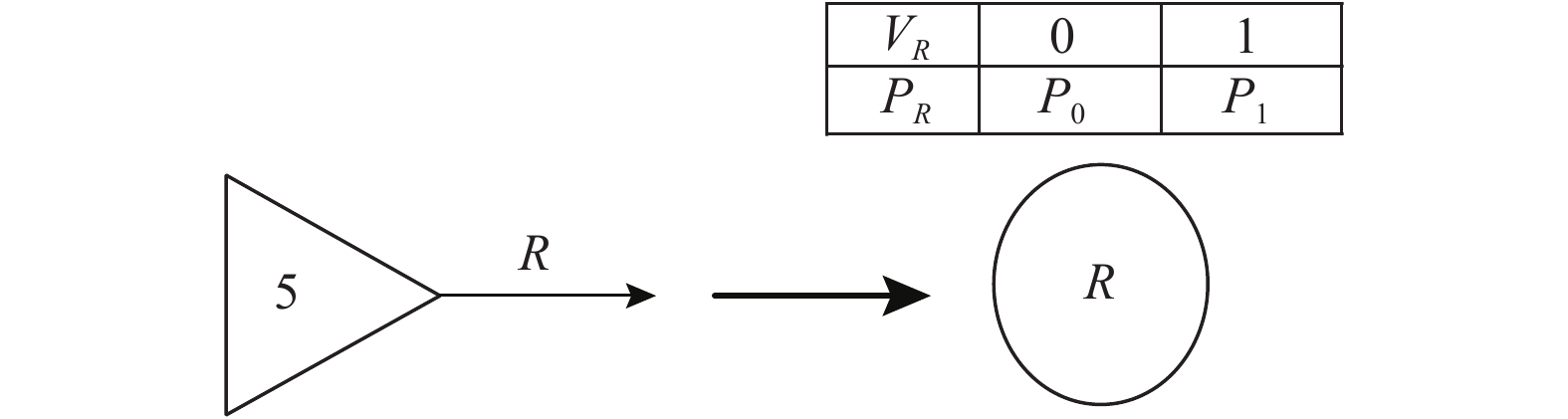
类型5操作符为信号发生器,用于模拟没有输入信号,只有输出信号的单元。在快递配送系统中,用于模拟各个子系统的影响因素。在映射到贝叶斯网络时,直接映射为贝叶斯网络中的根节点,得到的贝叶斯网络如图5所示。
|
图 5 第5类操作符及对应的贝叶斯网络 Fig. 5 Class 5 operator and corresponding bayesian network |
3) 第10、11类操作符。
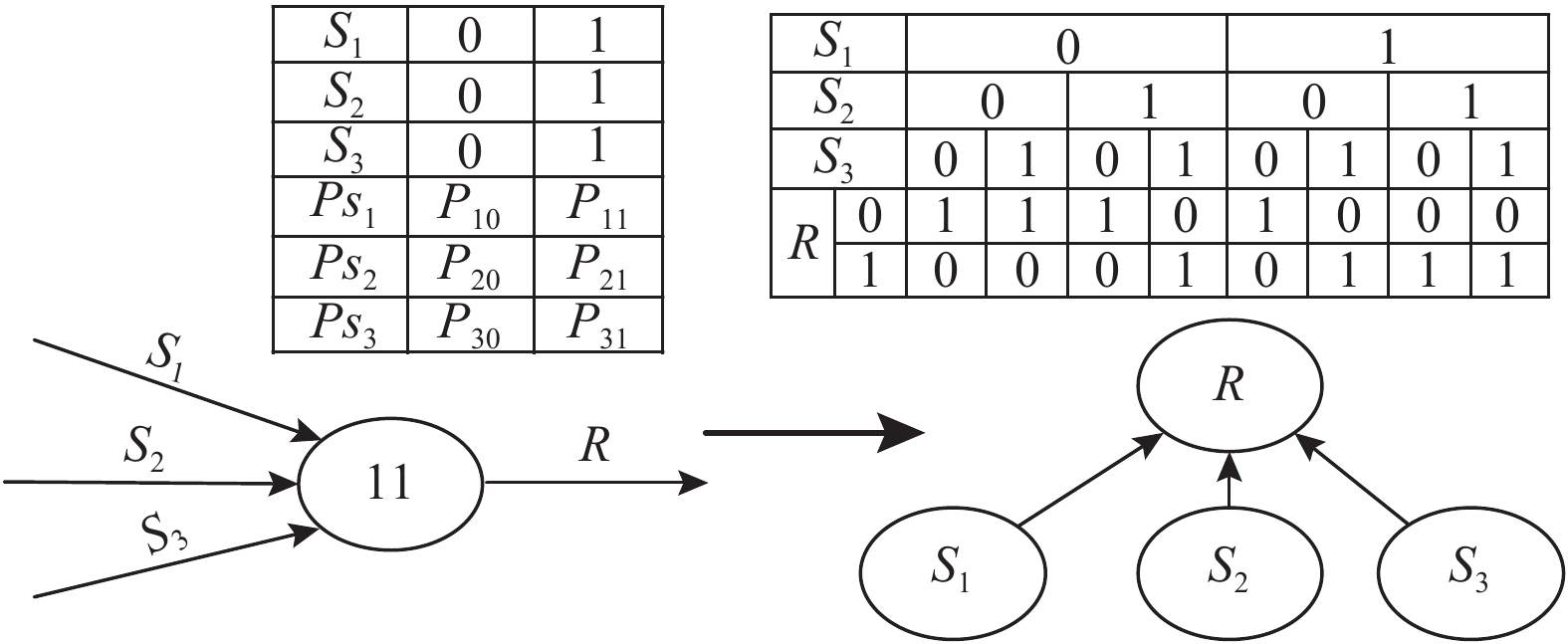
类型11操作符为M取K门,只有当M个输入信号中至少有K个输入成功时,单元才正常输出。在快递配送系统中,用来模拟具有复杂输入输出逻辑关系的虚拟操作符。第10类操作符—与门,是M取K门的特殊情况(K=1时),所以不重复赘述。本文主要以3取2为例说明第10、11类操作符的贝叶斯网络转换,得到的贝叶斯网络如图6所示。
|
图 6 第11类操作符及对应的贝叶斯网络 Fig. 6 Class 11 operator and corresponding bayesian network |
4) 第6类操作符。
类型6操作符为有条件信号而导通的元件,其中2个输入信号同时输入,单元才正常输出。在快递配送系统中,用来模拟具有与门逻辑的集散、中转、分拣、收件等子系统。由于类型6操作符也具有故障维修和正常工作2种状态,在贝叶斯网络映射中,需要转换为根节点,得到的贝叶斯网络如图7所示。

|
图 7 第6类操作符及对应的贝叶斯网络[12] Fig. 7 Class 6 operator and corresponding bayesian network |
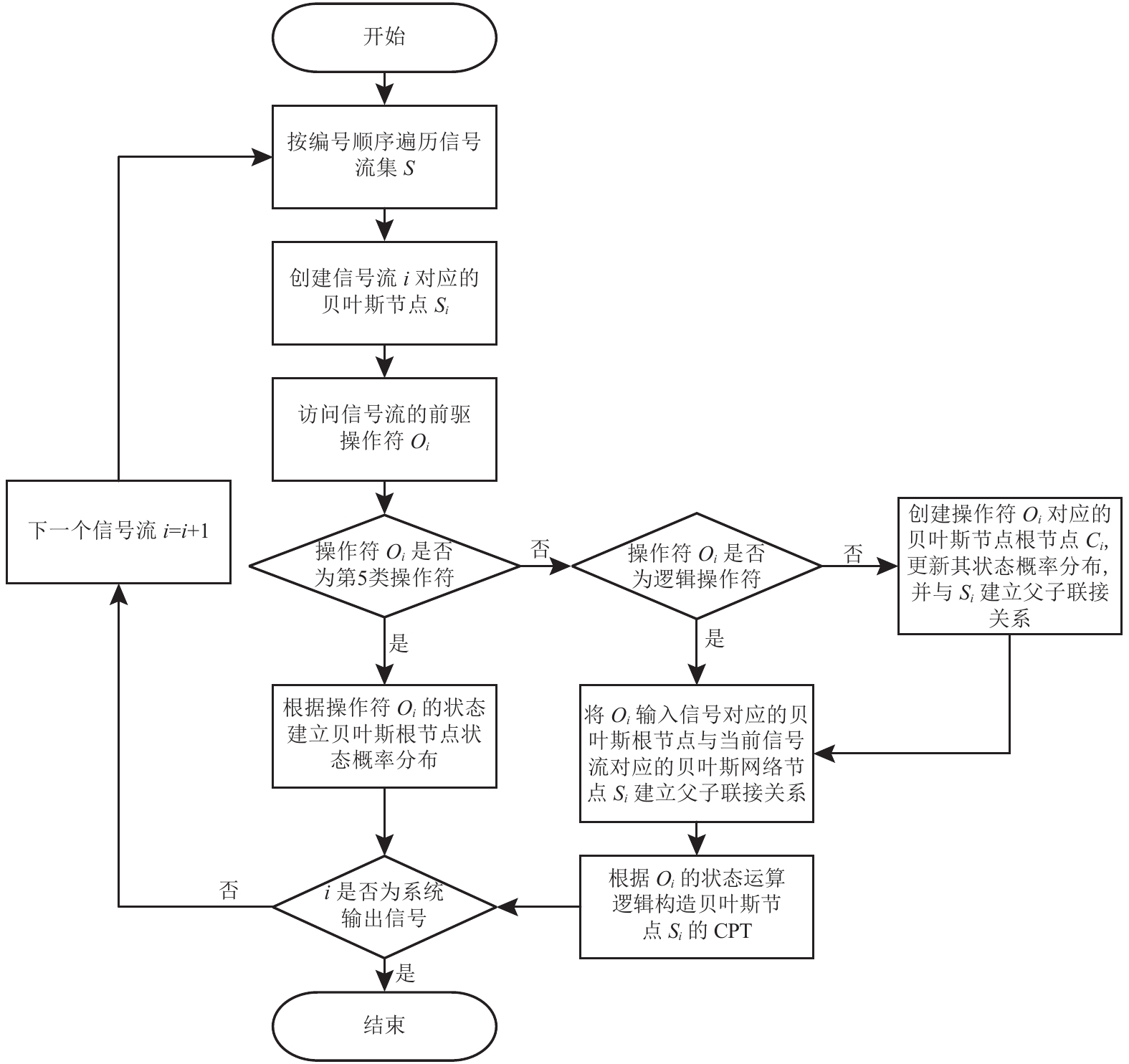
在使用贝叶斯-GO法进行可靠性分析的过程中,需要按照GO法的贝叶斯网络映射流程将GO图转化为贝叶斯网络,2.2.1节给出了快递配送系统GO法操作符的贝叶斯映射规则,具体的GO图转换为贝叶斯网络映射流程如图8所示。
|
图 8 GO法的贝叶斯网络映射流程图[12] Fig. 8 Algorithm for mapping GO chart into bayesian network |
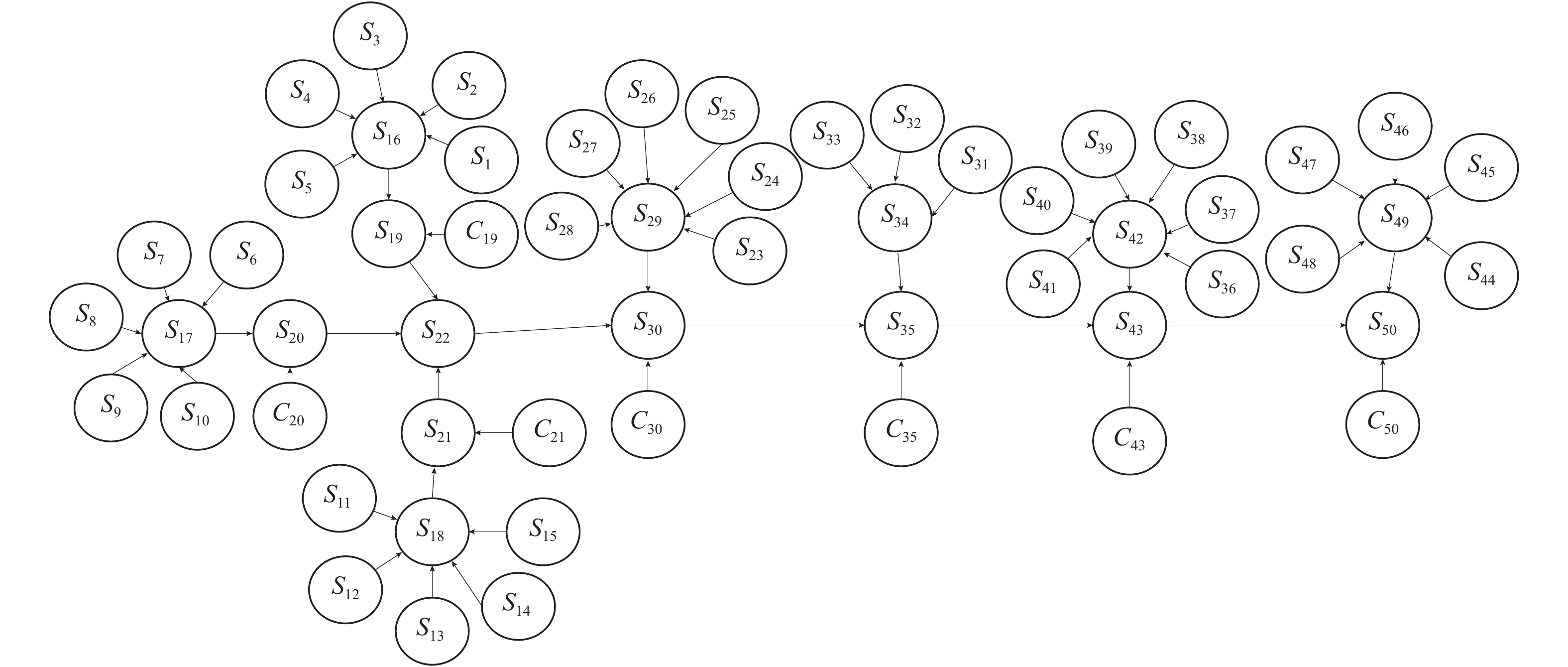
根据图3的快递配送系统GO图,按照2.2.2节的操作符映射流程,运用贝叶斯建模软件GeNle,将GO图转换为贝叶斯网络拓扑结构图,如图9所示,其中节点Si表示GO图中信号流编号i对应的贝叶斯网络节点,Ci表示第i个功能操作符对应的贝叶斯网络根节点,所有非时间影响因素节点均设置为故障维修、正常工作2种状态,时间影响因素节点分别设置为提前、正常、故障3种状态和故障、正常工作2种状态,进行对比分析。
|
图 9 快递配送系统贝叶斯网络 Fig. 9 Bayesian network of express delivery system |
本文选取上海市“天天快递”货运公司作为案例分析研究对象。“天天快递”品牌创建于1994年,公司业务包括市场采集、市场开发、物流配送、快件收派等,服务客户30万余家。客户群体遍及电子商务、纺织服装、医药化工、货代企业、进出口贸易、制造业等多个领域。但是其快递配送业务却饱受消费者投诉,根据2018年6月快递企业投诉排行榜数据显示:安能/天天/TNT申诉率为前3。通过企业内部配送系统故障维修和顾客投诉情况调研,并且对其上海市区域内2017—2018年度快递配送系统故障数据进行收集,经过数据清洗,整理统计得到快递配送系统中不同根节点所代表的可修单元的可靠性参数,其中故障、正常、提前概率统计以小时为单位计算。具体数据如表3所示。
| 表 3 快递配送系统根节点先验概率表 Tab. 3 Express distribution system root node prior probability table |
利用贝叶斯正反向推理算法进行可靠性评估和故障诊断时,除了表3中所需要的先验概率,还需要各个子节点的状态分布概率,根据2.2.1节操作符模型映射规则可以得到各个节点的状态分布概率。对快递配送系统进行故障诊断,假设快递配送系统发生故障,对输出信号进行故障注入,即将输出信号S50的故障维修概率PR(1)=1作为证据更新到贝叶斯网络中,重新推理计算,可以得到各根节点的后验概率分布。
采用GeNle软件进行推理计算,最后计算结果如表4所示,表中包括了贝叶斯网络中的所有子节点状态概率分布,即快递配送系统GO图中非初始信号流的状态概率分布。以上计算结果运行的硬件环境为4核1.6 GHz CPU、8 G内存,软件环境为GeNle Academic。
| 表 4 贝叶斯网络子节点后验概率分布表 Tab. 4 Bayesian network subnode probability distribution table |
由表4正向推理故障数据得到,系统成功即输出信号S50,正常工作概率为0.566 7,系统故障维修的概率为0.433 3,推理计算时间仅0.001 9 s。同时表3中反向推理故障数据,展示了快递配送系统故障失效情况下,各贝叶斯根节点的失效后验概率分布状况。在快递配送系统故障的情况下,S49的故障概率最高,S43、S35次之,说明收件子系统是快递配送系统的薄弱环节。因此,在快递配送系统发生故障的情况下,应该重点排除收件系统故障,其次排除中转、分拣子系统的问题。
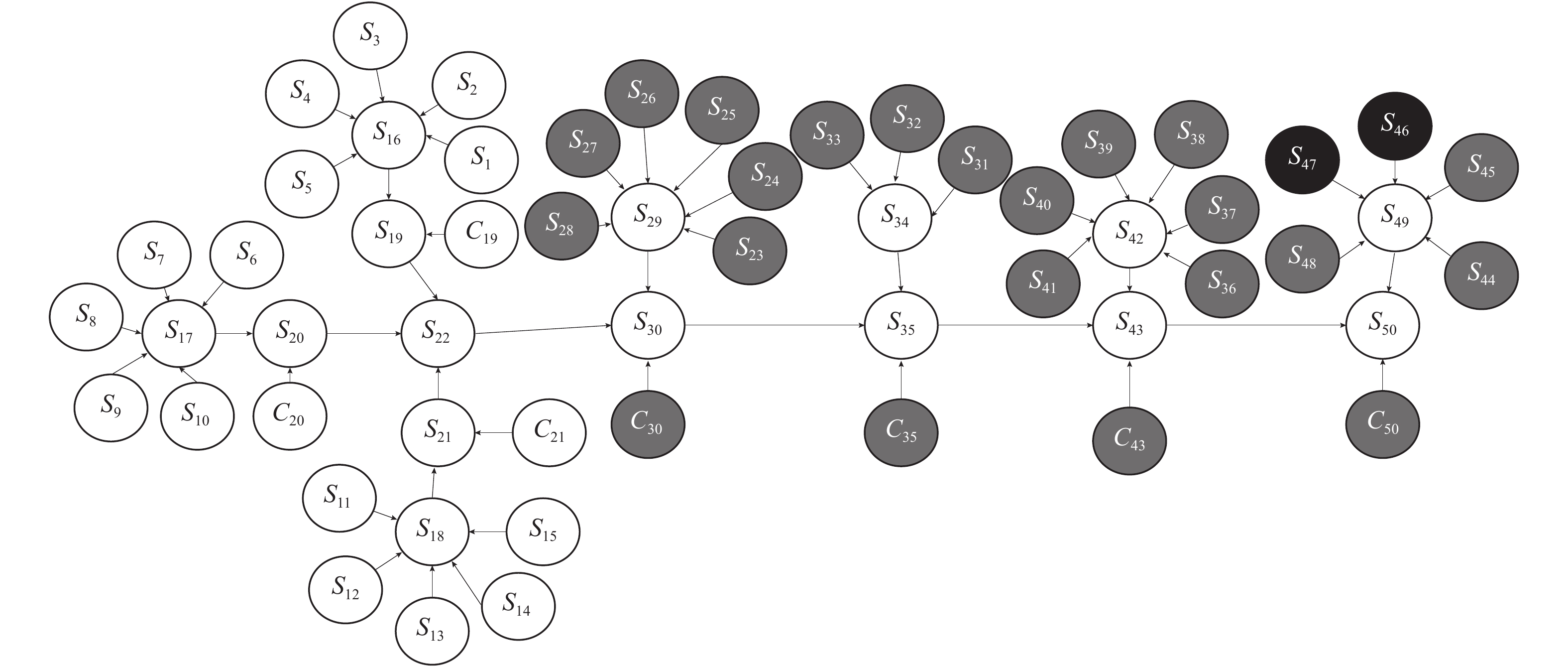
3.3 影响因素敏感度分析为了识别影响故障发生的主要影响因素,本文采用贝叶斯网络中各节点输出状态敏感性分析方法,将S50节点设置为目标节点,进行敏感性分析。GeNle软件计算灵敏度值,得到的分析结果如图10所示(颜色越深表示敏感度越高)。
|
图 10 快递配送系统敏感性分析 Fig. 10 Sensitivity analysis of express delivery system |
由图10的的敏感度值排序,可知S47、S46对S50影响最大,即收件过程中快递员的配送服务质量和寄件的损坏是快递配送系统可靠性的主要影响因素。其他的节点如S45、S33、S38、S39等对S50的影响也较为严重,说明寄件的丢失、损坏对系统可靠性的影响也较为显著。所以在收件环节,管理人员应该加强快递配送人员的业务培训,同时对寄件丢失、损坏、准时率的检测,也是提高整个快递配送系统可靠性的有效途径。
同时,将配送系统中各节点的工作状态,分别设置为不考虑提前状态、考虑提前状态2种情况,对比分析配送系统可靠性影响因素敏感度的变化,具体对比结果如表5所示。
| 表 5 考虑提前状态影响因素敏感度对比表 Tab. 5 Comparison of the sensitivity of the factors affecting the advance state |
由表5可知,在考虑提前状态下,寄件损坏、丢失的敏感度较高,而不考虑提前状态下,对于配送延时的敏感度较高。所以以往GO法对快递配送系统建模过程中,仅考虑快递配送各环节故障维修和正常工作状态,忽略提前状态,会对配送系统可靠性影响因素敏感度分析的准确性造成一定程度影响。
4 结论1) 相较于单独使用GO法,贝叶斯-GO法的推理计算过程仅耗时0.001 9 s,不需要考虑GO法中的复杂相关性,有效地避免了GO法计算复杂繁琐的缺点,而且能够利用贝叶斯网络的故障推理诊断能力,对快递配送系统中的薄弱环节和主要影响因素进行有效识别。同时,借助于成熟的贝叶斯软件,能够图形化地展现可靠性因素敏感度,降低了企业管理人员学习成本,有利于企业实际运用。
2) 收件子系统是快递配送系统的故障多发环节,而其中的快递员配送不及时、寄件丢失或者损坏是主要的影响因素。所以对于快递配送企业来说,收件系统应该作为其系统可靠性管理的主要对象,而强化快递配送员的培训和监督是提高快递配送系统可靠性的有效途径。
由于快递配送流程中,存在多种寄取件方式,本文只对客户网点自寄自取模式进行分析,且未考虑快递配送的动态变化过程,存在不足之处。而考虑多种寄取件方式,借助动态贝叶斯网络特性,对快递配送系统的动态可靠性进行分析,是未来的研究方向。
| [1] |
王进. 城市快递末端配送服务模式分类及影响因素[J].
商业经济研究, 2018(8): 81-85.
DOI: 10.3969/j.issn.1002-5863.2018.08.026. |
| [2] |
中华人民共和国国家邮政局. 关于2017年9月邮政业消费者申诉情况的通告[Z/OL]. (2017-10-20)[2018-12-25]. www.spb.gov.cn/xw/dtxx_15079/201710/t20171020_1381815.html
|
| [3] |
麻存瑞, 柏赟, 赵欣苗, 等. 快递配送车辆路径优化研究[J].
交通运输系统工程与信息, 2017, 17(4): 182-187.
MA Cunrui, BAI Yun, ZHAO Xinmiao, et al. Vehicle routing optimization on express distribution[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 182-187. |
| [4] |
张晓楠, 范厚明, 李剑锋. B2C物流配送网络双目标模糊选址模型与算法[J].
系统工程理论与实践, 2015, 35(5): 1202-1213.
ZHANG Xiaonan, FAN Houming, LI Jianfeng. Bi-objective fuzzy location model and algorithm for the design of logistics distribution network in B2C e-commerce[J]. Systems Engineering-Theory & Practice, 2015, 35(5): 1202-1213. |
| [5] |
付德强, 陈煜舟, 万晓榆. 自然灾害风险下区域应急储备设施选址可靠性研究[J].
运筹与管理, 2015, 24(3): 14-19.
FU Deqiang, CHEN Yuzhou, WAN Xiaoyu. The study on the reliable model for the regional emergency storage facility under the risk of natural disaster[J]. Operations Research and Management Science, 2015, 24(3): 14-19. DOI: 10.3969/j.issn.1007-3221.2015.03.004. |
| [6] |
MUNOZ-VILLAMIZAR A, MONTOYA-TORRES J R, FAULIN J. Impact of the use of electric vehicles in collaborative urban transport networks: a case study[J].
Transportation Research Part D: Transport and Environment, 2017, 50: 40-54.
DOI: 10.1016/j.trd.2016.10.018. |
| [7] |
KUTANOGLU E, MAHAJAN M. An inventory sharing and allocation method for a multi-location service parts logistics network with time-based service levels[J].
European Journal of Operational Research, 2009, 194(3): 728-742.
DOI: 10.1016/j.ejor.2007.12.032. |
| [8] |
许振宇, 任世科, 郭雪松, 等. 不确定条件下应急供应链可靠性评价模型[J].
运筹与管理, 2015, 24(3): 35-44.
XU Zhenyu, REN Shike, GUO Xuesong, et al. Evaluation of emergency supply chain reliability under uncertain information[J]. Operations Research and Management Science, 2015, 24(3): 35-44. DOI: 10.3969/j.issn.1007-3221.2015.03.007. |
| [9] |
张根保, 陈国华, 庞继红, 等. GO法在供应链可靠性诊断中的应用[J].
重庆大学学报, 2010, 33(12): 40-46.
ZHANG Genbao, CHEN Guohua, PANG Jihong, et al. Application of GO methodology in reliability analysis of supply chain[J]. Journal of Chongqing University, 2010, 33(12): 40-46. DOI: 10.11835/j.issn.1000-582X.2010.12.007. |
| [10] |
蔡鉴明, 曾峰. 基于GO法的供应链可靠性分析[J].
公路交通科技, 2007, 24(3): 141-144.
CAI Jianming, ZENG Feng. Reliability analysis of the supply chain based on the GO methodology[J]. Journal of Highway and Transportation Research and Development, 2007, 24(3): 141-144. DOI: 10.3969/j.issn.1002-0268.2007.03.034. |
| [11] |
胡思涛, 朱艳茹. 基于GO法的生鲜农产品供应链可靠性评价[J].
物流技术, 2013, 32(3): 214-216.
HU Sitao, ZHU Yanru. Evaluation of reliability of fresh farm produce supply chain based on GO method[J]. Logistics Technology, 2013, 32(3): 214-216. |
| [12] |
刘林林, 任羿, 王自力, 等. 基于贝叶斯网络的GO法模型算法[J].
系统工程与电子技术, 2015, 37(1): 212-218.
LIU Linlin, REN Yi, WANG Zili, et al. Algorithm based on Bayesian networks for GO methodology[J]. Systems Engineering and Electronics, 2015, 37(1): 212-218. |
| [13] |
田录林, 刘沛盛. 改进贝叶斯网络GO法在高压直流输电系统的可靠性分析[J].
高压电器, 2017, 53(7): 53-59+66.
TIAN Lulin, LIU Peisheng. Reliability analysis on HVDC transmission system based on improved bayesian networks GO methodology[J]. High Voltage Apparatus, 2017, 53(7): 53-59+66. |
| [14] |
陈洁, 陈国明, 李新宏, 等. 深水关井作业可靠性贝叶斯-GO法分析[J].
中国安全科学学报, 2016, 26(4): 144-149.
CHEN Jie, CHEN Guoming, LI Xinhong, et al. Reliability analysis of deep-water shut-in operation using Bayesian-GO approach[J]. China Safety Science Journal, 2016, 26(4): 144-149. |
| [15] |
沈祖培, 黄祥瑞. GO法原理及应用:一种系统可靠性分析方法[M]. 北京:清华大学出版社, 2004: 9-48.
|
| [16] |
倪玲霖. 轴辐式与点对点及组合式的快递网络特征分析[J].
统计与决策, 2010(20): 59-61.
|
| [17] |
谢广营, 韩云霞. 中国网购物流服务质量实证研究[J].
北京交通大学学报(社会科学版), 2016, 15(4): 102-114.
XIE Guangying, HAN Yunxia. An empirical research on the service quality of China's online shopping logistics[J]. Journal of Beijing Jiaotong University(Social Sciences Edition), 2016, 15(4): 102-114. DOI: 10.3969/j.issn.1672-8106.2016.04.013. |
| [18] |
戴君, 贾琪, 王晶. B2C电子商务环境下物流配送服务顾客满意度影响因素研究[J].
物流技术, 2014, 33(9): 166-170.
DAI Jun, JIA Qi, WANG Jing. Study on influence factors of customer satisfaction in logistics distribution services under B2C e-commerce environment[J]. Logistics Technology, 2014, 33(9): 166-170. DOI: 10.3969/j.issn.1005-152X.2014.09.057. |
| [19] |
张宏达, 戢晓峰, 吉选, 等. 基于时间可靠性的城市物流配送系统优化策略[J].
交通信息与安全, 2014, 32(2): 77-81.
ZHANG Hongda, JI Xiaofeng, JI xuan, et al. Optimization strategy of city logistics distribution system based on time reliability[J]. Journal of Transport Information and Safety, 2014, 32(2): 77-81. DOI: 10.3963/j.issn.1674-4861.2014.02.015. |
| [20] |
王振全, 于爱滨, 许开立. 城市危险化学品物流配送网络可靠性研究[J].
辽宁化工, 2015, 44(6): 654-656.
|
 2019, Vol. 22
2019, Vol. 22
