随着民航业进入高速发展时期，国内外航空市场竞争日益激烈。在这种市场背景下，提高民用飞机经济性尤为重要，而降低民用飞机的直接维修成本是解决这一问题的有效手段。在飞机研制初期的维修成本分析中，民机直接维修成本(direct maintenance cost，DMC)分析工作包括分配、预计和评估。在民机维修成本控制过程中，民机维修的目标成本分配是一关键步骤，在某种程度上决定了民机设计能否取得商业成功。维修成本分配的合理化可以有效地提高飞机维修经济性水平，确保飞机的市场竞争力^[1-2]。

国际上对于民机维修成本的研究始于20世纪40年代，包括NASA95方法、AEA2009方法、OPCOST方法、Liebeck方法和Harris方法^[3]。这些方法将维修成本分为机体和发动机2个部分。NASA95方法是将大部分模型和飞机的设计参数联系在一起，同时结合航空公司直接运营成本的计算方法^[4]；AEA2009方法广泛应用于经济分析和构型优化，采用较少的参数进行维修成本的预测^[5]；OPCOST是波音公司内部使用的预测DOC(direct operation cost)的软件系统，以ATA(air transport association)章节为基础，先根据原准机算出基本的维修成本，再根据起飞空重、起落架配置、刹车数、发动机数以及座位数等参数进行修正；Liebeck方法用于飞机构型优化分析^[6]；而Harris方法只适用于美国市场条件。国内对民机维修成本的研究起步较晚，主要集中于DMC的分配、预计和评估，提出了相似分配法、功能分解法和函数逼近法^[7-8]。在成本分配时，功能分解法以价值工程为基础，设计功能系统图，根据系统功能进行逐级划分，然后按功能评价值大小进行成本分配。此方法较依赖专家主观经验，易使结果出现较大误差^[9]。函数逼近法通过构建多项式函数，测算出商用飞机各部件成本在总成本中的比重，为商用飞机的成本管理提供依据^[8]。

鉴于功能分解法的不足，本文采用相似分配法。相似分配法的一般思路是首先确定类似机型的相似度，然后进行成本分配。现有的相似分配法确定机型权重时也较依赖专家主观经验，而熵权-TOPSIS (technique for order preference by similarity to ideal solution)通过加入客观的评价方法，避免了主观因素带来的影响。该方法已成功应用到风险决策分析、土地生态安全评价、环境质量测评和土地整理实施效益评价等多个方面，越来越受到人们的重视^[10]。本文应用熵权-TOPSIS方法确定类似机型设计参数的权重，然后采用加权距离计算类似机型的相似度，建立了一种新的民机直接维修成本分配模型，弥补了现有的相似分配法确定机型权重时的不足。

1 理论依据 1.1 熵权法

根据信息论观点，指标的变异程度反映其能提供多少信息量，从而影响指标的权重大小。而信息量的大小可用熵权来度量，信息量越大，熵权越小。熵权法是客观的评价指标权重的方法，其通过信息熵计算出各指标的熵权，再利用熵权对各指标进行权重的修正，为指标的评价提供更可靠的依据^[11]。

本文采用熵权法确定机型的设计参数权重，具体做法如下。若有m个评价机型，n个设计参数指标，初始评价矩阵 ${{C}} = {\left( {{x_{ij}}} \right)_{m \times n}},{x_{ij}} {\text{＞}} 0,\left( {i = 1,2, \cdots, m;j = }\right. $ $\left.{1,2, \cdots, n} \right)$ 。在实际应用中因为量纲差异，若遇到 ${x_{ij}} {\text{＜}} 0$ 的情况，要对数据做标准化处理。由于变量的取值范围为[0,1]，故要进行数据归一化处理， ${\theta _{ij}} = {{{x_{ij}}} /{\displaystyle\sum\limits_{i = 1}^m {{x_{ij}}} }}$ ，求出标准矩阵， ${\theta _{ij}}$ 为第j个设计参数下第i个机型的标值的比重， ${x_{ij}}$ 为第j个设计参数下第i个机型的评价值^[12]。

计算系统中第j个指标熵值 ${e_j}$ 为

$ \qquad{{{e}}_j} = - k\sum\limits_{j = 1}^n {{\theta _{ij}}} \ln {\theta _{ij}},\;\;j = 1,2, \cdots, n{\text{。}} $

(1)

其中， $k = {1 /{\ln m}}$ 。

计算第j个指标的熵权 ${W_j}$ 为

$ \qquad{{{W}}_j} = 1 - {e_j}/\sum\limits_{j = 1}^n {\left( {1 - {e_j}} \right)} {\text{。}} $

(2)

1.2 加权距离

求解相似度时由于某些因素之间的关系具有模糊性，同时要考虑各种因素的综合联系，采用常规的方法不易解决问题，可用模糊集合理论，即求解加权距离，获得贴近度^[13]。距离越小表示评价对象之间越接近。

加权距离包括很多种，考虑到各种距离的优缺点和计算的难易程度，本文选择欧氏距离作为处理权重的方法^[14]。

$ \qquad{d_{ij}} = \sqrt {\sum\limits_{l = 1}^n {{{\left( {{x_{il}} - {x_{jl}}} \right)}^2}} } {\text{。}} $

(3)

式中， ${x_{il}}$ 为第l个设计参数下第i个机型的评价值， ${x_{jl}}$ 类同。

1.3 TOPSIS模型

TOPSIS是“逼近于理想值的排序方法”，是系统工程中有限方案多目标分析的一种决策技术^[15]。TOPSIS法的核心思想是定义决策问题的最优解和最劣解的距离，最后计算各个方案与理想解的相对贴近度，进行方案的优劣排序。根据评价对象与理想解的贴近程度来评价，贴近度越接近1，说明评价对象水平越高^[16-17]。

正理想解

$ \qquad {s^ + } = \max \left( {{\gamma _{ij}}} \right),j = 1,2,\cdots, n{\text{；}} $

(4)

负理想解

$ \qquad {s^{\rm{ - }}} = \min \left( {{{{\gamma}} _{ij}}} \right),j = 1,2,\cdots, n{\text{。}} $

(5)

本文采用TOPSIS方法确定各类似机型与标准机型的贴近度，设计参数与正、负理想点的距离为

$ \quad\quad d_i^ + = \sqrt {\sum\limits_{j = 1}^{{n}} {\left[ {{W_j}{{\left( {{s^ + } - {{{\gamma}} _{ij}}} \right)}^2}} \right]} } {\text{；}} $

(6)

$ \quad\quad d_i^ - = \sqrt {\sum\limits_{j = 1}^{{n}} {\left[ {{W_j}{{\left( {{s^ - } - {\gamma _{ij}}} \right)}^2}} \right]} } {\text{。}} $

(7)

相对贴近度

$ \qquad{\sigma _i} = d_i^ - /\left( {d_i^ + + d_i^ - } \right),i = 1,2,\cdots, n{\text{。}} $

(8)

2 基于加权距离的熵权-TOPSIS分配模型

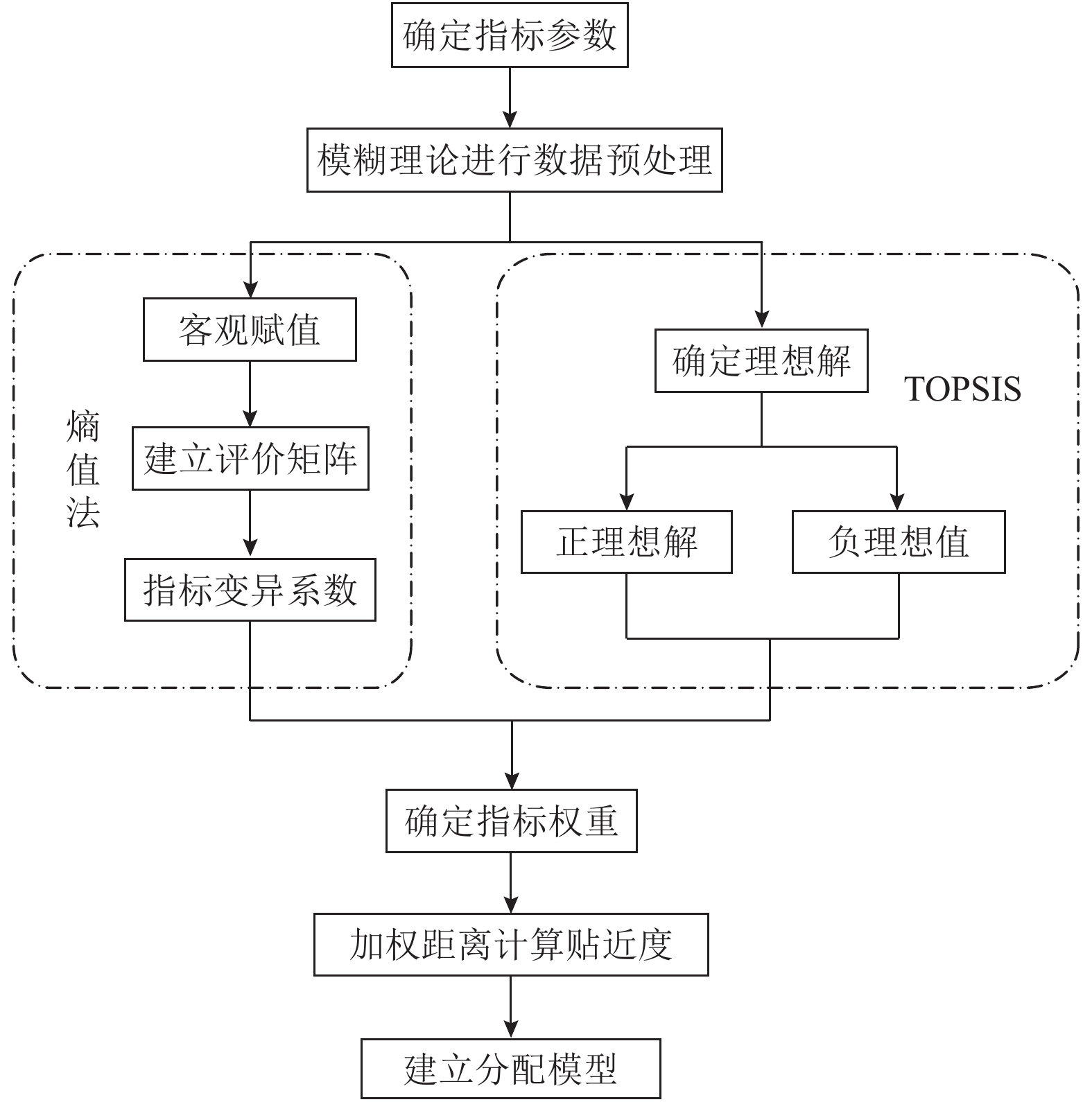
本文将熵权法与TOPSIS模型结合，用于评价各机型之间的相似性，建立了民机直接维修成本的分配模型^[15]，如图1所示。熵权-TOPSIS法^[18]为距离综合评价法，信息熵确定类似机型设计参数权重，TOPSIS模型寻求其余机型中的最优解和最劣解，然后应用加权距离构建目标民机与最优解和最劣解之间的距离，计算机型的相似度。

1) 数据预处理。本文采用以目标民机的特征为标准，运用模糊理论将其余相似机型与标准特征相比较得模糊集 ${\gamma }$ 。

若目标机型的设计参数矩阵为

$ \quad\quad {{A}} = \left[ {{a_j}} \right]{\text{，}} $

其余类似机型的设计参数矩阵为

$ \quad\quad{{B}} = \left[ {{b_{ij}}} \right]{\text{。}} $

(9)

则 ${{{\gamma}} _{ij}} = \left\{ \begin{array}{l}{b_{ij}}/{a_j},\;\;{b_{ij}} {\text{＜}} {a_j}{\text{；}}\\{a_j}/{b_{ij}},\;\;{b_{ij}} {\text{≥}} {a_j}{\text{。}}\end{array} \right. $

2) 计算信息熵。

令模糊熵 ${{{E}}_{ij}} = {{{\gamma}} _{ij}}$ ，

$ \quad\quad {{{e}}_j} ={{ {\Biggl({m\sum\limits_{j = 1}^n {{{{E}}_{ij}}} }}\Biggl)}^{-1}}{\text{。}} $

(10)

3) 由公式(2)~(8)计算获得贴近度。

4) 进行归一化处理，所得即为分配系数

$ \quad\quad \sigma _i' = {{{\sigma _i}} /{\sum\limits_{i = 1}^m {{\sigma _i}} }}{\text{。}} $

(11)

3 实例分析 3.1 机型相似性

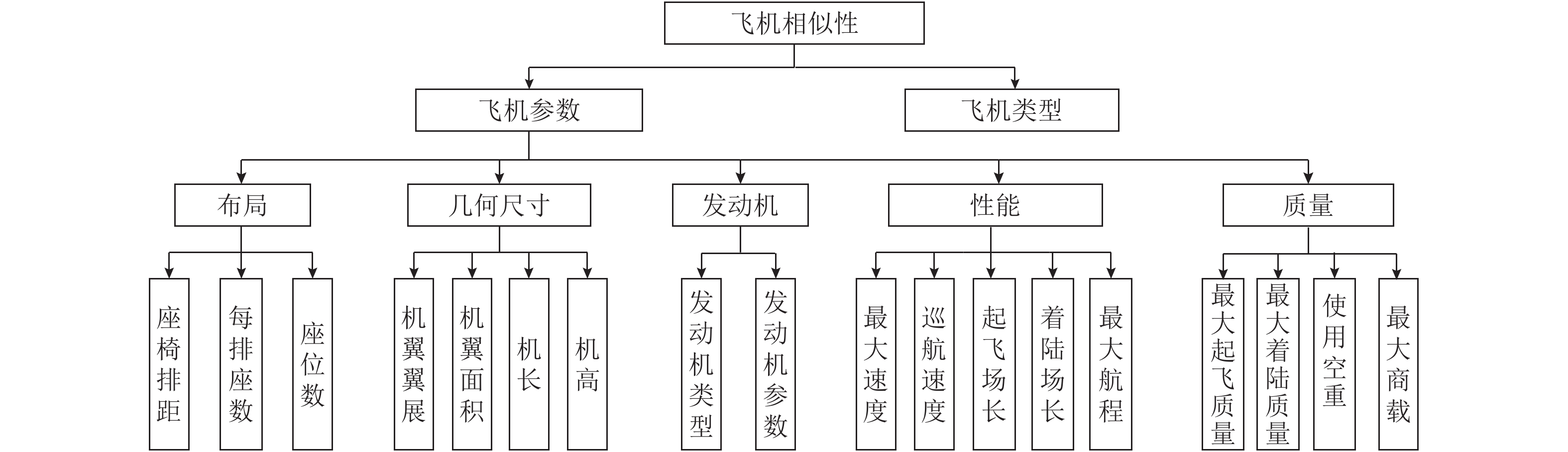
对于新研制的飞机来说，与其相似的机型不止一种，不同之处在于各机型与新机型的相似程度。衡量类似机型涉及到的参数层次关系如图2所示。本文从这些参数中选择影响较大的代表参数：座位数、机翼翼展、机长、巡航速度、最大航程、最大起飞质量和使用空重^[13]，再根据参数计算类似机型之间的相似度^[19-20]。

某商用公司生产型号为E的商用飞机，为了提高市场竞争力，达到民用飞机设计的维修经济性目标，需要对该型号飞机进行成本分配，表1为与该型号飞机类似的型号飞机A、B、C、D的设计参数数据。

在本实例中，以该民机E的特征为标准，其余类似机型与标准特征相比较得

$ {\text{模糊集}}\;\;{{{\gamma}} } = \left[ {\begin{array}{*{20}{c}} {0.91}\!\!&\!\!{0.91}\!\!&\!\!{1.00}\!\!&\!\!{0.91}\!\!&\!\!{0.86}\!\!&\!\!{0.93}\!\!&\!\!{0.92}\\ {0.95}\!\!&\!\!{0.91}\!\!&\!\!{0.82}\!\!&\!\!{0.89}\!\!&\!\!{0.85}\!\!&\!\!{0.97}\!\!&\!\!{0.90}\\ {0.94}\!\!&\!\!{0.77}\!\!&\!\!{0.60}\!\!&\!\!{0.60}\!\!&\!\!{0.75}\!\!&\!\!{0.92}\!\!&\!\!{0.68}\\ {0.96}\!\!&\!\!{0.87}\!\!&\!\!{0.75}\!\!&\!\!{0.81}\!\!&\!\!{0.79}\!\!&\!\!{0.99}\!\!&\!\!{0.71} \end{array}} \right]{\text{，}} $

信息熵 ${{{e}}} = \left[ {0.94,0.87,0.79,0.80,0.81,0.95,0.80} \right] $ ，

熵权 ${{{W}}} = \left[ {0.06,0.13,0.20,0.19,0.18,0.05,0.19} \right] $ 。

确定理想解。本文运用模糊集合理论将数据处理为模糊集，故本文的正理想解 ${s^ + }$ 取为1，负理想解 ${s^ - }$ 取为0。

经计算得加权距离、类似机型相似度及分配系数如表2所示。

3.2 直接维修成本分配

本文从相关文献和网络资料中整理出上述各类似机型的一些系统级维修成本数据，如表3所示，利用这些类似机型的历史经验数据对整机级直接维修成本进行分配。

因商业利益关系所能得到的成本数据较少，故验证结果具有一定的误差是合理的。起落架、燃油、空调系统的维修频率和维修工时较高，人工费用会有不同，分配结果存在较大误差；CPU系统精度要求较高，送修成本远高于人工费用，即离位维修费有较大不同，所得结果存在稍大误差；飞行操纵系统安全性要求较高，预防性维修成本会存在区别，各机型维修成本稍有不同；内饰/设备系统维修成本所占比重较大，涉及到客货舱、驾驶舱、厨房、厕所等的各种基础设备，若出现故障则直接替换新部件，故所得误差较小。所得新机型的各系统总成本误差在可接受范围内，而对于防火、氧气、水/污物等系统，结构相对简单，相应维修成本也较小，本文没有进行验证。

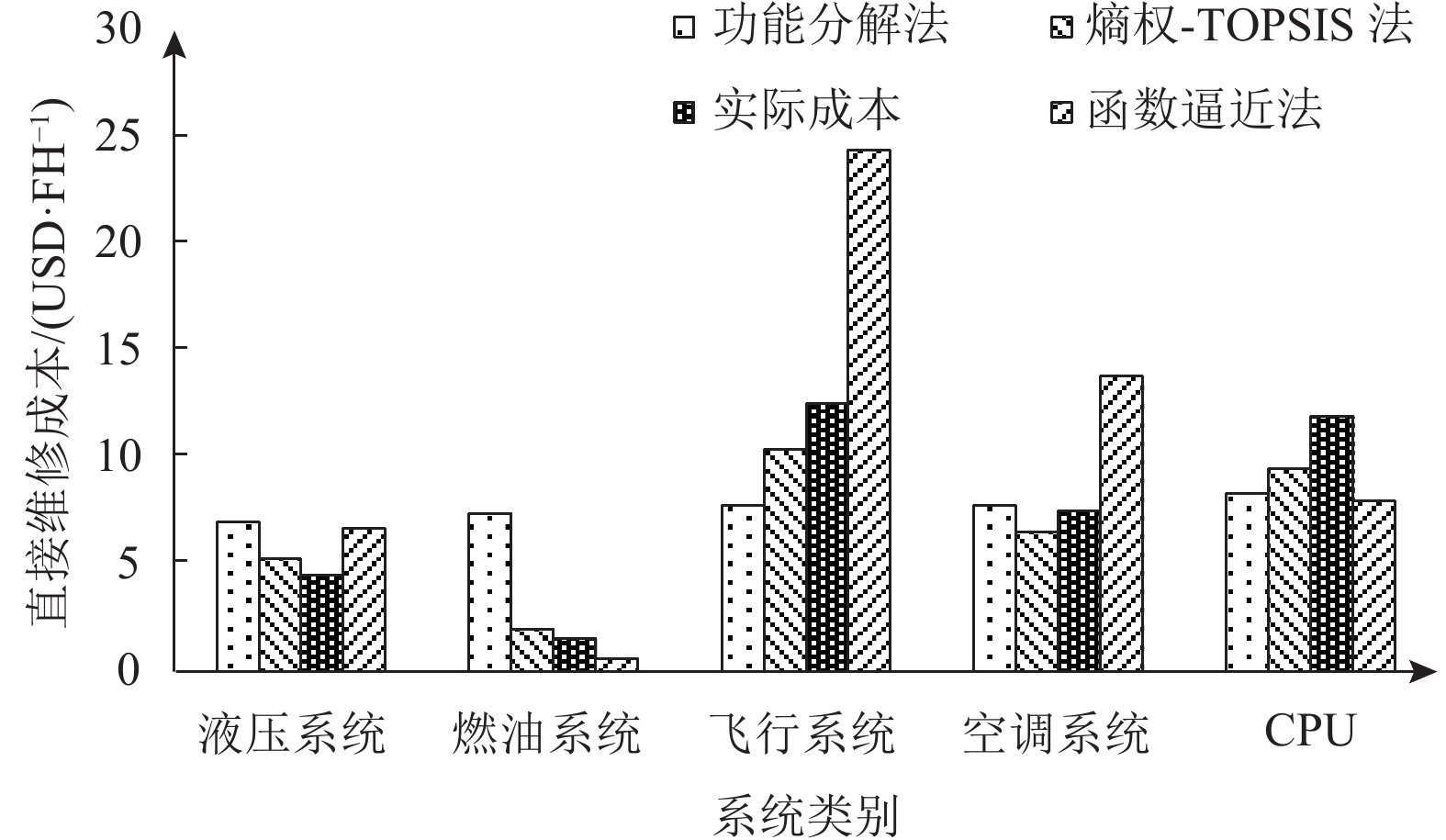
如图3所示，应用文献[8]中的函数逼近法和文献[9]中的功能分解法对成本进行了计算。从图中可以看出，本文方法所得结果与实际的直接维修成本值更接近，更符合实际情况。因为功能分解法根据专家经验主观地对各系统分配权重进行赋值，函数逼近法单一地建立多项式函数进行维修成本分配，没有考虑系统功能，所以这2种方法均会产生较大的误差。本文方法运用熵权法客观地确定了类似机型的设计参数权重，然后利用TOPSIS模型和加权距离构建目标民机与最优解和最劣解之间的距离，客观地得出分配权重，进而得到相似度，故所得结果与实际直接维修成本值更接近。

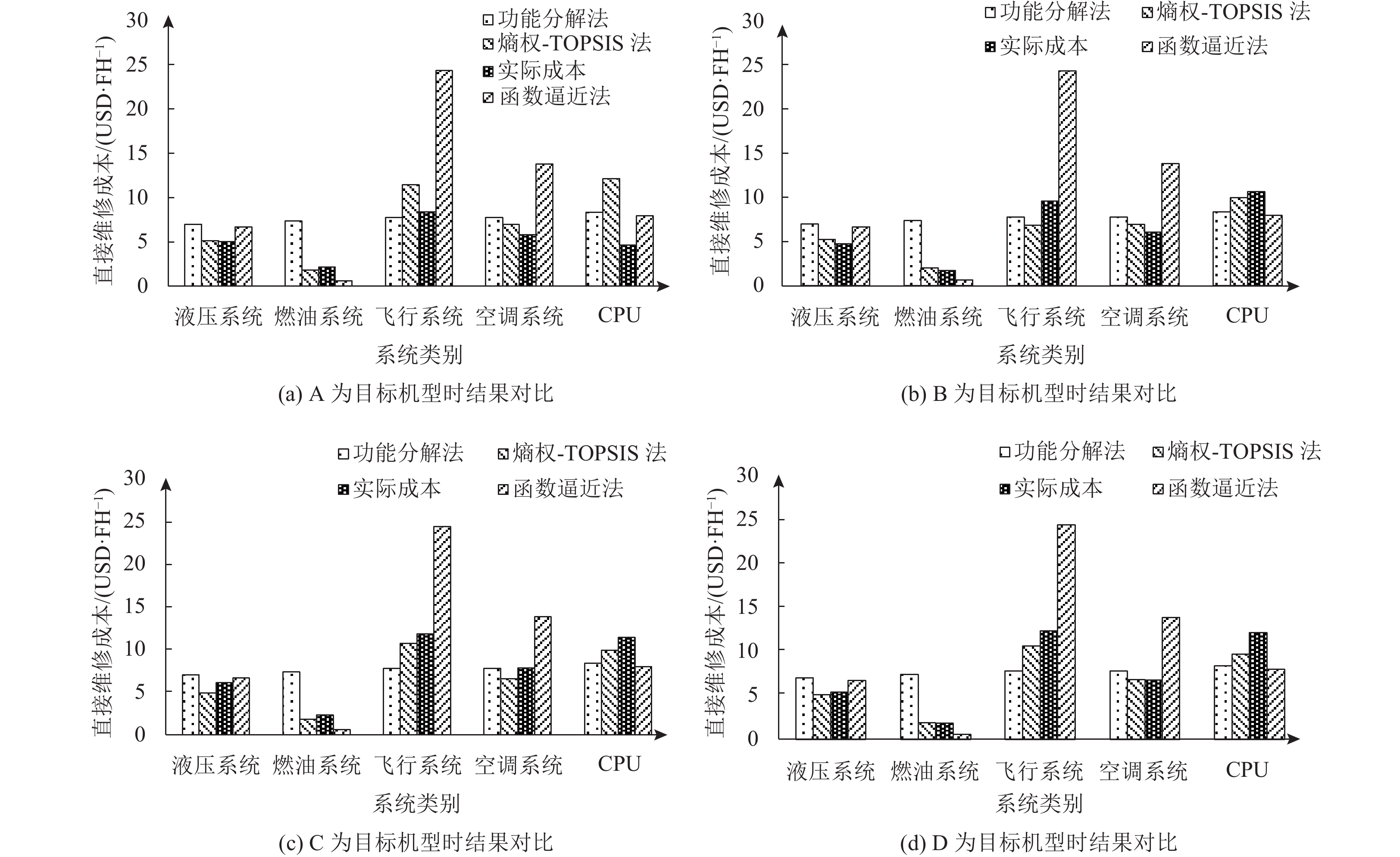
为了进一步验证本文所提方法的有效性，对A、B、C、D、E共5种机型做了交叉验证，所得结果对比如图4所示。通过对比可以看到：1) 分别以A、B、C和D为目标机型进行交叉验证时，采用功能分解法所求的燃油系统的直接维修成本与实际成本的误差较大，函数逼近法所求的飞行系统和空调系统的直接维修成本与实际成本误差偏大将近1倍；2) A机型为目标机型时，本文方法计算的飞行系统、CPU系统的分配值比其他几种机型作为目标机型时所得结果误差偏大；3) B、C、D和E机型分别为目标机型时，本文方法的计算结果均接近实际直接维修成本值；4) 5种机型进行交叉验证后发现本文方法的分配结果准确性高于功能分解法和函数逼近法。

4 结论

本文针对民机直接维修成本分配问题，应用信息熵确定类似机型设计参数权重，TOPSIS模型寻求其余机型中的最优解和最劣解，然后采用加权距离构建目标民机与最优解和最劣解之间的距离，计算机型的相似度，建立了民机直接维修成本分配模型，弥补了功能分解法和函数逼近法确定机型权重时的不足，对我国民机维修成本控制工作有重要的参考价值。

在实际操作中，飞机制造商可依照本文方法进行民机直接维修成本的分配，对本文的民机直接维修成本分配模型进一步验证及优化。