受工作性质以及工作条件的影响，民用航空助航灯光站(civil aviation lighting station,CALS)工作人员工作时，存在工作结果安全性能与稳定性能低、助航灯意外损坏情况的确认与修复能力低下以及反馈修复情况不及时等一系列问题^[1-2]。这会影响航容量的大小，严重情况下可能会造成停航等众多问题。于是，如何在最大程度上解决和降低上述问题的发生概率成为研究的重点。研究的出发点为通过设计合理的排班优化方法，有针对性地解决上述问题。通过提升CALS人员管理的工作效率，增强航班运行的安全性和可靠性，并有效地提高航空公司的经济效益^[3]。

由于助航灯光站在人员管理方面受到太多因素的影响，特别是助航灯光备件的更换频次以及特殊天气工况等因素^[4]，国内外的研究人员在此方面的研究比较少。目前与之比较相似的案例大多是在日常工业企业中的规划管理^[5]、医院护士排班管理^[6]、餐饮行业服务性人员的管理^[7]等，而近几年以护士排班优化的研究最为突出。国内外研究人员提出了众多的优化算法：Isken^[8]和Glass等^[9]提出的整数规划方法；He等^[10]采用的列生成算法；变领域的禁忌搜索算法^[11]；分散式的禁忌搜索算法^[12]以及Huang等^[13]提出的进化算法和Anwar等^[14]使用的超启发式算法等。对于CALS人员管理来说，从安全性问题上考虑，可以借鉴大型工业企业中的排班管理方案；相比之下，从突发性解决问题的角度考虑，医院中的排班管理方法与之存在相同点。

借鉴以上的研究分析结果，本文针对CALS人员管理的切实性以及特殊性，提出了一种改进的禁忌搜索算法。针对CALS人员管理几种不同的工作情况，该算法在禁忌搜索算法(tabu search)的基础上^[15]，提出了一种适合CALS人员管理的带权禁忌搜索算法。该算法引入了奖惩制度因子，能够实现针对性的优化管理。为能够增加管理的全面性，算法采用了分区领域动作搜索的方式，并且在其中设置了评估因子，对概率可忽略的领域进行忽略计算，极大地避免了结果重复，提高了管理的效率，以实现对CALS人员管理效率的优化。

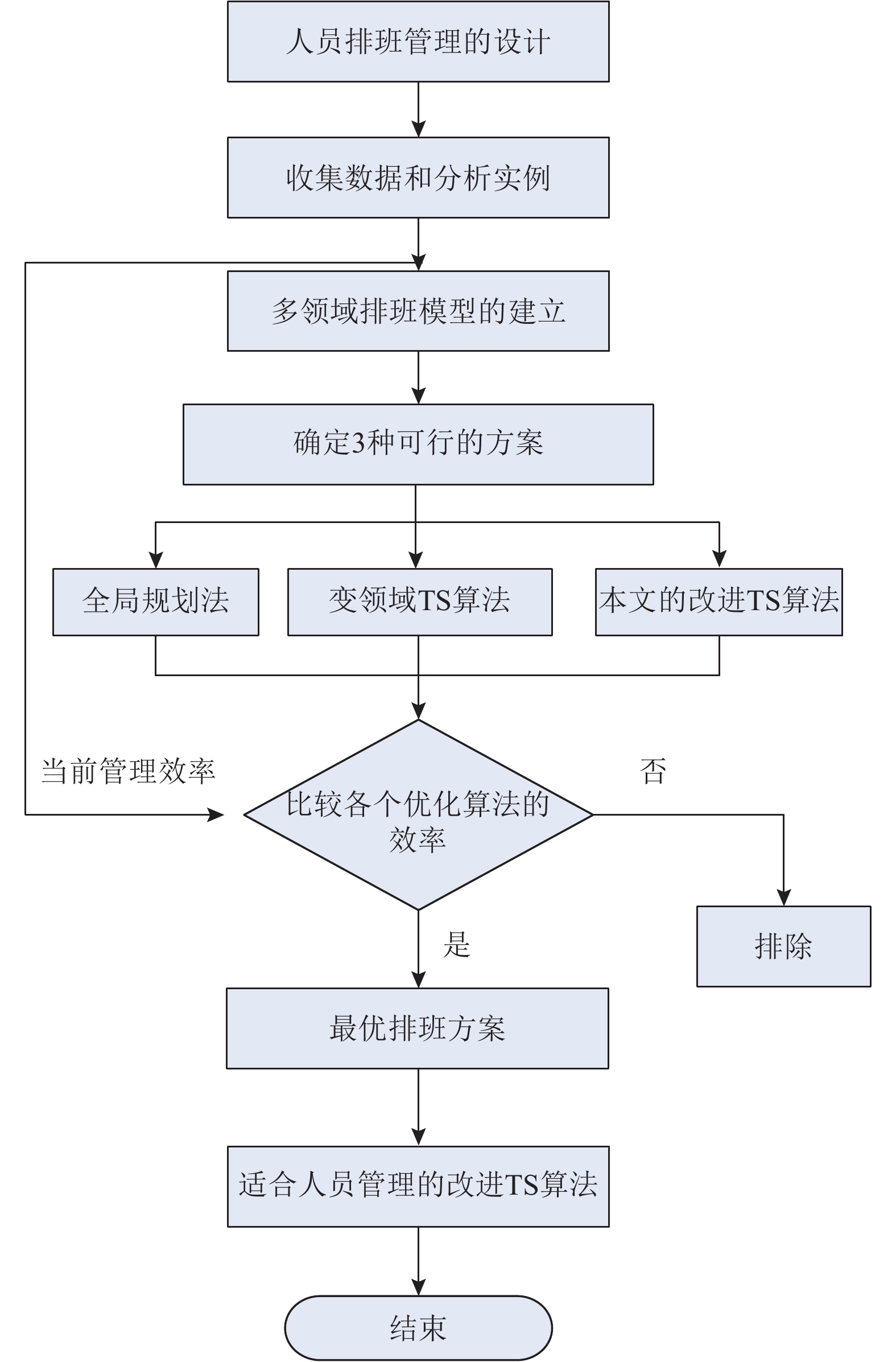
1 CALS人员总体排班管理分析 1.1 CALS人员排班管理总体设计分析

在对CALS人员进行排班规划时，首先需要明确工况以及限制工作人员工作的各种条件。具体到工作中，工作人员的工作主要分为灯光实时监控和灯光故障检测维护^[16]。实时监控不只是要求工作人员进行监控，也需要做好与机场总台之间的联系，确定飞机出入港的情况与时间，以便合理安排巡检维修人员的工作。因此针对整体的CALS人员管理，设计如图1所示的整体流程。

1.2 CALS人员排班管理模型的建立与分析

通过了解CALS在人员管理方面的具体情况，需要满足基本的优化目标：在保证CALS人员的工作效率以及基本的工作状态的基础上，有针对性地提高效率。在建立模型时，首先需要明确工作人员每天的工作班次以及工作人员所掌握的技能，例如白班和夜班、检查维修和实时监控等。在建模的过程中设置时间班次和技能组合成的单元槽，以此来进行分析。这样就可以得到(白班，检查维修)、(夜班，实时监控)等的单元槽。休息可以作为一个特殊的单元槽进行分析。建模时，主要通过对调查统计的数据情况进行分析，在已知工作人员的数量、排班周期以及每个单元槽的人数需求的情况下，按照较为高效的方法进行人员排班。在具体的实施过程中需要保证安排的工作人员能够在相应的单元槽内执行相应的技能。在整个排班的过程中，由于无法确定后续工作情况的变化，所以要进行增班、减班以及变换排班等多方面的考虑。另外，也需要考虑设置工作人员不可违背的硬性约束条件以及尽量避免违反的限制条件。

通过分析数据，建立了如表1所示的灯光站工作人员一周正常排班的计划模型表。在只考虑正常排班的情况下，以一周的计划为例，完成合理的排班分析。其中，令D为排班周期中各天组成的集合；N为员工的集合；H为班次的集合；K为技能的集合。 ${{X}^H}$ 为一个 $\left| N \right| \times \left| D \right|$ 的矩阵，表示各个工作人员在一周时间内被安排的班次； ${{X}^K}$ 为一个 $\left| N \right| \times \left| D \right|$ 的矩阵，表示工作人员在相应的班次上使用相应的技能； ${{X}^H}$ 和 ${{X}^K}$ 共同构成了正常排班情况下的模型矩阵 ${X}$ ，可以得出该模型下的每一个工作人员在一周之内的工作排班情况。

针对整个灯光站人员管理所要确定的优化条件以及目标为：以合理的排班方式对灯光站人员进行排班管理和提高灯光站工作人员的工作效率。

影响人员排班管理的决策变量主要需要考虑2个方面：1) 灯光站备件的定期维护以及定期寿命检测工作，这种情况下安排正常的如表1所示的工作排班即可；2) 灯光设备的突发性损坏和检测等情况，这种情况下需要进行加班或者换班的工作。

人员排班管理必须考虑4个约束条件(此条件不可违背)。Y₁ 为唯一工作量安排约束，这一条件在具体的排班设计中保证自动满足；Y₂ 为人员需求最小值设置，每天的排班人数不能小于设置的最少人数；Y₃ 为不允许连续排班，不可安排同一个工作人员在连续的2个班次中工作；Y₄ 为技能条件约束，必须要保证安排在某一特定单元槽内的工作人员具有与之要求相同的技能，保证工作的进行。在此以表1为例进行约束条件数学模型的分析如下。

$ \begin{split} & \qquad\forall n \in N,\forall d \in D,\forall h \in H,\forall k \in K{\text{。}}\\ & \qquad{Y_1}:({n_1},{d_1}) = ({h_1},{k_2})\cap [({n_3},{d_2}) = {\text{Ø}} ]{\text{；}}\\ & \qquad{Y_2}:{\text{在}}{d_1}{\text{天内}},\forall {n_x} \in N,{\rm{min}}\;(x) = 2,x {\text{≥}} 2{\text{；}}\\ & \qquad{Y_3}:({n_1},{d_1}) \!=\! ({h_1},{k_2}) \!\cap\! [({n_1},{d_1}) \!\ne \!({h_2},{k_2})] \!\cap\! \left[({n_1},{d_1}) \!\ne\! \right.\\ & \left. ({h_2},{k_1}) \right] \!\Rightarrow\! ({n_1},{d_2}) \!=\! [({h_1},{k_1})\!\parallel\! ({h_1},{k_2})\!\parallel\! ({h_2},{k_2})\!\parallel\! ({h_2},{k_1})\!\parallel \!{\text{Ø}} ]{\text{；}}\\ & \qquad{Y_4}:({n_1},{d_1}) = ({h_1},{k_x}) \cap [{k_x} = {k_2}]{\text{。}} \end{split} $

注意设置尽量避免违背限制条件如下。(此条件违背时，采取惩罚措施) 。S₁ 为最佳工作人数设置，工作人数设置不可过多，也不可小于最小值设置；S₂为连续工作时长设置，连续工作时长若出现不足或者是冗余的情况，则需要受到惩罚；S₃ 为工作班次不可连续约束，保证每一个工作人员不能连续在一天之内既在白天工作又在夜间工作；S₄ 为休息时间限定设置，工作人员的休息时间必须要保证在规定的区间内，不可超出或者少于规定的休息时间；S₅ 为工作偏好的限定，若某个工作人员请求不能够在某一天的某一班次进行工作，但仍被安排至这一天进行工作，则需要进行惩罚；S₆ 为周末合理化排班设置，必须要保证每个工作人员的周末工作安排合理：两天均工作或者两天均休息；S₇为总排班数约束，在整个排班周期中，保证每个工作人员的总工作天数必须在给定的范围内。

2 改进TS算法的分析

TS算法是由Glover^[17]于1986年提出的一种全局逐步寻优的搜索算法，也是一种模拟智力过程的“爬山”算法。为解决助航灯光站人员管理存在的问题，针对TS算法本身的特点以及CALS人员管理的特点，本文将TS算法作了一些改进。改进的TS算法在具体的计算过程中给每个员工设置奖惩因子。该权重的加入加强了对违反约束条件员工工作效率的优化。在进行整体全局分析时，算法引入不同的邻域动作，并且在其中设置了评估因子，对概率可忽略的领域进行忽略计算，极大地避免了结果重复，从而提高优化的效率。

通过对算法的分析，在保证不违背Y₁、Y₃、Y₄的前提下，初始解的设定是在一个周期内从第一天至最后一天依次进行排班，并且在排班的过程中，对于每周的每一天，需要统计所需技能的占有最小需求min D。在保证满足Y₂的条件下，根据拥有相对应技能的员工人数的比例确定先排哪个对应的班次。若对应技能的工作人员人手充足，排班比较容易满足，即可放在后面排；如人手比较短缺，则需要优先考虑。理论上，初始解的生成过程中会产生无法满足要求的非法解，但是由于最优化人数设置的原因，可以实现将非法解排除从而提高初始解的质量。

在具体的算法应用分析过程中，不仅要考虑单一的正常排班的情况，还需要考虑多领域的变化情况：增加排班、减少排班、变更排班以及交换排班。在具体的实验过程中需要保证的就是领域选择的概率。概率p由相应的权重c控制，初始时概率相同，在运行的过程中根据领域的变化动态调整c。每一次搜索领域内最优动作m时，会出现如式(1)所示的4种情况。

$ \qquad c \!=\! \left\{ \begin{array}{l} \!c \!+\! \lambda ({\varOmega _1} - c),m{\text{改进搜索的最优解}}{\text{；}}\\ \!c \!+\! \lambda ({\varOmega _2} - c),m{\text{改进当前解}}{\text{；}}\\ \!c \!+\! \lambda ({\varOmega _3} - c),m{\text{无改进但存在合法动作}}{\text{；}}\\ \!c \!+ \!\lambda ({\varOmega _4} - c),{\text{不存在合法动作}}{\text{。}} \end{array} \right.$

(1)

其中， ${\varOmega _1} {\text{＞}} {\varOmega _2} {\text{＞}} {\varOmega _3} {\text{＞}} {\varOmega _4} {\text{＞}} 0$ ，为基准值， $\lambda \in \left( {0,1} \right]$ ，控制c向基准值趋近的速度，并且 $\lambda $ 越大收敛速度越大。

确定邻域后，按照禁忌搜索的策略进行计算，在其过程中按照基本思路设置禁忌表，避免陷入局部最优陷阱。由于CALS员工排班问题存在着诸多约束与限制条件，所以在计算此问题时对于目标函数值的设置与计算就更加困难。并且在计算的过程中，不同领域的计算情况又存在很大的差异，大领域的运算量巨大。为了节约计算时间，每一次领域动作所生成的目标函数的变化量都被保存起来，形成统计计算的数据集，这有助于加快计算的进程。同时，需要记录最优动作及其引起的目标函数增量，当其他领域排班发生改变时，需要不断地更新最优的数据结果。

为了增加管理效率，算法设置了惩罚因子 $\omega $ 。在所有限制条件中，保证针对单一工作人员所考虑的限制条件计算的独立性，可对每一个可能存在的惩戒情况进行细分，将所有可能出现的惩罚情况总和表示为

$ \qquad{f^S}_j\left( {{X_i}} \right) = \sum\limits_{n \in N} {{\omega _n}} {f^S}_j\left( {{X_{i,n}}} \right){\text{。}} $

(2)

其中， ${f^S}_j\left( {{X_{i,n}}} \right)$ 表示解 ${X_i}$ 中员工n限制条件 ${S_j}$ 的惩罚； ${\omega _n}$ 为算法引入的员工n的惩罚权重。起始时所有员工的权重 ${\omega _n}$ 相等，在具体的实现过程中，将对该权重进行不断的调整。计算开始时，权重的初始值设置相同，搜索过程中通过增加惩戒较多人员的权重，有针对性地优先改进此类人员的排班计划。

3 CALS具体人员工作管理分析

在具体的算法应用分析过程中，考虑多领域的变化情况时，首先需要分析可能出现的排班变化情况，而对于其他变化情况可以分为以下几种情况：增加排班、减少排班、变更排班以及交换排班。

增加排班 　原定在第d天休息的员工n由于工作改动需要被安排在该工作领域中进行工作。可得该领域的集合为

$ \!\!\!\!\qquad{M_1}(X) = \left\{ \begin{array}{l} \left. {{m_1}(n,d,h,k)} \right|\forall n \in N,\forall d \in D{\text{，}} \\ \forall h \in H,\forall k \in K{\text{，}} \\ {{x}^H}_{n,d} = {\rm{ShiftOff}} \wedge h \ne {\rm{ShiftOff}}{\text{。}} \\ \end{array} \right\}{\text{。}} $

(3)

鉴于表1正常排班的情况，将原本在d₁天休息的员工n₅安排到单元槽(h₂,k₂)工作，其排班结果如表2所示。

减少排班 　原本在第d天工作的员工n，现在安排其在该班次进行休息。领域的集合为

$ \qquad{M_2}(X) = \left\{ \begin{array}{l} \left. {{m_2}(n,d)} \right|\forall n \in N,\forall d \in D{\text{，}} \\ {{x}^H}_{n,d} \ne \rm{ShiftOff}{\text{。}} \\ \end{array} \right\}{\text{。}} $

(4)

在正常排班的情况下，安排原本在d₁天工作的员工n₃休息，其排班结果如表3所示。

变更排班 　安排在第d天班次x上的员工进行变更，将其安排于其他班次工作。该领域的集合为

$ \!\!\!\!\!\!\!\!\!\!\qquad{M_3}(X) = \!\left\{ \begin{array}{l} \left. {{m_3}(n,d,h,k)} \right|\forall n \in N,\forall d \in D{\text{，}} \\ \forall h \in H,\forall k \in K{\text{，}} \\ {{x}^H}_{n,d} \ne {\rm{ShiftOff}} \wedge h \ne \\ {\rm{ShiftOff}} \wedge ({{x}^H}_{n,d} \ne h \vee {{x}^K}_{n,d} \ne k){\text{。}} \\ \end{array} \right\}{\text{。}} $

(5)

将第d₆天员工n₃原本安排到单元槽(h₂,k₂)工作变更为(h₁,k₁)，其结果如表4所示。

交换排班 　即为2个工作人员大面积的交换工作量。该领域的集合为

$ \!\!\!\!\!\!\quad{M_4}(X) =\left\{ \begin{array}{l} \left. {{m_4}({n_1},{n_2},{d_1},{d_2})} \right|\forall {n_1},{n_2} \in N{\text{，}} \\ \forall {d_1},{d_2} \in D{\text{，}} \\ {d_1} {\text{≤}} {d_2} \wedge (\sum\limits_{d = {d_1}}^{{d_2}} {C({{x}^H}_{{n_1},d} \ne {{x}^H}_{{n_2},d})} ) {\text{＞}} 0{\text{。}} \\ \end{array} \!\!\!\right\}{\text{。}}\!\!\!\!\!\!\!\!\!\!\! $

(6)

交换n₃和n₄从d₂到d₅天的排班如表5所示。

结合具体的CALS人员管理，通过调研和对现有数据的分析，对各类方法进行验证，统计其验证算例结果。在实验的过程中，进行了60组算例分析，其中包括4周内排班35个员工、8周内排班35个员工、4周内排班70个员工以及8周内排班70个员工等情况。选取有代表性的20组，并且统计不同方法下的结果，如表6所示。其中员工数、排班周数、文件编号、需求改变量编号构成了算例的命名方式。算例1 4n35-0-1-4-7-9为35个员工，在4周的工作中，初始值为0号文件夹中的数据，4周需求改变量文件编号分别为1,4,7,9。在求解的过程中，得到目标函数值越小证明模型分析的效果越好。结果如表6所示。

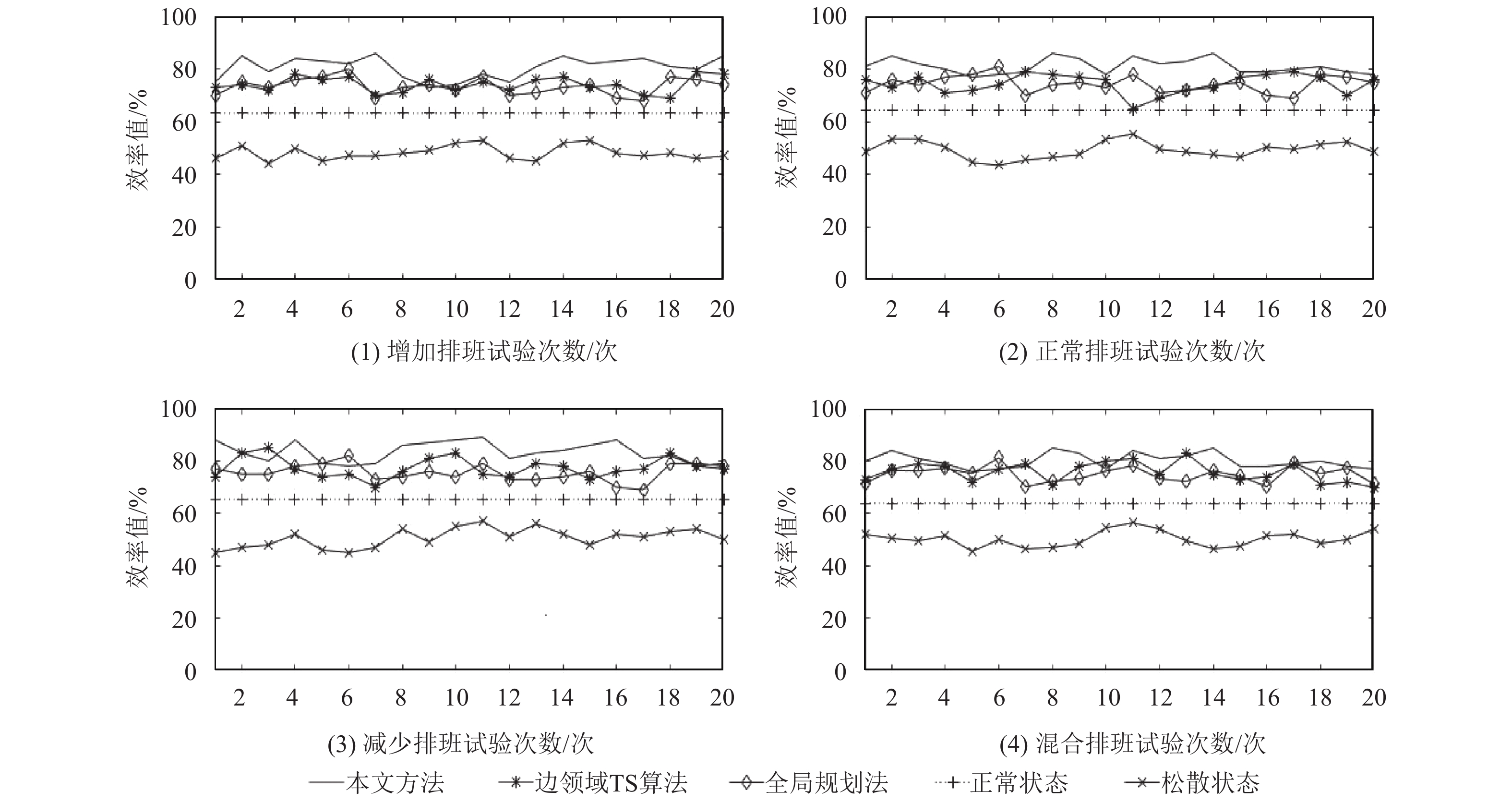
从目标函数值的变化可以得出，该方法的目标函数值小于其他2种方法，并且克服非法解(99 999)的产生，有较高的稳定性。鉴于CALS人员管理的情况，将结果转化为员工工作效率结果进行反映，得到不同工况下不同排班方法的工作效率，并对结果进行统计，得到如表7和图2所示的有效结果。

从仿真数据结果可以得出，通过对TS算法本身进行改进，并且设置惩罚权重，能够有效提高CALS人员管理的效率值至82.23%，相较于整体规划法的74.69%和变领域禁忌算法的77.27%分别提高了7.54%和4.96%。

4 结论

本文提出了一种适用于CALS人员管理的改进TS算法。针对CALS在人员管理方面存在的问题与缺陷，该方法以禁忌搜索为核心，改进了动态调整的惩罚权重，设计了多领域排班分析的情况，实现了针对性的优化。在进行建模时，有针对性地进行设计，并使之与现存的提高管理效率的方进行比较，对数据结果进行汇总分析，得到本方法的目标函数值小于其他方法的目标函数值。此外，从对有效效率值的结果分析中可以看出，本方法的加权有效效率值高达82.23%，相比其他方法提高了5%~8%。所以，本文的研究对提高CALS人员管理效率有一定的应用价值。