市场上小批量、多品种的货物越来越多,客户需求的不确定性以及个性化程度越来越高,这种趋势导致了客户订单中种类数目的增多和单品种订单数量的减少[1]。在现代板式家具行业中,传统的大规模生产库存模式已经不适应这种发展趋势,许多企业开始转向大规模定制生产。大规模定制的核心是在产品品种多样化和定制化急剧增加的情况下,不增加相应的成本并大规模生产个性化产品[2]。然而,定制化生产往往会带来2个问题,即工序非作业时间的增加以及原材料成本的上升。现代板式家具的生产环节虽然工序少,机器自动化程度较高,但在处理不同颜色以及不同厚度的板块时经常需要频繁调整机器设备,这大大降低了机器的设备利用率以及生产效率。同时,因为订单之间各不相同,若是按照单个的个性化订单安排生产,原材料的利用率会大大降低,原材料成本大幅上升。但是,通过合理的生产排产,可以最大程度地规避这2个问题。
关于制造型企业的生产排产,文献[3]对此作了梳理,并总结归纳出5个方面的排产问题。以生产设备能力为核心[4]的排产问题;以生产订单为核心[5]的排产问题;以工艺路线优化为核心[6]的排产问题;以生产成本控制为核心[7]的排产问题;以生产系统目标优化为核心[8]的排产问题。而这些排产问题都会涉及到订单如何组批这个关键问题。订单组批,即为提高设备的利用率以及原材料的利用率,将多个订单组合成一个批次去投放生产。为解决定制化生产带来的影响,许多家具企业往往采用订单组批的方式安排生产。
本文基于最小化生产调整时间以及最大化原材料利用率这2个出发点,提出了一种板式家具订单组批的启发式算法,通过大量的大规模算例进行了测试,并与其他启发式算法进行比较,最终验证了该算法的有效性。
1 数学模型 1.1 问题描述本文研究的是板式家具生产企业的订单组批问题。板式家具生产流程包含开料、封边、钻孔、清洗4道工序。假设每道工序上有m台机器设备,所有的板块都需要按顺序依次经过这4道工序,工序与工序之间的板块以固定数量的批次进行传递。板块的颜色和厚度是影响工序效率的因素。当板块颜色或厚度不同时,部分工序需要进行机器调整,产生机器调整时间T。已知受影响最大的工序是封边,其余工序的机器调整时间可忽略不计。假设到达的订单集合O为{
如何对订单进行组批,使得原材料的利用率最大化,以及机器调整时间最小化,为本文的研究内容。
1.2 数学模型数学模型的构建主要基于以下假设和前提:
1) 订单包含的板块数量及种类在有限范围内随机确定;
2) 一个订单只可以组批一次;
3) 批次与批次之间不会互相交叉混合;
4) 排样用的原料板面积为常数;
5) 封边工序在加工不同颜色和厚度的板块时需要调整机器设备;
6) 因为颜色和厚度而调整机器的时间相同;
7) 板块只有完成上一道工序才能进入下一道工序;
8) 订单需要在交货期内完成。
这些假设和前提是基于对中山市某板式家具企业生产基地的实地调研。据统计数据,除异形板外,绝大多数订单包含的板件均属于少数的某些尺寸大小,因此种类可以在有限范围内随机确定。绝大多数订单包含的板件数量在20~40块的范围内波动,因此可以假设订单包含的板块数量及种类满足某种随机分布。每个订单只能组批一次,并且不能跨批次组批,批次之间也不能相互交叉混合。这是因为订单多次组批意味着订单被拆分,会影响订单在分拣时的齐套性,导致后续工序的在制品数增多,增加了订单的分拣周期。而后续工序的堵塞又会反过来影响前面工序的生产。开料工序所使用的原料板通常为统一规格的标准大小,因此假设排样用的原料板面积为常数。封边工序在加工不同颜色或厚度的板块时,需要停下来更换封边带或调整机器卡位,这两部分的调整时间经过现场测时基本接近。
决策变量为
| $ {Y_{k,i,j}} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} 1,&{{\text{第}}k{\text{个批次的第}}i{\text{个订单的第}}j{\text{个板块}}}\\ {}&{\text{封边时与后一块板颜色或厚度不同}}; \end{array}\\ \begin{array}{*{20}{l}} 0,&{{\text{其他}}}{\text{。}} \end{array} \end{array} \right. $ |
问题的数学模型如下。
| $\quad\quad\min\left\{ \begin{array}{l} {Z_1} = \displaystyle\sum\limits_{k = 1}^a {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{Y_{k,i,j}}T} } }, \\ {Z_2} = \displaystyle\sum\limits_{k = 1}^a {\sum\limits_{l = 1}^b {p\frac{{S - {S_{kl}}}}{S}} }{\text{。}} \end{array} \right.$ | (1) |
| $\begin{split}&{\rm s.t.}\\ \quad\quad &\sum\limits_{k = 1}^a {\sum\limits_{l = 1}^b {{S_{kl}}} } {\text{≤}} abS;\end{split}$ | (2) |
| $\quad\quad p {\text{≥}} 1;$ | (3) |
| $\quad\quad\sum\limits_{k = 1}^a {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{Y_{k,i,j}}} } } {\text{≥}} 0;$ | (4) |
| $\quad\quad{t_{1,k,i,j}} + {t_1} {\text{≤}} {t_{2,k,i,j}};$ | (5) |
| $\quad\quad{t_{2,k,i,j}} + {Y_{k,i,j}}T + {t_2} {\text{≤}} {t_{3,k,i,j}};$ | (6) |
| $\quad\quad{t_{3,k,i,j}}{\rm{ + }}{t_3} {\text{≤}}{t_{4,k,i,j}};$ | (7) |
| $\quad\quad{t_{4,k,i,j}} + {t_4} {\text{≤}}{t_{5,k,i,j}};$ | (8) |
| $\quad\quad{t_{5,k,i,j}} + {t_5} {\text{≤}} {D_{k,i}}{\text{。}}$ | (9) |
式中,
a为批次数;
b为原料板数;
n 为订单数;
c为板块数;
式(1)表示问题的目标函数,其中,Z1表示最小化调整时间,Z2表示最小化废料率;式(2)表示所有板块的总排样面积小于总的原料板面积;式(3)表示排样废料利用率的惩罚系数,大于1表示废料率越高惩罚越重;式(4)表示总的调整次数大于或等于0;式(5)表示板块必须经过开料工序才能进入封边工序;式(6)表示板块只有经过封边工序才能进入钻孔工序;式(7)表示板块必须经过钻孔工序才能进入清洗工序;式(8)表示板块必须经过清洗工序才能开始包装;式(9)表示订单板块的生产必须满足交货期限的要求。
1.3 模型分析原问题是双目标问题,求解双目标问题通常有2种解法。第1种是化多为少,即把双目标化为比较容易求解的单目标,如通过线性加权法将2个目标加权转化为单目标问题求解;第2种叫序贯优化法,即把目标按其重要性给出一个序列,每次都在前一目标最优解集内求下一个目标最优解,直到求出共同的最优解。为了求得原问题的目标最优解,本文采用第2种方法。第1目标是最小化调整时间,把求解第1目标的结果作为约束条件,求解第2目标最小化排样废料率。
因为只有颜色和厚度发生改变才会引起封边工序的机器调整,因此,理论上批次最少的调整次数等于该批次订单的板块颜色种类数量
| $\quad\quad\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{Y_{k,i,j}}} } {\rm{ = }}CH {\text{。}}$ |
但是一个订单可能同时包含不同颜色和厚度的板,并且一个订单只能出现在唯一的一个批次中,所以理论最小值很难实现。因为家具订单基本只包含一种颜色,所以唯一的不确定因素为订单包含的厚度种类数量。如果将不同组合的厚度种类分开来,总共可以得到
| $\quad\quad\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{Y_{k,i,j}}} } \leqslant C\left( {{2^H} - 1} \right){\text{。}}$ |
因此,对第1个目标函数进行松弛,得到新的目标函数为
| $\quad\quad {\min} \;\; {Z = \sum\limits_{k = 1}^a {\sum\limits_{l = 1}^b {p\frac{{S - {S_{kl}}}}{S}} } } {\text{。}}$ |
同时,约束条件(4)变更为
| $\quad\quad 0 \leqslant \sum\limits_{k = 1}^a {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^c {{Y_{k,i,j}}} } } \leqslant aC\left( {{2^H} - 1} \right){\text{。}}$ |
至此,将双目标问题转化为单目标问题。
2 算法研究当所有的订单到达之后,所有的订单信息已知,就属于确定性问题,可以通过算法求得精确解。然而,当订单的数量到达一个规模时,求解的成本代价就会过高。以惠州的某家板式家具企业的生产数据为例,企业每天的日产能大约为17 500块板块,处理超过700个订单,板块包含的板件厚度种类数量少则1种,多则3~4种。生产的快节奏要求至多2 h就要进行一次组批,每次组批的订单数在30~50个不等,每次组批的板块数量大约1 000块。面对如此庞大的组批需求,如果使用精确求解算法,求解的时间显得过于漫长,无法满足企业实际的生产需要。因此,需要设计一个能够进行快速组批的启发式算法,来满足企业快速生产的需求。
2.1 算法设计关于订单组批问题,文献[9]已经证明大规模问题情况是NP难的,求解精确解是比较困难的。而在实际生产中,企业往往要求订单组批处理时间短,或是响应速度快。因此,启发式算法成为了许多学者研究的对象。Gibson等[10]提出了GS启发式算法用于大型仓储环境。在此基础上,Rosenwein[11]提出了MAA和COG启发式算法。上述3种启发式算法的基本思想是:通过合理规定的差异度函数计算出订单间的相似程度,并在此基础上对订单进行聚类,最终生成分批后的订单[12]。文献[13]提出了基于时间延迟的静态和动态2种不同状态下的订单分批方法;文献[14]则考虑了订单的完成期限,采用改进的固定时间窗订单分批启发式规则来求解模型,最小化平均有效订单服务时间。为了求得更为准确的解,许多学者也会研究如何运用智能算法进行订单组批。如Henn等[15]提出了基于禁忌搜索原理的方法,用于解决仓库分拣订单组批的问题。
实际生产过程中,工厂往往采用简单的启发式算法规则,简单易操作,有广泛的应用场景。文献[16]指出,一些简单的调度规则在经过某种方式的组合之后所形成的新组合规则有时候比之前的简单调度规则性能更好,效果更佳。
因此,基于以上的研究,本文提出一种基于板块颜色、厚度以及板块排样的订单组批算法,记为CHL。
CHL算法的步骤如下。
1) 输入参数,板块的颜色种类数量
2) 根据板块的颜色种类数量
| $\quad\quad Q = \left\{ {{Q_1},{Q_2}, \cdot \cdot \cdot ,{Q_u},u = CH} \right\}{\text{。}}$ |
3) 将订单划分到对应的订单类别中,如果有订单包含多种颜色或厚度,则将其作为单独的一种组合。
4) 针对第1个订单类别,根据板块总数量最多的订单优先原则选取第1个订单,根据板材规格大小比例
5) 根据步骤4)的原则继续选取订单,直到Sum≥阈值F,F为事先设定的板件数量值,通常由实际统计的板件数据给出,并且排样利用率
6) 当第1个订单类别的所有订单组批完毕后,对剩下的订单类别循环步骤4)到步骤6)的操作,直至所有订单类别均组批完毕。
7) 所有的组批批次
8) 根据封边机器数量计算每台封边机器的批次顺序,并输出最终的总调整时间
由于在现有的文献当中难以找到满足本文所研究问题的测试数据集,所以,本文以板式家具企业的实际生产数据为基础,在查阅大量相关文献,结合研究内容之后设计出本文的测试数据集。可能影响算法效果的因素有:封边机器的数量
| 表 1 影响因子 Tab. 1 Influence factors |
本文拟选取2种目前在工厂较为常见的简单的启发式规则算法,通过不同的水平组合成更多的不同的规则算法来与本文提出的启发式算法CHL进行对比分析。第1种是订单数量上限规则,即将超过某个阈值的订单数量作为一个批次,记为rule1。阈值可以取10、20、30、40、50共5个数值,分别对应调度规则rule1-10、rule1-20、rule1-30、rule1-40、rule1-50。第2种规则是将交货期与订单数量上限结合的算法,即先按交货期进行分类,再用订单数量上限规则算法进行组批,记为rule2。同样的,rule2算法取5个参数值,分别为调度规则rule2-10、rule2-20、rule2-30、rule2-40、rule2-50。与CHL算法一起,共同组成11个调度方法。为了验证设计算法与对比算法的准确性,本文选取分支定界算法求出精确值,对比结果。
3.3 仿真结果及分析在模拟算例中,考虑到封边机器的数量和板块的厚度,总共可分为6种参数配置。为了保证数据的可靠性,需要对每一种水平组合做多次仿真实验。考虑到可能因为测试算例的偶然性导致的结果偏小或偏大,至少应该做3次以上的实验。因此在每一种参数配置的情况下,都对11个调度方法分别进行10次仿真测试,即总共需要做660次实验。每次测试都是不同的1 000个订单的数据集,取其平均值作为相应结果,并记录每次仿真的中央处理器运行时间。以上所有算法的仿真测试均采用Matlab R2017a软件在中央处理器为Intel Core i7-7700HQ,2.80 GHz和内存16 GB的计算机上进行仿真实验。仿真指标主要包括每台设备的批次数BP,每台设备的调整时间TP以及排样利用率SR。仿真结果如表2~表4所示。
| 表 2 仿真实验结果(N=2) Tab. 2 Simulation results (N=2) |
| 表 3 仿真实验结果(N=3) Tab. 3 Simulation results (N=3) |
每种水平组合都进行了10次实验,这避免了因为订单数据集的偶然性引起的实验结果偏低或偏高的影响。为了验证计算结果的精确度,对同样的算例采用精确求解算法计算,结果如表5所示。
| 表 4 仿真实验结果(N=4) Tab. 4 Simulation results (N=4) |
| 表 5 精确解结果 Tab. 5 Exact solution results |
从表2~表4的数据中可以发现,随着订单数量上限阈值从10上升到50,总的批次数降低,每一台机器设备分配到的批次数也降低。同时,批次中订单的数量跟调整时间呈负相关关系,跟排样利用率呈正相关关系。并且,随着封边机器从2台增加到4台,在相同的调度规则的调配下,调整时间明显下降。而随着厚度种类数量从1种增加到2种,所有调度规则计算下的调整时间均出现了大幅上升。
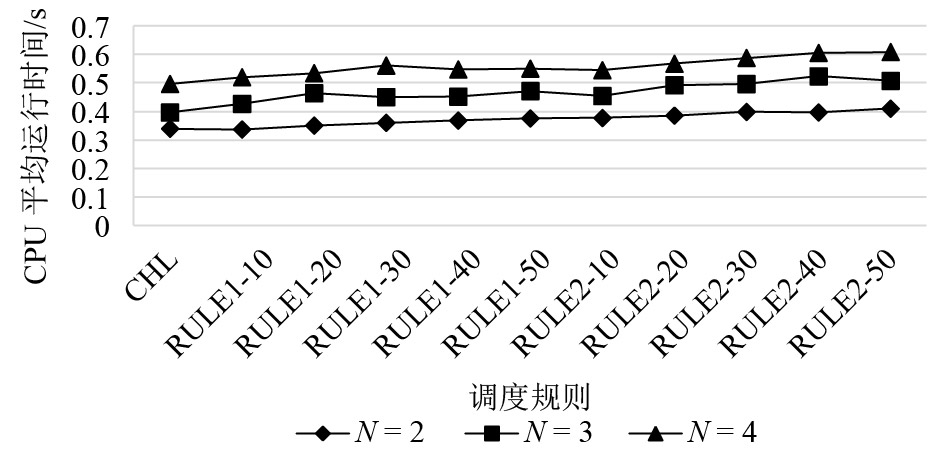
再将这几种调度算法所求的结果与精确解进行比较发现:不管在哪种环境条件下,CHL算法计算的工序调整时间结果都要大幅优于rule1算法和rule2算法。这说明了按照颜色和厚度事先分类对调整时间具有显著影响。而CHL算法在6种仿真环境下的平均调整时间约为24 min,接近精确解的17 min。在排样利用率方面,CHL算法虽然比rule1算法和rule2算法略低,但也超过了90%,基本满足了企业生产的基本要求。接着将所有调度规则的CPU平均运行时间做成折线图进行对比,结果如图1和图2所示。
|
图 1 调度规则CPU平均运行时间对比(H=18 mm) Fig. 1 Comparison of CPU average run time of dispatching rule (H=18 mm) |
|
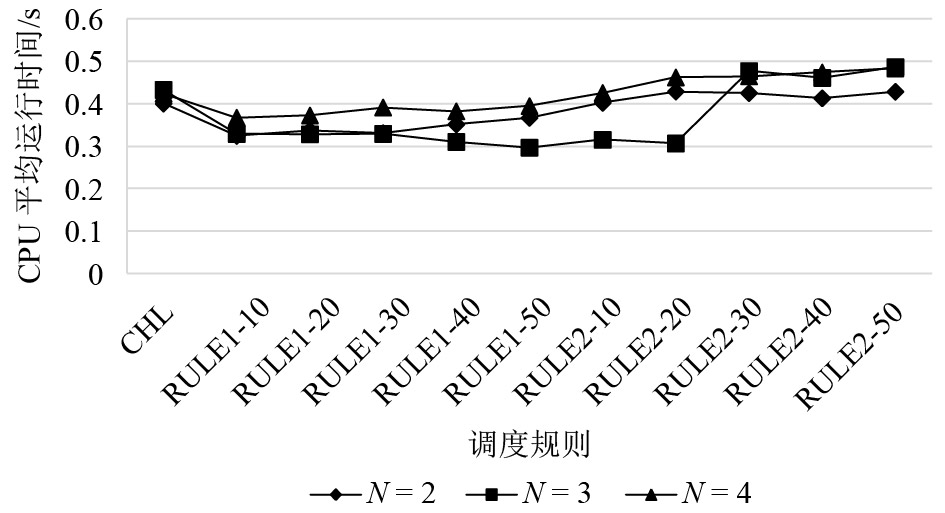
图 2 调度规则CPU平均运行时间对比(H=18 mm, 25 mm) Fig. 2 Comparison of CPU average run time of dispatching rule (H=18 mm, 25 mm) |
当只有1种厚度,3种颜色时,机器需要调整变化的情况较少,CHL算法表现出比rule1算法和rule2算法更快的计算速度。当厚度增加到2种,颜色保持3种时,CHL算法依然保持着快速的计算速度,与rule1和rule2算法基本相当。
本文采用了IBM公司的数学规划优化软件CPLEX对数学模型进行精确求解。CPLEX内置的分支定界算法在大规模问题上求解耗时过长。为了比较精确求解与CHL算法的速度,选择板件个数在50个以下的小规模算例进行对比。结果如表6所示。
| 表 6 精确求解时间(H=18 mm, 25 mm) Tab. 6 The speed of exact solution(H=18 mm, 25 mm) |
从表6可以看出,当其他条件不变,随着板件个数的增加,精确求解的时间快速增长,亦或者其他条件不变,随着机器数量的增加,求解的速度也快速变慢。
4 结论面向订单的离散型制造企业,在大规模定制生产的过程中,普遍面临着订单组批的问题。组批的规则与参数会影响到企业的生产指标。本文基于最小化工序调整时间以及最大化原材料利用率等目标,建立了一个数学模型,并设计了一个由组批规则组合构成的启发式算法。
为了研究组批规则与参数对生产指标的影响,本文基于某板式家具企业的实际情况设计了大规模的算例,并通过大量仿真分别收集了不同的数据。最后,本文对收集的数据进行了分析,并得出了相应的结论,即基于板块颜色和板块厚度的调度规则对订单分批的影响极大。
| [1] |
王艳艳. 并行自动分拣系统分拣任务及补货缓存优化研究[D]. 济南: 山东大学, 2012.
WANG Yanyan. Study on picking task and restocking buffer optimization of parallel automated picking system[D]. Jinan: Shandong University, 2012 |
| [2] |
约瑟夫·派恩二世. 大规模定制-企业竞争的新前沿[M]. 北京: 中国人民大学出版, 2000.
|
| [3] |
黄泽慧, 闫秀霞. 制造型企业生产排产研究综述与展望[J].
山东理工大学学报(自然科学版), 2012, 26(4): 81-86.
HUANG Zehui, YAN Xiuxia. The review and prospect of manufacturing enterprise production scheduling[J]. Journal of Shandong University of Technology(Natural Science Edition), 2012, 26(4): 81-86. DOI: 10.3969/j.issn.1672-6197.2012.04.018. |
| [4] |
周维, 程娟珠, 韩伟. 离散型制造企业基于设备的生产排产优化研究[J].
现代制造工程, 2015(5): 43-48.
ZHOU Wei, CHENG Juanzhu, HAN Wei. Research on the optimization scheme of production scheduling based on equipment in discrete manufacturing enterprise[J]. Modern Manufacturing Engineering, 2015(5): 43-48. DOI: 10.3969/j.issn.1671-3133.2015.05.009. |
| [5] |
王易. 纺织机械制造企业生产排产研究与系统应用[D]. 武汉: 武汉理工大学, 2014.
WANG Yi. Research of production scheduling and application of system for textile machinery manufacturing enterprise[D]. Wuhan: Wuhan University Of Technology, 2014. |
| [6] |
刘青, 白素宏, 卢军辉. 转炉特钢流程连铸-轧钢生产排产系统[J].
北京科技大学学报, 2008, 30(5): 566-570.
LIU Qing, BAI Suhong, LU Junhui. Production plan schedule for the casting-rolling process in BOF special steel plants[J]. Journal of University of Science and Technology Beijing, 2008, 30(5): 566-570. DOI: 10.3321/j.issn:1001-053X.2008.05.024. |
| [7] |
张贵军, 丁情, 王柳静, 等. 柔性车间生产排产调度优化方法[J].
计算机科学, 2018, 45(2): 269-275.
ZHANG Guijun, DING Qing, WANG Liujing, et al. Optimization method of production scheduling in flexible job[J]. Computer Science, 2018, 45(2): 269-275. |
| [8] |
倪庆楼. TOC方法在W工厂生产排产中的应用研究[D]. 广州: 华南理工大学, 2011.
NI Qinglou. One production planning method and it’s using research at W factory[D]. Guangzhou : South China University of Technology, 2011. |
| [9] |
HWANG H C, CHANG S. Order consolidation for batch processing[J].
Journal of Combinatorial Optimization, 2005, 9(1): 121-138.
DOI: 10.1007/s10878-005-5488-z. |
| [10] |
GIBSON D R, SHARP G P. Order batching procedures[J].
European Journal of Operational Research, 1992, 58(1): 57-67.
DOI: 10.1016/0377-2217(92)90235-2. |
| [11] |
ROSENWEIN M B. A comparison of heuristics for the problem of batching orders for warehouse selection[J].
International Journal of Production Research, 1996, 34(3): 657-664.
DOI: 10.1080/00207549608904926. |
| [12] |
伍经纬, 蔡临宁. 订单分批算法的适用性研究[J].
工业工程与管理, 2007, 12(4): 104-107.
WU Jingwei, CAI Linning. Applicability analysis of different order batching algorithms[J]. Industrial Engineering and Management, 2007, 12(4): 104-107. DOI: 10.3969/j.issn.1007-5429.2007.04.023. |
| [13] |
马士华, 文坚. 基于时间延迟的订单分批策略研究[J].
工业工程与管理, 2004, 4(6): 1-4.
MA Shihua, WEN Jian. The order batching strategies based on time postponement[J]. Industrial Engineering and Management, 2004, 4(6): 1-4. DOI: 10.3969/j.issn.1007-5429.2005.06.001. |
| [14] |
王旭坪, 张珺, 马骏. 考虑完成期限的电子商务在线订单分批模型及算法[J].
管理科学, 2014, 27(6): 103-113.
WANG Xuping, ZHANG Jun, MA Jun. E-commerce on-line order batching model and algorithm: considering due time[J]. Journal of Management Science, 2014, 27(6): 103-113. DOI: 10.3969/j.issn.1672-0334.2014.06.009. |
| [15] |
HENN S, WÄSCHER G. Tabu search heuristics for the order batching problem in manual order picking systems[J].
European Journal of Operational Research, 2012, 222(3): 484-494.
DOI: 10.1016/j.ejor.2012.05.049. |
| [16] |
HOLTHAUS O. Design of efficient job shop scheduling rules[J].
Computers & Industrial Engineering, 1998, 33(1-2): 249-252.
|
 2019, Vol. 22
2019, Vol. 22