2. 中国航天科工集团 第九总设计部,湖北 武汉 430040
2. The 9th Designing of China Aerospace Science Industry Corp., Wuhan 430040, China
传统的车辆路径问题是以最小化总行程为目标,从经济学的角度进行研究[1-3]。随着低碳环保问题越来越受到重视,绿色物流的概念随之被提出[4]。绿色物流的主要问题之一是减少二氧化碳排放量,缓解运输活动对空气污染和全球变暖的严重影响,同时提高配送效率,推动环境友好型物流的发展。针对绿色供应链的特点,研究人员提出了许多新的优化模型,这些模型既考虑了经济成本,也考虑了二氧化碳的排放[5-8]。
冷链物流作为物流行业中的一种特殊的运输方式,由于其运输的产品多为易腐、易变质的产品,所以其运输过程必须在较短的时间内完成,以减少产品的损耗,进而达到降低成本的目的。缪小红等[9]建立了考虑时间窗问题的数学模型,并使用改进遗传算法对冷链物流配送路径进行优化;周咏等[10]则是考虑了同时送取货物的冷链物流配送情况。王维军等[11]使用改进的智能水滴算法对构建的冷链物流配送模型进行求解,结果表明该算法对于解决考虑时间窗的优化问题更准确。Amorim等[12]针对葡萄牙一家冷链物流企业面临的实际配送问题提出了多约束VRP模型。Drezner等[13]研究了冷链配送中心选址对于易腐产品配送过程总成本的影响。
本文基于绿色物流的理念,结合冷链物流的配送过程特点,考虑了传统物流配送中的固定成本及运输成本以外,由于冷链物流在运输过程中使用空调等降温设备,导致了冷链物流的高耗能、高排放的缺点,因此还分析了由于车辆运输及其制冷设备消耗燃油造成的碳税成本,以及低温冷藏货物因配送迟到而造成的货损成本,综合以上成本分析,构建优化模型,并使用全局人工鱼群算法对具体案例进行求解。
1 基于绿色供应链的冷链物流配送路径优化 1.1 问题描述及假设本文研究了一个冷链物流配送中心为N个客户使用低温冷藏车进行配送货物的路径优化问题。根据绿色物流的理念及冷链物流货物的特点,在传统的车辆路径优化问题考虑的固定成本及运输成本以外,加入了碳税成本及货损成本。问题的假设如下。
1) 冷链物流配送中心存货充足,拥有K辆同一型号冷藏配送车,最大载重量相同且已知,在配送过程之中降温设备保持工作,功率恒定且相同;
2) 每辆配送车从配送中心出发,完成配送任务后返回配送中心,在配送过程中仅送货不取货;
3) 每个客户的需求量及其位置已知,每个客户只能且必须由一辆车服务一次;
4) 每个客户都有要求的配送时间窗,超过配送时间后,货物就会变质产生货损成本,且与超额时间成线性关系;
5) 不同的车辆在两个客户进行配送任务时,行驶速度只与当前时段有关。
1.2 参数和变量根据建立模型的需要,本文设置了以下参数。
K:配送中心拥有的卡车数量;
f:每辆冷藏车的固定成本;
dij:客户i和j之间的距离;
Q:冷藏车的最大载货重量;
α:车辆在不制冷情况下每公里油耗量;
Vij:客户i和j之间的车辆行驶速度;
tsi:客户i被服务的时间;
P:车载制冷设备功率;
β:车载发电机燃油消耗率;
γ:燃油单价;
tik:车辆k到达客户i的时间;
[ETi,LTi]:客户i接收配送货物的时间窗,其中ETi是客户i开始接收货物的开始时间;LTi是客户i要求的完成配送任务的结束时间;
ai:客户i接收的单位货物单位时间的货损成本;
qi:客户i的需求量;
C:碳税价格;
ρ:燃油的CO2排放系数;
xijk:决策变量,配送车辆k从客户i行驶到客户j,xijk=1;否则,xijk=0;
yik:决策变量,客户i由配送车辆k服务,yik=1;否则,yik=0。
1.3 车辆行驶速度计算模型中车辆行驶速度Vk经常被假设为恒定值[14-16],但是车辆在实际运行时是不可能以恒定速度行驶,经常是在最大和最小速度限制内行驶,这可以使用三角分布进行更为准确的表示[17]。
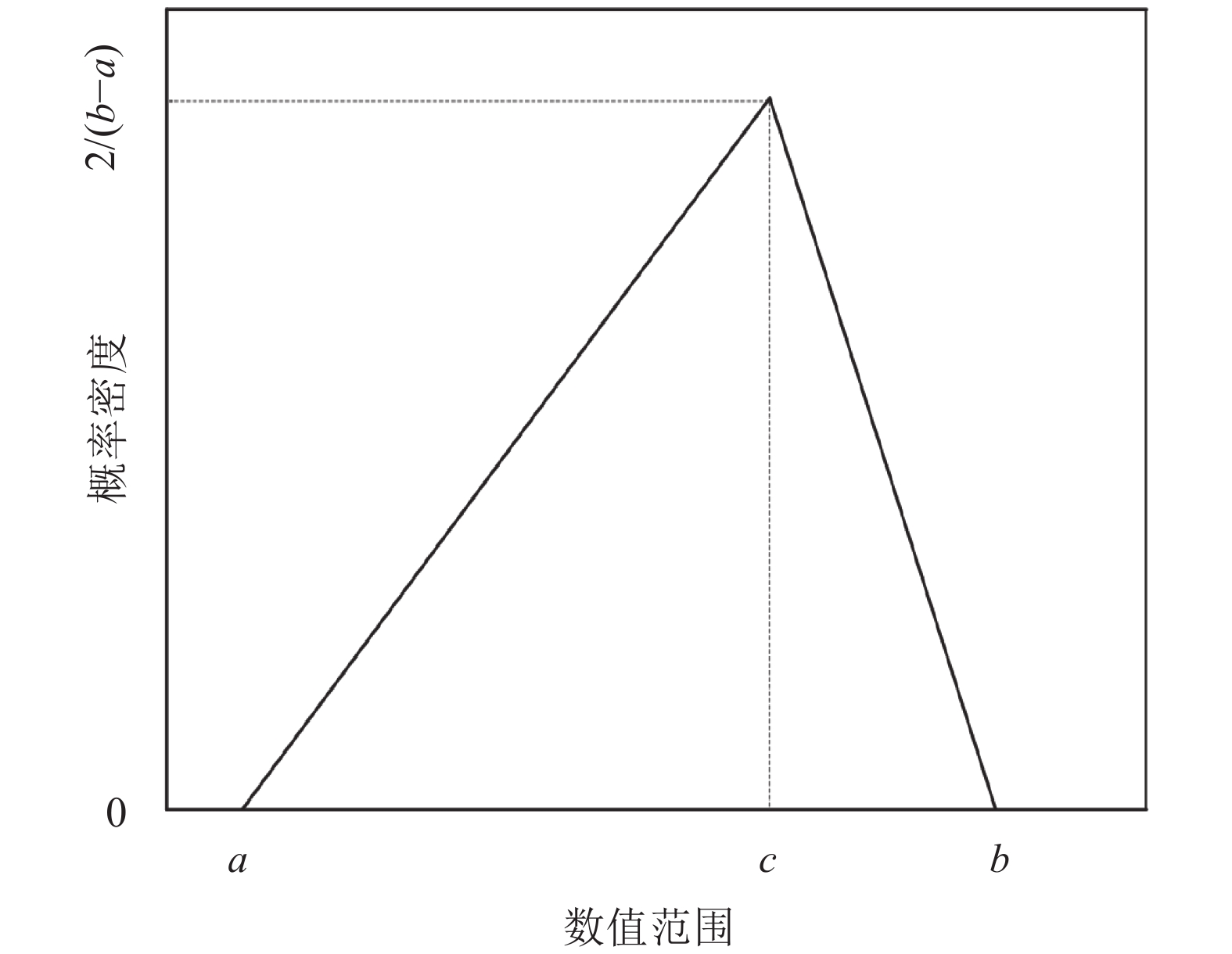
三角分布是一个连续分布,具有最小值a,最大值b以及众数c,并且a≤c≤b,如图1所示。其概率密度函数如式(1)所示。
| $\quad\quad{{f}}\left( {{x}} \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{x {\text{<}} a};\\ {\dfrac{{2\left( {x - a} \right)}}{{\left( {b - a} \right)\left( {c - a} \right)}},}&{a {\text{≤}} x {\text{≤}} c};\\ {\dfrac{{2\left( {b - x} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}},}&{c {\text{≤}} x {\text{≤}} b};\\ {0,}&{x > b}{\text{。}} \end{array}} \right.$ | (1) |
|
图 1 三角分布 Fig. 1 Triangular distribution |
已知三角分布的概率密度分布,即可求出其均值。则车辆的变速行驶均值Vk如式(2)所示。
| $\begin{split} &\quad\quad{V_k} = E\left( X \right) = \mathop \int \nolimits_a^b xf\left( x \right){\rm d}x=\\ &\mathop \int \nolimits_a^c x\dfrac{{2\left( {x - a} \right)}}{{\left( {b - a} \right)\left( {c - a} \right)}}{\rm d}x + \mathop \int \nolimits_c^b x\dfrac{{2\left( {b - x} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}}{\rm d}x{\text{。}} \end{split}$ | (2) |
每辆配送车在使用时都会产生一定的固定费用,比如配送人员的工资,配送车辆的定期维护成本等等。该冷链配送中心共有K辆车配送车,每辆车的固定成本均为f,则车辆的固定成本C1为
| $\quad\quad {C_1} = \mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{j = 1}^N fx_{0j}^k{\text{。}}$ | (3) |
在配送过程中,每辆车所消耗的燃油被分为两个部分,一部分是配送车辆在配送过程中用于产生动力的油耗,另一部分是为制冷设备供电所产生的油耗。
1) 配送过程车辆运输燃油消耗量。
配送过程车辆运输燃油消耗量Q1可以表示为
| $\quad\quad{Q_1} = \alpha \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{j = 0}^N \mathop \sum \limits_{k = 1}^K {d_{ij}}x_{ij}^k{\text{。}}$ | (4) |
2) 配送过程车辆制冷燃油消耗量。
冷藏车在配送过程中制冷设备保持工作以达到保持低温的目的,在完成配送任务后返回配送中心的路程中停止制冷。制冷设备的供电由配送车辆消耗燃油带动发电机供电,在此过程中将会增加燃油的消耗量。配送过程车辆制冷燃油消耗量Q2可以表示为
| $\begin{split}&\quad\quad{Q_2} = \beta P\left( {\mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{j = 1}^N \mathop \sum \limits_{k = 1}^K {d_{ij}}x_{ij}^k/{V_{ij}} +}\right.\\ &\left.{ \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K {\rm max}\left\{ {0,{\rm E}{{\rm T}_i} - t_i^k} \right\} + \mathop \sum \limits_{i = 1}^N {t_{{\rm s}i}}} \right){\text{。}}\end{split}$ | (5) |
3) 配送过程燃油成本。
配送过程燃油消耗总量等于配送过程车辆运输燃油消耗量及车辆制冷燃油消耗量之和。因此配送过程燃油成本C2可以表示为
| $\quad\quad{C_2} = \gamma \left( {{Q_1} + {Q_2}} \right){\text{。}}$ | (6) |
如果配送车辆在配送时间窗结束之前完成客户i配送任务,即tik+tsi≤LTi,则不产生货损成本;如果配送车辆在配送时间窗结束之后完成客户i配送任务,即tik+tsi≥LTi,则产生货损成本。单位重量货损成本Pi设定如下。
| $\quad\quad {p_i} = \left\{ {\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!\!{0,\quad\quad \quad\quad \quad\quad t_i^k + {t_{{\rm s}i}} {\text{≤}} {{\rm LT}_i}};\\ {{a_i}\left( {t_i^k + {t_{{\rm s}i}} - {{\rm LT}_i}} \right),t_i^k + {t_{{\rm s}i}}{\text{>}} {{\rm LT}_i}}{\text{。}} \end{array}} \right.$ | (7) |
由此在配送过程中所产生的货损成本C3可以表示为
| $\quad\quad{C_3} = \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K {p_i}{q_i}y_i^k{\text{。}}$ | (8) |
本文中冷链分配过程的碳排放产生在2个方面:配送过程车辆运输燃油消耗及车辆制冷燃油消耗的碳排放。对于配送过程中燃料消耗产生的二氧化碳排放量,本文表示为:碳排放量=燃料消耗×二氧化碳排放系数[18]。本文引入碳税机制来计算碳排放成本,即碳排放成本=碳税×碳排放量。碳排放总成本C4可表示为
| $\quad\quad{C_4} = C\rho \left( {{Q_1} + {Q_2}} \right){\text{。}}$ | (9) |
通过对车辆固定成本、燃油成本、货损成本、碳税成本4个优化目标的综合分析,基于绿色物流的冷链物流配送路径优化模型如下。
| $\begin{split} &\quad\quad{\rm{min}}\;{\rm{C}} = {C_1} + {C_2} + {C_3} + {C_4} = \mathop \sum \limits_{k = 1}^k \mathop \sum \limits_{j = 1}^n fx_{0j}^k + \\ & \gamma \left( {\alpha \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k + \beta P\left( {\mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{j = 1}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k/{V_{ij}} +}\right.}\right.\\ &\left.{\left.{ \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K \max\left\{ {0,{{\rm ET}_i} - t_i^k} \right\} + \mathop \sum \limits_{i = 1}^N {t_{si}}} \right)} \right)+\mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K {p_i}{q_i}y_i^k + \\ & C\rho \left( {\alpha \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k + \beta P\left( {\mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{j = 1}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k/{V_{ij}} +}\right.}\right. \\ & \left.{\left.{ \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K \max\left\{ {0,{{\rm ET}_i} - t_i^k} \right\} + \mathop \sum \limits_{i = 1}^N {t_{si}}} \right)} \right)=\mathop \sum \limits_{k = 1}^k \mathop \sum \limits_{j = 1}^n fx_{0j}^k +\\ & \left( {\gamma + C\rho } \right)\left( {\alpha \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k + \beta P\left( {\mathop \sum \limits_{i = 0}^N \mathop \sum \limits_{j = 1}^N \mathop \sum \limits_{K = 1}^K {d_{ij}}x_{ij}^k/{V_{ij}} +}\right.}\right.\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ &\left.{\left.{\mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K \max\left\{ {0,{{\rm ET}_i} - t_i^k} \right\} + \mathop \sum \limits_{i = 1}^N {t_{si}}} \right)} \right) + \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K {p_i}{q_i}y_i^k{\text{。}}\!\!\!\!\! \end{split} $ | (10) |
约束条件:
| $\quad\quad\mathop \sum \limits_{k = 1}^K y_i^k = \left\{ {\begin{array}{*{20}{l}} {1,}&{i = 1,2, \cdots, N};\\ {K,}&{i = 0}{\text{。}} \end{array}} \right.$ | (11) |
| $\quad\quad\mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{j = 1}^N x_{0j}^k {\text{≤}} K;$ | (12) |
| $\quad\quad\mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{i = 1}^N y_i^k = N;$ | (13) |
| $\quad\quad\mathop \sum \limits_{j = 1}^N x_{0j}^k = \mathop \sum \limits_{j = 1}^N x_{j0}^k {\text{≤}} 1,k = 1,2, \cdots, K;$ | (14) |
| $\quad\quad\mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{k = 1}^K y_i^k{q_i} {\text{≤}} Q;$ | (15) |
| $\quad\quad t_j^k = {\rm{max}}\{ t_i^k,{{\rm ET}_i}\} + {t_{si}} + {d_{ij}}x_{ij}^k/{V_{ij}}{\text{。}}$ | (16) |
其中,目标函数(10)是最小化总成本;约束(11)和(12)表示在配送中心总共有K辆冷藏车,且被派出的车辆数不超过K,每个客户只能由一辆冷藏车进行服务;约束(13)确保每个客户都能接受服务;约束(14)限制了每辆冷藏车必须从配送中心出发,配送任务结束后返回配送中心;约束(15)保证了每条线路上所有客户的需求量不超过车辆k的最大载重量;约束(16)保持2个客户节点的服务时间连续性。
2 全局人工鱼群算法设计 2.1 全局人工鱼群算法基本人工鱼群算法通过模拟自然界中鱼群的觅食、聚群以及追尾等行为,采集局部的最优信息,逐步淘汰较差信息进而达到全局最优化的目标。因为采用局部寻优的行为,所以基本人工鱼群算法容易出现早熟现象,极易局部最优[19]。全局人工鱼群算法通过在人工鱼群的位置更新模式中引入全局最优信息,提高了算法的全局寻优能力,并引入了人工鱼的吞食行为,克服了基本人工鱼群算法的缺点。全局人工鱼群算法变量主要包括鱼群总数N、个体鱼状态
1) 觅食行为。
个体鱼的当前状态为Xi,在其视野范围内任意选择一个状态Xj,
| $\quad\quad{X_j} = {X_i} + {\rm Visual} \cdot {\rm Rand}()\text{。}$ | (17) |
式中,Rand为0~1间的随机数。在求解最小值问题时,如果Yi>Yj,那么下一步就向Xj及Xbest_af的向量和方向前进一步,则
| ${{X}}_i^{t + 1} = {{X}}_i^t + \left( {\frac{{\left( {{X_j} - {{X}}_i^t} \right) + \left( {{X_{{\rm best}\_af}} - {{X}}_i^t} \right)}}{{\parallel \left( {{X_j} - {X}_i^t} \right) + \left( {{X_{{\rm best}\_af}} - {{X}}_i^t} \right)\parallel }}} \right) \cdot {\rm Step} \cdot {\rm Rand}(){\text{。}}$ | (18) |
如果Yi<Yj,则继续任意选择一个状态进行比较,在进行Try_number次数后仍然不能满足,则随机向前移动,
| $\quad\quad{{X}}_i^{t + 1} = {{X}}_i^t + {\rm Visual} \cdot {\rm Rand}(){\text{。}}$ | (19) |
2) 聚群行为。
个体鱼的当前状态为Xi,搜索当前邻域Dij(Dij<Visual)内的个体数目nf以及邻域中心位置Xc。如果
| ${{X}}_i^{t + 1} = {{X}}_i^t + \left( {\frac{{\left( {{X_c} - {{X}}_i^t} \right) + \left( {{X_{{\rm best}\_{\rm af}}} - {{X}}_i^t} \right)}}{{\parallel \left( {{X_c} - {{X}}_i^t} \right) + \left( {{X_{{\rm best}\_{\rm af}}} - {{X}}_i^t} \right)\parallel }}} \right) \cdot {\rm Step} \cdot {\rm Rand}(){\text{。}}$ | (20) |
如果不能满足
3) 追尾行为。
个体鱼的当前状态为Xi,搜索当前邻域dij(dij<Visual)内其他个体鱼中Yj最小的个体鱼Xj。如果
| ${{X}}_i^{t + 1} = {{X}}_i^t + \left( {\frac{{\left( {{X_j} - {{X}}_i^t} \right) + \left( {{X_{{\rm best}\_{\rm af}}} - {{X}}_i^t} \right)}}{{\parallel \left( {{X_j} - {{X}}_i^t} \right) + \left( {{X_{{\rm best}\_{\rm af}}} - {{X}}_i^t} \right)\parallel }}} \right) \cdot {\rm Step} \cdot {\rm Rand}(){\text{。}}$ | (21) |
如果不能满足
4) 跳跃行为。
算法在进行n次迭代后,个体鱼进行所有每个行为以后的Y值不再发生较大的变化,此时所有的个体鱼都陷入了局部极值,跳跃行为可以随机地改变部分个体鱼的参数,使其跳出此时的局部最优值区域。
| $\quad\quad {X_{\rm some}}\left( {{{t}} + 1} \right) = {X_{\rm some}}\left( t \right) + \beta \cdot {\rm Visual} \cdot {\rm Rand}(){\text{。}}$ | (22) |
5) 吞食行为。
当算法迭代到总迭代次数的一半时,在求解最大值问题时,存在一条个体鱼的Y值低于T_value;或者在求解最小值问题时,存在一条个体鱼的Y值高于T_value,该个体鱼所占有的空间将被释放,此时鱼群总数Af_total=Af_total-1。
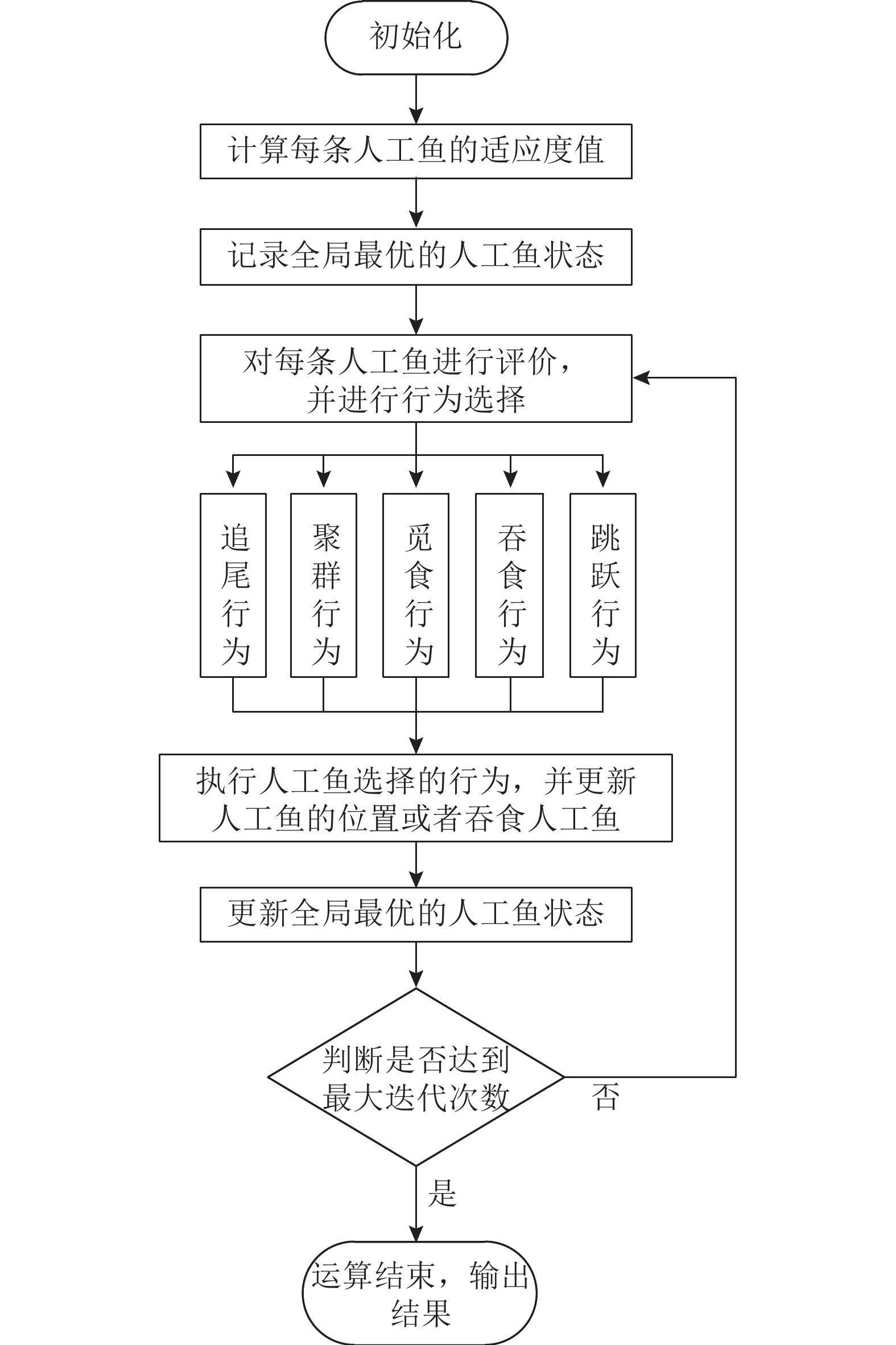
2.3 算法实现步骤全局人工鱼群算法流程图如图2所示。具体算法步骤如下。
|
图 2 全局人工鱼群算法流程 Fig. 2 Flow chart of global artificial fish swarm algorithm |
1) 进行初始化设置,包括鱼群的数量Total、个体鱼的初始位置、视野Visual、步长Step、最大迭代次数gen、尝试次数Try_number、拥挤度因子δ和执行吞食行为的阈值T_value;
2) 计算每个个体鱼的适应度值,并记录全局最优的人工鱼的状态;
3) 对每条人工鱼进行评价,选择其下一步要进行的行为,包括觅食行为、聚群行为、追尾行为、吞食行为和跳跃行为;
4) 执行第(3)步选择的行为,基于全局信息和局部信息更新个体鱼的位置信息;
5) 更新全局最优人工鱼的状态;
6) 若达到最大迭代次数就输出结果,否则跳转到第(2)步。
3 案例应用 3.1 案例分析设有一个配送中心L0和8个客户,配送中心拥有5台载重量为10 t的同一型号冷藏配送车。每个客户的需求量、服务时长、服务时间窗及单位货物单位时间的货损成本如表1所示。配送中心L0与每个客户间的距离如表2所示。在城市中进行配送,车辆的行驶速度通常与行驶的时间段有关[20],根据式(2)将配送时间窗[8:00,14:00]分为4个不同的时间段,分别计算配送车辆在相应时间段内的平均速度,如表3所示。
| 表 1 客户相关参数 Tab. 1 Parameters of customers |
设每辆冷藏车的固定成本f为500元/次,车辆在不制冷情况下每公里油耗量α为0.16 L,车载制冷设备功率P为6 000 w,车载发电机燃油消耗率β为0.3 L/kWh,燃油单价γ为7.14元/L,碳税价格C的平均值为0.027 元/kg,燃油的CO2碳排放系数ρ按每升燃油产生2.3 kg CO2进行计算[20]。
| 表 2 两点之间距离 Tab. 2 Distance between two points |
| 表 3 分时段车辆行驶速度 Tab. 3 Vehicle speed in different time periods |
本案例采用全局人工鱼群算法进行求解。根据已有的文献[19]以及大量的实验,设置鱼群的数量Total=150、视野Visual=3、步长Step=0.5、最大迭代次数gen=1000、尝试次数Try_number=200、拥挤度因子δ=0.618和执行吞食行为的阈值T_value=1.2×Xbest_af,即个体鱼的Y值是最佳位置的Y值1.2倍时,该个体鱼就会被吞食。
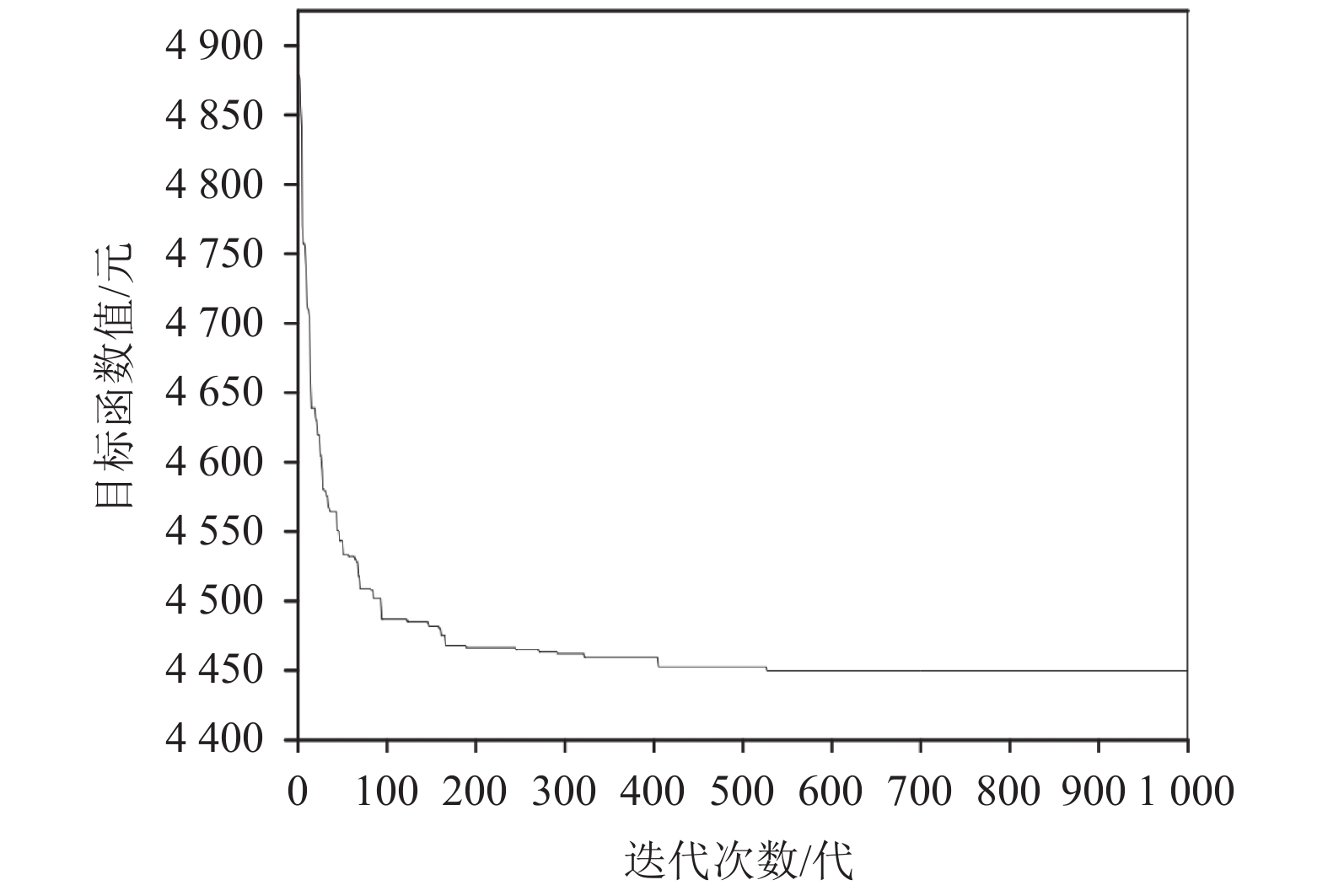
经过计算,迭代情况如图3所示,该配送系统的最低成本约为4 456元。通过算法得到本案例最优目标函数结果的配送路径如表4所示。从图3中可以看到在迭代过程中,在前100次的迭代收敛速度较后面的迭代的收敛速度要快,在300代至400代,400代至500代之间目标函数值几乎不发生改变,在540代左右得到最优目标函数值。
|
图 3 迭代示意图 Fig. 3 Iterative schematic |
| 表 4 最优配送路径结果 Tab. 4 Results of the optimal delivery path |
本文针对冷链物流高排放、高能耗的特点,分析了传统物流考虑的各项成本。根据绿色物流的理念,考虑了冷链物流配送过程中的碳税成本及货损成本,并以各成本之和最小为优化目标构造了数学模型。为了避免基本人工鱼群算法极易陷入局部最优的问题,设计了全局人工鱼群算法,并对具体案例进行求解。案例结果表明,本文构造的数学模型和全局人工鱼群算法能够有效地解决考虑碳税成本的冷链物流配送路径优化问题,对此类问题有着一定的理论指导和参考价值。
| [1] |
KIM K C, SUN J U, LEE S W. A hierarchical approach to vehicle routing and scheduling with sequential services using the genetic algorithm[J].
International Journal of Industrial Engineering Theory Applications & Practice, 2013, 20(1): 99-113.
|
| [2] |
BRANDSTÄTTER C, REIMANN M. The line-haul feeder vehicle routing problem: mathematical model formulation and heuristic approaches[J].
European Journal of Operational Research, 2018, 270(1): 157-170.
DOI: 10.1016/j.ejor.2018.03.014. |
| [3] |
AHKAMIRAAD A, WANG Y. Capacitated and multiple cross-docked vehicle routing problem with pickup, delivery, and time windows[J].
Computers & Industrial Engineering, 2018, 119: 76-85.
|
| [4] |
ERDOĞAN S, MILLER-HOOKS E. A green vehicle routing problem[J].
Transportation Research Part E Logistics & Transportation Review, 2012, 48(1): 100-114.
|
| [5] |
KWON Y J, CHOI Y J, LEE D H. Heterogeneous fixed fleet vehicle routing considering carbon emission[J].
Transportation Research Part D Transport & Environment, 2013, 23(8): 81-89.
|
| [6] |
FRANCESCHETTI A, HONHON D, WOENSEL T V, et al. The time-dependent pollution-routing problem[J].
Transportation Research Part B, 2013, 56: 265-293.
DOI: 10.1016/j.trb.2013.08.008. |
| [7] |
DEMIR E, BEKTAŞ T, LAPORTE G. A review of recent research on green road freight transportation[J].
European Journal of Operational Research, 2014, 237(3): 775-793.
DOI: 10.1016/j.ejor.2013.12.033. |
| [8] |
XIAO Y, KONAK A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion[J].
Transportation Research Part E, 2016, 88: 146-166.
DOI: 10.1016/j.tre.2016.01.011. |
| [9] |
缪小红, 周新年, 林森, 等. 第3方冷链物流配送路径优化研究[J].
运筹与管理, 2011, 20(4): 32-28.
MIAO Xiaohong, ZHOU Xinnian, LIN Sen, et al. Study on routing optimization for cold-chain logistics distribution of 3PL[J]. Operations Research and Management Science, 2011, 20(4): 32-28. DOI: 10.3969/j.issn.1007-3221.2011.04.005. |
| [10] |
周咏, 计莹峰, 杨华龙, 等. 冷链物流同时送取货车辆路径优化[J].
数学的实践与认识, 2016, 46(20): 18-26.
ZHOU Yong, JI Yingfeng, YANG Hualong, et al. Optimization of vehicle routing problem with simultaneous delivery and pickup for cold chain logistics[J]. Mathematics in Practice and Theory, 2016, 46(20): 18-26. |
| [11] |
王维军, 罗伟. 基于改进智能水滴算法的冷链物流配送路径优化问题研究[J].
工业工程, 2017, 20(2): 38-43.
WANG Weijun, LUO Wei. A research of cold chain logistic distribution path optimization based on the improved intelligent water drop algorithm[J]. Industrial Engineering Journal, 2017, 20(2): 38-43. DOI: 10.3969/j.issn.1007-7375.e16-2292. |
| [12] |
AMORIM P, PARRAGH S N, SPERANDIO F, et al. A rich vehicle routing problem dealing with perishable food: a case study[J].
TOP, 2014, 22(2): 489-508.
DOI: 10.1007/s11750-012-0266-4. |
| [13] |
DREZNER Z, SCOTT C H. Location of a distribution center for a perishable product[J].
Mathematical Methods of Operations Research, 2013, 78(3): 301-314.
DOI: 10.1007/s00186-013-0445-6. |
| [14] |
张亚明, 李娜. 基于精英单亲遗传算法的冷链物流VRP模型优化研究[J].
数学的实践与认识, 2016, 46(4): 87-96.
ZHANG Yaming, LI Na. Research on elite selection based partheno-genetic algorithm under optimized cold-chain logistics VRP model[J]. Mathematical Methods of Operations Research, 2016, 46(4): 87-96. |
| [15] |
LEGGIERI V, HAOUARI M. A practical solution approach for the green vehicle routing problem[J].
Transportation Research Part E Logistics & Transportation Review, 2017, 104(23): 97-112.
|
| [16] |
YIN P Y, CHUANG Y L. Adaptive memory artificial bee colony algorithm for green vehicle routing with cross-docking[J].
Applied Mathematical Modeling, 2016, 40(21-22): 9302-9315.
DOI: 10.1016/j.apm.2016.06.013. |
| [17] |
POONTHALIR G, NADARAJAN R. A fuel efficient green vehicle routing problem with varying speed constraint (F-GVRP)[J].
Expert Systems with Applications, 2018, 100(1): 131-144.
|
| [18] |
OTTMAR R D. Wildland fire emissions, carbon and climate: modeling fuel consumption[J].
Forest Ecology & Management, 2014, 317(2): 41-50.
|
| [19] |
黄务兰, 张涛. 基于改进全局人工鱼群算法的VRPSPDTW研究[J].
计算机工程与应用, 2016, 52(21): 21-29.
HUANG Wulan, ZHANG Tao. VRPSPDTW based on improved global artificial fish swarm algorithm[J]. Computer Engineering and Applications, 2016, 52(21): 21-29. DOI: 10.3778/j.issn.1002-8331.1603-0309. |
| [20] |
张如云, 刘清. 考虑低碳的城市配送车辆路径优化模型研究[J].
工业工程与管理, 2015, 20(4): 29-34.
ZHANG Ruyun, LIU Qing. CO2 emission minimizing for the time-dependent VRP in urban area [J]. Industrial Engineering and Management, 2015, 20(4): 29-34. DOI: 10.3969/j.issn.1007-5429.2015.04.005. |
 2019, Vol. 22
2019, Vol. 22