混合属性广义灰靶决策方法,是将决策方案的指标由实数值拓展为混合属性值,而其对决策方案靶心距的处理也有别于传统的方法[1-3]。传统的混合属性广义灰靶决策方法对靶心距的获取主要采用的是欧氏距离的方法[4]。而混合属性广义灰靶决策方法的决策依据最初采用的是接近度的方法[1-3],后来又产生了以Kullback-Leibler(K-L)距离为决策依据的方法[5]。文献[6-7]研究了广义灰靶决策方法中在确定性实数情况下决策方案靶心指标可由决策者的选择偏好和理想偏好所决定,而不同的决策者偏好所决定的靶心对决策方案存在着一定的影响:决策者正或负理想属性偏好所确定的正或负靶心都能够缩小方案指标之间的差距,即具有使决策方案指标聚类的作用。而涉及到混合属性广义灰靶决策方法,其靶心指标同样可以由决策者的不同属性偏好所决定。即混合属性广义灰靶决策方法的靶心指标,可以比较方便地替换为非方案本身所确定的靶心。基于以上特性,可以探索混合属性广义灰靶决策方法所具有的模式识别功能。
模式识别是根据已有的某一行为或对象的特征来判别尚未确定的行为或对象所属类别的方法[8]。模式识别当前已经得到了广泛而深入的应用和研究。在众多的研究中,对涉及实数、模糊数等混合指标属性的模式识别或分类方法的研究成果也比较丰富[9-10]。已有的涉及区间数或模糊数等不确定数的模式识别中主要有3类方法,一是采用模糊集的方法来进行处理[11-12];二是将不确定数采用类似确定数的方法进行规范化,然后采用计算待识别目标与基准模式距离的方法进行模式识别[13-14];三是将不确定数转化为包含了“确定+不确定”的二元联系数并视为向量的方法来进行处理[15]。
混合属性广义灰靶决策方法用于模式识别的具体思路如下。将标准的各类模式分别作为待识别对象的靶心,而以待识别的目标作为各决策方案;然后分别计算各待识别的目标(决策方案)与各个不同的靶心指标向量的广义靶心距(接近度或其他决策的依据);最后,分别选择出各方案与不同的标准模式最接近的广义靶心距,即识别为该类模式。
1 基础理论 1.1 不确定性灰数定义1:记R为实数域,称
(a)如果
(b)如果
(c) 如果
定义2:记R为实数域,称A+Bi为二元联系数,其中A,B∈R,i∈[-1,1],A表示确定的项,B表示不确定的项,i是一个变动的项,它的存在统一了不确定数的确定性和不确定性[16-17]。
设有不确定性灰数
| $ \quad\quad \bar x = \frac{1}{p}\sum\limits_{j = 1}^p {{x_j}} , $ | (1) |
| $ \quad\quad S = \sqrt {\frac{1}{{(p - 1)}}\sum\limits_{j = 1}^p {({x_j} - \overline x } {)^2}} , $ | (2) |
| $ \quad\quad {\rm VS} = \max \left\{ {\left| {{x^{\rm L}} - \overline x } \right|,\left| {{x^{\rm U}} - \overline x } \right|} \right\}, $ | (3) |
| $ \quad\quad v = \min \left\{ {S,{\rm VS}} \right\}{\text{。}} $ | (4) |
式(1)~(4)中均值
定义3:设
| $ \quad\quad u(\overline x ,v) = A + Bi = \overline x + vi,\;i \in [ - 1,1], $ | (5) |
为对
定义4:设向量
| $ \quad\quad|{ X}| = \sqrt {\sum\limits_{t = 1}^n {x_t^2} } , $ | (6) |
为向量X的模。
定义5:设
| $ \quad\quad {{\mathop{\rm Prj}\nolimits} _{ Y}}({ X}) = \frac{{\displaystyle\sum\limits_{t = 1}^n {{x_t}{y_t}} }}{{\sqrt {\displaystyle\sum\limits_{t = 1}^n {x_t^2} \displaystyle\sum\limits_{t = 1}^n {y_t^2} } }}\sqrt {\displaystyle\sum\limits_{t = 1}^n {x_t^2} } = \frac{{\displaystyle\sum\limits_{t = 1}^n {{x_t}{y_t}} }}{{\sqrt {\displaystyle\sum\limits_{t = 1}^n {y_t^2} } }}, $ | (7) |
为向量X在向量Y上的投影。一般地,
定义6:设rst为基准指标向量Yst的模,pst为指标向量Xst在Yst上的投影,则
| $ \quad\quad{d_{st}} = |{r_{st}} - {p_{st}}| ,s = 1 ,\cdots, n;t = 1 ,\cdots, m $ | (8) |
为投影值pst与基准指标向量Yst的模rst的距离,称为接近度[1]。
2 混合属性广义灰靶决策方法的模式识别框架 2.1 混合属性广义灰靶决策方法的特点 2.1.1 混合属性广义灰靶决策方法靶心的可变性灰靶决策方法靶心的确定最初是由决策方案各属性的最优值来决定。而随着研究的深入,灰靶决策方法的靶心亦可以由决策者的偏好确定。引入决策者的偏好靶心,决定了混合属性广义灰靶决策方法靶心获得的灵活性。而由决策者偏好所确定的靶心对决策方案为确定性实数值决策方案的影响在相关文献中已有研究[6-7]。同样,混合属性广义灰靶决策方法由决策者偏好所确定的靶心肯定对决策方案存在一定的影响,但是影响的范围和程度存在着不确定性。
2.1.2 混合属性广义灰靶决策方法具有可扩展性混合属性广义灰靶决策方法是遵循灰靶决策方法的基本原理,但在具体的运算方法和决策依据上不同于传统的决策方法。这种决策方法的特点是其具有可扩展性。最早的涉及混合属性的广义灰靶决策方法是采用通常的距离的方法,主要是欧氏距离。后来产生了以向量的接近度为决策依据的方法;而最新的混合属性广义灰靶决策则采用的是以K-L距离为决策依据的方法。混合属性广义灰靶决策的一个显著特点是存在着含有不确定性的灰数,而如何在运算过程中保持这些不确定数所含有的信息少丢失,不被过度地扭曲是确保决策精确性的关键。基于上述分析,混合属性广义灰靶决策方法的决策依据不仅仅限于传统的距离方法,而是随着研究的深入有新的理论和方法不断地加以拓展。
2.1.3 混合属性广义灰靶决策方法具有模式识别功能的关键混合属性广义灰靶决策方法具有模式识别的关键是其决策依据(靶心距)的可拓展性以及靶心的可变动性。混合属性广义灰靶决策方法中决策依据的可拓展性为进行模式识别提供了最根本的保障,如可以根据模式识别的不同情形选择不同的靶心距确定方法。而靶心在灰靶决策方法中是各方案的标准或希望达到的目标。当混合属性的靶心全部换成标准模式的数据时,各决策方案与靶心的距离最近或最相似,则就越可能会被认定为某种模式。需要注意的是当应用灰靶决策方法进行模式识别时,由于标准模式可能有多种,所以其靶心指标向量不唯一。
2.2 混合属性广义灰靶决策方法的模式识别框架设有方案集
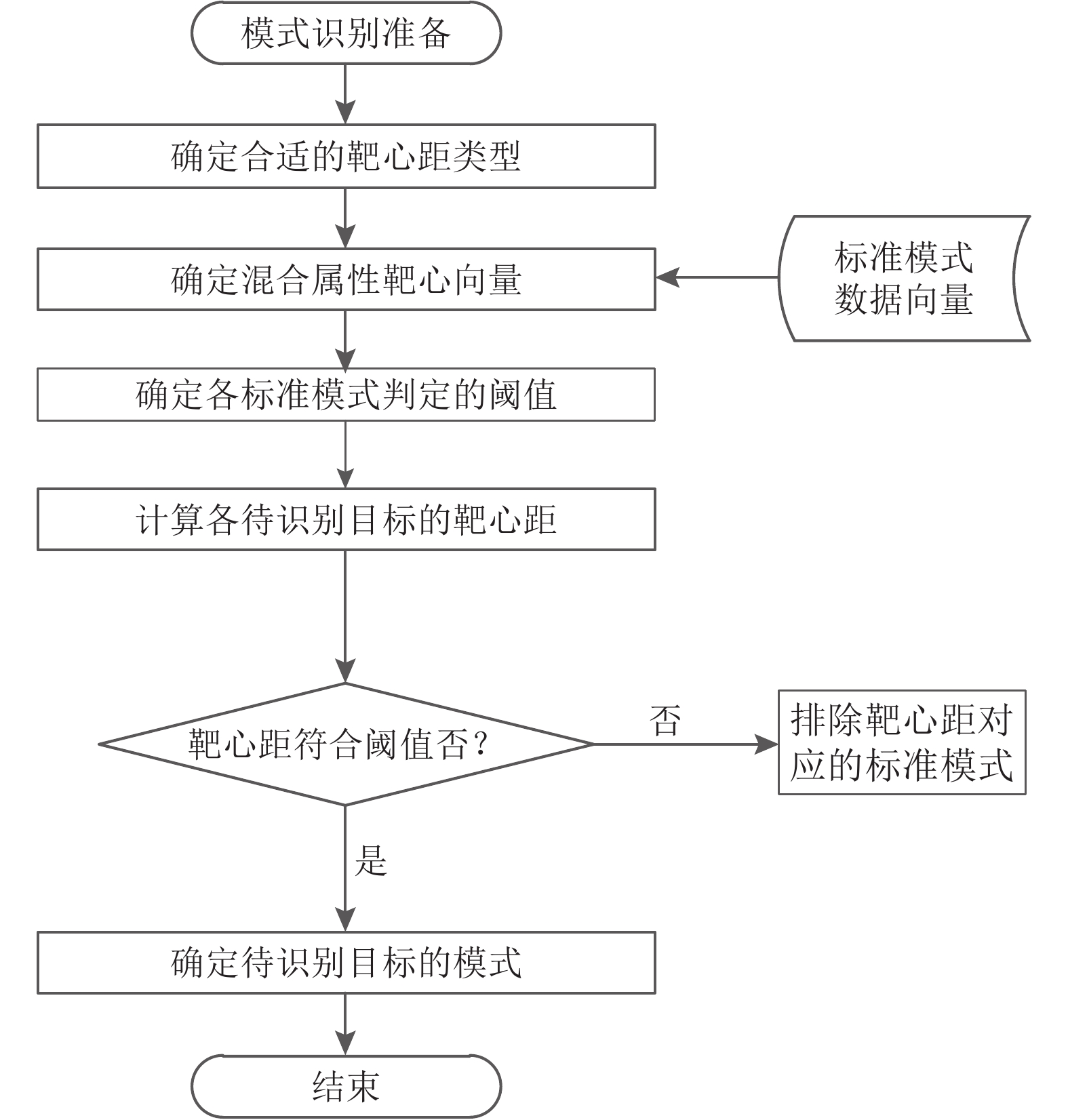
|
图 1 混合属性广义灰靶决策方法模式识别的一般框架 Fig. 1 Framework of pattern recognition of generalised grey target decision method for mixed attributes |
设已知特征模式的向量有n1种,记为
其次确定待识别目标样本。其数据同样是采用混合指标属性来表达的,此处设待识别的目标为n2个,可以记为
无论是模式特征(靶心)的数据表示还是待识别目标的数据表示均采用混合属性的表示方法。为便于处理,这里采用将各类属性值统一转化为二元联系数,然后视这些二元“确定+不确定”联系数为联系数向量,即表示为“A+Bi”的形式。需要说明的是当数据为实数时,二元联系数的表示形式为“A+0i”的形式,即实数转化为二元联系数时不确定项为“0”。
具体转化方法是采用式(1)~(4)计算出二元联系数的确定项和不确定项参数,然后将所有类型的数据最终转化为式(5)表示的二元联系数。
2.2.3 计算各待识别目标的单指标广义靶心距灰靶决策对各方案的优劣排序需要根据其靶心距来确定。随着决策理论研究的深入,单纯的以距离为决策依据的方法拓展为采用接近度,以及采用K-L距离的方法。本文采用接近度来作为决策分析的依据。
根据式(6)~(8),以待识别目标的样本向量分别与基准的模式特征向量求解各单指标的接近度。然后再运用线性归一化式(9)将各个属性下的接近度进行规范化处理,使得各属性下的接近度具有可比性。
| $ \quad\quad{z_{ij}} = \frac{{{d_{ij}}}}{{\displaystyle\sum\limits_{i = 1}^m {{d_{ij}}} }}, i = 1, \cdots, n;j = 1 ,\cdots, m{\text{。}} $ | (9) |
式(9)中dij为未经规范化的单指标接近度,而zij为经过归范化后的单指标接近度。
2.2.4 计算综合靶心距并进行模式识别根据所求得各方案针对相应模式向量的单指标的广义靶心距,在各属性下进行归一化处理。得到归一化后的单指标广义靶心距后,则可以对各属性下各方案的单指标靶心距进行集成。当然,在集成的时候可以根据各属性目标的重要性程度对其赋予不同的权重。最终模式的识别是以综合(加权)的最小的靶心距为最可能的识别模式。在进行模式识别时,首先需要求其满足设定的阈值
本文采用综合接近度作为靶心决策的依据。综合接近度的计算公式为
| $ \quad\quad{I_i} = \sum\limits_{j = 1}^m {{z_{ij}}} , \;\; i = 1, \cdots, n{\text{。}} $ | (10) |
然后比较各待识别目标与基准模式特征向量的归一化综合接近度,以综合接近度越小待识别的目标与其所对应的模式越接近,最小的接近度可以判别为最符合相应的模式。当然,也可以根据实际情况的需要为各个不同的属性赋以权重,即可得到加权的综合接近度,可得到
| $ \quad\quad{I_{W_{i}}} = \sum\limits_{j = 1}^m {{w_j}{z_{ij}}} , \;\; i = 1, \cdots, n{\text{。}} $ | (11) |
其中,wj为某属性Aj的权重,故
有2个不同的投资企业欲选择适合自己的投资模式。投资方案的评估指标有投资额(万元)、期望净现值(万元)、风险损失值(万元)和研发能力,分别用A1~A4表示。其中,A1、A2为区间灰数;A3为三角灰数;A4为梯形灰数。S1~S4表示为较为成功的4种投资模式,而y1、y2为2个投资企业的基本情况,要求作出合理的投资模式选择,数据如表1和表2所示。
| 表 1 各基准模式(靶心)的指标值 Tab. 1 Data pertaining to the basic patterns |
| 表 2 各待识别目标方案的指标值 Tab. 2 Data for the researched objects |
首先根据式(1)~(4)计算表1和表2中各指标值转换为二元联系数的参数,其结果见表3所示。
然后,根据式(5)将各属性方案及标准模式的指标值转换为二元联系数,其结果见表4所示。
| 表 3 基准模式及待识别目标的参数1) Tab. 3 Parameters of the basic patterns and the researched objects |
| 表 4 各属性方案及标准模式的指标值转化为联系数 Tab. 4 Connection numbers of the basic patterns and the objects from mixed values |
首先,采用式(6)~(8)计算出各属性下各待识别目标与不同的基准特征模式向量的接近度,见表5。
| 表 5 各属性下各待识别目标的联系数向量与基准特征值向量的接近度 Tab. 5 Proximities of all index vectors with the basic index vectors |
表5中yi-Sj表示待识别对象yi与基准特征模式Sj的接近度。
其次,采用式(9)对各属性下待识别目标与不同的基准特征模式向量的接近度进行归一化处理,使得各个属性的接近度之间具有可比性,结果见表6。
| 表 6 归一化各属性下各待识别目标的联系数向量与基准特征值向量的接近度 Tab. 6 Normalised proximities of all index vectors with the basic index vectors |
然后,采用式(10)计算出各个待识别目标分别针对不同的基准特征的综合接近度,见表7。
| 表 7 各待识别目标对基准特征模式的综合接近度 Tab. 7 Integrated proximities of all researched objects with the basic patterns |
若预先设定的接近度阈值为
本文分析了混合属性广义灰靶决策方法具有决策依据可扩展性,靶心的确定具有可变动性的特点,提出了将混合属性广义灰靶决策方法应用到模式识别的思路。结合模式识别的一般方法,给出了混合属性广义灰靶决策方法应用于模式识别的一般框架,并以一个算例验证了混合属性广义灰靶决策方法的模式识别功能。混合属性广义灰靶决策方法用于模式识别的一个特点是不仅能够给出待识别目标的最可能模式,而且还可以给出备选的可能模式。
| [1] |
MA Jinshan, JI Changsheng. Generalized grey target decision method for mixed attributes based on connection number[J].
Journal of Applied Mathematics, 2014, 2014: 1-8.
DOI: 10.1155/2014/763543. |
| [2] |
MA Jinshan. Generalised grey target decision method for mixed attributes with index weights containing uncertain numbers[J].
Journal of Intelligent and Fuzzy Systems, 2018, 34(1): 625-632.
DOI: 10.3233/JIFS-17851. |
| [3] |
马金山. 指标及权重均为混合数据类型的广义灰靶决策方法[J].
统计与决策, 2018(7): 58-61.
MA Jinshan. Generalized grey target decision method for mixed data types of indices and weights[J]. Statistics and Decision, 2018(7): 58-61. |
| [4] |
沈春光, 党耀国, 裴玲玲. 混合型多指标灰靶决策模型研究[J].
统计与决策, 2010(12): 17-20.
SHEN Chunguang, DANG Yaoguo, PEI Lingling. Hybrid multi-attribute decision model of grey target[J]. Statistics and Decision, 2010(12): 17-20. |
| [5] |
MA Jinshan. Generalized grey target decision method for mixed attributes based on kullback-leibler distance[J].
Entropy, 2018, 20(7): 523.
DOI: 10.3390/e20070523. |
| [6] |
MA Jinshan. Grey target decision method for a variable target centre based on the decision maker’s preferences[J].
Journal of Applied Mathematics, 2014, 2014: 1-6.
DOI: 10.1155/2014/572529. |
| [7] |
马金山, 孙静. 基于决策者偏好的正负靶心灰靶决策方法[J].
科技管理研究, 2014, 34(23): 185-190.
MA Jinshan, SUN Jing. Grey target decision method for positive and negative target centers based on decision maker's preferences[J]. Science and Technology Management Research, 2014, 34(23): 185-190. DOI: 10.3969/j.issn.1000-7695.2014.23.035. |
| [8] |
范会敏, 王浩. 模式识别方法概述[J].
电子设计工程, 2012, 20(19): 48-51.
FAN Huimin, WANG Hao. An overview of the pattern recognition methods[J]. Electronic Design Engineering, 2012, 20(19): 48-51. DOI: 10.3969/j.issn.1674-6236.2012.19.015. |
| [9] |
AHMAD A, DEY L. A k-means type clustering algorithm for subspace clustering of mixed numeric and categorical data-sets[J].
Pattern Recognition Letters, 2011, 32(7): 1062-1069.
DOI: 10.1016/j.patrec.2011.02.017. |
| [10] |
THONG Phamhuy, SON Lehoang. Picture fuzzy clustering for complex data[J].
Engineering Applications of Artificial Intelligence, 2016, 56: 121-130.
DOI: 10.1016/j.engappai.2016.08.009. |
| [11] |
楚俊峰, 王应明. 基于新的区间直觉模糊集相似性测度的模式识别[J].
计算机工程与应用, 2013, 49(9): 140-143.
CHU Junfeng, WANG Yingming. Method of pattern recognition based on new similarity measure of interval-valued intuitionistic fuzzy set[J]. Computer Engineering and Applications, 2013, 49(9): 140-143. DOI: 10.3778/j.issn.1002-8331.1111-0263. |
| [12] |
CHEN Shyiming, CHANG Chiahao. A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition[J].
Information Sciences, 2015, 291: 96-114.
DOI: 10.1016/j.ins.2014.07.033. |
| [13] |
WAN Shuping. Applying triangular fuzzy number for multi‐sensor object recognition[J].
Kybernetes, 2011, 40(3/4): 589-599.
DOI: 10.1108/03684921111133755. |
| [14] |
张肃, 程启月, 解瑶, 等. 不确定空情信息条件下的意图识别方法[J].
空军工程大学学报(自然科学版), 2008, 9(3): 50-53.
ZHANG Su, CHENG Qiyue, XIE Yao, et al. A method of inference intention with uncertain aerial information[J]. Journal of Air Force Engineering University (Natural Science Edition), 2008, 9(3): 50-53. DOI: 10.3969/j.issn.1009-3516.2008.03.012. |
| [15] |
刘秀梅, 赵克勤. 基于联系数的不确定空情意图识别[J].
智能系统学报, 2012, 7(5): 450-456.
LIU Xiumei, ZHAO Keqin. Inference method on intention with uncertain aerial information based on the connection number[J]. CAAI Transactions on Intelligent Systems, 2012, 7(5): 450-456. DOI: 10.3969/j.issn.1673-4785.201206016. |
| [16] |
赵克勤. 二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用[J].
智能系统学报, 2008, 3(6): 476-486.
ZHAO Keqin. The theoretical basis and basic algorithm of binary conection A+Bi and its application in AI[J]. CAAI Transactions on Intelligent Systems, 2008, 3(6): 476-486. |
| [17] |
赵克勤. 基于集对分析的不确定性多属性决策模型与算法[J].
智能系统学报, 2010, 5(1): 41-50.
ZHAO Keqin. Decision making algorithm based on set par analysis for use when facing multiple uncertain in attributes[J]. CAAI Transactions on Intelligent Systems, 2010, 5(1): 41-50. |
 2019, Vol. 22
2019, Vol. 22