2. 中南大学 交通运输工程学院,湖南 长沙 410075
2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China
备件库存优化是设备维护管理和售后保障的重点问题。当设备发生故障时,必须及时提供备件对设备进行维修,否则将导致巨大的停机损失[1],因此备件库存是设备制造企业维持其售后服务水平的基本保障。设备备件普遍具有价值高、专用性强、需求发生的随机性大等特点,这增加了库存管理决策的难度,如果维持较高的库存水平,则会导致成本增加,同时增大备件的陈旧和退化等风险;而库存水平过低,又会降低设备制造企业的售后服务水平,因而备件库存优化的问题仍是目前备件管理研究的难点之一。
设备备件库存优化的研究集中于多级、多品种结构的备件库存系统建模与优化问题。Sherbrooke[2-4]首先提出了多级备件库存的Metric经典模型并开展了延伸性研究,讨论了可维修备件单基地库存模型、考虑定期补给和冗余度的Metric模型、Mod-Metric模型、Vari-Metric模型等。此后众多学者在Metric经典模型基础上进行了扩展研究,提出了涉及设备可靠性[5-6]、备件可维修性[7-9]、横向转运[10-13]、冗余系统[14]、库存老化[15]等影响因素的一系列模型。但Metric及其扩展模型是对备件库存系统的近似描述,只有在各库存站点的备件需求相互独立且服从参数相同的稳态概率分布的假设下才能得到合理的优化结果。徐晓燕[16]认为,随着设备的使用和老化,相邻时间段上的设备需求会有一定的自相关性;熊浩[17]针对相关性需求提出用“系统整体需求”作为库存优化的依据,但未分析相关性变化对库存策略的影响;Tsai等[18]指出,由于基层仓库依赖于同一个中央仓库的备件库存情况,因此备件交货时间不是独立的,当这种相关性很大时,Metric经典模型将导致不正确的库存决策。可见,备件库存结构体系的层次级别越复杂,备件需求之间的相互影响作用就越大,对库存优化决策的影响越显著。本文针对基层库存需求具有相关关系的情况,基于(S–1,S)库存管理策略,建立考虑需求相关性的多级备件库存模型,利用Monte Carlo仿真及遗传算法对模型进行优化求解,并讨论需求相关性对库存决策的影响。
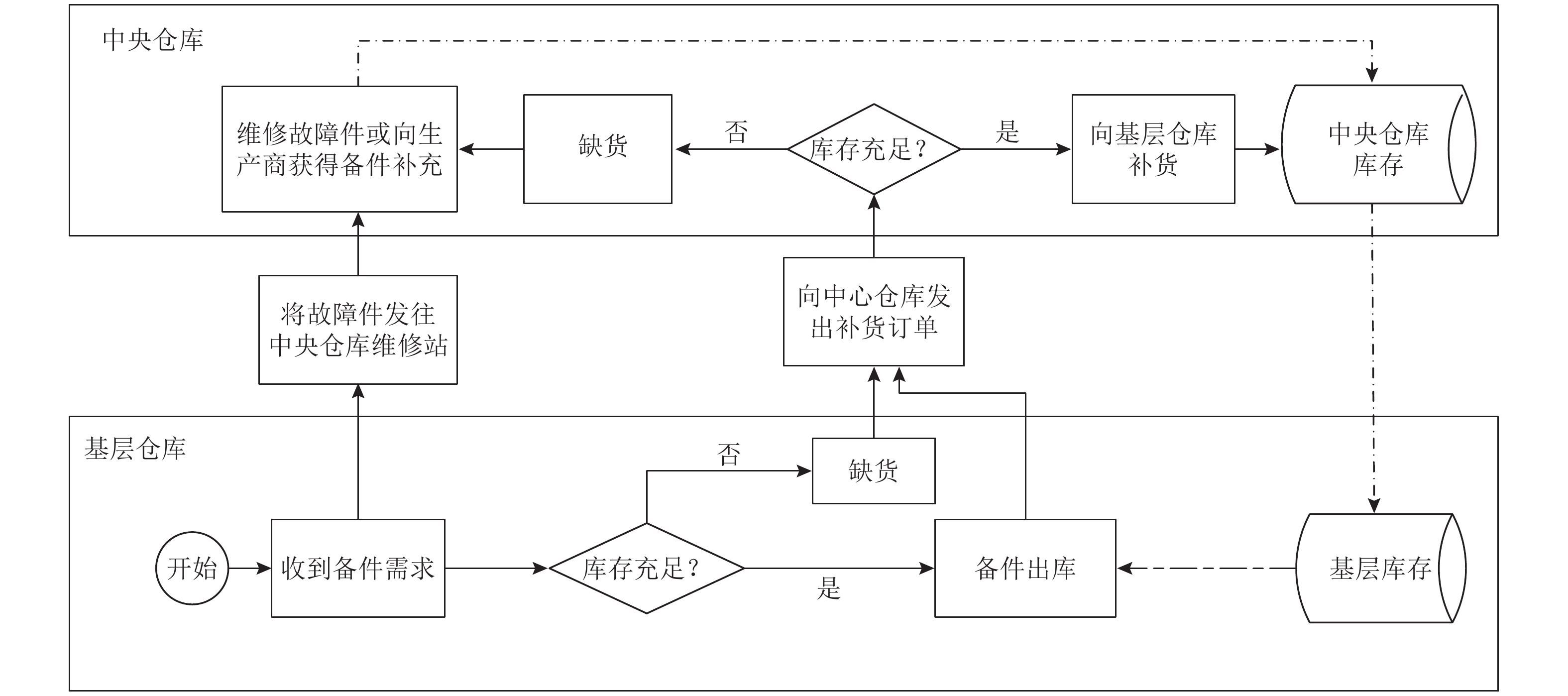
1 设备备件两级库存问题的描述考虑一个两级备件库存系统,系统的第1级为1个中央仓库,它包括1个仓储中心和1个维修中心;第2级由若干个面向设备用户的基层仓库组成,备件在两级仓库中都有一定的储备量。当某基层仓库所服务的设备发生故障时,维修人员申请1件备件以替换故障件,如果基层仓库有库存,则提供备件并向中心仓库发出相应数量的补货订单,同时将故障件送到中央仓库进行维修;如果基层仓库库存不足,则该备件缺货,相应设备处于停机状态直到中央仓库补充的备件到库。对基层仓库发来的订单,中央仓库如果有库存,则对各基层仓库的订单按“先到先得”的原则发货;如果中央仓库库存不足,则中央仓库缺货直到故障件修好或者向生产商获得备件补充并重新入库。库存系统结构如图1所示。
|
图 1 两级备件库存系统结构 Fig. 1 Structure of two echelon spare parts inventory system |
图1所描述的备件消耗与补充过程中的备件数量关系,可用式(1)表示为
| $\quad\quad { S} = {\rm OH} + D - {\rm BO}{\text{。}}$ | (1) |
其中,S为备件的库存水平;OH为备件仓库中的可用库存;D为待接收备件数量,包括了在修理、等待维修的备件以及运输在途的备件数量;BO为备件短缺数。根据图1的流程,当采用连续监视库存的(S–1,S)策略时,在任意时刻t,可用备件库存OH和待接收备件D的总量一直维持在库存水平S上。当D的数量等于S时,OH正好等于0;当D的数量大于S时,备件库存发生短缺,短缺量为BO。
顾客向基层仓库报告设备故障到获得备件以供维修的时间称为顾客响应时间。由于设备发生故障会给顾客造成停工损失,因此,顾客响应时间的大小直接决定了备件供应服务的水平,当基层仓库有库存时,响应时间很短,可近似为0;若基层仓库缺货,响应时间等于中央仓库与基层仓库之间的运输时间;若中央仓库也缺货,则顾客响应时间等于中央仓库的补货时间加上中央仓库与基层仓库之间的运输时间。当客户响应时间超过给定的服务时间限制时,库存系统需要向顾客支付相应的缺货罚金。可以看出,顾客响应时间是一个随机变量。它由备件需求的发生量以及需求发生时刻的备件库存量来决定。由于中央仓库与基层仓库采用协同供应机制,因此,在任何基层仓库发生的需求,都会影响整个备件库存系统的响应能力。需要制定合理的库存策略,保证以尽可能少的库存成本,满足顾客对备件需求响应速度的要求。
2 模型的建立 2.1 基本假设为构建上述备件库存决策问题的数学模型,现规定以下基本假设条件。
1) 对备件的库存控制采用(S–1,S)策略;
2) 由顾客向基层仓库报告设备故障而发生的备件需求为随机变量,设备故障发生的时间间隔服从参数为λ的指数分布;
3) 不同基层仓库的同类型备件需求量之间有两两相关性,其相关系数用相关系数矩阵
4) 故障件的维修时间服从均值为
5) 不考虑基层仓库之间的横向调拨;
6) 故障件均可修复,且修复后与新备件无差别;
7) 中央仓库与各基地仓库之间的运输时间为固定值。
2.2 模型变量和参数的定义设备备件的集合可表示为
S为决策向量,
系统变量和主要参数定义如下。
λil为基层仓库l中备件i需求发生的时间间隔;
ci0为备件i在中央仓库的单位库存成本;
cil为备件i在仓库l的的单位库存成本,其中
cp为备件延迟交货产生的缺货成本;
ti0为故障件i在中央仓库的修复时间;
tl为中央仓库到基层仓库l的运输时间,运输时间与备件的类型无关;
τl为顾客对基层仓库l响应时间的可接受阈值;
Ril(Sil)表示当库存水平为Sil时,基层仓库l对备件i的响应时间。
2.3 备件库存模型备件库存优化的目标一般采用期望短缺数或需求满足率来衡量,但它们度量的主要是库存系统在数量上的供货能力。而目前装备保障企业越来越重视备件供应的及时性对装备产品售后服务水平的重要影响,因此提出以库存总成本最小化为优化目标,以顾客对系统响应时间的要求,即响应时间为主要约束条件。
通常情况下,为便于故障件的维修和库存管理,中央仓库的维修中心与仓储中心之间的距离是很近的,因此两者之间的运输时间可忽略不计,中央仓库的补货延迟时间可以近似为故障件i在中央仓库的修复时间ti0。为便于计算,假定从中央仓库到基层仓库的运输时间tl为常数。设在任意时间点,顾客对仓库l中备件i的需求量为dil,则Ril(Sil)表示当库存水平为Sil时基层仓库l对备件i的响应时间,可由式(2)表示。
| $\quad\quad{R_{il}}\left( {{S_{\!\! il}}} \right){\rm{ = }}\left\{ \!\!\!\!{\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {0,} & {{\text{当}}{d_{il}} {\text{≤}} {S_{\!\! il}}}; \end{array}}\\ {\begin{array}{*{20}{c}} {{t_l},} & {{\text{当}}{d_{il}} {\text{>}} {S_{\!\! il}}{\text{且}}\displaystyle\sum\limits_{l = 1}^v {{d_{il}} {\text{≤}} {S_0}} }; \end{array}}\\ {\begin{array}{*{20}{c}} {{t_l} + {t_{i0}}}, & {{\text{当}}{d_{il}}{\text{>}} {S_{\!\! il}}{\text{且}}\displaystyle\sum\limits_{l = 1}^v {{d_{il}} {\text{>}} {S_0}} }{\text{。}}\!\!\!\! \end{array}} \end{array}} \right.$ | (2) |
当基层仓库l有备件i供应时,基层仓库对顾客需求的响应时间为0;当基层仓库l的备件i缺货时,若上一级的中央仓库有备件i的库存,则由中央仓库发送该备件,此时,基层仓库对顾客需求的响应时间等于备件i从中央仓库运送到基层仓库的运输时间tl。若中央仓库也缺货,则基层仓库需要等待中央仓库补充库存后才能获得备件i,因此顾客响应时间等于中央仓库的补货时间t0加上备件i从中央仓库运送到基层仓库的运输时间tl。
需要强调的是,在这个两级备件库存系统中,由于所有基层仓库都向中央仓库发出订单请求,它们的备件需求都由同一个中央仓库来满足。因此,各基层仓库的备件i的渠道量之间存在一定的相关关系,从而使得各基层仓库对顾客的响应时间之间也产生相关关系。也就是说,基层仓库l的期望顾客响应时间是由整个系统的库存水平决策变量S(S0,
以库存总成本最小化作为模型的优化目标,以顾客对系统响应时间的要求即响应时间作为模型的约束条件。建立大型服务备件两级库存系统的优化模型,如式(3)所示。
| $\quad\quad \left\{\begin{array}{l} \min\displaystyle\sum\limits_{i = 1}^u {\left( {{c_i}{S_{\!\! i0}} + \displaystyle\sum\limits_{l = 1}^v {{c_i}{S_{\!\! il}}} } \right)} + \displaystyle\sum\limits_{l = 1}^v {{c_{\rm p}}} {R_{il}}\left( {{S_{\!\! il}}} \right){\text{。}}\\ {\rm s.t}\;\;\;\;E\left[ {{R_l}\left( { S} \right)} \right] {\text{≤}} {\tau _l};\\ \;\;\;\;\;\;\;{S_{il}} {\text{≥}} 0,\; i = 1,2, \cdots ,u;\;l = 0,1,2, \cdots ,v{\text{。}} \end{array}\right.$ | (3) |
目标函数由2部分组成,第1部分为中央仓库和基层各仓库的库存成本;第2部分为顾客平均响应时间超过服务时间约束而产生的罚金。约束条件表明各基层仓库对顾客的期望响应时间不能超过顾客可容忍的响应时间限制。
Metric模型在计算备件库存系统服务水平的时候,应用了Palm定理的假设,即备件的维修响应时间是相互独立的。但是在实际应用中,由于中央仓库的维修供应能力显然受到来自各个下级仓库订单请求的影响,从而造成维修响应时间的相关性,Palm定理在此条件下不再适用,要寻找一个通用的公式来描述备件的期望顾客响应时间是很困难的。因此,本文采用Monte Carlo仿真方法,通过样本均值逼近法估计预期响应时间的期望值E[Rl(S)]。
顾客响应时间可以定义为:当系统整体库存水平为S时,一定时期内顾客在仓库l等待备件所花费的总时间与该时间段内备件的总需求数量的比值,计算公式如(4)所示。
| $\quad\quad{R_l}\left( { S} \right) = \frac{{\displaystyle\sum\limits_{i = 1}^u {{R_{il}}({{S}_{\!\! i}})} }}{{\displaystyle\sum\limits_{i = 1}^u {{Q_{il}}} }}{\text{。}}$ | (4) |
其中,Qil表示一定时期里顾客对基层仓库l的备件i的总需求数量。
由于基层仓库的期望顾客响应时间依赖于仓库的整体库存水平,即向量S的取值,而不仅仅依赖于发生需求的基层仓库的库存水平Sl,因此难以用概率公式来描述顾客响应时间,本文通过时序仿真求得Rl(S)的样本均值,从而推算Rl(S)期望值的估计值。
由前述定义可知,随机变量
| $\begin{split} &\quad\quad E\left[ {{R_l}\left( { S} \right)} \right] = \mathop {\lim }\limits_{N \to \infty } \frac{{\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{R_{il}}\left( {{ S},{T_k}} \right)} } }}{{\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{Q_{il}}\left( {{T_k}} \right)} } }}=\\ & \frac{{\mathop {\lim }\limits_{N \to \infty } {N^{ - 1}}\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{R_{il}}\left( {{ S},{T_k}} \right)} } }}{{\mathop {\lim }\limits_{N \to \infty } {N^{ - 1}}\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{Q_{il}}\left( {{T_k}} \right)} } }}{\text{。}} \end{split}$ | (5) |
当N趋向于无穷大时,根据大数定律,可将响应时间的样本均值作为其期望值的近似估计,因而可得式(6)。
| $\quad\quad E\left[ {{R_l}\left( { S} \right)} \right] = {\bar R_l}\left( {{ S};N} \right) = \frac{{{N^{ - 1}}\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{R_{il}}\left( {{ S},{T_k}} \right)} } }}{{{N^{ - 1}}\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{i = 1}^u {{Q_{il}}\left( {{T_k}} \right)} } }}{\text{。}}$ | (6) |
求得各基层仓库的期望响应时间后,将Ril(Sil)和E[Rl(S)]代入式(3),则可通过对决策模型的求解,进一步得出设备备件的最优库存决策。
3 基于Nataf变换的备件库存系统模型 3.1 基于Nataf变换的备件需求相关性模型Metric及其改进模型都基于需求独立的假设,而由于设备的种类、生产时间、使用条件、维护管理方式等因素影响,供应渠道内对应的备件需求实际具有不同程度的相关性。因此需要寻求一种变换方法,利用已知的边缘概率密度函数和相关性系数来获得备件需求联合概率密度的数学描述。Nataf变换法能够利用独立的标准正态分布样本生成服从特定的概率分布、满足特定相关性条件的随机样本[19],因而正好能实现独立随机变量到相关随机变量概率描述的变换,从而为构建相关性需求的服务备件库存模型提供条件。
考虑不同类备件的需求相互独立,而同类备件在不同基层仓库的需求具有相关性的情况,分别对每类备件进行需求时间序列的抽样,因而在下面的分析中,略去表示备件类别的下标i。
设备件两级库存系统中,v个基层仓库的某类备件需求发生的间隔时间为随机向量
| $\begin{split} &\quad\quad{\rho _{ab}} = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\dfrac{{({x_a} - {\mu _a})}}{{{\sigma _a}}}\dfrac{{({x_b} - {\mu _b})}}{{{\sigma _b}}}} } {f_{ab}}({x_a},{x_b}){\rm d}{x_a}{\rm d}{x_b},\!\!\!\!\!\!\!\!\!\!\\ & a,b = 1,2, \cdots ,v{\text{。}} \end{split}$ | (7) |
式中,μa和μb分别为xa和xb的数学期望;σa和σb为xa和xb的标准差;
引入标准正态随机向量
| $\quad\quad\left\{\begin{array}{l} {y_h} = \varPhi _h^{^{ - 1}}\left( {{F_h}({x_h})} \right),\\ {x_h} = F_h^{^{ - 1}}\left( {{\varPhi _h}({y_h})} \right),\\ h = 1,2, \cdots ,v{\text{。}} \end{array}\right.$ | (8) |
式中,
根据Nataf概率变换原理,可以通过隐函数求导法则,将各基层仓库需求随机变量的联合概率密度函数转换为用标准正态分布变量表示的形式,如式(9)所示。
| $\quad\quad{f_{ab}}({x_a},{x_b}) = {f_a}({x_a}){f_b}({x_b})\frac{{{\varphi _2}({{ y}_a},{{ y}_b},{\rho {_{0ab}^{}}})}}{{\varphi ({{ y}_a})\varphi ({{ y}_b})}}{\text{。}}$ | (9) |
式中,
| ${\varphi _2}({{ y}_a},{{ y}_b},{\rho _{0ab}^{}}) \!=\! \frac{1}{{2\!\pi \sqrt {\det ( {{\rho _{0ab}^{}}} )} }}\exp \left( { \!-\! \frac{1}{2}{{\left( {{{ y}_a},{{ y}_b}} \right)}^{\rm{T}}}\!{\rho _{0ab}^{}}\!\left( {{{ y}_a},{{ y}_b}} \right)}\! \right)\!{\text{。}}$ | (10) |
对ρ0进行Choleskey分解,可得
| $\quad\quad{{\rho} _0} = \left[ \begin{array}{l} 1\;\;\;\;\;\;\;{{\rho} _{0ab}^{}}\\ {\rho _{0ab}^{}}\;\;1 \end{array} \right] = {{ B}_0}{ B}_0^{\rm T}{\text{。}}$ | (11) |
其中,
| $\quad\quad{({z_a},{z_b})^{\rm{T}}} = { B}_0^{ - 1}{({{ y}_a},{{ y}_b})^{\rm{T}}}{\text{。}}$ | (12) |
把式(8)、式(9)代入式(7),同时结合式(12)可得带隐含参数
| $\begin{split} &\quad\quad{\rho _{ab}} = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\dfrac{{({x_a} - {\mu_a})}}{{{\sigma _a}}}\dfrac{{({x_b} - {\mu_b})}}{{{\sigma _b}}}\varphi ({z_a})\varphi ({z_b})} } {\rm d}{z_a}{\rm d}{z_b},\!\!\!\!\!\!\!\!\!\!\!\!\!\\ & a,b = 1,2, \cdots ,v{\text{。}} \end{split}$ | (13) |
联立式(8)、(11)和(12),可以求出
在生产实际中,不同基层仓库中任意备件的需求相关性系数可通过对历史需求数据的统计分析获得。假设基层仓库a和b中某类备件需求的历史统计数据分别为时间序列xa和xb,则需求相关性系数可用式(14)进行估算。
| $\quad\quad{\rho _{xy}} = \frac{{\displaystyle\sum\limits_{i = 1}^G {\left( {{x_{ai}} - {e_a}} \right)\left( {{x_{bi}} - {e_b}} \right)} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^G {{{\left( {{x_{ai}} - {e_a}} \right)}^2}} } \sqrt {\displaystyle\sum\limits_{i = 1}^G {{{\left( {{x_{bi}} - {e_b}} \right)}^2}} } }}{\text{。}}$ | (14) |
其中,G为历史统计数据的样本量;
根据相关性模型,可得备件需求过程的仿真步骤如下。
步骤1 假设v个基层仓库中某类备件需求发生的时间间隔为随机变量
| $\begin{split} &\quad\quad{\rho _{ab}} - \displaystyle\sum\limits_{p = 1}^m {\displaystyle\sum\limits_{q = 1}^m {{\omega _p}{\omega _q}\dfrac{{({x_{ap}} - {\mu _a})}}{{{\sigma _a}}}\dfrac{{({x_{bq}} - {\mu _b})}}{{{\sigma _b}}}} } = 0,\\ & b = 1,2,a - 1,a + 1, \cdots ,v{\text{。}} \end{split}$ | (15) |
其中,m为积分节点数;ωp、ωq为权值。积分节点和权值可参考文献[20]得出。
步骤2 应用弦截法对式(14)进行求解,得出隐含参数ρ0ab的值,并代入式(11)求出B0。
步骤3 对v个基层仓库的中备件的需求发生时间间隔按指数分布进行抽样,生成v个互相独立的随机变量zk,得到v维随机向量
步骤4 利用式(8)把y转换为具有相关性的随机向量x,即得到各基层仓库备件相关性需求发生的时间间隔。
步骤5 通过x根据式(1)表示的库存变化关系,结合式(2)求得基层仓库l对备件i的响应时间Ril。
步骤6 计算统计量,转到步骤3。重复该过程直到满足收敛条件或约定次数停止。根据式(6),则可求得各基层仓库的期望响应时间E[Rl(S)]。
3.3 库存模型的优化求解备件库存优化配置模型的求解方法以解析法较为常见,如边际分析法、分枝定界法等。解析法适用于能够对库存系统各渠道上的需求量用概率分布函数进行完整描述的情况。而当考虑备件需求的相关性时,在供应渠道上的备件数量难以用精确的解析式表达,同时,当基层仓库和备件数量较多时,也难以单纯地通过仿真,利用枚举法在庞大的解空间里搜索最优解。由于遗传算法是一种并行启发式算法,适用于大规模的优化求解问题,因此,可结合遗传算法对模型进行优化求解。其主要步骤如下。
步骤1 生成M个初始可行解
步骤2 利用Monte Carlo抽样生成各基层仓库的需求基础样本,并利用Nataf变换将基础样本转换成具有相关性的需求样本序列。
步骤3 根据3.2节所述的仿真步骤求得
步骤4 令适应度函数为
| $\quad\quad f = A - \left[ {\sum\limits_{i = 1}^u {\left( {{c_i}{S_{i0}} + \sum\limits_{l = 1}^v {{c_i}{S_{il}}} } \right)} + \sum\limits_{l = 1}^v {{c_{\rm p}}} {R_{il}}\left( {{S_{il}}} \right)} \right]{\text{。}}$ |
其中,A为足够大的常数,通常取值为预计的最大成本费用。将
步骤5 通过交叉、变异等操作产生新的种群。
步骤6 重复步骤2~5直至满足仿真停止条件,或完成指定的循环次数;选择适应度最高的个体作为最优解。
4 算例分析 4.1 仿真试验设有一个由3个基层仓库站点和1个中央仓库组成的两级备件库存系统,考虑系统中只有1类备件、备件的单机安装数为1的情况。基层站点不具备备件的修复能力,所有故障件均在中央仓库进行修复并重新补充到库存系统中。备件故障发生的时间间隔服从λ1=2×10–3的指数分布;中央仓库对故障备件的修复时间服从均值为θ1=0.06的指数分布。基层站点从发出补货申请到接收到中央仓库补给的平均时间为10 d,客户响应时间可接受阈值为15 d,在备件缺货期间,企业须向客户支付70 元/d的缺货罚金。该备件在中央仓库和基层仓库的单位存货成本分别为60 元/件和80 元/件。
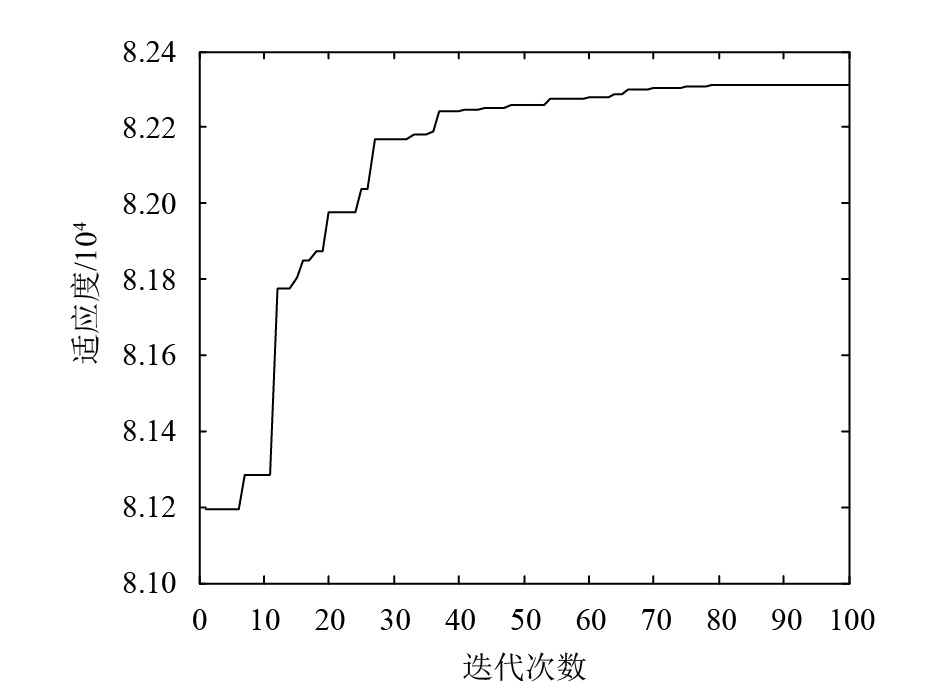
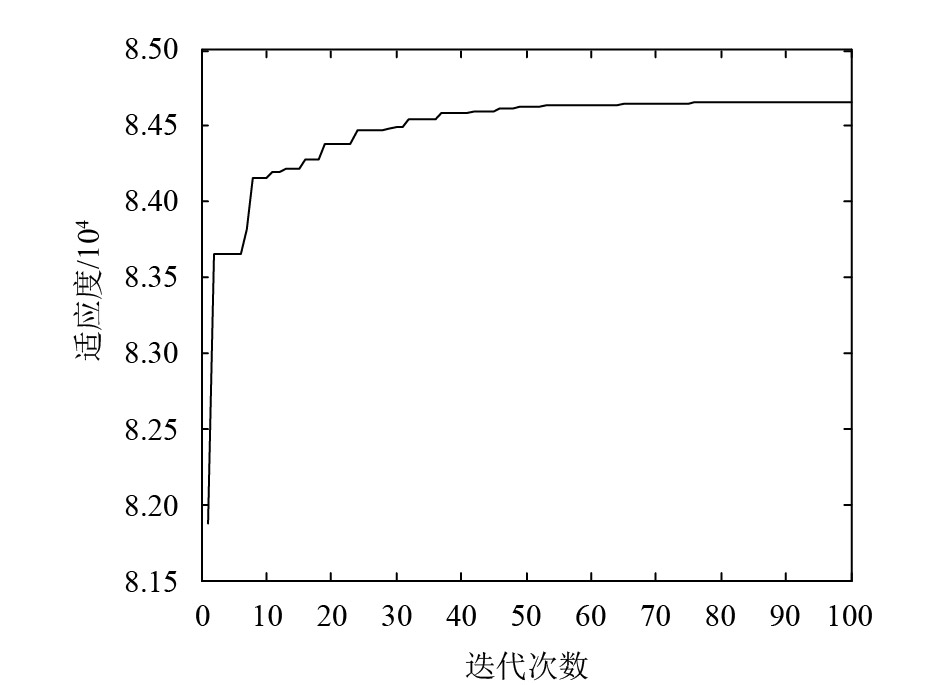
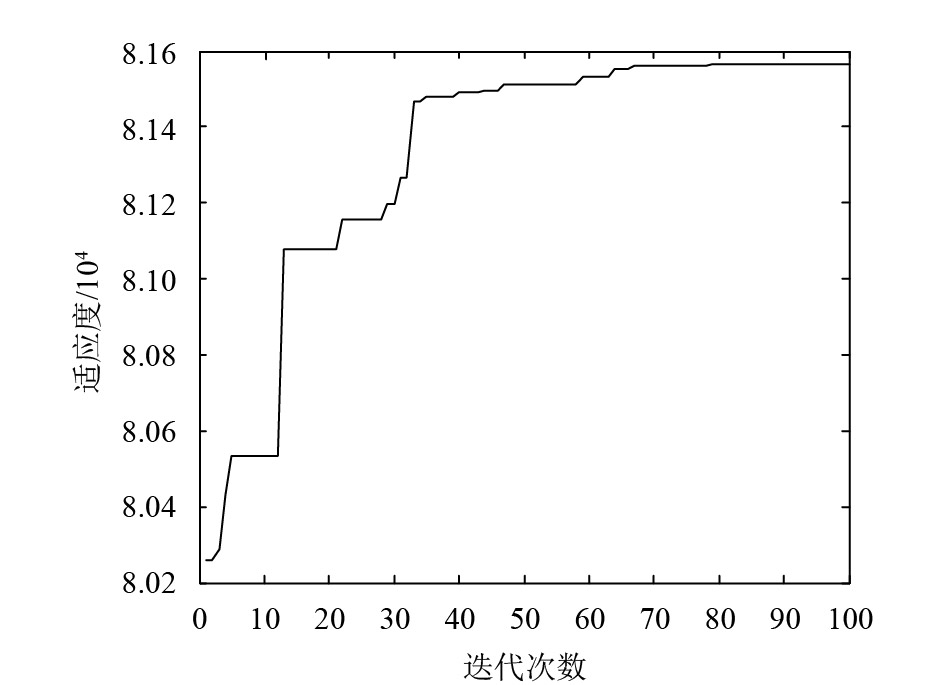
将库存需求的相关性系数分别取值为0.1~0.9,步长为0.1,在Matlab平台上编写仿真和模型优化求解程序。在不同相关系数设定条件下,经过100代进化后均达到收敛。图2~图6分别为相关系数设定为0.1、0.3、0.5、0.7、0.9时的库存策略寻优轨迹。
|
图 2 需求相关系数为0.1的库存策略寻优轨迹 Fig. 2 Inventory strategy optimization trajectory with demand correlation coefficient of 0.1 |

|
图 3 需求相关系数为0.3的库存策略寻优轨迹 Fig. 3 Inventory strategy optimization trajectory with demand correlation coefficient of 0.3 |
|
图 4 需求相关系数为0.5的库存策略寻优轨迹 Fig. 4 Inventory strategy optimization trajectory with demand correlation coefficient of 0.5 |
|
图 5 需求相关系数为0.7的库存策略寻优轨迹 Fig. 5 Inventory strategy optimization trajectory with demand correlation coefficient of 0.7 |
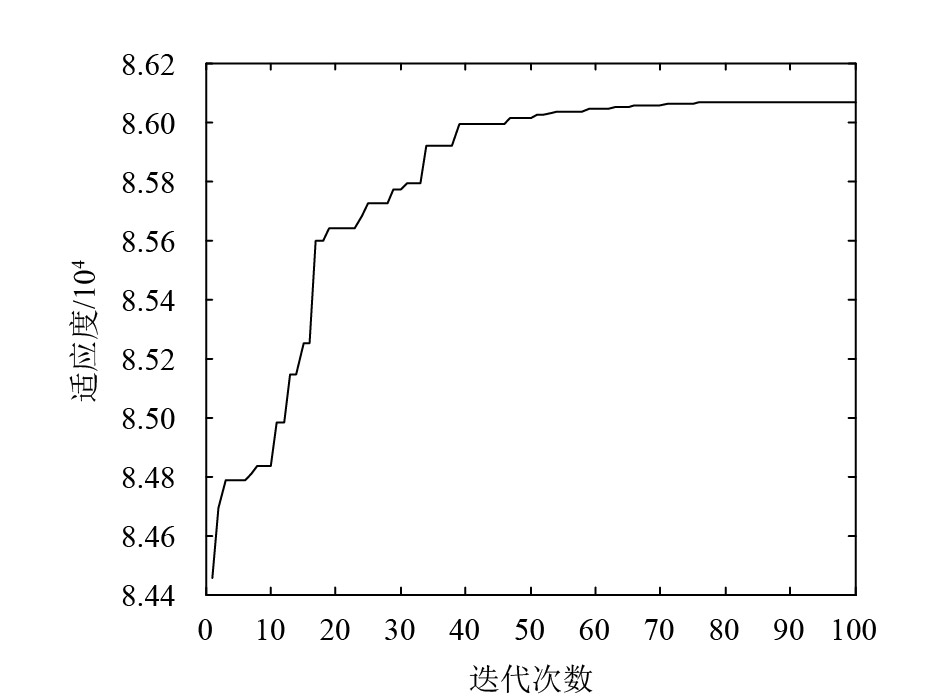
|
图 6 需求相关系数为0.9的库存策略寻优轨迹 Fig. 6 Inventory strategy optimization trajectory with demand correlation coefficient of 0.9 |
表1记录了在不考虑需求相关性以及需求相关性系数从0.1到0.9的条件下,该两级备件库存系统的库存优化配置策略及相应的总成本。
| 表 1 不同相关系数设定下的最优决策 Tab. 1 Optimal decision under the setting of different correlation coefficients |
图7表示各仓库站点优化后的库存水平配置随需求相关系数变化的趋势,系统总成本的变化趋势如图8所示。
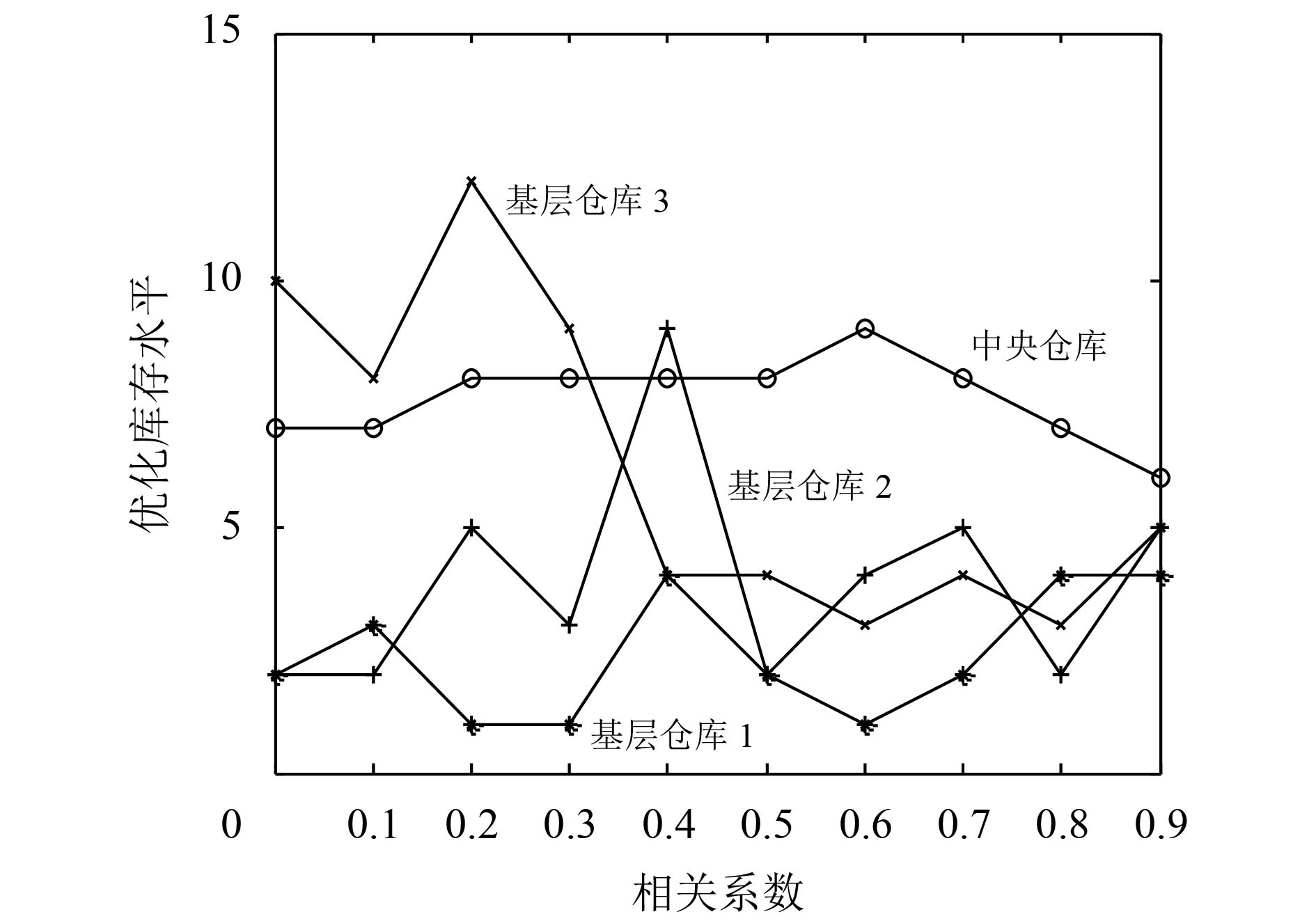
|
图 7 最优库存水平随需求相关系数变化的趋势 Fig. 7 Trends of optimal inventory levels with demand correlation coefficient |
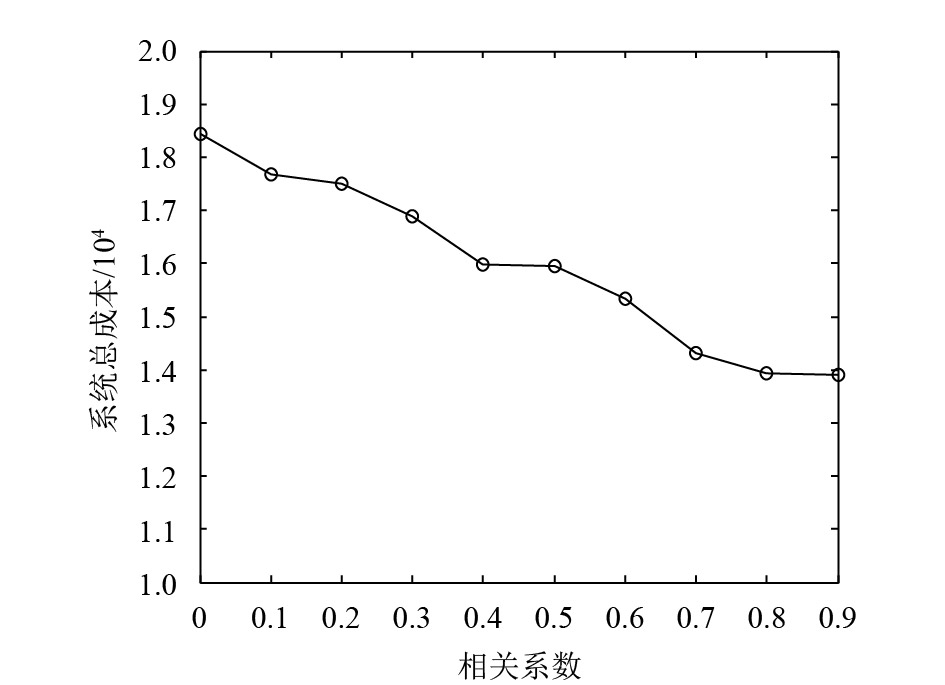
|
图 8 系统总成本随需求相关系数变化的趋势 Fig. 8 Trends in total system cost versus demand correlation coefficient |
从仿真试验可以得出以下分析结果。
1) 当各基层仓库的服务备件需求的相关性增大时,结合相关性影响进行库存优化能进一步降低系统总成本。从表1可看出,当不考虑备件需求的相关性时,根据模型(2)和(3)求得优化后中央仓库和基层1~基层3的库存水平分别为7、2、2、10,库存总成本包括备件的存货成本和缺货成本两项,为18 436元;而考虑备件需求之间的相关性后,优化后的库存系统总成本随着需求相关性的增加,呈现逐渐减少的趋势。这表明,当各基层仓库的服务备件需求相互独立时,系统各站点的需求差异性较大,需求发生时间和数量的参差性导致库存系统需要付出较高的存货成本以满足规定的服务响应时间约束,或者通过支付较高的缺货罚金以减少存货成本,从而增加库存总成本。随着基层备件需求相关性的增加,由图7可看出,当相关系数大于0.6时,基层仓库之间的需求共性趋于明显,参差性减弱,中央仓库容易把握各基层的需求总趋势,从而可以利用优化模型降低库存水平,提高服务响应能力。
2) 服务备件需求相关性对各级站点库存水平的影响是非线性的。由图7可看出,当备件需求之间的相关系数从0.1逐渐增加到0.6的过程中,中央仓库的最优库存水平缓慢增长,各基层仓库的最优库存水平差异较大;当相关系数从0.6持续增长到0.9时,中央仓库的最优库存水平则缓慢下降,各基层仓库的最优库存水平趋于平均,在图中表现为各基层的最优库存水平曲线逐渐相互靠近。以相关系数为0.2时的库存水平优化结果为例,中央和基层库存水平分别为8、1、5、12,3个基层仓库的库存水平最大相差10个库存单位,随着相关系数逐渐增大,基层仓库的最优库存水平差异值减小。发生这一现象的主要原因在于:随着基层仓库需求相关系数的增大,各基层仓库的备件需求体现出一定的共性,主要表现在基层仓库需求发生的时间点和数量相近,从而增加了中央仓库的短期供货压力,因此中央仓库的库存水平增加。而当相关系数进一步增大(本例中大于0.6)时,基层仓库需求的共性逐渐明显,体现为基层仓库库存水平之间的差值减小,中央仓的安全库存部分转移到基层仓库,缓解了中央仓库的备货压力,从而在一定程度上降低了系统总成本。以相关系数为0.9时的库存优化决策为例,中央仓库库存水平减少到6个单位,各基层仓库的库存水平略有增加,分别为4、5、5,基层仓库之间的库存差异减少。在这一策略下,库存系统总成本为13 894元,低于相关系数为0.2时的17 494元。
3) 在考虑需求相关性的情况下,中央仓库对系统总成本的调控能力比基层仓库高。从仿真过程可看出,当需求的相关系数小于0.5时,优先考虑对中央仓库的库存水平进行微调往往能达到较满意的成本控制目标,而当需求相关性大于0.5并逐渐增加时,则要同时调整中央和基层的库存水平。但是各基层仓库的备件需求之间高度相关的情况是较少的,因此在设备备件库存系统中,中央仓库的供货能力、成本和效率对整个库存系统的效能起着重要的作用。
4.3 管理启示从仿真结果可以看出,随着备件库存系统层次的增加以及协同管理方式的应用,各库存节点上的备件需求不是独立的,备件库存结构体系的层次级别越复杂,备件需求之间的相互影响作用就越大。此时若忽略需求相关性的影响,则容易导致不正确的库存决策。在多级备件库存系统中,随着备件需求相关性系数的增加,需求曲线发生非线性波动,加剧了牛鞭效应对库存决策的影响。因此,加强中央仓库与基层仓库供求信息的实时共享,针对系统总体需求建立计及相关性影响因素的需求预测机制显得尤为重要。由于中央仓库比基层库存节点具有更强的供给调节和成本控制能力,在满足给定顾客服务水平的条件下,优先考虑基于中央仓库的备件库存调度策略能减少需求波动对库存决策的影响、有效地找到系统服务水平与系统总体成本的最佳结合点。
5 结论设备备件的库存系统一般为多层级、多站点协同运作的复杂结构,备件需求之间往往具有一定的相关性,传统库存模型难以对其供需过程进行精确的描述。本文引入Nataf变换方法,提出了考虑备件需求相关性影响的两级库存优化模型,结合Monte Carlo仿真和遗传算法进行优化求解,对不同相关系数条件下的最优库存策略进行了比较分析。结果表明,服务备件需求的相关性对库存系统的优化决策和系统总成本有非线性影响,考虑需求相关性的大小进行库存优化决策,能提高备件库存系统的服务水平。加强中央仓库与基层仓库的信息共享,对各基层仓库所服务的大型设备实施统一的设备维护保养方案等措施都能提升各基层仓库之间的协同能力。在此基础上调整库存水平,能够在满足规定的售后服务水平的条件下进一步降低库存系统的总成本。
| [1] |
顾玉琦, 王正肖, 潘晓弘. 基于服务的慢速流动备件储量问题[J].
浙江大学学报(工学版), 2009, 43(12): 2264-2267.
GU Yuqi, WANG Zhengxiao, PAN Xiaohong. Service based reserves of slow moving spare parts[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(12): 2264-2267. DOI: 10.3785/j.issn.1008-973X.2009.12.024. |
| [2] |
SHERBROOKE C C. Metric: a mulit-echelon technique for recoverable item control[J].
Operations Research Letters, 1968, 16(1): 122-141.
|
| [3] |
SHERBROOKE C C. VARI-METRIC: improved approximation for multi-indenture, multi-echelon availability[J].
Operations Research, 1986, 34(2): 311-319.
|
| [4] |
SHERBROOKE C C. Multiechelon inventory systems with lateral supply[J].
Naval Research Logistics, 1992, 39(1): 29-40.
DOI: 10.1002/(ISSN)1520-6750. |
| [5] |
MUCKSTADT J A. A model for a multi-item, multi-echelon, multi-indenture inventory system[J].
Management Science, 1973, 20(4): 472-481.
|
| [6] |
PARK Jaehun, BAE Hyerim, BAE Joonsoo. Cross-evaluation-based weighted linear optimization for multi-criteria ABC inventory classification[J].
Computers & Industrial Engineering, 2014, 76(1): 40-48.
|
| [7] |
LOWAS A F, CIARALLO F W. Reliability and operations: keys to lumpy aircraft spare parts demands[J].
Journal of Air Transport Management, 2016, 50: 30-40.
DOI: 10.1016/j.jairtraman.2015.09.004. |
| [8] |
POPPE J, BASTEN R J I, BOUTE R N, et al. Numerical study of inventory management under various maintenance polici-es[J].
Reliability Engineering & System Safety, 2017, 168: 262-273.
|
| [9] |
徐立, 李庆民, 李华, 等. 非抢占维修优先权下的多级备件库存优化[J].
海军工程大学学报, 2016, 28(2): 92-97.
XU Li, LI Qingmin, LI Hua, et al. Optimization of spare parts inventory for multi-echelon support system under non-preemptive priorities[J]. Journal of Naval University of Engineering, 2016, 28(2): 92-97. |
| [10] |
PASCUAL R, SANTELICES G, LÜER-VILLAGRA A, et al. Optimal repairable spare-parts procurement policy under total business volume discount environment[J].
Reliability Engineering & System Safety, 2016, 159: 276-282.
|
| [11] |
刘任洋, 李庆民, 李华. 基于横向转运策略的可修件三级库存优化模型[J].
航空学报, 2014, 35(12): 3341-3349.
LIU Renyang, LI Qingmin, LI Hua. Optimal model of three-echelon inventory for repairable spare parts with lateral transshipments strategy[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3341-3349. |
| [12] |
PATRIARCA R, COSTANTINO F, DI GRAVIO G. Inventory model for a multi-echelon system with unidirectional lateral transshipment[J].
Expert Systems with Applications, 2016, 65: 372-382.
DOI: 10.1016/j.eswa.2016.09.001. |
| [13] |
阮旻智, 刘任洋. 随机需求下多层级备件的横向转运配置优化模型[J].
系统工程理论与实践, 2016, 36(10): 2689-2698.
RUAN Minzhi, LIU Renyang. Configuration and optimization model for multi-indenture spares with lateral transshipments under stochastic demand[J]. Systems Engineering-Theory & Practice, 2016, 36(10): 2689-2698. DOI: 10.12011/1000-6788(2016)10-2689-10. |
| [14] |
DE SMIDT-DESTOMBES K S, VAN ELST N P, BARROS A I, et al. A spare parts model with cold-standby redundancy on system level[J].
Computers & Operations Research, 2011, 38(7): 985-991.
|
| [15] |
BEHFARD S, VAN DER HEIJDEN M C, A. HANBALI A Al, et al.. Last time buy and repair decisions for spare parts[J].
European Journal of Operational Research, 2015, 244(2): 498-510.
DOI: 10.1016/j.ejor.2015.02.003. |
| [16] |
徐晓燕. 一种基于需求特性分类的备件库存管理方法及其实证研究[J].
系统工程理论与实践, 2006, 26(2): 64-69.
XU Xiaoyan. A demand classification based approach of inventory management for spare-parts and its application[J]. Systems Engineering – Theory & Practice, 2006, 26(2): 64-69. |
| [17] |
熊浩. 二级库存系统中库存策略的比较研究[J].
系统工程理论与实践, 2007, 27(6): 100-104.
XIONG Hao. Introduction of the relationship between safety stock and transshipment in two-echelon systems[J]. Systems Engineering – Theory & Practice, 2007, 27(6): 100-104. DOI: 10.3321/j.issn:1000-6788.2007.06.015. |
| [18] |
TSAI Shing Chih, LIU Chung Hung. A simulation-based decision support system for a multi-echelon inventory problem with service level constraints[J].
Computers & Operations Research, 2015, 53: 118-127.
|
| [19] |
李洪双, 吕震宙, 袁修开. 基于Nataf变换的点估计法[J].
科学通报, 2008, 53(6): 627-632.
LI Hongshuang, LYU Zhenzhou, YUAN Xiukai. Point estimation method based on Nataf transform[J]. Chinese Science Bulletin, 2008, 53(6): 627-632. DOI: 10.3321/j.issn:0023-074X.2008.06.004. |
| [20] |
李庆扬. 数值计算原理[M]. 北京: 清华大学出版社, 2000.
|
 2019, Vol. 22
2019, Vol. 22